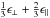| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | C2 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117624e | |
| Published online | 18 September 2012 | |
Variations on a theme – the evolution of hydrocarbon solids (Corrigendum)
II. Optical property modelling – the optEC(s) model ⋆
1 Institut d’Astrophysique Spatiale, CNRS, IAS UMR 8617, 91405 Orsay, France
e-mail: Anthony.Jones@ias.u-psud.fr
2 Université Paris Sud, IAS UMR 8617, 91405 Orsay, France
Key words: dust, extinction / ISM: general / errata, addenda
Data files are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/545/C2
In the computation of the complex refractive index data for the original published version of this article, and in the following article Jones (2012), there was an error in the calculation of the IR band intensities. This error results in small changes in the 3 μm region bands and an underestimation of the band strengths and continua at longer wavelengths for hydrogen-rich a-C:H materials (XH ≳ 0.23 ≡ Eg ≳ 1 eV). The conclusions of the paper are unchanged, except as indicated in the following, where an updated version of the relevant figure and, if necessary, the accompanying text is given. The section headings and figure numbers are the same as those used in the originally-published paper. The refractive index data that were originally made available through the CDS have now been replaced with corrected data.
Additionally, there was an error in the overly-complicated reasoning in the deduction of the a-C(:H) particle photo-processing time-scales in Sect. 5.1 of this paper and also in Sect. 5.2 of the following paper (Jones 2012). The photo-processing time-scale is simply the inverse of the photo-darkening rate, ΛUV,pd, given in Eq. (31). A new and modified version of Sect. 5.1, which replaces the previously published version, is given below.
4.3. The addition of IR bands into the k determination
In Fig. 8 the band gap colour-coding for the data were reversed. The correct caption is now given but the data in this figure are unaffected by the error noted above.
Figure 9 shows the updated refractive index data for bulk a-C:H materials. The most significant differences are apparent in k and occur for large band gap materials with Eg ≳ 1 eV. The IR band strengths for λ > 4 μm and the long-wavelength continua are enhanced with respect to the previous results. The real part of the refractive index, n, is not significantly affected.
 |
Fig. 8 The adopted wavelength-dependent IR cross-section per carbon atom, σC, in Mb (1 Mb = 10-18 cm2) for the eRCN model. The upper curves (violet) are for the H-rich, wide band gap materials and the cross-sections, in the 8 μm region, decrease with decreasing XH ≡ Eg from top to bottom – Eg = 2.5 (violet), 2.25 (cobalt), 2.0 (blue), 1.75 (green), 1.5 (yellow), 1.25 (orange), 1.0 (brown) and 0.75 eV (red). |
 |
Fig. 9 The imaginary part, k (upper), and derived real part, n (lower), of the refractive index data for the suite of a-C(:H) materials predicted by the optEC(s) model as a function of Eg (see Table 1 for the line colour-coding). |
4.5. A detailed look at the optEC(s) data
The optEC(s) a-C:H data in Fig. 11 have been updated.
 |
Fig. 11 The smooth, coloured lines show the optEC(s) model-derived imaginary (top) and real (bottom) parts of the refractive index (large band gap, violet, to low band gap, grey). The lines with data points are the laboratory-measured and model-derived data (see references earlier for the sources). The upper black lines with data points show the data for graphite (Draine & Lee 1984) and the purple and violet lines with data points show the data for diamond (Edwards & Philipp 1985; Lewis et al. 1989). |
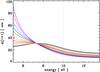 |
Fig. 15 The depth, d1, at which τ = 1 for optEC(s) model data. The vertical grey line marks the assumed lower limit for photons capable of photo-dissociating CH bonds in the assumed a-C(:H) materials. |
5.1. a-C(:H) processing time-scales
A key question here is: what are the critical photo-processing time-scales that determine the evolution of a-C(:H) materials in the ISM? We now examine this is some detail but return to the issue again in a following paper where we consider the added complication of size effects.
In Fig. 15 we show the depth, d1 (in nm), at which the optical depth, τ, for photons of a given energy is unity (i.e., τ = 1), for the derived a-C(:H) optical properties. What this shows is that, for all the derived materials, photons with E ≳ 7 eV are able to penetrate the entire particle volume for grains smaller than a few tens of nm in radius. This then also implies that the surfaces of larger grains can only be UV/EUV photo-processed to depths of the order of a few tens of nm by photons with energies greater than ~7 eV. Such photons, above some threshold energy, will then lead to a-C(:H) grain photo-darkening (photo-processing).
We can estimate a UV/EUV photo-darkening rate, ΛUV,pd, for carbonaceous dust subject to a given radiation field using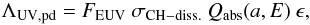 (1)where FEUV is the dissociating photon flux, σCH − diss. is the CH bond photo-dissociation cross-section, Qabs(a,E) is the particle absorption efficiency and ϵ is a photo-darkening efficiency, which takes into account that photon absorption can also lead to heating and fluorescence (e.g., Sorrell 1990). Based on CH4 photo-dissociation cross-section studies in the EUV (Welch & Judge 1972; Gruzdkov et al. 1994) we adopt a value of σCH − diss. = 10-19 cm2 centred at ~107 nm (11.6 eV) and (somewhat conservatively) assume a bandwidth of 33 nm (10 − 13.6 eV). At UV/EUV wavelengths the photon flux, FEUV, appropriate to the local ISRF, can be approximated by FEUV ≈ 106 photons cm-2 s-1 nm-1 (Henry 2002). Integrated over the assumed 33 nm bandwidth for the photo-dissociation cross-section, this then yields FEUV ≃ 3 × 107 photons cm-2 s-1. For large grains at these wavelengths Qabs(a, EUV) ~ 1 (i.e., the short-wavelength, linear behaviour in the λQabs(a, EUV)/a plot in Fig. 16 below). The photo-darkening (or aromatisation) time-scale for the outer ≃ 20 nm of large a-C(:H) particles, τUV,pd, is then simply the inverse of the photo-darkening time-scale, i.e.,
(1)where FEUV is the dissociating photon flux, σCH − diss. is the CH bond photo-dissociation cross-section, Qabs(a,E) is the particle absorption efficiency and ϵ is a photo-darkening efficiency, which takes into account that photon absorption can also lead to heating and fluorescence (e.g., Sorrell 1990). Based on CH4 photo-dissociation cross-section studies in the EUV (Welch & Judge 1972; Gruzdkov et al. 1994) we adopt a value of σCH − diss. = 10-19 cm2 centred at ~107 nm (11.6 eV) and (somewhat conservatively) assume a bandwidth of 33 nm (10 − 13.6 eV). At UV/EUV wavelengths the photon flux, FEUV, appropriate to the local ISRF, can be approximated by FEUV ≈ 106 photons cm-2 s-1 nm-1 (Henry 2002). Integrated over the assumed 33 nm bandwidth for the photo-dissociation cross-section, this then yields FEUV ≃ 3 × 107 photons cm-2 s-1. For large grains at these wavelengths Qabs(a, EUV) ~ 1 (i.e., the short-wavelength, linear behaviour in the λQabs(a, EUV)/a plot in Fig. 16 below). The photo-darkening (or aromatisation) time-scale for the outer ≃ 20 nm of large a-C(:H) particles, τUV,pd, is then simply the inverse of the photo-darkening time-scale, i.e., 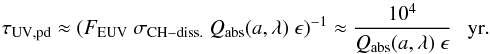 (2)If we assume a per bond photo-darkening efficiency of ϵ = 0.1, rather than the per grain photofission efficiency of 10-3 adopted by Sorrell (1990), this yields an ≈ 20 nm outer-layer photo-darkening time-scale of ≈ 105 yr for large a-C(:H) grains (a > 20 nm) in the diffuse ISM. In photo-dissociation regions where the local radiation field can be orders of magnitude over that of the diffuse ISM (e.g., a factor of ≃ 104 higher for the Orion PDR) these timescales will be significantly shorter. For example, in a PDR with a radiation field 100 (104) times that of the diffuse ISM, the outer-layer photo-darkening timescales reduce to ≈ 103 yr ( ≈ 10 yr) for large particles. However, in all of these cases the complete photo-processing of the particle is not possible because core material, at depths greater than a few tens of nm, is likely to be unaffected by photo-darkening. Thus, the large carbonaceous grains in the ISM can retain an H-rich interior, as indicated by observations (e.g., Dartois et al. 2004a,b).
(2)If we assume a per bond photo-darkening efficiency of ϵ = 0.1, rather than the per grain photofission efficiency of 10-3 adopted by Sorrell (1990), this yields an ≈ 20 nm outer-layer photo-darkening time-scale of ≈ 105 yr for large a-C(:H) grains (a > 20 nm) in the diffuse ISM. In photo-dissociation regions where the local radiation field can be orders of magnitude over that of the diffuse ISM (e.g., a factor of ≃ 104 higher for the Orion PDR) these timescales will be significantly shorter. For example, in a PDR with a radiation field 100 (104) times that of the diffuse ISM, the outer-layer photo-darkening timescales reduce to ≈ 103 yr ( ≈ 10 yr) for large particles. However, in all of these cases the complete photo-processing of the particle is not possible because core material, at depths greater than a few tens of nm, is likely to be unaffected by photo-darkening. Thus, the large carbonaceous grains in the ISM can retain an H-rich interior, as indicated by observations (e.g., Dartois et al. 2004a,b).
 |
Fig. 16 The optEC(s) model extinction and absorption coefficient data, for clarity plotted as λQext/a (solid lines) and λQabs/a (dashed lines), as a function of Eg and wavelength for 100 nm radius particles. From top to bottom on the right the dashed blue lines indicate wavelength dependencies, λ − β, where β = 1, 1.5 and 2. |
The above a-C:H UV processing can also perhaps be considered to engender a sort of band gap “velocity”, i.e., dEg/dt, which will principally depend upon the local ISRF in the diffuse ISM or given PDR and that only apply to the outer few tens of nm of large particles (a > 20 nm). The band gap “velocity”, dEg/dt, derived from the above, can be expressed as ![\begin{equation} \frac{{\rm d}E_{\rm g}}{{\rm d}t} \approx \Lambda_{\rm UV,pd} \ E_{\rm g}(t) \approx 10^{-4} \ Q_{\rm abs}(a,\lambda) \ \epsilon \ E_{\rm g}(t) \ \ \ \ \left[{\rm eV\ yr}^{-1}\right], \label{eq_dEgdt} \end{equation}](/articles/aa/full_html/2012/09/aa17624e-11/aa17624e-11-eq56.png) (3)which yields a band gap velocity of ≈ 10-4 ϵ Eg(t) eV yr-1, where Eg(t) is the band gap at time t.
(3)which yields a band gap velocity of ≈ 10-4 ϵ Eg(t) eV yr-1, where Eg(t) is the band gap at time t.
However, we note that the above determination may only give an upper limit to the a-C(:H) aromatisation time-scale because it concerns only the direct photo-dissociation of CH bonds by EUV photons. To this must be added the thermal effects due to photon absorption leading to grain heating to temperatures sufficiently high for H atom loss by thermal annealing to occur.
Thermal processing effects on amorphous hydrocarbons, and the associated kinetics, have been studied in detail by Duley (1996). Using the data of Smith (1984) he showed that, for H atom loss leading to band gap closing, the reaction can be described in terms of a thermally activated process, i.e., 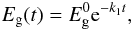 (4)where
(4)where 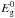 eV is the initial band gap (taken to be 2.2 eV) and the rate constant k1 = Ae − ΔH/T (where A = 6.8 s-1 and the activation energy ΔH = 8000 ± 2000 K). With this approach Duley (1996) finds that, for a temperature of 350 K (typical of the extended atmospheres of evolved stars such as IRC+10216), band gap closure ( ≡ aromatisation) can occur on a time-scale of ≈ 10 yr. Thus, it appears that a thermal processing effect could be important but only if sufficiently high temperatures can be maintained long enough for thermally-driven aromatisation to occur. For grains in the ISM or in PDRs, where grain temperatures are considerably lower than 350 K for large particles in thermal equilibrium with the ISRF (T ≃ 20 K), or can only be achieved for very short time-scales in stochastically-heated small particles (for periods of the order of a few seconds every month, i.e., ≈ one millionth of their time), the aromatisation time-scales will be considerably longer than 10 yr and probably of the order of, at least, several millions of years. Given that thermal processing is probably only going to be important for stochastically-heated, small a-C(:H) grains we will re-examine this process when we specifically consider grain size effects.
eV is the initial band gap (taken to be 2.2 eV) and the rate constant k1 = Ae − ΔH/T (where A = 6.8 s-1 and the activation energy ΔH = 8000 ± 2000 K). With this approach Duley (1996) finds that, for a temperature of 350 K (typical of the extended atmospheres of evolved stars such as IRC+10216), band gap closure ( ≡ aromatisation) can occur on a time-scale of ≈ 10 yr. Thus, it appears that a thermal processing effect could be important but only if sufficiently high temperatures can be maintained long enough for thermally-driven aromatisation to occur. For grains in the ISM or in PDRs, where grain temperatures are considerably lower than 350 K for large particles in thermal equilibrium with the ISRF (T ≃ 20 K), or can only be achieved for very short time-scales in stochastically-heated small particles (for periods of the order of a few seconds every month, i.e., ≈ one millionth of their time), the aromatisation time-scales will be considerably longer than 10 yr and probably of the order of, at least, several millions of years. Given that thermal processing is probably only going to be important for stochastically-heated, small a-C(:H) grains we will re-examine this process when we specifically consider grain size effects.
 |
Fig. 17 The optEC(s) model extinction/absorption coefficient data at FIR-mm wavelengths, plotted as Qext/a and normalised at 10 μm, as a function of Eg for 100 nm radius particles. From top to bottom, the grey dashed lines indicate wavelength dependencies, λ − β, where β = 1, 1.5, 2, 2.5 and 3. |
 |
Fig. 18 The predicted emissivity slope, β, at FIR-mm wavelengths as a function of Eg for 100 nm radius particles: blue (at 100 μm), green (at 300 μm) and red (at 1 mm); lower, middle and upper lines, respectively. |
5.3. a-C(:H) extinction and absorption
The data in Figs. 16–18 have been re-calculated based on the corrected complex indices of refraction for a-C(:H). The plot axis intervals are the same as in the originally-published versions in order to allow a direct comparison. The effects of the increased band strengths and enhanced continua at long wavelengths (λ ≳ 20 μm), in large band gap (Eg ≳ 1 eV) a-C:H materials, are evident in Fig. 16.
In Fig. 17 the corrected data do not lead to any significant changes other than the enhanced bands at the shortest wavelengths.
For a-C:H materials with band gaps larger than ~1 eV Fig. 18 now shows a weaker effect and slightly lower absolute values of β at FIR-mm wavelengths. The changes are most marked for Eg = 1 − 1.5 eV materials and for β in the λ ~ 100 μm region. Hence, the last sentence of the last itemized point should read:
-
...As the band gap further reduces(Eg ~ 1.5 eV → −0.1 eV) β first increases to ≈ 2.7 for Eg = 1 eV, drops to ≈ 1.3 at Eg = 0.1 eV, and then rises to 1.7 for the smallest band gap material with Eg = −0.1 eV.
In the upper plot in Fig. 18 the same β(Eg) data is shown plotted in logarithmic form over a narrower range of Eg in order to allow a comparison with β vs. Tdust plots, where Tdust could be considered a proxy for Eg, implying that higher band gap materials are to be found in lower dust temperature-higher extinction regions, as might be expected by the accretion of increasingly hydrogen-rich a-C:H materials in denser regions of the ISM (e.g., Jones et al. 1990).
5.4. Scattering by a-C(:H) grains at mid-IR wavelengths
The first part of the second paragraph of this section should now read:
In Fig. 19 we show Qext and Qsca, and also the ratio of scattering to extinction Qsca/Qext, as a function of Eg for 100 nm grains. What this figure shows is, that for a fixed grain size, large band gap a-C(:H) materials ( eV) exhibit almost pure scattering behaviour at wavelengths from 0.5 to 5 μm (0.2 − 2 μm-1), with sharp downturns at the positions of the strong IR C − H resonances in the 3 μm region. We note that the scattering fraction (see Fig. 19) decreases as the band gap of the material decreases but is still significant for materials with band gaps as low as 1.5 eV...
eV) exhibit almost pure scattering behaviour at wavelengths from 0.5 to 5 μm (0.2 − 2 μm-1), with sharp downturns at the positions of the strong IR C − H resonances in the 3 μm region. We note that the scattering fraction (see Fig. 19) decreases as the band gap of the material decreases but is still significant for materials with band gaps as low as 1.5 eV...
 |
Fig. 19 Qext (dashed), Qsca (triple-dotted-dashed) and Qsca/Qext (solid lines) as a function of Eg (0, 0.5, 1.0, 1.25, 1.5, 2.0 and 2.5 eV, from bottom to top) for grains of radius a = 100 nm. |
References
- Dartois, E., Marco, O., Muñoz-Caro, G. M., et al. 2004a, A&A, 423, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Muñoz Caro, G. M., Deboffle, D., & d’Hendecourt, L. 2004b, A&A, 423, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Duley, W. W. 1996, MNRAS, 283, 343 [NASA ADS] [Google Scholar]
- Edwards, D. F., & Philipp, H. R. 1985, Handbook of Optical Constants of Solids, ed. E. D. Polik (New York: Academic Press), 665 [Google Scholar]
- Gruzdkov, Y. A., Watanabe, K., Sawabe, K., & Matsumoto, Y. 1994, Chem. Phys. Lett., 227, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. C. 2002, ApJ, 570, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P. 2012, A&A, 542, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Duley, W. W., & Williams, D. A. 1990, QJRAS, 31, 567 [NASA ADS] [Google Scholar]
- Lewis, R. S., Anders, E., & Draine, B. T. 1989, Nature, 339, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, F. W. 1984, J. Appl. Phys., 55, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Sorrell, W. H. 1990, MNRAS, 243, 570 [NASA ADS] [Google Scholar]
- Welch, A. R., & Judge, D. L. 1972, J. Chem. Phys., 57, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Tauc analysis of the available data
The a-C:H data in the Tauc analysis wavelength (right hand) plots presented in Figs. A.2 to A.4 have been corrected.
 |
Fig. A.2 As per Figs. 5 and A.1 but for the Rouleau & Martin (1991) data. |
 |
Fig. A.3 As per Fig. A.1 but for the Jena DDOP amorphous carbon data. Also shown for comparison are the data for graphite using the usual |
 |
Fig. A.4 As per Fig. A.1 but for the Zubko et al. (1996) data. |
Appendix B: The derived optical constants compared with the available data
 |
Fig. B.3 Same as Fig. B.1 but for the Rouleau & Martin (1991) data. |
The imaginary part of the complex indices of refraction, k, in Figs. B.3 to B.5 have been corrected. The corresponding changes in real parts of the complex refractive indices, n, are not discernable in this type of plot and these figures are therefore not reproduced here.
 |
Fig. B.4 Same as Fig. B.1 but for the Jena DDOP amorphous carbon data. |
 |
Fig. B.5 Same as Fig. B.1 but for the Zubko et al. (1996) data. |
© ESO, 2012
All Figures
 |
Fig. 8 The adopted wavelength-dependent IR cross-section per carbon atom, σC, in Mb (1 Mb = 10-18 cm2) for the eRCN model. The upper curves (violet) are for the H-rich, wide band gap materials and the cross-sections, in the 8 μm region, decrease with decreasing XH ≡ Eg from top to bottom – Eg = 2.5 (violet), 2.25 (cobalt), 2.0 (blue), 1.75 (green), 1.5 (yellow), 1.25 (orange), 1.0 (brown) and 0.75 eV (red). |
| In the text | |
 |
Fig. 9 The imaginary part, k (upper), and derived real part, n (lower), of the refractive index data for the suite of a-C(:H) materials predicted by the optEC(s) model as a function of Eg (see Table 1 for the line colour-coding). |
| In the text | |
 |
Fig. 11 The smooth, coloured lines show the optEC(s) model-derived imaginary (top) and real (bottom) parts of the refractive index (large band gap, violet, to low band gap, grey). The lines with data points are the laboratory-measured and model-derived data (see references earlier for the sources). The upper black lines with data points show the data for graphite (Draine & Lee 1984) and the purple and violet lines with data points show the data for diamond (Edwards & Philipp 1985; Lewis et al. 1989). |
| In the text | |
 |
Fig. 15 The depth, d1, at which τ = 1 for optEC(s) model data. The vertical grey line marks the assumed lower limit for photons capable of photo-dissociating CH bonds in the assumed a-C(:H) materials. |
| In the text | |
 |
Fig. 16 The optEC(s) model extinction and absorption coefficient data, for clarity plotted as λQext/a (solid lines) and λQabs/a (dashed lines), as a function of Eg and wavelength for 100 nm radius particles. From top to bottom on the right the dashed blue lines indicate wavelength dependencies, λ − β, where β = 1, 1.5 and 2. |
| In the text | |
 |
Fig. 17 The optEC(s) model extinction/absorption coefficient data at FIR-mm wavelengths, plotted as Qext/a and normalised at 10 μm, as a function of Eg for 100 nm radius particles. From top to bottom, the grey dashed lines indicate wavelength dependencies, λ − β, where β = 1, 1.5, 2, 2.5 and 3. |
| In the text | |
 |
Fig. 18 The predicted emissivity slope, β, at FIR-mm wavelengths as a function of Eg for 100 nm radius particles: blue (at 100 μm), green (at 300 μm) and red (at 1 mm); lower, middle and upper lines, respectively. |
| In the text | |
 |
Fig. 19 Qext (dashed), Qsca (triple-dotted-dashed) and Qsca/Qext (solid lines) as a function of Eg (0, 0.5, 1.0, 1.25, 1.5, 2.0 and 2.5 eV, from bottom to top) for grains of radius a = 100 nm. |
| In the text | |
 |
Fig. A.2 As per Figs. 5 and A.1 but for the Rouleau & Martin (1991) data. |
| In the text | |
 |
Fig. A.3 As per Fig. A.1 but for the Jena DDOP amorphous carbon data. Also shown for comparison are the data for graphite using the usual |
| In the text | |
 |
Fig. A.4 As per Fig. A.1 but for the Zubko et al. (1996) data. |
| In the text | |
 |
Fig. B.3 Same as Fig. B.1 but for the Rouleau & Martin (1991) data. |
| In the text | |
 |
Fig. B.4 Same as Fig. B.1 but for the Jena DDOP amorphous carbon data. |
| In the text | |
 |
Fig. B.5 Same as Fig. B.1 but for the Zubko et al. (1996) data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.