Magnetic field induced by strong transverse plasmons in ultra-relativistic electron-positron plasmas

Y. Liu; X. Q. Li; S. Q. Liu

doi:10.1051/0004-6361/201218921

Home

All issues

Volume 544 (August 2012)

A&A, 544 (2012) A151

Full HTML

Free Access

Issue		A&A Volume 544, August 2012


Article Number		A151
Number of page(s)		11
Section		Astrophysical processes
DOI		https://doi.org/10.1051/0004-6361/201218921
Published online		21 August 2012

A&A 544, A151 (2012)

Magnetic field induced by strong transverse plasmons in ultra-relativistic electron-positron plasmas

Y. Liu¹, X. Q. Li² and S. Q. Liu³

¹ School of Sciences, Nantong University, 226019 Nantong, PR China
e-mail: yliu1886@live.cn
² Department of Physics, Nanjing Normal University, 210097 Nanjing, PR China
³ School of Sciences, Nanchang University, 330047 Nanchang, PR China

Received: 31 January 2012
Accepted: 4 July 2012

Abstract

Context. We investigated the generation of localized magnetic fields in an ultra-relativistic non-isothermal electron-positron plasma by strong electromagnetic plasmons.

Aims. The results obtained can be used to explain the origin of small-scale magnetic fields in the internal shock region of gamma-ray bursts with ultra-relativistic electron positron plasmas.

Methods. The generation of magnetic fields was investigated with kinetic Vlasov Maxwell equations.

Results. The self-generated magnetic field will collapse for modulation instability, leading to spatially highly intermittent magnetic fluxes, whose characteristic scale is much larger than relativistic plasma skin depth, which in turn is conducive to the generation of the long-life small-scale magnetic fields in the internal shock region of gamma-ray bursts.

Key words: gamma-ray burst: general / magnetic fields / relativistic processes / plasmas

© ESO, 2012

1. Introduction

The prompt emission and afterglows of gamma-ray bursts (GRBs) are generally believed to be produced by synchrotron emission. Although the synchrotron emission can adequately explain the observed afterglow spectra and light curves, yet there are some problems in fitting the observed prompt γ-ray spectrum. On the one hand, the theoretically predicted spectrum in the low-energy part of the synchrotron spectrum contradicts the much harder spectra observed. Considering the fast cooling of electrons by synchrotron emission (Cohen et al. 1997), this problem will be even more severe. On the other hand, many observational spectra showed turnoff points and energy excesses in the higher frequency parts. These problems may be caused by a significant decrease of the synchrotron emission mechanism in which the magnetic field should be uniform throughout the shocked region.

Medvedev (2000) proposed that the prompt emission is produced by jitter radiation, which arises if the magnetic field’s correlation length is smaller than the region over which an electron emits the synchrotron radiation seen by a given observer. This radiative mechanism has been applied successfully to the research of gamma-ray bursts (Medvedev 2006; Mao & Wang 2011) and their afterglows (Workman et al. 2008; Morsony et al. 2009). To overcome that the electron cooling time is much shorter than the dynamical time (Ghisellini et al. 2000), Pe’er & Zhang (2006) put forward that the magnetic field created by the internal shocks decays on a length scale much shorter than the comoving width of the plasma. Under this assumption synchrotron radiation can reproduce the observed prompt emission spectra of the majority of the bursts. Deng et al. (2005) applied the synchro-curvature mechanism instead of the synchrotron mechanism to explain the spectra of gamma-ray bursts. They demonstrated that if the curvature radius of magnetic fields is much smaller than the scale of the emission area, many observational spectra with turnoff points and energy excesses in the higher frequency parts can be fit nicely. These theories indicate the turbulent small-scale magnetic field is crucial for our understanding of GRBs.

Medvedev & Loeb (1999) suggested that the relativistic Weibel instability can generate strong small-scale magnetic fields in the collisionless shocks of GRBs. However, Gruzinov (2001) raised the concern that this magnetic field will maintain its equipartition magnitude only over a skin depth δ, they decay there on a timescale 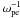$ω_{pe}^{-1}$ $\hbox{$\omega _{\rm pe}^{-1} $}$ due to phase-space mixing, but generic synchrotron emission scenarios take place on longer timescales, ranging from 10⁵ to 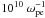$10^{10} ω_{pe}^{-1}$ $\hbox{$10^{10} ~\omega _{\rm pe}^{-1} $}$ . Magnetic field decay may be alleviated via an inverse cascade from small to large scales. An inverse cascade via current filament merging operates strongly in the foreshock region (Silva et al. 2003). However, Katz et al. (2007) suggested via self-similar arguments that the inverse cascade does not operate downstream of the shock. Chang et al. (2008) investigated the idea by two-dimensional particle-in-cell numerical simulations. These authors found that filament merging does occur, but is confined to the foreshock, where the filaments exist, and there is little evidence of magnetic clumps merging in the downstream. Hence, the magnetic energy should evaporate in the downstream region. Therefore, Chang and collaborators concluded that initially unmagnetized relativistic shocks in electron-positron plasmas are unable to form persistent downstream magnetic fields, if there are no additional physical processes that create longer wavelength, more persistent fields. In this paper we investigate the generation of magnetic fields in the relativistic EP plasma from a different perspective.

Pulupa et al. (2010) examined 178 interplanetary shocks observed by the Wind spacecraft. They found 43 produced upstream Langmuir waves, as that shown by enhancements in wave power near the plasma frequency. In the foreshock region, the reflected electron beams create unstable bump-on-tail electron distribution functions, which excite a Landau resonance and create electrostatic oscillations known as Langmuir waves. Medvedev & Loeb (1999) also pointed out that if the colliding shells do not possess similar densities, the growth rate of the instability decreases or even shuts off beyond a particular density contrast. In this regime, the shock may be dominated by electrostatic (Langmuir) turbulence. The Langmuir waves undergo a mode conversion process and generate electromagnetic waves at the plasma frequency. There is a continuous transfer from Langmuir waves to transverse plasmons and back, and their energy densities are approximately the same, average over time, W^l ≈ W^T (Kaplan & Tsytovich 1973; Liu et al. 2008).

The prompt γ-rays in the GRBs are assumed to be produced by internal shock that may be dominated by the ultra-relativistic electron-positron pairs (Medvedev et al. 2005). In our previous paper we have come to the conclusion that the interaction of transverse plasmons with isothermal ultra-relativistic EP plasma will not excite magnetic field (Liu & Liu 2011). The reason is that the same mass and the opposite charge of EP pairs leads to the cancellation of magnetic currents, while one can expect that the spontaneous magnetic field maybe present for non-isothermal ultra-relativistic EP plasma, i.e., T_e ≠ T_p. Tkaczyk (1993) used a non-isothermal EP plasma model to explain the observed spectra of gamma ray bursts. He suggested that the relaxation time may exceed the annihilation time when temperature of electron and positron are significantly different, and argued that in the emission region of the gamma burst source the temperature of electrons and positrons can be different because of, i) the additional heating mechanism of the electrons or the positrons is in action; or, ii) turbulent motion causes the injection of the hot plasma to the cool region; or, iii) a strong magnetic field. For the sake of simplicity, we assume that electron thermal temperature is much higher than that of positrons, i.e., T_e ≫ T_p (Karpman et al. 1975). The dispersion relation for an electromagnetic wave with frequency close to ω_P in the plasma is (Mikhailovskii 1980) 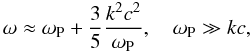$ω \approx ω_{P} + \frac{3}{5} \frac{k^{2} c^{2}}{ω_{P}}, ω_{P} ≫ kc,$ $\begin{equation} \label{eq1} \omega \approx \omega _{\rm P} + \frac{3}{5}\frac{k^2c^2}{\omega _{\rm P} }, \quad \omega _{\rm P} \gg kc, \end{equation}$ (1)in which 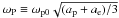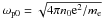$ω_{P} \equiv ω_{p 0} \sqrt{(a_{p} + a_{e}) / 3}$ $\hbox{$\omega _{\rm P} \equiv \omega _{\rm p0} \sqrt { (a_{\rm p} + a_{\rm e}) / 3} $}$ , $ω_{p 0} = \sqrt{4 π n_{0} e^{2} / m_{e}}$ $\hbox{$\omega _{\rm p0} = \sqrt {4\pi n_{0} {\rm e}^2 / m_{\rm e} } $}$ is the positron (or electron) plasma frequency; a_p,e = m_ec²/T_p,e, for ultra-relativistic case a_p,e ≪ 1; n₀, m_e, e and T_p,e are the particle density for electrons and positrons in equilibrium state, the electron rest mass, the electron charge magnitude, and the thermal temperature of positrons and electrons, respectively. This wave is undamped in a collisionless unmagnetized plasma because its phase velocity always exceeds the speed of light. Hence, they cannot resonate with plasma particles. It is extremely difficult for the oscillations to escape the plasma because the refraction index of the wave is very close to zero. This means that once the mode is excited, it will stay at the source region where there are strong nonlinear wave-wave and wave-particle interactions. It is convenient to call the transverse mode of Eq. (1) transverse plasmon. In the following, we will theoretically investigate the low-frequency magnetic filed generated by the transverse electromagnetic plasmons with dispersion (1). Qualitatively understanding the excitation of magnetic fields by transverse plasmons is quite straightforward: low-frequency nonlinear currents excited by high-frequency transverse plasmons via wave-wave and wave-particle interactions lead to the generation of quasi-static magnetic field.

An important property that distinguishes high-temperature relativistic plasmas from normal fluids is that the plasmas are to a first approximation collisionless (O’Neil & Coroniti 1999). In view of this fact, the governing equations for the magnetic field generated in the interactions of transverse plasmons with ultra-relativistic non-isothermal EP plasmas are derived from Vlasov-Maxwell equations, in which nonlinear wave-wave and wave-particle interactions are taken into consideration. The modulation instability of finite transverse plasmons shows that the characteristic scale of the spontaneous magnetic field is much larger than the relativistic plasma skin depth. Therefore, one can expect that the magnetic field will have a longer lifetime than the field generated by Weibel instability. Our theory may provide a new insight into the origin of magnetic fields in the internal shocks of GRBs.

2. Nonlinear governing equations for the interactions of transverse plasmons with non-isothermal ultra-relativistic EP plasmas

2.1. Fundamental theory in the framework of Vlasov-Maxwell equation

If the exited energy density of a perturbed field E^T is much lower than the thermal one, i.e., 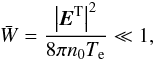$W̅ = \frac{{| E^{T} |}^{2}}{8 π n_{0} T_{e}} ≪ 1,$ $\begin{equation} \label{eq2} \bar {W} = \frac{\left| {{{\vec E}}^{\rm T}} \right|^2}{8\pi n_{0} T_{\rm e} } \ll 1, \end{equation}$ (2)the perturbed distribution function of plasma particles can be expanded in powers of the field E^T (Tsytovich 1977). In this case, taking the well-known kinetic Vlasov equation as well as the Maxwell equations into consideration, following the method introduced by Li & Ma (1993), one can obtain the equations for a transverse field 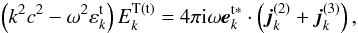$({k^{2} c^{2} - ω^{2} ε_{k}^{t}}^{)} E_{k}^{T (t)} = 4 π i ω e_{k}^{t *} \cdot ({j_{k}^{(2)} + j_{k}^{(3)}}^{)},$ $\begin{equation} \label{eq3} \left( {k^2c^2 - \omega ^2\varepsilon _{k}^{\rm t} } \right)E_{k}^{\rm T(t)} = 4\pi {\rm i}\omega {{\vec e}}_{k}^{\rm t * } \cdot \left( {{{\vec j}}_{k}^{(2)} + {{\vec j}}_{k}^{(3)} } \right), \end{equation}$ (3)and for longitudinal field 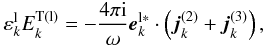$ε_{k}^{l} E_{k}^{T (l)} = - \frac{4 π i}{ω} e_{k}^{l *} \cdot ({j_{k}^{(2)} + j_{k}^{(3)}}^{)},$ $\begin{equation} \label{eq4} \varepsilon _{k}^{\rm l} E_{k}^{\rm T(l)} = - \frac{4\pi {\rm i}}{\omega }{{\vec e}}_{k}^{\rm l * } \cdot \left( {{{\vec j}}_{k}^{(2)} + {\rm {\vec j}}_{k}^{(3)} } \right), \end{equation}$ (4)where only the nonlinear currents up to the third order have been considered. 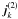$j_{k}^{(2)}$ $\hbox{${{\vec j}}_{k}^{(2)}$}$ is the second-order nonlinear current 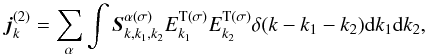$j_{k}^{(2)} = \sum_{α} \int S_{k, k_{1}, k_{2}}^{α (σ)} E_{k_{1}}^{T (σ)} E_{k_{2}}^{T (σ)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2},$ $\begin{equation} \label{eq5} {{\vec j}}_{k}^{(2)} = \sum\limits_\alpha {\int {{\rm {\vec S}}_{k,k_1 ,k_2 }^{\alpha (\sigma )} } } E_{k_1 }^{\rm T(\sigma )} E_{k_2 }^{\rm T(\sigma )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2 , \end{equation}$ (5)the third-order nonlinear current $j_{k}^{(3)} = \sum_{α} \int G_{k, k_{1}, k_{2}, k_{3}}^{α (σ)} E_{k_{1}}^{T (σ)} E_{k_{2}}^{T (σ)} E_{k_{3}}^{T (σ)} δ (k - k_{1} - k_{2} - k_{3}) d k_{1} d k_{2} d k_{3},$ $\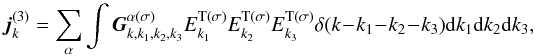begin{equation} \label{eq6} {{\vec j}}_{k}^{(3)} = \sum\limits_\alpha {\int {{\rm {\vec G}}_{k,k_1 ,k_2 ,k_3 }^{\alpha (\sigma )} } } E_{k_1 }^{\rm T(\sigma )} E_{k_2 }^{\rm T(\sigma )} E_{k_3 }^{\rm T(\sigma )} \delta (k - k_1 - k_2 - k_3 ){\rm d}k_1 {\rm d}k_2 {\rm d}k_3 , \end{equation}$ (6)with $\begin{matrix} S_{k, k_{1}, k_{2}}^{α (σ)} & = & - q_{α}^{3} \int \frac{v}{ω - k \cdot v + i ε} ({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{σ} \cdot \frac{\partial}{\partial p}) \\ G_{k, k_{1}, k_{2}, k_{3}}^{α (σ)} & = & i q_{α}^{4} \int \frac{v}{ω - k \cdot v + i ε} \\ \times (\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} σ \\ k_{1} \end{matrix} \cdot \frac{\partial}{\partial p}) \frac{1}{(ω - ω_{1}) - (k_{1} - k_{2}) \cdot v + i ε} \end{matrix}$ $\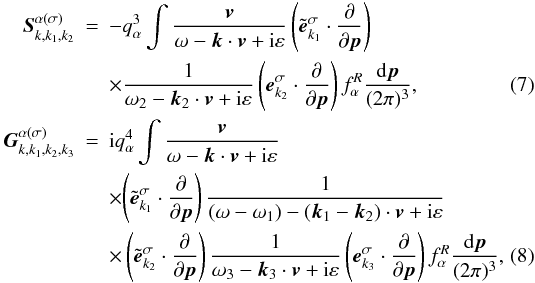begin{eqnarray} {{\vec S}}_{k,k_{1},k_{2}}^{\alpha (\sigma )} &=&-q_{\alpha }^{3}\int {\frac{{{\vec v}}}{\omega -{{\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {{\tilde{{\vec e}}}_{k_{1}}^{\sigma }\cdot \frac{\partial }{\partial {{\vec p}} }}\right) } \notag \\ &&\times{\frac{1}{\omega _{2}-{{\vec k}}_{2}\cdot {{\vec v}} +{\rm i}\varepsilon }\left( {{{\vec e}}_{{k}_{2}}^{\sigma }\cdot \frac{\partial }{\partial {{\vec p}}}}\right) f_{\alpha }^{R} }\frac{{\rm d}{{\vec p}}}{(2\pi )^{3}}, \label{eq7} \\ {{\vec G}}_{k,k_{1},k_{2},k_{3}}^{\alpha (\sigma )} &=&{\rm i}q_{\alpha }^{4}\int {\frac{{{\vec v}}}{\omega -{{\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon }} \notag \\ &&\times{\left( {\tilde{{\vec e}}_{{k}_{1}}^{\sigma }\cdot \frac{ \partial }{\partial {\vec p}}}\right) \frac{1}{(\omega -\omega _{1})-( {\vec k}_{1}-{\vec k}_{2})\cdot {{\vec v}} +{\rm i}\varepsilon }} \notag \\ &&\times\left( {\tilde{{\vec e}}_{k_{2}}^{\sigma }\cdot \frac{ \partial }{\partial {\vec p}}}\right) \frac{1}{\omega _{3}-{{\vec k}}_{3}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {{{\vec e}}_{ {k}_{3}}^{\sigma }\cdot \frac{\partial }{\partial { {\vec p}}}}\right) f_{\alpha }^{R}\frac{{\rm d}{{\vec p}}}{(2\pi )^{3}}, \label{eq8} \end{eqnarray}$ in which ∗ denotes the conjugate; 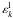$ε_{k}^{l}$ $\hbox{$\varepsilon _{k}^{\rm l} $}$ and $ε_{k}^{t}$ $\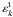hbox{$\varepsilon _{k}^{\rm t} $}$ are transverse and longitudinal dielectric constants; the term iε arises from the Landau rule (Lifshitz & Pitaevskii 1981); 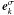$e_{k}^{σ}$ $\hbox{${\vec e}_{k}^\sigma $}$ is unit polarization vector for σ-mode (for transverse mode, σ = t, and for longitudinal mode, σ = l); 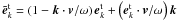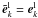$\begin{matrix} _{˜} \\ e \end{matrix} \begin{matrix} t \\ k \end{matrix} = (1 - k \cdot v / ω) e_{k}^{t} + {}^{(}{e_{k}^{t} \cdot v / ω}^{)} k$ $\hbox{$\tilde { {\vec {e}}}_{k}^{\rm t} = \left( {1 - {{\vec k}} \cdot {{\vec v}} / \omega } \right){{\vec e}}_{k}^{\rm t} + \left( {{{\vec e}}_{k}^{\rm t} \cdot {{\vec v}} / \omega } \right){{\vec k}}$}$ , $\begin{matrix} _{˜} \\ e \end{matrix} \begin{matrix} l \\ k \end{matrix} = e_{k}^{l}$ $\hbox{$\tilde {\vec {e}}_{k}^{\rm l} = {\vec e}_{k}^{\rm l}$}$ . It is worth noting that under the high-frequency approximation, i.e, ω ≈ ω_P ≫ kc, one derives 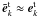$\begin{matrix} _{˜} \\ e \end{matrix} \begin{matrix} t \\ k \end{matrix} \approx e_{k}^{t}$ $\hbox{$\tilde{\vec {e}}_{k}^{\rm t} \approx {\rm {\vec e}}_{k}^{\rm t} $}$ . The δ functions in Eqs. (5) and (6) represent the conservation of energy and momentum. $f_{α}^{R}$ $\hbox{$f_\alpha ^R$}$ is the equilibrium distribution function of plasma particles. 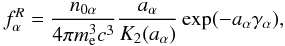Liang (1982) had mentioned that even collisionless plasmas can maintain near-Maxwellian distributions via collective processes, thus, we may take the distribution function of particles in equilibrium unperturbed state to be (Jüttner 1911) $f_{α}^{R} = \frac{n_{0 α}}{4 π m_{e}^{3} c^{3}} \frac{a_{α}}{K_{2} (a_{α})} \exp (- a_{α} γ_{α}),$ $\begin{equation} \label{eq9} f_\alpha ^R = \frac{n_{0\alpha } }{4\pi m_{\rm e}^3 c^3}\frac{a_\alpha }{K_2 (a_\alpha )}\exp ( - a_\alpha \gamma _\alpha ), \end{equation}$ (9)where $γ_{α} = \sqrt{1 + p_{α}^{2} / (m_{e} c)^{2}}$ $\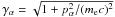hbox{$\gamma _\alpha = \sqrt {1 + p_\alpha ^2 / (m_{\rm e} c)^2} $}$ is the usual Lorentz factor, K₂ is the second kind modified Bessel function of the second order.

From Eqs. (7) and (8) one can see 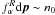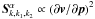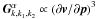$f_{α}^{R} d p ~ n_{0}$ $\hbox{$f_\alpha ^R {\rm d}{{\vec p}} \sim n_0 $}$ , $S_{k, k_{1}, k_{2}}^{α} \propto {(\partial v / \partial p)}^{2}$ $\hbox{${{\vec S}}_{k,k_1 ,k_2 }^\alpha \propto \left( {\partial {{\vec v}} / \partial {{\vec p}}} \right)^2$}$ , $G_{k, k_{1}, k_{2}}^{α} \propto {(\partial v / \partial p)}^{3}$ $\hbox{${{\vec G}}_{k,k_1 ,k_2 }^\alpha \propto \left( {\partial {{\vec v}} / \partial {{\vec p}}} \right)^3$}$ . Considering the relativistic effects, one has 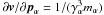$\partial v / \partial p_{α} = 1 / (γ_{α}^{3} m_{α})$ $\hbox{${\partial {\vec v} / \partial {{\vec p}}_\alpha} = 1/({\gamma _\alpha ^3 }{m_\alpha }) $}$ . Since the distribution function (9) has an exponential form, the characteristic value of γ_α ~ 1/a_α. When T_e ≫ T_p, the characteristic value of γ_e is much higher than that of γ_p. Therefore, the nonlinear currents produced by the electrons can be neglected. That is to say, one can take α = p and omit the symbol ∑ in Eqs. (5) and (6).

2.2. Self-generated low-frequency magnetic fields

The low-frequency nonlinear current is generated by nonlinear interactions of two intense waves that propagate in opposite directions, leading to the the low-frequency transverse and longitudinal fields. Now, we study the low-frequency transverse field, i.e., 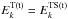$E_{k}^{T (t)} = E_{k}^{TS (t)}$ $\hbox{$E_{k}^{\rm T(t)} = E_{k}^{\rm TS(t)} $}$ in Eq. (3). Only considering the second order of 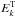$E_{k}^{T}$ $\hbox{$E_{k}^{\rm T} $}$ , Eq. (3) gives (Li & Ma 1993) 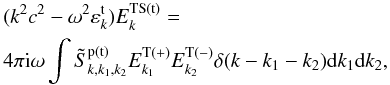$\begin{matrix} (k^{2} c^{2} - ω^{2} ε_{k}^{t}) E_{k}^{TS (t)} = \\ 4 π i ω \int {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} E_{k_{1}}^{T (+)} E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2}, \end{matrix}$ $\begin{eqnarray} \label{eq10} &&(k^2c^2 - \omega ^2\varepsilon _{k}^{\rm t} )E_{k}^{\rm TS(t)} = \nonumber\\&&4\pi {\rm i}\omega \int {\tilde {S}_{k,k_1 ,k_2 }^{\rm p(t)} E_{k_1 }^{\rm T( + )} E_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2 } , \end{eqnarray}$ (10)in which + and – denote positive and negative high-frequency fields, k₁ = (k₁,ω₁) and k₂ = (k₂,ω₂) are four-dimensional wave vectors for positive and negative high-frequency transverse fields, k = (k,ω) is the four-dimensional wave vector for low-frequency transverse fields. The interaction matrix 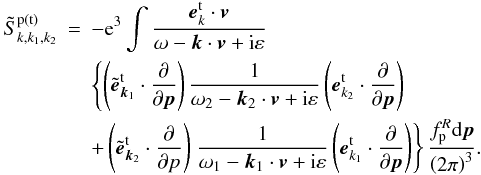$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} & = & - e^{3} \int \frac{e_{k}^{t} \cdot v}{ω - k \cdot v + i ε} \\ {(\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{1} \end{matrix} \cdot \frac{\partial}{\partial p}) \frac{1}{ω_{2} - k_{2} \cdot v + i ε} (e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p(t)} &=&-{\rm e}^{3}\int {\frac{{{\vec e}} _{k}^{\rm t}\cdot {{\vec v}}}{\omega -{{\vec k}}\cdot { {\vec v}}+{\rm i}\varepsilon }} \notag \\ &&{\left\{ {\left( {\tilde{{\vec e}}_{{\vec k}_{1}}^{\rm t}\cdot \frac{\partial }{\partial {\vec p}}}\right) \frac{1}{\omega _{2}-{ {\vec k}}_{2}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {{ {\vec e}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) }\right. } \notag \\ &&+\left( {\tilde{{\vec e}}_{{\vec k}_{2}}^{\rm t}\cdot \frac{ \partial }{\partial {p}}}\right) \left. {\frac{1}{\omega _{1}-{ {\vec k}}_{1}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {{ {\vec e}}_{{k}_{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) }\right\} \frac{f_{\rm p}^{R}{\rm d}{{\vec p}} }{\left( {2\pi }\right) ^{3}}. \label{eq11} \end{eqnarray}$ (11)Here and below we assume that all field quantities and their differentials satisfy the natural boundary condition, i.e., they are to be zero at infinity. Under the assumption of low-frequency fields kc ≪ ω ≪ ω_P, of high-frequency fields ω₁ ≈ − ω₂ ≈ ω_P, and the isotropic distribution of positrons, the interaction matrix Eq. (11) can be reduced to be (see Appendix A) ${S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} \approx - \frac{1}{4 π} \frac{e ω_{pp}^{2}}{m_{p} ω ω_{P}^{2}} Λ e_{k}^{t *} \cdot [{k \times ({e_{k_{1}}^{t} \times e_{k_{2}}^{t}}^{)}}^{]},$ $\begin{equation} \label{eq12} \tilde {S}_{k,k_1 ,k_2 }^{\rm p\left( {t} \right)} \approx -\frac{1}{4\pi }\frac{e\omega _{\rm pp}^2 }{m_{\rm p} \omega \omega _{\rm P}^2 }\Lambda {{\vec e}}_{k}^{\rm t\ast } \cdot \left[ {{{\vec k}}\times \left( {{{\vec e}}_{{k}_1 }^{\rm t} \times {{\vec e}}_{{k}_2 }^{\rm t} } \right)} \right], \end{equation}$ (12)where $Λ = {}^{⟨}{γ_{p}^{-4}}^{⟩} - 2 {}^{⟨}{γ_{p}^{-6}}^{⟩}$ $\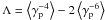hbox{$\Lambda=\left\langle {\gamma _{\rm p}^{ - 4} } \right\rangle-2\left\langle {\gamma _{\rm p}^{ - 6} } \right\rangle$}$ , in which, 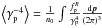${}^{⟨}{γ_{p}^{-4}}^{⟩} = \frac{1}{n_{0}}^{\int} \frac{f_{p}^{R}}{γ_{p}^{4}} \frac{d p}{{(2 π)}^{3}}$ $\hbox{$\left\langle {\gamma _{\rm p}^{ - 4} } \right\rangle = \frac{1}{n_0} \int {\frac{f_{\rm p}^R }{\gamma _{\rm p}^4 }\frac{{\rm d}{\vec p}}{\left( {2\pi } \right)^3}} $}$ and ${}^{⟨}{γ_{p}^{-6}}^{⟩} = \frac{1}{n_{0}}^{\int} \frac{f_{p}^{R}}{γ_{p}^{6}} \frac{d p}{{(2 π)}^{3}}$ $\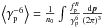hbox{$\left\langle {\gamma _{\rm p}^{ - 6} } \right\rangle = \frac{1}{n_0}\int {\frac{f_{\rm p}^R }{\gamma _{\rm p}^6 }} \frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right)^3}$}$ .

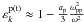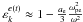The transverse dielectric constants for ultra-relativistic positrons and electrons are $ε_{k}^{p (t)} \approx 1 - \frac{a_{p}}{3} \frac{ω_{pp}^{2}}{ω^{2}}$ $\hbox{$\varepsilon _{k}^{\rm p(t)} \approx 1 - \frac{a_{\rm p} }{3}\frac{\omega _{\rm pp}^2 }{\omega ^2}$}$ and $ε_{k}^{e (t)} \approx 1 - \frac{a_{e}}{3} \frac{ω_{pe}^{2}}{ω^{2}}$ $\hbox{$\varepsilon _{k}^{e(t)} \approx 1 - \frac{a_{\rm e} }{3}\frac{\omega _{\rm pe}^2 }{\omega ^2}$}$ , for kc ≪ ω ≪ ω_P, respectively (Mikhailovskii 1980). Correspondingly, one can arrive at 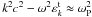$k^{2} c^{2} - ω^{2} ε_{k}^{t} \approx ω_{P}^{2}$ $\hbox{$k^2c^2 - \omega ^2\varepsilon _{k}^{\rm t} \approx \omega _{\rm P}^2 $}$ . Here, we used the formula 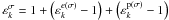$ε_{k}^{σ} = 1 + {}^{(}{ε_{k}^{e (σ)} - 1}^{)} + {}^{(}{ε_{k}^{p (σ)} - 1}^{)}$ $\hbox{$ \varepsilon _{k}^\sigma = 1 + \left( {\varepsilon _{k}^{e(\sigma)} - 1} \right) + \left( {\varepsilon _{k}^{\rm p(\sigma)} - 1} \right)$}$ . Therefore, substituting Eqs. (12) into (11) yields 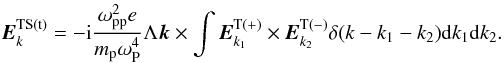$E_{k}^{TS (t)} = - i \frac{ω_{pp}^{2} e}{m_{p} ω_{P}^{4}} Λ k \times \int E_{k_{1}}^{T (+)} \times E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} .$ $\begin{equation} \label{eq13} {{\vec E}}_{k}^{\rm TS(t)} = -{\rm i}\frac{\omega _{\rm pp}^2 e}{m_{\rm p} \omega _{\rm P}^4 } \Lambda {{\vec k}}\times \int {{{\vec E}}_{k_1 }^{\rm T( + )} \times {{\vec E}}_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2 }. \end{equation}$ (13)Timing both sides of Eq. (13) with k, and taking Faraday’s law into consideration, i.e., 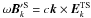$ω B_{k}^{′S} = c k \times E_{k}^{TS}$ $\hbox{$\omega {\vec B}_{k}^{\prime \rm S} = c{{\vec k}}\times {\vec E}_{k}^{\rm TS} $}$ , the equation for spontaneous low-frequency magnetic field in Fourier space can be obtained 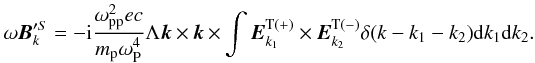$ω B_{k}^{' S} = - i \frac{ω_{pp}^{2} ec}{m_{p} ω_{P}^{4}} Λ k \times k \times \int E_{k_{1}}^{T (+)} \times E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} .$ $\begin{equation} \label{eq14} \omega {\vec B}_{k}^{\prime S} =- {\rm i}\frac{\omega _{\rm pp}^2 ec}{m_{\rm p} \omega _{\rm P}^4 }\Lambda {{\vec k}}\times {\vec k}\times \int {{{\vec E}}_{k_1 }^{\rm T( + )} \times {\vec E}_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2 }. \end{equation}$ (14)From above equation, one can find that the self-generated magnetic field is exited by the nonlinear wave-wave coupling.

2.3. High-frequency transverse field

If 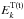$E_{k}^{T (t)}$ $\hbox{$E_{k}^{\rm T(t)} $}$ in the left-hand side of Eq. (3) is a positive high-frequency transverse field, i.e., 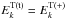$E_{k}^{T (t)} = E_{k}^{T (+)}$ $\hbox{$E_{k}^{\rm T(t)} = E_{k}^{\rm T( + )} $}$ . The quadratic terms in Eq. (5) should be the product of high-frequency and low-frequency fields: 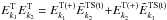$E_{k_{1}}^{T} E_{k_{2}}^{T} = E_{k_{1}}^{T (+)} {E_{k_{2}}^{TS (t)}}_{˜} + E_{k_{2}}^{T (+)} {E_{k_{1}}^{TS (t)}}_{˜}$ $\hbox{$E_{k_1 }^{\rm T} E_{k_2 }^{\rm T} = E_{k_1 }^{\rm T( + )} \tilde {E}_{k_2 }^{\rm TS(t)} { + }E_{k_2 }^{\rm T( + )} \tilde {E}_{k_1 }^{\rm TS(t)} $}$ . The three field products included in the current 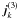$j_{k}^{(3)}$ $\hbox{${{\vec j}}_{k}^{(3)} $}$ can be expressed in terms of the triple product of high-frequency fields and a mixed cubic product of high-frequency and low-frequency fields. Considering Eq. (11), this mixed term is indeed the product of four high-frequency fields, which is of higher order. Then, 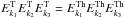$E_{k_{1}}^{T} E_{k_{2}}^{T} E_{k_{3}}^{T} = E_{k_{1}}^{Th} E_{k_{2}}^{Th} E_{k_{3}}^{Th}$ $\hbox{$E_{k_1 }^{\rm T} E_{k_2 }^{\rm T} E_{k_3 }^{\rm T} = E_{k_1 }^{\rm Th} E_{k_2 }^{\rm Th} E_{k_3 }^{\rm Th} $}$ . Because the presence of the factor (ω − ω₁) − (k₁ − k₂)·v + iε in the integral expression for 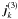$j_{k}^{(3)}$ $\hbox{${\vec j}_{k}^{(3)} $}$ is important when 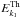$E_{k_{1}}^{Th}$ $\hbox{$E_{k_1 }^{\rm Th} $}$ is the perturbed field with positive frequency. As a result, $E_{k_{1}}^{T} E_{k_{2}}^{T} E_{k_{3}}^{T} = E_{k_{1}}^{T (+)} [E_{k_{2}}^{T (+)} E_{k_{3}}^{T (-)} + E_{k_{2}}^{T (-)} E_{k_{3}}^{T (+)}]$ $\hbox{$E_{k_1 }^{\rm T} E_{k_2 }^{\rm T} E_{k_3 }^{\rm T} = E_{k_1 }^{\rm T( + )} [E_{k_2 }^{\rm T( + )} E_{k_3 }^{\rm T( - )} + E_{k_2 }^{\rm T( - )} E_{k_3 }^{\rm T( + )} ]$}$ . Now, we obtain the high-frequency field equation from Eq. 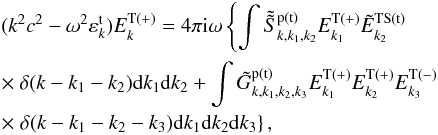(3) (Li & Ma 1993) $\begin{matrix} (k^{2} c^{2} - ω^{2} ε_{k}^{t}) E_{k}^{T (+)} = 4 π i ω {\int \begin{matrix} ˜ \\ \begin{matrix} ˜ \end{matrix} \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)} E_{k_{1}}^{T (+)} {E_{k_{2}}^{TS (t)}}_{˜} \\ \times δ (k - k_{1} - k_{2}) d k_{1} d k_{2} + \int {G_{k, k_{1}, k_{2}, k_{3}}^{p (t)}}_{˜} E_{k_{1}}^{T (+)} E_{k_{2}}^{T (+)} E_{k_{3}}^{T (-)} \end{matrix}$ $\begin{eqnarray} &&(k^{2}c^{2}-\omega ^{2}\varepsilon _{k}^{\rm t})E_{k}^{\rm T(+)}=4\pi {\rm i}\omega \left\{ {\int {\tilde{\tilde{S}}_{k,k_{1},k_{2}}^{\rm p(t)}E_{k_{1}}^{\rm T(+)}}} \tilde{E}_{k_{2}}^{\rm TS(t)}\right. \notag \\ &&\times\ \delta (k-k_{1}-k_{2}){\rm d}k_{1}{\rm d}k_{2}+{\int {\tilde{G} _{k,k_{1},k_{2},k_{3}}^{\rm p(t)}E_{k_{1}}^{\rm T(+)}E_{k_{2}}^{\rm T(+)}E_{k_{3}}^{\rm T(-)} }} \notag \\ &&\times \left. {{\delta (k-k_{1}-k_{2}-k_{3}){\rm d}k_{1}{\rm d}k_{2}{\rm d}k_{3}}}\right\} , \label{eq15} \end{eqnarray}$ (15)in which the matrix element for two positive and one negative high-frequency transverse field coupling to positive high-frequency transverse field is $\begin{matrix} {G_{k, k_{1}, k_{2}, k_{3}}^{p (t)}}_{˜} & = & i e^{4} \int \frac{(e_{k}^{t *} \cdot v)}{ω - k \cdot v + i ε} \\ \times {\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot \frac{\partial}{\partial p} \frac{1}{({ω - ω_{1}}^{)} - (k - k_{1}) \cdot v + i ε} \\ \times {\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{2} \end{matrix} \cdot \frac{\partial}{\partial p} \frac{1}{ω_{3} - k_{3} \cdot v + i ε} (e_{k_{3}}^{t} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\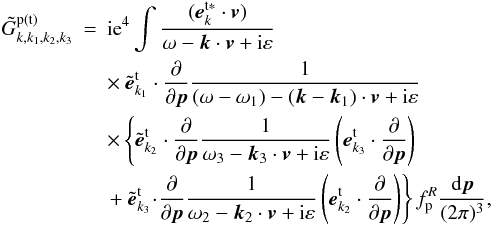begin{eqnarray} \tilde{G}_{k,k_{1},k_{2},k_{3}}^{\rm p(t)} &=&{\rm i}{\rm e}^{4}\int {\frac{({{\vec e}}_{{k}}^{\rm t\ast }\cdot {{\vec v}})}{\omega - {{\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon }} \notag \\ &&\times\ {{\tilde{{\vec e}}}_{{k}_{1}}^{\rm t}\cdot \frac{ \partial }{\partial {{\vec p}}}\frac{1}{\left( {\omega -\omega _{1}} \right) -\left( {{{\vec k}}-{{\vec k}}_{1}}\right) \cdot {{\vec v}}+{\rm i}\varepsilon }} \notag \\ &&\times \left\{ {\tilde{{{\vec e}}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}\frac{1}{\omega _{3}- {\vec k}_{3}\cdot {{\vec v}}+{\rm i}\varepsilon }}\left( {\vec e}_{{k}_{3}}^{\rm t}\cdot \frac{\partial }{\partial{{\vec p}}}\right) \right. \notag \\ && \left. {+ \ \tilde{{{\vec e}}}_{{k}_{3}}^{\rm t}\!\cdot\! 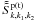\frac{\partial }{\partial {{\vec p}}}\frac{1}{\omega _{2}-{ {\vec k}}_{2}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {{ {\vec e}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) }\right\} f_{\rm p}^{R}\frac{{\rm d}{{\vec p}}}{ (2\pi )^{3}}, \, \label{eq16} \end{eqnarray}$ (16)and $\begin{matrix} _{˜} \\ _{˜} \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)}$ $\hbox{$\tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p(t)} $}$ is the same as 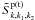${S_{k, k_{1}, k_{2}}^{p (t)}}_{˜}$ $\hbox{$\tilde {S}_{k,k_1 ,k_2 }^{\rm p(t)} $}$ , except that k₂ is the four-dimensional wave vector for the low-frequency transverse field. The low-frequency transverse field E^TS(t) for the fusion process of Eq. (11) may be different from the low-frequency field 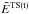$\begin{matrix} ˜ \\ E^{TS (t)} \end{matrix}$ $\hbox{$\tilde {E}^{\rm TS(t)} $}$ for the decay process in Eq. (15). According to the semi-classical theory, the decay/fusion interactions can determine the intensity of the low-frequency field 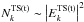$N_{k}^{TS (t)} ~ {| E_{k}^{TS (t)} |}^{2}$ $\hbox{$N_{k}^{\rm TS(t)} \sim \left| {E_{k}^{\rm TS(t)} } \right|^2$}$ . In other words, they differ by a phase factor exp(iϕ): 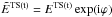$\begin{matrix} _{˜} \\ E^{TS (t)} \end{matrix} = E^{TS (t)} \exp (i ϕ)$ $\hbox{$\tilde {E}^{\rm TS(t)} = E^{\rm TS(t)} \exp ({\rm i}\varphi )$}$ (Li & Ma 1993).

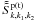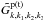To obtain the high-frequency transverse field equation, one should estimate the nonlinear interaction matrixes $\begin{matrix} _{˜} \\ _{˜} \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)}$ $\hbox{$\tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p(t)} $}$ and ${G_{k, k_{1}, k_{2}, k_{3}}^{p (t)}}_{˜}$ $\hbox{$\tilde {G}_{k,k_1 ,k_2 ,k_3 }^{\rm p(t)} $}$ in detail. Considering that ω₁ ≈ ω_P ≫ k₁c and ω ≈ ω_P ≫ kc for high-frequency transverse fields, k₂c ≪ ω₂ ≪ ω_P and 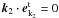$k_{2} \cdot e_{k_{2}}^{t} = 0$ $\hbox{${\rm {\vec k}}_2 \cdot {{\vec e}}_{{\rm { k}}_2 }^{\rm t} = 0$}$ for the low-frequency transverse field, after straightforward manipulation, one can obtain (see Appendix B ) $\begin{matrix} ˜ \\ ˜ \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)} \approx - \frac{1}{4 π} \frac{ω_{pp}^{2} e}{ω m_{p} ω_{P} c} ⟨ {γ_{p}^{-4}}^{⟩} e_{k}^{t *} \cdot [e_{k_{1}}^{t} \times (\frac{k_{2} c}{ω_{2}} \times e_{k_{2}}^{t})] .$ $\begin{equation} \label{eq17} \tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p\left( t \right)} \approx - \frac{1}{4\pi }\frac{\omega _{\rm pp}^2 e}{\omega m_{\rm p} \omega _{\rm P} c}\left\langle {\gamma _{\rm p}^{ - 4} } \right\rangle {\vec e}_{k}^{\rm t{\rm {\bf \ast }}} \cdot \left[ {{\vec e}_{{{k}}_1 }^{\rm t} \times \left( {\frac{{\vec k}_2 c}{\omega _2}\times {{\vec e}}_{{k}_2 }^{\rm t} } \right)} \right]. \end{equation}$ (17)Integrating Eq. (16) by parts, and considering ω ≈ ω_P ≫ kc, Eq. (16) can be written as $\begin{matrix} i ω {G_{k, k_{1,} k_{2,} k_{3}}^{p (t)}}_{˜} & = & e^{4} \begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t * \\ k \end{matrix} \cdot {\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \int \frac{1}{γ_{p}^{3} m_{p}} \frac{1}{({ω - ω_{1}}^{)} - (k - k_{1}) \cdot v + i ε} \\ \times {(\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{2} \end{matrix} \cdot \frac{\partial}{\partial p}) \frac{e_{k_{3}}^{t} \cdot \frac{\partial}{\partial p}}{ω_{3} - k_{3} \cdot v + i ε} \end{matrix}$ $\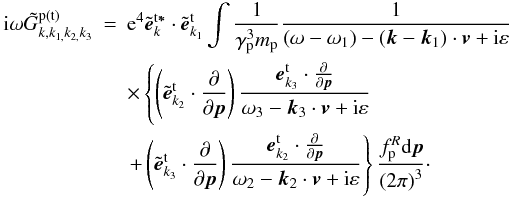begin{eqnarray} {\rm i}\omega \tilde{G}_{k,k_{1,}k_{2,}k_{3}}^{\rm p(t)} &=&{\rm e}^{4}\tilde{\vec e}_{{k}}^{\rm t{{\vec \ast }}}\cdot {\tilde{ {\vec e}}}_{{k}_{1}}^{\rm t}\int {\frac{1}{\gamma _{\rm p}^{3}m_{\rm p} }\frac{1}{\left( {\omega -\omega _{1}}\right) -\left( {{{\vec k}}- {{\vec k}}_{1}}\right) \cdot {{\vec v}}+{\rm i}\varepsilon }} \notag \\ &&\times\left\{ {\left( {\tilde{{{\vec e}}}_{{k} _{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \frac{ {{\vec e}}_{{k}_{3}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}{\omega _{3}-{{\vec k}}_{3}\cdot {{\vec v}}+{\rm i}\varepsilon }}\right. \notag \\ &&\left. {+\left( {\tilde{{{\vec e}}}_{{k} _{3}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \frac{ {{\vec e}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}{\omega _{2}-{{\vec k}}_{2}\cdot {{\vec v}}+{\rm i}\varepsilon }}\right\} \frac{f_{\rm p}^{R}{\rm d}{ {\vec p}}}{\left( {2\pi }\right) ^{3}}\cdot \label{eq18} \end{eqnarray}$ (18)Regarding that the characteristic Lorentz factor for positrons γ_p ~ 1/a_p, the above equation can be simplified to 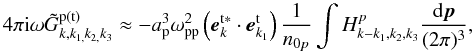$4 π i ω {G_{k, k_{1,} k_{2,} k_{3}}^{p (t)}}_{˜} \approx - a_{p}^{3} ω_{pp}^{2} ({e_{k}^{t *} \cdot e_{k_{1}}^{t}}^{)} \frac{1}{n_{0 p}} \int H_{k - k_{1}, k_{2}, k_{3}}^{p} \frac{d p}{(2 π)^{3}},$ $\begin{equation} \label{eq19} 4\pi {\rm i}\omega \tilde {G}^{\rm p(t)}_{k,k_{1,} k_{2,} k_3 } \approx - a_{\rm p}^3 \omega _{\rm pp}^2 \left( {{{\vec e}}_{k}^{\rm t{\rm {\bf \ast }}} \cdot {{\vec e}}_{{k}_1 }^{\rm t} } \right)\frac{1}{n_{0p} }\int {H_{k - k_1 ,k_2 ,k_3 }^p \frac{ {\rm d}{{\vec p}}}{(2\pi )^3}}, \end{equation}$ (19)where $\begin{matrix} H_{k - k_{1}, k_{2}, k_{3}}^{p} & = & - \frac{e^{2}}{(ω - ω_{1}) - (k - k_{1}) \cdot v + i ε} \\ \times [\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{2} \end{matrix} \cdot \frac{\partial}{\partial p} \frac{1}{ω_{3} - k_{3} \cdot v + i ε} e_{k_{3}}^{t} \cdot \frac{\partial}{\partial p} \end{matrix}$ $\begin{eqnarray} H_{k-k_{1},k_{2},k_{3}}^{\rm p} &=&-\frac{{\rm e}^{2}}{(\omega -\omega _{1})-({ {\vec k}}-{{\vec k}}_{1})\cdot {{\vec v}}+{\rm i}\varepsilon } \notag \\ &&\times\left[ {\tilde{{{\vec e}}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}\frac{1}{\omega _{3}-{ {\vec k}}_{3}\cdot {{\vec v}}+{\rm i}\varepsilon }{{\vec e}}_{ {k}_{3}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p }}}}\right. \notag \\ &&\left. {+{\tilde{{\vec e}}}_{{k}_{3}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}\frac{1}{\omega _{2}-{ {\vec k}}_{2}\cdot {{\vec v}}+{\rm i}\varepsilon }{{\vec e}}_{ {k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p }}}}\right] f_{\rm p}^{R}. 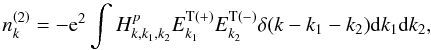\label{eq20} \end{eqnarray}$ (20)The second-order low-frequency density perturbation produced by the interaction of two high-frequency transverse fields propagating in opposite directions is (Li & Ma 1993) $n \begin{matrix} (2) \\ k \end{matrix} = - e^{2} \int H_{k, k_{1}, k_{2}}^{p} E_{k_{1}}^{T (+)} E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2},$ $\begin{equation} \label{eq21} n_{k}^{\left( 2 \right)} = - {\rm e}^2\int {H_{k,k_1 ,k_2 }^p E_{k_1 }^{\rm T( + )} E_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2}, \end{equation}$ (21)where $H_{k, k_{1}, k_{2}}^{p}$ $\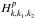hbox{$H_{k,k_1 ,k_2 }^p $}$ is the same as 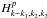$H_{k - k_{1}, k_{2}, k_{3}}^{p}$ $\hbox{$H_{k - k_1 ,k_2 ,k_3 }^p $}$ , except k − k₁ → k, k₂ → k₁, k₃ → k₂. Here we should mention that k in Eq. (21) and k − k₁ in Eq. (19) are four-dimensional wave vectors for low-frequency perturbations. Comparing Eqs. (21) and (19), the last term on the right-hand side of Eq. (15) can be written as 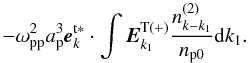$- ω_{pp}^{2} a_{p}^{3} e_{k}^{t *} \cdot \int E_{k_{1}}^{T (+)} \frac{n \begin{matrix} (2) \\ k - k_{1} \end{matrix}}{n_{p 0}} d k_{1} .$ $\begin{equation} \label{eq22} - \omega _{\rm pp}^2 a_{\rm p}^3 {{\vec e}}_{k}^{\rm t{\rm {\bf \ast }}} \cdot \int {{{\vec E}}_{k_1 }^{\rm T( + )} \frac{n_{k - k_1 }^{\left( 2 \right)} }{n_{\rm p0} }{\rm d}k_1 }. \end{equation}$ (22)Similarly, from Eqs. (17) the first term on the right-hand side of Eq. (15) is 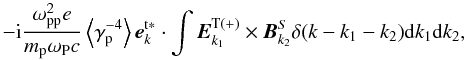$- i \frac{ω_{pp}^{2} e}{m_{p} ω_{P} c} ⟨ {γ_{p}^{-4}}^{⟩} e_{k}^{t *} \cdot \int E_{k_{1}}^{T (+)} \times B_{k_{2}}^{S} δ (k - k_{1} - k_{2}) d k_{1} d k_{2},$ $\begin{equation} \label{eq23} - {\rm i}\frac{\omega _{\rm pp}^2 e}{m_{\rm p} \omega _{\rm P} c}\left\langle {\gamma _{\rm p}^{ - 4} } \right\rangle {{\vec e}}_{k}^{\rm t{\rm {\bf \ast }}} \cdot \int {{{\vec E}}_{k_1 }^{\rm T( + )} \times {\vec B}_{k_2 }^S \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2 }, \end{equation}$ (23)in which, $ω B_{k_{2}}^{S} = c k_{2} \times {\begin{matrix} _{˜} \\ E \end{matrix}}_{k_{2}}^{TS (t)}$ $\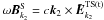hbox{$\omega {\rm {\vec B}}_{k_2}^{\rm S} = c{\vec k}_2 \times {\rm \tilde {\vec E}}_{k_2 }^{\rm TS(t)} $}$ .

Substituting Eqs. (22), and (23) into Eq. (15) yields 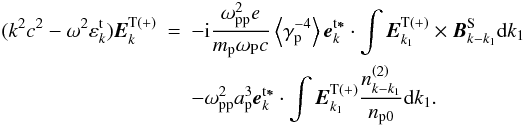$\begin{matrix} (k^{2} c^{2} - ω^{2} ε_{k}^{t}) E_{k}^{T (+)} & = & - i \frac{ω_{pp}^{2} e}{m_{p} ω_{P} c} ⟨ {γ_{p}^{-4}}^{⟩} e_{k}^{t *} \cdot \int E_{k_{1}}^{T (+)} \times B_{k - k_{1}}^{S} d k_{1} \end{matrix}$ $\begin{eqnarray} (k^{2}c^{2}-\omega ^{2}\varepsilon _{k}^{\rm t}){{\vec E}}_{k}^{\rm T(+)} &=&-{\rm i}\frac{\omega _{\rm pp}^{2}e}{m_{\rm p}\omega _{\rm P}c}\left\langle {\gamma _{\rm p}^{-4}}\right\rangle {{\vec e}}_{{k}}^{\rm t{ {\vec \ast }}}\cdot \int {{{\vec E}}_{k_{1}}^{\rm T(+)}\times { {\vec B}}_{k-k_{1}}^{\rm S}{\rm d}k_{1}} \notag \\ &&-\omega _{\rm pp}^{2}a_{\rm p}^{3}{{\vec e}}_{{k}}^{\rm t {{\vec \ast }}}\cdot \int {{{\vec E}}_{k_{1}}^{\rm T(+)}\frac{ n_{k-k_{1}}^{\left( 2\right) }}{n_{\rm p0}}{\rm d}k_{1}}. \label{eq24} \end{eqnarray}$ (24)

2.4. Low-frequency density perturbation

It has been shown that the transverse field, produced by positive and negative high-frequency fields, would not result in a linear density perturbation, for 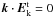$k \cdot E_{k}^{t} = 0$ $\hbox{${{\vec k}} \cdot {{\vec E}}_{{\rm { k}} }^{\rm t} = 0$}$ (Li & Ma 1993). However, the low-frequency longitudinal field produced by the coupling of high-frequency fields may produce low-frequency density perturbations.

From Eq. (4) the field equation for a low-frequency longitudinal field is (Li & Ma 1993) 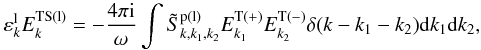$ε_{k}^{l} E_{k}^{TS (l)} = - \frac{4 π i}{ω} \int {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} E_{k_{1}}^{T (+)} E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2},$ $\begin{equation} \label{eq25} \varepsilon _{k}^{\rm l} E_{k}^{\rm TS(l)} = - \frac{4\pi {\rm i}}{\omega }\int {\tilde {S}_{k,k_1 ,k_2 }^{\rm p(l)} E_{k_1 }^{\rm T( + )} E_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2 }, \end{equation}$ (25)in which k, k₁ and k₂ are the four-dimensional wave vectors for low-frequency longitudinal fields and positive and negative high-frequency transverse fields, respectively. And the interaction matrix 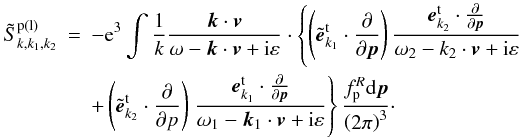$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} & = & - e^{3} \int \frac{1}{k} \frac{k \cdot v}{ω - k \cdot v + i ε} \cdot {(\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{1} \end{matrix} \cdot \frac{\partial}{\partial p}) \frac{e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}}{ω_{2} - k_{2} \cdot v + i ε} \\ + (\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{2} \end{matrix} \cdot \frac{\partial}{∂p}) \frac{e_{k_{1}}^{t} \cdot \frac{\partial}{\partial p}}{ω_{1} - k_{1} \cdot v + i ε} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix} \frac{f_{p}^{R} d p}{{({2 π}^{)}}^{3}} \cdot \end{matrix}$ $\begin{eqnarray} \label{eq26} \tilde {S}_{k,k_1 ,k_2 }^{\rm p\left( l \right)} &=& - {\rm e}^3\int {\frac{1}{k}\frac{{{\vec k}} \cdot {{\vec v}}}{\omega - {{\vec k}} \cdot {{\vec v}} + {\rm i}\varepsilon } \cdot \left\{ {\left( {\tilde {\vec {e}}_{k_1 }^{\rm t} \cdot \frac{\partial }{\partial {{\vec p}}}} \right)\frac{{\vec e}_{k_2 }^{\rm t} \cdot \frac{\partial }{\partial {\vec p}}}{\omega _2 - k_2 \cdot {{\vec v}} + {\rm i}\varepsilon }} \right.} \nonumber\\ &&+ \left( {\tilde {\vec {e}}_{k_2 }^{\rm t} \cdot \frac{\partial }{\partial {p}}} \right)\left. {\frac{{\vec e}_{k_1 }^{\rm t} \cdot \frac{\partial }{\partial {\vec p}}}{\omega _1 - {\vec k}_1 \cdot {{\vec v}} + {\rm i}\varepsilon }} \right\} \frac{f_{\rm p} ^R{\rm d}{{\vec p}}}{\left( {2\pi } \right)^3}\cdot \end{eqnarray}$ (26)Following the similar procedure to obtain Eq. (17), the above equation can be reduced to (see Appendix C) 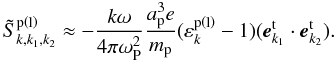${S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} \approx - \frac{kω}{4 π ω_{P}^{2}} \frac{a_{p}^{3} e}{m_{p}} (ε_{k}^{p (l)} - 1) (e_{k_{1}}^{t} \cdot e_{k_{2}}^{t}) .$ $\begin{equation} \label{eq27} \tilde {S}_{k,k_1 ,k_2 }^{\rm p\left( l \right)} \approx - \frac{k\omega }{4\pi \omega _{\rm P}^2 }\frac{a_{\rm p}^3 e}{m_{\rm p} }(\varepsilon _{k}^{\rm p\left( l \right)} - 1)({{\vec e}}_{k_1 }^{\rm t} \cdot {{\vec e}}_{k_2 }^{\rm t} ).\vspace*{-2.5mm} \end{equation}$ (27)Substituting Eq. (27) into (25), the low-frequency longitudinal field equation becomes 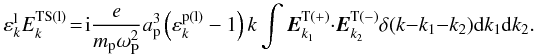$ε_{k}^{l} E_{k}^{TS (l)} = i \frac{e}{m_{p} ω_{P}^{2}} a_{p}^{3} ({ε_{k}^{p (l)} - 1}^{)} k \int E_{k_{1}}^{T (+)} \cdot E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} .$ $\begin{equation} \label{eq28} \varepsilon _{k}^{\rm l} E_{k}^{\rm TS(l)} \!=\! {\rm i}\frac{e}{m_{\rm p} \omega _{\rm P}^2 }a_{\rm p}^3 \left( {\varepsilon _{k}^{\rm p\left( l \right)} - 1} \right)k\int {{{\vec E}}_{k_1 }^{\rm T( + )} } \cdot {\vec E}_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2){\rm d}k_1 {\rm d}k_2.\vspace*{-4.5mm} \end{equation}$ (28)The linear low-frequency density perturbation resulting from the low-frequency longitudinal field is (Li & Ma 1993) 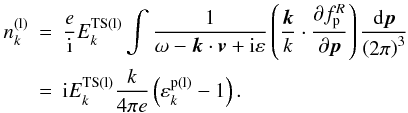$\begin{matrix} n_{k}^{(l)} & = & \frac{e}{i} E_{k}^{TS (l)} \int \frac{1}{ω - k \cdot v + i ε} (\frac{k}{k} \cdot \frac{\partial f_{p}^{R}}{\partial p}) \frac{d p}{{({2 π}^{)}}^{3}} \\ = \end{matrix}$ $\begin{eqnarray} n_{k}^{\rm (l)} &=&\frac{e}{\rm i}E_{k}^{\rm TS(l)}\int {\frac{1}{\omega -{ {\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {\frac{{ {\vec k}}}{k}\cdot \frac{\partial f_{\rm p}^{R}}{\partial {{\vec p}}}} \right) \frac{{\rm d}{{\vec p}}}{\left( {2\pi }\right) ^{3}}} \notag \\ &=&{\rm i}E_{k}^{\rm TS(l)}\frac{k}{4\pi e}\left( {\varepsilon _{k}^{\rm p\left( l\right) }-1}\right). \label{eq29} \end{eqnarray}$ (29)When ω_P ≫ ω ≫ kc, the longitudinal dielectric for positrons is 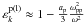$ε_{k}^{p (l)} \approx 1 - \frac{a_{p}}{3} \frac{ω_{pp}^{2}}{ω^{2}}$ $\hbox{$ \varepsilon _{k}^{\rm p(l)} \approx 1 - \frac{a_{\rm p} }{{3}}\frac{\omega _{\rm pp}^2 }{\omega ^2}$}$ (Mikhailovskii 1980). Combining Eqs. (28) and (29), the first-order linear density perturbation is 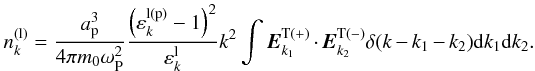$n_{k}^{(l)} = \frac{a_{p}^{3}}{4 π m_{0} ω_{P}^{2}} \frac{{({ε_{k}^{l (p)} - 1}^{)}}^{2}}{ε_{k}^{l}} k^{2} \int E_{k_{1}}^{T (+)} \cdot E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} .$ $\begin{equation} \label{eq30} n_{k}^{\rm (l)} = \frac{a_{\rm p}^3 }{4\pi m_0 \omega _{\rm P}^2 }\frac{\left( {\varepsilon _{k}^{\rm l(p)} - 1} \right)^2}{\varepsilon _{k}^{\rm l} }k^2\int {{{\vec E}}_{k_1 }^{\rm T( + )} } \cdot {\vec E}_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2. \end{equation}$ (30)The second-order low-frequency density perturbation produced by the interaction of two high-frequency transverse fields can be derived from Eq. (21). Integrating the interaction matrix Eq. (26) by parts yields 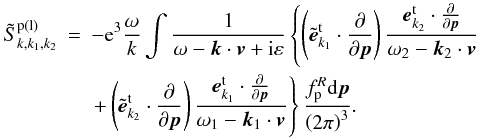$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} & = & - e^{3} \frac{ω}{k} \int \frac{1}{ω - k \cdot v + i ε} {(\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{1} \end{matrix} \cdot \frac{\partial}{\partial p}) \frac{e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}}{ω_{2} - k_{2} \cdot v} \end{matrix}$ $\begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p(l)} &=&-{\rm e}^{3}\frac{\omega }{k}\int {\frac{1}{ \omega -{{\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon }}\left\{ { \left( {\tilde{{{\vec e}}}_{{k}_{1}}^{\rm t}\cdot \frac{ \partial }{\partial {{\vec p}}}}\right) \frac{{{\vec e}}_{ {k}_{{{2}}}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}{\omega _{2}-{{\vec k}}_{{ {2}}}\cdot {{\vec v}}}}\right. \notag \\ &&\left. {+\left( {{\tilde{{\vec e}}}_{{k} _{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \frac{ {{\vec e}}_{{k}_{{{1}}}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}{\omega _{1}-{{\vec k }}_{{1}}\cdot {{\vec v}}}}\right\} \frac{f_{\rm p}^{R}{\rm d }{{\vec p}}}{\left( {{2}\pi }\right) ^{3}}. \label{eq31} \end{eqnarray}$ (31)Therefore, Eq. (21) can be rewritten as 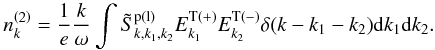$n \begin{matrix} (2) \\ k \end{matrix} = \frac{1}{e} \frac{k}{ω} \int {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} E_{k_{1}}^{T (+)} E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} .$ $\begin{equation} \label{eq32} n_{k}^{\left( 2 \right)} = \frac{1}{e}\frac{k}{\omega }\int {\tilde {S}_{k,k_1 ,k_2 }^{\rm p(l)} E_{k_1 }^{\rm T( + )} E_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2}. \end{equation}$ (32)Combining Eqs. (27) and (32) yields 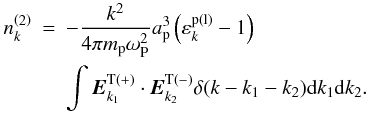$\begin{matrix} n \begin{matrix} (2) \\ k \end{matrix} & = & - \frac{k^{2}}{4 π m_{p} ω_{P}^{2}} a_{p}^{3} ({ε_{k}^{p (l)} - 1}^{)} \\ \int E_{k_{1}}^{T (+)} \cdot E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} . \end{matrix}$ $\begin{eqnarray*} n_{k}^{\left( 2\right) } &=&-\frac{k^{2}}{4\pi m_{\rm p}\omega _{\rm P}^{2}} a_{\rm p}^{3}\left( {\varepsilon _{k}^{\rm p(l)}-1}\right) \\ &&\int {{{\vec E}}_{k_{1}}^{\rm T\left( +\right) }\cdot {{\vec E}}_{k_{2}}^{\rm T\left( -\right) }\delta (k-k_{1}-k_{2}){\rm d}k_{1}{\rm d}k_{2}}. \end{eqnarray*}$ Thus, the total density perturbation for positrons is 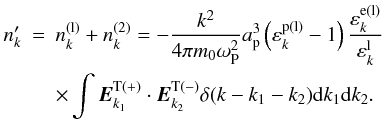$\begin{matrix} n_{k}^{'} & = & n_{k}^{(l)} + n_{k}^{(2)} = - \frac{k^{2}}{4 π m_{0} ω_{P}^{2}} a_{p}^{3} ({ε_{k}^{p (l)} - 1}^{)} \frac{ε_{k}^{e (l)}}{ε_{k}^{l}} \end{matrix}$ $\begin{eqnarray} {n}_{k}^{\prime } &=&n_{k}^{\rm (l)}+n_{k}^{(2)}=-\frac{k^{2}}{4\pi m_{0}\omega _{\rm P}^{2}}a_{\rm p}^{3}\left( {\varepsilon _{k}^{\rm p(l)}-1}\right) \frac{ \varepsilon _{k}^{\rm e(l)}}{\varepsilon _{k}^{\rm l}} \notag \\ &&\times\int {{{\vec E}}_{k_{1}}^{\rm T(+)}}\cdot {{\vec E}} _{k_{2}}^{\rm T(-)}\delta (k-k_{1}-k_{2}){\rm d}k_{1}{\rm d}k_{2}. \label{eq33} \end{eqnarray}$ (33)The low-frequency longitudinal dielectric for electrons is 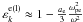$ε_{k}^{e (l)} \approx 1 - \frac{a_{e}}{3} \frac{ω_{pe}^{2}}{ω^{2}}$ $\hbox{$\varepsilon _{k}^{\rm e(l)} \approx 1 - \frac{a_{\rm e} }{{3}}\frac{\omega _{\rm pe}^2 }{\omega ^2}$}$ when ω_P ≫ ω ≫ kc (Mikhailovskii 1980). Therefore, Eq. (33) can be converted into 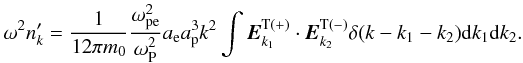$ω^{2} n_{k}^{'} = \frac{1}{12 π m_{0}} \frac{ω_{pe}^{2}}{ω_{P}^{2}} a_{e} a_{p}^{3} k^{2} \int E_{k_{1}}^{T (+)} \cdot E_{k_{2}}^{T (-)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} .$ $\begin{equation} \label{eq34} \omega ^2{n}'_{k} = \frac{1}{{12}\pi m_0 }\frac{\omega _{\rm pe}^2 }{\omega _{\rm P}^2 }a_{\rm e} a_{\rm p}^3 k^2\int {{{\vec E}}_{k_1 }^{\rm T( + )} } \cdot {{\vec E}}_{k_2 }^{\rm T( - )} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2. \end{equation}$ (34)In the case involving longitudinal fields, one needs to add the following term to the right-hand side of Eq. (15): 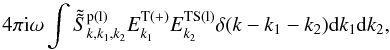$4 π i ω \int \begin{matrix} ˜ \\ ˜ \end{matrix} S_{k, k_{1}, k_{2}}^{p (l)} E_{k_{1}}^{T (+)} E_{k_{2}}^{TS (l)} δ (k - k_{1} - k_{2}) d k_{1} d k_{2},$ $\begin{equation} \label{eq35} 4\pi {\rm i}\omega \int {\tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p(l)} E_{k_1 }^{\rm T( + )} E_{k_2 }^{\rm TS(l)} \delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2}, \end{equation}$ (35)in which 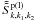$\begin{matrix} _{˜} \\ _{˜} \end{matrix} S_{k, k_{1}, k_{2}}^{p (l)}$ $\hbox{$\tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p(l)} $}$ is the same as 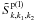${S_{k, k_{1}, k_{2}}^{p (l)}}_{˜}$ $\hbox{$\tilde {S}_{k,k_1 ,k_2 }^{\rm p(l)} $}$ , except that k₂ is the four-dimensional wave vector for the low-frequency longitudinal field, 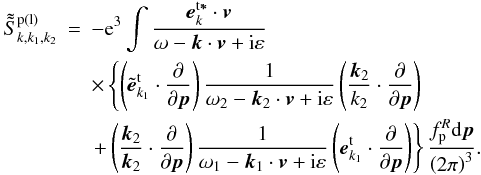$\begin{matrix} \begin{matrix} ˜ \\ \begin{matrix} ˜ \end{matrix} \end{matrix} S_{k, k_{1}, k_{2}}^{p (l)} & = & - e^{3} \int \frac{e_{k}^{t *} \cdot v}{ω - k \cdot v + i ε} \\ \times {(\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{1} \end{matrix} \cdot \frac{\partial}{\partial p}) \frac{1}{ω_{2} - k_{2} \cdot v + i ε} (\frac{k_{2}}{k_{2}} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\begin{eqnarray} \tilde{\tilde{S}}_{k,k_{1},k_{2}}^{\rm p(l)} &=&-{\rm e}^{3}\int {\frac{{ {\vec e}}_{{k}}^{\rm t{{\vec \ast }}}\cdot { {\vec v}}}{\omega -{{\vec k}}\cdot {{\vec v}} +{\rm i}\varepsilon }} \notag \\ &&\times\left\{ {\left( {\tilde{{{\vec e}}}_{{k}_{{ {1}}}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}} \right) \frac{1}{\omega _{2}-{{\vec k}}_{2}\cdot {{\vec v}} +{\rm i}\varepsilon }\left( {\frac{{{\vec k}}_{2}}{k_{2}}\cdot \frac{ \partial }{\partial {{\vec p}}}}\right) }\right. \notag \\ &&\left. {+\left( {\frac{{{\vec k}}_{2}}{{\vec k}_{2}}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \frac{1}{\omega _{1}-{{\vec k}}_{1}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {{{\vec e}}_{ {k}_{{{1}}}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}\right) }\right\} \frac{f_{\rm p}^{R}{\rm d}{ {\vec p}}}{\left( {2\pi }\right) ^{3}}. \label{eq36} \end{eqnarray}$ (36)Similarly as the derivation of interaction matrix 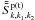$\begin{matrix} _{˜} \\ _{˜} \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)}$ $\hbox{$\tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p \left( {t} \right)} $}$ , Eq. (36) can be simplified as 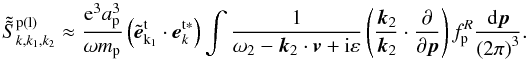$\begin{matrix} ˜ \\ ˜ \end{matrix} S_{k, k_{1}, k_{2}}^{p (l)} \approx \frac{e^{3} a_{p}^{3}}{ω m_{p}} ({\begin{matrix} ˜ \\ e \end{matrix} \begin{matrix} t \\ k_{1} \end{matrix} \cdot e_{k}^{t *}}^{)} \int \frac{1}{ω_{2} - k_{2} \cdot v + i ε} (\frac{k_{2}}{k_{2}} \cdot \frac{\partial}{\partial p}) f_{p}^{R} \frac{d p}{{({2 π}^{)}}^{3}} .$ $\begin{equation} \label{eq37} \tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p(l)} \approx \frac{{\rm e}^3a_{\rm p}^3 }{\omega m_{\rm p} }\left( {\tilde {\vec {e}}_{{\rm {k}}_{1} }^{\rm t} \cdot {{\vec e}}_{k}^{\rm t{\rm {\bf \ast }}} } \right)\int {\frac{1}{\omega _2 - {\vec k}_2 \cdot {{\vec v}} + {\rm i}\varepsilon }\left( {\frac{{\vec k}_2 }{{\vec k}_2 } \cdot \frac{\partial }{\partial {{\vec p}}}} \right)f_{\rm p}^R } \frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right)^3}. \end{equation}$ (37)Considering Eqs. (29) and (37), Eq. (35) can be written as 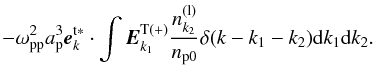$- ω_{pp}^{2} a_{p}^{3} e_{k}^{t *} \cdot \int E_{k_{1}}^{T (+)} \frac{n_{k_{2}}^{(l)}}{n_{p 0}} δ (k - k_{1} - k_{2}) d k_{1} d k_{2} .$ $\begin{equation} \label{eq38} - \omega _{\rm pp}^2 a_{\rm p}^3 {{\vec e}}_{k}^{\rm t{\rm {\bf \ast }}} \cdot \int {{{\vec E}}_{k_1 }^{\rm T( + )} \frac{n_{k_2 }^{\rm (l)} }{n_{\rm p0} }\delta (k - k_1 - k_2 ){\rm d}k_1 {\rm d}k_2}. \end{equation}$ (38)Taking Eq. (38) into account, one obtains from Eq. (24) 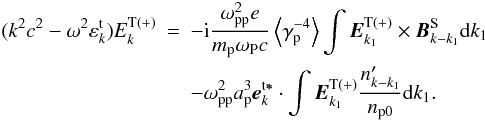$\begin{matrix} (k^{2} c^{2} - ω^{2} ε_{k}^{t}) E_{k}^{T (+)} & = & - i \frac{ω_{pp}^{2} e}{m_{p} ω_{P} c} ⟨ {γ_{p}^{-4}}^{⟩} \int E_{k_{1}}^{T (+)} \times B_{k - k_{1}}^{S} d k_{1} \end{matrix}$ $\begin{eqnarray} (k^{2}c^{2}-\omega ^{2}\varepsilon _{k}^{\rm t})E_{k}^{\rm T(+)} &=&-{\rm i}\frac{\omega _{\rm pp}^{2}e}{m_{\rm p}\omega _{\rm P}c}\left\langle {\gamma _{\rm p}^{-4}}\right\rangle \int {{{\vec E}}_{k_{1}}^{\rm T(+)}\times {{\vec B}} _{k-k_{1}}^{\rm S}{\rm d}k_{1}} \notag \\ &&-\omega _{\rm pp}^{2}a_{\rm p}^{3}{{\vec e}}_{{k}}^{\rm t {{\vec \ast }}}\cdot \int {{{\vec E}}_{k_{1}}^{\rm T(+)}\frac{ n_{k-k_{1}}^{\prime }}{n_{\rm p0}}{\rm d}k_{1}}. \label{eq39} \end{eqnarray}$ (39)For ω ≈ ω_P ≫ kc, the transverse dielectric 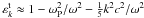$ε_{k}^{t} \approx 1 - ω_{P}^{2} / ω^{2} - \frac{1}{5} k^{2} c^{2} / ω^{2}$ $\hbox{$\varepsilon _{k}^{\rm t} \approx 1 - {\omega _{\rm P}^2 }/{\omega ^2}-\frac{1}{5}k^2 c^2/\omega ^2$}$ (Mikhailovskii 1980). Hence, Eq. ( 39) can be written as 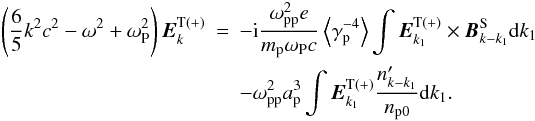$\begin{matrix} (\frac{6}{5} k^{2} c^{2} - ω^{2} + ω_{P}^{2}) E_{k}^{T (+)} & = & - i \frac{ω_{pp}^{2} e}{m_{p} ω_{P} c} ⟨ {γ_{p}^{-4}}^{⟩} \int E_{k_{1}}^{T (+)} \times B_{k - k_{1}}^{S} d k_{1} \end{matrix}$ $\begin{eqnarray} \left(\frac{6}{5}k^{2}c^{2}-\omega ^{2}+\omega _{\rm P}^{2}\right){{\vec E}}_{k}^{\rm T(+)} &=&-{\rm i} \frac{\omega _{\rm pp}^{2}e}{m_{\rm p}\omega _{\rm P}c}\left\langle {\gamma _{\rm p}^{-4}} \right\rangle \int {{{\vec E}}_{k_{1}}^{\rm T(+)}\times {{\vec B}}_{k-k_{1}}^{\rm S}{\rm d}k_{1}} \notag \\ &&-\omega _{\rm pp}^{2}a_{\rm p}^{3}\int {{{\vec E}}_{k_{1}}^{\rm T(+)}\frac{{n} _{k-k_{1}}^{\prime }}{n_{\rm p0}}{\rm d}k_{1}}. \label{eq40} \end{eqnarray}$ (40)

2.5. Nonlinear governing equation in coordinate space

For transverse plasmons near the frequency ω_P, the high-frequency electric field 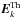$E_{k}^{Th}$ $\hbox{${{\vec E}}_{k}^{\rm Th} $}$ can be expressed as (Robinson 1997) 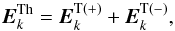$E_{k}^{Th} = E_{k}^{T (+)} + E_{k}^{T (-)},$ $\begin{equation} \label{eq41} {{\vec E}}_{k}^{\rm Th} = {{\vec E}}_{k}^{\rm T( + )} + {\rm {\vec E}}_{k}^{\rm T( - )}, \end{equation}$ (41)in which 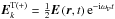$E_{k}^{T (+)} = \frac{1}{2} E {}^{(}{r,t}^{)} e^{- i ω_{P} t}$ $\hbox{${{\vec E}}_{k}^{\rm T( + )} = \frac{1}{2}{\vec E}\left( {{\vec r},t} \right){\rm e}^{ - {\rm i}\omega _{\rm P} {t}}$}$ , and $E_{k}^{T (-)} = \frac{1}{2} E {}^{(}{r,t}^{)}^{*} e^{i ω_{P} t}$ $\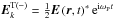hbox{${\rm {\vec E}}_{k}^{\rm T( - )} = \frac{1}{2}{{\vec E}}\left( {{\vec r},t} \right)^\ast {\rm e}^{{\rm i}\omega _{\rm P} {t}}$}$ , $E {}^{(}{r,t}^{)}$ $\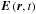hbox{${{\vec E}}\left( {{ {\vec r}},t} \right)$}$ varying very slowly compared with ω_P is the complex envelope for the high-frequency fields. Using the following Fourier transformations 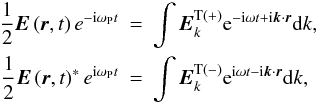$\begin{matrix} \frac{1}{2} E ({r,t}^{)} e^{- i ω_{P} t} & = & \int E_{k}^{T (+)} e^{- i ωt + i k \cdot r} d k, \\ \frac{1}{2} E {({r,t}^{)}}^{*} e^{i ω_{P} t} & = \end{matrix}$ $\begin{eqnarray} \frac{1}{2}{{\vec E}}\left( {{{\vec r}},t}\right) {e} ^{-{\rm i}\omega _{\rm P} {t}} &=&\int {{{\vec E}}_{k}^{\rm T(+)}{\rm e}^{-{\rm i}\omega t+{\rm i} {{\vec k}}\cdot {{\vec r}}}{\rm d}k}, \notag \\ \frac{1}{2}{{\vec E}}\left( {{{\vec r}},t}\right) ^{\ast }{ e}^{{\rm i}\omega _{\rm P} {t}} &=&\int {{{\vec E}}_{k}^{\rm T(-)}{\rm e}^{{\rm i}\omega {t}-{\rm i} {{\vec k}}\cdot {{\vec r}}}{\rm d}k}, \label{eq42} \end{eqnarray}$ (42)Equations (34), (40) and (14) can be transformed into coordinate space $\begin{matrix} \frac{\partial^{2}}{\partial t^{2}} \frac{n (r,t)}{n_{p 0}} = c^{2} a_{p}^{2} \nabla^{2} \frac{{| E (r,t) |}^{2}}{16 π n_{p 0} T_{e}}, \\ \frac{2 i}{ω_{P}} \frac{\partial}{∂t} E (r,t) - \frac{6}{5} \frac{c^{2}}{ω_{P}^{2}} \nabla \times \nabla \times E (r,t) \\ \frac{\partial}{∂t} B (r, t) = i \frac{3}{4} \frac{ec}{m_{p} a_{p} ω_{P}^{2}} Λ∇ \times \nabla \times [E (r,t) \times E^{*} (r,t)] . \end{matrix}$ $\begin{eqnarray} \label{eq43} &&\frac{\partial ^2}{\partial t^2}\frac{n({{\vec r}},t)}{n_{\rm p0} } = c^2a_{\rm p}^2 \nabla ^2\frac{\left| {{{\vec E}}({{\vec r}},t)} \right|^2}{16\pi n_{\rm p0} T_{\rm e} }, \\ &&\frac{2\rm i}{\omega _{\rm P}}\frac{\partial }{\partial t}{{\vec E}}( {{\vec r}},t)-\frac{6}{5}\frac{c^{2}}{\omega _{\rm P}^{2}}\nabla \times \nabla \times {{\vec E}}({{\vec r}},t) \notag \\ &&-{\rm i}\frac{3}{a_{\rm p}}\frac{e}{m_{\rm p}\omega _{\rm P}c}\left\langle {\gamma _{\rm p}^{-4}} \right\rangle {{\vec E}}({{\vec r}},t)\times { {\vec B}}({{\vec r}},t)-3a_{\rm p}^{2}{{\vec E}}({ {\vec r}},t)\frac{{n}^{\prime }({{\vec r}},t)}{n_{\rm p0}} =0,~~~~~~~~~~~~ \label{eq44} \\ \label{eq45} &&\frac{\partial }{\partial t}{{\vec B}}({{\vec r}}{,}t) = {\rm i} \frac{3}{4}\frac{ec}{m_{\rm p} a_{\rm p} \omega _{\rm P}^2 } \Lambda \nabla \times \nabla \times [{{\vec E}}({{\vec r}},t)\times {{\vec E}} ^\ast ({{\vec r}},t)]. \end{eqnarray}$ In deriving Eq. 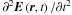(44), we have neglected the term $\partial^{2} E {}^{(}{r,t}^{)} / \partial t^{2}$ $\hbox{$\partial ^2{{\vec E}}\left( {{{\vec r}},t} \right) / \partial t^2$}$ when the slow change envelope 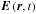$E {}^{(}{r,t}^{)}$ $\hbox{${{\vec E}}\left( {{{\vec r}} ,t} \right)$}$ satisfies the condition ∂ln|E(r,t)|/∂t ≪ ω_P. To obtain a real magnetic field with low-frequency, we have put ϕ = −π/2.

Introducing the following dimensionless parameters 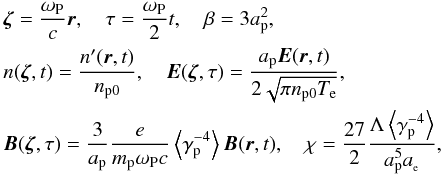$\begin{matrix} ζ = \frac{ω_{P}}{c} r, τ = \frac{ω_{P}}{2} t, β = 3 a_{p}^{2}, \\ n (ζ,t) = \frac{n^{'} (r,t)}{n_{p 0}}, E (ζ,τ) = \frac{a_{p} E (r,t)}{2 \sqrt{π n_{p 0} T_{e}}}, \\ B (ζ,τ) = \frac{3}{a_{p}} \frac{e}{m_{p} ω_{P} c} ⟨ {γ_{p}^{-4}}^{⟩} B (r,t), χ = \frac{27}{2} \frac{Λ ⟨ {γ_{p}^{-4}}^{⟩}}{a_{p}^{5} a_{e}}, \end{matrix}$ $\begin{eqnarray*} &&{{\vec \zeta }} =\frac{\omega _{\rm P}}{c}{{\vec r}},\quad \tau =\frac{\omega _{\rm P}}{2}t,\quad \beta =3a_{\rm p}^{2}, \\ && n({{\vec \zeta }},t) =\frac{{n}^{\prime }({{\vec r} },t)}{n_{\rm p0}},\quad {{\vec E}}({{\vec \zeta }},\tau )= \frac{a_{\rm p}{{\vec E}}({{\vec r}},t)}{2\sqrt{\pi n_{\rm p0}T_{\rm e} }}, \\ &&{{\vec B}}({{\vec \zeta }},\tau ) =\frac{3}{a_{\rm p}}\frac{e }{m_{\rm p}\omega _{\rm P}c}\left\langle {\gamma _{\rm p}^{-4}}\right\rangle { {\vec B}}({{\vec r}},t),\quad \chi =\frac{27}{2}\frac{\Lambda \left\langle {\gamma _{\rm p}^{-4}}\right\rangle }{a_{\rm p}^{5}a_{_{\rm e}}}, \end{eqnarray*}$ Equations (43), (44) and (45) can be transformed into $\begin{matrix} \frac{\partial^{2}}{\partial τ^{2}} n (ζ,τ) = \nabla^{2} {| E (ζ,τ) |}^{2}, \\ i \frac{\partial}{∂τ} E (ζ,τ) - \frac{6}{5} \nabla \times \nabla \times E (ζ,τ) - β E (ζ,τ) n (ζ,τ) \\ - i E (ζ,τ) \times B (ζ,τ) = 0, \\ \frac{\partial}{∂τ} B (ζ,τ) = i χ \nabla \times \nabla \times [E (ζ,τ) \times E^{*} (ζ,τ)] . \end{matrix}$ $\begin{eqnarray} \label{eq46} &&\frac{\partial ^2}{\partial \tau ^2}n({\rm {\bf \zeta }},\tau ) = \nabla ^2\left| {{{\vec E}}({\rm {\bf \zeta }},\tau )} \right|^2, \\ \label{eq47} &&{\rm i}\frac{\partial }{\partial \tau }{{\vec E}}({\rm {\bf \zeta }},\tau ) - \frac{6}{5} \nabla \times \nabla \times {\rm {\vec E}}({\rm {\bf \zeta }},\tau ) - \beta {{\vec E}}({\rm {\bf \zeta }},\tau )n({\rm {\bf \zeta }},\tau ) \nonumber\\ &&- {\rm i}{{\vec E}}({\rm {\bf \zeta }},\tau )\times {\vec B}({\rm {\bf \zeta }},\tau ) = 0, \\ \label{eq48} &&\frac{\partial }{\partial \tau }{\vec B}({\rm {\bf \zeta }},\tau ) = {\rm i}\chi \nabla \times \nabla \times [{\vec E}({\rm {\bf \zeta }},\tau )\times {{\vec E}}^\ast ({\rm {\bf \zeta }},\tau )]. \end{eqnarray}$ Indeed, Eqs. (46)–(48) are a set of equations that can describe the magnetic field generated by the transverse plasmons in non-isothermal ultra-relativistic EP plasmas. Equation (46) characterizes the density variation caused by the divergence of ponderomotive force on the right side of Eq. (46). And Eq. (48) describes the evolution of the slowly varying magnetic field, which is set up by beats of the high-frequency transverse plasmons; as was discussed, the term E(ζ,τ) × E^∗(ζ,τ) in (48) is the field “spin” (Thornhill & Haar 1978). The last term in the left-hand side of Eq. (47) describes the phase inhomogeneity via B(ζ,τ) and the third term represents the shift in plasma frequency caused by plasma density fluctuations.

We have followed the theory developed by Li & Ma (1993) in which the magnetic field is generated by transverse plasmons in non-relativistic regime. This theory had been generalized to the generation of magnetic field in plasmas containing ultra-relativistic electrons and non-relativistic ions (Li et al. 2008), and used to investigate the nonlinear behavior of transverse plasmons in isothermal ultra-relativistic EP plasmas (Liu & Liu 2011). If similar physical processes are taken into account, there are some similarities between the paper and those mentioned above. However, our work is different from the previous works in the following aspects:

1)
the special relativistic theory limits the particle speed to lessthan the speed of light, which allows us to calculate the integrals inthe interaction matrix for a fully relativistic regime by focusingour analysis on the large-scale superluminal waves; i.e.,kc ≪ ω, which is different from the papers mentioned above;
2)
the net nonlinear magnetization currents in the paper are determined by ultra-relativistic positrons, whereas in the works of Li & Ma (1993) and Li et al. (2008), it is dominantly produced by non-relativistic electrons and by non-relativistic ions, respectively. In the case of isothermal EP plasmas, there are no net nonlinear magnetization currents (Liu & Liu 2011).

3. Linear analysis for transverse perturbations

Now we examine the problem of the stability of monochromatic waves in the Liapunov sense in the framework of Eqs. (46)–(48). It is easily examined that the following form of plane wave, $E_{0} = E_{00} \exp [i (k_{0} \cdot ξ - ω_{0} τ)], B_{0} = 0, n_{0} = 0,$ $\begin{equation} \label{eq49} {{\vec E}}_0 = {{\vec E}}_{00} \exp \left[ {{\rm i}\left( {{{\vec k}}_0 \cdot {\rm {\bf \xi }} - \omega _0 \tau } \right)} \right], \quad {\vec B}_0 = 0, \quad n_0 = 0, \end{equation}$ (49)is a solution of Eqs. 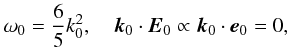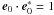(46)–(48), provided that $ω_{0} = \frac{6}{5} k_{0}^{2}, k_{0} \cdot E_{0} \propto k_{0} \cdot e_{0} = 0,$ $\begin{equation} \label{eq50} \omega _0 = \frac{6}{5} k_0^2 , \quad {{\vec k}}_0 \cdot {{\vec E}}_0 \propto {{\vec k}}_0 \cdot {{\vec e}}_0 = 0, \end{equation}$ (50)e₀ is a unit vector: $e_{0} \cdot e_{0}^{*} = 1$ $\hbox{${{\vec e}}_0 \cdot {{\vec e}}_0^\ast = 1$}$ .

To investigate the stability of the solution, we assume the presence of small perturbations (δE, δB, δn) to the solution, if the disturbance is amplified, then the solution is unstable in the Liapunov sense. Linearizing Eqs. (46)–(48) with respect to the perturbations yields $\begin{matrix} (δn)_{ττ} = \nabla^{2} [E_{0} \cdot δ E^{*} + E_{0}^{*} \cdot δ E], \\ i (δ E)_{τ} - \nabla \times \nabla \times δ E = βδn E_{0} + i E_{0} \times δ B, \\ (δ B)_{τ} = i χ \nabla \times \nabla \times [E_{0} \times δ E^{*} + δ E \times E_{0}^{*}] . \end{matrix}$ $\begin{eqnarray} \label{eq51} &&(\delta n )_{\tau \tau } = \nabla ^2[{{\vec E}}_{0} \cdot \delta {{\vec E}}^\ast + {{\vec E}}_{0}^\ast \cdot \delta {{\vec E}} ], \\ \label{eq52} &&{\rm i}(\delta {{\vec E}} )_\tau - \nabla \times \nabla \times \delta {{\vec E}} = \beta \delta n {{\vec E}}_{0} + {\rm i}{{\vec E}}_{0} \times \delta {\vec B}, \\ \label{eq53} &&(\delta {\vec B} )_\tau = {\rm i}\chi \nabla \times \nabla \times [{{\vec E}}_{0} \times \delta {{\vec E}}^\ast + \delta {{\vec E}} \times {{\vec E}}_{0}^\ast ]. \end{eqnarray}$ We study the following forms of the transverse perturbations: $\begin{matrix} δn & = & \frac{1}{2} n {\exp [i (k \cdot ξ - ωτ)] + \exp [- i (k \cdot ξ - ωτ)]}, \\ δ B & = & \frac{1}{2} B {\exp [i (k \cdot ξ - ωτ)] + \exp [- i (k \cdot ξ - ωτ)]}, \\ δ E & = & {E \exp [i (k \cdot ξ - ωτ)] + E^{+} \exp [- i (k \cdot ξ - ωτ)]} \end{matrix}$ $\begin{eqnarray} \label{eq54} \delta n &=& \frac{1}{2}n\left\{ {\exp [{\rm i}({{\vec k}} \cdot {\rm {\bf \xi }} - \omega \tau )] + \exp [ - {\rm i}({{\vec k}} \cdot {\rm {\bf \xi }} - \omega \tau )]} \right\}, \\ \label{eq55} \delta {\vec B} &=& \frac{1}{2}{\vec B}\left\{ {\exp [{\rm i}({{\vec k}} \cdot {\rm {\bf \xi }} - \omega \tau )] + \exp [ - {\rm i}({{\vec k}} \cdot {\rm {\bf \xi }} - \omega \tau )]} \right\}, \\ \delta {{\vec E}} &=&\left\{ {{{\vec E}}\exp [{\rm i}({ {\vec k}}\cdot {{\vec \xi }}-\omega \tau )]+{{\vec E}} ^{+}\exp [-{\rm i}({{\vec k}}\cdot {{\vec \xi }}-\omega \tau )]} \right\} \notag \\ &&\quad\times \exp [{\rm i}({{\vec k}}_{0}\cdot {{\vec \xi }}-\omega _{0}\tau )], \label{eq56} \end{eqnarray}$ where E, E⁺ are transverse perturbations: $E = E e_{1}, E^{+} = E^{*} e_{2}^{+}, e_{1} ⊥ (k + k_{0}), e_{2}^{+} ⊥ (k - k_{0}),$ $\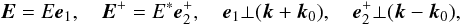begin{equation} \label{eq57} {{\vec E}} = E{{\vec e}}_1, \quad {{\vec E}}^ + = E^\ast {{\vec e}}_2^ +, \quad {{\vec e}}_1 \bot ({\rm {\vec k}} + {{\vec k}}_0 ), \quad {{\vec e}}_2^ + \bot ({\rm {\vec k}} - {{\vec k}}_0 ), \end{equation}$ (57)where e₁, 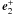$e_{2}^{+}$ $\hbox{${{\vec e}}_2^ + $}$ are real unit vectors.

Substituting Eqs. (49), (50), (54) and (56) into Eq. (51) yields $\frac{n}{2} ω^{2} = k^{2} [E (e_{2}^{+} \cdot E_{00}) + E (e_{1} \cdot E_{00}^{*})] .$ $\begin{equation} \label{eq58} \frac{n}{2}\omega ^2 = k^2[E({{\vec e}}_2^ + \cdot {{\vec E}}_{00} ) + E({{\vec e}}_1 \cdot {\vec E}_{00}^\ast )]. \end{equation}$ (58)Similarly, we obtain from Eq. 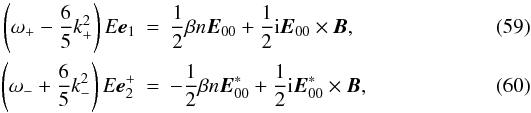(52), $\begin{matrix} (ω_{+} - \frac{6}{5} k_{+}^{2}) E e_{1} & = & \frac{1}{2} βn E_{00} + \frac{1}{2} i E_{00} \times B, \\ (ω_{-} + \frac{6}{5} k_{-}^{2}) E e_{2}^{+} & = & - \frac{1}{2} βn E_{00}^{*} + \frac{1}{2} {i E}_{00}^{*} \times B, \end{matrix}$ $\begin{eqnarray} \label{eq59} \left(\omega _ + - \frac{6}{5}k_ + ^2 \right)E{{\vec e}}_1 &=& \frac{1}{2}\beta n{{\vec E}}_{00} + \frac{1}{2} {\rm i}{\vec E}_{00} \times {\vec B}, \\ \label{eq60} \left(\omega _ - + \frac{6}{5} k_ - ^2 \right)E{{\vec e}}_2^ + &=& - \frac{1}{2}\beta n{{\vec E}}_{00}^\ast + \frac{1}{2}{\rm i {\vec E}}_{00}^\ast \times {\vec B}, \end{eqnarray}$ where $ω_{\pm} = ω \pm ω_{0}, k_{\pm} = k \pm k_{0} .$ $\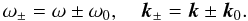begin{equation} \label{eq61} \omega _\pm = \omega \pm \omega _0, \quad {\vec k}_\pm = {{\vec k}}\pm {{\vec k}}_0. \end{equation}$ (61)Combining Eqs. (58)–(61), one can obtain $n [ω^{2} - \frac{\frac{12}{5} β k^{4} {| E_{00} |}^{2}}{(ω - \frac{12}{5} k \cdot k_{0})^{2} - \frac{36}{25} k^{4}}] = - i \frac{\frac{12}{5} k^{4} B \cdot (E_{00} \times E_{00}^{*})}{(ω - \frac{12}{5} k \cdot k_{0})^{2} - \frac{36}{25} k^{4}} \cdot$ $\begin{equation} \label{eq63} n\left[ {\omega ^2 - \frac{\frac{12}{5}\beta k^4\left| {{{\vec E}}_{00} } \right|^2}{(\omega - \frac{12}{5}{{\vec k}} \cdot {{\vec k}}_0 )^2 -\frac{36}{25} k^4}} \right] = - {\rm i}\frac{\frac{12}{5}k^4{\vec B} \cdot ({{\vec E}}_{00} \times {{\vec E}}_{00}^\ast )}{(\omega - \frac{12}{5}{{\vec k}} \cdot {{\vec k}}_0 )^2 -\frac{36}{25} k^4}\cdot \end{equation}$ (62)From Eq. (53), we easily arrive at $\begin{matrix} ω B & = & 2 χ k^{2} E E_{00} [(e_{2}^{+} \times e_{0}) - \frac{E_{00}^{*}}{E_{00}} (e_{1} \times e_{0}^{*}) \end{matrix}$ $\begin{eqnarray} \omega {{\vec B}} &=&2\chi k^{2}EE_{00}\left[ {({{\vec e}} _{2}^{+}\times {{\vec e}}_{0})-\frac{E_{00}^{\ast }}{E_{00}}({ {\vec e}}_{1}\times {{\vec e}}_{0}^{\ast })}\right. \notag \\ &&\left. {+\frac{E_{00}^{\ast }}{E_{00}}{{\vec e}}_{{{k} }}{{\vec e}}_{{k}}\cdot ({{\vec e}} _{1}\times {{\vec e}}_{0}^{\ast })-{{\vec e}}_{{ {k}}}{{\vec e}}_{{k}}\cdot ({{\vec e }}_{2}^{+}\times {{\vec e}}_{0})}\right]. \label{eq64} \end{eqnarray}$ (63)Doting the both sides of Eq. 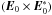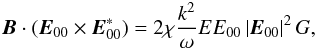(63) with $(E_{0} \times E_{0}^{*})$ $\hbox{$({\vec E}_0 \times {{\vec E}}_0^\ast )$}$ yields $B \cdot (E_{00} \times E_{00}^{*}) = 2 χ \frac{k^{2}}{ω} E E_{00} {| E_{00} |}^{2} G,$ $\begin{equation} \label{eq66} {\vec B} \cdot ({{\vec E}}_{00} \times {\rm {\vec E}}_{00}^\ast ) = 2\chi \frac{k^2}{\omega }EE_{00} \left| {{\rm {\vec E}}_{00} } \right|^2G, \end{equation}$ (64)where $\begin{matrix} G & = & [(e_{2}^{+} \cdot e_{0}) - (e_{2}^{+} \cdot e_{0}^{*}) (e_{0} \cdot e_{0})] \\ - \frac{E_{00}^{*}}{E_{00}} [(e_{1} \cdot e_{0}) (e_{0}^{*} \cdot e_{0}^{*}) - (e_{1} \cdot e_{0}^{*})] \\ + \frac{E_{00}^{*}}{E_{00}} [e_{k} \cdot (e_{0} \times e_{0}^{*})] [e_{k} \cdot (e_{1} \times e_{0}^{*})] \end{matrix}$ $\begin{eqnarray} G &=&[({{\vec e}}_{2}^{+}\cdot {{\vec e}}_{0})-({ {\vec e}}_{2}^{+}\cdot {{\vec e}}_{0}^{\ast })({{\vec e}} _{0}\cdot {{\vec e}}_{0})] \notag \\ &&-\frac{E_{00}^{\ast }}{E_{00}}[({{\vec e}}_{1}\cdot {{\vec e}}_{0})({{\vec e}}_{0}^{\ast }\cdot {{\vec e}}_{0}^{\ast })-({{\vec e}}_{1}\cdot {{\vec e}}_{0}^{\ast })] \notag \\ &&+\frac{E_{00}^{\ast }}{E_{00}}[{{\vec e}}_{{k} }\cdot ({{\vec e}}_{0}\times {{\vec e}}_{0}^{\ast })][ {{\vec e}}_{{k}}\cdot ({{\vec e}} _{1}\times {{\vec e}}_{0}^{\ast })] \notag \\ &&-[{{\vec e}}_{{k}}\cdot ({{\vec e}} _{0}\times {{\vec e}}_{0}^{\ast })][{{\vec e}}_{{ {\vec k}}}\cdot ({{\vec e}}_{2}^{+}\times {{\vec e}} _{0})]. 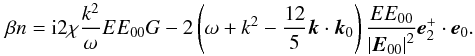\label{eq67} \end{eqnarray}$ (65)Equations (60) and (64) yield $βn = i 2 χ \frac{k^{2}}{ω} E E_{00} G - 2 (ω + k^{2} - \frac{12}{5} k \cdot k_{0}) \frac{E E_{00}}{{| E_{00} |}^{2}} e_{2}^{+} \cdot e_{0} .$ $\begin{equation} \label{eq68} \beta n = {\rm i}2\chi \frac{k^2}{\omega }EE_{00} G - 2\left(\omega + k^2 - \frac{12}{5}{{\vec k}} \cdot {{\vec k}}_0 \right)\frac{EE_{00} }{\left| {{{\vec E}}_{00} } \right|^2}{\vec e}_2^ + \cdot {{\vec e}}_0. \end{equation}$ (66)Therefore, the following dispersion relation $\begin{matrix} [(ω + k^{2} - \frac{12}{5} k \cdot k_{0}) e_{2}^{+} \cdot e_{0} - i χ {| E_{00} |}^{2} G \frac{k^{2}}{ω}] \\ \times [ω^{2} - \frac{\frac{12}{5} β k^{4} {| E_{00} |}^{2}}{(ω - \frac{12}{5} k \cdot k_{0})^{2} - \frac{36}{25} k^{4}}] = \end{matrix}$ $\begin{eqnarray} &&\left[ {\left(\omega +k^{2}-\frac{12}{5}{{\vec k}}\cdot {{\vec k}}_{0}\right) {{\vec e}}_{2}^{+}\cdot {{\vec e}}_{0}-{\rm i}\chi \left\vert { {{\vec E}}_{00}}\right\vert ^{2}G\frac{k^{2}}{\omega }}\right] \nonumber \\ &&\times\left[ {\omega ^{2}-\frac{\frac{12}{5}\beta k^{4}\left\vert {{{\vec E}}_{00}} \right\vert ^{2}}{(\omega -\frac{12}{5}{{\vec k}}\cdot {{\vec k}} _{0})^{2}-\frac{36}{25}k^{4}}}\right] =\nonumber\\ &&\hspace*{3mm}{\rm i}\frac{\frac{12}{5}\chi \beta \left\vert {{{\vec E }}_{00}}\right\vert ^{4}G}{(\omega -\frac{12}{5}{{\vec k}}\cdot {{\vec k}}_{0})^{2}-\frac{36}{25}k^{4}}\frac{k^{6}}{\omega } \label{eq69} \end{eqnarray}$ (67)can be obtained from Eqs. (62), (64) and (66). The dispersion Eq. (67) is quite complicated in general. For the purpose of obtaining a simple analytical result, we assume e₀ is a real vector. Now, the dispersion Eq. 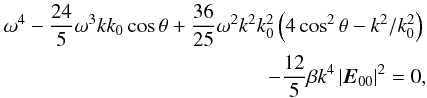(67) is reduced to $\begin{matrix} ω^{4} - \frac{24}{5} ω^{3} k k_{0} \cos θ + \frac{36}{25} ω^{2} k^{2} k_{0}^{2} ({4 \cos^{2} θ - k^{2} / k_{0}^{2}}^{)} \\ - \frac{12}{5} β k^{4} {| E_{00} |}^{2} = 0, \end{matrix}$ $\begin{eqnarray} \label{eq70} \omega ^4 - \frac{24}{5}\omega ^3kk_0 \cos \theta +\frac{36}{25} \omega ^2k^2k_0^2 \left( {4\cos ^2\theta - k^2 / k_0^2 } \right) \notag \\ - \frac{12}{5}\beta k^4\left| {{\vec E}_{00} } \right|^2 = 0, \end{eqnarray}$ (68)where θ is the angle between k and k₀. If one takes θ = π/2, the above equation can be written as 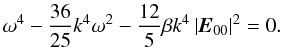$ω^{4} - \frac{36}{25} k^{4} ω^{2} - \frac{12}{5} β k^{4} {| E_{00} |}^{2} = 0.$ $\begin{equation} \label{eq71} \omega ^4 - \frac{36}{25}k^4\omega ^2 - \frac{12}{5}\beta k^4\left| {{{\vec E}}_{00} } \right|^2 = 0. \end{equation}$ (69)The roots of Eq. (69) are $ω^{2} = \frac{18}{25} k^{4} [1 \pm \sqrt{1 + \frac{250}{54} β {| E_{00} |}^{2} / k^{4}}] .$ $\begin{equation} \label{eq72} \omega ^2 =\frac{18}{25}k^4\left[ {1\pm \sqrt {1 + \frac{250}{54}\beta \left| {{{\vec E}}_{00} } \right|^2 / k^4} } \right]. \end{equation}$ (70)Obviously, Eq. (70) has imaginary roots, i.e., there will be instability. From Eq. (70) we obtain the instability growth rate, Γ = Im(ω), $Γ^{2} = \frac{18}{25} k^{4} [\sqrt{1 + \frac{250}{54} β {| E_{00} |}^{2} / k^{4}} - 1] .$ $\begin{equation} \label{eq73} \Gamma ^2 = \frac{18}{25}k^4\left[ {\sqrt {1 + \frac{250}{54}\beta \left| {{{\vec E}}_{00} } \right|^2 / k^4}-1 } \right]. \end{equation}$ (71)From above analysis, one can conclude that the spontaneous magnetic field is modulationally unstable. Naturally, the mode with the highest growth rate, Γ_max, dominates and sets the characteristic length scale of the magnetic field fluctuations, x_c ~ 1/k_max, k_max is the wave number at which the maximum growth rate occurs. The ultrarelativistic expressions for Γ_max and k_max are given by Eq. (67). The dispersion Eq. (67) is so complicated that numerical calculation is the only way to obtain a general knowledge of the growth rate and characteristic scale of self-generated magnetic field.

Fig. 1

Growth rate with respect to the wave number calculated from Eq. (68). The different lines in each figure correspond to different θ. a) W₀ = 0.1,a_p = 0.05, b) W₀ = 0.1,a_p = 0.02, c) W₀ = 0.1,a_p = 0.01, d) W₀ = 0.01,a_p = 0.05, e) W₀ = 0.001,a_p = 0.05.

During numerical calculation we find that the maximum growth rate and the corresponding k_max obtained from Eq. (67) are weakly depended on a_e, and the results are similar to that calculated from Eq. (68). It means the terms containing χ in Eq. (67) are negligible. In the following, the dispersion curves for different values of a_p and 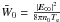$W̅_{0} = \frac{{| E_{00} |}^{2}}{8 π n_{0} T_{e}}$ $\hbox{$\bar {W}_0=\frac{\left| {{{\vec E}}_{00}} \right|^2}{8\pi n_{0} T_{\rm e} } $}$ are presented in accordance with Eq. (68). Figure 1 shows the growth rate of modulation instability with respect to k for k₀ = 0.05 and θ varies from 0 to π. Figures 1a–c are calculated at a_p = 0.05, 0.02 and 0.01, respectively, in which 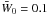$\hbox{$\bar {W}_0 = 0.1$}$ . Figures 1d, and e are calculated at 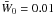$\hbox{$\bar {W}_0 = 0.01$}$ and 0.001, respectively, in which a_p = 0.05. The maximum growth rate and corresponding characteristic scale in units of ω_P/2 and c/ω_P are 4.4 × 10^-3 and 7.2 for Fig. 1a, 1.1 × 10^-3 and 9.5 for Fig. 1b, 4.3 × 10^-4 and 9.8 for Fig. 1c, 1.8 × 10^-3 and 9.0 for Fig. 1d, and 8.0 × 10^-4 and 9.7 for Fig. 1e.

With increasing positrons temperature, the scale of the magnetic field will increase, and the growth rate will decrease, as can be seen from Figs. 1a–c. In contrast, increasing the amplitude of the wave field results in the decrease of the magnetic field scale and an increase of the growth rate. Therefore, one can conclude that strong turbulence fields favor of the generation of strong localized magnetic field. The modulation instability and the growth rate should be determined by the temperature difference of electrons and positrons, whereas the assumption of T_e ≫ T_p leads them to weakly depend on the electron temperature. If the difference of temperature is finite, the effects of electrons on the nonlinear currents should be taken into consideration.

4. Discussions and conclusions

The modulation interaction between the transverse plasmons and the low-frequency density fluctuation will lead the wave field collapse into a localized rarified region where the strong wave field is trapped. In the density caviton there will be a strong highly intermittent magnetic field, which can be inferred from Eq. (48). Regarding this, we seek a self-similar collapse solution for the nonlinear self-generated magnetic field within the framework of Eqs. (46)–(48). Assuming the characteristic time-space scales of n, E and B to be τ and ζ, then from Eqs. (46) and (48) one has 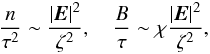$\frac{n}{τ^{2}} ~ \frac{| E |^{2}}{ζ^{2}}, \frac{B}{τ} ~ χ \frac{| E |^{2}}{ζ^{2}},$ $\begin{equation} \label{eq74} \frac{n}{\tau ^2} \sim \frac{\vert {{\vec E}}\vert ^2}{\zeta ^2}, \quad \frac{B}{\tau } \sim \chi \frac{\vert {\vec E}\vert ^2}{\zeta ^2}, \end{equation}$ (72)where τ′ = τ₀ − τ, τ₀ corresponds to the final state of collapse, as mentioned above, the perturbed fields become too strong for the condition of Eq. (2) to be valid.

Using Eq. (72), the order of magnitudes of the terms in Eq. (47) can be read as 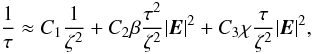$\frac{1}{τ} \approx C_{1} \frac{1}{ζ^{2}} + C_{2} β \frac{τ^{2}}{ζ^{2}} | E |^{2} + C_{3} χ \frac{τ}{ζ^{2}} | E |^{2},$ $\begin{equation} \label{eq75} \frac{1}{\tau } \approx C_1 \frac{1}{\zeta ^2} + C_2 \beta \frac{\tau ^2}{\zeta ^2}\vert {{\vec E}}\vert ^2 + C_3 \chi \frac{\tau }{\zeta ^2}\vert {{\vec E}}\vert ^2, \end{equation}$ (73)where C₁, C₂ and C₃ are constants on the order of unity. One can readily derive 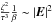$\frac{ζ^{2}}{τ^{3}} \frac{1}{β} ~ | E |^{2}$ $\hbox{$ \frac{\zeta ^2}{\tau ^3}\frac{1}{\beta } \sim \vert {{\vec E}}\vert ^2$}$ , provided that the first term and the last term in the right-hand side of Eq. (73) are balanced, which implies 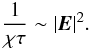$\frac{1}{χτ} ~ | E |^{2} .$ $\begin{equation} \label{eq76} \frac{1}{\chi \tau } \sim \vert {{\vec E}}\vert ^2. \end{equation}$ (74)Therefore, there is 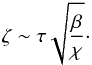$ζ ~ τ \sqrt{\frac{β}{χ}} \cdot$ $\begin{equation} \label{eq77} \zeta \sim \tau \sqrt {\frac{\beta }{\chi }} \cdot \end{equation}$ (75)From the Eq. (47), one can obtain $\begin{matrix} i \frac{\partial}{∂τ} {| E (ζ,τ) |}^{2} + \frac{6}{5} \nabla \cdot [(\nabla \times E^{*} (ζ,τ)) \times E (ζ,τ) \\ - (\nabla \times E (ζ,τ)) \times E^{*} (ζ,τ)] = 0. \end{matrix}$ $\begin{eqnarray} &{\rm i}\frac{\partial }{\partial \tau }\left\vert {{{\vec E}}({ {\vec \zeta }},\tau )}\right\vert ^{2}+\frac{6 }{5 }\nabla \cdot \left[ {\left( {\nabla \times {{\vec E}}^{\ast }({{\vec \zeta }},\tau )}\right) \times {{\vec E}}({{\vec \zeta }},\tau )}\right. \notag \\ &\left. {-\left( {\nabla \times {{\vec E}}({{\vec \zeta }} ,\tau )}\right) \times {{\vec E}}^{\ast }({{\vec \zeta }} ,\tau )}\right] =0. 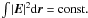\label{eq78} \end{eqnarray}$ (76)Integrating the above equation over all space yields the conservation of the plasmon number ${}^{\int}{| E |}^{2} d r = const .$ $\hbox{$ \int {\left| {{\vec E}} \right|} ^2\mbox{d}{\vec r} = \mbox{const}.$}$ Generally, the modulational instability will lead to an anisotropic collapse of the magnetic field, resulting in an pancake-like structure with a scale ζ and radius R (R ≫ ζ). This leads to 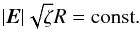$| E | \sqrt{ζ} R = const .$ $\begin{equation} \label{eq79} \vert {{\vec E}}\vert \sqrt \zeta R = \mbox{const.} \end{equation}$ (77)We try to find a solution in the form 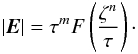$| E | = τ^{m} F (\frac{ζ^{n}}{τ}) \cdot$ $\begin{equation} \label{eq80} \vert {{\vec E}}\vert = \tau ^m {F}\left( {\frac{\zeta ^n}{\tau }} \right)\cdot \end{equation}$ (78)Then, Eqs. (74) and (77) become 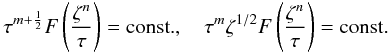$τ^{m + \frac{1}{2}} F (\frac{ζ^{n}}{τ}) = const ., τ^{m} ζ^{1 / 2} F (\frac{ζ^{n}}{τ}) = const .$ $\begin{equation} \label{eq81} \tau ^{m + \frac{1}{2}}{F}\left( {\frac{\zeta ^n}{\tau }} \right) = \mbox{const.}, \quad \tau ^m\zeta ^{1 / 2}{F}\left( {\frac{\zeta ^n}{\tau }} \right) = \mbox{const.} \end{equation}$ (79)Taking account of the Eq. (74), one derives 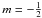$m = - \frac{1}{2}$ $\hbox{$m = - \frac{1}{2}$}$ and n = 1. Thus, a self-similar collapse solution can be asymptotically shown as 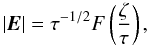$| E | = τ^{- 1 / 2} F (\frac{ζ}{τ}),$ $\begin{equation} \label{eq82} \vert {{\vec E}}\vert = \tau ^{ - 1 / 2}F\left( {\frac{\zeta }{\tau }} \right), \end{equation}$ (80)with R ~ const. Here, F is a function determined by the initial conditions. Assuming ζ_f is the scale to stop the collapse, the maximum growth rate 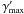$γ_{\max}^{'}$ $\hbox{${\gamma }'_{\max } $}$ by the nonlinear collapse motion could be obtained from the self-similar Eq. (80) as 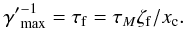${γ^{'}}_{\max}^{-1} = τ_{f} = τ_{M} ζ_{f} / x_{c} .$ $\begin{equation} \label{eq83} {\gamma '}_{\max }^{ - 1} = \tau _{\rm f} = \tau _M \zeta _{\rm f} / x_{\rm c}. \end{equation}$ (81)There is evidence that the nonlinear collapse growth rate is always higher than that of the linear instability (Li & Ma 1993; Li et al. 2008), which results in ζ_f < x_c.

The magnitude of the magnetic field in dimensionless form can be estimated from Eq. (48) as 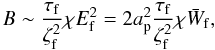$B ~ \frac{τ_{f}}{ζ_{f}^{2}} χ E_{f}^{2} = 2 a_{p}^{2} \frac{τ_{f}}{ζ_{f}^{2}} χ W̅ f,$ $\begin{equation} \label{eq84} B \sim \frac{\tau _{\rm f} }{\zeta_{\rm f}^2 }\chi E_{\rm f}^2 = 2a_{\rm p}^2 \frac{\tau _{\rm f} }{\zeta_{\rm f}^2 }\chi \bar {W}_{\rm f}, \end{equation}$ (82)where 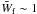$\hbox{$\bar {W}_{\rm f} \sim 1 $}$ is the wave density in the final state. In dimensional units, 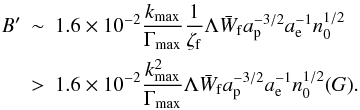$\begin{matrix} B^{'} & ~ & 1.6 \times 10^{-2} \frac{k_{\max}}{Γ_{\max}} \frac{1}{ζ_{f}} Λ W̅ f a_{p}^{- 3 / 2} a_{e}^{-1} n_{0}^{1 / 2} \\ > \end{matrix}$ $\begin{eqnarray} {B}^{\prime } &\sim &1.6\times 10^{-2}\frac{k_{\max }}{\Gamma _{\max }}\frac{ 1}{\zeta _{\rm f}}\Lambda \bar{W}_{\rm f}a_{\rm p}^{-3/2}a_{\rm e}^{-1}n_{0}^{1/2} \notag \\ &>&1.6\times 10^{-2}\frac{k_{\max }^{2}}{\Gamma _{\max }}\Lambda \bar{W} _{\rm f}a_{\rm p}^{-3/2}a_{\rm e}^{-1}n_{0}^{1/2}(G). \label{eq85} \end{eqnarray}$ (83)For the magnetic field in the internal shock region of GRB, one may take the characteristic Lorentz factor for electrons to be 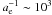$a_{e}^{-1} ~ 10^{3}$ $\hbox{$a_{\rm e}^{ - 1} \sim 10^3$}$ , and the particle density for electrons and positrons n₀ ~ 3 × 10¹⁰ cm^-3 (Medvedev & Loeb 1999). Assuming 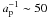$a_{p}^{-1} ~ 50$ $\hbox{$a_{\rm p}^{ - 1} \sim 50$}$ and the initial wave density 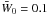$\hbox{$\bar {W}_0 = 0.1$}$ , the dimensionless maximum growth rate and the corresponding wave number from Fig. 1b are Γ_max = 1.1 × 10^-3 and k_max = 0.105, respectively. The dimensional growth rate of the spontaneous magnetic field is 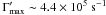$Γ_{\max}^{'} ~ 4.4 \times 10^{5} s^{-1}$ $\hbox{${\Gamma }'_{\max } \sim 4.4 \times 10^5~\mbox{s}^{ - 1}$}$ . The characteristic e-folding time for the field (~10^-6 s) is much shorter than the duration parameter T90, which is the time over which a burst emits from 5% of its total measured counts to 95%. This means that the self-generated magnetic field can be assumed to be invariant with time during T90. In addition, the characteristic scale of the magnetic field is x_c ~ 3.6 × 10² cm. Taking the final wave density in a localized region to be 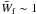$\hbox{$\bar {W}_{\rm f} \sim 1$}$ , the magnitude of this magnetic field is probably higher than 10⁴ G. Our results are consistent with the prediction made by Deng et al. (2005). In their model, gamma-ray burst spectra can be explained by the synchro-curvature mechanism with the curvature and the strength of magnetic field to be ~100 cm and 10⁴ G respectively. In conclusion, we have investigated the nonlinear evolution of EM turbulence with frequency ω ≈ ω_P in the non-isothermal ultra-relativistic EP plasma from a kinetic way. We revealed that the coupling of transverse plasmons, low-frequency density perturbation, and spontaneous magnetic field that arise from the nonlinear wave-wave and wave-particle interactions can be self-consistently described by Eqs. (46)–(48). The linear stability analysis showed that the transverse perturbation is modulation-unstable, which will lead the magnetic field to grow and form spatially highly intermittent magnetic fluxes. The instability, weakly depending on the spontaneous magnetic field, is dominantly caused by the modulation interaction between the transverse plasmons and the low-frequency density perturbation. Our numerical results imply that the growth rate of the instability and the characteristic scale of the magnetic field are determined by the field intensity and the effective temperature of the positrons. The characteristic scale is much larger than that of the Weibel instability, which is on the order of the collisionless skin depth. The Landau damping of the field will be much weaker than that of the field generated by Weibel instability, which is conducive to the generation of the long-life small-scale magnetic fields in the internal shock region of GRBs. The results we obtained can give a plausible explanation for the origin of the long-term small-scale magnetic field needed to explain the prompt GMBs spectrum. We focused on the generation of the small-scale magnetic field in the region of the internal shock of GRBs by transverse plasmons. The macro-equipartition parameters and the macro-energy transfer, including energy dissipation along the GRB jet and the temporal variability observed in GRBs, are beyond the main purpose of our manuscript, and we will investigate these significant problems in future. It is worth noting that our model is based on the different temperature of electrons and the positrons; this point needs an additional confirmation from observations.

Acknowledgments

The project was supported by the International S&T Cooperation Program of China (2009DFA02320), Program for Innovative Research Team in Jiangxi Province (2010DQB00900), the National Basic Research Program of China (973 Program) (No. 2010CB635112) and National Natural Science Foundation of China under grant No. 11178002.

References

Chang, P., Spitkovsky, A., & Arons, J. 2008, ApJ, 674, 378 [Google Scholar]
Cohen, E. J., Katz, I., Piran, T., et al. 1997, ApJ, 488, 330 [NASA ADS] [CrossRef] [Google Scholar]
Deng, X. L., Xia, T. S., & Liu, J. 2005, A&A, 443, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ghisellini, G., Celotti, A., & Lazzati, D. 2000, MNRAS, 313, L1 [NASA ADS] [CrossRef] [Google Scholar]
Gruzinov, A. 2001, ApJ, 563, L15 [NASA ADS] [CrossRef] [Google Scholar]
Jüttner, F. 1911, Ann. der Phys., 34, 856 [Google Scholar]
Kaplan, S. A., & Tsytovich, V. N. 1973, Plasma Astrophysics (London: Pergamon Press) [Google Scholar]
Karpman, V. I., Norman, C. A., ter Haar, D., & Tsytovich, V. N. 1975, Phys. Scripta, 11, 271 [Google Scholar]
Katz, B., Keshet, U., & Waxman, E. 2007, ApJ, 655, 375 [NASA ADS] [CrossRef] [Google Scholar]
Li, X. Q., & Ma, Y. H. 1993, A&A, 270, 534 [NASA ADS] [Google Scholar]
Li, X. Q., Liu, S. Q., & Tao, X. Y. 2008, Contrib. Plasma Phys., 48, 361 [NASA ADS] [CrossRef] [Google Scholar]
Liang, E. P. 1982, Nature, 299, 321 [NASA ADS] [CrossRef] [Google Scholar]
Lifshitz, E. N., & Pitaevskii, L. P. 1981, Physical Kinetics (Oxford: Pergamon Press) [Google Scholar]
Liu, Y., & Liu, S. Q. 2011, Contrib. Plasma Phys., 51, 698 [NASA ADS] [CrossRef] [Google Scholar]
Liu, X. L., Liu, S. Q., & Yang, X. S. 2008, Phys. Plasmas, 15, 032302 [NASA ADS] [CrossRef] [Google Scholar]
Mao, J., & Wang, J. 2011, ApJ, 731, 26 [NASA ADS] [CrossRef] [Google Scholar]
Medvedev, M. V. 2000, ApJ, 540, 704 [NASA ADS] [CrossRef] [Google Scholar]
Medvedev, M. V. 2006, ApJ, 637, 869 [NASA ADS] [CrossRef] [Google Scholar]
Medvedev, M. V., & Loeb, A. 1999, ApJ, 526, 697 [NASA ADS] [CrossRef] [Google Scholar]
Medvedev, M. V., Fiore, M., Fonseca, R. A., Silva, L. O., & Mori, W. B. 2005, ApJ, 618, L75 [NASA ADS] [CrossRef] [Google Scholar]
Mikhailovskii, A. B. 1980, Plasma Phys., 22, 133 [NASA ADS] [CrossRef] [Google Scholar]
Morsony, B. J., Workman, J. C., Lazzati, D., & Medvedev, M. V. 2009, MNRAS, 392, 1397 [NASA ADS] [CrossRef] [Google Scholar]
O’Neil, T. M., & Coroniti, F. V. 1999, Rev. Mod. Phys., 71, S404 [CrossRef] [Google Scholar]
Pe’er, A., & Zhang, B. 2006, ApJ, 653, 454 [NASA ADS] [CrossRef] [Google Scholar]
Pulupa, M. P., Bale, S. D., & Kasper, J. C. 2010, J. Geophys. Res., 115, A04106 [NASA ADS] [Google Scholar]
Robinson, P. A. 1997, Rev. Mod. Phys., 69, 507 [NASA ADS] [CrossRef] [Google Scholar]
Silva, L. O., Fonseca, R. A., Tonge, J. W., et al. 2003, ApJ, 596, L121 [Google Scholar]
Thornhill, S. G., & Ter Haar, D. 1978, Phys. Rep., 43, 43 [NASA ADS] [CrossRef] [Google Scholar]
Tkaczyk, W. 1993 Unthermalized Plasma in Phebus and BATSE Gamma Ray Bursts Sources. 23rd International Cosmic Ray Conference, 1, eds. D. A. Leahy, R. B. Hickws, & D. Venkatesan (Singapore: World Scientific), 124 [Google Scholar]
Tsytovich, V. N. 1977, Theory of turbulent plasma (New York: Consultants Bureau) [Google Scholar]
Workman, J. C., Morsony, B. J., Lazzati, D., & Medvedev, M. V. 2008, MNRAS, 386, 199 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Calculation of the matrix 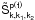${S_{k, k_{1}, k_{2}}^{p (t)}}_{˜}$ $\hbox{$\mathsf{\tilde {S}_{k,k_1 ,k_2}^{p\left( {t} \right)}}$}$

Expanding the differentiation in close brackets of Eq. (11), one can obtain 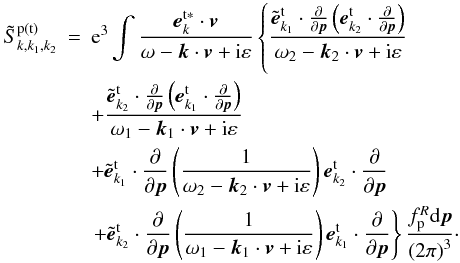$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} & = & e^{3} \int \frac{e_{k}^{t *} \cdot v}{ω - k \cdot v + i ε} {\frac{{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot \frac{\partial}{\partial p} (e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p})}{ω_{2} - k_{2} \cdot v + i ε} \\ + \frac{{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{2}}^{t} \cdot \frac{\partial}{\partial p} (e_{k_{1}}^{t} \cdot \frac{\partial}{\partial p})}{ω_{1} - k_{1} \cdot v + i ε} \\ + {\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot \frac{\partial}{\partial p} (\frac{1}{ω_{2} - k_{2} \cdot v + i ε}) e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p} \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( t\right) } &=&{\rm e}^{3}\int {\frac{{ {\vec e}}_{k}^{\rm t\ast }\cdot {{\vec v}}}{\omega -{{\vec k} }\cdot {{\vec v}}+{\rm i}\varepsilon }\left\{ {\frac{{\tilde{ {\vec e}}}_{{k}_{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}\left( {{{\vec e}}_{{k} _{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) }{ \omega _{2}-{{\vec k}}_{2}\cdot {{\vec v}}+{\rm i}\varepsilon }} \right. } \notag \\ &&{+\frac{{\tilde{{\vec e}}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}\left( {{{\vec e}}_{ {k}_{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p }}}}\right) }{\omega _{1}-{{\vec k}}_{1}\cdot {{\vec v}} +{\rm i}\varepsilon }} \notag \\ &&{+{\tilde{{\vec e}}}_{{k}_{1}}^{\rm t}\cdot \frac{ \partial }{\partial {{\vec p}}}\left( {\frac{1}{\omega _{2}-{ {\vec k}}_{2}\cdot {{\vec v}}+{\rm i}\varepsilon }}\right) { {\vec e}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}} \notag \\ &&\left. {+{\tilde{{\vec e}}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}\left( {\frac{1}{\omega _{1}- {{\vec k}}_{1}\cdot {{\vec v}}+{\rm i}\varepsilon }}\right) {{\vec e}}_{{k}_{1}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}\right\} \frac{f_{\rm p}^{R}{\rm d}{{\vec p}} }{\left( {2\pi }\right) ^{3}}\cdot \label{eqa1} \end{eqnarray}$ (A.1)We define $\begin{matrix} H & = & [\frac{1}{ω_{2} - k_{2} \cdot v} ({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}) (e_{k_{1}}^{t} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} H &=&\left[ \frac{1}{\omega _{2}-{{\vec k}}_{2}\cdot { {\vec v}}}{\left( {{\tilde{{\vec e}}}_{{k} _{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \left( {{{\vec e}}_{{k}_{1}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}\right) }\right. \notag \\ &&\left. {+\frac{1}{\omega _{1}-{{\vec k}}_{1}\cdot {{\vec v}}}\left( {{\tilde{{\vec e}}}_{{k}_{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \left( {{ {\vec e}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) }\right] f_{\rm p}^{R}. \label{eqa2} \end{eqnarray}$ (A.2)For positive high-frequency and negative high-frequency transverse fields with ω₁ ≈ − ω₂ ≈ ω_P ≫ kc, Eq. ( A.2) can be written as $H \approx \frac{1}{ω_{P}} [({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}) (e_{k_{1}}^{t} \cdot \frac{\partial}{\partial p}) - ({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot \frac{\partial}{\partial p}) (e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p})] f_{p}^{R} .$ $\begin{equation*} H \approx \frac{1}{\omega _{\rm P} }\left[ {\left( {{\tilde {{\vec e}}}_{ {k}_2 }^{\rm t} \cdot \frac{\partial }{\partial {{\vec p}} }} \right)\left( {{{\vec e}}_{{k}_1 }^{\rm t} \cdot \frac{ \partial }{\partial {{\vec p}}}} \right) - \left( {{\tilde { {\vec e}}}_{{k}_1 }^{\rm t} \cdot \frac{\partial }{\partial {{\vec p}}}} \right)\left( {{{\vec e}}_{{k} _2 }^{\rm t} \cdot \frac{\partial }{\partial {{\vec p}}}} \right)} \right] f_{\rm p} ^R. 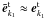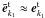\end{equation*}$ Under the high-frequency approximation, there are ${\begin{matrix} _{˜} \\ e \end{matrix}}_{k_{1}}^{t} \approx e_{k_{1}}^{t}$ $\hbox{${\tilde { {\vec e}}}_{{k}_1 }^{\rm t} \approx {{\vec e}}_{{{k}}_1 }^{\rm t}$}$ and ${\begin{matrix} _{˜} \\ e \end{matrix}}_{k_{1}}^{t} \approx e_{k_{1}}^{t}$ $\hbox{${\tilde {{\vec e}}}_{{k}_1 }^{\rm t} \approx{{\vec e}}_{{k}_1 }^{\rm t}$}$ . Now, it is easy to obtain H ≈ 0. Therefore, Eq. (A.1) can be reduced to 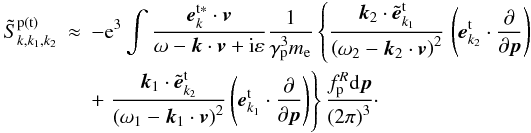$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} & \approx & - e^{3} \int \frac{e_{k}^{t *} \cdot v}{ω - k \cdot v + i ε} \frac{1}{γ_{p}^{3} m_{e}} {\frac{k_{2} \cdot {\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t}}{{(ω_{2} - k_{2} \cdot v)}^{2}} (e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( {t}\right) } & \approx & -{\rm e}^{3}\int {\frac{ {{\vec e}}_{k}^{\rm t\ast }\cdot {{\vec v}}}{\omega -{ {\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon }\frac{1}{\gamma _{\rm p}^{3}m_{\rm e}} \left\{ {\frac{{{\vec k}}_2\cdot {\tilde{ {\vec e}}}_{{k}_{1}}^{\rm t}}{\left( {\omega _{2}-{ {\vec k}}_{2}\cdot {{\vec v}}}\right) ^{2}}}\right. }\left( { {{\vec e}}_{{k}_{2}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}\right) \notag \\ &&+\left. {\frac{{{\vec k}}_{1}\cdot {\tilde{{\vec e}}}_{ {k}_{2}}^{\rm t}}{\left( {\omega _{1}-{{\vec k}} _{1}\cdot {{\vec v}}}\right) ^{2}}\left( {{{\vec e}}_{ {k}_{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p }}}}\right) }\right\} \frac{f_{\rm p}^{R}{\rm d}{{\vec p}}}{\left( {2\pi } \right) ^{3}}\cdot \label{eqa3} \end{eqnarray}$ (A.3)When the equilibrium distribution of positrons ( 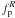$f_{p}^{R}$ $\hbox{$f_{\rm p}^{R}$}$ ) is isotropic, one has 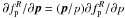$\partial f_{p}^{R} / \partial p = (p / p) \partial f_{p}^{R} / ∂p$ $\hbox{${\partial f_{\rm p}^R }/{\partial {{\vec p}}} = ({{\vec p}}/ p){\partial f_{\rm p}^R } /\partial p$}$ . Under the high-frequency approximation, Eq. (A.3) can be written as $\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} & \approx & - e^{3} \int \frac{1}{γ_{p}^{3} m_{e}} \frac{1}{ω - k \cdot v + i ε} [\frac{({k_{2} \cdot e_{k_{1}}^{t}}^{)} ({e_{k_{2}}^{t} \cdot v}^{)}}{{(ω_{2} - k_{2} \cdot v)}^{2}} \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( {t}\right) } &\approx &-{\rm e}^{3}\int {\frac{1 }{\gamma _{\rm p}^{3}m_{\rm e}}\frac{1}{\omega -{{\vec k}}\cdot { {\vec v}}+{\rm i}\varepsilon }\left[ {\frac{\left( {{{\vec k}}_{{ 2}}\cdot {{\vec e}}_{{k}_{1}}^{\rm t}}\right) \left( { {{\vec e}}_{{k}_{2}}^{\rm t}\cdot {{\vec v}}} \right) }{\left( {\omega _{2}-{{\vec k}}_{2}\cdot {{\vec v} }}\right) ^{2}}}\right. } \notag \\ &&+\left. \frac{\left( {{{\vec k}}_{1}\cdot {{\vec e}}_{ {k}_{2}}^{\rm t}}\right) \left( {{{\vec e}}_{{ {\vec k}}_{1}}^{\rm t}\cdot {{\vec v}}}\right) }{\left( {\omega _{1}- {{\vec k}}_{1}\cdot {{\vec v}}}\right) ^{2}}\right] \left( {{{\vec e}}_{k}^{\rm t\ast }\cdot \frac{\partial }{\partial { {\vec p}}}}\right) f_{\rm p}^{R}\frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right) ^{3}}\cdot \label{eqa4} \end{eqnarray}$ (A.4)Taking account of |ω₁| ≈ |ω₂| ≈ ω_P ≫ kc, the above equation can be approximated to be $\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} & \approx & - \frac{e^{3}}{m_{e} ω_{P}^{2}} \int \frac{[{({k_{2} \cdot e_{k_{1}}^{t}}^{)} ({e_{k_{2}}^{t} \cdot v}^{)} + ({k_{1} \cdot e_{k_{2}}^{t}}^{)} ({e_{k_{1}}^{t} \cdot v}^{)}}^{]}}{γ_{p}^{3} (ω - k \cdot v + i ε)} \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( {t}\right) } &\approx &-\frac{{\rm e}^{3}}{ m_{\rm e}\omega _{{P}}^{{2}}}\int {\frac{\left[ {\left( {{{\vec k}} _{2}\cdot {{\vec e}}_{{k}_{1}}^{\rm t}}\right) \left( { {{\vec e}}_{{k}_{2}}^{\rm t}\cdot {{\vec v}}} \right) +\left( {{{\vec k}}_{1}\cdot {{\vec e}}_{{ {k}}_{2}}^{\rm t}}\right) \left( {{{\vec e}}_{{k} _{1}}^{\rm t}\cdot {{\vec v}}}\right) }\right] }{\gamma _{\rm p}^{3}{\left( \omega -{{\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon \right) }}} \notag \\ &&\left( {{{\vec e}}_{k}^{\rm t\ast }\cdot \frac{\partial }{\partial {{\vec p}}}}\right) f_{\rm p}^{R}\frac{{\rm d}{{\vec p}}}{\left( { 2\pi }\right) ^{3}}\cdot \label{eqa5} \end{eqnarray}$ (A.5)After integration by parts, there is $\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} = \frac{e^{3}}{m_{e}^{2} ω_{P}^{2}} \int \frac{1}{γ_{p}^{3}} (e_{k}^{t *} \cdot \frac{\partial}{\partial v}) \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} &&\tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( {t}\right) } =\frac{{\rm e}^{3}}{ m_{\rm e}^{2}\omega _{\rm P}^{2}}\int {\frac{{1}}{\gamma _{\rm p}^{3}}\left( {{ {\vec e}}_{k}^{\rm t\ast }\cdot \frac{\partial }{\partial {{\vec v}}}} \right) } \notag \\ &&\times{\left\{ {\frac{{\left[ {\left( {{{\vec k}}_{2}\cdot { {\vec e}}_{{k}_{1}}^{\rm t}}\right) \left( {{{\vec e}} _{{k}_{2}}^{\rm t}\cdot {{\vec v}}}\right) +\left( { {{\vec k}}_{1}\cdot {{\vec e}}_{{k} _{2}}^{\rm t}}\right) \left( {{{\vec e}}_{{k} _{1}}^{\rm t}\cdot {{\vec v}}}\right) }\right] }}{\gamma _{\rm p}^{3}{ \left( \omega -{{\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon \right) }}}\right\} }\frac{f_{\rm p}^{R}{\rm d}{{\vec p}}}{\left( {2\pi } \right) ^{3}}\cdot \label{eqa6} \end{eqnarray}$ (A.6)After a series of algebraic calculations, and considering ω ≫ kc, Eq. (A.6) can be written as $\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} & \approx & \frac{e^{3}}{m_{e}^{2} ω_{P}^{2} ω} {\int \frac{3}{γ_{p}^{4}} [{({e_{k_{1}}^{t} \times e_{k_{2}}^{t}}^{)} \cdot (k \times v) ({e_{k}^{t *} \cdot v}^{)}}^{]} \frac{f_{p}^{R}}{c^{2}} \frac{d p}{{({2 π}^{)}}^{3}} \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( {t}\right) } &\approx &\frac{{\rm e}^{3}}{ m_{\rm e}^{{2}}\omega _{{\rm P}}^{{2}}\omega }\Biggl\{ {{\int {\frac{3}{\gamma _{\rm p }^{4}}\left[ {\left( {{{\vec e}}_{{k} _{1}}^{\rm t}\times {{\vec e}}_{{k}_{2}}^{\rm t}}\right) \cdot \left( {{\vec {k}}\times {{\vec v}}}\right) \left( { {\vec {e}}_{k}^{\rm t\ast }\cdot {{\vec v}}}\right) }\right] } \frac{f_{\rm p}^{R}}{c^{2}}\frac{{\rm d}{\vec {p}}}{\left( {2\pi }\right) ^{3} }}} \nonumber \\ &&{+} {{n_{0}{\vec {e}}_{k}^{\rm t\ast }\cdot \left[ {{ \vec {e}}_{{{k}}_{2}}^{\rm t}\left( {{\vec {k}}_{ 2}\cdot {\vec {e}}_{{{k}}_{1}}^{\rm t}} \right) +{\vec {e}}_{{{k}}_{1 }}^{\rm t}\left( {{\vec {k}}_{1}\cdot {\vec {e}}_{{ {k}}_{2}}^{\rm t}}\right) }\right] \left\langle {\gamma _{\rm p}^{-6}} \right\rangle }}\Biggl\} \label{eqa7}. \end{eqnarray}$ (A.7)The first term on the right-hand side of Eq. 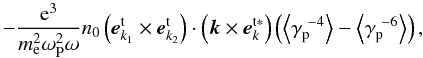(A.7) can be read as $- \frac{e^{3}}{m_{e}^{2} ω_{P}^{2} ω} n_{0} ({e_{k_{1}}^{t} \times e_{k_{2}}^{t}}^{)} \cdot ({k \times e_{k}^{t *}}^{)} ({⟨ {γ_{p}^{- 4}}^{⟩} - ⟨ {γ_{p}^{- 6}}^{⟩}}^{)},$ $\appendix \setcounter{section}{1} \begin{equation} \label{eqa8} -\frac{{\rm e}^3}{m_{\rm e}^{2} \omega _{\rm P}^{2} \omega }n_0 \left( {{\vec {e}}_{ {{k}}_1 }^{\rm t} \times {\vec e}_{{k} _2}^{\rm t}} \right) \cdot \left( {{\vec {k}}\times {\vec {e}} _{k}^{\rm t\ast } } \right)\left( {\left\langle {\gamma _{\rm p} ^{{\ - 4}} } \right\rangle - \left\langle {\gamma _{\rm p} ^{{\ - 6}} } \right\rangle } \right), \end{equation}$ (A.8)where the following expression has been used 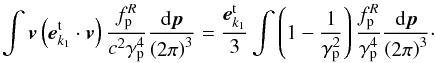$\int v ({e_{k_{1}}^{t} \cdot v}^{)} \frac{f_{p}^{R}}{c^{2} γ_{p}^{4}} \frac{d p}{{({2 π}^{)}}^{3}} = \frac{e_{k_{1}}^{t}}{3} \int (1 - \frac{1}{γ_{p}^{2}}) \frac{f_{p}^{R}}{γ_{p}^{4}} \frac{d p}{{({2 π}^{)}}^{3}} \cdot$ $\appendix \setcounter{section}{1} \begin{equation} \label{eqa9} \int {{\vec {v}}\left( {{\vec {e}}_{{{k}}_{ 1} }^{\rm t} \cdot {{\vec v}}} \right)\frac{f_{\rm p}^R }{ c^2\gamma _{\rm p} ^4 }\frac{{\rm d}{\vec {p}}}{\left( {2\pi } \right)^3} } = \frac{{\vec {e}}_{{{k}}_{1} }^{\rm t} }{3}\int {\left( {1 - \frac{1}{\gamma _{\rm p} ^2 }} \right)\frac{f_{\rm p}^R }{ \gamma _{\rm p} ^4 }\frac{{\rm d}{\vec {p}}}{\left( {2\pi } \right)^3}} \cdot \end{equation}$ (A.9)Taking the δ-function in Eq. (11) into account, one can arrive at k₂ = k₁ − k, in which k₁ and k₂ are positive and negative wave vectors, respectively. Thus, the second term on the right-hand side of (A.7) can be reduced to $\frac{e^{3} n_{0}}{m_{e}^{2} ω ω_{P}^{2}} e_{k}^{t *} \cdot [{e_{k_{2}}^{t} ({k_{2} \cdot e_{k_{1}}^{t}}^{)} + e_{k_{1}}^{t} ({k_{1} \cdot e_{k_{2}}^{t}}^{)}}^{]} ⟨ {γ_{p}^{- 6}}^{⟩} .$ $\appendix \setcounter{section}{1} \begin{equation} \label{eqa10} \frac{{\rm e}^3n_0 }{m_{\rm e}^{2} \omega \omega _{\rm P}^{2} }{\vec {e}}_{k}^{\rm t\ast } \cdot \left[ {{\vec {e}}_{{{k}}_2 }^{\rm t} \left( { {\vec {k}}_{2} \cdot {\vec {e}}_{{ {k}}_1 }^{\rm t} } \right) + {\vec {e}}_{{{k}}_{ 1} }^{\rm t} \left( {{{\vec k}}_1 \cdot {\vec { e}}_{{{k}}_2 }^{\rm t} } \right)} \right]\left\langle {\gamma _{\rm p}^{{\ - 6}} } \right\rangle. \end{equation}$ (A.10)Combining (A.8) and (A.10) yields ${S_{k, k_{1}, k_{2}}^{p (t)}}_{˜} = - \frac{e^{3} n_{0}}{m_{e}^{2} ω ω_{P}^{2}} e_{k}^{t *} \cdot [{k \times ({e_{k_{1}}^{t} \times e_{k_{2}}^{t}}^{)}}^{]} ({⟨ {γ_{p}^{- 4}}^{⟩} - 2 ⟨ {γ_{p}^{- 6}}^{⟩}}^{)} .$ $\appendix \setcounter{section}{1} \begin{equation} \label{eqa11} \tilde {S}_{k,k_1 ,k_2 }^{\rm p \left( {t} \right)} = - \frac{{\rm e}^3n_0 }{ m_{\rm e}^{2} \omega \omega _{\rm P}^{2} }{\vec {e}}_{k}^{\rm t\ast } \cdot \left[ { {\vec {k}}\times \left( {{\vec {e}}_{{{k}}_1 }^{\rm t} \times {\vec {e}}_{{{k}}_2 }^{\rm t} } \right)} \right] \left( {\left\langle {\gamma _{\rm p}^{{\ - 4}} } \right\rangle - 2\left\langle { \gamma _{\rm p}^{{\ - 6}} } \right\rangle } \right). \end{equation}$ (A.11)

Appendix B: Calculation of the matrix 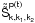${\begin{matrix} ˜ \\ ˜ \end{matrix} S}_{k, k_{1}, k_{2}}^{p (t)}$ $\hbox{$\mathsf{{\tilde{\tilde{S}}}_{k,k_1 ,k_2 }^{p(t)} }$}$

The matrix 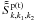$\begin{matrix} _{˜} \\ _{˜} \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)}$ $\hbox{$\tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p \left( t \right)}$}$ can be written as 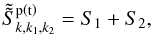$\begin{matrix} ˜ \\ ˜ \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)} = S_{1} + S_{2},$ $\appendix \setcounter{section}{2} \begin{equation} \label{eqb1} \tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p \left( t \right)} = S_1 + S_2 , \end{equation}$ (B.1)in which $\begin{matrix} S_{1} & = & - e^{3} \int \frac{e_{k}^{t *} \cdot v}{ω - k \cdot v + i ε} ({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\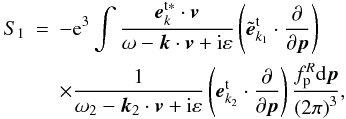appendix \setcounter{section}{2} \begin{eqnarray} S_{1} &=&-{\rm e}^{3}\int \frac{{{\vec e}}_{{ {k}}}^{\rm t {{\ast }}}\cdot {\vec {v}}}{\omega -{\vec {k} }\cdot {{\vec v}}+{\rm i}\varepsilon } \left( {\tilde{\vec e}}_{ k_1}^{\rm t}\cdot \frac{\partial }{\partial {\vec p}}\right) \notag \\ &&\times\frac{1}{\omega _{2}-{{\vec k}}_{2}\cdot {{\vec v}} +{\rm i}\varepsilon }\left( {{{\vec e}}_{k _{2}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \frac{ f_{\rm p}^{R}{\rm d}{{\vec p}}}{\left( {2\pi }\right) ^{3}}, \label{eqb2} \end{eqnarray}$ (B.2) $\begin{matrix} S_{2} & = & - e^{3} \int \frac{e_{k}^{t *} \cdot v}{ω - k \cdot v + i ε} ({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\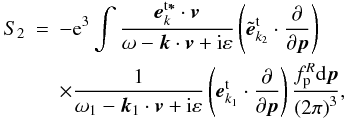appendix \setcounter{section}{2} \begin{eqnarray} S_{2} &=&-{\rm e}^{3}\int {\frac{{{\vec e}}_{{{ k}}}^{\rm t {{\vec \ast }}}\cdot {{\vec v}}}{\omega -{{\vec k} }\cdot {{\vec v}}+{\rm i}\varepsilon }}\left( {{{ \tilde{\vec e}}} _{k_{2}}^{\rm t}\cdot \frac{\partial }{\partial { {\vec p}}}}\right) \notag \\ &&\times\frac{1}{\omega _{1}-{{\vec k}}_{1}\cdot {{\vec v}} +{\rm i}\varepsilon }\left( {{{\vec e}}_{{{k}} _{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}}\right) \frac{ f_{\rm p}^{R}{\rm d}{{\vec p}}}{\left( {2\pi }\right) ^{3}}, \label{eqb3} \end{eqnarray}$ (B.3)where k₁ = (k₁,ω₁) and k = (k,ω) are four-dimensional wave vectors for the high-frequency transverse field, k₂ = (k₂,ω₂) is the four-dimensional wave vector for the low-frequency transverse field.

Integrating Eq. (B.2) by parts, and considering ω ≫ kc, one derives 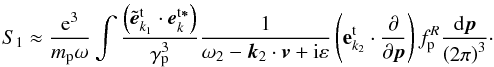$S_{1} \approx \frac{e^{3}}{m_{p} ω} \int \frac{({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot e_{k}^{t *}^{)}}{γ_{p}^{3}} \frac{1}{ω_{2} - k_{2} \cdot v + i ε} (e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}) f_{p}^{R} \frac{d p}{{({2 π}^{)}}^{3}} \cdot$ $\appendix \setcounter{section}{2} \begin{equation} S_{1}\approx \frac{{\rm e}^{3}}{m_{\rm p }\omega }\int {\frac{\left( { {\tilde{{\vec e}}}_{{{k}}_{1 }}^{\rm t}\cdot {{\vec e}}_{{{k}}}^{\rm t{{\vec \ast }}}}\right) }{\gamma _{\rm p }^{3}}\frac{1}{\omega _{2}-{{\vec k}} _{2}\cdot {{\vec v}}+{\rm i}\varepsilon }\left( {{\mathbf{e}}_{ {k}_{2}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}\right) f_{\rm p }^{R}}\frac{{\rm d}{{\vec p}}}{\left( {2\pi }\right) ^{3}}\cdot \label{eqb4} \end{equation}$ (B.4)Integrating Eq. (B.4) by parts, and considering 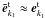${\begin{matrix} _{˜} \\ e \end{matrix}}_{k_{1}}^{t} \approx e_{k_{1}}^{t}$ $\hbox{${\tilde {{\vec e}}}_{{{ k}}_{1} }^{\rm t} \approx { {\vec e}}_{k_{1} }^{\rm t} $}$ if kc ≪ ω₁ ≈ ω_P, Eq. (B.4) can be read as 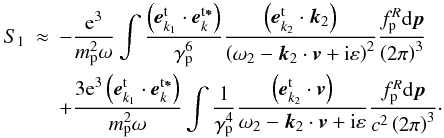$\begin{matrix} S_{1} & \approx & - \frac{e^{3}}{m_{p}^{2} ω} \int \frac{({e_{k_{1}}^{t} \cdot e_{k}^{t *}}^{)}}{γ_{p}^{6}} \frac{({e_{k_{2}}^{t} \cdot k_{2}}^{)}}{{(ω_{2} - k_{2} \cdot v + i ε)}^{2}} \frac{f_{p}^{R} d p}{{({2 π}^{)}}^{3}} \end{matrix}$ $\appendix \setcounter{section}{2} \begin{eqnarray} S_{1} &\approx &-\frac{{\rm e}^{3}}{m_{\rm p }^{2}\omega }\int {\frac{ \left( {{{\vec e}}_{{{k}}_{1 }}^{\rm t}\cdot {{\vec e}}_{k}^{\rm t{{\vec \ast }}}}\right) }{\gamma _{\rm p }^{6}} {\frac{\left( {{{\vec e}} _{ k_{2}}^{\rm t}\cdot {{\vec k}}_{2} }\right) }{\left( {\omega _{2}-{{\vec k}}_{2}\cdot {{\vec v }}+{\rm i}\varepsilon }\right) ^{2}}} }\frac{f_{\rm p }^{R}{ \rm d}{ {\vec p}}}{\left( {2\pi }\right) ^{3}} \nonumber \\ &&{+}\frac{{3}{\rm e}^{3}\left( {{{\vec e}}_{k _{1}}^{\rm t}\cdot {{\vec e}}_{{k}}^{\rm t {{\vec \ast }}}}\right) }{m_{\rm p}^2 \omega }\int {\frac{1}{\gamma _{\rm p }^{4}}\frac{\left( {{{\vec e}}_{{k}_{ 2}}^{\rm t}\cdot {{\vec v}}}\right) }{\omega _{2}- {{\vec k}}_{2}\cdot {{\vec v}}+{\rm i}\varepsilon }}\frac{ f_{\rm p }^{R}{\rm d}{{\vec p}}}{c^{2}\left( {2\pi }\right) ^{3}}\cdot\label{eqb5} \end{eqnarray}$ (B.5)For the transverse field, i.e. 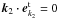$k_{2} \cdot e_{k_{2}}^{t} = 0$ $\hbox{$ {{\vec k}}_2 \cdot {{\vec e}}_{{{k}}_{ 2} }^{\rm t}= 0$}$ , and considering the facts ω₂ ≫ k₂c, there is 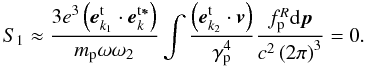$S_{1} \approx \frac{3 e^{3} ({e_{k_{1}}^{t} \cdot e_{k}^{t *}}^{)}}{m_{p} ω ω_{2}} \int \frac{({e_{k_{2}}^{t} \cdot v}^{)}}{γ_{p}^{4}} \frac{f_{p}^{R} d p}{c^{2} {({2 π}^{)}}^{3}} = 0.$ $\appendix \setcounter{section}{2} \begin{equation} \label{eqb6} S_1 \approx \frac{{3}e ^3 \left( {{{\vec e}}_{{ {k}}_{1} }^{\rm t} \cdot {{\vec e}}_{{ {k}}}^{\rm t{{\vec \ast }}} } \right)}{m_{\rm p} \omega \omega _2 }\int {\frac{\left( {{{\vec e}}_{{{k}}_{{ 2}} }^{\rm t} \cdot {{\vec v}}} \right)}{\gamma _{\rm p} ^{4} }} \frac{f_{\rm p} ^R {\rm d}{{\vec p}}}{c^{2}\left( {2\pi } \right)^3}=0. \end{equation}$ (B.6)In view of the isotropic distribution of the positrons in equilibrium state, it is easy to obtain S₁ = 0.

Integrating Eq. (B.3) by parts, if k₁c ≪ ω₁ ≈ ω_P, similarly as the calculation of Eq. (B.4), one can obtain 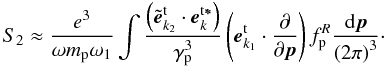$S_{2} \approx \frac{e^{3}}{ω m_{p} ω_{1}} \int \frac{({\begin{matrix} ˜ \\ e \end{matrix}}_{k_{2}}^{t} \cdot e_{k}^{t *}^{)}}{γ_{p}^{3}} (e_{k_{1}}^{t} \cdot \frac{\partial}{\partial p}) f_{p}^{R} \frac{d p}{{({2 π}^{)}}^{3}} \cdot$ $\appendix \setcounter{section}{2} \begin{equation} \label{eqb7} S_2 \approx \frac{e ^3 }{\omega m_{\rm p} \omega _1 }\int {\frac{\left( {{\tilde {{\vec e}}}_{{{k}}_{2} }^{\rm t} \cdot {{\vec e}}_{{{k}}}^{\rm t{{\vec \ast }}} } \right)}{\gamma _{\rm p} ^3 }\left( {{{\vec e}}_{{{k}} _{1} }^{\rm t} \cdot \frac{\partial }{\partial {{\vec p} }}} \right)f_{\rm p} ^R } \frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right)^3}\cdot \end{equation}$ (B.7)Integrating the above equation by parts, one derives $\begin{matrix} S_{2} = - \frac{e^{3}}{ω m_{p}^{2} ω_{1}} \int \frac{1}{γ_{p}^{6}} (e_{k_{1}}^{t} \cdot \frac{\partial}{\partial v}) \\ \times \begin{matrix} ⎧ \\ ⎪ \\ ⎪ \\ ⎨ \\ ⎪ \\ ⎪ \\ ⎩ \end{matrix} [e_{k_{2}}^{t} (1 - \frac{k_{2} \cdot v}{ω_{2}}) + \frac{e_{k_{2}}^{t} \cdot v}{ω_{2}} k_{2}] \cdot e_{k}^{t *} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix} f_{p}^{R} \frac{d p}{{({2 π}^{)}}^{3}} + \frac{3 e^{3}}{ω m_{p}^{2} ω_{1} c^{2}} \\ \times \int \frac{e_{k_{1}}^{t} \cdot v}{γ_{p}^{4}} \begin{matrix} ⎧ \\ ⎪ \\ ⎪ \\ ⎨ \\ ⎪ \\ ⎪ \\ ⎩ \end{matrix} [e_{k_{2}}^{t} (1 - \frac{k_{2} \cdot v}{ω_{2}}) + \frac{e_{k_{2}}^{t} \cdot v}{ω_{2}} k_{2}] \cdot e_{k}^{t *} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix} f_{p}^{R} \frac{d p}{{({2 π}^{)}}^{3}} \cdot \end{matrix}$ $\appendix \setcounter{section}{2} \begin{eqnarray} &&S_{2}=-\frac{{\rm e}^{3}}{\omega m_{\rm p}^{2}\omega _{1}}\int {\frac{1}{\gamma _{\rm p}^{6}}\left( {{{\vec e}}_{k_{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec v}}}}\right) } \notag \\ &&\times{\left\{ {\left[ {{{\vec e}}_{k_{{2} }}^{\rm t}\left( {1-\frac{{{\vec k}}_{2}\cdot {{\vec v}}}{ \omega _{2}}}\right) +\frac{{{\vec e}}_{{{ k}} _{2}}^{\rm t}\cdot {{\vec v}}}{\omega _{2}}{{\vec k}}_{2}} \right] \cdot {{\vec e}}_{{{k}}}^{\rm t{{\vec \ast }}}}\right\} }f_{\rm p}^{R}\frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right) ^{3}}+\frac{3 {\rm e}^3}{\omega m_{\rm p}^{2}\omega _{1}c^{2}} \notag \\ &&\times\int {\frac{{{\vec e}}_{{{k}}_{1}}^{\rm t}\cdot { {\vec v}}}{\gamma _{\rm p}^{4}}\left\{ {\left[ {{{\vec e}}_{{ {k}}_{2}}^{\rm t}\left( {1-\frac{{{\vec k}}_{2}\cdot { {\vec v}}}{\omega _{2}}}\right) +\frac{{{\vec e}}_{{ {k}}_{2}}^{\rm t}\cdot {{\vec v}}}{\omega _{2}}{{\vec k} }_{2}}\right] \cdot {{\vec e}}_{{{k}}}^{\rm t{ {\vec \ast }}}}\right\} f_{\rm p}^{R}\frac{{\rm d}{{\vec p}}}{\left( { 2\pi }\right) ^{3}}}\cdot \notag \\ \label{eqb8} \end{eqnarray}$ (B.8)The first term of Eq. (B.8) can be written as $- \frac{e^{3}}{ω m_{p}^{2} ω_{1} ω_{2}} e_{k}^{t *} \cdot [{e_{k_{1}}^{t} \times ({k_{2} \times e_{k_{2}}^{t}}^{)}}^{]} \int \frac{f_{p}^{R}}{γ_{p}^{6}} \frac{d p}{{({2 π}^{)}}^{3}},$ $\appendix \setcounter{section}{2} \begin{equation} \label{eqb9} - \frac{e ^3 }{\omega m_{\rm p} ^{2} \omega _1 \omega _2}{ {\vec e}}_{{{k}}}^{\rm t{{\vec \ast }}} \cdot \left[ { {{\vec e}}_{k_{1} }^{\rm t} \times \left( {{{\vec k}}_{2} \times {{\vec e}} _{{k}_{2} }^{\rm t} } \right)} \right]\int { \frac{f_{\rm p} ^R }{\gamma _{\rm p} ^6 }} \frac{{\rm d}{{\vec p}}}{ \left( {2\pi } \right)^3}, \end{equation}$ (B.9)and the second can be read as $\begin{matrix} - \frac{3 e^{3}}{ω m_{p}^{2} ω_{1}} (\frac{k_{2}}{ω_{2}} \times e_{k_{2}}^{t}) \cdot [e_{k}^{t *} \times \int v ({e_{k_{1}}^{t} \cdot v}^{)} \frac{f_{p}^{R}}{c^{2} γ_{p}^{4}} \frac{d p}{{({2 π}^{)}}^{3}}] = \end{matrix}$ $\appendix \setcounter{section}{2} \begin{eqnarray} &&-\frac{3{\rm e}^{3}}{\omega m_{\rm p}^{2}\omega _{1}}\left( {\frac{{{\vec k} }_{2}}{\omega _{2}}\times {{\vec e}}_{k_{2}}^{\rm t}} \right) \cdot \left[ {{{\vec e}}_{{{k}}}^{\rm t{ {\vec \ast }}}\times \int {{{\vec v}}\left( {{{\vec e}}_{ k_{1}}^{\rm t}\cdot {{\vec v}}}\right) \frac{f_{\rm p}^{R} }{c^{2}\gamma _{\rm p}^{4}}\frac{{\rm d}{{\vec p}}}{\left( {2\pi }\right) ^{3}}}}\right] = \notag \\ &&-\frac{{\rm e}^3}{\omega m_{\rm p}^{2}\omega _{1}}\left( \frac{{{ {\vec k}}_{2}}}{\omega _{2}}{\times {{\vec e}}_{{k }_{2}}^{\rm t}}\right) \cdot \left( {{{\vec e}}_{{{k}}}^{\rm t {{\vec \ast }}}\times {{\vec e}}_{k _{1}}^{\rm t}}\right) \int {\left( {1-\frac{1}{\gamma _{\rm p}^{2}}}\right) \frac{ f_{\rm p}^{R}}{\gamma _{\rm p}^{4}}\frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right) ^{3}}}, \label{eqb10} \end{eqnarray}$ (B.10)where Eq. (B.9) was used.

Combining Eqs. (B.9) and (B.10), and considering ω₁ ≈ ω_P, one obtains $\begin{matrix} ˜ \\ ˜ \end{matrix} S_{k, k_{1}, k_{2}}^{p (t)} \approx - \frac{1}{4 π} \frac{ω_{pp}^{2} e}{ω m_{p} ω_{P} c} ⟨ {γ_{p}^{-4}}^{⟩} e_{k}^{t *} \cdot [e_{k_{1}}^{t} \times (\frac{k_{2} c}{ω_{2}} \times e_{k_{2}}^{t})] .$ $\appendix \setcounter{section}{2} \begin{equation} \label{eqb11} \tilde {\tilde {S}}_{k,k_1 ,k_2 }^{\rm p \left( t \right)} \approx - \frac{1}{ 4\pi }\frac{\omega _{\rm pp }^2 e }{\omega m_{\rm p} \omega _{\rm P} c} \left\langle {\gamma _{\rm p} ^{ - 4} } \right\rangle {{\vec e}}_{ {{\vec k}}}^{\rm t{{\vec \ast }}} \cdot \left[ {{ {\vec e}}_{{k}_{1} }^{\rm t} \times \left( { \frac{{{\vec k}}_{2} c}{\omega {\ }_2}\times {{\vec e}}_{k_{2} }^{\rm t} } \right)} \right]. \end{equation}$ (B.11)

Appendix C: Calculation of the matrix 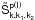${S_{k, k_{1}, k_{2}}^{p (l)}}_{˜}$ $\hbox{$\mathsf{\tilde {S}_{k,k_1 ,k_2 }^{p\left( l \right)}}$}$

Completing the derivation in brackets of the interaction matrix 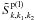${S_{k, k_{1}, k_{2}}^{p (l)}}_{˜}$ $\hbox{$\tilde {S}_{k,k_1 ,k_2 }^{\rm p\left( l \right)}$}$ , for H ≈ 0, one derives 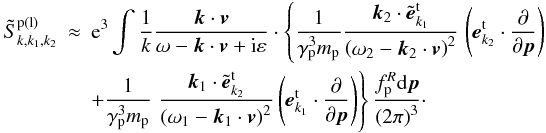$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} & \approx & e^{3} \int \frac{1}{k} \frac{k \cdot v}{ω - k \cdot v + i ε} \cdot {\frac{1}{γ_{p}^{3} m_{p}} \frac{k_{2} \cdot {\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t}}{{(ω_{2} - k_{2} \cdot v)}^{2}} (e_{k_{2}}^{t} \cdot \frac{\partial}{\partial p}) \end{matrix}$ $\appendix \setcounter{section}{3} \begin{eqnarray} \tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( l\right) } &\approx &{\rm e}^{3}\int {\frac{1}{k }\frac{{{\vec k}}\cdot {{\vec v}}}{\omega -{{\vec k}}\cdot {{\vec v}}+{\rm i}\varepsilon }\cdot \left\{ {\frac{1}{\gamma _{\rm p}^{3}m_{\rm p}}\frac{{{\vec k}}_{2}\cdot {\tilde{{\vec e}}} _{{k}_{1}}^{\rm t}}{\left( {\omega _{2}-{{\vec k}} _{2}\cdot {{\vec v}}}\right) ^{2}}}\right. }\left( {{{\vec e}}_{k_{2}}^{\rm t}\cdot \frac{\partial }{\partial { {\vec p}}}}\right) \nonumber \\ &&+\frac{1}{\gamma _{\rm p}^{3}m_{\rm p}}\left. {\frac{{{\vec k}}_{1}\cdot {\tilde{{\vec e}}}_{{k}_{2}}^{\rm t}}{\left( {\omega _{1}-{{\vec k}}_{1}\cdot {{\vec v}}}\right) ^{2}}\left( { {{\vec e}}_{{k}_{1}}^{\rm t}\cdot \frac{\partial }{ \partial {{\vec p}}}}\right) }\right\} \frac{f_{\rm p}^{R}{\rm d}{ {\vec p}}}{\left( {2\pi }\right) ^{3}}\cdot \label{eqC1} \end{eqnarray}$ (C.1)Considering the isotropic distribution of positrons, the first integration of Eq. (C.1 ) can be read as $\begin{matrix} \int \frac{1}{ω - k \cdot v + i ε} (\frac{k}{k} \cdot \frac{\partial f_{p}^{R}}{\partial p}) \\ \times [{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot \frac{\partial}{\partial p} \frac{e_{k_{2}}^{t} \cdot v}{ω_{2} - k_{2} \cdot v} - \frac{{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot e_{k_{2}}^{t}}{ω_{2} - k_{2} \cdot v} \frac{1}{γ_{p}^{3} m_{p}}] \frac{d p}{(2 π)^{3}} \cdot \end{matrix}$ $\appendix \setcounter{section}{3} \begin{eqnarray*} &&\int {\frac{1}{\omega -{{\vec k}}\cdot {{\vec v}} +{\rm i}\varepsilon }\left( {\frac{{{\vec k}}}{k}\cdot \frac{\partial f_{\rm p}^{R}}{\partial {{\vec p}}}}\right) } \\ &&\times\left[ {{\tilde{{\vec e}}}_{{k}_{1}}^{\rm t}\cdot \frac{\partial }{\partial {{\vec p}}}\frac{{{\vec e}}_{ {k}_{2}}^{\rm t}\cdot {{\vec v}}}{\omega _{2}-{ {\vec k}}_{2}\cdot {{\vec v}}}-\frac{{\tilde{{\vec e}}}_{ {k}_{1}}^{\rm t}\cdot {{\vec e}}_{{k} _{2}}^{\rm t}}{\omega _{2}-{{\vec k}}_{2}\cdot {{\vec v}}} \frac{1}{\gamma _{\rm p}^{3}m_{\rm p}}}\right] \frac{{\rm d}{{\vec p}}}{(2\pi )^{3}}\cdot \end{eqnarray*}$ Similarly, the second integration can be obtained through $\frac{{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot e_{k_{2}}^{t}}{ω_{2} - k_{2} \cdot v} + \frac{{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{2}}^{t} \cdot e_{k_{1}}^{t}}{ω_{1} - k_{1} \cdot v} \approx \frac{1}{ω_{1}} [{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{2}}^{t} \cdot e_{k_{1}}^{t} - {\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot e_{k_{2}}^{t}^{]} \approx 0.$ $\begin{equation*} \frac{{\tilde {{\vec e}}}_{{k}_1 }^{\rm t} \cdot { {\vec e}}_{{k}_2 }^{\rm t} }{\omega _2 - {{\vec k}}_2 \cdot {{\vec v}}} + \frac{{\tilde {{\vec e}}}_{{ {k}}_2 }^{\rm t} \cdot {{\vec e}}_{{k}_1 }^{\rm t} }{ \omega _1 - {{\vec k}}_1 \cdot {{\vec v}}} \approx \frac{1 }{\omega _1 }\left[ {{\tilde {{\vec e}}}_{{k}_2 }^{\rm t} \cdot {{\vec e}}_{{k}_1 }^{\rm t} - {\tilde { {\vec e}}}_{{k}_1 }^{\rm t} \cdot {{\vec e}}_{{ {k}}_2 }^{\rm t} } \right] \approx 0. \end{equation*}$ Therefore, Eq. (C.1) can be written as $\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} & \approx & - \frac{q_{p}^{3}}{m_{p}} \int \frac{1}{γ_{p}^{3}} \frac{1}{ω - k \cdot v + i ε} (\frac{k}{k} \cdot \frac{\partial f_{p}^{R}}{\partial p}) \\ \times {\frac{{\begin{matrix} ˜ \\ e \end{matrix}}_{k_{1}}^{t} \cdot e_{k_{2}}^{t}}{{(ω_{2} - k_{2} \cdot v)}^{2}} ω_{2} + \frac{e_{k_{2}}^{t} \cdot e_{k_{1}}^{t}}{{(ω_{1} - k_{1} \cdot v)}^{2}} ω_{1} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix} \frac{d p}{({2 π}^{)}} \cdot \end{matrix}$ $\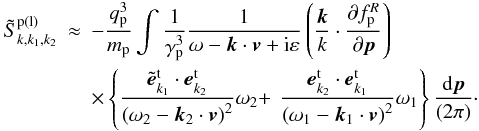appendix \setcounter{section}{3} \begin{eqnarray*} \tilde{S}_{k,k_{1},k_{2}}^{\rm p\left( l\right) } &\approx &-\frac{q_{\rm p}^{3}}{ m_{\rm p}}\int {\frac{1}{\gamma _{\rm p}^{3}}\frac{1}{\omega -{{\vec k}} \cdot {{\vec v}}+{\rm i}\varepsilon }}\left( {\frac{{{\vec k}}}{k }\cdot \frac{\partial f_{\rm p}^{R}}{\partial {{\vec p}}}}\right) \\ &&\times\left\{ {\frac{{\tilde{{\vec e}}}_{{k} _{1}}^{\rm t}\cdot {{\vec e}}_{k_{2}}^{\rm t}}{\left( { \omega _{2}-{{\vec k}}_{2}\cdot {{\vec v}}}\right) ^{2}} \omega _{2}+}\right. \left. {\frac{{{\vec e}}_{{k} _{2}}^{\rm t}\cdot {{\vec e}}_{{k}_{1}}^{\rm t}}{\left( { \omega _{1}-{{\vec k}}_{1}\cdot {{\vec v}}}\right) ^{2}} \omega _{1}}\right\} \frac{{\rm d}{{\vec p}}}{\left( {2\pi }\right) }\cdot \end{eqnarray*}$ For ω₁ ≈ − ω₂ ≈ ω_P ≫ kc, the above equation can be approximately written as 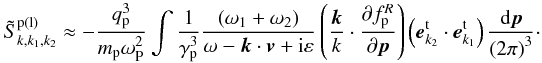$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} \approx - \frac{q_{p}^{3}}{m_{p} ω_{P}^{2}} \int \frac{1}{γ_{p}^{3}} \frac{({ω_{1} + ω_{2}}^{)}}{ω - k \cdot v + i ε} (\frac{k}{k} \cdot \frac{\partial f_{p}^{R}}{\partial p}) ({e_{k_{2}}^{t} \cdot e_{k_{1}}^{t}}^{)} \frac{d p}{{({2 π}^{)}}^{3}} \cdot \end{matrix}$ $\appendix \setcounter{section}{3} \begin{eqnarray*} \tilde {S}_{k,k_1 ,k_2 }^{\rm p\left( l \right)} \approx - \frac{q_{\rm p}^3 }{m_{\rm p} \omega _{\rm P}^2 }\int {\frac{1}{\gamma _{\rm p}^3 }\frac{\left( {\omega _1 + \omega _2 } \right)}{\omega - {{\vec k}} \cdot {{\vec v}} + {\rm i}\varepsilon }\left( {\frac{{{\vec k}}}{k} \cdot \frac{\partial f_{\rm p} ^R}{\partial {{\vec p}}}} \right)} \left( {{{\vec e}}_{ {k}_2 }^{\rm t} \cdot {{\vec e}}_{{k}_1 }^{\rm t} } \right)\frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right)^3}\cdot \end{eqnarray*}$ In view of δ-function in Eq. (25), i.e., ω = ω₁ + ω₂, one derives 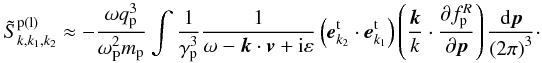$\begin{matrix} {S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} \approx - \frac{ω q_{p}^{3}}{ω_{P}^{2} m_{p}} \int \frac{1}{γ_{p}^{3}} \frac{1}{ω - k \cdot v + i ε} ({e_{k_{2}}^{t} \cdot e_{k_{1}}^{t}}^{)} (\frac{k}{k} \cdot \frac{\partial f_{p}^{R}}{\partial p}) \frac{d p}{{({2 π}^{)}}^{3}} \cdot \end{matrix}$ $\appendix \setcounter{section}{3} \begin{eqnarray*} \tilde {S}_{k,k_1 ,k_2 }^{\rm p\left( l \right)} \approx - \frac{\omega q_{\rm p}^3 }{ \omega _{\rm P}^2 m_{\rm p} }\int {\frac{1}{\gamma _{\rm p}^3 }\frac{1}{\omega - { {\vec k}} \cdot {{\vec v}} + {\rm i}\varepsilon }} \left( {{ {\vec e}}_{{k}_2 }^{\rm t} \cdot {{\vec e}}_{{k}_{1} }^{\rm t} } \right)\left( {\frac{{{\vec k}}}{k} \cdot \frac{\partial f_{\rm p} ^R}{\partial {{\vec p}}}} \right) \frac{{\rm d}{{\vec p}}}{\left( {2\pi } \right)^3}\cdot \end{eqnarray*}$ Following the similar procedure to obtain Eq. (19), the above equation can be reduced to 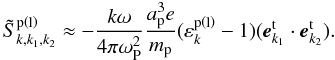${S_{k, k_{1}, k_{2}}^{p (l)}}_{˜} \approx - \frac{kω}{4 π ω_{P}^{2}} \frac{a_{p}^{3} e}{m_{p}} (ε_{k}^{p (l)} - 1) (e_{k_{1}}^{t} \cdot e_{k_{2}}^{t}) .$ $\appendix \setcounter{section}{3} \begin{equation} \label{eqC2} \tilde {S}_{k,k_1 ,k_2 }^{\rm p\left( l \right)} \approx - \frac{k\omega }{4\pi \omega _{\rm P}^2 }\frac{a_{\rm p}^3 e}{m_{\rm p} }(\varepsilon _{k}^{\rm p\left( l \right)} - 1)( {{\vec e}}_{{k}_1 }^{\rm t} \cdot {{\vec e}}_{ {k}_2 }^{\rm t} ). \end{equation}$ (C.2)

All Figures

	Fig. 1 Growth rate with respect to the wave number calculated from Eq. (68). The different lines in each figure correspond to different θ. a) W₀ = 0.1,a_p = 0.05, b) W₀ = 0.1,a_p = 0.02, c) W₀ = 0.1,a_p = 0.01, d) W₀ = 0.01,a_p = 0.05, e) W₀ = 0.001,a_p = 0.05.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Chang, P., Spitkovsky, A., & Arons, J. 2008, ApJ, 674, 378 [Google Scholar]

[2] Cohen, E. J., Katz, I., Piran, T., et al. 1997, ApJ, 488, 330 [NASA ADS] [CrossRef] [Google Scholar]

[3] Deng, X. L., Xia, T. S., & Liu, J. 2005, A&A, 443, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[4] Ghisellini, G., Celotti, A., & Lazzati, D. 2000, MNRAS, 313, L1 [NASA ADS] [CrossRef] [Google Scholar]

[5] Gruzinov, A. 2001, ApJ, 563, L15 [NASA ADS] [CrossRef] [Google Scholar]

[6] Jüttner, F. 1911, Ann. der Phys., 34, 856 [Google Scholar]

[7] Kaplan, S. A., & Tsytovich, V. N. 1973, Plasma Astrophysics (London: Pergamon Press) [Google Scholar]

[8] Karpman, V. I., Norman, C. A., ter Haar, D., & Tsytovich, V. N. 1975, Phys. Scripta, 11, 271 [Google Scholar]

[9] Katz, B., Keshet, U., & Waxman, E. 2007, ApJ, 655, 375 [NASA ADS] [CrossRef] [Google Scholar]

[10] Li, X. Q., & Ma, Y. H. 1993, A&A, 270, 534 [NASA ADS] [Google Scholar]

[11] Li, X. Q., Liu, S. Q., & Tao, X. Y. 2008, Contrib. Plasma Phys., 48, 361 [NASA ADS] [CrossRef] [Google Scholar]

[12] Liang, E. P. 1982, Nature, 299, 321 [NASA ADS] [CrossRef] [Google Scholar]

[13] Lifshitz, E. N., & Pitaevskii, L. P. 1981, Physical Kinetics (Oxford: Pergamon Press) [Google Scholar]

[14] Liu, Y., & Liu, S. Q. 2011, Contrib. Plasma Phys., 51, 698 [NASA ADS] [CrossRef] [Google Scholar]

[15] Liu, X. L., Liu, S. Q., & Yang, X. S. 2008, Phys. Plasmas, 15, 032302 [NASA ADS] [CrossRef] [Google Scholar]

[16] Mao, J., & Wang, J. 2011, ApJ, 731, 26 [NASA ADS] [CrossRef] [Google Scholar]

[17] Medvedev, M. V. 2000, ApJ, 540, 704 [NASA ADS] [CrossRef] [Google Scholar]

[18] Medvedev, M. V. 2006, ApJ, 637, 869 [NASA ADS] [CrossRef] [Google Scholar]

[19] Medvedev, M. V., & Loeb, A. 1999, ApJ, 526, 697 [NASA ADS] [CrossRef] [Google Scholar]

[20] Medvedev, M. V., Fiore, M., Fonseca, R. A., Silva, L. O., & Mori, W. B. 2005, ApJ, 618, L75 [NASA ADS] [CrossRef] [Google Scholar]

[21] Mikhailovskii, A. B. 1980, Plasma Phys., 22, 133 [NASA ADS] [CrossRef] [Google Scholar]

[22] Morsony, B. J., Workman, J. C., Lazzati, D., & Medvedev, M. V. 2009, MNRAS, 392, 1397 [NASA ADS] [CrossRef] [Google Scholar]

[23] O’Neil, T. M., & Coroniti, F. V. 1999, Rev. Mod. Phys., 71, S404 [CrossRef] [Google Scholar]

[24] Pe’er, A., & Zhang, B. 2006, ApJ, 653, 454 [NASA ADS] [CrossRef] [Google Scholar]

[25] Pulupa, M. P., Bale, S. D., & Kasper, J. C. 2010, J. Geophys. Res., 115, A04106 [NASA ADS] [Google Scholar]

[26] Robinson, P. A. 1997, Rev. Mod. Phys., 69, 507 [NASA ADS] [CrossRef] [Google Scholar]

[27] Silva, L. O., Fonseca, R. A., Tonge, J. W., et al. 2003, ApJ, 596, L121 [Google Scholar]

[28] Thornhill, S. G., & Ter Haar, D. 1978, Phys. Rep., 43, 43 [NASA ADS] [CrossRef] [Google Scholar]

[29] Tkaczyk, W. 1993 Unthermalized Plasma in Phebus and BATSE Gamma Ray Bursts Sources. 23rd International Cosmic Ray Conference, 1, eds. D. A. Leahy, R. B. Hickws, & D. Venkatesan (Singapore: World Scientific), 124 [Google Scholar]

[30] Tsytovich, V. N. 1977, Theory of turbulent plasma (New York: Consultants Bureau) [Google Scholar]

[31] Workman, J. C., Morsony, B. J., Lazzati, D., & Medvedev, M. V. 2008, MNRAS, 386, 199 [NASA ADS] [CrossRef] [Google Scholar]

Magnetic field induced by strong transverse plasmons in ultra-relativistic electron-positron plasmas

1. Introduction

2. Nonlinear governing equations for the interactions of transverse plasmons with non-isothermal ultra-relativistic EP plasmas

2.1. Fundamental theory in the framework of Vlasov-Maxwell equation

2.2. Self-generated low-frequency magnetic fields

2.3. High-frequency transverse field

2.4. Low-frequency density perturbation

2.5. Nonlinear governing equation in coordinate space

3. Linear analysis for transverse perturbations

4. Discussions and conclusions

Acknowledgments

References

Appendix A: Calculation of the matrix Sk,k1,k2p(t)˜

Appendix B: Calculation of the matrix ˜˜Sk,k1,k2p(t)

Appendix C: Calculation of the matrix Sk,k1,k2p(l)˜

All Figures

Appendix A: Calculation of the matrix ${S_{k, k_{1}, k_{2}}^{p (t)}}_{˜}$ $\hbox{$\mathsf{\tilde {S}_{k,k_1 ,k_2}^{p\left( {t} \right)}}$}$

Appendix B: Calculation of the matrix ${\begin{matrix} ˜ \\ ˜ \end{matrix} S}_{k, k_{1}, k_{2}}^{p (t)}$ $\hbox{$\mathsf{{\tilde{\tilde{S}}}_{k,k_1 ,k_2 }^{p(t)} }$}$

Appendix C: Calculation of the matrix ${S_{k, k_{1}, k_{2}}^{p (l)}}_{˜}$ $\hbox{$\mathsf{\tilde {S}_{k,k_1 ,k_2 }^{p\left( l \right)}}$}$