| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219267 | |
| Published online | 03 July 2012 | |
Shape reconstruction of irregular bodies with multiple complementary data sources
Department of MathematicsTampere University of Technology,
PO Box 553
33101
Tampere,
Finland
e-mail: mikko.kaasalainen@tut.fi
Received: 22 March 2012
Accepted: 14 May 2012
We discuss inversion methods for shape reconstruction with complementary data sources. The current main sources are photometry, adaptive optics or other images, occultation timings, and interferometry, and the procedure can readily be extended to include range-Doppler radar and thermal infrared data as well. We introduce the octantoid, a generally applicable shape support that can be automatically used for surface types encountered in planetary research, including strongly nonconvex or non-starlike shapes. We present models of Kleopatra and Hermione from multimodal data as examples of this approach. An important concept in this approach is the optimal weighting of the various data modes. We define the maximum compatibility estimate, a multimodal generalization of the maximum likelihood estimate, for this purpose. We also present a specific version of the procedure for asteroid flyby missions, with which one can reconstruct the complete shape of the target by using the flyby-based map of a part of the surface together with other available data. Finally, we show that the relative volume error of a shape solution is usually approximately equal to the relative shape error rather than its multiple. Our algorithms are trivially parallelizable, so running the code on a CUDA-enabled graphics processing unit is some two orders of magnitude faster than the usual single-processor mode.
Key words: methods: data analysis / methods: numerical / techniques: high angular resolution / techniques: interferometric / techniques: photometric / minor planets, asteroids: general
© ESO, 2012
1. Introduction
Photometric measurements, i.e., lightcurves (sparse or dense), are the main data source for the physical modelling of asteroids. This is because they are in principle available for all targets that can be observed in the first place, and they allow a unique (usually global convex) shape and pole/period solution (Kaasalainen et al. 1992, 2001; Ďurech & Kaasalainen 2003; Kaasalainen 2004; Ďurech et al. 2005; Kaasalainen & Lamberg 2006, henceforth KL06). Lightcurves can also be used to determine more complex spin states (Kaasalainen 2001; Kaasalainen et al. 2007; Scheirich et al. 2010) or colour maps over the surface using filters of various wavelengths (Nathues et al. 2005). Other data sources providing more detailed information are available for a much smaller portion of asteroids. In addition to space mission targets, these include asteroids that have a large enough apparent diameter for some resolution in adaptive optics images, interferometric measurements, or occultation timings, or come close enough for radar observations. Though this portion is relatively small, it nevertheless comprises several hundreds or even thousands of targets, so standard procedures for analysing these in the same way as lightcurve-only targets are necessary. In KL06, it was shown that all the aforementioned data types are different versions of generalized projections of the objects, and hence have some common mathematical properties.
The most natural way of modelling targets with datasets from various data sources is to combine all the datasets and analyse them simultaneously. In Kaasalainen (2011, henceforth K11), a general scheme was introduced for combining lightcurves and adaptive optics images to produce more detailed nonconvex shape models, and the uniqueness properties and computational aspects of the problem were discussed. The ground truth validating this scheme via the Lutetia flyby of the Rosetta probe (Sierks et al. 2011) was presented in Carry et al. (2012). Occultation timings are essentially profile projections of the object and can be modelled in the same way as adaptive optics profiles (Ďurech et al. 2012). The use of interferometric data is described in KL06 and, in more detail, in this paper. Radar data have been used for modelling tens of asteroids (Ostro et al. 2002; Magri et al. 2011, and references therein), and the uniqueness properties and information content of these were discussed in KL06. Including radar data in our formalism is straightforward, and we discuss this in a forthcoming paper.
This paper is an addition to a series of reports on our ongoing project of using all available data sources to model asteroids. The aim of this paper is to expand and complement the formalism of the aforementioned papers to include i) a shape support for general shapes, including non-starlike ones (Sects. 2 and 3.1); ii) interferometric measurements (Sect. 3.2); and iii) a technique for modelling the complete asteroid surface using flyby images combined with other data (Sect. 6). In addition, we present some examples of these (Sect. 5) and review the principle of finding the optimal weights for various data modalities (Sect. 4). We discuss future work in Sect. 7.
2. General shape representation: octantoids
Our aim is to find a general surface parametrization for the reconstruction of non-starlike shapes from generalized projections. A popular approach is the usual spherical harmonics representation in which each coordinate function is represented independently as a spherical harmonics series (see, e.g., Zacharopoulos et al. 2006). However, while this parametrization is powerful enough to represent any shape that can be parametrized on the unit sphere S2 (with sufficient continuity properties), it requires excessive smoothness regularization during the inversion process. What is more, the actual topology of the mesh of the evaluation points on the surface may change during iteration (which does not happen in the starlike case): the mesh can cross itself and become “tangled” as its vertices are allowed to move freely. Thus, instead of trying to find a regularization method to stabilize the surface topology, we decided to try a different approach of defining a representation that is general enough to represent non-starlike asteroid shapes, yet more stable than the usual spherical harmonics representation in the inversion process.
We consider surfaces that can be represented in the form 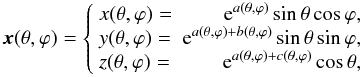 (1)where a, b, and c are linear combinations of the (real) spherical harmonic functions
(1)where a, b, and c are linear combinations of the (real) spherical harmonic functions 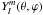 , with coefficients {alm} , {blm} , and {clm} , respectively. The coordinates (θ,ϕ), 0 ≤ θ ≤ π, 0 ≤ ϕ < 2π, parametrize the surface on the unit sphere S2 but do not represent any physical directions such as polar coordinates. We use the exponential representation to ensure that the generalized radii ea, ea + b, and ea + c are all positive.
, with coefficients {alm} , {blm} , and {clm} , respectively. The coordinates (θ,ϕ), 0 ≤ θ ≤ π, 0 ≤ ϕ < 2π, parametrize the surface on the unit sphere S2 but do not represent any physical directions such as polar coordinates. We use the exponential representation to ensure that the generalized radii ea, ea + b, and ea + c are all positive.
It is clear that our representation is more restrictive than the general spherical harmonics representation, for the coordinate functions cannot change sign within each S2-octant. We call shapes that can be rendered in the form (1) octantoids. For a body to be an octantoid, it must be possible to choose the origin (inside the body) and coordinate axes such that if the body is cut along the coordinate planes, there is only one piece from each octant (and the pieces join together smoothly). For example, the ellipsoid is the simplest octantoid, as it can be represented by Eq. (1) by choosing the functions a, b, and c to be constants so that the semiaxes are the generalized radii. A curved banana is an example of a strongly non-starlike octantoid. From irregular small asteroids to planets, the currently known shapes of solar system bodies are octantoids. A non-octantoid body is typically made of sculpted material with great tensile strength and has a markedly twisted shape, whereas processes guided by gravitation (accumulation etc.) tend to favour octantoid shapes.
The usual representation for starlike shapes can be obtained by setting b = c = 0 in the parametrization of Eq. (1). If we think of starlike surfaces as our basic “stable” shapes, an intuitively obvious measure for shape complexity is a weighted norm of the coefficients {blm} and {clm} (and possibly {alm}). We thus define 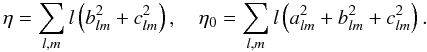 (2)We note that for an ellipsoid η = 0 = η0, as the only nonzero coefficients are a00, b00, and c00. This reflects the compact information content of the octantoid parametrization: representing an ellipsoid in the more usual starlike formulation with b = c = 0 would require an infinite spherical harmonics series for a. Using η0 also formally solves the nonuniqueness problem of the choice of (θ,ϕ): for a given octantoid, the optimal parametrization is the one with the smallest η0 (when the spherical harmonics series are truncated at some lmax).
(2)We note that for an ellipsoid η = 0 = η0, as the only nonzero coefficients are a00, b00, and c00. This reflects the compact information content of the octantoid parametrization: representing an ellipsoid in the more usual starlike formulation with b = c = 0 would require an infinite spherical harmonics series for a. Using η0 also formally solves the nonuniqueness problem of the choice of (θ,ϕ): for a given octantoid, the optimal parametrization is the one with the smallest η0 (when the spherical harmonics series are truncated at some lmax).
For the inversion algorithm, we assume that our surface is represented as a polytope with triangular facets. The vertex locations (θi, ϕi), i = 1,...,N, on the parametrizing unit sphere are obtained from a triangular mesh of the size N on the sphere, with any usual mesh topology (vertex connections; cf., e.g., Kaasalainen et al. 2001), and the actual vertex locations are then given by Eq. (1). Enforcing small values of η (or η0) as regularization greatly stabilizes the procedure and improves convergence.
The regularization measure of Eq. (2) mostly affects the global surface shape. A regularization method for smoothing out more local irregularities is often required. We define a smoothing regularization function (K11), designed to minimize the sum of local nonconvex features, as 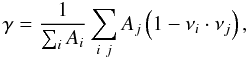 (3)where Ai is the area of the facet i and νi its unit normal vector, ν ∈ S2. The sum is over all those facets j that are adjacent to the facet i and tilted above its plane. In the same vein, we introduce a physical regularization function for non-monolithic bodies by constraining the gravitational slope so that steep rubble-pile slopes are avoided:
(3)where Ai is the area of the facet i and νi its unit normal vector, ν ∈ S2. The sum is over all those facets j that are adjacent to the facet i and tilted above its plane. In the same vein, we introduce a physical regularization function for non-monolithic bodies by constraining the gravitational slope so that steep rubble-pile slopes are avoided: ![\begin{equation} \phi=\frac{1}{\sum_i A_i} \sum_i A_{i}[1-\nu_i\cdot\nabla\Phi(x_i)], \label{slope} \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq34.png) (4)where xi is the centroid of the facet i, and Φ(x) is the gravitational potential computed from the tetrahedra formed by the centroid of the body and the facet triangles (see, e.g., Werner 1994). The gravitational slope for the facet i is arccos [νi·∇Φ(xi)] .
(4)where xi is the centroid of the facet i, and Φ(x) is the gravitational potential computed from the tetrahedra formed by the centroid of the body and the facet triangles (see, e.g., Werner 1994). The gravitational slope for the facet i is arccos [νi·∇Φ(xi)] .
The octantoid form of Eq. (1) can also be written for a set of independent vertices (rather than spherical harmonics series) by using a(θi, ϕi),b(θi, ϕi), and c(θi, ϕi) as a set of 3N free parameters, with smoothness regularization and, for instance, a penalty function f(b,c) to suppress deviation from starlike shapes: 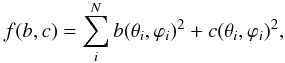 (5)where b and c represent the set of values b(θi, ϕi) and c(θi, ϕi).
(5)where b and c represent the set of values b(θi, ϕi) and c(θi, ϕi).
3. Data modes and their modelling
3.1. Non-starlike contours
The theoretical aspects of shape inversion from generalized profiles were extensively studied in KL06 and K11. Here we restrict ourselves to some practical observations of the goodness-of-fit measure and the optimization process.
Let ω and ω0 be, respectively, the viewing and the illumination directions; ω0,ω ∈ S2. As the surface is no longer convex, the set of facets approximating the visible and illuminated portion 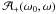 of the surface is determined by ray-tracing. A computationally fast form of this determination, approximate but sufficiently accurate for most of our purposes and easily refinable for higher accuracy, was given in Kaasalainen et al. (2001). A facet with the unit normal vector ν is in
of the surface is determined by ray-tracing. A computationally fast form of this determination, approximate but sufficiently accurate for most of our purposes and easily refinable for higher accuracy, was given in Kaasalainen et al. (2001). A facet with the unit normal vector ν is in 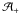 if the dot products ω·ν and ω0·ν are both positive, and the rays from the facet centroid to the directions ω and ω0 do not intersect any other facet.
if the dot products ω·ν and ω0·ν are both positive, and the rays from the facet centroid to the directions ω and ω0 do not intersect any other facet.
The use of the image boundary contours is necessary because it is considerably more reliable than using the pixel brightness values of adaptive optics images. The contour mode is also faster than the pixel one. For reliable pixel values, the goodness-of-fit measure of especially non-starlike objects is easiest to formulate in the pixel space. However, even in these cases the use of boundary contours is often necessary if one wishes to employ efficient gradient-based optimization procedures. An algorithm for constructing the outer shadow and limb boundary of the projection of a polyhedron was outlined in K11. However, for a general non-starlike object, the construction is too time-consuming and complex to be used in an inversion algorithm. Instead, we construct an approximate image boundary ∂ℬ(ω0,ω) of the object ℬ using a two-step algorithm:
-
1.
Construct the set ℰ of edges that are shared by a facet in
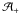 and one not in it. The actual outer projection boundary (profile contour) of the object is not necessarily well approximated by the projection of this set of line segments, since ℰ usually also contains edges that are caused by other concavities and shadows, but are not part of the true outer boundary.
and one not in it. The actual outer projection boundary (profile contour) of the object is not necessarily well approximated by the projection of this set of line segments, since ℰ usually also contains edges that are caused by other concavities and shadows, but are not part of the true outer boundary. -
2.
Project the edges found in step 1 onto the plane defined by the viewing direction ω. With line sweeping, remove those edges from the set that are contained between edges in both the horizontal and vertical directions in the projection plane. This set of two-dimensional line segments is denoted by ∂ℬ(ω0,ω).
We define the distance d(e,P0) between a point P0 and a line segment e with end points P1 and P2 as follows. Let d1(e,P0) be the perpendicular distance of the point P0 from the line defined by P1 and P2 if its projection is inside the line segment, and d2(e,P0) be the smaller one of the distances (P0, P1) and (P0, P2). We can then set 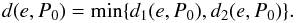 (6)A goodness-of-fit measure between the model boundary ∂ℬ and a set ϰ of the observed profile contour points ϰi can be defined as follows:
(6)A goodness-of-fit measure between the model boundary ∂ℬ and a set ϰ of the observed profile contour points ϰi can be defined as follows: 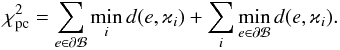 (7)We usually assume that the displacement of the model profile contour from the observed contour in the viewing plane is unknown. The optimal offset parameters must then be determined during the inversion as in K11.
(7)We usually assume that the displacement of the model profile contour from the observed contour in the viewing plane is unknown. The optimal offset parameters must then be determined during the inversion as in K11.
3.2. Interferometry
As our second data source, we consider the interferometric projection operator (KL06). An interferometric curve is essentially obtained by projecting the image of the object on the POS to an interferometric base line in the same plane and convolving it with a point-spread-like instrument response function. In our case, the base line is one of the orthogonal axes of the Fine Guidance Sensor of the Hubble Space Telescope (HST/FGS), but the procedure presented here is generic for any interferometric case. To be more precise, the final observable response function S(x) of the HST/FGS can be computed by convolving the brightness distribution I(u,v) of the image of the object on the plane-of-sky (POS) with the template transfer function T(x) of the instrument: 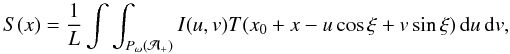 (8)where
(8)where 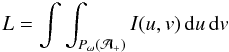 (9)is the total brightness of the visible and illuminated part of the object,
(9)is the total brightness of the visible and illuminated part of the object, 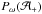 denotes the POS projection of
denotes the POS projection of 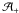 , and ξ is the angle between the image u-axis and the FGS base line x-axis. A similar measurement is made in the y-direction perpendicular to x, and the parameters x0 and y0 are the location offset values of the object w.r.t. the FGS coordinates.
, and ξ is the angle between the image u-axis and the FGS base line x-axis. A similar measurement is made in the y-direction perpendicular to x, and the parameters x0 and y0 are the location offset values of the object w.r.t. the FGS coordinates.
The template transfer function T(x) cannot usually be written in an analytical form and is thus given as a set of sampled values. To obtain a continuous function, the transfer function is linearly interpolated between the sampled points so that we have a form suitable for gradient-based optimization (i.e., all parameters to be adjusted have existing and locally continuous partial derivatives w.r.t. the goodness-of-fit measure).
For a polytope, the integral can be easily computed for practical inversion. The visible and illuminated facets are determined by ray-tracing using the same approach as in the previous section1. In this case, we evaluate an integral over the POS, so we must have a sufficiently high resolution for the sampling points (u,v) even if the polyhedral model itself is not in high resolution. Indeed, it is computationally much more efficient to sprinkle each facet with a number of sampling points than to use many very small facets. For each facet fi with ω·ν and ω0·ν positive, we generate N points {pij} , j = 1...N, uniformly distributed within the facet. The value of N, typically of order N ~ 10, depends on the resolution of the instrument, the size of the facets, and the apparent size of the target on the POS; this is simple to probe by noting when the numerical approximation of S(x) with some test case starts to converge to the desired accuracy. The point pij on the facet fi is visible if the rays from the point pij to the directions ω and ω0 do not intersect any other facet. The integral in Eq. (8) can then be approximated as the sum 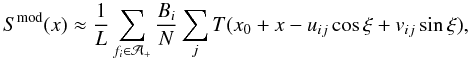 (10)where (uij, vij) is the projection of the point pij onto the plane defined by ω, Bi is the brightness of the facet fi, and the inner sum is over all of those points in the facet that are visible and illuminated. The goodness-of-fit measure
(10)where (uij, vij) is the projection of the point pij onto the plane defined by ω, Bi is the brightness of the facet fi, and the inner sum is over all of those points in the facet that are visible and illuminated. The goodness-of-fit measure 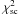 for an interferometric S-curve of M data points is of the usual form
for an interferometric S-curve of M data points is of the usual form ![\begin{equation} \chi^2_{\rm sc}=\sum_{i=1}^M \left[S^{\rm obs}(x_i)-S^{\rm mod}(x_i)\right]^2. \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq95.png) (11)
(11)
4. Maximum compatibility estimate
In our problem of combining lightcurves and other data sources, the data modalities are complementary but incommensurable, which causes an additional problem: how exactly is the combined dataset defined? Ideally, the solution of the inverse problem should be independent of, e.g., noise level estimates or scale factors such as physical units. It should reflect the best compatibility estimate and the optimal relative weight factors of the data modes: how much does each mode bring reliable information into the solution? In this sense, one can even separate subsets of a single data mode: should data obtained in one set of conditions be weighted more than those acquired in another? This problem was addressed in K11, where a rigorous definition of the maximum compatibility estimate – a multimodal generalization of the maximum likelihood estimate – was derived. For convenience, we briefly review this formulation.
Let us choose as goodness-of-fit measures some functions δi, i = 1,...,n, of n data modalities. Typically, δ is the usual χ2-fit form. Our task is to construct a joint δtot with well-defined weighting for each data mode: 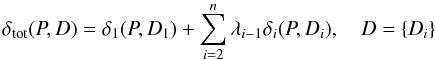 (12)(to which regularization functions g(P) can be added), where Di denotes the data from the source i, and P is the set of model parameter values.
(12)(to which regularization functions g(P) can be added), where Di denotes the data from the source i, and P is the set of model parameter values.
The principle of deriving the maximum compatibility estimate is easiest first to describe in two dimensions. We can plot the separate fit levels for each δi, obtained by minimizing δtot at various λ in the (log δ1, log δ2)-plane, denoting ![\begin{eqnarray} x(\lambda)&=&\log\delta_1\left[\arg\min_P \delta_{\rm tot}(P)\vert_\lambda\right],\\\nonumber y(\lambda)&=&\log\delta_2\left[\arg\min_P \delta_{\rm tot}(P)\vert_\lambda\right], \end{eqnarray}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq108.png) (13)(the logarithm keeps the shape of the plot invariant in, e.g., unit conversions as multiplicative factors in δi are converted to translations in the plot plane). We can also translate the origin to (X,Y) given by
(13)(the logarithm keeps the shape of the plot invariant in, e.g., unit conversions as multiplicative factors in δi are converted to translations in the plot plane). We can also translate the origin to (X,Y) given by 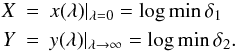 (14)A suitable choice of λ then corresponds to the point closest to (X,Y). Figure 1 is a schematic plot of this: the dashed line is an (x,y)-plot for a dataset with two well compatible data sources, while the dot-dash line portrays a case with some apparent mutual discrepancies.
(14)A suitable choice of λ then corresponds to the point closest to (X,Y). Figure 1 is a schematic plot of this: the dashed line is an (x,y)-plot for a dataset with two well compatible data sources, while the dot-dash line portrays a case with some apparent mutual discrepancies.
 |
Fig. 1 A schematic of the curve [x(λ),y(λ)] and the maximum compatibility estimate (the point closest to the new origin at the intersection of the dotted lines). The dashed line corresponds to a case with closely compatible data sources, while dot-dash indicates a case with systematic errors in models and/or data. The weight parameter λ for data mode 2 increases from left (λ = 0) to right (λ = ∞) on a curve. |
The parameter vector P0![\begin{equation} P_0=\arg\min_P\left(\left[\log\delta_1(P)-X\right]^2+\left[\log\delta_2(P)- Y\right]^2\right)\label{mce} \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq115.png) (15)is called the maximum compatibility estimate (MCE). The maximum compatibility weight (MCW) λ0 is given by
(15)is called the maximum compatibility estimate (MCE). The maximum compatibility weight (MCW) λ0 is given by ![\begin{equation} \lambda_0=\arg\min_\lambda \Big([x(\lambda)-X]^2+[y(\lambda)- Y]^2\Big).\label{lambda0} \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq117.png) (16)We note that, in this formalism, P0 can be found directly as a solution of an optimization problem in the usual manner, without having to determine λ0. It is, however, useful to make the plot with different values of λ to see how well the data modalities are compatible with each other in general (see Fig. 1 and the discussion in K11).
(16)We note that, in this formalism, P0 can be found directly as a solution of an optimization problem in the usual manner, without having to determine λ0. It is, however, useful to make the plot with different values of λ to see how well the data modalities are compatible with each other in general (see Fig. 1 and the discussion in K11).
The above is straightforward to generalize to n functions δi and n − 1 parameters λi describing the position on an n − 1-dimensional hypersurface. The MCE is ![\begin{equation} P_0=\arg\min\sum_{i=1}^n\left[\log\frac{\delta_i(P)}{\delta_{i0}}\right]^2, \quad\delta_{i0}:=\min\delta_i(P),\label{p0} \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq120.png) (17)and the MCW is, with λ ∈ Rn − 1,
(17)and the MCW is, with λ ∈ Rn − 1, ![\begin{equation} \lambda_0=\arg\min\sum_{i=1}^n\left[\log \frac{\hat\delta_{i,{\rm tot}}(\lambda)}{\delta_{i0}}\right]^2, \,\,\hat\delta_{i,{\rm tot}}(\lambda):= \left\{\delta_i\left\vert\min\delta_{\rm tot};\lambda\right.\right\}. \label{l0} \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq122.png) (18)
(18)
5. Examples: Kleopatra and Hermione
As an example of our shape representation and the inversion process, we consider two asteroids with complicated shapes: (216) Kleopatra and (121) Hermione. For the general goodness-of-fit measure, we choose 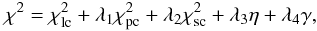 (19)where
(19)where 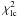 ,
, 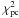 , and
, and 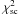 are the fits obtained from the lightcurves, profile contours, and S-curves, respectively. Optimal weight coefficients λi can be determined using the maximum compatibility procedure described above. For smoothness and to keep the procedure stable and ensure convergence, we use the two regularization functions η and γ discussed above. We can also use physical constraints: the function φ of Eq. (4) and one that strives to align the principal axis of the maximum moment of inertia with the rotation axis of the object (K11). However, for these two asteroids, these regularization measures are apparently not required: the inertia tilt is less than 5° and the average gravitational slope is small for all shape versions obtained.
are the fits obtained from the lightcurves, profile contours, and S-curves, respectively. Optimal weight coefficients λi can be determined using the maximum compatibility procedure described above. For smoothness and to keep the procedure stable and ensure convergence, we use the two regularization functions η and γ discussed above. We can also use physical constraints: the function φ of Eq. (4) and one that strives to align the principal axis of the maximum moment of inertia with the rotation axis of the object (K11). However, for these two asteroids, these regularization measures are apparently not required: the inertia tilt is less than 5° and the average gravitational slope is small for all shape versions obtained.
In addition to the shape parameters {alm} , {blm} , {clm} , the spin direction angles β, λ, and the rotation period P, we also determine optimal offset parameters for each profile contour and S-curve. The parameters minimizing Eq. (19) are found using the Levenberg-Marquardt optimization algorithm as in Kaasalainen et al. (2001). The reconstructed shape is no longer necessarily unique since it is a compromise between several data sources and regularization functions. However, even if the depiction of fine detail varies among the solutions, the overall shape is usually relatively stable, regardless of the weighting between the data sources. The truncation point of the spherical harmonics series reflects this level of resolution.
Our algorithm is implemented in MATLAB and C. The computational performance is strongly enhanced by CUDA-enabled programming of the graphics processing unit (GPU). This is a general feature of most algorithms dealing with the computational problems of generalized projections because they are highly parallelizable due to the discretization of the surface by facets. The GPU-version is over two orders of magnitude faster than running the same code in CPU-only mode, so its use is strongly recommended. An alternative approach is grid computation. With GPU programming, the inversion result is typically obtained in less than a minute, and with moderately sized datasets in seconds.
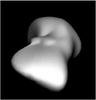 |
Fig. 2 Kleopatra reconstructed from lightcurves, AO, and interferometric data. |
For the asteroid Kleopatra, we used 46 lightcurves, 18 profile contours from adaptive optics images (Descamps et al. 2011), and 30 interferometric HST/FGS observations (Hestroffer et al. 2002). Interestingly enough, shape solutions obtained from the lightcurves and profile contours alone show almost none of the bifurcated structure attributed to the asteroid (Ostro et al. 2001). This is mostly due to the limited observation geometries and inaccuracies in the data. Thus the bifurcation evident in the full LC+AO+HST model of Fig. 2 is almost exclusively based on HST/FGS data. The model fits the dataset better than the radar model (see the comparison in Descamps et al. 2011). It has a bifurcated structure in common with the radar model, but the details of the two models are different.
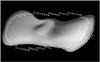 |
Fig. 3 An adaptive optics contour (white crosses) with systematic errors. |
 |
Fig. 4 A typical HST/FGS S-curve fitted by the Kleopatra model. |
An interesting feature is that the datasets from the different modalities are not very compatible with each other. Using all the data sources with the maximum compatibility estimate yields a compromise that clearly fits none of the single-source datasets as well as a single-source model would. This is a typical signature of systematic errors in data (cf. Fig. 3) and/or the model used in inversion (see the discussion in K11). Nevertheless, such erroneous data cannot always be discarded. For example, AO contours such as that in Fig. 3 do stabilize the result as they contain important information on the size and orientation. The radar data should be included in the complete dataset for a more refined model, but even then the current datasets from different sources are likely to be somewhat at odds with each other. However, this is perhaps not so atypical when the data are acquired by instruments working at their resolution limits.
 |
Fig. 5 Sample fits of the reconstructed Kleopatra model to the AO data. |
The rotational parameters for our solution are P = 5.38528 ± 0.00001 h, β = +21°, and λ = 73°, ± 8° of arc, close to (and halfway between) the ones presented in Ostro et al. (2001) and Descamps et al. (2011). Assuming a homogeneous density, the mean gravitational slope is 15°, indicating that the solution is physically feasible. Sample HST/FGS and AO fits are shown in Figs. 4 (best revealing the bifurcated structure) and 5.
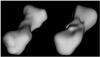 |
Fig. 6 A radar-based test model (left) and its reconstruction (right) from simulated Kleopatra data. |
Using the radar-based model, we simulated data with the same observing geometries as in our real dataset, and the resulting model, compared with the original one, is shown in Fig. 6. The spherical harmonics series were truncated at l = 6. This demonstrates that our octantoid model is powerful enough to represent complicated non-starlike shapes, and that the dataset should facilitate the construction of a reliable model if there were no systematic and/or modelling errors. The model is insensitive to typical random noise in the data sources. (Note that our original and inversion models are entirely different in their surface representations, so this result is not overoptimistic due to “inverse crime”.) As it is, the jury is still out: all models and data sources of Kleopatra are somewhat discrepant with each other, so only additional disk-resolved data will help us to construct a reliable model.
For a quick estimate of which features in our model are due to the data and which are mostly the result of regularization and parametrization, we use the following greatly simplified but illustrative approach. A vertex (or a set of nearby vertices) is sequentially displaced in the normal direction, and the model fit to the data is computed. If the fit remains essentially unchanged, the facets surrounding the vertex are coloured white (we use a black-and-white classification for clarity). This method mostly reveals the effect of AO contours and their aspect coverage: the white areas are poorly constrained by the disk-resolved data. Figure 7 confirms that we do not have enough data for a reliable reconstruction of all the features. Most of the purported details in the model are due to LC and HST data, and the AO geometries are limited in addition to the systematic error due to fuzzy images, poor weather conditions, etc. AO contours can usually be extracted more reliably than here (cf. Carry et al. 2010). We emphasize that, in multimodal inverse problems, the whole is indeed more than the sum of its parts: even a limited coverage of the surface by AO contours (or HST/FGS measurements) constrains the model details from photometry considerably more than if lightcurves were used alone. In this sense, Fig. 7 can be compared with the plots in Keller et al. (2010) and Carry et al. (2012) that portray parts of Steins and Lutetia in different colours corresponding to the datasets used. We will investigate issues related to error analysis in more detail in future work.
 |
Fig. 7 Uncertain regions (white) of the Kleopatra reconstruction. |
For the asteroid Hermione, we used 41 lightcurves and 6 profile contours (the same dataset as in Descamps et al. 2009). Only one of the profile contours seems to display bifurcation-like features. As can be seen from Figs. 8 and 9, the apparent bifurcation in the AO image can, in fact, be explained by a large indentation on the asteroid’s surface, and this is (for the given dataset) a more probable solution than actual bifurcated features. The rotational parameters for our solution are P = 5.55088 ± 0.00001 h, β = +14°, and λ = 4°, ±6° of arc, which are virtually the same as in Descamps et al. (2009). The shape result is also essentially the same as in Descamps et al. (2009), but the octantoid representation helps to resolve the valley-type concavity and explains the AO contours better than a starlike parametrization. The smoothness regularization level required to explain the contours typically causes obvious artificial details in other parts of the surface as can be seen in Fig. 9. For a more refined version of the model, these can be smoothed out locally.
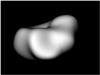 |
Fig. 8 Hermione reconstructed from lightcurves and AO data. |
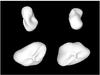 |
Fig. 9 Hermione model fits to the AO contours (white dots). The ridge-like structure visible in the two lower images is an artifact of the chosen smoothness level. |
6. Tailoring the procedure to flyby missions
6.1. Modelling the dark side
Asteroid flybys by space probes form an important class of dataset combination. During a flyby, only about half of the asteroid’s surface is usually seen (here denoted by 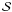 ) as the other half remains in darkness. To complete a model of the whole surface, we must use other data to reconstruct the unseen part
) as the other half remains in darkness. To complete a model of the whole surface, we must use other data to reconstruct the unseen part 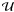 , and in this process the probe-based model of
, and in this process the probe-based model of 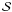 is important in constraining the possible solutions for
is important in constraining the possible solutions for 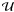 . Because of this,
. Because of this, 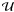 , though never directly seen, can be reconstructed in more detail than in the usual case of ground-based observations only. We remark that this setup is rather different from that in Simonelli et al. (1994), where some minor parts of the probe-based model of the asteroid Gaspra were refined using lightcurve data. Here we consider a problem in which there is no probe-based model for a large portion of the surface at all.
, though never directly seen, can be reconstructed in more detail than in the usual case of ground-based observations only. We remark that this setup is rather different from that in Simonelli et al. (1994), where some minor parts of the probe-based model of the asteroid Gaspra were refined using lightcurve data. Here we consider a problem in which there is no probe-based model for a large portion of the surface at all.
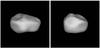 |
Fig. 10 Equatorial views of Lutetia reconstructed from space probe (upper part) and ground-based data (lower part). |
The reconstruction procedure described here was successfully used in the flybys of the Rosetta probe past the asteroids Steins (Keller et al. 2010) and Lutetia (Sierks et al. 2011), and can be used in any flyby missions. Sample views of the Lutetia model are shown in Fig. 10; a more detailed description of the model is given in Carry et al. (2012) and Jorda et al. (in prep.).
Our problem of reconstructing the body ℬ is of the form 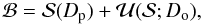 (20)where Dp are space-probe image and position data, and Do are other data: ground-based observations and typically lightcurves measured by the probe prior to the flyby.
(20)where Dp are space-probe image and position data, and Do are other data: ground-based observations and typically lightcurves measured by the probe prior to the flyby.
We define two terms necessary for the reconstruction algorithm. By the limb boundary ℒ(ω) we mean, in a polyhedral representation of the surface, that an edge of ℒ(ω) is any edge common to two facets with ω·ν of opposite signs, when ω is the projection direction and ν the outward normal of a facet. By the envelope, we mean the boundary of the set of those points in space (in the asteroid’s frame of reference) that can be in the asteroid without contradicting the spacecraft images; i.e., points that would not appear as protrusions outside the limb boundaries or inside the shadowed regions in the images. The envelope is not necessarily a closed surface. More exactly, the envelope is the intersection of the cylinder continuations (see K11) of all the projection boundaries  formed by the outermost projections of ℒ(ω) of
formed by the outermost projections of ℒ(ω) of  , in the sense of Sect. 3.1 (ω is the direction of the spacecraft seen from the asteroid), and those of ℒ(ω0) of
, in the sense of Sect. 3.1 (ω is the direction of the spacecraft seen from the asteroid), and those of ℒ(ω0) of 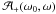 . When ω0 ≠ ω,
. When ω0 ≠ ω, 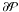 are not closed curves, but they can be completed as closed ones by assuming some maximal limb projections for the target in the shadowed areas. In other words, the envelope is made closed by making physical assumptions of the maximal size of the object in the regions where the envelope is not determined by the spacecraft images. For starlike bodies, we can denote the envelope by the function env(θ,ϕ), where (θ,ϕ) are spherical coordinates.
are not closed curves, but they can be completed as closed ones by assuming some maximal limb projections for the target in the shadowed areas. In other words, the envelope is made closed by making physical assumptions of the maximal size of the object in the regions where the envelope is not determined by the spacecraft images. For starlike bodies, we can denote the envelope by the function env(θ,ϕ), where (θ,ϕ) are spherical coordinates.
The flyby reconstruction procedure, given the reconstruction of  by standard procedures (Capanna et al., in prep.), is a modification of the general multimodal case. Here we assume a starlike body for clarity; i.e., each vertex can be described by its radius r(θ,ϕ) in the direction (θ,ϕ) (measured from some centre inside the body). We note that, in this procedure, the part
by standard procedures (Capanna et al., in prep.), is a modification of the general multimodal case. Here we assume a starlike body for clarity; i.e., each vertex can be described by its radius r(θ,ϕ) in the direction (θ,ϕ) (measured from some centre inside the body). We note that, in this procedure, the part 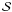 is assumed to be exact, i.e., fully consistent with the spacecraft images. Thus the images themselves need not be used in this approach; we only need the directions ω0 and ω for each flyby image if the step 2(b) below is used (these are known because the shape part
is assumed to be exact, i.e., fully consistent with the spacecraft images. Thus the images themselves need not be used in this approach; we only need the directions ω0 and ω for each flyby image if the step 2(b) below is used (these are known because the shape part 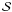 is known). The algorithm is as follows:
is known). The algorithm is as follows:
-
1.
Fix the flyby-determined vertices of
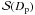 , and choose the directions (θi, ϕi), i = 1,...,N for the adjustable vertices of the surface part
, and choose the directions (θi, ϕi), i = 1,...,N for the adjustable vertices of the surface part 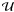 ; these can be picked with some tessellation scheme, or they follow as by-products of the determination of
; these can be picked with some tessellation scheme, or they follow as by-products of the determination of 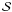 . A practical scheme is to represent the adjustable vertices by the positive-valued exponential spherical harmonics series
. A practical scheme is to represent the adjustable vertices by the positive-valued exponential spherical harmonics series ![\begin{equation} r(\theta,\varphi)=\exp\Big[\sum_{lm} c_{lm}Y_l^m(\theta,\varphi)\Big], \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq162.png) (21)but the radii can be taken as separate parameters as well. The series representation provides a smoothing and regularizing element, and reduces the number of parameters. The resolution level expected for
(21)but the radii can be taken as separate parameters as well. The series representation provides a smoothing and regularizing element, and reduces the number of parameters. The resolution level expected for 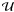 can typically be represented by a series with 6 ≤ lmax ≤ 8. The procedure and regularization functions for minimizing χ2 are as described in the general cases above and in K11. The initial guesses for clm can be obtained, e.g., from an ellipsoid best matching
can typically be represented by a series with 6 ≤ lmax ≤ 8. The procedure and regularization functions for minimizing χ2 are as described in the general cases above and in K11. The initial guesses for clm can be obtained, e.g., from an ellipsoid best matching 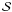 or they can be some plausible values resulting as by-products of the flyby-determination of
or they can be some plausible values resulting as by-products of the flyby-determination of 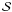 . The latter are useful as they initially join
. The latter are useful as they initially join 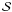 and
and 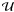 smoothly together. The flyby-determination usually also fixes the pole direction of the object since its orientation (and hence the zero-time and zero-rotation phase) at some epoch during the flyby is fixed. This defines the asterocentric frame of reference. The rotation period is usually left adjustable as the long time span of other data constrains it more accurately than the flyby data.
smoothly together. The flyby-determination usually also fixes the pole direction of the object since its orientation (and hence the zero-time and zero-rotation phase) at some epoch during the flyby is fixed. This defines the asterocentric frame of reference. The rotation period is usually left adjustable as the long time span of other data constrains it more accurately than the flyby data. -
2.
-
(a)
The
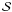 model may provide an envelope env(θ,ϕ) as well. The radii of
model may provide an envelope env(θ,ϕ) as well. The radii of 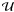 can be explicitly constrained to lie within the envelope with
can be explicitly constrained to lie within the envelope with 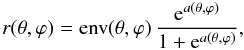 (22)where a(θ,ϕ) is a spherical harmonics series (or a parameter for an independent vertex). In our experience, however, this often weakens the convergence of the algorithm. In such cases, or if no envelope is available, it is best to use the more approximate but also more robust version (b) below.
(22)where a(θ,ϕ) is a spherical harmonics series (or a parameter for an independent vertex). In our experience, however, this often weakens the convergence of the algorithm. In such cases, or if no envelope is available, it is best to use the more approximate but also more robust version (b) below. -
(b)
Constraints equivalent to an envelope can be enforced by vertex retraction using the projection directions of the flyby images (for a detailed description of the profiles of polyhedra and the terms used below, see K11). In the following, the projections are checked in all the directions of the flyby images, and the direction Ω is, in turn, both Ω = ω and Ω = ω0 for each image (this takes care of both the shadow and limb boundaries seen from the spacecraft). For each
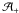 vertex i of
vertex i of 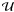 , check whether its projected radius p(αi;Ω) (from the origin at the direction αi in the projection plane) is larger than the radius
, check whether its projected radius p(αi;Ω) (from the origin at the direction αi in the projection plane) is larger than the radius 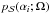 of an intersection of the radius line with an ℒ(Ω) edge of
of an intersection of the radius line with an ℒ(Ω) edge of 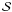 in
in 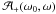 . If yes, retract according to the nearest smaller value
. If yes, retract according to the nearest smaller value 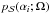 of projected radius:
of projected radius: 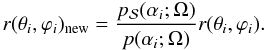 (23)The retraction produces a shape that is consistent with probe images, i.e., is within the shape envelope, while the effect of the retraction on χ2 is usually negligible since few model vertices from step 1 are expected to lie outside the envelope if the data are good (and, e.g., inertia tensor regularization is used).
(23)The retraction produces a shape that is consistent with probe images, i.e., is within the shape envelope, while the effect of the retraction on χ2 is usually negligible since few model vertices from step 1 are expected to lie outside the envelope if the data are good (and, e.g., inertia tensor regularization is used).
-
(a)
-
3.
For the vertices of
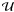 within some angular distance δ on S2 from the
within some angular distance δ on S2 from the 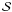 /
/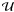 boundary, use the neighbouring radii (again within some suitable distance) for averaging ri → ⟨r⟩ to smooth out any unrealistic indentations that may occur near the
boundary, use the neighbouring radii (again within some suitable distance) for averaging ri → ⟨r⟩ to smooth out any unrealistic indentations that may occur near the 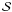 /
/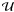 boundary. Bulges at the boundary are ruled out by step 2 at the start, but after averaging go back to retraction (step 2) if necessary. Again, the effect of this smoothing on χ2 is usually negligible.
boundary. Bulges at the boundary are ruled out by step 2 at the start, but after averaging go back to retraction (step 2) if necessary. Again, the effect of this smoothing on χ2 is usually negligible. -
4.
The result obtained is a set of vertices of
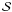 and
and 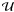 joined smoothly together. Since
joined smoothly together. Since 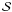 can usually be given with a level of resolution much higher than one that would affect the model fit of the other data Do, it is computationally advantageous to use a low-resolution version of
can usually be given with a level of resolution much higher than one that would affect the model fit of the other data Do, it is computationally advantageous to use a low-resolution version of 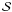 in the procedure. Once
in the procedure. Once 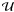 is determined, it can be glued to any higher-resolution version of
is determined, it can be glued to any higher-resolution version of 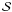 at will. Such glueing can be done without an explicit definition of the complete vertex circuits of the boundaries of
at will. Such glueing can be done without an explicit definition of the complete vertex circuits of the boundaries of 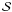 and
and 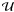 . First create sets of
. First create sets of 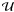 and
and 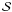 facet triangle edges that occur only once in their respective facet lists: these are boundary edges. Then connect each boundary vertex of one set to the nearest one of the other set. This results in triangles or (non-planar) quadrangles in the region between the boundaries, and the quadrangles can be split into triangles as desired.
facet triangle edges that occur only once in their respective facet lists: these are boundary edges. Then connect each boundary vertex of one set to the nearest one of the other set. This results in triangles or (non-planar) quadrangles in the region between the boundaries, and the quadrangles can be split into triangles as desired.
6.2. Distributions of derived quantities: note on volume uncertainty
A typical quantity derived from a shape model is its volume. The uncertainty in the volume is related to the shape uncertainty somewhat in the sense of a marginal distribution, so we briefly discuss this aspect. The uncertainty estimate of the volume was, for example, important in deducing the density of the asteroid Lutetia, and confirming that it was indeed at the high end of the estimated densities of asteroids (Sierks et al. 2011). When using normal distributions for radius- or volumelike variables x here, we assume that the distributions p(x) are narrow enough so that p(x) = 0, x ≤ h for all practical purposes for some h > 0.
Consider first a sphere with the centre of pR(R) at some R0. With 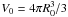 , we have, from pR(R) dR = pV(V) dV,
, we have, from pR(R) dR = pV(V) dV, ![\begin{equation} p_V(V)=\frac{1}{3}\left(\frac{3}{4\pi}\right)^{1/3} p_R\left[\left(\frac{3V}{4\pi}\right)^{1/3}\right]V^{-2/3}, \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq183.png) (24)which, for a Gaussian normal distribution
(24)which, for a Gaussian normal distribution 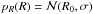 (here σ denotes the relative standard deviation w.r.t. R0), is well approximated by
(here σ denotes the relative standard deviation w.r.t. R0), is well approximated by 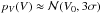 , consistent with the basic approximation from dV/V = 3dR/R (the top of the distribution is at a slightly smaller value than V0 due to the V−2/3-term).
, consistent with the basic approximation from dV/V = 3dR/R (the top of the distribution is at a slightly smaller value than V0 due to the V−2/3-term).
For an ellipsoid with semiaxes a,b, and c, using V = 4πabc/3, we take V to be a variable, and change c = 3V/(4πab) so that 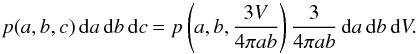 (25)The marginal distribution p(V) is thus given by
(25)The marginal distribution p(V) is thus given by 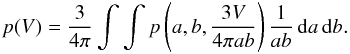 (26)For a0 = b0 = c0 = l and
(26)For a0 = b0 = c0 = l and 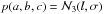 , where
, where 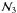 is a three-dimensional multivariate normal distribution with equal means and deviations, p(V) is approximated by
is a three-dimensional multivariate normal distribution with equal means and deviations, p(V) is approximated by 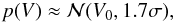 (27)already strongly in contrast with the spherical case and the basic approximation ΔV/V ≈ 3σ. The distribution of p(V) is more concentrated because the shape of the ellipsoid can change in all semiaxis directions. If the shape stayed the same and only the size changed, p(a,b,c) would only lie along a line in the (a,b,c)-space rather than sample the whole space.
(27)already strongly in contrast with the spherical case and the basic approximation ΔV/V ≈ 3σ. The distribution of p(V) is more concentrated because the shape of the ellipsoid can change in all semiaxis directions. If the shape stayed the same and only the size changed, p(a,b,c) would only lie along a line in the (a,b,c)-space rather than sample the whole space.
For general cases, the integral is replaced by a cumulative distribution function C(V) over N MCMC samples, i.e., ![\begin{equation} C(V_i)=i/N, \quad V_i=V[{\cal S}_i(p(x))], \end{equation}](/articles/aa/full_html/2012/07/aa19267-12/aa19267-12-eq205.png) (28)for i = 1,...N, and
(28)for i = 1,...N, and 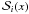 denotes the ith randomly drawn sample from the distribution p(x) of the shape parameters x, and the draws are sorted in ascending order of Vi. For numerical purposes, obtaining p(V) = dC(V)/dV is unstable, so it is easier to work with C(V) and, e.g., fit the parameters V0 and σV of a normal distribution
denotes the ith randomly drawn sample from the distribution p(x) of the shape parameters x, and the draws are sorted in ascending order of Vi. For numerical purposes, obtaining p(V) = dC(V)/dV is unstable, so it is easier to work with C(V) and, e.g., fit the parameters V0 and σV of a normal distribution 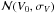 to C(V) using the Gaussian cumulative integral
to C(V) using the Gaussian cumulative integral 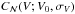 .
.
For a sphere with i.i.d. radii for each octant, we have 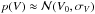 with σV ≈ σR, while a further division into four parts of equal solid angles for each octant already yields σV ≈ 0.5 σR. A needle-cushionlike division into infinitely many parts thus yields p(V) = δ(V − V0) (regardless of σ), i.e., a step function for C(V). This emphasizes that, if we have a multiparameter shape model with polyhedral radii ri, the relative volume uncertainty can be smaller than the relative radius uncertainty: 0 < ΔV/V < Δr/⟨r⟩ even when ri are correlated by a smoothness constraint. The fluctuations of r effectively cancel out most of each other as far as the total volume is concerned. As a rule of thumb, the approximation ΔV/V ≈ Δr/⟨r⟩ is more appropriate than 3Δr/⟨r⟩ when the shape uncertainty is not dominated by a scale factor for size (cf. Carry et al. 2012).
with σV ≈ σR, while a further division into four parts of equal solid angles for each octant already yields σV ≈ 0.5 σR. A needle-cushionlike division into infinitely many parts thus yields p(V) = δ(V − V0) (regardless of σ), i.e., a step function for C(V). This emphasizes that, if we have a multiparameter shape model with polyhedral radii ri, the relative volume uncertainty can be smaller than the relative radius uncertainty: 0 < ΔV/V < Δr/⟨r⟩ even when ri are correlated by a smoothness constraint. The fluctuations of r effectively cancel out most of each other as far as the total volume is concerned. As a rule of thumb, the approximation ΔV/V ≈ Δr/⟨r⟩ is more appropriate than 3Δr/⟨r⟩ when the shape uncertainty is not dominated by a scale factor for size (cf. Carry et al. 2012).
7. Discussion
We have presented methods for expanding the sets of data sources and surface types in multimodal asteroid modelling. The most plausible compromise between the datasets is given by the maximum compatibility estimate. We emphasize the mutual “synergy” effect of multimodal data in constraining shape details. This is particularly striking when partial flyby data are available. As discussed in Sierks et al. (2011) and Carry et al. (2012), the fixed flyby-determined portion of the surface greatly constrains the allowed solutions for the dark side  even when its data are disk-integrated only. Thus the solution based on photometry is considerably more restricted than if photometry were used alone. This allows the construction of large-scale nonconvex features on the dark side. The same phenomenon can be seen in the cases where good AO contours are combined with photometry. The power of this approach is demonstrated in Carry et al. (2012), where the match of the ground-based Lutetia model (published prior to the flyby) to the flyby images was shown to be remarkably good. What is more, the ground-based Lutetia data were not special in any way: the AO contours contained several systematic errors, and their aspect coverage of the target was not especially good. Of the examples presented here, the quality of the Hermione dataset is roughly similar to that of Lutetia. The octantoid parametrization allows the modelling of non-starlike features, which in the case of Hermione best explains the kidney-bean shaped AO images as views of the shadow of a large indentation. Kleopatra, on the other hand, turned out to be something of a riddle. In spite of the many available data modes, a valid model cannot be constructed yet as the data (plus the model from radar, the fourth source) are mutually inconsistent. Disk-resolved data (with fewer systematic errors) at complementary observing geometries are needed to establish a reliable multimodal reconstruction.
even when its data are disk-integrated only. Thus the solution based on photometry is considerably more restricted than if photometry were used alone. This allows the construction of large-scale nonconvex features on the dark side. The same phenomenon can be seen in the cases where good AO contours are combined with photometry. The power of this approach is demonstrated in Carry et al. (2012), where the match of the ground-based Lutetia model (published prior to the flyby) to the flyby images was shown to be remarkably good. What is more, the ground-based Lutetia data were not special in any way: the AO contours contained several systematic errors, and their aspect coverage of the target was not especially good. Of the examples presented here, the quality of the Hermione dataset is roughly similar to that of Lutetia. The octantoid parametrization allows the modelling of non-starlike features, which in the case of Hermione best explains the kidney-bean shaped AO images as views of the shadow of a large indentation. Kleopatra, on the other hand, turned out to be something of a riddle. In spite of the many available data modes, a valid model cannot be constructed yet as the data (plus the model from radar, the fourth source) are mutually inconsistent. Disk-resolved data (with fewer systematic errors) at complementary observing geometries are needed to establish a reliable multimodal reconstruction.
Reliability estimates are important in any schemes that produce detailed asteroid shape models from indirect data of various types and quality. Assessing the reliability of depicted surface features is not a simple task as the uncertainties are typically dominated by systematic errors, “unknown unknowns” rather than “known unknowns” in both data and the model setup. This makes practically all standard procedures for uncertainty evaluation (such as MCMC) more or less deficient and overoptimistic in our case. We will study this problem and develop estimation procedures in the future versions of the modelling software package described below. A further aspect of this is observation/experiment design. Using reliability estimates, we can predict how observations made at various geometries can improve the result. This should improve the time efficiency and planning of observation campaigns.
Our inversion procedures are incorporated in a continuously updated software package that is downloadable at the DAMIT asteroid modelling website2. Asteroid models and the data used in constructing them are available there as well (Ďurech et al. 2010). GPU programming typically speeds up the computation by a factor of more than one hundred. This makes the inversion very fast and allows, e.g., time-efficient Monte Carlo sampling. The software will be described in a separate paper (Ďurech et al., in prep.). The first public version of the package contains procedures for lightcurve inversion; the second one will provide the routines for analysing lightcurves, occultation timings, adaptive-optics (or other) images, and interferometric data simultaneously. Radar and thermal infrared data will be added to the source options in a forthcoming version. We will also study the use of level sets and control point sets in analysing bifurcated and other complex shape structures in a general manner. One of the advantages of level sets is their ability to provide a continuous sequence of models from a connected bifurcated shape to a separated binary one without having to change the model setup.
The mathematical properties of generalized projections are helpful here from the computational point of view. We essentially have a common routine for computing the POS image of the target, and each data mode is just a different way of sampling that image. This makes it easy to add a plug-in module for a data source.
Acknowledgments
This work was supported by the Academy of Finland project “Modelling and applications of stochastic and regular surfaces in inverse problems”. We thank Franck Marchis, Daniel Hestroffer, and Pascal Descamps for the datasets of Hermione and Kleopatra, and Josef Ďurech and Benoit Carry for discussions and comments.
References
- Carry, B., Dumas, C., Kaasalainen, M., et al. 2010, Icarus, 205, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B., Kaasalainen, M., Merline, W., et al. 2012, Planet. Space Sci., 60, 200 [Google Scholar]
- Descamps, P., Marchis, F., Ďurech, J., et al. 2009, Icarus, 203, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Descamps, P., Marchis, F., Berthier, J., et al. 2011, Icarus, 211, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Ďurech, J., & Kaasalainen, M. 2003, A&A, 404, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Grav, T., Jedicke, R., et al. 2005, Earth Moon Planets, 97, 179 [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Kaasalainen, M., Herald, D., et al. 2011, Icarus, 214, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Hestroffer, D., Tanga, P., Cellino, A., et al. 2002, A&A, 391, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M. 2001, A&A, 376, 302 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M. 2004, A&A, 422, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M. 2011, Inv. Prob. Imag., 5, 37 (K11) [Google Scholar]
- Kaasalainen, M., & Lamberg, L. 2006, Inv. Prob., 22, 749 (KL06) [Google Scholar]
- Kaasalainen, M., Lamberg, L., Lumme, K., & Bowell, E. 1992, A&A, 259, 318 [NASA ADS] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Ďurech, J., Warner, B., et al. 2007, Nature, 446, 420 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Keller, H. U., Barbieri, C., Koschny, D., et al. 2010, Science, 327, 190 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nathues, A., Mottola, S., Kaasalainen, M., & Neukum, G. 2005, Icarus, 173, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Magri, C., Howell, E., Nolan, M., et al. 2011, Icarus, 214, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Ostro, S. J., Hudson, R. S., Nolan, M., et al. 2000, Science, 288, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Ostro, S. J., Hudson, R. S., Benner, L., et al. 2002, Asteroids III, eds. W. Bottke, A. Cellino, P. Paolicchi, & R. Binzel, 151 [Google Scholar]
- Scheirich, P., Ďurech, J., Pravec, P., et al. 2010, Met. Plan. Sci., 4, 1804 [Google Scholar]
- Sierks, H., Lamy, P., Barbieri, C., et al. 2011, Science, 334, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Simonelli, D., Veverka, J., Thomas, P., & Helfenstein, P. 1994, Icarus, 114, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, R. 1994, Cel. Mech. Dyn. Ast., 59, 253. [NASA ADS] [CrossRef] [Google Scholar]
- Zacharopoulos, A. D., Arridge, S. R., Dorn, O., et al. 2006, Inv. Prob., 22, 1509 [Google Scholar]
All Figures
 |
Fig. 1 A schematic of the curve [x(λ),y(λ)] and the maximum compatibility estimate (the point closest to the new origin at the intersection of the dotted lines). The dashed line corresponds to a case with closely compatible data sources, while dot-dash indicates a case with systematic errors in models and/or data. The weight parameter λ for data mode 2 increases from left (λ = 0) to right (λ = ∞) on a curve. |
| In the text | |
 |
Fig. 2 Kleopatra reconstructed from lightcurves, AO, and interferometric data. |
| In the text | |
 |
Fig. 3 An adaptive optics contour (white crosses) with systematic errors. |
| In the text | |
 |
Fig. 4 A typical HST/FGS S-curve fitted by the Kleopatra model. |
| In the text | |
 |
Fig. 5 Sample fits of the reconstructed Kleopatra model to the AO data. |
| In the text | |
 |
Fig. 6 A radar-based test model (left) and its reconstruction (right) from simulated Kleopatra data. |
| In the text | |
 |
Fig. 7 Uncertain regions (white) of the Kleopatra reconstruction. |
| In the text | |
 |
Fig. 8 Hermione reconstructed from lightcurves and AO data. |
| In the text | |
 |
Fig. 9 Hermione model fits to the AO contours (white dots). The ridge-like structure visible in the two lower images is an artifact of the chosen smoothness level. |
| In the text | |
 |
Fig. 10 Equatorial views of Lutetia reconstructed from space probe (upper part) and ground-based data (lower part). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


