| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 12 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201219062 | |
| Published online | 02 July 2012 | |
High-velocity stars in the cores of globular clusters: the illustrative case of NGC 2808⋆
1 European Southern Observatory (ESO), Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
e-mail: nluetzge@eso.org
2 Max-Planck Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching, Germany
3 Department of Physics and Astronomy, University of Leicester, Leicester, LE1 7RH, UK
4 Astronomy Department, University of Texas at Austin, Austin, TX 78712, USA
5 School of Mathematics and Physics, University of Queensland, Brisbane, QLD 4072, Australia
6 Instituto de Astronomia, Universidad Nacional Autonoma de Mexico (UNAM), A.P. 70-264, 04510 Mexico, Mexico
7 1. Physikalisches Institut, Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
8 Sterrewacht Leiden, Leiden University, Postbus 9513, 2300 RA Leiden, The Netherlands
Received: 17 February 2012
Accepted: 15 May 2012
Context. We report the detection of five high-velocity stars in the core of the globular cluster NGC 2808. The stars lie on the red giant branch and show total velocities between 40 and 45 km s-1. For a core velocity dispersion σc = 13.4 km s-1, this corresponds to up to 3.4σc. These velocities are close to the estimated escape velocity (~50 km s-1) and suggest an ejection from the core. Two of these stars have been confirmed in our recent integral field spectroscopy data and we will discuss them in more detail here. These two red giants are located at a projected distance of ~0.3 pc from the center. According to their positions on the color magnitude diagram, both stars are cluster members.
Aims. We investigate several possible origins for the high velocities of the stars and conceivable ejection mechanisms. Since the velocities are close to the escape velocity, it is not obvious whether the stars are bound or unbound to the cluster. We therefore consider both cases in our analysis.
Methods. We perform numerical simulations of three-body dynamical encounters between binaries and single stars and compare the resulting velocity distributions of escapers with the velocities of our stars. If the stars are bound, the encounters must have taken place when the stars were still on the main sequence. We compare the predictions for a single dynamical encounter with a compact object with those of a sequence of two-body encounters due to relaxation. If the stars are unbound, the encounter must have taken place recently, when the stars were already in the giant phase.
Results. After including binary fractions and black-hole retention fractions, projection effects, and detection probabilities from Monte-Carlo simulations, we estimate the expected numbers of detections for all the different scenarios. Based on these numbers, we conclude that the most likely scenario is that the stars are bound and were accelerated by a single encounter between a binary of main-sequence stars and a ~10 M⊙ black hole. Finally, we discuss the origin of previously discovered fast stars in globular clusters, and conclude that the case of NGC 2808 is most likely a representative case for most other detections of fast stars in globular clusters. We show that with the present analysis we are able to explain high-velocity stars in the clusters M3 and 47 Tucanae with simple dynamical encounters.
Key words: globular clusters: individual: NGC 2808 / stars: kinematics and dynamics
© ESO, 2012
1. Introduction
High-velocity stars in globular clusters have been a puzzle to astronomers since the beginning of velocity measurements. Especially finding fast giant stars in the core of globular clusters has drawn attention. Gunn & Griffin (1979) found two fast stars which they called “interlopers” in the globular cluster M3. The stars are located in the core of the cluster, both at a projected distance of about 20′′ from the center. With radial velocities of 17.0 km s-1 and −22.9 km s-1 relative to the cluster, they move with 3.5 and 4.5 times the central velocity dispersion (σc = 4.9 km s-1), respectively. Due to the high systemic velocity of the cluster itself (Vr ~ −147 km s-1) the possibility of these stars being field stars is rather low. Meylan et al. (1991) found a similar case for the globular cluster 47 Tucanae. The stars which they found have radial velocities of −36.7 km s-1 and 32.4 km s-1 in the reference frame of the cluster which corresponds to 4.0 and 3.6 times the core velocity dispersion σc = 9.1 km s-1. Despite the fact that the low systemic velocity of the cluster does not allow for an accurate kinematic statement on the membership of these two stars, their position in the color − magnitude diagram and the high Galactic latitude of 47 Tucanae (b = −44°) both argue for membership.
 |
Fig. 1 ARGUS field of view (left) and velocity map of NGC 2808 (right). Visible as bright blue spots are the two high-velocity stars FS1 and FS2. Marked with the dashed blue line is FS4, the star which does not dominate its spaxel and therefore is not detectable. The blue cross marks the center of the cluster. |
Plausible mechanisms to explain these high-velocity stars are ejection from the core by recoil from an encounter between a single star and a binary, between two binary stars, between a binary and an intermediate-mass black hole (IMBH) at the center or even from encounters of stars with an IMBH binary (e.g. Gualandris et al. 2004, 2005; Baumgardt et al. 2006; Gvaramadze et al. 2009; Mapelli et al. 2005). It has been recently suggested that globular clusters may contain central black holes in the mass range of 103 − 104 M⊙ (Miller & Hamilton 2002; Baumgardt et al. 2005) which fall on top of the relation between the velocity dispersion and black hole mass seen for galaxies (e.g. Ferrarese & Merritt 2000; Gebhardt et al. 2000). Kinematic signatures for intermediate-mass black holes have been found in the globular clusters ω Centauri (Noyola et al. 2008, 2010), G1 in M 31 (Gebhardt et al. 2002, 2005) and NGC 6388 (Lützgendorf et al. 2011). High velocity stars are predicted in globular clusters which host intermediate-mass black holes. Therefore it is important to study such stars in more detail when observed in a globular cluster.
The globular cluster NGC 2808 is of high interest in many regards. From the photometric side, it has a complex extended horizontal branch (Harris 1974; Ferraro et al. 1990) which shows puzzling discontinuities in the stellar distribution along its blue tail. Furthermore, Piotto et al. (2007) found a triple main sequence after accurate photometric and proper motion analysis with deep Hubble Space Telescope (HST) data. This indicates the existence of three sub-populations with an age of ~12.5 Gyr and different metallicities. The kinematic properties of NGC 2808 are also unusual. By analyzing Fabry-Perot data, Gebhardt et al. (2012) found rotation in the outer parts of the cluster with a maximum rotation velocity of Vrot ~ 5 km s-1. The latest radial velocity measurements of the cluster core by Lützgendorf et al. (2012) have shown that NGC 2808 most probably does not host an intermediate-mass black hole: the best fit model is consistent with no IMBH and gives an upper limit of MBH < 1 × 104 M⊙.
In this work we report on the discovery of five high-velocity stars in NGC 2808 and discuss several explanations and ejection scenarios for the two stars found in our integral field spectroscopy observations. In Sect. 2 we explain the observations and the method of obtaining single star velocities with integral field spectroscopy. Further, we introduce a second data set used for velocity measurements taken from a Fabry-Perot instrument. At the end of the first Section we determine the escape velocity of NGC 2808. Section 3 is dedicated to the discussion of alternative explanations for the observed high velocities including foreground stars, binaries and atmospheric active stars. Section 4 describes the analysis of the Maxwellian velocity distribution and the probabilities of these stars resulting from relaxation while Sect. 5 describes the dynamical three-body simulations in order to find the most likely acceleration scenario for the two fast stars. In Sect. 6 we briefly discuss other cases of fast star detections in globular clusters. Finally, we summarize our results and list our conclusions in Sect. 7.
Radial velocities and photometric properties of the two fast stars FS1 and FS2.
 |
Fig. 2 Kinematic properties of the five high-velocity stars. Left: the histogram of the Fabry-Perot data in the core of NGC 2808. Marked with colors are five high velocity stars FS1 to FS5. Right: the escape-velocity profile (solid line) and its uncertainties (dotted line) obtained from the density profile overplotted by the total velocities and projected positions of the five fast stars. |
2. Radial velocities
The data we use were obtained with the GIRAFFE spectrograph of the FLAMES (Fiber Large Array Multi Element Spectrograph) instrument at the Very Large Telescope (VLT) in ARGUS (Large Integral Field Unit). For more details on the observations and reductions we refer to Lützgendorf et al. (2012). From these data we construct a velocity map which is shown in Fig. 1 together with the corresponding field of view from the HST image. The two fast stars are visible as bright “blue” spots and are labeled with FS1 and FS2 in the maps. To estimate their velocities, we use the output of a shot noise routine described in Lützgendorf et al. (2012). This routine computes for every spaxel the number of stars that contribute to the light of the spaxel and indicates which spaxels are dominated by a single star. With this information we find the spaxel to which our two (bright) fast stars contribute with more than 80% of the light and use the radial velocities derived for these spaxels as the ones of the stars. These velocities are corrected for the systemic velocity of the cluster (Vr = 93.6 km s-1, Lützgendorf et al. 2012).
A second measurement is obtained from the dataset observed by Gebhardt et al. (2012) with the Rutgers Fabry Perot on the Blanco 4-m telescope at Cerro Tololo Inter-American Observatory (CTIO). This dataset contains 3634 stars and covers the center of the cluster as well as regions up to 4 arcmin radius. We match this dataset with our photometric catalog from the HST image and identify the two fast stars. Despite crowding in the inner regions, the two stars are resolved and can be identified in the Fabry-Perot dataset. In addition to FS1 and FS2, we find three more stars with velocities values between 36.0 km s-1 and 42.0 km s-1 inside the core radius labeled with FS3, FS4 and FS5. Table 1 lists the velocity measurements of all the stars as well as other properties derived from the HST data. Besides FS1 and FS2 only FS4 is also located inside the field of view of the combined ARGUS pointing (see Fig. 1). However, due to its low contribution of ~55% to the single spaxel we measure a much lower velocity in the IFU data than with the Fabry-Perot. The remaining stars lie outside the IFU pointing. Figure 2 shows the histogram of the radial velocities inside the core from the Fabry-Perot data set. The five fast stars are color-coded and visible as outliers of the distribution.
In addition to the spectroscopic data sets we also received proper motions for four out of the five stars (private communication, Jay Anderson). As listed in Table 1 the proper motions indicate that all stars are cluster members and increase the total velocities up to 40−45 km s-1. FS3, unfortunately, lies outside the proper motion dataset and therefore can only be assigned a lower limit of velocity. Since our measurements are only complete for FS1 and FS2 we decided to limit the following analysis to these two stars.
 |
Fig. 3 Fabry-Perot photometric points for FS1. Overplotted is the best fit of the model for the Hα line. |
Figure 3 shows the photometric data points of the Fabry-Perot for FS1 and the best fit to its spectrum. The data of FS1 is not well reproduced by the model (solid line). In order to compare velocities from both datasets the velocities are corrected for the systemic motion of the cluster by computing the average velocity of the central region. The results from both data sets show high velocities for these stars. However, for FS1 the two measurements differ by 7 km s-1, i.e. more than 1σ, from each other. The star is close to the saturation limit and therefore causes difficulties when measuring the velocity. Also, measuring individual velocities with integrated light can lead to larger errors since other stars always contribute some amount of light to the analyzed spectrum. For FS2 the measurements agree within the error bars. Thus, the difference for FS1 is probably not due to a systematic shift. The discrepancy for FS1 can have several reasons: a) the velocity of this star is variable. This suggests a binary or long period variable and is discussed in more detail in Sect. 3. b) At least one of the measurements is affected by a large error. Considering the quality of the fit of the Fabry-Perot data we consider the spectroscopic measurement more accurate.
As a next step, we calculate the escape velocity of the cluster as a function of radius. This value gives the information needed to decide whether the stars are bound or unbound. We obtain an escape velocity profile by parametrizing our surface-brightness profile with a multi-gaussian expansion (MGE, Emsellem et al. 1994) as implemented in the Jeans anisotropic models (JAM) by Cappellari (2008). The parametrization allows an easy way of deprojecting the profile after multiplying it with the derived M/L profile from our kinematic fits (see Lützgendorf et al. 2012). The gravitational potential generated by the deprojected density of stars is given by Eq. (39) of Emsellem et al. (1994): 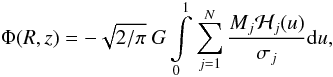 (1)where G is the gravitational constant, Mj and σj the enclosed mass and the dispersion of each of the N Gaussians, respectively and with
(1)where G is the gravitational constant, Mj and σj the enclosed mass and the dispersion of each of the N Gaussians, respectively and with ![\begin{equation} \label{eq:hi} \mathcal{H}_j(u) = \frac{\mathrm{exp}\left\{ \frac{-u^2}{2\sigma_j^2} \left[ R^2 + \frac{z^2}{1-\left(1-q_j^2\right)u^2}\right]\right\}}{\sqrt{1-\left(1-q_j^2\right)u^2}}, \end{equation}](/articles/aa/full_html/2012/07/aa19062-12/aa19062-12-eq116.png) (2)a function of the integration variable u, the deprojected axial ratio 0 ≤ qj ≤ 1, and the cylindrical coordinates R and z.
(2)a function of the integration variable u, the deprojected axial ratio 0 ≤ qj ≤ 1, and the cylindrical coordinates R and z.
The escape-velocity profile is then evaluated by calculating the difference in the potential at a radius of r and the potential at the tidal radius (rt = 35 pc, Harris 1996) as given by the equation: 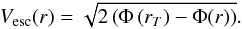 (3)The resulting profile is shown in Fig. 2. Overplotted are the velocities of the five stars at their projected radii. Since the radii are projected, they only give a lower limit on the actual distance from the center. Considering the uncertainties of the stellar velocities and of the escape velocity from the cluster, we find that star FS4 is consistent with being both bound and unbound. The remaining stars appear to be bound, but given the large velocity uncertainties we will also investigate ejection mechanisms in the unbound regime.
(3)The resulting profile is shown in Fig. 2. Overplotted are the velocities of the five stars at their projected radii. Since the radii are projected, they only give a lower limit on the actual distance from the center. Considering the uncertainties of the stellar velocities and of the escape velocity from the cluster, we find that star FS4 is consistent with being both bound and unbound. The remaining stars appear to be bound, but given the large velocity uncertainties we will also investigate ejection mechanisms in the unbound regime.
3. Possible explanations
Despite the uncertainties in the exact velocity, both stars lie more than 3σc above the systemic velocity of the cluster, where σc = (13.4 ± 0.2) km s-1 (Lützgendorf et al. 2012) represents the central velocity dispersion. Before investigating dynamical acceleration scenarios for the stars, we consider possible alternative explanations for the high velocities.
 |
Fig. 4 Color − magnitude diagram of NGC 2808 overplotted with the positions of the high-velocity stars FS1 to FS4. All of them are located on the red giant branch or the horizontal branch and therefore most likely cluster members. |
3.1. Foreground stars
The first possibility we consider is that the two stars are field stars and therefore moving with a different velocity than the cluster. We identify the two stars in our HST image (see Fig. 1) and study their position on the color − magnitude diagram (CMD) which was obtained in Lützgendorf et al. (2012). Figure 4 shows the position of all the stars in the CMD. Both stars are located on the giant branch, which suggests cluster membership. The three other stars are also most likely cluster members. FS1 is the brightest star in our pointing and sits at the top of the giant branch. The fact that the brightest star in our dataset is also the fastest is suspicious. This star is most likely a long period variable star and will be discussed in more detail in Sect. 3.3. The second star (FS2), however, lies in the central part of the giant branch about one magnitude fainter than FS1 and does not seem to show any peculiar photometric properties.
The fact that both stars lie on the giant branch of the cluster does not strictly exclude them from being foreground stars. Stars at a distance of a few hundred pc may also appear superposed on the giant branch of NGC 2808. In the case of FS2, a lower main sequence foreground star would be projected up on the giant branch if its apparent magnitude was increased by 8 to 9 mag. This would imply that the star is located 40 − 60 times closer than a giant of similar apparent magnitude. That is, at a distance of 240 − 150 pc from us. FS1 is even more extreme. With a color (B − V) ~ 1.9, an equivalent dwarf star would have an apparent brightness increased by more than 12 mag. This would mean that the star is 240 times closer to the sun than its giant equivalent and therefore at 40 pc distance from us.
In general the probability of contamination through galactic field stars is rather low. According to a galactic model by Ratnatunga & Bahcall (1985), the estimated number of field stars per square arcminute projected onto the central regions of NGC 2808 is 3.4 × 10-2 for 0.8 < (B − V) < 1.3 (FS2) and 1.8 × 10-3 for (B − V) > 1.3 (FS1). The stellar population synthesis model of the Milky Way by Robin et al. (2004) can also be used to predict the number of foreground stars expected in this part of the sky. For a field of view of 0.5 arcmin2 at the position of l = 282.19°, b = −11.25°, the model does not predict any stars in the observed magnitude ranges (mV = 13.5 − 14.5 mag, mI = 11.5 − 13.0 mag). Also, the high radial velocity of NGC 2808 makes it easier to distinguish between field stars and cluster members.
Finally, neither star shows peculiar motions in the plane of the sky and the tangential velocities fall inside the velocity distribution of the cluster (see Table 1). This strongly argues for membership and a dynamical connection between the stars and cluster. Considering all these facts, we conclude that both stars are giants and associated to the cluster.
3.2. Binaries
The binary fraction in typical globular clusters is about 10% (e.g. Rubenstein & Bailyn 1997; Davis et al. 2008; Dalessandro et al. 2011). Due to their higher dynamical mass, binaries tend to sink to the cluster center and become more concentrated in that region. This is why it is likely that binaries are present in our field of view. The possibility that these two fast stars are binaries, however, is rather low.
The fact that we measure very similar radial velocities at different epochs (IFU and Fabry-Perot datasets) with a time difference of 15 years already speaks against a binary scenario. Within this time period we should have seen large differences between the two measurements if the velocities were periodical. If we assume that the radial velocities that we measure for our two stars are their orbital velocities, a ~ 1 M⊙ companion would imply a separation of ~ 0.5 AU. The two stars are located on the giant branch and their radii are of about 7 R⊙ (FS1) and 70 R⊙ (FS2) (most likely lower limits), which are comparable to the presumed separation. This would indicate that these systems are in deep contact and that we should see signatures of accretion and mass transfer in the form of X-ray and UV excesses. Servillat et al. (2008) obtained X-ray observations with Chandra for the core of NGC 2808. Comparing their observations with our image, we see no match between our two stars and any of the X-ray sources detected. We also investigate a near and a far UV image obtained with the Space Telescope Imaging Spectrograph (STIS) on board the HST (Program ID: 8511). The stars are visible in the near UV but no source was detected in the far UV image. We conclude that these stars show no excess in either X-ray and UV which excludes almost all scenarios of contact binaries.
Sommariva et al. (2009) investigate the binary fraction of the globular cluster M4 via spectroscopy. They find 57 binary star candidates out of 2469 observed stars with 4 candidates inside the core radius. Looking at their table of candidates we find 7 binaries which show velocities > 20 km s-1 in one of their orbital phases. Since the velocity dispersion of NGC 2808 is over twice as high as the one of M4 (~4 km s-1), total velocities around 40 km s-1 would be possible if the binary itself approached with a velocity > 20 km s-1. However, all high velocity binaries in M4 lie in the upper main sequence and the turn-off region. There is no high velocity binary observed on the giant branch. To make a quantitative statement, we estimated the expected fraction of binaries with these properties and velocities higher than 45 km s-1 with binary population synthesis.
We assume a binary fraction of 10% and use a log-normal orbital period distribution with a mean of ⟨ log (P/days) ⟩ = 4.8 and a sigma of 2.3 as obtained by Duquennoy & Mayor (1991). The binary components are chosen randomly from an evolved (over 12 Gyr) Kroupa initial mass function (IMF) to account for the age of NGC 2808. For the eccentricities we assume a thermal distribution of f(e) = 2e. Thus, for every binary we compute M1, M2, P and e. From P we derive the semi-major axis a and place both components (M1,M2) at random positions in their orbits. We then distribute the binary orientation randomly in space and add systemic velocities drawn from a velocity distribution with σ = 13.4 km s-1. Finally we observe the binaries from a random position and count how often a giant star or main-sequence star with M > 0.8 M⊙ has velocities | V | > 45 km s-1. As additional boundary conditions we required that the pericenter distance of the binary is larger than the sum of the stellar radii, i.e. a(1e) > (R ∗ 1 + R ∗ 2).
Among the 1000 bright stars in our pointing we expect 0.0054 stars like FS2 (R ∗ ~ 7 R⊙) and only 0.00012 stars like FS1 (R ∗ ~ 70 R⊙) if their velocities originate from orbital binary velocities. To summarize, it is possible but highly unlikely that the high velocities we observe are due to orbital velocities in binary systems.
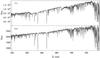 |
Fig. 5 Spectra of the two fast stars extracted from the ARGUS integral field unit in the Calcium Triplet region. The lines of both stars are narrow and confirm the assumption that both stars are giants. |
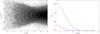 |
Fig. 6 Monte Carlo simulations of recovering the radial velocities of v = 44 km s-1 and v = 37 km s-1 as a function of the magnitude of the star. The left panel shows the measured velocities of every spaxel from the 106 realizations as a density contour plot. The magenta and green lines mark the detection limits of 42 km s-1 and 35 km s-1 for FS1 and FS2 respectively. A spaxel with a velocity lower than 2 km s-1 (which corresponds to the error bars) minus the actual radial velocity is not considered to be a detection anymore. The right panel visualizes the probability of detecting a star with a radial velocity of 44 km s-1 (magenta) and 37 km s-1 (green) as well as their smoothed curves. |
3.3. Atmospheric active stars
Another possibility is that these stars have active atmospheres, such as strong stellar winds or expanding shells which we would see as approaching velocities. According to its location in the CMD, FS1 is most likely a Mira star. Studies have shown that the amplitudes of Mira pulsations do not exceed 30 km s-1 (e.g. Hinkle 1978; Hinkle et al. 1982; Hinkle et al. 1997; Lebzelter et al. 2000; Lebzelter et al. 2005; Lebzelter & Wood 2011). Our stars show velocities faster than this limit. However, an explanation could be that these stars have radial velocities of about 20 km s-1 on top of their Mira pulsations.
Lebzelter & Wood (2011) recently investigated the long period variables of NGC 2808. Unfortunately, they had to exclude the inner regions of the cluster due to crowding. We identify their long period variable stars in our pointing and found two matches. The first one is LW 15 with a period of 332 days while the second one, LW 7, does not have a precise position and is therefore an uncertain candidate with a period of 21 days. We use the matches in our pointing to compare these spectra with our two fast stars. The spectra of the fast stars are shown in Fig. 5. No conspicuous features were found in the Mira spectra nor in the spectra of the fast stars. The lack of studies of Mira spectra in the optical range, especially in the Calcium Triplet region, prevents us from making comparisons with other measurements.
Another argument against the pulsation velocities is the fact that optical lines usually form in the upper atmospheres where no shock waves can be observed. Also, these optical velocities are nearly always directed inward relative to the stellar center-of-mass as found by Wood (1979).
It is worth mentioning that we found no asymmetry in any of the lines used to measure the radial velocity. Assuming that the high velocity would come from an atmospheric effect, such as winds or expanding shells, one would expect the lines to be either asymmetric like p-Cygni profiles or even split into two parts which is often observed in Mira variables (e.g. Scholz 1992; Lamers & Cassinelli 1999).
We conclude that thermal pulsations are an explanation for the high velocities of our two stars seem rather unlikely. The range of velocities reached by these pulsations is not high enough to explain the peculiar motions of the stars and unlikely to be strongly represented in optical lines.
4. The bound case – Maxwellian distribution
Having established that the most likely scenario is that the two stars do indeed have velocities exceeding more than three times the velocity dispersion of the cluster, we investigate possible acceleration mechanisms of dynamical nature. We first consider the case in which we assume that the stars are bound to the cluster. Under this assumption, the stars could have been accelerated either through encounters as giants or in their main-sequence stage. For the latter the acceleration can occur through either many two-body encounters or a single encounter with a more massive object. In this Section we discuss the first scenario and the likelihood of observing such an event.
4.1. Acceleration through uncorrelated two-body encounters
The first possibility we consider is that the stars acquired their high velocities through relaxation, i.e. a sequence of uncorrelated, distant encounters with other cluster stars over long timescales. In such a case they would be bound to the cluster and belong to the tail of the three-dimensional Maxwellian velocity distribution which is established by relaxation. However, stars with velocities ~ 3.5σ are quite rare. The chance of detection decreases even more if one also considers the probability of detecting the high-velocity star in an integral-field unit (IFU) since the star has to be very bright to be detected. The final probability is composed of the probability of a Maxwellian velocity distribution with a certain velocity dispersion producing a high velocity star, the number of stars in our pointing and the probability of detecting such a star in our pointing.
In order to make a quantitative statement we calculate these probabilities in the following way. We use the velocity dispersion profile obtained in Lützgendorf et al. (2012) to estimate σ at the position of the two fast stars. From this, we find that the stars have velocities of 3.2 and 3.1 times their local velocity dispersion. The probability of finding a star with a total velocity V or higher from a three-dimensional Maxwellian velocity distribution is then given by: ![\begin{equation} \label{eq:fraction} p(x) = 1 - \left[{\rm erf}\left(\frac{x}{\sqrt{2}}\right) - \sqrt{\frac{2}{\pi}}x{\rm e}^{-x^2/2}\right], \end{equation}](/articles/aa/full_html/2012/07/aa19062-12/aa19062-12-eq172.png) (4)with x = V/σ.
(4)with x = V/σ.
With this information we can calculate how many stars we would expect among all the stars in the pointing using the stars which have been found in the HST image. In order to obtain the detection probability we run Monte Carlo simulations for 106 spaxels. For each simulated spaxel we draw 10 stars from the luminosity function. For 9 of them, we assign random total velocities from a Maxwellian velocity distribution with σ = 13.4 km s-1 as well as a random spatial orientation. The tenth star is always assigned a velocity value of 44 km s-1. We build the spaxel in the following way: for each star we take the template spectrum, scale it with the flux of the star, and shift it with the amount of its projected radial velocity. Then we combine all 10 spectra to a single spaxel spectrum. The velocity of each spaxel is measured using the penalized pixel-fitting (pPXF) program developed by Cappellari & Emsellem (2004) as described in Lützgendorf et al. (2012). Figure 6 shows the result of the Monte Carlo simulations. Plotted are all the 106 measured spaxel velocities as a function of the magnitude of the star with V = 44 km s-1 in the form of a density contour. This shows that the probability of detecting a high velocity star strongly decreases with the magnitude of the star.
In order to calculate the detection probability, we set the detection limit equal to the minimal velocities within the error bars (2 km s-1), 42 km s-1 for FS1 and 35 km s-1 for FS2. Spaxel with velocities below this limit are not considered to be a detection anymore. The probability is obtained by deriving the fraction of stars which are faster than these limits in overlapping bins of 100 stars each. The right panel of Fig. 6 shows the smoothed curve of the probability for FS1 (magenta) and FS2 (green). The plot shows that the probability to detect a star with a radial velocity of 37 km s-1 in the IFU is higher by almost a factor of 5 than a star with 44 km s-1 in the radial component and that for stars fainter than mV = 17 both velocities are not detectable anymore.
To derive the expected number of stars with this configuration we multiply the luminosity function of stars in our pointing with the probability from the Maxwellian distribution and the detection probability from the Monte Carlo simulations and integrate over all magnitudes for both stars. As a final result we derive:  For further analysis we also derive the pure detection probability fb, which accounts for (1) the geometric probability that the velocity component along the line of sight exceeds a certain threshold velocity, and (2) the probability that the star is massive and bright enough to be detected in the IFU. The probabilities are derived in the same way as described above but without multiplying by the probability from the Maxwellian distribution. Thus we integrate only the probability function from the Monte Carlo simulations multiplied by the number of stars over the entire magnitude range. The derived detection probabilities for stars like FS1 and FS2 are fb,FS1 = 4 × 10-4 and fb,FS2 = 4 × 10-3, respectively.
For further analysis we also derive the pure detection probability fb, which accounts for (1) the geometric probability that the velocity component along the line of sight exceeds a certain threshold velocity, and (2) the probability that the star is massive and bright enough to be detected in the IFU. The probabilities are derived in the same way as described above but without multiplying by the probability from the Maxwellian distribution. Thus we integrate only the probability function from the Monte Carlo simulations multiplied by the number of stars over the entire magnitude range. The derived detection probabilities for stars like FS1 and FS2 are fb,FS1 = 4 × 10-4 and fb,FS2 = 4 × 10-3, respectively.
We conclude that neither FS1 nor FS2 is likely to originate from the Maxwellian velocity distribution. The probability for a star such as FS2 is higher than that for FS1 by an order of magnitude but still too low to explain the observations with this mechanism. It is therefore unlikely that FS1 and FS2 acquired their high velocities through relaxation and we study other acceleration scenarios in the following Sections.
5. Dynamical encounters
The numbers we derive from the analysis of the Maxwellian distribution and observational effects are too small to explain the observed stars. Therefore we test for alternative acceleration scenarios due to dynamical three-body encounters of two different types of stars (main-sequence stars and giants) as described in this section.
5.1. Acceleration in the main-sequence stage
Here we study a scenario in which FS1 and/or FS2 were accelerated by a single dynamical encounter at some time during the main-sequence stage. To test this possibility we perform numerical three-body scattering experiments (e.g. Hills & Fullerton 1980; Hut & Bahcall 1983; Sigurdsson & Phinney 1993; Heggie et al. 1996; Gvaramadze et al. 2008, 2009; Gvaramadze & Gualandris 2011) involving main-sequence stellar binaries and single stars/compact objects of different kinds. The simulations are carried out with the sigma3 package included in the STARLAB software environment (McMillan & Hut 1996).
We adopt a mass of m = 0.8 M⊙ and a radius of R = 0.8 (M/M⊙)0.7 R⊙ (Habets & Heintze 1981) for both stars, and we set the characteristic ejection velocity to Vej = 45 km s-1. We consider four types of binary-single star encounters, which are detailed in Table 2: (1) encounters with a main-sequence star of the same mass; (2) encounters with a 0.8 M⊙ white-dwarf; (3) encounters with a 1.4 M⊙ neutron star and (4) encounters with a 10 M⊙ black hole. We consider a fifth type of encounters, between a binary containing a main-sequence star and a stellar mass black hole and single stars. Such binaries originate from the encounters of stellar binaries with single black holes.
 |
Fig. 7 Branching ratios versus initial binary separation for the outcomes of encounters between a stellar binary and a main-sequence star E1 (left) or a stellar mass black hole E4 (right). The label “runaway” refers to encounters that produce an escaper with velocity larger than 45 km s-1. |
Dynamical encounters between a main-sequence stellar binary and a single star.
We first discuss the simulations involving stellar binaries. As is typical in three-body scatterings, we use a Monte Carlo approach to randomly generate the angles that define the spatial orientation of the binary with respect to the incoming star. The binary eccentricity is randomly drawn from a thermal distribution (Heggie 1975), having set a maximum value to guarantee that the binary components do not come into contact at the first pericenter passage. The impact parameter b is randomized according to an equal probability distribution for b2 with a maximum value that is determined automatically for each set of experiments (see Gualandris et al. 2004, for a detailed description). The relative velocity between the single star and the binary center of mass is set equal to the cluster velocity dispersion. We vary the initial semi-major axis of the binary from a minimum value amin = 0.05 AU set by the radii of the stars to a maximum value amax = 10 AU.
While stars are treated as point particles in the integrations, all inter-particle distances are monitored to identify physical collisions when the distance between any two stars becomes equal to the sum of their radii. Since we are interested in the ejection of stars with high velocity, we neglect all encounters that result in a physical collision. While it is a priori possible to eject collision products during dynamical encounters, the fact that stars FS1 and FS2 lie precisely on the color − magnitude diagram of the cluster strongly argues against such a scenario.
Possible outcomes of three-body encounters include: flybys of the single star past the binary (F), exchanges of the incoming star into the binary (E), with ejection of one of the binary components, ionization (I) of the binary where three single stars get ejected, and collisions. For each type of encounter listed in Table 2, we consider all outcomes resulting in the ejection of (at least) one main-sequence star, and record the ejection velocity. Ionizations are rare and, for our set of parameters, only occur in the case of encounters with a black hole. In all the other cases, the binaries are too hard to be broken apart by the incoming star (see Fig. 7). In the case of encounters between equal mass stars, the binary is always too hard to be unbound by the incoming star.
Figure 7 gives the branching ratios, i.e. the fraction of all encounters resulting in a particular outcome, as a function of the initial binary separation, for model E1 and E4. The relative importance of flybys, exchanges and mergers is a strong function of the binary semi-major axis, with mergers occurring in about 40% of the cases for the tightest binaries.
 |
Fig. 8 Average ejection velocities of all main-sequence escapers for the different types of encounters considered. For model E5, we adopt a black hole mass of 30 M⊙. The dotted horizontal line marks the characteristic velocity of the runaways. |
The average velocity of all main-sequence escapers is shown in Fig. 8 for all types of encounters. Encounters with a main-sequence star produce average recoil velocities significantly lower than required for the observed runaways, for all considered values of the binary semi-major axis. Encounters with white dwarfs and neutron stars produce only slightly larger velocities, and reach the required 45 km s-1 only for the tightest binaries. Encounters with a stellar mass black hole, on the other hand, result in typical ejection velocities in excess of 45 km s-1 for all values of a ~ < 0.4 AU. Given that these are average velocities, large velocities can occasionally be achieved even for larger separations.
If encounters with stellar-mass black holes lead to exchanges, they are expected to produce a star-black hole binary that will then interact with the dominant population of single, main-sequence stars. We find that such binaries typically have large eccentricities. For this reason, when simulating encounters of type E5, we generate binaries with a suprathermal eccentricity distribution. The branching ratios for this process are shown in Fig. 9. Most encounters of this kind result in simple flybys or mergers. The average velocity of escaping main-sequence stars is given in Fig. 8 for the case of a 30 M⊙ black hole. Only binaries with separation ≲ 0.1 AU produce average velocities larger than 45 km s-1. On average, higher black holes masses do not result in larger ejection velocities, because a larger fraction of encounters results in a collision.
 |
Fig. 9 Branching ratios versus initial binary separation for the outcomes of encounters of type E5, in the case of a black hole of 30 M⊙. |
The rate of ejection of runaway stars like FS1 and FS2 by encounters with a compact object can be estimated as 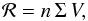 (7)where n is number density of stars in the core, Σ is the cross-section for the process and V is the relative velocity between the binary and the black hole. The cross section can be derived from the scattering experiments as
(7)where n is number density of stars in the core, Σ is the cross-section for the process and V is the relative velocity between the binary and the black hole. The cross section can be derived from the scattering experiments as 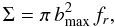 (8)where bmax represents the maximum impact parameter for the process under consideration and fr is the fraction of encounters resulting in escapers with velocity larger than 45 km s-1 (see Fig. 11). The rate for interactions is therefore
(8)where bmax represents the maximum impact parameter for the process under consideration and fr is the fraction of encounters resulting in escapers with velocity larger than 45 km s-1 (see Fig. 11). The rate for interactions is therefore 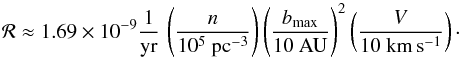 (9)Finally, we multiply the event rate ℛ as a function of the binary semi-major axis by the distribution function of the semi-major axis taken from Duquennoy & Mayor (1991). The final rates are shown in Fig. 10, where we assume a relative velocity equal to the dispersion velocity in the core V = 13 km s-1, and a stellar density n = 105 pc-3. We obtain the central density by extrapolating our density profile (n(0) = 106 pc-3) and multiplying this by a binary fraction of 10%. We caution that this is a mere working estimate derived from the total estimated stellar mass and the structural parameters of the cluster, and ℛ scales linearly with the stellar density. The final rate is derived by integrating over all a.
(9)Finally, we multiply the event rate ℛ as a function of the binary semi-major axis by the distribution function of the semi-major axis taken from Duquennoy & Mayor (1991). The final rates are shown in Fig. 10, where we assume a relative velocity equal to the dispersion velocity in the core V = 13 km s-1, and a stellar density n = 105 pc-3. We obtain the central density by extrapolating our density profile (n(0) = 106 pc-3) and multiplying this by a binary fraction of 10%. We caution that this is a mere working estimate derived from the total estimated stellar mass and the structural parameters of the cluster, and ℛ scales linearly with the stellar density. The final rate is derived by integrating over all a.
The number of events producing runaway stars with velocity ≳ 45 km s-1 is then 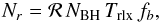 (10)where NBH is the number of BHs to be found in the core, Trlx is the relaxation time of the core (the high velocity of the stars should decrease due to two-body relaxation within this time scale) and fb the detection probability as obtained in Sect. 4.1.
(10)where NBH is the number of BHs to be found in the core, Trlx is the relaxation time of the core (the high velocity of the stars should decrease due to two-body relaxation within this time scale) and fb the detection probability as obtained in Sect. 4.1.
 |
Fig. 10 Event rates of the different encounters as a function of the separation multiplied by the distribution function of the semi-major axis. From this the final event rate can be achieved by integrating over the values for the semi-major axis. |
Estimating the number of black holes in the cluster core is not straightforward. There are two factors which play a major role. The first one is the black hole retention fraction fret, i.e. the fraction of black holes that does not escape the cluster due to kick velocities acquired during their formation. The second factor is how efficiently equal-mass black holes eject themselves from the cluster core by building a subcore through mass segregation. This process would leave only a few (0 − 3) black holes in the cluster (e.g. Sigurdsson & Hernquist 1993; Kulkarni et al. 1993; Miller & Hamilton 2002; O’Leary et al. 2006). However, Mackey et al. (2007) find different results. In their N-body simulations, larger numbers of black holes are retained because the ejection rate of black holes decreases as the subcluster evolves. In order to estimate an appropriate number of black holes in the core of the globular cluster we use results from our own N-body simulations which are described in Lützgendorf et al. (in prep.). Our results show that for a model with a retention fraction of fret = 0.3 and N = 128 000 particles there are only one or two black holes remaining after 12 Gyr. For higher retention fractions such as fret = 1.0 this number increases to 20 black holes after 12 Gyr. With N = 50 000 stars remaining, these values correspond to black-hole fractions of fBH = NBH/N ∗ = 2 × 10-5 and 4 × 10-4 respectively, equivalent to 20 to 500 black holes in a cluster with 1 × 106 stars. These values are lower limits though, since we are not only interested in the number of black holes at the current time, but more so in the average number of black holes over the entire lifetime of the cluster. Therefore, an average black hole number of NBH ~ 100 seems adequate as a first-order estimate.
 |
Fig. 11 Branching ratios versus initial binary separation for the outcomes of encounters between a stellar binary and a black hole of 10 M⊙ (model B2). The label “runaway” refers to encounters that produce an escaper with velocity larger than 45 km s-1. |
 |
Fig. 12 Average ejection velocity in runs B1 (left) and B2 (right) as a function of the initial binary semi-major axis. Different lines refer to different values of the BH mass, MBH = 10, 20, 50, 100 M⊙, respectively, from bottom to top. Dotted lines indicate the required ejection velocity of 45 km s-1. |
Adopting a relaxation time Trlx = 108 yr (Harris 1996), we find the expected number of runaway stars produced by encounters between a main-sequence binary and a stellar mass black hole to be: ![\begin{eqnarray} \label{eq:msenc} N_{r,\rm FS1} & = & 0.3 \ \rm{stars} \\[1.5mm] N_{r,\rm FS2} & = & 3.4 \ \rm{stars}. \end{eqnarray}](/articles/aa/full_html/2012/07/aa19062-12/aa19062-12-eq223.png) The fact that the expected number of stars like FS1 is an order of magnitude lower than that of FS2 comes from the detection probabilities. A star like FS1 is less likely to be observed due to its brightness and the fact that its velocity vector has almost no tangential component. The expected number of stars like FS2 is in good agreement with our observation of the four other fast stars in NGC 2808.
The fact that the expected number of stars like FS1 is an order of magnitude lower than that of FS2 comes from the detection probabilities. A star like FS1 is less likely to be observed due to its brightness and the fact that its velocity vector has almost no tangential component. The expected number of stars like FS2 is in good agreement with our observation of the four other fast stars in NGC 2808.
Keeping in mind all the uncertainties that enter these estimates, we consider both of these numbers consistent with the observation of one star like FS1 and one like FS2.
5.2. The unbound case – acceleration in the giant phase
The measured velocities for stars FS1 and FS2 are very close to the cluster escape velocity. This makes it hard to establish whether the two stars are bound or unbound to the cluster. Here we consider the case in which FS1 and/or FS2 received a recoil velocity during a recent dynamical encounter large enough to unbind them from the cluster.
We test the possibility that FS1 and FS2 were ejected from the cluster core by a dynamical encounter by performing numerical three-body scattering experiments similar to the ones described in Sect. 5.1. In this case, considering an ejection velocity of 45 km s-1 and the current projected distance of ~ 0.3 pc from the cluster center, we can assume that the encounters that accelerated the two stars took place when the stars were already in the giant phase. This is an important assumption, and the one that distinguishes the encounters described in this section from those in 5.1. Collisions in close encounters affect giant stars much more than they affect main-sequence stars due to the larger radii, and therefore larger cross-sections, of the giants.
Dynamical encounters between a binary and a single star.
We consider three main types of binary-single star encounters, which are detailed in Table 3: (1) encounters involving only giant stars (models G1, G2); (2) encounters involving giant and main-sequence stars (models M1, M2, M3, M4); and (3) encounters between a binary of giant stars and a black hole (BH) (of both the stellar and intermediate-mass kind). For each type of encounter listed in Table 3, we consider all outcomes resulting in the ejection of (at least) one giant star, and record the ejection velocity. Since we are interested in the ejection of giant stars with large velocities, we neglect all cases of collisions.
Encounters of star FS1 and FS2 with other giants (case G1 and G2), or main-sequence stars (case M1, M2, M3, M4) result in ejection velocities always much lower than 45 km s-1, for any value of the initial binary separation. It thus ruled out that any of the two high velocity giants were ejected by encounters with stars of the same mass, whether giants or main-sequence stars.
We also consider the case of encounters with black holes (BHs) of different masses. Figure 11 gives the branching ratios, as a function of the initial binary separation, for model B2. The relative importance of mergers and exchanges depends sensitively on the binary semi-major axis, with mergers occurring in more than 50% of the cases for a ~ < 0.2 AU.
 |
Fig. 13 Distribution of ejection velocities in encounters between a binary of giant stars and a black hole (case B1). The three panels refer to BHs of different mass: 10,50,100 M⊙, from left to right. The binary separation is set to 1 AU. |
Average ejection velocities as a function of the initial binary semi-major axis are shown in Fig. 12, for models B1 and B2, and for different values of the BH mass MBH = 10,20,50,100 M⊙. Velocity distributions for case B1 are shown in Fig. 13 for BH masses of 10,50,100 M⊙ and the smallest value of the binary semi-major axis a = 1 AU. We find that stellar-mass BHs are sufficient to accelerate star FS2 to velocities of ~ 45 km s-1 for any value of the binary separation, and no BH of intermediate mass is required in the cluster to explain its velocity. Average ejection velocities for star FS1 are somewhat lower, due to the much larger size and therefore to the much larger number of close encounters that end with a collision. However, if we look at the distributions of ejection velocities for model B1, which are shown in Fig. 13 for the case a = 1 AU, we find that a 10 M⊙ black hole is sufficient to produce ejection velocities of 40 − 45 km s-1.
We compute the ejection rates for this ejection mechanism in the same way as in Sect. 5.1. To obtain the final number of ejected stars, however, the relaxation time in Eq. (8) needs to be replaced with the crossing time of the core. With a typical velocity of 13 km s-1, the crossing time for a core diameter of 1.4 pc is Tcr ~ 105 yr. This results in a final number of events as listed in Table 4. It is clear that the higher the black hole mass, the more stars with velocities larger than 45 km s-1 are produced. However, even a black hole of 103 M⊙ would not be enough to produce an acceptable number of stars to explain the observations.
We conclude that a dynamical encounter between a binary of giant stars and a stellar-mass black hole of ≳ 10 M⊙ can produce giant stars with velocities ~45 km s-1. However, the number of expected fast stars produced by this mechanism is one to three orders of magnitudes lower than our observations show. The reasons for this discrepancy are, on the one hand, the lower ejection rates due to the shorter timescales in which the stars will disappear from the field of view and, on the other hand, the fact that giant stars are less likely to achieve large velocities than main-sequence stars. For these reasons, this scenario is unlikely to have accelerated the observed runaways.
Expected numbers of stars if accelerated by an encounter of a giant and a massive black hole.
6. Comparison with other globular clusters
In Sect. 1 we mentioned the cases of M3 and 47 Tuc and their high-velocity stars. Meylan et al. (1991) argued that the two fast stars in 47 Tuc, which move with 3.6σc and 4.8σc, must have been recently accelerated by encounters with a giant star, similar to our unbound case. The reason for this assumption is the fact that the velocities of these stars (V1 = −36.7 km s-1, V2 = 32.4 km s-1) are, within the errors, equal to the escape velocity Vesc = 35.38 km s-1 (Peterson & King 1975). This is a very similar situation to our case and therefore we would be more cautious in claiming the stars are bound or unbound. The argument of Meylan et al. (1991) that these stars could only recently have been accelerated is questionable. Furthermore, even if the velocities of the stars exceed the escape velocity by a few km s-1, the probability that the stars are able to actually escape the cluster immediately remains low, since they are only able to escape by passing through small apertures near the Lagrange points L1 and L2. This can result in a significant delay of the escape of stars (Fukushige & Heggie 2000). For this reason it is a valid hypothesis that these stars also got accelerated in their main-sequence stage. Because the central density1 log (ρ0/pc-3) = 4.88 and core relaxation time log (tc/yr) = 7.85 (Harris 1996) of 47 Tuc are very similar to the values of NGC 2808, the expected numbers of fast stars will be close to our derived numbers.
In the case of M3 the central velocity dispersion is lower than the one of NGC 2808 by 50% (σc = 4.9 km s-1). However, it is important to note that the absolute velocity dispersion is not the key factor, but rather its value relative to the velocities of the high-velocity stars. Gunn & Griffin (1979) measured velocities of 17.0 km s-1 and − 22.9 km s-1 for two stars which are most likely cluster members. Again, these velocities lie in the same range as the escape velocity (Vesc = 20.81 km s-1) but, as in the two previous cases, do not exceed this limit by much. The only difference with NGC 2808 and 47 Tuc is the central density of log (ρ0) = 3.57. This would lower othe expected number of high-velocity stars by an order of magnitude. Since this would most strongly affect the prediction for the unbound case, the most likely scenario for M3 is still that the stars are bound and were accelerated by a dynamical encounter with a massive object while they were in the main sequence phase.
The globular cluster NGC 6752 shows two millisecond pulsars outside the core: a recycled binary pulsar at more than three half-mass radii and a single pulsar at 1.4 half-mass radii. Such systems suggest the presence of a massive object in the center of the cluster. Colpi et al. (2002, 2003) show that the off-center location of the pulsars can be explained with scattering from a binary of stellar mass black holes or a single intermediate-mass black hole. This supports the idea that high-velocity stars in globular clusters may be produced by single or binary black holes.
7. Summary and conclusions
We detect five high-velocity stars in the globular cluster NGC 2808 using integral field unit spectroscopy as well as Fabry-Perot data for individual stars. All stars are ~ 0.3 − 0.5 pc away from the cluster center and their velocities correspond to 3.6 − 4.1σc, where σc is the velocity dispersion in the core. All stars are very likely to be cluster members due to their positions in the CMD. Furthermore, we find that the proper motions of the stars are in good agreement with the proper-motion distribution.
For the case of the two fast stars found in the integral-field unit, we discuss various scenarios which could explain their peculiar motions. By performing a binary synthesis and looking at HST far UV and near UV images, we exclude the possibility of these stars being close binaries. Furthermore, we discuss the possibility of atmospherically active stars such as long period variables and conclude that this scenario can also be excluded due to a lack of spectroscopic evidence and general inconsistency with the observed velocity range.
The measured velocities of the stars are close to the estimated escape velocity from NGC 2808. For this reason, we consider two cases of acceleration: the bound case, in which the stars were accelerated while in the main-sequence stage; and the unbound case, in which the acceleration must have taken place recently. We perform numerical three-body scattering experiments for both cases. In the bound case we also test the possibility that these stars belong to the tail of the Maxwellian velocity distribution by means of Monte Carlo simulations. In the case of three-body encounters of main-sequence stars and compact objects (the bound case) we consider four types of encounters: (1) encounters with a main-sequence star of the same mass; (2) encounters with a 0.8 M⊙ white-dwarf; (3) encounters with a 1.4 M⊙ neutron star and (4) encounters with a ~ 10 M⊙ black hole. To obtain the expected numbers of ejected stars, we calculate the event rates of each encounter producing a star with a velocity larger than 45 km s-1 as a function of the binary separation. Combining the rates with the log-normal orbital period distribution obtained by Duquennoy & Mayor (1991), we obtain the total event rate by integration.
Similarly, we test for the possibility of encounters with giant stars (the unbound case). As an input, we take the estimated properties of the two stars (radius and mass) and consider three main types of binary-single star encounters: encounters between giants, encounters of giant and main-sequence stars, and encounters including a black hole. We find that all encounters including only stars result in much lower escape velocities than the observed ones. Encounters between a binary of giants and a black hole, however, result in velocity distributions which peak at the observed velocities. Especially a black hole of MBH ~ 10 M⊙ and a binary separation of a = 1 AU predicts velocities around 40 km s-1 for star FS1. For star FS2, any separation produces large enough ejection velocities.
The scattering experiments show that no intermediate-mass black hole is needed in order to accelerate the stars to their velocities. Furthermore, only the encounters of main-sequence stars and compact objects have rates high enough to explain the observed stars. This leads us to the conclusion that the stars are bound and were accelerated by an encounter with a ~ 10 M⊙ stellar black hole. This cluster must thus have a high concentration of stellar-mass black holes in its center in order to make such an encounter likely enough to be observed. This is in agreement with the latest results on the central kinematics of NGC 2808 where no intermediate-mass black hole is detected Lützgendorf et al. (2012). Such a retention of stellar remnants in evolving globular clusters is also in line with theoretical expectations, which allow up to 30% − 50% of the cluster mass to be constituted by remnants (Baumgardt & Makino 2003; Kruijssen 2009).
We compare our results with the two other known cases in which high velocity stars were detected in globular clusters, M3 and 47 Tuc. These cases are very similar to NGC 2808 and might therefore be explained with the same arguments. The high-velocity stars in these clusters are most probably products of encounters of main-sequence binaries with a massive black hole. For further analysis, N-body simulations could help verifying these results by running specific simulations dedicated to the statistics of fast stars and their origin. When combined with an analysis as carried out in this paper, this provides a general prediction for the origin of high-velocity stars in globular clusters.
Acknowledgments
We thank Thomas Lebzelter, Mathieu Servillat and Dietrich Baade for sharing their knowledge and expertise. Also, special thanks go to Jay Anderson and his group for providing us with the proper motions and for the strong support of this project. This research was supported by the DFG cluster of excellence Origin and Structure of the Universe (www.universe-cluster.de). H.B. acknowledges support from the Australian Research Council through Future Fellowship grant FT0991052. We thank the referee, Steinn Sigurdsson, for constructive comments that helped improve the paper.
References
- Baumgardt, H., & Makino, J. 2003, MNRAS, 340, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Makino, J., & Hut, P. 2005, ApJ, 620, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Gualandris, A., & Portegies Zwart, S. 2006, MNRAS, 372, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2008, MNRAS, 390, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., Possenti, A., & Gualandris, A. 2002, ApJ, 570, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., Mapelli, M., & Possenti, A. 2003, ApJ, 599, 1260 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessandro, E., Lanzoni, B., Beccari, G., et al. 2011, ApJ, 743, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, D. S., Richer, H. B., Anderson, J., et al. 2008, AJ, 135, 2155 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Emsellem, E., Monnet, G., & Bacon, R. 1994, A&A, 285, 723 [NASA ADS] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Clementini, G., Fusi Pecci, F., Buonanno, R., & Alcaino, G. 1990, A&AS, 84, 59 [NASA ADS] [Google Scholar]
- Fukushige, T., & Heggie, D. C. 2000, MNRAS, 318, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Pryor, C., O’Connell, R. D., Williams, T. B., & Hesser, J. E. 2000, AJ, 119, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Rich, R. M., & Ho, L. C. 2002, ApJ, 578, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Rich, R. M., & Ho, L. C. 2005, ApJ, 634, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Second, A., Third, A., et al. 2012, A&A, 533, A36 [Google Scholar]
- Gualandris, A., PortegiesZwart, S., & Eggleton, P. P. 2004, MNRAS, 350, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Gualandris, A., Portegies Zwart, S., & Sipior, M. S. 2005, MNRAS, 363, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Griffin, R. F. 1979, AJ, 84, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., & Gualandris, A. 2011, MNRAS, 410, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., Gualandris, A., & Portegies Zwart, S. 2008, MNRAS, 385, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., Gualandris, A., & Portegies Zwart, S. 2009, MNRAS, 396, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Habets, G. M. H. J., & Heintze, J. R. W. 1981, A&AS, 46, 193 [NASA ADS] [Google Scholar]
- Harris, W. E. 1974, ApJ, 192, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C., Hut, P., & McMillan, S. L. W. 1996, ApJ, 467, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G., & Fullerton, L. W. 1980, AJ, 85, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H. 1978, ApJ, 220, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K., Hall, D., & Ridgway, S. 1982, ApJ, 252, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., Lebzelter, T., & Scharlach, W. W. G. 1997, AJ, 114, 2686 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P., & Bahcall, J. N. 1983, ApJ, 268, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D. 2009, A&A, 507, 1409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulkarni, S. R., Hut, P., & McMillan, S. 1993, Nature, 364, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to Stellar Winds (Cambridge University Press) [Google Scholar]
- Lebzelter, T., & Wood, P. R. 2011, A&A, 529, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebzelter, T., Kiss, L. L., & Hinkle, K. H. 2000, A&A, 361, 167 [NASA ADS] [Google Scholar]
- Lebzelter, T., Wood, P., Hinkle, K., Joyce, R., & Fekel, F. 2005, A&A, 432, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lützgendorf, N., Kissler-Patig, M., Noyola, E., et al. 2011, A&A, 533, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lützgendorf, N., Kissler-Patig, M., Gebhardt, K., et al. 2012, A&A, 542, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, A. D., Wilkinson, M. I., Davies, M. B., & Gilmore, G. F. 2007, MNRAS, 379, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Colpi, M., Possenti, A., & Sigurdsson, S. 2005, MNRAS, 364, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, S. L. W., & Hut, P. 1996, ApJ, 467, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, G., Dubath, P., & Mayor, M. 1991, ApJ, 383, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. C., & Hamilton, D. P. 2002, MNRAS, 330, 232 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Noyola, E., Gebhardt, K., & Bergmann, M. 2008, ApJ, 676, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., Gebhardt, K., Kissler-Patig, M., et al. 2010, ApJ, 719, L60 [NASA ADS] [CrossRef] [Google Scholar]
- O’Leary, R. M., Rasio, F. A., Fregeau, J. M., Ivanova, N., & O’Shaughnessy, R. 2006, ApJ, 637, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, C. J., & King, I. R. 1975, AJ, 80, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Ratnatunga, K. U., & Bahcall, J. N. 1985, ApJS, 59, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2004, A&A, 416, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubenstein, E. P., & Bailyn, C. D. 1997, ApJ, 474, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, M. 1992, A&A, 253, 203 [NASA ADS] [Google Scholar]
- Servillat, M., Dieball, A., Webb, N. A., et al. 2008, A&A, 490, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sigurdsson, S., & Hernquist, L. 1993, Nature, 364, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., & Phinney, E. S. 1993, ApJ, 415, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Sommariva, V., Piotto, G., Rejkuba, M., et al. 2009, A&A, 493, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, P. R. 1979, ApJ, 227, 220 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Expected numbers of stars if accelerated by an encounter of a giant and a massive black hole.
All Figures
 |
Fig. 1 ARGUS field of view (left) and velocity map of NGC 2808 (right). Visible as bright blue spots are the two high-velocity stars FS1 and FS2. Marked with the dashed blue line is FS4, the star which does not dominate its spaxel and therefore is not detectable. The blue cross marks the center of the cluster. |
| In the text | |
 |
Fig. 2 Kinematic properties of the five high-velocity stars. Left: the histogram of the Fabry-Perot data in the core of NGC 2808. Marked with colors are five high velocity stars FS1 to FS5. Right: the escape-velocity profile (solid line) and its uncertainties (dotted line) obtained from the density profile overplotted by the total velocities and projected positions of the five fast stars. |
| In the text | |
 |
Fig. 3 Fabry-Perot photometric points for FS1. Overplotted is the best fit of the model for the Hα line. |
| In the text | |
 |
Fig. 4 Color − magnitude diagram of NGC 2808 overplotted with the positions of the high-velocity stars FS1 to FS4. All of them are located on the red giant branch or the horizontal branch and therefore most likely cluster members. |
| In the text | |
 |
Fig. 5 Spectra of the two fast stars extracted from the ARGUS integral field unit in the Calcium Triplet region. The lines of both stars are narrow and confirm the assumption that both stars are giants. |
| In the text | |
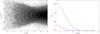 |
Fig. 6 Monte Carlo simulations of recovering the radial velocities of v = 44 km s-1 and v = 37 km s-1 as a function of the magnitude of the star. The left panel shows the measured velocities of every spaxel from the 106 realizations as a density contour plot. The magenta and green lines mark the detection limits of 42 km s-1 and 35 km s-1 for FS1 and FS2 respectively. A spaxel with a velocity lower than 2 km s-1 (which corresponds to the error bars) minus the actual radial velocity is not considered to be a detection anymore. The right panel visualizes the probability of detecting a star with a radial velocity of 44 km s-1 (magenta) and 37 km s-1 (green) as well as their smoothed curves. |
| In the text | |
 |
Fig. 7 Branching ratios versus initial binary separation for the outcomes of encounters between a stellar binary and a main-sequence star E1 (left) or a stellar mass black hole E4 (right). The label “runaway” refers to encounters that produce an escaper with velocity larger than 45 km s-1. |
| In the text | |
 |
Fig. 8 Average ejection velocities of all main-sequence escapers for the different types of encounters considered. For model E5, we adopt a black hole mass of 30 M⊙. The dotted horizontal line marks the characteristic velocity of the runaways. |
| In the text | |
 |
Fig. 9 Branching ratios versus initial binary separation for the outcomes of encounters of type E5, in the case of a black hole of 30 M⊙. |
| In the text | |
 |
Fig. 10 Event rates of the different encounters as a function of the separation multiplied by the distribution function of the semi-major axis. From this the final event rate can be achieved by integrating over the values for the semi-major axis. |
| In the text | |
 |
Fig. 11 Branching ratios versus initial binary separation for the outcomes of encounters between a stellar binary and a black hole of 10 M⊙ (model B2). The label “runaway” refers to encounters that produce an escaper with velocity larger than 45 km s-1. |
| In the text | |
 |
Fig. 12 Average ejection velocity in runs B1 (left) and B2 (right) as a function of the initial binary semi-major axis. Different lines refer to different values of the BH mass, MBH = 10, 20, 50, 100 M⊙, respectively, from bottom to top. Dotted lines indicate the required ejection velocity of 45 km s-1. |
| In the text | |
 |
Fig. 13 Distribution of ejection velocities in encounters between a binary of giant stars and a black hole (case B1). The three panels refer to BHs of different mass: 10,50,100 M⊙, from left to right. The binary separation is set to 1 AU. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


