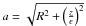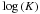| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 19 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201118646 | |
| Published online | 09 July 2012 | |
Gaia Universe model snapshot
A statistical analysis of the expected contents of the Gaia catalogue⋆
1
Institut Utinam, CNRS UMR6213, Université de Franche-Comté, Observatoire de
Besançon,
Besançon,
France
e-mail: annie.robin@obs-besancon.fr
2
Dept. Astronomia i Meteorologia ICCUB-IEEC, Martí i Franquès
1, Barcelona,
Spain
e-mail: xluri@am.ub.es
3
GEPI, Observatoire de Paris, CNRS, Université Paris
Diderot, 5 place Jules
Janssen, 92190
Meudon,
France
4
Department of Astrophysics Astronomy & Mechanics,
Faculty of Physics, University of Athens, Athens, Greece
5
OAT, Torino, Italy
6
Observatoire de Genève, Sauverny,
Switzerland
7 SIM, Faculdade de Ciências, Universidade de Lisboa, Portugal
8
Observatoire de la Côte d’Azur, Nice, France
9
Institut d’Astrophysique de Paris, France
Received: 13 December 2011
Accepted: 27 January 2012
Context. This study has been developed in the framework of the computational simulations that are executed for the preparation of the ESA Gaia astrometric mission.
Aims. We focus on describing the objects and characteristics that Gaia will potentially observe without taking into consideration instrumental effects (detection efficiency, observing errors).
Methods. The theoretical Universe model prepared for the Gaia simulation has been statistically analysed at a given time. Ingredients of the model are described, with the greatest emplasis on the stellar content, the double and multiple stars, and variability.
Results. In this simulation the errors have not yet been included. Hence we estimated the number of objects and their theoretical photometric, astrometric and spectroscopic characteristics if they are perfectly detected. We show that Gaia will be able to potentially observe 1.1 billion of stars (single or part of multiple star systems) of which about 2% are variable stars and 3% have one or two exoplanets. At the extragalactic level, observations will be potentially composed of several millions of galaxies, half a million to 1 million quasars and about 50 000 supernovae that will occur during the five years of the mission.
Key words: methods: data analysis / Galaxy: stellar content / catalogs / Galaxy: structure / galaxies: statistics / stars: statistics
The catalogue is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/543/A100
© ESO, 2012
1. Introduction
The ESA Gaia astrometric mission has been designed for solving one of the most difficult, yet deeply fundamental challenges in modern astronomy: to create an extraordinarily precise 3D map of about a billion stars throughout our Galaxy and beyond (Perryman et al. 2001).
The survey aims to reach completeness at Vlim ~ 20−25 mag depending on the colour of the object, with astrometric accuracies of about 10 μas at V = 15. In the process, it will map stellar motions and provide detailed physical properties of each observed star: characterising their luminosity, temperature, gravity and elemental composition. Additionally, it will perform the detection and orbital classification of tens of thousands of extra-solar planetary systems, and a comprehensive survey of some 105−106 minor bodies in our solar system, as well as galaxies in the nearby Universe and distant quasars.
This massive stellar census will provide the basic observational data to tackle important questions related to the origin, structure, and evolutionary history of our Galaxy and will enable new tests of general relativity and cosmology.
Clearly, the Gaia data analysis will be an enormous task in terms of expertise, effort and dedicated computing power. To cope with this, the Data Processing and Analysis Consortium (DPAC) is a large pan-European team of expert scientists and software developers who are officially responsible for the Gaia data processing and analysis1. The consortium is divided into specialized units with a unique set of processing tasks known as coordination units (CUs). More precisely, the CU2 is the task force in charge of the simulation needs for the work of other CUs, ensuring that reliable data simulations are available for the various stages of the data processing and analysis development. One key piece of the simulation software developed by CU2 for Gaia is the universe model which generates the astronomical sources.
The main goal of the present paper is to analyse the content of a full sky snapshot (for a given moment in time) of the universe model. With that objective in mind, the article has been organized to have two main parts: in Sect. 2, the principal components of the Gaia simulator are introduced, while the results of the analysis are detailed in Sect. 3, complemented with a wide variety of diagrams and charts.
To understand those results properly, it is important to remark that four passbands (and their corresponding magnitudes) are associated with the Gaia instruments: G, GBP, GRP, and 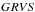 (see Fig. 1).
(see Fig. 1).
 |
Fig. 1 Gaia G, GBP , GRP, and GRVS passbands. |
As described in Jordi et al. (2010), from the astrometric measurements of unfiltered (white) light, Gaia will yield G magnitudes in a very broad band that covers the 350–1000 nm wavelength range. The G band can be related to the Johnson-Cousins V and IC passband by the following approximation (Jordi et al. 2010) for unreddened stars: 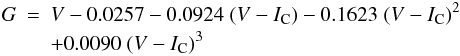 (1)for −0.4 < V − I ≲ 6. The approximation can be simplified to G − V = 0.0 ± 0.1 for the range −0.4 < V − I < 1.4.
(1)for −0.4 < V − I ≲ 6. The approximation can be simplified to G − V = 0.0 ± 0.1 for the range −0.4 < V − I < 1.4.
Additionally, the spectrophotometric instrument (Jordi et al. 2010) consists of two low-resolution slitless spectrographs named “blue photometer” (BP) and “red photometer” (RP). They cover the wavelength intervals 330–680 nm and 650–1050 nm, and their total flux will yield GBP and GRP magnitudes. For the brighter stars, Gaia also features a high-resolution (R = 11 500) integral field spectrograph in the range 847–874 nm around the CaII triplet, named Radial Velocity Spectrometer (RVS). Its integrated flux will provide the GRVS magnitude.
The RVS will provide the radial velocities of stars up to GRVS = 17 with precisions ranging from 15 km s-1 at the faint end to 1 km s-1 or better at the bright end. Individual abundances of key chemical elements (e.g. Ca, Mg and Si) will be derived for stars up to GRVS = 12.
Colour equations to transform Gaia photometric systems to the Johnson, SDSS and Hipparcos photometric systems can be found in Jordi et al. (2010).
The catalogue described here is available at the CDS.
2. Gaia simulator
Gaia will acquire an enormous quantity of complex and extremely precise data that will be transmitted daily to a ground station. By the end of Gaia’s operational life, around 150 terabytes (1014 bytes) will have been transmitted to Earth: some 1000 times the raw volume from the related Hipparcos mission.
An extensive and sophisticated Gaia data processing mechanism is required to yield meaningful results from the collected data. To this aim, an automatic system has been designed to generate the simulated data required for the development and testing of the massive data reduction software.
The Gaia simulator has been organized around a common tool box (named GaiaSimu library) containing a universe model, an instrument model and other utilities, such as numerical methods and astronomical tools. This common tool box is used by several specialized components:
-
GOG (Gaia Object Generator).
Provides simulations of number counts and lists of observable objects from the universe model. It is designed to directly simulate catalogue data.
-
GIBIS (Gaia Instrument and Basic Image Simulator).
Simulates how the Gaia instruments will observe the sky at the pixel level, using realistic models of the astronomical sources and of the instrument properties.
-
GASS (GAia System Simulator).
In charge of massive simulations of the raw telemetry stream generated by Gaia.
As a component of the GaiaSimu library, the universe model aims at simulating the characteristics of all the different types of objects that Gaia will observe: their spatial distribution, photometry, kinematics, and spectra.
To handle the simulation, the sky is partitioned with a Hierarchical Triangular Mesh (HTM) (Kunszt et al. 2001), which subdivides the spherical surface into triangles in a recursive/multi-level process which can be higher or lower depending on the area density. The first level divides the northern and southern sphere into four areas each, which are identified by the letter N or S, respectively, and a number from 0 to 3. The second level for one of these areas (for instance, “S1”) is generated by subdividing it into four new triangles as stated in Fig. 2. At each level, the area of the different triangles is almost the same.
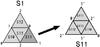 |
Fig. 2 Hierarchical Triangular Mesh subdivisions scheme: Each triangle has three vertices labelled 0, 1 and 2. When the area is subdivided into four new triangles, the opposite midpoints are labelled 0′, 1′ and 2′, respectively, and the central triangle is suffixed with a 3. |
The universe model is designed to generate lists of astronomical sources in given regions of the sky, represented by a concrete HTM area of a given maximum level. In the present simulation the HTM level is 8, giving a mean size of about 0.1 square degree for each triangular tile.
The distributions of these objects and the statistics of observables should be as realistic as possible, while the algorithms have been optimized so that the simulations can be performed in reasonable time. Random seeds are fixed to regenerate the same sources at each new generation and in each of the three simulators.
The object generation process is divided into three main modules:
-
Solar system object generator such as planets, satellites,asteroids, comets, etc. This generator is based on a database ofknown objects and has not been activated in the present statisticalanalysis (Tanga 2011).
-
Galactic object generator based on the Besançon Galaxy model (BGM from now on). It creates stellar sources taking into account extinction, star variability, existence of binary systems, and exoplanets.
-
Extragalactic objects generator such as unresolved galaxies, QSOs, and supernovae.
In the following subsections, the generation of the different types of objects and the computation of their relevant characteristics are described.
2.1. Galactic objects
Galactic objects are generated from a model based on BGM (Robin et al. 2003), which provides the distribution of the stars, their intrinsic parameters, and their motions. The stellar population synthesis combines
-
theoretical considerations such as stellar evolution, galacticevolution, and dynamics;
-
observational facts such as the local luminosity function, the age-velocity dispersion relation, the age-metallicity relation.
The result is a comprehensive description of the stellar components of the Galaxy with their physical characteristics (e.g. temperature, mass, gravity, chemical composition, and motions).
The Galaxy model is formed by four stellar populations constructed with different model parameters. For each population the stellar content is defined by the Hess diagram according to the age and metallicity characteristics. The populations considered here are
-
The thin disc: young stars with solar metallicity in the mean. It isadditionally divided into seven isothermal components of agesvarying from 0–0.15 Gyr for the youngest to7–10 Gyr for the oldest.
-
The thick disc: in terms of metallicity, age and kinematics, stars are intermediate between the thin disc and the stellar halo.
-
The stellar halo (or spheroid): old and metal-poor stars.
-
The outer bulge: old stars with metallicities similar to those of the thin disc.
The simulations are performed using the equation of stellar statistics. Specifying a direction and a distance rmax, the model generates a star catalogue using the following equation:
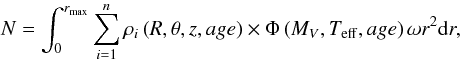 (2)where ρ(R,θ,z, age) is the stellar density law with galactocentric coordinates
(2)where ρ(R,θ,z, age) is the stellar density law with galactocentric coordinates 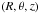 , described in Tables 1 and 2, Φ(MV,Teff,age) is the number of stars per square parsec in a given cell of the HR diagram (MV,Teff, age) for a given age range near the sun, ω is the solid angle and r the distance to the sun.
, described in Tables 1 and 2, Φ(MV,Teff,age) is the number of stars per square parsec in a given cell of the HR diagram (MV,Teff, age) for a given age range near the sun, ω is the solid angle and r the distance to the sun.
The functions ρ(R,θ,z,age) (density laws) and Φ(MV,Teff,age) (Hess diagrams) are specific for each population, and established using theoretical and empirical constraints, as described below.
In a given volume element with an expected density of N, ≈ N stars are generated using a Poisson distribution. After generating the corresponding number of stars, each star is assigned its intrinsic attributes (age, effective temperature, bolometric magnitude, U, V, W velocities, distance) and corresponding observational parameters (apparent magnitudes, colours, proper motions, radial velocities, etc.) and is finally affected by the implemented 3D extinction model from Drimmel et al. (2003).
2.1.1. Density laws
Local mass density ρ0 and axis ratios ϵ for different populations and as a function of age for the thin disc.
Density laws allow one to extrapolate to the rest of the Galaxy what is observed in the solar neighbourhood (i.e. local densities). The density law of each population has been described in Robin et al. (2003). However, the disc and bulge density were slightly changed. The revised density laws are given in Table 2. It is worth noting that the local density assigned to the seven subpopulations of the thin disc and its scale height z was defined by a dynamically self-consistent process using the Galactic potential and Boltzmann equations (Bienaymé et al. 1987). In this table the density formulae do not include the warp and flare, for simplicity, which are added as a modification of the position and thickness of the mid-plane.
The flare is the increase of the thickness of the disc with galactocentric distance: 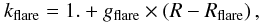 (3)with gflare = 0.545 × 10-6 pc-1 and Rflare = 9500 pc. The warp is modelled as a symmetrical S-shape warp with a linear slope of 0.09 starting at galactocentric distance of 8400 pc (Reylé et al. 2009). Moreover, a spiral structure was added with two arms, as determined in a preliminary study by De Amores & Robin (in prep.). The parameters of the arms are given in Table 3.
(3)with gflare = 0.545 × 10-6 pc-1 and Rflare = 9500 pc. The warp is modelled as a symmetrical S-shape warp with a linear slope of 0.09 starting at galactocentric distance of 8400 pc (Reylé et al. 2009). Moreover, a spiral structure was added with two arms, as determined in a preliminary study by De Amores & Robin (in prep.). The parameters of the arms are given in Table 3.
2.1.2. Magnitude – temperature – age distribution
The distribution of stars in the HR diagram 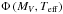 is based on the initial mass function (IMF) and star formation rate (SFR) observed in the solar neighbourhood (see Table 4). For each population, the SFR determines how much stellar mass is created at a given formation epoch, while the IMF distributes this mass to stars of different sizes. Then, the model brings every star that is created in each formation epoch to the present day, considering evolutionary tracks and the population age.
is based on the initial mass function (IMF) and star formation rate (SFR) observed in the solar neighbourhood (see Table 4). For each population, the SFR determines how much stellar mass is created at a given formation epoch, while the IMF distributes this mass to stars of different sizes. Then, the model brings every star that is created in each formation epoch to the present day, considering evolutionary tracks and the population age.
For the thin disc, the distribution in the Hess diagram splits into several age bins. It is obtained from an evolutionary model, which starts with a mass of gas, generates stars of different masses assuming an IMF and a SFR history, and makes these stars evolve along evolutionary tracks. The evolution model is described in Haywood et al. (1997a,b). It produces a file describing the distribution of stars per element volume in the space (MV, Teff, age). Similar Hess diagrams are also produced for the bulge, the thick disc and the spheroid populations, assuming a single burst of star formation and ages of 10 Gyr, 11 Gyr, and 14 Gyr, respectively, using the Bergbush & VandenBerg (1992) isochrones.
Parameters of the two arms of the spiral structure.
The stellar luminosity function is that of primary stars (single stars, or primary stars in multiple systems) and is normalised to the luminosity functions in the solar neighbourhood (Reid et al. 2002).
A summary of age and metallicities, star formation history and IMF for each population is given in Tables 4 and 5.
White dwarfs are taken into account using the Wood (1992) luminosity function for the disc and Chabrier (1999) for the halo. Additionally, some rare objects such as Be stars, peculiar metallicity stars and Wolf Rayet stars were also added (see Sect. 2.1.7).
IMF and SFR for each population for primary stars.
Age, metallicity, and radial metallicity gradients.
Alpha element abundances and metallicity relation.
2.1.3. Metallicity
In contrast to Robin et al. (2003), the metallicities [Fe/H] were computed through an empirical age-metallicity relation ψ(Z,age) from Haywood (2008). The mean thick disc and spheroid metallicities were also revised. For each age and population component the metallicity was drawn from a Gaussian, with a mean and a dispersion as given in Table 5. We also accounted for the radial metallicity gradient for the thin disc, −0.7 dex/kpc, but not for any vertical metallicity gradient.
2.1.4. Alpha elements – metallicity relation
Alpha element abundances are computed as a function of the population and the metallicity. For the spheroid, the abundance in the alpha elements is drawn from a random around a mean value, while for the thin disc, thick disc, and bulge populations it depends on [Fe/H]. Formulas are given in Table 6.
2.1.5. Age – velocity dispersion
The age-velocity dispersion relation is obtained from Gomez et al. (1997) for the thin disc, while Ojha et al. (1996) and Ojha et al. (1999) determined the velocity ellipsoid of the thick disc, that was used in the model (see Table 7). In the computation of the asymmetric drift we assumed a radial gradient of the velocity dispersion 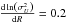 for the disc.
for the disc.
Velocity dispersions, asymmetric drift Vad at the solar position, and velocity dispersion gradient.
2.1.6. Stellar rotation
The rotation of each star is simulated following specifications from Cox et al. (2000). The rotation velocity is computed as a function of luminosity and spectral type. Then vsini is computed for random values of the inclination of the star’s rotation axis.
2.1.7. Rare objects
For the needs of the simulator, some rare objects were added to the BGM Hess diagram:
Be stars: this is a transient state of B-type stars with a gaseous disc that is formed of material ejected from the star (Be stars are typically variable). Prominent emission lines of hydrogen are found in its spectrum because stellar ultraviolet light in the gaseous disc is reprocessed. Additionally, infrared excess and polarization is detected as a result from the scattering of stellar light in the disc.
Oe and Be stars are simulated as a proportion of 29% of O7-B4 stars, 20% of B5-B7 stars, and 3% of B8-B9 stars (Jaschek et al. 1988; Zorec & Briot 1997). For these objects, we linked the ratio between the envelope radius and the stellar radius with the line strength so that we were able to determine their spectrum. Over the time, this ratio changed between 1.2 and 6.9 to simulate the variation of the emission lines.
Two types of peculiar metallicity stars are simulated, following Kurtz (1982), Kochukhov (2007), and Stift & Alecian (2009) for A and B stars that have a much slower rotation than normal:
-
Am stars have strong and often variable absorption lines of metalssuch as zinc, strontium, zirconium, and barium, and deficienciesof others, such as calcium and scandium. These anomalies withrespect to A-type stars arise because the elements that absorbmore light are pushed towards the surface, while others sink underthe force of gravity. [en-tity!#x20!] In the model, 12% ofA stars on the main sequence in the Teff range 7400 K–10 200 K are set to be Amstars. Of these Am stars, 70% belong to a binary systemwith a period from 2.5 to 100 days. They are forced to beslow rotators: 67% have a projection of rotation velocityvsin i < 50 km s-1 and 23% have 50 < vsin i < 100[en-tity!#xa0!]km s-1.
-
Ap/Bp stars present overabundances of some metals, such as strontium, chromium, europium, praseodymium and neodymium, which might be connected to the present magnetic fields which are stronger than that of classical A or B type stars. In the simulation, 8% of A and B stars on the main sequence in the Teff range 8000 K–15 000 K are set to be Ap or Bp stars. They are forced to have a lower rotation: vsin i < 120 km s-1.
Wolf Rayet (WR) stars are hot and massive stars with a high rate of mass loss through a very strong stellar wind. There are three classes based on their spectra: the WN stars (nitrogen-dominant, some carbon), WC stars (carbon-dominant, no nitrogen) and the rare WO stars with C/O < 1.
The WR densities are computed following the observed statistics from the VIIth catalogue of Galactic Wolf-Rayet stars of van der Hucht (2001). The local column density of WR stars is 2.9 × 10-6 pc-2 or volume density 2.37 × 10-8 pc-3. Among them, 50% are WN, 46% are WC and 3.6% are WO. The absolute magnitude, colours, effective temperature, gravity, and mass were estimated from the literature. The masses and effective temperature vary considerably from one author to another. As a conservative value, it is assumed that the WR stars have masses of 10 M⊙ in the mean, an absolute V magnitude of –4, a gravity of –0.5, and an effective temperature of 50 000 K.
2.1.8. Binary systems
The BGM model produces only single stars whose densities were normalized to follow the luminosity function (LF) of single stars and primaries in the solar neighbourhood (Reid et al. 2002). The IMF, inferred from the LF and the mass-luminosity relation, covers the mass range down to the hydrogen burning limit, and includes disc stars down to MV = 24. It corresponds to spectral types down to about L5.
In the Gaia simulation multiple star systems are generated with some probability (Arenou 2011) that increases with the mass of the primary star obtained from the BGM model.
The mass of the companion is then obtained through a given statistical relation 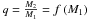 , which depends on period and mass ranges. Moreover it is checked that the total number of stars and their distribution is compatible with the statistical observations and that the pairing is realistic. The mass and age of the secondary determines physical parameters computed using the Hess diagram distribution in the Besançon model.But, it appears that, for PMS stars, some pairing were done in some cases with main-sequence stars, due to the resolution in age which is not good enough to distinguish them. It will be improved in futur simulations.
, which depends on period and mass ranges. Moreover it is checked that the total number of stars and their distribution is compatible with the statistical observations and that the pairing is realistic. The mass and age of the secondary determines physical parameters computed using the Hess diagram distribution in the Besançon model.But, it appears that, for PMS stars, some pairing were done in some cases with main-sequence stars, due to the resolution in age which is not good enough to distinguish them. It will be improved in futur simulations.
It is worth noting that while observationally, the primary of a system is conventionally the brighter, our model uses the other convention, i.e. the primary is the one with the largest mass, and consequently the generated mass ratio is constrained to be 0 < q ≤ 1.
The separation of the components (AU) was chosen with a Gaussian probability with different mean values depending on the stars’ masses (a smaller average separation for low-mass stars). Through Kepler’s third law, the separation and masses then give the orbital period. The average orbital eccentricity (a perfect circular orbit corresponds to e = 0) depends on the period by the following relation: ![\begin{equation} E\left[e\right]=a\left(b-{\rm e}^{-c\log\left(P\right)}\right), \end{equation}](/articles/aa/full_html/2012/07/aa18646-11/aa18646-11-eq136.png) (4)where a,b, and c are constants with different values depending on the star’s spectral type (values can be found in Table 1 of Arenou 2010).
(4)where a,b, and c are constants with different values depending on the star’s spectral type (values can be found in Table 1 of Arenou 2010).
To describe the orientation of the orbit, three angles are chosen randomly:
-
the argument of the periastron ω2 uniformly in [0, 2π[;
-
the position angle of the node Ω uniformly in [0, 2π[;
-
the inclination i uniformly random in
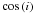 .
.
The moment at which stars are closest together (the periastron date T) is also chosen uniformly between 0 and the period P.
Characteristics of the variable types. Localisation in the (spectral type, luminosity class) diagram, probability of a star to be variable in this region, stellar population, and metallicity, respectively.
Much effort was made to ensure that the simulated multiple star numbers agree with the latest fractions known from available observations. A more detailed description can be found in Arenou (2011).
Although we here describe the content of the universe model at a fixed moment in time, we recall that the model is being used to simulate the Gaia observations. Thus, obviously, the astrometric, photometric, and spectroscopic observables of a multiple system vary in time according to the orbital properties. This means that, e.g. the apparent path of the photocentre of an unresolved binary will reflect the orbital motion through positional and radial velocity changes, or that the light curve of an eclipsing binary will vary in each band.
Light curves of the regular or semi-regular variable stars where 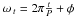 (P is the period, φ is the phase).
(P is the period, φ is the phase).
2.1.9. Variable stars
-
Regular and semi-regular variables
Depending on their position in the HR diagram, the generated stars have a probability of being one of the six types of regular and semi-regular variable stars considered in the simulator:
-
Cepheids:
Supergiant stars that undergo pulsations with very regular periods of the order of days to months. Their luminosity is directly related to their period of variation.
-
δScuti:
Similar to Cepheids, but somewhat fainter, and with shorter periods.
-
RR Lyrae:
Much more common than Cepheids, but also much less luminous. Their period is shorter, typically less than one day. They are classified into
- RRab:
Asymmetric light curves (these are the majority);
- RRc:
Nearly symmetric light curves (sometimes sinusoidal).
- RRab:
-
Gamma Doradus:
Display variations in luminosity due to non-radial pulsations of their surface. Periods of the order of one day.
-
RoAp:
Rapidly oscillating Ap stars are a subtype of the Ap star class (see Sect. 2.1.7) that exhibit short-timescale rapid photometric or radial velocity variations. Periods of the order of minutes.
-
ZZceti:
Pulsating white dwarf with hydrogen atmosphere. These stars have periods between seconds to minutes.
-
Miras:
Cool red supergiants, which are undergoing very long pulsations (of the order of months).
-
Semiregular:
Usually red giants or supergiants that show a definite period on occasion, but also go through periods of irregular variation. Periods lie in the range from 20 to more than 2000 days.
-
ACV (α Canes Venaticorum):
Stars with strong magnetic fields whose variability is caused by axial rotation with respect to the observer.
A summary of the variable type characteristics is given in Table 8 and the description of their light curve is given in Table 9.
Period and amplitude are taken randomly from a 2D-distribution defined for each variability type (Eyer et al. 2005). For Cepheids, a period-luminosity relation is also included log(P) = (− MV + 1.42)/2.78 (Molinaro et al. 2011). For Miras the relation is log(P) = (− MBol + 2.06)/2.54 (Feast et al. 1989). The different light curve models for each variability type are described in Reylé et al. (2007).
The variation of the radius and radial velocity are computed accordingly to the light variation for stars with radial pulsations (RRab, RRc, Cepheids, δ Scuti, SemiRegular, and Miras).
-
Dwarf and classical novae
Dwarf novae and classical novae are cataclysmic variable stars consisting of close binary star systems in which one of the components is a white dwarf that accretes matter from its companion.
Classical novae result from the fusion and detonation of accreted hydrogen, while current theory suggests that dwarf novae result from instability in the accretion disc that leads to releases of large amounts of gravitational potential energy. The luminosity of dwarf novae is lower than that of classical novae and it increases with the recurrence interval and the orbital period.
The model simulates half of the white dwarfs in close binary systems with periods shorter than 14 h as dwarf novae. The light curve is simulated by a linear increase followed by an exponential decrease. The time between two bursts, the amplitude, the rising time, and the decay time are drawn from Gaussian distributions derived from OGLE observations (Wyrzykowski & Skowron, priv. comm.).
The other half of the white dwarfs in these systems is simulated as classical novae.
-
M-dwarf flares
Flares are caused by magnetic reconnection in the stellar atmospheres. These events can produce dramatic increases in brightness when they take place in M dwarfs and brown dwarfs.
The statistics used in the model for M-dwarf flares are mainly based on Kowalski et al. (2009) and their study on SDSS data: 0.1% of M0-M1 dwarfs, 0.6% of M2-M3 dwarfs, and 5.6% of M4-M6 dwarfs are flaring. The light curve for magnitude m is described as follows: 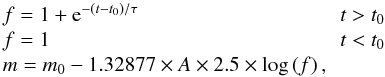 (5)where t0 is the time of the maximum, τ is the decay time (in days, random between 1 and 15 min), m0 is the baseline magnitude of the source star, A is the amplitude in magnitudes (drawn from a Gaussian distribution with σ = 1 and x0 = 1.2).
(5)where t0 is the time of the maximum, τ is the decay time (in days, random between 1 and 15 min), m0 is the baseline magnitude of the source star, A is the amplitude in magnitudes (drawn from a Gaussian distribution with σ = 1 and x0 = 1.2).
-
Eclipsing binaries
Eclipsing binaries, while being variables, are treated as binaries and the eclipses are computed from the orbits of the components. See Sect. 2.1.8.
-
Microlensing events
Gravitational microlensing is an astronomical phenomenon due to the gravitational lens effect, where distribution of matter between a distant source and an observer is capable of bending (lensing) the light from the source. The magnification effect permits the observation of faint objects such as brown dwarfs.
In the model, microlensing effects are generated assuming a map of event rates as a function of Galactic coordinates (l,b). The probabilities of lensing over the sky are drawn from the study of Han (2008). This probabilistic treatment is not based on the real existence of a modelled lens close to the line of sight of the source, it simply uses the lensing probability to randomly generate microlensing events for a given source during the five-year observing period.
The Einstein crossing time is also a function of the direction of observation in the bulge, obtained from the same paper. The Einstein time of the simulated events is drawn from a Gaussian distribution centred on the mean Einstein time. The impact parameter follows a flat distribution from 0 to 1. The time of maximum is uniformely distributed and completely random, from the beginning to the end of the mission. The Paczynski formula (Paczynski 1986) is used to compute the light curve.
2.1.10. Exoplanets
One or two extra-solar planets are generated with distributions in true mass Mp and orbital period P resembling those of Tabachnik & Tremaine (2002), which constitutes quite a reasonable approximation to the observed distributions as of today, and extrapolated down to the masses close to the mass of Earth. A detailed description can be found in Sozzetti et al. (2009).
Semi-major axes are derived given the star mass, planet mass, and period. Eccentricities are drawn from a power-law-type distribution, where full circular orbits (e = 0.0) are assumed for periods of less than six days. All orbital angles (i, ω and Ω) are drawn from uniform distributions. Observed correlations between different parameters (e.g, P and Mp ) are reproduced.
Assumed parameters of the Magellanic Clouds.
Simple prescriptions for the radius (assuming a mass-radius relationship from available structural models, see e.g. Baraffe et al. 2003), effective temperature, phase, and albedo (assuming toy models for the atmospheres, such as a Lambert sphere) are provided, based on the present-day observational evidence.
For every dwarf star generated of spectral type between F and mid-K, the likelihood that it harbours a planet of given mass and period depends on its metal abundance according to the Fischer & Valenti (2005) and Sozzetti et al. (2009) prescriptions. For the time being, we do not simulate planets around double and multiple stars.
The astrometric displacement, spectroscopic radial velocity amplitude, and photometric dimming (when transiting) induced by a planet on the parent star, and their evolution in time, are presently computed from orbital components similarly to double stellar systems.
2.2. Extragalactic objects
2.2.1. Resolved galaxies
To simulate the Magellanic Clouds, catalogues of stars and their characteristics (magnitudes B, V, I, Teff, log (g), spectral type) were obtained from the literature (Belcheva et al., priv. comm.).
For the astrometry, because a star by star distance is missing, a single proper motion and radial velocity for all stars of both clouds is assumed. Chemical abundances are also extimated from the mean abundance taken from the literature. The resulting values and their references are given in Table 10. For simulating the depth of the Clouds a Gaussian distribution is assumed along the line of sight with a sigma given in the table.
Stellar masses were estimated for each star from polynomial fits of the mass as a function of B − V colour, for several ranges of log (g), based on Padova isochrones for a metallicity of z = 0.003 for the LMC and z = 0.0013 for the SMC. The gravities were estimated from the effective temperature and luminosity class, but is very difficult to assert from the available observables. Hence the resulting HR diagrams for the Magellanic Clouds are not as well defined and reliable as they would be from theoretical isochrones.
2.2.2. Unresolved galaxies
Most galaxies observable by Gaia will not be resolved in their individual stars. These unresolved galaxies are simulated using the Stuff (catalogue generation) and Skymaker (shape/image simulation) codes from Bertin (2009), adapted to Gaia by Dollet (2004) and Krone-Martins et al. (2008).
This simulator generates a catalogue of galaxies with a 2D uniform distribution and a number density distribution in each Hubble type sampled from Schechter’s luminosity function (Fioc & Rocca-Volmerange 1999). The LF follows a shape from Schechter (1976). Parameters of the luminosity function in the Schechter formalism are given for each Hubble type in Table 11. Each galaxy is assembled as a sum of a disc and a spheroid, they are located at their redshift and luminosity and K corrections are applied. The algorithm returns the position for each galaxy, its magnitude, B/T relation, disc size, bulge size, bulge flatness, redshift, position angles, and V − I.
The adopted library of synthetic spectra at low resolution was created Tsalmantza et al. (2009) based on the Pegase-2 code (Fioc & Rocca-Volmerange 1997)2. Nine Hubble types are available (including Quenched Star Forming Galaxies or QSFG) (Tsalmantza et al. 2009), with five different inclinations (0.00, 22.5, 45.0, 67.5, 90.0) for non-elliptical galaxies, and at 11 redshifts (from 0. to 2. by step of 0.2). For all inclinations, the Pegase-2 spectra were computed with internal extinction by transfer model with two geometries either slab or spheroid, depending on type.
The resulting percentages per type, given in Table 26, reflect the numbers expected without applying the Gaia source detection and prioritization algorithms. De facto, the detection efficiency will be better for unresolved galaxies with a prominent bulge and for nucleated galaxies, hence the effective Gaia catalogue will have percentages different from those given in the table.
Parameters defining the luminosity function in the Schechter formalism for different galaxy types at z = 0, from Fioc & Rocca-Volmerange (1999).
2.2.3. Quasars
Quasars are simulated from the scheme proposed in Slezak & Mignard (2007). To summarise, lists of sources were generated with similar statistical properties as the SDSS, but extrapolated to G = 20.5 (the SDSS sample being complete to i = 19.1) and taking into account the flatter slope expected at the faint end of the QSO luminosity distribution. The space density per bin of magnitude and the luminosity function should be very close to the actual sky distribution. Because bright quasars are saturated in the SDSS, the catalogue is complemented by the Véron-Cetty & Véron (2006) catalogue of nearby QSOs.
The equatorial coordinates were generated from a uniform drawing on the sphere in each of the subpopulations defined by its redshift. No screening was applied in the vicinity of the Galactic plane since this will result directly from the application of the absorption and reddening model at a later stage. Distance indicators can be derived for each object from its redshift value by specifying a cosmological model. Because each of these sources lies at cosmological distances, a nearly zero (10-6 mas) parallax was assigned to all of them (equivalent to an Euclidean distance of about 1 Gpc) to avoid possible overflow/underflow problems in the simulation.
In principle, distant sources are assumed to be co-moving with the general expansion of the distant Universe and have no transverse motion. However, the observer is not at rest with respect to the distant Universe and the accelerated motion around the Galactic centre, or more generally, that of the Local Group towards the Virgo cluster is the source of a spurious proper motion with a systematic pattern. This has been discussed in many places (Kovalevsky 2003; Mignard 2005). Eventually, the effect of the acceleration (centripetal acceleration of the solar system) will show up as a small proper motion of the quasars, or stated differently, we will see the motion of the quasars on a tiny fraction of the aberration ellipse whose period is 250 million years. This effect is simulated directly in the quasar catalogue, and the equations are given in Slezak & Mignard (2007). This explains their not null proper motions in the output catalogue.
2.2.4. Supernovae
A set of supernovae (SN) are generated associated with galaxies, with a proportion for each Hubble type, as given in Table 12. Numbers of SNIIs are computed from the local star formation rate at 13 Gyr (z = 0) and IMF for M ∗ (Bj) galaxy types as predicted by the code PEGASE.2. Theoretical SNIa numbers follow the SNII/SNIa ratios from Greggio & Renzini (1983). In this case, the SN is situated at a distance randomly selected at less than a disc radius from the parent galaxy, and a correction is applied which accounts for the inclination.
Predictions of SNII and SNIa numbers exploding per century for the M* (Bj) galaxies defined in Table 11.
Another set of SN are generated randomly on the sky to simulate SN on host galaxies that are too faint in surface brightness to be detected by Gaia.
Four SN types are available with a total probability of occuring determined to give at the end 6366 SN per steradian during the five year mission (from estimations by Belokurov & Evans 2003). For each SN generated, a type is attributed from the associated probability, and the absolute magnitude is computed from a Gaussian drawing centred on the absolute magnitude and the dispersion of the type corresponding to the cosmic scatter. These parameters are given in Table 13. Supernova light curves were provided by Peter Nugent3. It is assumed that the SN varies in the same way at each wavelength and the light curve in V was taken as reference.
Parameters for each supernova type taken from Belokurov & Evans (2003).
2.3. Extinction model
The extinction model, applied to Galactic and extragalatic objects, is based on the dust distribution model of Drimmel et al. (2003). This full 3D extinction model is a strong improvement over previous generations of extinction models because it includes both a smooth diffuse absorption distribution for a disc and the spiral structure and smaller-scale corrections based on the integrated dust emission measured from the far-infrared. The extinction law is from Cardelli et al. (1989).
3. Gaia Universe Model Snapshot (GUMS)
The Gaia Universe Model Snapshot (GUMS) is part of the GOG component of the Gaia simulator. It was used to generate a synthetic catalogue of objects from the universe model that simulates the real environment where Gaia will observe (down to G = 20) for a given static time t0.
This snapshot is what Gaia will be able to potentially observe, but not what it will really detect, since satellite instrument specifications and the available error models are not taken into account in the present statistical analysis4.
The generated universe model snapshot was analysed by using the Gog Analysis Tool (GAT) statistics framework, which produces all types of diagnostic statistics that allow its scientific validation (e.g. star density distributions, HR diagrams, distributions of the properties of the stars). The visual representation of the most interesting results introduced in this article were generated using Python, Healpy and Matplotlib (Hunter 2007).
The simulation was performed with MareNostrum, one of the most powerful supercomputers in Europe managed by the Barcelona Supercomputing Center. The execution took 20 000 h (equivalent to 28 months) of computation time distributed in 20 jobs, each one using between 16 and 128 CPUs. MareNostrum runs a SUSE Linux Enterprise Server 10SP2 and its 2560 nodes are powered by two dual-core IBM 64-bit PowerPC 970MP processors running at 2.3 GHz.
3.1. Galactic objects overview
-
Gless than 20 mag
In general terms, the universe model has generated a total number of 1 000 000 000 galactic objects of which ~49% are single stars and ~51% are stellar systems formed by stars with planets and binary/multiple stars.
Individually, the model has created 1 600 000 000 stars of which about 32% are single stars with magnitude G less than 20 (potentially observable by Gaia) and 68% correspond to stars in multiple systems (Table 14). This last group is formed by stars whose magnitude G is less than 20 as a system but, in some cases, the isolated components can have a magnitude G exceeding 20, which will not be individually detectable by Gaia.
Considering only the magnitude limit in G and ignoring the angular separation of multiple systems, Gaia could be able to individually observe up to 1 100 000 000 stars (69%) in single and multiple systems.
-
GRVSless than 17 mag
For GRVS magnitudes limited to 17, the model has generated 370 000 000 galactic objects of which ~43% are single stars and ~57% are stellar systems formed by stars with planets and binary/multiple stars.
Concretely, the RVS instrument could potentially provide radial velocities for up to 390 000 000 stars in single and multiple systems if the limit in angular separation and resolution power are ignored (Table 14).
-
GRVSless than 12 mag
The model has generated 13 100 000 galactic objects with GRVS less than 12, of which ~27% are single stars and ~73% are stellar systems formed by stars with planets and binary/multiple stars.
Again, if the limits in angular separation and resolution power are ignored, the RVS instrument could measure individual abundances of key chemical elements (metallicities) for ~13 000 000 stars (Table 14).
Numbers and percentages of single stars and multiple systems generated by the universe model over the total number of stars.
3.2. Star distribution
The distribution of stars in the sky was plotted using a Hierarchical equal area isolatitude pixelisation, also known as Healpix projection. Unlike the HTM internal representation of the sky explained in Sect. 2, Healpix provides areas of identical size that are useful for comparison.
 |
Fig. 3 Total sky distribution of stars for different magnitudes. Top down: G < 20, GRVS < 17 and GRVS < 12. Colour scale indicates the log 10 of the number of stars per square degree. |
The number of stars on every region of the sky varies significantly depending on the band (Fig. 3) and the population (Fig. 4). In this last case, it is clear how the galactic centre is concentrated in the middle of the galaxy with only 10% of stars, while the thin disc is the densest region (67%), as stated in Table 15.
The effects of the extinction model caused by the interstellar material of the Galaxy, predominantly atomic and molecular hydrogen and significant amounts of dust, is clearly visible in these representations of the sky.
Percentages of stars of each population, calculated over the total number of stars for each respective column.
A projected representation in heliocentric-galactic coordinates of the stellar distribution shows how the majority of the generated stars are denser near the sun position, located at the origin of the XYZ coordinate system, and the bulge at 8.5 kpc away (Fig. 5). Specially from a top perspective (XY view), the extinction effect is clearly seen which produces windows where stars can be observed that are farther away. One also notices the sudden density drop towards the anticentre, which is due to the edge of the disc, which is assumed to be at a galactocentric distance of 14 kpc, following Robin et al. (1992).
The distribution of stars according to the G magnitude varies depending on the stellar population, which is particularly different for the bulge (Fig. 6).
 |
Fig. 4 Stellar distribution split by population (G < 20). Left to right, top down: thin disc, thick disc, spheroid, and bulge. Colour scale indicates the log 10 of the number of stars per square degree. |
 |
Fig. 5 Distribution of stars in heliocentric Cartesian coordinates (G < 20): top (XY), side (XZ) and front (YZ) perspectives. Colour scale indicates the log 10 of the number of stars per square parsec. |
3.3. Star classification
As expected, the most abundant group of stars belong to the main-sequence class (69%), followed by subgiants (15%) and giants (14%). The complete star luminosity classification is given in Table 16.
The star distribution as a function of G can be found in Fig. 7. Main sequence stars present the biggest exponential increase, relatively similar to subgiants. The population of white dwarfs increases significantly starting at magnitude G = 14. It is also interesting how supergiants decrease in number because they are intrinsically so bright and because of the peak that bright giants present at G = 14.5. For both of them, the decrease corresponds mainly to the distance of the edge of the disc in the Galactic plane.
Percentages of each luminosity class of generated stars, calculated over the total number of stars for each respective column.
The spectral classification of stars (Table 17) shows that G types are the most numerous (38%), followed by K types (28%) and F types (23%).
Percentages of each spectral type of generated stars, calculated over the total number of stars for each respective column.
 |
Fig. 6 G distribution split by stellar population. The bump for the bulge is due to the red clump, which is seen at I = 15 in Baade’s window. |
 |
Fig. 7 Star distribution split by luminosity class for G < 20. |
HR diagrams were generated for different populations (Fig. 8). The thin disc population represents the most complete one in terms of luminosity classes and spectral type distribution. The thin disc sequence of AGB stars going roughly from –4 to +17 in Mv is due to the heavy internal reddening of this population in visual bands. Isochrones can be clearly identified for thick disc, spheroid, and bulge populations because they are assumed to be generated in single bursts. Additionally, all populations present a fraction of the white dwarfs generated by the model.
 |
Fig. 8 HR Diagram of stars split by population (left to right, top down): thin disc, thick disc, spheroid and bulge. colour scale indicates the log 10 of the number of stars per 0.025 |
From the population perspective (Fig. 9), its is natural that bulge stars are concentrated at smaller parallaxes (farther distances) while the rest increases from the Sun’s position until the magnitude limit is reached and only brighter stars can be observed.
On the other hand, from a spectral type perspective, Fig. 10 presents the different parallax distributions for each type. Concrete numbers can be found in Table 18 for specific parallaxes 240 μas, 480 μas, and 960 μas5, which corresponds to distances of 4167 pc, 2083 pc, and 1042 pc.
 |
Fig. 9 Stellar parallax split by populations. |
 |
Fig. 10 Stellar parallax split by spectral type. |
As mentioned in the introduction, the RVS instrument will be able to measure abundances of key chemical elements (e.g. Ca, Mg and Si) for stars up to GRVS = 12. Metallicities and their relation to the abundances of alpha elements is presented in Fig. 11 split by population. Alpha element abundances are mostly reliable except at metallicity higher than 0.5, owing to the formulation, which is extrapolated. It will be corrected in a future version.
3.4. Kinematics
Proper motion of stars and radial velocity are represented in Fig. 12. Means are located at 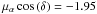 mas/year and μδ = −2.78 mas/year, which are affected by the motion of the Sun with regards to the local standard of rest.
mas/year and μδ = −2.78 mas/year, which are affected by the motion of the Sun with regards to the local standard of rest.
 |
Fig. 11 Metallicity-alpha elements relation for GRVS < 12. Colour scale indicates the log 10 of the number of stars per 0.05 [Fe/H] and 0.04 [α/Fe] . |
 |
Fig. 12 Proper motion of stars μαcosδ, μδ and radial velocity VR. Colour scale indicates the log 10 of the number of stars per 2.4 mas/year (km s-1 in case of VR) and 1.0 mag. |
Older stars, which present poorest metallicities, tend to have lowest velocities on the V axis compared to the solar local standard of rest (Fig. 13) following the so-called asymmetric drift. The approximate mean V velocities are –48 km s-1 for the thin disc, –98 km s-1 for the thick disc, –243 km s-1 for the spheroid, and –116 km s-1 for the bulge.
 |
Fig. 13 Metallicity and V-axis velocity relation split by population (left to right, top down): thin disc, thick disc, spheroid, and bulge. Colour scale indicates the log 10 of the number of stars per 0.05 [Fe/H] and 6 km s-1. |
3.5. Variable stars
From the total amount of 1 600 000 000 individual stars generated by the model, ~1.8% are variable stars (of the variable types included in the universe model). They are composed of 6 800 000 single stars (~25% of the total variable stars) with magnitude G less than 20 (observable by Gaia if their maximum magnitude is reached at least once during the mission) and 21 000 000 stars in multiple systems (~75%). However, as explained in Sect. 3.1, this last group is formed by stars that have magnitude G less than 20 as a system but, in some cases, its isolated components can have a magnitude G higher than 20 and will not be individually detectable by Gaia.
Again, only taking into consideration magnitude G and ignoring the angular separation of multiple systems, Gaia could be able to observe up to 21 500 000 variable stars in single and multiple systems (~2% of the total individually observable stars exposed in Sect. 3.1).
Radial velocities will be measurable for 16 000 000 variable stars with GRVS < 17, while metallicities will be available for 2 000 000 variable stars (~1%) with GRVS < 12 (see Table 19).
Overview of variable stars. Percentages were calculated over the total variable stars.
By variability type, δ scuti are the most abundant representing the 49% of the variable stars, followed by semiregulars (42%) and microlenses (4.3%) as seen in Table 20. However, microlenses are highly related to denser regions of the galaxy, as shown in Fig. 14, and they can involve stars of any kind. The rest of variability types are strongly related to different locations in the HR diagram (Fig. 15).
3.6. Binary stars
As seen in Sect. 3.1, the model has generated 410 000 000 binary systems. Therefore about 820 000 000 stars were generated, but it is important to remark that not all of them will be individually observable by Gaia. Some systems may have components with magnitude G fainter than 20 (although the integrated magnitude is brighter) and others may be so close together that they cannot be resolved (although they can be detected by other means).
The majority of the primary stars are from the main sequence (67%), of which the most popular combination is a double main-sequence star system (62%). Subgiants and giants as primary coupled with a main-sequence star are the second and third most probable systems (16% and 14% respectively). In general terms, the distribution is coherent with star formation and evolution theories (e.g. supergiants are not accompanied by white dwarfs), see Table 21.
The magnitude difference versus angular separation between components is shown in Fig. 16. While main-sequence pairs should produce only negative magnitude differences, the presence of white dwarf primaries with small red dwarf companions produces the asymmetrical shape of the figure (recalling that “primary” here means the more massive). To give a hint of the angular resolution capabilities of Gaia, we can assume it at a first step as nearly diffraction-limited and correctly sampled with pixel size ≈ 59 mas. Figure 16 thus shows that a small fraction only of binaries with moderate magnitude differences will be resolved.
The mean separation of binary systems is 30 AU, and they present a mean orbital period of about 250 years (Fig. 17). While only pairs with periods shorter than a decade may have their orbit determined by Gaia, a significative fraction of binaries will be detected through the astrometric “acceleration” of their motion.
 |
Fig. 14 Sky distribution of microlenses that could take place during the 5 years of the mission. Colour scale indicates the log 10 of the number of microlenses per square degree. |
Star distribution by variability type.
 |
Fig. 15 HR diagram split by variability type. |
 |
Fig. 16 G difference and angular separation relation for binaries. Colour scale indicates the log 10 of the number of binaries per 0.25 difference in magnitude and 0.1 in log (mas). |
 |
Fig. 17 Period-eccentricity relation for binaries. Colour scale indicates the log 10 of the number of binaries per 0.01 difference in eccentricity and 0.13log (days). |
Binary stars classified depending on the luminosity class combination.
3.7. Stars with planets
A total number of 34 000 000 planets were generated and associated to 27 500 000 single stars (~2.6% of the total individually observable stars exposed in Sect. 3.1), implying that 25% of the stars were generated with two planets (Table 22). No exoplanets are associated to multiple systems in this version of the model.
The majority of stars with planets belong to the main sequence (66%), followed by giants (17%) and subgiants (16.8%) as shown in Table 23. Only 8% of stars have a planet that produces eclipses.
On the other hand, stars with solar or higher metallicities present a higher probability of having a planet than stars poorer in metals (Fig. 18).
Overview of stars with planets.
Luminosity class of stars with planets.
 |
Fig. 18 Metallicity distribution of stars with planets. |
Finally, 77% of stars with planets belong to the thin disc population, while 11% are in the bulge, 11% in the thick disc, and 0.4% in the spheroid (Fig. 19).
 |
Fig. 19 G distribution of stars with planets split by population. |
3.8. Extragalactic objects
An overview of the simulated extragalactic objects is presented in Table 24. In addition to the stars presented in the previous sections, the model generates 8 800 000 additional stars that belong to the Magellanic Clouds. The distribution in spectral type of LMC and SMC stars is given in Table 25. Again, the most abundant spectral type are G stars (46%), followed by K types (33%) and A types (17%). There are no F-type stars reachable by Gaia, because the magnitude cut at the cloud distance selects only the upper part of the HR diagram including massive stars on the blue side, and late-type giants and supergiants on the red side.
The model generated 38 000 000 unresolved galaxies. However, due to the on board thresholding algorithm optimized for point sources, a significant fraction of these galaxies will not have their data transfered to Earth. Gaia will be able to measure radial velocities for only 8% and metal abundances for 0.01% of them. The most frequent galaxy type are spirals (58% considering Sa, Sb, Sc, Sd, Sbc), followed by irregulars (25%) and ellipticals (13% adding E2 and E-S0), as seen in Table 26.
Overview of extragalactic objects.
Spectral types of stars from LMC/SMC.
Additionally, 1 000 000 quasars were generated and the model predicts 50 000 supernovae that will occur during the five years of mission, 77% of which are Ia type (Table 27).
Percentages of each supernova type calculated over 50 000 supernovae.
The sky distribution of these three types of objects is shown in Fig. 20.
 |
Fig. 20 Total sky distribution of unresolved galaxies, quasars, and supernovae. Colour scale indicates the log 10 of the number of objects per square degree. |
Regarding redshifts, galaxies go up to z ~ 0.75, while the most distant quasars are at z ~ 5. Magnitudes also present a different pattern depending on the type of object, as shown in Fig. 21.
 |
Fig. 21 Redshift and G relation for galaxies and QSOs. Colour scale indicates the log 10 of the number of objects per 0.05 mag and 0.05 redshift difference. |
4. Conclusions
Gaia will be able to provide a much more precise and complete view of the Galaxy than its predecessor Hipparcos, which means a huge increase in the total number of stars (Table 28) known in the solar neighbourhood (Table 29).
Comparison of Hipparcos and Gaia characteristics and the predicted number of stars, variables, and binaries presented in this study.
Number of nearby stars (within 25 pc) detected by Hipparcos compared with the predicted number of stars in the universe model.
The Gaia universe model, and other population synthesis models in general, can be useful tools for survey preparation. In this particular case, it has been possible to obtain a general idea of the numbers, percentages, and distribution of different objects and characteristics of the environment that Gaia can potentially observe and measure.
Additionally, the analysis of the snapshot has facilitated the detection of several aspects that are to be improved. Therefore, it has been a quite fruitful quality assurance process from a scientific point of view.
Looking forward, the next reasonable step would be to repeat the same analysis but taking into consideration the instrument specifications and the available error models. By convolving it with the idealized universe model presented in this paper, it will be possible to evaluate the impact of the instrumental effects on the actual composition of the Gaia catalogue. In the meantime the simulated catalogue presented in this paper will be available at the CDS.
Internal referred documents from the Gaia mission can be found at http://www.rssd.esa.int/index.php?project=GAIA&page=Library_Livelink
Gaia performances and error models are described at http://www.rssd.esa.int/index.php?page=Science_Performance&project=GAIA
Acknowledgments
The development of the Universe Model and of the GOG simulator used here have been possible thanks to contributions from many people. We warmly acknowledge the contributions from Mary Kontizas, Laurent Eyer, Guillaume Debouzy, Oscar Martínez, Raul Borrachero, Jordi Peralta, and Claire Dollet. This work has been possible thanks to the European Science Foundation (ESF) and its funding for the activity entitled “Gaia Research for European Astronomy Training”, as well as the infrastructure used for the computation in the Barcelona Supercomputing Center (MareNostrum). This work was supported by the MICINN (Spanish Ministry of Science and Innovation) – FEDER through grant AYA2009-14648-C02-01 and CONSOLIDER CSD2007-00050.
References
- Arenou, F. 2010, The simulated multiple stars, Tech. Rep., Observatoire de Paris-Meudon, GAIA-C2-SP-OPM-FA-054 [Google Scholar]
- Arenou, F. 2011, in International Workshop Double and Multiple Stars: Dynamics, Physics, and Instrumentation, ed. J. A. Docobo, V. S. Tamazian, & Y. Y. Balega, AIP Conf. Ser., 1346, 107 [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belokurov, V. A., & Evans, N. W. 2003, MNRAS, 341, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., & Feltzing, S. 2009, in The Galactic Plane, in depth and across the spectrum, ed. N. W. Janet Drew, Melvin Hoare, XXVIIth IAU General Assembly, Rio de Janeiro, 15, 789 [Google Scholar]
- Bergbush, P., & VandenBerg, D. 1992, ApJS, 81, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2009, MmSAI, 80, 422 [Google Scholar]
- Bienaymé, O., Robin, A. C., & Crézé, M. 1987, A&A, 180, 94 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 1999, ApJ, 513, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, E., Méndez, R. A., Pedreros, M. H., et al. 2009, AJ, 137, 4339 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N., Becker, S. A., & Pesnell, W. D. 2000, in Theoretical Stellar Evolution, ed. A. N. Cox (New York: Springer-Verlag), 499 [Google Scholar]
- Dollet, C. 2004, Ph.D. Thesis, Tech. Rep., Université de Nice [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., & Lopez-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eyer, L., Robin, A., Evans, D. W., & Reylé, C. 2005, Implementation of variable stars in the Galactic model, I. General concept, Tech. Rep., Observatoire de Genève, VSWG-LE-002 [Google Scholar]
- Feast, M. W., Glass, I. S., Whitelock, P. A., & Catchpole, R. M. 1989, MNRAS, 241, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1999, A&A, 344, 393 [NASA ADS] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, A. E., Grenier, S., Udry, S., et al. 1997, in Publ., ESA Spec. Publ., 402, 621 [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2011, A&A, 530, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greggio, L., & Renzini, A. 1983, A&A, 118, 217 [NASA ADS] [Google Scholar]
- Han, C. 2008, ApJ, 681, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Robin, A. C., & Crézé, M. 1997a, A&A, 320, 428 [NASA ADS] [Google Scholar]
- Haywood, M., Robin, A. C., & Crézé, M. 1997b, A&A, 320, 440 [NASA ADS] [Google Scholar]
- Hilditch, R. W., Howarth, I. D., & Harries, T. J. 2005, MNRAS, 357, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Computing In Science & Engineering, 9, 90 [Google Scholar]
- Jaschek, C., Jaschek, M., Egret, D., & Andrillat, Y. 1988, A&A, 192, 285 [NASA ADS] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O. 2007, Communications in Asteroseismology, 150, 39 [Google Scholar]
- Kontizas, M., Bellas-Velidis, I., Rocca-Volmerange, B., et al. 2011, in EAS Publ. Ser., 45, 337 [Google Scholar]
- Kovalevsky, J. 2003, A&A, 404, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kowalski, A. F., Hawley, S. L., Hilton, E. J., et al. 2009, AJ, 138, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Krone-Martins, A. G. O., Ducourant, C., Teixeira, R., & Luri, X. 2008, in IAU Symp. 248, ed. W. J. Jin, I. Platais, & M. A. C. Perryman, 276 [Google Scholar]
- Kunszt, P. Z., Szalay, A. S., & Thakar, A. R. 2001, in Mining the Sky, ed. A. J. Banday, S. Zaroubi, & M. Bartelmann, 631 [Google Scholar]
- Kurtz, D. W. 1982, MNRAS, 200, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Macri, L. M., Stanek, K. Z., Bersier, D., Greenhill, L. J., & Reid, M. J. 2006, ApJ, 652, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA Spec. Publ., 576, 5 [Google Scholar]
- Molinaro, R., Ripepi, V., Marconi, M., et al. 2011, MNRAS, 413, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Ryan, S. G., & Beers, T. C. 2001, ApJ, 561, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Ojha, D., Bienayme, O., Robin, A., Crézé, M., & Mohan, V. 1996, A&A, 311, 456 [NASA ADS] [Google Scholar]
- Ojha, D. K., Bienaymé, O., Mohan, V., & Robin, A. C. 1999, A&A, 351, 945 [NASA ADS] [Google Scholar]
- Paczynski, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, I. N., Gizis, J. E., & Hawley, S. L. 2002, AJ, 124, 2721 [NASA ADS] [CrossRef] [Google Scholar]
- Reylé, C., Robin, A., Arenou, F., & Grux, E. 2007, Universe Model Interface Control Document, Tech. Rep., Obs. de Besançon, Obs. de Paris-Meudon, GAIA-C2-SP-LAOB-CR-001 [Google Scholar]
- Reylé, C., Marshall, D. J., Robin, A. C., & Schultheis, M. 2009, A&A, 495, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Crézé, M., & Mohan, V. 1992, ApJ, 400, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derriére, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, S., Zaritsky, D., & Kennicutt, Jr., R. C. 2000, AJ, 119, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Slezak, E., & Mignard, F. 2007, A realistic QSO Catalogue for the Gaia Universe Model, Tech. Rep., Observatoire de la Côte d’Azur, GAIA-C2-TN-OCA-ES-001-1 [Google Scholar]
- Sozzetti, A., Torres, G., Latham, D. W., et al. 2009, ApJ, 697, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Stift, M. J., & Alecian, G. 2009, MNRAS, 394, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, S., & Subramaniam, A. 2009, A&A, 496, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabachnik, S., & Tremaine, S. 2002, MNRAS, 335, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Tanga, P. 2011, in EAS Publ. Ser., 45, 225 [Google Scholar]
- Tsalmantza, P., Kontizas, M., Rocca-Volmerange, B., et al. 2009, A&A, 504, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Hucht, K. A. 2001, New Astron. Rev., 45, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, M. A. 1992, ApJ, 386, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Zorec, J., & Briot, D. 1997, A&A, 318, 443 [NASA ADS] [Google Scholar]
All Tables
Local mass density ρ0 and axis ratios ϵ for different populations and as a function of age for the thin disc.
Velocity dispersions, asymmetric drift Vad at the solar position, and velocity dispersion gradient.
Characteristics of the variable types. Localisation in the (spectral type, luminosity class) diagram, probability of a star to be variable in this region, stellar population, and metallicity, respectively.
Light curves of the regular or semi-regular variable stars where 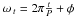 (P is the period, φ is the phase).
(P is the period, φ is the phase).
Parameters defining the luminosity function in the Schechter formalism for different galaxy types at z = 0, from Fioc & Rocca-Volmerange (1999).
Predictions of SNII and SNIa numbers exploding per century for the M* (Bj) galaxies defined in Table 11.
Numbers and percentages of single stars and multiple systems generated by the universe model over the total number of stars.
Percentages of stars of each population, calculated over the total number of stars for each respective column.
Percentages of each luminosity class of generated stars, calculated over the total number of stars for each respective column.
Percentages of each spectral type of generated stars, calculated over the total number of stars for each respective column.
Overview of variable stars. Percentages were calculated over the total variable stars.
Comparison of Hipparcos and Gaia characteristics and the predicted number of stars, variables, and binaries presented in this study.
Number of nearby stars (within 25 pc) detected by Hipparcos compared with the predicted number of stars in the universe model.
All Figures
 |
Fig. 1 Gaia G, GBP , GRP, and GRVS passbands. |
| In the text | |
 |
Fig. 2 Hierarchical Triangular Mesh subdivisions scheme: Each triangle has three vertices labelled 0, 1 and 2. When the area is subdivided into four new triangles, the opposite midpoints are labelled 0′, 1′ and 2′, respectively, and the central triangle is suffixed with a 3. |
| In the text | |
 |
Fig. 3 Total sky distribution of stars for different magnitudes. Top down: G < 20, GRVS < 17 and GRVS < 12. Colour scale indicates the log 10 of the number of stars per square degree. |
| In the text | |
 |
Fig. 4 Stellar distribution split by population (G < 20). Left to right, top down: thin disc, thick disc, spheroid, and bulge. Colour scale indicates the log 10 of the number of stars per square degree. |
| In the text | |
 |
Fig. 5 Distribution of stars in heliocentric Cartesian coordinates (G < 20): top (XY), side (XZ) and front (YZ) perspectives. Colour scale indicates the log 10 of the number of stars per square parsec. |
| In the text | |
 |
Fig. 6 G distribution split by stellar population. The bump for the bulge is due to the red clump, which is seen at I = 15 in Baade’s window. |
| In the text | |
 |
Fig. 7 Star distribution split by luminosity class for G < 20. |
| In the text | |
 |
Fig. 8 HR Diagram of stars split by population (left to right, top down): thin disc, thick disc, spheroid and bulge. colour scale indicates the log 10 of the number of stars per 0.025 |
| In the text | |
 |
Fig. 9 Stellar parallax split by populations. |
| In the text | |
 |
Fig. 10 Stellar parallax split by spectral type. |
| In the text | |
 |
Fig. 11 Metallicity-alpha elements relation for GRVS < 12. Colour scale indicates the log 10 of the number of stars per 0.05 [Fe/H] and 0.04 [α/Fe] . |
| In the text | |
 |
Fig. 12 Proper motion of stars μαcosδ, μδ and radial velocity VR. Colour scale indicates the log 10 of the number of stars per 2.4 mas/year (km s-1 in case of VR) and 1.0 mag. |
| In the text | |
 |
Fig. 13 Metallicity and V-axis velocity relation split by population (left to right, top down): thin disc, thick disc, spheroid, and bulge. Colour scale indicates the log 10 of the number of stars per 0.05 [Fe/H] and 6 km s-1. |
| In the text | |
 |
Fig. 14 Sky distribution of microlenses that could take place during the 5 years of the mission. Colour scale indicates the log 10 of the number of microlenses per square degree. |
| In the text | |
 |
Fig. 15 HR diagram split by variability type. |
| In the text | |
 |
Fig. 16 G difference and angular separation relation for binaries. Colour scale indicates the log 10 of the number of binaries per 0.25 difference in magnitude and 0.1 in log (mas). |
| In the text | |
 |
Fig. 17 Period-eccentricity relation for binaries. Colour scale indicates the log 10 of the number of binaries per 0.01 difference in eccentricity and 0.13log (days). |
| In the text | |
 |
Fig. 18 Metallicity distribution of stars with planets. |
| In the text | |
 |
Fig. 19 G distribution of stars with planets split by population. |
| In the text | |
 |
Fig. 20 Total sky distribution of unresolved galaxies, quasars, and supernovae. Colour scale indicates the log 10 of the number of objects per square degree. |
| In the text | |
 |
Fig. 21 Redshift and G relation for galaxies and QSOs. Colour scale indicates the log 10 of the number of objects per 0.05 mag and 0.05 redshift difference. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.