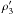| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A157 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201118560 | |
| Published online | 16 July 2012 | |
Hyperons in neutron-star cores and a 2 M⊙ pulsar
1 N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
e-mail: ilona.bednarek@us.edu.pl, bejger@camk.edu.pl; haensel@camk.edu.pl; jlz@camk.edu.pl
2 Department of Astrophysics and Cosmology, Institute of Physics, University of Silesia, Uniwersytecka 4, 40-007 Katowice, Poland
Received: 1 December 2011
Accepted: 16 April 2012
Context. A recent measurement of the mass of PSR J1614-2230 rules out most existing models of the equation of state (EOS) of dense matter that is subjected to the high-density softening caused by either hyperonization or a phase transition to either quark matter or a boson condensate.
Aims. We attempt to resolve the apparent differences between the predictions derived from up-to-date hypernuclear data, which include the appearance of hyperons at about three nuclear densities and the existence of a M = 2.0 M⊙ neutron star.
Methods. We consider a non-linear relativistic mean field (RMF) model involving the baryon octet coupled to meson fields. An effective Lagrangian includes quartic terms in the meson fields. The values of the model parameters are obtained by fitting the semi-empirical parameters of nuclear matter at the saturation point, as well as potential wells for hyperons in nuclear matter and the strength of the Λ − Λ attraction in double-Λ hypernuclei.
Results. We propose a non-linear RMF model that is consistent with up-to-date semi-empirical nuclear and hypernuclear data and allows for neutron stars with hyperon cores and M > 2 M⊙. The model involves hidden-strangeness scalar and vector mesons, coupled only to hyperons, and quartic terms involving vector meson fields.
Conclusions. Our EOS involving hyperons is stiffer than the corresponding nucleonic EOS (in which hyperons are artificially suppressed) above five nuclear densities. The required stiffening is generated by the quartic terms involving the hidden-strangeness vector meson.
Key words: dense matter / equation of state / stars: neutron
© ESO, 2012
1. Introduction
A recent measurement of the mass of PSR J1614-2230, 1.97 ± 0.04 M⊙ (Demorest et al. 2010), puts a stringent constraint on the equation of state (EOS) of dense matter in neutron star cores. In the light of this measurement, EOSs of dense matter, which are based on the modern many-body theories and the realistic strong-interaction model, lead to a puzzle. On the one hand, interactions consistent with the available experimental data on hypernuclei, predict the presence of hyperons at densities exceeding 2–3ρ0, where ρ0 = 2.7 × 1014 g cm-3 (corresponding to the baryon number density n0 = 0.16 fm-3) is the normal nuclear density. On the other hand, the inevitable softening of the EOS, due to the hyperonization, implies that the maximum allowable mass is Mmax ≲ 1.5 M⊙ (see, e.g. Burgio et al. 2011; Vidana et al. 2011, and references therein). Such a low value of Mmax is only marginally consistent with that of 1.44 M⊙ measured for the Hulse-Taylor pulsar, but has been placed in doubt by that of 1.67 ± 0.04 M⊙ for PSR J1903-0327 (Champion et al. 2008; a more precise value was obtained by Freire et al. 2011). Vidana et al. (2011) noted that this problem cannot be solved by adding an ad hoc extremely stiff repulsive three-body contribution to the EOS.
We consider neutron star cores composed of baryons, electrons, and muons. Baryons and leptons are in weak-interaction equilibrium. Hyperons appear at density ρ1 (baryon density n1). For ρ < ρ1, only nucleons are present. For ρ > ρ1, matter contains a mixture of nucleons and hyperons. This state (phase) is denoted NH. We also consider a “reference dense-matter model” with hyperons artificially suppressed. This purely nucleon state is denoted N. The corresponding EOSs are denoted EOS.NH and EOS.N. These EOSs coincide for ρ < ρ1.
A too low 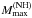 is not an inevitable feature of neutron stars with hyperon cores. Bonanno & Sedrakian (2012) obtained
is not an inevitable feature of neutron stars with hyperon cores. Bonanno & Sedrakian (2012) obtained 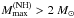 , starting from an extremely stiff relativistic mean field model NL3 EOS.N, which yielded
, starting from an extremely stiff relativistic mean field model NL3 EOS.N, which yielded 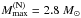 (close to the absolute upper bound on Mmax stemming from causality, e.g., Haensel et al. 2007). Bonanno & Sedrakian (2012) extend the NL3 model to the hyperon sector, and get
(close to the absolute upper bound on Mmax stemming from causality, e.g., Haensel et al. 2007). Bonanno & Sedrakian (2012) extend the NL3 model to the hyperon sector, and get 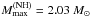 . Massive stars with hyperon cores exist there because of the extreme stiffness of the EOS.N, and the nuclear-matter parameter (the slope of symmetry energy versus density) L = 118 MeV is significantly higher than its semi-empirical estimates.
. Massive stars with hyperon cores exist there because of the extreme stiffness of the EOS.N, and the nuclear-matter parameter (the slope of symmetry energy versus density) L = 118 MeV is significantly higher than its semi-empirical estimates.
In our approach, we keep L (and the stiffness of the EOS.N near ρ0) within the semi-empirical estimates (i.e., those obtained within a model of atomic nuclei, hence model-dependent values). Our EOS.N at high density is stiff, but not extremely stiff: 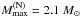 . In general,
. In general, 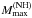 is essentially determined by the ρ ≳ 5ρ0 segment of the EOS.NH. Hence if the hyperon softening occurs at 2–3ρ0, then, to get a sufficiently high Mmax, the softening must be followed by a sufficiently strong stiffening of EOS.NH for ρ ≳ 5ρ0. One has therefore to identify a mechanism that stiffens the EOS.NH at these densities. For our model of EOS.N, in order to yield
is essentially determined by the ρ ≳ 5ρ0 segment of the EOS.NH. Hence if the hyperon softening occurs at 2–3ρ0, then, to get a sufficiently high Mmax, the softening must be followed by a sufficiently strong stiffening of EOS.NH for ρ ≳ 5ρ0. One has therefore to identify a mechanism that stiffens the EOS.NH at these densities. For our model of EOS.N, in order to yield 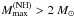 , the EOS.NH for ρ ≳ 5ρ0 should be actually stiffer than the EOS.N one. Simultaneously, the NH phase has to be stable (thermodynamically preferred over the N one). We derive a constraint on the EOS.NH resulting from the conditions mentioned above, and discuss the consequences of the violation of this constraint.
, the EOS.NH for ρ ≳ 5ρ0 should be actually stiffer than the EOS.N one. Simultaneously, the NH phase has to be stable (thermodynamically preferred over the N one). We derive a constraint on the EOS.NH resulting from the conditions mentioned above, and discuss the consequences of the violation of this constraint.
In our discussion, we restrict ourselves to hadronic matter, and do not consider the possibility of quark deconfinement. Because of the surface effects and electrical screening in a quark plasma, a transition to quark matter would occur at nearly constant pressure and with an only slightly smoothed density jump (see, e.g., Endo et al. 2006, and references therein). A reasonable scenario is: softening of the N phase by hyperonization at 2–3ρ0, followed by softening of the NH phase by quark deconfinement at a significantly higher density. Bonanno & Sedrakian (2012) show that assuming NL3 EOS.NH, a transition to quark matter occurring after hyperonization could be consistent with the detection of 2 M⊙ neutron star provided that the vector repulsion in quark matter is sufficiently strong and quark deconfinement takes place near the maximum NS mass. For our EOS.NH, getting 2 M⊙ with a quark core would require a very fine tuning, and we do not consider such an unlikely possibility.
The problem of an interplay between attraction (softening) and repulsion (stiffening) in dense hadronic matter can be formulated in simple terms using a modern effective field theory, involving baryon and meson fields. In the case of nucleon matter, such a theory can be put on a firm theoretical basis, starting from quantum chromodynamics (QCD) (Walecka 2004, and references therein). Such an effective theory can be solvable within the mean field approximation and can give a satisfactory description of a wealth of nuclear physics data if the coupling of nucleons to the scalar meson field σ, and two vector meson fields: ωμ and 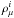 , is considered. Here, μ and i denote the space-time and isospin-space components of the field. An effective Lagrangian contains quadratic and quartic terms in vector fields, and quadratic, cubic, and quartic terms in scalar fields. While σ yields an attraction to bind nuclei, vector meson fields generate repulsion to saturate nuclear matter at ρ0. Numerical coefficients in the effective Lagrangian are fixed by fitting a wealth of nuclear data (Sugahara & Toki 1994). The effective model is then extended to include the hyperon sector. Two meson fields with “hidden strangeness” (
, is considered. Here, μ and i denote the space-time and isospin-space components of the field. An effective Lagrangian contains quadratic and quartic terms in vector fields, and quadratic, cubic, and quartic terms in scalar fields. While σ yields an attraction to bind nuclei, vector meson fields generate repulsion to saturate nuclear matter at ρ0. Numerical coefficients in the effective Lagrangian are fixed by fitting a wealth of nuclear data (Sugahara & Toki 1994). The effective model is then extended to include the hyperon sector. Two meson fields with “hidden strangeness” (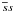 ) are added: scalar σ∗ (quadratic terms) and vector-isovector
) are added: scalar σ∗ (quadratic terms) and vector-isovector 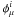 (quadratic and quartic terms). These fields couple only to hyperons (Schaffner et al. 1994). An important constraint on the hyperon sector of Lagrangian results from the existing evaluations of the depth of the potential well acting on a single zero-momentum hyperon in nuclear matter,
(quadratic and quartic terms). These fields couple only to hyperons (Schaffner et al. 1994). An important constraint on the hyperon sector of Lagrangian results from the existing evaluations of the depth of the potential well acting on a single zero-momentum hyperon in nuclear matter, 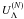 ,
, 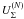 , and
, and  (binding energy of a hyperon in nuclear matter is
(binding energy of a hyperon in nuclear matter is 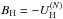 ). An effective theory of hadronic matter described in the general terms above and solved in the mean field approximation are referred to as a non-linear relativistic mean field model (non-linear RMF, Bednarek & Mańka 2009).
). An effective theory of hadronic matter described in the general terms above and solved in the mean field approximation are referred to as a non-linear relativistic mean field model (non-linear RMF, Bednarek & Mańka 2009).
There exist a few older and simpler models of NH matter that predict that 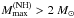 . These models are based on the relativistic mean field Lagrangian involving an octet of baryons coupled to the σ, ωμ, and
. These models are based on the relativistic mean field Lagrangian involving an octet of baryons coupled to the σ, ωμ, and 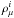 meson fields (quadratic terms in the Lagrangian), with additional cubic and quartic σ self-interaction terms (for a review, see Glendenning 1996). The mean field solutions of the field equations are referred to collectively as the relativistic mean field (RMF) model. Glendenning & Moszkowski (1991) can exceed 2 M⊙ assuming high nuclear matter incompressibility, K = 300 MeV, and a strong Λ − σ attraction, balanced by a Λ − ω repulsion to be consistent with an experimental
meson fields (quadratic terms in the Lagrangian), with additional cubic and quartic σ self-interaction terms (for a review, see Glendenning 1996). The mean field solutions of the field equations are referred to collectively as the relativistic mean field (RMF) model. Glendenning & Moszkowski (1991) can exceed 2 M⊙ assuming high nuclear matter incompressibility, K = 300 MeV, and a strong Λ − σ attraction, balanced by a Λ − ω repulsion to be consistent with an experimental 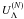 . Experimental constraints on UΣ and UΞ in nuclear matter are not applied. It is assumed that all hyperons in the baryon octet have the same coupling as Λ.
. Experimental constraints on UΣ and UΞ in nuclear matter are not applied. It is assumed that all hyperons in the baryon octet have the same coupling as Λ.
A model similar to that of Glendenning & Moszkowski (1991) was used to obtain 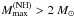 by Bombaci et al. (2008). Dexheimer & Schramm (2008) applied a hadronic chiral model of NH matter. They treated mesons and the baryon octet as flavor-SU(3) multiplets. For one form of the quartic term in the vector-meson fields, they obtained
by Bombaci et al. (2008). Dexheimer & Schramm (2008) applied a hadronic chiral model of NH matter. They treated mesons and the baryon octet as flavor-SU(3) multiplets. For one form of the quartic term in the vector-meson fields, they obtained 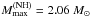 .
.
Two specific ways of ensuring that 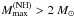 have been proposed. The first way, chosen in both our work and Weissenborn et al. (2012b,a), consists in introducing a hyperon repulsion due to a hidden-strangeness vector meson φμ that couples only to hyperons. The second way, pointed out in Weissenborn et al. (2012a), consists in making vector-meson – hyperon repulsion stronger by going from the SU(6) symmetry relations to the SU(3) ones. In contrast to Weissenborn et al. (2012a), we keep the vector-meson – hyperon coupling constants at their SU(6) values.
have been proposed. The first way, chosen in both our work and Weissenborn et al. (2012b,a), consists in introducing a hyperon repulsion due to a hidden-strangeness vector meson φμ that couples only to hyperons. The second way, pointed out in Weissenborn et al. (2012a), consists in making vector-meson – hyperon repulsion stronger by going from the SU(6) symmetry relations to the SU(3) ones. In contrast to Weissenborn et al. (2012a), we keep the vector-meson – hyperon coupling constants at their SU(6) values.
In the present paper, we propose a resolution to the problem of the “hyperonization − Mmax > 2 M⊙” using a specific realization of the non-linear RMF model of hadronic matter (Bednarek & Mańka 2009). The non-linear RMF model of NH matter is presented in Sect. 2. Experimental constraints from nuclear and hypernuclear physics are described in Sect. 3. A particular EOS.NH is described in Sect. 4. A model of PSR J1614-2230 with a hyperon core is presented in Sect. 5. The problem of the high-density instability of the NH phase and the M − R relation for neutron stars models are discussed in Sect. 6. Finally, in Sect. 7 we summarize the results of the paper, compare them with results obtained by other authors, and present our conclusions.
Preliminary results of our work were presented at the MODE-SNR-PWN Workshop in Bordeaux, France, November 15 − 17, 2010, and in a poster at the CompStar 2011 Workshop in Catania, Italy, May 9–12, 2011.
2. Non-linear RMF model of hyperon cores
Our adopted model was formulated by Bednarek & Mańka (2009). The octet of baryons includes a nucleon doublet N and six of the lowest-mass hyperons H: Λ singlet, Σ triplet, and Ξ doublet. The uniform number density of each baryon species B is denoted nB (B = n,p,Λ,...).
In the nucleon sector, the meson fields are: scalar σ, vector ωμ, and vector-isovector 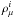 . The generalization of the non-linear RMF model to the baryon octet is done in the following way. Additional “hidden-strangeness” mesons, namely scalar
. The generalization of the non-linear RMF model to the baryon octet is done in the following way. Additional “hidden-strangeness” mesons, namely scalar 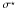 and vector φμ, are introduced. They couple only to hyperons, such that gNσ ⋆ = gNφ = 0. The vector-meson coupling constants to hyperons are assumed to fulfill the relations stemming from the SU(6) symmetry (additive quark model) of hadrons
and vector φμ, are introduced. They couple only to hyperons, such that gNσ ⋆ = gNφ = 0. The vector-meson coupling constants to hyperons are assumed to fulfill the relations stemming from the SU(6) symmetry (additive quark model) of hadrons 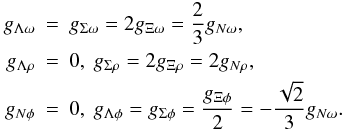 (1)Similar symmetry relations can be obtained for the coupling constants of the scalar mesons, but they are not used in the present model. We instead adjust them to fit experimental estimates of
(1)Similar symmetry relations can be obtained for the coupling constants of the scalar mesons, but they are not used in the present model. We instead adjust them to fit experimental estimates of 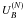 .
.
At fixed {nB} (B = n,p,Λ,... ), and assuming vanishing baryon currents, the hadronic Lagrangian density ℒhad is used to derive the equations of motion for the meson fields. Static solutions are found assuming that baryonic matter is isotropic and uniform. The mean-field approximation, neglecting quantum corrections, is used: σ − → ⟨ σ ⟩ = s0, ωμ − → ⟨ ωμ ⟩ = w0δμ0, 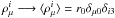 ,
, 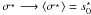 , φμ − → ⟨ φμ ⟩ = f0δμ0. The resulting Lagrangian density function ℒhad consists of three components,
, φμ − → ⟨ φμ ⟩ = f0δμ0. The resulting Lagrangian density function ℒhad consists of three components, 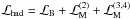 . The component ℒB is obtained from the free-baryon Lagrangian by replacing bare baryon masses mB (B = n,p,Λ,...) by the effective ones,
. The component ℒB is obtained from the free-baryon Lagrangian by replacing bare baryon masses mB (B = n,p,Λ,...) by the effective ones, 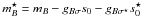 . The quadratic (interaction) component
. The quadratic (interaction) component 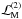 contains terms proportional to
contains terms proportional to 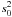 ,
, 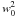 ,
, 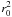 ,
, 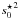 , and
, and 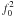 . The interaction component
. The interaction component 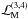 contains cubic and quartic terms in s0, and quartic vector-meson terms proportional to
contains cubic and quartic terms in s0, and quartic vector-meson terms proportional to  ,
,  , and
, and 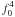 and the cross terms proportional to
and the cross terms proportional to 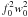 ,
,  , and
, and 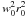 .
.
The hadronic Lagrangian density function ℒhad is then used to calculate the hadron energy-density as a function of partial baryon densities {nB}, ℰhad({nB}). To simplify the formulae, we use the units in which ħ = c = 1, except where indicated otherwise. Calculations done for the considered model (Bednarek & Mańka 2009) lead to the following explicit formulae for the hadron contribution to the energy density ℰ and pressure P (we note that the original equations of Bednarek & Mańka contain several misprints that are corrected below; for the sake of simplicity, we use a shorthand notation gNσ ≡ gσ,gNω ≡ gω,... ) 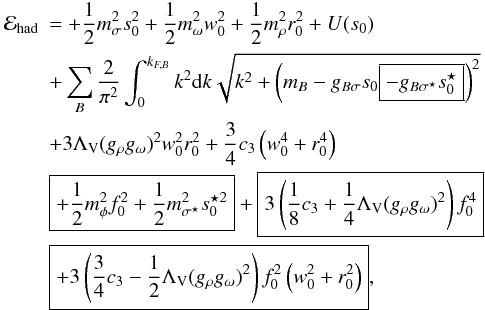 (2)
(2)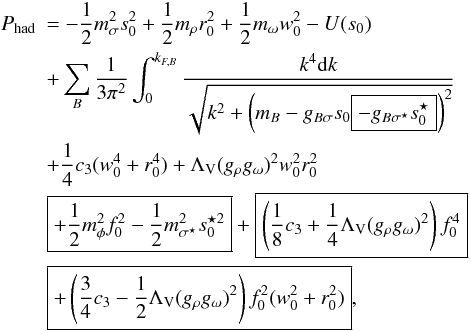 (3)where the non-linear σ-self-interaction potential is
(3)where the non-linear σ-self-interaction potential is 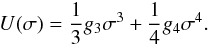 (4)The terms vanishing in purely nucleon (zero strangeness) matter are presented above in rectangles.
(4)The terms vanishing in purely nucleon (zero strangeness) matter are presented above in rectangles.
The quartic terms in ℰhad and Phad deserve additional explanations. Their form stems from the chiral SU(3) symmetry of the baryon-meson and meson-meson interactions. The coefficients of the quartic terms involve two phenomenological parameters, c3 and ΛV.
We first consider the quartic terms in the nucleon sector. The vector-isoscalar quartic term ( ) was included in the TM1 model of Sugahara & Toki (1994). However, the TM1 model was constructed to describe atomic nuclei, hence is valid for both nuclear matter near saturation density and a small neutron excess. It is to be expected that extrapolation to supranuclear density and large neutron excess would necessitate a richer isospin and density dependence of the model Lagrangian than assumed in the TM1 model. Bednarek & Mańka (2009) proposed to do this by enlarging the quartic terms by adding a vector-isovector one (
) was included in the TM1 model of Sugahara & Toki (1994). However, the TM1 model was constructed to describe atomic nuclei, hence is valid for both nuclear matter near saturation density and a small neutron excess. It is to be expected that extrapolation to supranuclear density and large neutron excess would necessitate a richer isospin and density dependence of the model Lagrangian than assumed in the TM1 model. Bednarek & Mańka (2009) proposed to do this by enlarging the quartic terms by adding a vector-isovector one ( ) and a cross-term (
) and a cross-term (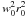 ). The strengths of the quartic terms are determined by two parameters, ΛV and c3, instead of only one in the TM1 model of Sugahara & Toki (1994). This allows a good fitting of not only (semi-empirical estimates of) nuclear symmetry energy and incompressibility, but also the slope parameter L, and simultaneously yields Mmax > 1.97 M⊙.
). The strengths of the quartic terms are determined by two parameters, ΛV and c3, instead of only one in the TM1 model of Sugahara & Toki (1994). This allows a good fitting of not only (semi-empirical estimates of) nuclear symmetry energy and incompressibility, but also the slope parameter L, and simultaneously yields Mmax > 1.97 M⊙.
As shown in Bednarek & Mańka (2009), the chiral SU(3) symmetry yields a suitable extension of the quartic terms to the hyperon sector, the same c3 and ΛV entering the quartic-terms coefficients. Additional quartic terms in the hyperon sector are generated by the hidden-strangeness vector-isoscalar field f0.
3. Determination of parameters of non-linear RMF model
We denote the neutron excess in nuclear matter by δ = (nn − np)/nb. The energy per nucleon (excluding the nucleon rest energy) is E(nb,δ). An analysis of a wealth of data on heavy atomic nuclei can yield the parameters of nuclear matter near the saturation point, corresponding to the minimum of energy per nucleon, Es, reached at nb = ns and δ = 0. The results are model-dependent and therefore they are called semi-empirical. Other semi-empirical parameters are: the symmetry energy Ss, the incompressibility Ks, and the symmetry-energy slope parameter L, 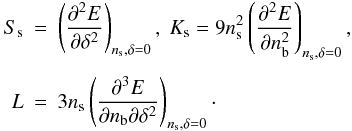 (5)Studies of hypernuclei and of Σ − atoms allow us to evaluate the potential energy of a single zero-momentum hyperon in symmetric nuclear matter,
(5)Studies of hypernuclei and of Σ − atoms allow us to evaluate the potential energy of a single zero-momentum hyperon in symmetric nuclear matter, 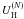 . The non-linear RMF yields following expression for this quantity:
. The non-linear RMF yields following expression for this quantity: 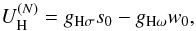 (6)which should be calculated at ns and δ = 0. The semi-empirical estimates are
(6)which should be calculated at ns and δ = 0. The semi-empirical estimates are  MeV,
MeV, 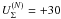 MeV, and
MeV, and 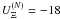 MeV (Schaffner-Bielich & Gal 2000). Equation (6) is then used to determine gΛσ, gΣσ, and gΞσ.
MeV (Schaffner-Bielich & Gal 2000). Equation (6) is then used to determine gΛσ, gΣσ, and gΞσ.
As we consider the NH phase, which contains finite fractions of hyperons, we need information on the hyperon-hyperon interaction. Studies of double-Λ hypernuclei suggest that the Λ − Λ interaction is attractive. In the mean-field approximation, it can be characterized by the potential well of a zero-momentum Λ in Λ-matter. In our model we get a general expression for the potential energy of a zero-momentum hyperon H′ in H-matter 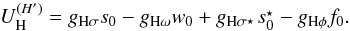 (7)The latest (very uncertain) semi-empirical estimate coming from double-Λ hypernuclei is
(7)The latest (very uncertain) semi-empirical estimate coming from double-Λ hypernuclei is 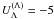 MeV (Takahashi et al. 2001; Song et al. 2003). Equation (7) is then used to determine
MeV (Takahashi et al. 2001; Song et al. 2003). Equation (7) is then used to determine 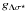 . For
. For 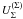 and
and 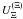 , no data exist. We therefore estimate them using the relations
, no data exist. We therefore estimate them using the relations 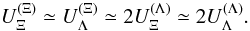 (8)These relations were established based on one-boson exchange models and semi-empirical evaluation of the strength of the Λ − Λ attraction (Schaffner et al. 1994).
(8)These relations were established based on one-boson exchange models and semi-empirical evaluation of the strength of the Λ − Λ attraction (Schaffner et al. 1994).
Our aim is to adjust the parameters of our Lagrangian to reproduce, to within a few percent, ten semi-empirical nuclear and hyper-nuclear data. As we have mentioned in the introduction, the term “semi-empirical” refers to an indirect, model-dependent way of extracting these parameters from a wealth of experimental data. We first consider five nuclear matter parameters at saturation. The modern models used to extract the nuclear matter data are energy-density functionals of a sufficiently rich structure. Their parameters are adjusted to fit the masses and charge-radii (and often some additional data) of a broad sample (some thousands) of atomic nuclei. An extrapolation to the limiting case of infinite nuclear matter is then made, yielding semi-empirical values of ns, Es, Ks, Ss, and L. The scatter in the values of the nuclear-matter parameters extracted in this way visualizes the model dependence of the procedure used. In particular, systematic differences are noticed for Ks: non-relativistic models give typically 210–240 MeV, while the relativistic ones yield larger values 260–290 MeV. The starting point for our Lagrangian, Sect. 2, was a very successful relativistic model TM1 (Sugahara & Toki 1994), and therefore we kept its values of ns, Es, and Ks. Our results for the nuclear matter parameters at saturation are presented in Table 3.
Our adjustement of the isovector parameters in Lagrangian density, namely gρ and ΛV, deserves additional explanation. We performed this by employing existing information on the density dependence of the symmetry energy, that is, we used not only the value of the symmetry energy at saturation, Ss, but also a semi-empirical estimate of symmetry energy at nb ≈ 0.1 fm-3, 26.67 MeV, which determined the value of L (Horowitz & Piekarewicz 2001). This influenced the EOS of neutron matter, because E(nb,1) ≈ E(nb,0.5) + S(nb) (see, e.g., Haensel et al. 2007).
4. EOS of neutron-star matter
The total energy density and the total pressure are the sums of the contributions of hadrons and leptons, because the contributions of the electromagnetic interaction to these quantities are negligibly small, and leptons (electrons and muons) can be treated as ideal Fermi gases, such that 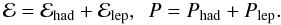 (9)The (total) baryon number density is
(9)The (total) baryon number density is 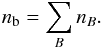 (10)Imposing electrical charge neutrality and beta equilibrium, one gets a system of non-linear equations for the particle species fractions Yi = ni/nb. At a given nb the equilibrium fractions are
(10)Imposing electrical charge neutrality and beta equilibrium, one gets a system of non-linear equations for the particle species fractions Yi = ni/nb. At a given nb the equilibrium fractions are 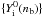 and the energy density and pressure become functions only of nb. For the sake of comparison, we consider not only a general EOS involving nucleons and hyperons, EOS.NH, but also an EOS of nucleon matter, EOS.N, with artificially suppressed hyperons (see Sect. 1).
and the energy density and pressure become functions only of nb. For the sake of comparison, we consider not only a general EOS involving nucleons and hyperons, EOS.NH, but also an EOS of nucleon matter, EOS.N, with artificially suppressed hyperons (see Sect. 1).
Expression for Phad, Eq.(3), shows that hyperons produce new repulsive quartic terms involving f0, w0, and r0. The dependence of the EOS on ΛV turns out to be quite strong. All other parameters are determined by the conditions of reproducing nuclear and hypernuclear data (i.e., near the saturation point of nuclear matter), and the high-density stiffness of EOS.NH increases monotonically with increasing ΛV. In what follows, we use ΛV = 0.0165, which as we see yields a high-density stiffness of the EOS.NH consistent with 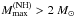 , while keeping good agreement with semi-empirical nuclear matter parameters. This EOS.NH is referred to hereafter as BM165.
, while keeping good agreement with semi-empirical nuclear matter parameters. This EOS.NH is referred to hereafter as BM165.
The parameters of the BM165 model, and the values of ten semi-empirical nuclear and hyper-nuclear parameters given by this model, are presented in Tables 1–4.
BM165 model of hadronic matter.
BM165 model of hadronic matter.
BM165 model of hadronic matter.
BM165 model of hadronic matter.
The thermodynamical equilibrium of the NH matter imposes relations between the chemical potentials of hyperons present in dense matter, nucleons, and leptons. These relations can be expressed in the general form (see, e.g., Haensel et al. 2007)  (11)where
(11)where 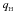 is the charge of the hyperon H in units of the proton charge. The threshold density for the appearance of hyperons H,
is the charge of the hyperon H in units of the proton charge. The threshold density for the appearance of hyperons H, 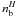 , is determined by the enthalpy of a single hyperon H in beta-equilibrated dense matter
, is determined by the enthalpy of a single hyperon H in beta-equilibrated dense matter 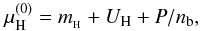 (12)where UH is the potential energy of this hyperon. For
(12)where UH is the potential energy of this hyperon. For 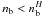 ,
, 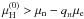 , and H decays in a weak interaction process. At the threshold density, a single H in dense matter is stable so that
, and H decays in a weak interaction process. At the threshold density, a single H in dense matter is stable so that 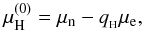 (13)and for
(13)and for 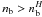 , the density of stable H grows with increasing nb.
, the density of stable H grows with increasing nb.
For the BM165 model, the first hyperon to appear is Λ at 6.3 × 1014 g cm-3 (0.35 fm-3), where 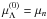 . The next hyperon is Ξ − , which appears at 7.7 × 1014 g cm-3 (0.42 fm-3), where
. The next hyperon is Ξ − , which appears at 7.7 × 1014 g cm-3 (0.42 fm-3), where 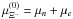 . A repulsive
. A repulsive 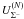 implies that Σ − appears at significantly higher density than Ξ − , namely 1.23 × 1015 g cm-3 (0.63 fm-3), even though mΣ − < mΞ − .
implies that Σ − appears at significantly higher density than Ξ − , namely 1.23 × 1015 g cm-3 (0.63 fm-3), even though mΣ − < mΞ − .
The order of appearance of hyperons in dense matter deserves a comment. For a long time, in view of the lack of experimental information on 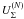 and
and  , they were assumed to be similar to
, they were assumed to be similar to 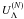 . Consequently, Σ − was found to be the first hyperon to appear, not the lightest hyperon Λ, because the (unfavorable) effect of mΣ − > mΛ was weaker than the (favorable) effect of the presence of μe in the threshold condition
. Consequently, Σ − was found to be the first hyperon to appear, not the lightest hyperon Λ, because the (unfavorable) effect of mΣ − > mΛ was weaker than the (favorable) effect of the presence of μe in the threshold condition 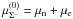 (see, e.g., Haensel et al. 2007). However, the large positive (repulsive)
(see, e.g., Haensel et al. 2007). However, the large positive (repulsive) 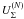 derived by analyses of the Σ − -atoms pushes
derived by analyses of the Σ − -atoms pushes 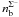 well above
well above  . Consequently, Σ − is the last, instead of the first, hyperon to appear in a neutron star core (Fig. 2).
. Consequently, Σ − is the last, instead of the first, hyperon to appear in a neutron star core (Fig. 2).
The appearance of hyperons leads to significant softening of the EOS.NH compared to EOS.N (Fig. 1). To be able to model neutron stars with M > 2M⊙, the EOS.NH has necessarily to significantly stiffen at higher densities. The curve PNH(ρ) crosses the PN(ρ) one at ρ2 = 1.76 × 1014 g cm-3 (n2 = 0.85 fm-3), and at higher density the EOS.NH is stiffer than the EOS.N.
In reality, the difference PNH − PN is limited by the stability of the NH phase against the re-conversion into the N phase. We assume that the matter is in beta equilibrium. At T = 0, the small change in energy per baryon dE is related to the small change in the baryon density dnb by 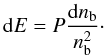 (14)Therefore, the condition for the stability of the NH phase (against the conversion into the N one)
(14)Therefore, the condition for the stability of the NH phase (against the conversion into the N one) 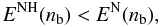 (15)implies that
(15)implies that 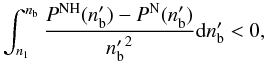 (16)where n1 is the density at the first hyperon threshold. For the BM165 model, n1 = 0.35 fm-3.
(16)where n1 is the density at the first hyperon threshold. For the BM165 model, n1 = 0.35 fm-3.
 |
Fig. 1 Equations of state EOS.N and EOS.NH calculated using the BM165 model. Hyperons appear at point 1 and the EOS.NH crosses the EOS.N one at point 2. |
 |
Fig. 2 Number fractions of the constituents of dense matter in beta equilibrium, Yi = ni/nb, versus baryon density, nb. Dotted lines: EOS.N. Solid lines: EOS.NH. |
 |
Fig. 3 EOS BM165 in the vicinity of the high-density NH-N phase transition, where 2 is the crossing of the the N and NH pressures, 3 represents the density and pressure of the NH phase at the phase coexistence, and 3′ is the density and pressure of the N phase at the phase coexistence. Horizontal segment 33′ is the pressure at the first order phase transition. Were the NH phase to be (sufficiently) stable until reaching a maximum mass, maximum (central) density in stable stars would correspond to the asterisk sign, ρc,max = ρ ∗ . For the fully equilibrated hadronic matter ρc,max is slightly higher than |
5. A model of PSR J1614-2230
To get a complete EOS of the neutron-star interior, the BM165 EOS of the liquid core was supplemented by an EOS of the crust. We used the EOS of the inner crust of Douchin & Haensel (2001), the model of Haensel & Pichon (1994) for the outer crust down to 108 g cm-3, and the classical model of Baym et al. (1971) for the outer layer with ρ < 108 g cm-3. A model of a neutron star of gravitational mass 1.97 M⊙, rotating rigidly at 317 Hz, was calculated using the two-dimensional rotstar code from the LORENE library1 implementing the formulation of Bonazzola et al. (1993). The circumferential equatorial radius of neutron star is Req = 11.83 km, its central density ρc = 1.73 × 1014 g cm-3, and its central baryon density nc = 0.834 fm-3. At 317 Hz, polar flattening is rather small: the radial coordinate at the equator is only 200 m larger than that at the pole. The number fractions of the particle species Yi = ni/nb in the liquid core of neutron star, are plotted versus the radial coordinate r in Fig.4. The radius of the hyperon core is 8.36 km. The strangeness per baryon at the star’s center is (S/Nb) = −0.35.
6. High-density instability of the NH phase and neutron star models
Violation of the inequality (16) indicates that the NH phase is unstable with respect to a conversion into a purely nucleon (N) one. Thermodynamic equilibrium of dense matter at pressure P corresponds to the minimum of the baryon chemical potential μb = (ℰ + P)/nb. An equilibrium phase-transition NH − → N occurs at P3 such that 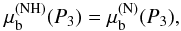 (17)and is accompanied by a density jump from ρ3 = ρ(NH)(P3) = 2.58 × 1015 g cm-3 (n3 = 1.105 fm-3) on the NH side to
(17)and is accompanied by a density jump from ρ3 = ρ(NH)(P3) = 2.58 × 1015 g cm-3 (n3 = 1.105 fm-3) on the NH side to 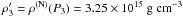 (
(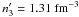 ) on the N side. The BM165 EOS in the vicinity of P3 = 1.05 × 1036 erg cm-3 is shown in Fig.3. The softening of the EOS for P > P3 is twofold. First, there is a constant pressure sector of the EOS (corresponding to the vanishing compression modulus!). Second, there is a transition to the N-phase, which is significantly softer than the NH one.
) on the N side. The BM165 EOS in the vicinity of P3 = 1.05 × 1036 erg cm-3 is shown in Fig.3. The softening of the EOS for P > P3 is twofold. First, there is a constant pressure sector of the EOS (corresponding to the vanishing compression modulus!). Second, there is a transition to the N-phase, which is significantly softer than the NH one.
The reaction of the stellar structure to the (first order) phase transition (NH − → N) can be described by the linear response theory formulated in Zdunik et al. (1987). This theory describes stellar configurations in the vicinity of a star that has a central pressure equal to P3. In our case, this region of stellar configurations is very small because we are close to the maximum mass. The crucial parameter, determining the stability of the star with a small core of the denser phase (N), is the relative density jump at phase transition pressure, P3 of 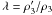 . The stability condition for a star with a small N-core is
. The stability condition for a star with a small N-core is 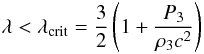 (18)(see Sect. 3.4 of Zdunik et al. 1987). In our case, the condition in Eq. (18) is fulfilled, because λ = 1.27 while λcrit = 2.18. Consequently, there is a (very small) region of stable configurations with the N-phase core. In reality, this region is very narrow: the maximum mass of non-rotating stars is reached for a central pressure Pc,max that is only higher by 0.04% than the pressure at the phase transition, P3.
(18)(see Sect. 3.4 of Zdunik et al. 1987). In our case, the condition in Eq. (18) is fulfilled, because λ = 1.27 while λcrit = 2.18. Consequently, there is a (very small) region of stable configurations with the N-phase core. In reality, this region is very narrow: the maximum mass of non-rotating stars is reached for a central pressure Pc,max that is only higher by 0.04% than the pressure at the phase transition, P3.
 |
Fig. 4 The logarithm of the number fractions of the constituents of dense matter, log 10(Yi), versus circumferential radius, in the liquid core of a 1.97 M⊙ star model based on the BM165 EOS. |
 |
Fig. 5 Gravitational stellar mass, M, versus circumferential radius, R, calculated for the EOS.N and EOS.NH. Only stable configurations are displayed. Inset: effect of rotation at f = 317 Hz on the M – equatorial circumferential radius curve near Mmax. |
We plot in Fig.5 the M − R relations for non-rotating neutron stars, and those rotating at 317 Hz, based on the BM165 EOS. Stars with M > 1.4 M⊙ have a hyperon core. The flattening of the M(R) curve due to the hyperon softening of the EOS is significant. However, it remains possible to achieve 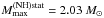 , which is smaller than
, which is smaller than  by only 0.07 M⊙. Rotation at 317 Hz, as measured for PSR J1614-2230, increases
by only 0.07 M⊙. Rotation at 317 Hz, as measured for PSR J1614-2230, increases 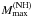 to 2.04 M⊙ (see zoomed inset of Fig.5).
to 2.04 M⊙ (see zoomed inset of Fig.5).
7. Discussion and conclusions
We have constructed a model of the hyperon cores of neutron stars that allows for the existence of neutron star of 2 M⊙. The model is consistent with ten semi-empirical evaluations of nuclear and hyper-nuclear matter parameters. As an additional constraint, we have imposed SU(6) symmetry relations between the coupling constants of baryons and vector mesons. In spite of this, by introducing two hidden-strangeness meson fields (scalar and vector) coupled only to hyperons, we have been able to reproduce four semi-empirical parameters stemming from hypernuclear physics.
In contrast to the NL3 model, which was used by Bonanno & Sedrakian (2012), our symmetry energy is not unusually “stiff” near the saturation point: we get L = 74 MeV, compared to L = 118 MeV for NL3 (Agrawal et al. 2005). Consistently, our EOS.N is not unusually stiff, and yields for NS with nucleon cores 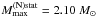 , which to be contrasted with the NL3 value of 2.8 M⊙. The hyperon softening for the model of Bonanno & Sedrakian (2012) is dramatic, and leads to
, which to be contrasted with the NL3 value of 2.8 M⊙. The hyperon softening for the model of Bonanno & Sedrakian (2012) is dramatic, and leads to 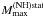 , which is lower by nearly 0.8 M⊙ than the N one. In our case, getting
, which is lower by nearly 0.8 M⊙ than the N one. In our case, getting 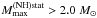 is conditioned by the high-density vector interactions in the hyperon sector, which are not excluded in view of our lack of knowledge of high-density hyperon interactions. A similar solution was proposed Weissenborn et al. (2012b,a), who obtained the stiffening of the EOS.NH from the φ meson coupled to hyperons.
is conditioned by the high-density vector interactions in the hyperon sector, which are not excluded in view of our lack of knowledge of high-density hyperon interactions. A similar solution was proposed Weissenborn et al. (2012b,a), who obtained the stiffening of the EOS.NH from the φ meson coupled to hyperons.
Our EOS.NH becomes stiffer than the EOS.N for ρ ≳ 5ρ0, and its stiffness grows with density. This leads eventually to the instability of the NH matter with respect to the conversion into the N state, softening the EOS due to the first order phase transition. The maximum density at which the stable NH phase can exist actually determines our 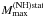 , which is only 0.07 M⊙ lower than
, which is only 0.07 M⊙ lower than  . The rotation at 317 Hz, as measured for PSR J1614-2230, increases
. The rotation at 317 Hz, as measured for PSR J1614-2230, increases 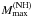 by 0.01 M⊙, to 2.04 M⊙. Breaking the SU(6) symmetry for the vector-meson couplings to hyperons, in a similar way to Weissenborn et al. (2012a), can make the value of
by 0.01 M⊙, to 2.04 M⊙. Breaking the SU(6) symmetry for the vector-meson couplings to hyperons, in a similar way to Weissenborn et al. (2012a), can make the value of 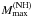 even higher.
even higher.
In the present paper, we have restricted ourselves to the hadronic forms of matter. A consistent treatment of the phase transition to the quark phase in the neutron star core would require the use of the QCD for both hadronic and quark phases. As the transition occurs in the strong-coupling regime, one is forced to use different models that separately describe the baryon and the quark phases. An approach based on an effective model of the QCD of quark matter (Nambu-Jona-Lasinio) and NL3 for the hadronic phase, used by Bonanno & Sedrakian (2012) indicates that to get Mmax > 2 M⊙, vector repulsion in quark matter should be sufficiently strong. In any case, the maximum mass obtained by them is very close to that reached at a central density equal to the deconfinement density.
Acknowledgments
We are deeply grateful to Mikhail E. Gusakov for his invaluable help in detecting and removing some errors in earlier versions of the present work. We are also indebted to him for his difficult but inspiring questions referring to the physics of dense matter. We are grateful to Verônica Antocheviz Dexheimer for pointing out one of the missing references. This work was partially supported by the Polish MNiSW research grant no. N N203 512838, by the LEA Astro-PF, and by the European Science Foundation CompStar RNP. MB acknowledges the support of Marie Curie Fellowship no. ERG-2007-224793 within the 7th European Community Framework Programme.
References
- Agrawal, B. K., Shlomo, S., & Kim Au, V. 2005, EpJ A, 25, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Pethick, C., & Sutherland, P. 1971, ApJ, 170, 299 [Google Scholar]
- Bednarek, I., & Manka, R. 2009, J. Phys. G Nucl. Phys., 36, 095201 [NASA ADS] [CrossRef] [Google Scholar]
- Bombaci, I., Panda, P. K., Providencia, C., & Vidana, I. 2008, Phys. Rev. D, 77, 083002 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, L., & Sedrakian, A. 2012, A&A, 539, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marck, J.-A. 1993, A&A, 278, 421 [NASA ADS] [Google Scholar]
- Burgio, G. F., Schulze, H.-J., & Li, A. 2011, Phys. Rev. C, 83, 025804 [NASA ADS] [CrossRef] [Google Scholar]
- Champion, D. J., Ransom, S. M., Lazarus, P., et al. 2008, Science, 320, 1309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chatterjee, D., & Schaeffner-Bielich, J. 2011, Poster presented at CompStar2011 Workshop, Catania, Italy [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dexheimer, V., & Schramm, S. 2008, ApJ, 683, 943 [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endo, T., Maruyama, T., Chiba, S., & Tatsumi, T. 2006, Prog. Theor. Phys., 115, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C., Bassa, C. G., Wex, N., et al. 2011, MNRAS, 412, 2763 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 1985, ApJ, 293, 470 [Google Scholar]
- Glendenning, N. K. 1996, Compact Stars. Nuclear Physics, Particle Physics, and General Relativity (New York: Springer) [Google Scholar]
- Glendenning, N. K., & Moszkowski, S. A. 1991, Phys. Rev. Lett., 67, 2414 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Haensel, P., & Pichon, B. 1994, A&A, 283, 313 [NASA ADS] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1. Equation of State and Structure (New York: Springer) [Google Scholar]
- Horowitz, C. J., & Piekarewicz, J. 2001, Phys. Rev. Lett., 86, 5647 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schaffner, J., Dover, C. B., Gal, A., et al. 1994, Ann. Phys. (NY), 235, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Schaffner-Bielich, J., & Gal, A. 2000, Phys. Rev. C, 62, 034311 [NASA ADS] [CrossRef] [Google Scholar]
- Song, H. Q., Su, R. K., Lu, D. H., & Qian, W. L. 2003, Phys. Rev. C, 68, 055201 [NASA ADS] [CrossRef] [Google Scholar]
- Sugahara, Y., & Toki, H. 1994, Nucl. Phys. A, 579, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, H., Ahn, J. K., Akikawa, H., et al. 2001, Phys. Rev. Lett., 87, 212502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vidana, I., Logoteta, D., Providencia, C., & Bombaci, I. 2011, Europhys. Lett., 94, 11002 [Google Scholar]
- Walecka, J. D. 2004, Theoret. Nucl. Subnucl. Phys., 2nd ed. (World Scientific: Imperial College Press) [Google Scholar]
- Weissenborn, S., Chatterjee, D., & Schaffner-Bielich, J. 2012a, Phys. Rev. C, 85, 065802 [NASA ADS] [CrossRef] [Google Scholar]
- Weissenborn, S., Chatterjee, D., & Schaffner-Bielich, J. 2012b, Nucl. Phys. A, 881, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L., Haensel, P., & Schaeffer, R. 1987, A&A, 172, 95 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Equations of state EOS.N and EOS.NH calculated using the BM165 model. Hyperons appear at point 1 and the EOS.NH crosses the EOS.N one at point 2. |
| In the text | |
 |
Fig. 2 Number fractions of the constituents of dense matter in beta equilibrium, Yi = ni/nb, versus baryon density, nb. Dotted lines: EOS.N. Solid lines: EOS.NH. |
| In the text | |
 |
Fig. 3 EOS BM165 in the vicinity of the high-density NH-N phase transition, where 2 is the crossing of the the N and NH pressures, 3 represents the density and pressure of the NH phase at the phase coexistence, and 3′ is the density and pressure of the N phase at the phase coexistence. Horizontal segment 33′ is the pressure at the first order phase transition. Were the NH phase to be (sufficiently) stable until reaching a maximum mass, maximum (central) density in stable stars would correspond to the asterisk sign, ρc,max = ρ ∗ . For the fully equilibrated hadronic matter ρc,max is slightly higher than |
| In the text | |
 |
Fig. 4 The logarithm of the number fractions of the constituents of dense matter, log 10(Yi), versus circumferential radius, in the liquid core of a 1.97 M⊙ star model based on the BM165 EOS. |
| In the text | |
 |
Fig. 5 Gravitational stellar mass, M, versus circumferential radius, R, calculated for the EOS.N and EOS.NH. Only stable configurations are displayed. Inset: effect of rotation at f = 317 Hz on the M – equatorial circumferential radius curve near Mmax. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.