| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117835 | |
| Published online | 11 July 2012 | |
A phenomenological model for the X-ray spectrum of nova V2491 Cygni
1
SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA
Utrecht, The
Netherlands
e-mail: c.pinto@sron.nl
2
ESAC European Space Astronomy Center, PO Box 78, 28691 Villanueva
de la Canada, Madrid,
Spain
3
Department of Astrophysics/IMAPP, Radboud
University, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
Received: 5 August 2011
Accepted: 10 June 2012
The X-ray flux of nova V2491 Cyg reached a maximum some forty days after optical maximum. The X-ray spectrum at that time, obtained with the RGS of XMM-Newton, shows deep, blue-shifted absorption by ions of a wide range of ionization. We show that the deep absorption lines of the X-ray spectrum at maximum, and those observed nine days later, are well described by a phenomenological model with emission from a central blackbody and from a collisionally ionized plasma (CIE). The blackbody spectrum (BB) is absorbed by three main highly ionized expanding shells; the CIE and BB are absorbed by cold circumstellar and interstellar matter that includes dust. The outflow density does not decrease monotonically with distance. The abundances of the shells indicate that they were ejected from an O-Ne white dwarf. We show that the variations on time scales of hours in the X-ray spectrum are caused by a combination of variation in the central source and in the column density of the ionized shells. Our phenomenological model gives the best description so far of the supersoft X-ray spectrum of nova V2491 Cyg, but underpredicts, by a large factor, the optical and ultraviolet flux. The X-ray part of the spectrum must originate from a very different layer in the expanding envelope, presumably much closer to the white dwarf than the layers responsible for the optical/ultraviolet spectrum. This is confirmed by the absence of any correlation between the X-ray and UV/optical observed fluxes.
Key words: novae, cataclysmic variables / nuclear reactions, nucleosynthesis, abundances / X-rays: binaries / stars: abundances / circumstellar matter / dust, extinction
© ESO, 2012
1. Introduction
The sensitivity to soft X-rays of the EXOSAT satellite enabled the first discovery of X-rays from a classical nova, GQ Mus, in April 1984 (Oegelman et al. 1984). The ROSAT satellite detected it almost eight years later, in February 1992, and found it to have a very soft blackbody-like spectrum with kTeff ~ 28 eV (Oegelman et al. 1993). ROSAT observations of other novae in our galaxy showed that only a small fraction of novae are detected in X-rays (Oegelman et al. 1993; Orio et al. 2001).
The spectrum of GQ Mus is very soft, comparable to
the spectra of a new class of supersoft X-ray sources (SSS) discovered with ROSAT in the
Large Magellanic Cloud, with temperatures 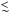 100 eV in blackbody fits to their spectra
(Trümper et al. 1991; Greiner et al. 1991). The favored explanation for the X-ray spectra of the
supersoft sources such as GQ Mus is hydrogen burning at the surface of a white dwarf, of
material accreted from a companion star. The class of supersoft X-ray sources shows a large
variety, some sources being permanent and others transient, and with wide different types of
companion stars (see review by Kahabka & van den Heuvel
1997). Observation campaigns with ROSAT, XMM-Newton and
Chandra in M 31 show that most of the supersoft sources are classical
novae (Pietsch et al. 2005; Henze et al. 2010). Recently, Henze et al.
(2011) argued that the high fraction of novae without detected SSS emission might
be explained by the incomplete coverage.
100 eV in blackbody fits to their spectra
(Trümper et al. 1991; Greiner et al. 1991). The favored explanation for the X-ray spectra of the
supersoft sources such as GQ Mus is hydrogen burning at the surface of a white dwarf, of
material accreted from a companion star. The class of supersoft X-ray sources shows a large
variety, some sources being permanent and others transient, and with wide different types of
companion stars (see review by Kahabka & van den Heuvel
1997). Observation campaigns with ROSAT, XMM-Newton and
Chandra in M 31 show that most of the supersoft sources are classical
novae (Pietsch et al. 2005; Henze et al. 2010). Recently, Henze et al.
(2011) argued that the high fraction of novae without detected SSS emission might
be explained by the incomplete coverage.
The model fits of the supersoft X-ray spectra have become increasingly sophisticated over the years. Blackbody fits indicated high super-Eddington luminosities for the ROSAT sources. Heise et al. (1994) showed that the fit of local thermodynamic equilibrium (LTE) model atmospheres to the ROSAT data brought their bolometric luminosity below the Eddington limit for temperatures ≤60 eV. For temperatures ≥100 eV, Hartmann & Heise (1997) showed that the differences between bolometric luminosities for ROSAT supersoft sources derived from blackbody, LTE and NLTE models are much smaller, the main difference being that NLTE models may give appreciable flux above 0.4 keV (i.e. in the “hard” ROSAT band). A new level of sophistication is reached by Petz et al. (2005), who fit NLTE model spectra of expanding atmospheres, thus taking into account the outflow inherent in the nova phenomenon. Even the most sophisticated model fails to fit the observed continuum of the nova V4743 Sgr at λ < 30 Å, and also does not match the depth of the absorption lines (Fig. 3 of Petz et al. 2005; Rauch & Werner 2010).With regard to the X-ray spectra of V2491 Cyg, the best published atmosphere model does not reproduce the observed line velocities or the observed line depths, as clearly visible in Fig. 11 of Ness et al. (2011), for example in the N vii 1s–2p line at 24.8 Å. Atmosphere models so far also fail to reproduce the wide range of ionization levels simultaneously present in the observed spectra: e.g. O v to O viii in V2491 Cyg (see Figs. 1−4 below).
 |
Fig. 1 Best fit to the first observation A.1 (see also Table 1). The rest-frame wavelengths of all main transitions are displayed. |
 |
Fig. 2 Best fit to the second observation A.2. |
 |
Fig. 3 Best fit to the third observation A.3. |
 |
Fig. 4 Best fit to the fourth observation B. |
What is the reason for this failure? If there are shocks in the expanding nova envelope, the assumption of a standard atmosphere whose density decreases monotonically outward, breaks down. The rapid X-ray variability observed in some novae indicates that the expanding envelope and/or the luminosity from the deeper layers are not stationary and/or not spherically symmetric, invalidating another assumption in atmosphere models. In this paper we therefore investigate a pilot model of a quite different nature, in which separate expanding shells absorb the spectrum of an underlying central source. In this first study, we describe the central source as a blackbody spectrum. We apply our simple model to the XMM-Newton RGS spectra obtained from the nova V2491 Cyg to investigate whether this model gives a better description of the continuum and line absorption; whether the short-term variability is due to changes in the source or in the absorption; and whether the model allows determining of the chemical abundances in the expanding envelope.
Nova V2491 Cyg was discovered on April 10, 2008, at V = 7.7 (Nakano et al. 2008). The optical flux declined from this peak in the course of the following months, interrupted by a brief second maximum at the end of April. Ultraviolet and X-ray fluxes of the V2491 Cyg were obtained with the Swift satellite: the ultraviolet flux declined in tandem with the optical flux (measured through May and June), whereas the X-ray luminosity rose from a marginal detection on April 11 to a peak more than a thousand times brighter some 40 days later (Page et al. 2010). Lightcurves of optical, ultraviolet and X-ray are shown in Fig. 4 of Page et al. (2010). In the Swift X-ray range (0.3–8 keV) the spectrum peaks strongly near 0.4–0.5 keV during the X-ray maximum and has a flatter (i.e. harder) energy distribution before and after X-ray maximum (see Fig. 3 of Page et al. 2010).
From a relation between maximum magnitude of novae and their rate of decline, a distance of 10.5 kpc has been estimated for V2491 Cyg by Helton et al. (2008). The optical flux was already declining during the first measurements, and therefore the actual flux maximum may have been higher than the flux of the first measurement: this would imply a smaller distance.
The interstellar reddening E(B − V) = 0.43 has been estimated from the ratio of the O I lines at 0.84 and 1.13 micron (Rudy et al. 2008), and may be converted into a hydrogen column NH = 2.4 × 1025 m2 using the relation determined by Predehl & Schmitt (1995).
The X-ray spectra described in this paper were obtained with XMM-Newton just before the X-ray maximum, and some nine days later, when the X-ray flux had declined by an order of magnitude.
Our paper is structured as follows. In Sect. 2 we describe the XMM-Newton data and provide a brief description of the four spectra that we will analyze. In Sect. 3 we describe a basic model and apply it to the spectra. In Sect. 4 we discuss several variant models and their applications. In Sect. 5 we discuss our model fits and in Sect. 6 we summarize our conclusions and outline prospects for improvements to the models.
2. Data and brief description of the spectra
The data discussed in this paper were obtained during two observations with XMM-Newton, as described in Ness et al. (2011). The first observation started at day 39.86, measured from the initial optical discovery on 2008 April 10.73 UT, and lasted 39 280 s. During this first observation the RGS countrate varied strongly: from about 15 cts/s during the first 7500 s it dropped to a minimum near 3 cts/s lasting some 6000 s, and then rose to a maximum of about 18 cts/s for the final 16 000 s of the observation. We follow Ness et al. (2011) in defining three spectra for this first observation, spectrum A.1 obtained during the initial plateau; spectrum A.2 during the minimum flux; and spectrum A.3 during the final high-flux plateau, (see Fig. 3 of Ness et al. 2011). The second observation started on day 49.62, and showed a countrate that varied only mildly around 3 cts/s during the 31 700 s observation. All data from this observation are collected in the fourth spectrum, spectrum B.
We analyzed the 7–38 Å (1.77–0.33 keV) first order spectra of the RGS detector, using SPEX version 2.02.03 (Kaastra et al. 1996).
We show the four spectra derived from the XMM-Newton RGS observations in Figs. 1–4 (see also Figs. 6 and 7 of Ness et al. 2011). The most prominent features are the neutral oxygen absorption edge near 23 Å with the corresponding 1s–2p absorption line at 23.5 Å. The neutral nitrogen 1s–2p absorption line near 31.2 Å is also visible, but the neutral iron L2 and L3 edges that one expects near 17.15 and 17.45 Å are weak. Ness et al. (2011) identify 1s–3p and 1s–4p lines of O vii near these wavelengths. Indeed, absorption lines from O v to O viii are detected, blueshifted with respect to the rest frame wavelength; examples include O viii near 19 Å, O vii at 21.5 Å, and N vii at 24.5 Å. The blueshift indicates that the absorbing matter is expanding, and the wide range of ionization levels indicates that several expansion shells are involved.
Lines of highly ionized neon and oxygen are also detected at the rest frame wavelengths; examples are Ne x at 12.1 Å, Ne ix at 13.4 Å, O viii at 19.0 Å, and O vii at 21.6 Å. A strong feature is also seen near 29.3 Å, close to the forbidden N vi line at 29.5 Å.
3. The basic model
As a first attempt to describe the spectrum Fλ
we used a multi-component model which may be written symbolically as
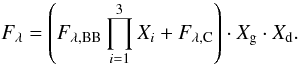 (1)The components in this model and their
parameters are
(1)The components in this model and their
parameters are
-
the blackbody fluxFλ,BB(R,Teff) characterized by the radius R and effective temperature Teff,
-
three photo-ionized absorbers Xi(Ni,O,ξi,vi,σi,(A/O)i), each characterized by the column density for oxygen Ni,O, the ionization parameter ξi, the outflow velocity vi, the velocity width σi, and the abundances of various elements with respect to oxygen (A/O)i. The number of absorbers is in principle free: we added absorbers until the fit did not significantly improve anymore (as indicated by the Δ χ2; see Table 1). In this case, this leads to at least three absorbers.
-
the flux from a collisionally ionized plasma Fλ,C(EM,T,σC,(ANe)C,(Mg/Ne)C), characterized by the emission measure
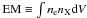 , the
temperature T, the turbulent velocity σC,
the neon abundance (ANe)C, and the abundance
ratio of magnesium to neon (Mg/Ne)C,
, the
temperature T, the turbulent velocity σC,
the neon abundance (ANe)C, and the abundance
ratio of magnesium to neon (Mg/Ne)C, -
the absorption by interstellar or circumstellar gas Xg(NH,Tg,Ag), characterized by the hydrogen column NH, the temperature Tg, and the abundances for each element Ag, and
-
the absorption by interstellar dust Xd(Nd,O), characterized by the column of oxygen in the dust Nd,O.
To correctly describe the interstellar absorption Xg with high spectral resolution, we used the SPEX model hot, adjusting its temperature Tg at a low value (near 1 eV), suitable for the (nearly) neutral component of the ISM. This model describes the transmission through a layer of collisionally ionized plasma. We give abundances of the ISM normalized on proto-solar values; here and in the following, when we refer to proto-solar values we use those given by Lodders & Palme (2009).
The detailed form of the Fe L edge near 17.2–17.7 Å and the O K edge near 22.7–23.2 Å may be affected by the presence of these elements in molecules in dust (Paerels et al. 2001). The absorption Xd by such molecules is described in SPEX with amol (Pinto et al. 2010). In the spectra of V2491 Cyg, the iron feature is weak, and thus we only constrain oxygen compounds in the interstellar dust.
A highly ionized absorber Xi is modeled in SPEX with the xabs model, which gives the transmission of a slab of photo-ionized material. Before this model is applied, one must compute the ionization levels, and for this we used version C08.00 of Cloudy (for a description of an earlier version, see Ferland et al. 1998). Cloudy computes the ionization balance of a gas for the ionization parameter ξ ≡ L/(nr2), a measure of the number of photons per particle (for a light source with luminosity L at distance r of the gas with number density n), and a given spectral energy distribution (SED). The form of the energy distribution is important, because a soft irradiating spectrum leads to a different ionization equilibrium than a hard irradiating spectrum with the same luminosity. The energy distribution that we used for V2491 Cyg is shown in Fig. 5. It has been computed through all available archival data from IR to X-ray energies: IR fluxes from Naik et al. (2009), optical from Hachisu & Kato (2009), UV and soft X-ray from Ness et al. (2011), and hard X-ray from Page et al. (2010). We have taken their fluxes and models in each wavelength band and corrected for the Galactic interstellar extinction by assuming a NH = 2.5 × 1025 m-2, which represents an average between our fits and those found in the literature. The total luminosity of this SED is 1.15 × 1033 W, of which the X-rays, roughly described as a blackbody with the temperature of 110 eV (blue dash-dotted line in Fig. 5), contribute 6.23 × 1032 W.
 |
Fig. 5 Unabsorbed SED used for V2491 Cyg (solid line and data points). We also show the unabsorbed blackbody emission (blue dashed-dotted line) and the observed absorbed fluxes (red dotted line). |
The abundances of the highly ionized absorber are obviously also important for calculating the ionization structure. To compute the ionization levels we used proto-solar abundances. In principle, once we determined the abundances of the highly ionized absorbers from our spectral fit, the computation of the ionization structure should be iterated for these new abundances. In this pilot study, however, we have not performed this iteration.
To limit the number of free parameters, we limited the number of independent abundances in the basic model as follows. The flux Fλ,C of collisionally ionized plasma dominates only at wavelengths λ < 15 Å in the spectra of V2491 Cyg and at these wavelengths only magnesium and neon contribute to the emission. We determined the Mg and Ne abundances from this part of the spectrum, and assumed that the abundances thus determined for the collisionally ionized plasma are also valid for the highly ionized absorbers Xi. Conversely, we determined the column of O, and the number ratios of C, N, Si, S, Ar, Ca, Fe with respect to oxygen from the absorption lines of the highly ionized absorbers Xi, assuming that these ratios are the same for all three highly ionized absorbing shells. We then assumed that the ratios found for the highly ionized absorbing shells also apply to the collisionally ionized plasma.
The reason for listing abundances with respect to oxygen is that these are much better constrained by the observed spectrum than abundances with respect to hydrogen, because hydrogen only contributes to the X-ray spectrum as a source of free electrons. The ionized hydrogen of the hot nova shell only affects the spectral normalization, but not the shape in the RGS spectra.
3.1. Application to spectrum A.3
We applied the basic model first to the spectrum with the highest signal-to-noise ratio, spectrum A.3. To be able to use χ2 statistics, we binned the RGS data in bins of about 1/3 of the spectral resolution of ~0.065 Å of the first-order RGS spectrum. To ensure a minimum of 10 counts/bin we in addition rebinned the raw data at the shortest wavelengths. This led to rebinning by factors 10, 5 and 2 in the ranges 7–11 Å, 11–15 Å, and 15–38 Å, respectively.
In a first step we fit a preliminary model, in which we ignore the highly ionized absorption shells Xi and the dust absorption lines Xd, This provided us with initial estimates for the blackbody and collisionally ionized plasma, which we then entered as starting values in the full model fitting. The value that we derived for the temperature of the collisionally ionized plasma was determined mostly from the spectrum at λ < 15 Å, and more specifically from the ratio between the Ne ix and Ne x 1s–2p lines in this region. For this reason we fixed the plasma temperature T in the full model fitting at the value found from the preliminary fit.
The resulting values of the parameters for the full model are listed in Table 1, and the resulting model spectrum is shown in Fig. 3.
The radius of the blackbody emitter, 17 600 km, is several times the radius of a white dwarf (which decreases from ≃ 9000 km for a 0.6 M⊙ white dwarf to ≃ 3000 km at 1.3 M⊙; see Eq. (27) of Nauenberg 1972; Provencal et al. 2002). This implies that the photospheric surface lies in the expanding layers. With the temperature of 1.4 × 106 K, the blackbody has a bolometric luminosity LBB = 8.5 × 1032 W.
To describe the high-ionization absorption lines, we required three distinct Xi components. An outflow with constant velocity and constant mass flux Ṁ, has nr2 ∝ Ṁ/v and therefore ξ is constant with radius. If the velocity increases with radius, as in a homologous expansion, we expect ξ to increase with radius. This agrees with our finding that the shell with the highest ionization parameter ξi has the highest velocity. However, our finding that the shell with the intermediate velocity has the lowest ξi is puzzling. This result may be due to systematic errors in the velocities of weak shells 2 and 3, caused by the difficulty in separating the velocity dispersion and shift in the absorption lines of these relatively weak shells (see also Sect. 3.1.2).
The lines of C vi, Ar xvi and S xiv are weak compared to the oxygen lines, and this results in number ratios C/O, Ar/O and S/O much lower than solar. For Ca we can only give an upper limit to the Ca/O ratio. We estimated the hydrogen column by assuming a proto-solar O/H ratio.
The relative strengths of the O vii γ plus Fe i L edge at 17.2−17.7 Å and the oxygen features at 22.7–23.2 Å indicate an Fe/O ratio lower than proto-solar. This suggests that Fe may be depleted by dust. Indeed, we prefer to describe the broad absorption feature at 22.7–23.3 Å with a dusty-molecule component of silicates plus a gaseous component of O ii, with about 10% of the total oxygen in each of these two components. The alternative explanation with low-ionization O ii-iv in gaseous form only is less appealing because it requires a very high velocity dispersion.
3.1.1. Deviations
There are some features that limit the quality of the fit. Most of them show broad emission-like features and are much more relevant in the low-continuum spectra. Indeed, in the high-flux spectra these features are well hidden by both strong continuum and absorption lines. The strongest lines are at 18.4 Å, 19.0 Å, 19.2 Å, 21.5 Å, 21.9 Å, 26.5 Å, 27.5 Å, and 29.35 Å. Most of the emission lines are less blueshifted than the absorption line of the same transition, thus the emission should originate from a broader region of the shell. This would explain the whole line shape similar to a P Cygni profile. There are also a few absorption lines not reproduced by the model at 19.8 Å, 25.8 Å, 29.1 Å, and 29.7 Å, which have already been reported by Ness et al. (2011) as unidentified lines. These lines could represent an additional slower (− 2000 km s-1) expanding layer because their projected wavelengths are consistent with O v, Ca xiii, Ar xiii, and Fe xvi/Al xi transitions. However, as mentioned above, these absorption lines are so much weaker than the strong ones that the inclusion of an additional layer does not provide a significant improvement to the fit.
3.1.2. Systematic errors
In Table 1, only the relatively small statistical parameter errors are given, which are likely much smaller than the combined statistical plus systematic uncertainties. The statistical errors are a proxy for the quality data, while systematic uncertainties are the main limitation for the accuracy of our results. A few parameters are highly model-dependent or have a degenerate value. Both the velocity dispersion and the blueshift of the shell layers have this problem. The complexity of the absorption lines plus the presence of weak emission lines complicate the modeling because the different components could mix with each other. This can happen to the components that refer to the weak unresolved emission lines (layers 2 and 3). Thus, the conclusion of different expansion velocities in two low-ionization layers is less certain than, e.g., the fact that the highest-ionization layer has a higher velocity shift and broadening.
3.2. Application to Spectra A.1, A.2 and B
In fitting the other X-ray spectra of V2491 Cyg, which have somewhat lower signal-to-noise ratio, we fixed the velocity dispersion of the collisionally ionized plasma, as well as the (relative) abundances of this plasma, of the highly ionized absorbers Xi, and of the cold absorption component Xg to the values determined for spectrum A.3. The resulting values of the other parameters are collected in Table 1, and the spectral fits are shown in Figs. 1–4, respectively.
The blackbody radius of spectrum A.1 is similar to that of spectrum A.3, but the temperature is lower by a quarter, and as a result the bolometric luminosity is lower by 50%; within the RGS band the blackbody flux is lower by 60%. For the collisionally ionized plasma, the temperature is same in the spectrum A.1 as in spectrum A.3, but the emission measure, and therefore also the luminosity, is lower by 45% in the former. As regards the highly ionized absorption shells, all parameters are similar in the Spectra A.1 and A.3, with the exception of the column of the shell with the highest ionization, 1.5 times bigger in A.1, and the column of the shell with the middle ionization, which in spectrum A.1 was 0.5 times that of A.3. Finally, the columns of the cold absorbers Xg and Xd both are markedly higher, by factors 1.3 and 1.2, respectively, in spectrum A.1 with respect to A.3.
The blackbody radius of spectrum A.2 is only 10 000 km, and thus closer to the white dwarf surface. One might expect a higher temperature there, but the observation shows a lower temperature, ten percent lower even than the low temperature of spectrum A.1. The luminosity of the blackbody accordingly is just 10% in spectrum A.2 of that in spectrum A.1. The emission measure of the collisionally ionized plasma in spectrum A.2 is intermediate between those before in spectrum A.1 and after in spectrum A.3, at unchanged temperature. The ionization parameter of all three high-ionization absorption shells is lower in spectrum A.2. The column of the shell with the highest ionization has increased by a factor of almost three between spectrum A.1 and spectrum A.2; in contrast, the columns of the other two shells have plunged. The column of the cold absorbing gas is the same in spectrum A.2 and spectrum A.1, but the column of the dust is much higher in spectrum A.2.
The strong changes in the spectral components well within the eleven hours of the first XMM-Newton observation are striking; we will investigate these in more detail in Sects. 4 and 5.
Almost ten days later, during the second observation of V2491 Cyg with XMM-Newton, the radius of the blackbody component had shrunk to 1900 km. This remarkably low value would imply that only part of the surface of the white dwarf has this high temperature; or alternatively that the white dwarf is more massive than 1.3 M⊙. The luminosity of the blackbody component has declined to LBB = 3.8 × 1030 W. The emission measure of the collisionally ionized plasma has decreased, but its temperature has increased, and as a result its luminosity now is LCIE = 1.45 × 1028 W, to a large extent within the RGS band (see Table 1).
The ionization levels of the three highly ionized absorbers have dropped, as have the columns of shells 2 and 3, between Spectra A.1 or A.3 and spectrum B; the column of the highest ionization shell, shell 1, has increased. The column of the cold gas absorber has dropped by some 10%, but the column of the dust component has increased by a factor 1.7. In general, the relative changes of the parameters of spectrum B with respect to those of Spectra A.1 and A.3 are similar qualitatively, if not quantitatively, to the changes of the spectrum with the lowest countrate during the first observation, i.e. spectrum A.2.
4. Variant models
To test the robustness of some of the results from the basic models, we have fitted some variant models. The topics that we wish to investigate in particular are the nature of the hot absorption shells and the cause of the changes during the first observation.
4.1. The hot absorption shells and the bolometric luminosity
In the basic model the hot ionized absorber consists of three shells, all with the same abundances, but with distinct ionization parameters ξi.
As an alternative we have fitted a continuous absorption measure distribution (AMD), using the SPEX model warm, to spectrum A.3 (see Table 2 and Fig. 6). We found that an initially continuous distribution in the course of the fitting procedure collapses to discrete components, compatible with the findings of our basic model. The model confirms the presence of at least two discrete ionization ranges with discrete velocities, represented by log ξ = 3.50−3.75 and log ξ ≥ 4.75, which are consistent with what we have found with separate xabs components (see Table 1). The warm model uses the same velocity for the whole range of ξ, but the observed spectrum shows a relation between ionization and velocity, and this causes the warm model fit to be decidedly worse than the basic model (χ2/d.o.f. = 17 300/1480).
Absorption measure distribution.
We have also fitted spectrum A.3 with some models in which we fit the abundances separately for each shell; this does not improve the fits significantly.
While the limited number of absorbers suggests the presence of discrete shells with different velocities and a non-monotonous ξ distribution, we note that any number of absorbers and therefore a continuous distribution is possible. The two strong peaks in the absorption measure distribution suggest the presence of two main absorbers. However, the high velocities make difficult to believe that the shells might be stable throughout the first month after the outburst and argue in favor of a continuous distribution.
The temperatures of the hot absorbing shells imply that hydrogen is fully ionized. This means that the hydrogen column of these shells is badly constrained, and for this reason we give the abundances of the various elements with respect to oxygen, fixing the hydrogen column to the proto-solar hydrogen-to-oxygen ratio in the basic model. The main effect of the presence of hydrogen is that photons that initially move from the central source in our direction are scattered into another direction. In the fully spherically symmetric case, these photons are replaced by photons moving initially in other directions that are scattered into our direction by Thompson scattering. The slab model that we used for the absorbing shell assumes that each photon from the central source that is scattered within the shell does not reach the observer, and is not replaced by photons from initially other directions. In the presence of hydrogen, the number of electrons in the shell is much higher than in the absence of hydrogen, and a much higher number of photons is scattered. For a given observed number of photons, the slab model with hydrogen leads to a much higher number of source photons incident on the shell than the model without hydrogen.
Whether this implementation of the model is valid for V2491 Cyg is not clear. The rapid variations between spectra A.1, A.2 and A.3 may suggest that spherical symmetry does not apply. If spherical symmetry does apply, however, the number of photons should not be corrected for scattering, i.e. the luminosity of the central source will be much lower than found with the slab model. To investigate the magnitude of this effect we considered first a variant model in which we set the hydrogen content of the three shells to zero, but kept the helium. To good approximation, the electron scattering of the photons from the central source does not depend on energy within the RGS range, and thus the parameters of the fit are not affected, other than that the luminosity of the central source is reduced. In particular, the temperature of the blackbody is the same as in the basic model. Therefore we computed the luminosity for the blackbody emitter for the model in which the photon number is not corrected for electron scattering in the absorption shells by fixing all parameters to the values of the basic model, and then recomputed the luminosity of the emitter for spectrum A.3. This luminosity, at 3.92 × 1031 W, and with it the radius, at 3780 km, are much smaller than in the basic model.
This reasoning applies equally to a second variant model where we set the hydrogen and helium content both to zero. For spectrum A.3 the temperature again is the same as in the basic model, but the luminosity and radius drop to 2.14 × 1031 W and 2790 km, respectively. Table 3 lists the variation of the parameters with assumed hydrogen and/or helium content for the slab model, or alternatively the variation with increasing spherical symmetry.
Radii and luminosities of the central blackbody emitter.
Computing the ionization equilibria with Cloudy we assumed that the ultraviolet/optical flux is emitted by the central source. If instead it is emitted elsewhere, it may not contribute to the ionization of the shells. For this reason, we have calculated the ionization balance of the shells when the UV fluxes in the adopted SED were decreased by up to two orders of magnitude. The bolometric luminosity decreased by less than 5%, while the newly-fitted ionization parameters of the shells are systematically lower by 15–25%. The non-monotonous ξ structure as seen in Fig. 6 is still preserved and the other main physical parameters such as column densities and abundances are consistent within the errors. The overall scenario thus is unaffected.
4.2. The changes between spectra A.2 and A.3
The dramatic changes in brightness of the X-ray source during the first observation with XMM-Newton are explained in the basic model by a drop in the luminosity of the central blackbody emitter, combined with changes in the column of the ionized absorption shells. The luminosity drop of the central source is the result of a smaller radius and a lower temperature (see Table 3). In the variant models discussed in the previous section, where the hydrogen and helium contents of the absorption shells are set to zero, the drop in luminosity between A.3 and A.2 is much less pronounced, since in these models the lower temperature of spectrum A.2 is partially offset by a larger radius (Table 3). It is remarkable that R in the models with reduced hydrogen and helium contents drops monotonically with time; in the basic model R increases between spectrum A.2 and spectrum A.3.
To investigate whether it is possible to describe the change between spectra A.2 and A.3 with a change in the blackbody and collisionally ionized emitters only, we fitted spectrum A.2 with an alternative model, in which all parameters related to the absorption components were fixed to the values for spectrum A.3, and only the parameters for the blackbody and for the collisionally ionized plasma were allowed to change. The resulting fit is significantly worse (χ2 ≃ 5000, as compared to the best basic fit χ2 ≃ 4000). The χ2 for this fit is dominated by the bad fit to the emission between 25–29 Å, and around 16 Å.
To investigate whether the lower luminosity may be explained by increased absorption due to increased columns of the ionized shells only, we fit spectrum A.2 with a model in which the parameters for the central emitters are fixed to the best values of the basic model for spectrum A.3, and only the columns and ionization parameters of the shells were allowed to vary. The best fit with this variant model has χ2 ≃ 5500, significantly worse than the basic fit for spectrum A.2.
To investigate whether the lower luminosity may be explained by increased absorption due
to an increased column of the neutral gas and/or an increased column of the dust, we fit
spectrum A.2 with a model in which the columns of the neutral gas and of the dust are
fitted, but all other parameters were fixed to the best-fit parameters of the basic model
for spectrum A.3. This gives a poor fit, with χ2 ≃ 8000. A
model in which the central emitter is only partially absorbed by an increased neutral
hydrogen column does not fit the spectrum at all, because the H I absorption is strongest
at 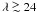 Å, a part of the spectrum that remains
relatively bright. Therefore, we can exclude absorption by cold clumpy material.
Å, a part of the spectrum that remains
relatively bright. Therefore, we can exclude absorption by cold clumpy material.
Finally, we have checked whether an addition of a radiative recombination continuum (RRC) to the model of spectrum A.2 improves the fit. The presence of this emission is suggested by emission features near 16.8 Å and 18.4 Å. We take into account the recombination of the most relevant ions of took, nitrogen and oxygen. The addition of RRC to the model does not lead to a significant improvement of the fit.
4.3. Derived mass loss rates and model consistency
Our fits to the spectra imply a mass loss rate 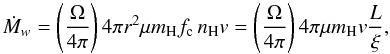 (2)where μ is the mean atomic
weight in units of the hydrogen mass mH,
fc is a factor allowing for clumpiness of the density
distribution (fc ≤ 1), and where Ω = 4π in
the case of spherical symmetry. The observed spectrum gives ξ and
v for each shell, almost independent of L. With the
parameters of the standard model fit to spectrum A.3, we obtained the mass loss rates
listed in Table 4. Note that these values are valid
for one time interval only – i.e. the time of maximum X-ray flux, and thus may
overestimate the outflow-rate averaged over the outburst. From Eq. (2) we note in addition that the derived value
of Ṁw scales with the luminosity
L of the central source, and thus will be smaller when the layers are
hydrogen- and/or helium-poor (see Table 3), and also when the layers are spherically
symmetric, in which case the xabs model overestimates the central luminosity.
(2)where μ is the mean atomic
weight in units of the hydrogen mass mH,
fc is a factor allowing for clumpiness of the density
distribution (fc ≤ 1), and where Ω = 4π in
the case of spherical symmetry. The observed spectrum gives ξ and
v for each shell, almost independent of L. With the
parameters of the standard model fit to spectrum A.3, we obtained the mass loss rates
listed in Table 4. Note that these values are valid
for one time interval only – i.e. the time of maximum X-ray flux, and thus may
overestimate the outflow-rate averaged over the outburst. From Eq. (2) we note in addition that the derived value
of Ṁw scales with the luminosity
L of the central source, and thus will be smaller when the layers are
hydrogen- and/or helium-poor (see Table 3), and also when the layers are spherically
symmetric, in which case the xabs model overestimates the central luminosity.
The depths of the absorption lines, combined with the fitted abundances, are converted to
the hydrogen column density 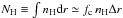 where ΔR is a typical
length scale. Our model implies that this length scale is shorter than the distance to the
central source, Δr ≡ βr < r, and
this may be used to obtain an upper limit to the distance r:
where ΔR is a typical
length scale. Our model implies that this length scale is shorter than the distance to the
central source, Δr ≡ βr < r, and
this may be used to obtain an upper limit to the distance r:
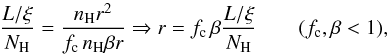 (3)and from this a lower limit to the density
(3)and from this a lower limit to the density
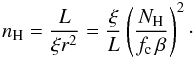 (4)Note that the definition and computation of
ξ involves the physical density (i.e. not the space-averaged density),
and therefore does not contain the clumpiness factor fc. The
mean atomic weight μ is 1.42 for proto-solar H-He abundances and 3.58 for
H-He abundances decreased by two orders of magnitude.
(4)Note that the definition and computation of
ξ involves the physical density (i.e. not the space-averaged density),
and therefore does not contain the clumpiness factor fc. The
mean atomic weight μ is 1.42 for proto-solar H-He abundances and 3.58 for
H-He abundances decreased by two orders of magnitude.
Derived mass loss rates and shell parameters.
Another interesting parameter is the time scale at which the gas in the outflow adjusts its ionization balance. This may be calculated from the ionization balance and ξ-values of the fits. Through the SPEX tool rec_time we determined the O viii recombination times for layers 1 and 2. They spread between a few (H-He rich slabs) to up to ten (H-He poor slabs) seconds, which means that the gas is responding instantaneously to the variations of the photo-ionizing continuum of the source and that the observed features are linked to the variability of the source.
5. Discussion
From our fits it is clear that the central blackbody emission varies rapidly during our first observation on a time scale of hours. The variations are likely exaggerated by the slab model: in full spherical symmetry, and also in the absence of hydrogen and helium in the ionized absorption shells, the changes are still significant, but much less so. Forty days into the nova outburst, we may well be looking at shells whose abundances are affected by nuclear reactions. Indeed, the abundances that we derive for carbon, nitrogen and oxygen indicate that this is the case. This implies that the hydrogen and helium abundances of absorption shells are much lower than solar, in comparison to the elements just mentioned. Even in the absence of spherical symmetry, therefore, the variation of the central source is less pronounced than implied by our basic model, and probably agrees better with the numbers found for the models in which the absorption shells contain no hydrogen and/or helium.
The response time required for the ionization equilibrium of shells to respond to changes in the ionizing continuum is a few seconds, which means that the photo-ionization balance of the shells responds almost instantaneously to variations in the source flux and that its luminosity might indeed have changed. The mass loss rate in our standard model for spectrum A.3 for the third shell in particular is rather high compared to the common limits 10-4−10-3 M⊙/yr found for other novae (Kovetz et al. 1987; Kato & Hachisu 1989; Smith & Owocki 2006). The derived mass loss rates for all three layers are lower in the models with reduced hydrogen and/or helium content of the absorbing shells.
As discussed in Sect. 4.1, the blueshifted absorption lines are caused by photons from the central source that initially move in our direction and are scattered into another direction. If the dimension of the shell is large with respect to the size of the white dwarf, and if the optical depth of the shell in the lines is not too high, this will lead to a P Cygni profile, because we see photons initially moving in other directions and then scattered into our direction in emission, both blue- and red-shifted. The emission and absorption should have equal strength. In the spectrum of V2491 Cyg this is clearly not the case. One explanation is that the shell is not large with respect to the white dwarf, so that a large part of the receding half is occulted. Similarly, a high optical depth in the shell may cause photons scattered from the receding half of the shell to be reabsorbed before escaping in our direction. And finally, a large asymmetry in the shell may also reduce the strength of the redshifted emission.
Carbon and sulfur are about an order of magnitude less abundant than nitrogen and oxygen, and elements such as silicon, argon and calcium are much less abundant. This suggests that the white dwarf in V2491 Cyg is an O-Ne and not a C-O white dwarf. The strength of the Ne ix-x lines as compared to the C v-vi lines supports this conclusion, as do observations in other wavelength regions (Lynch et al. 2008; Helton et al. 2008; Naik et al. 2009; Munari et al. 2011).
The strongest feature in all X-ray spectra is the rest frame O i K-edge around 23.0 Å, which is well reproduced in the fits together with the corresponding O i 1s–2p absorption line at 23.5 Å. Other features of the cold CSM/ISM are the Fe i L-edge around 17.5 Å and the N i 1–2p absorption line at 31.2 Å, both well fitted by our models. Neutral oxygen and nitrogen are highly overabundant, whereas iron is slightly overabundant, with respect to solar abundances. This suggests that part of the cold absorption originates in enriched circumstellar matter close to V2491 Cyg. The reduction of the column and the decrease in temperature of the cold absorber between spectra A.1 and B suggests that the CSM column is mostly derived from the current nova outburst, and still expanding, albeit slowly. Page et al. (2010) suggested that the reduction of the column stops at 2.2 × 1025 m-2 some time after our second observation. This final value then corresponds to the interstellar component. If the total O i column is equally divided between CSM and ISM, the ISM may have a near-solar abundance for oxygen, and sub-solar abundance for iron, implying that iron is depleted by dust.
The optical flux defines the nova outburst, and thus clearly must come from the expanding nova envelope; the ultraviolet flux changes in tandem with the optical flux, and therefore also originates from the nova envelope. As can be seen from Fig. 5, our model fails to predict the correct level of the ultraviolet and optical fluxes by several orders of magnitude. This indicates that our model applies only, if at all, to the X-ray part of the spectrum, which must originate from a very different layer in the expanding envelope, presumably much closer to the white dwarf than the layers responsible for the optical/ultraviolet spectrum. This conclusion is confirmed by the observation that the marked changes in the X-ray flux during the first XMM-Newton observation are not accompanied by changes in the optical and/or ultraviolet fluxes.
Because the absorption lines from the shells are shifted from the rest wavelengths by the high outflow velocities, and because hot atmospheres do not show deep absorption lines even at the rest wavelengths using a blackbody spectrum as the central source is not as poor choice as might appear at first sight. As a first test we have tried a model atmosphere spectrum that replaces the blackbody as the central source. Following Ness et al. (2011) we used the best fitting TMAP model of Rauch & Werner (2010) (007, with log g = 9 and T = 106 K). This provides an even worse fit with χ2 = 15 with three shells, 18 with two shells, 32 with just one shell and 59 without any photo-ionized absorber (instead of 7 from the BB fit) because O viii/N vii line ratio (the most important in the spectrum) cannot be reproduced by the atmosphere model. It may be necessary to consider models with different abundances and outflows which, however, are currently not available and we therefore refrain from a systematic parameter study of the atmosphere model parameters.
6. Conclusions and prospects
Our spectral analysis of nova V2491 Cyg suggests that the absorption by highly-ionized ions is caused by non-monotonous, possibly discrete, ejecta shells with different outflow velocities and ionization levels. Variations on time scales of hours occur both in the luminosity of the central source and in the ionization level and columns of the absorption shells. We find that in our scenario of photo-ionization equilibrium the expanding gas is responding almost instantaneously to the variations in the source ionizing continuum. Our upper limits for the mass loss rate of each shell agree with those estimated for other novae, especially if the shells are depleted in hydrogen.
The values derived from the fits for the luminosity and radius of the central source depend on the nature of the models that are applied, and therefore must be considered uncertain. In the spherically symmetric case, however, the radius of the central emitter of X-rays decreases monotonically with time, and therefore must be in the increasingly transparent expanding nova envelope. The values derived for the abundances in the ionized absorption shells do not depend on the details of the models, and therefore may be considered more secure. These abundances indicate that the white dwarf in V2491 Cyg is an O-Ne white dwarf.
Improvements to our pilot models can be made in several ways. First, it would be useful to replace the central blackbody emitter with an appropriate white-dwarf atmosphere model. We have tested a model in which the TMAP model substitutes the blackbody, but is still absorbed by the three shells. However, this model provides even poorer results than those obtained with our standard fits with a blackbody continuum. In the future atmosphere models must take into account different abundances and outflows.
Second, it will be necessary to iterate between the computation of the ionization structure of the ionizing shells for a given spectral energy distribution, and the computation of the spectral energy distribution and elemental abundances from the fit, for each of the four observed spectra separately. For this improvement it is also necessary to determine the distance more reliably: a close distance implies a lower luminosity and thereby a lower ionization parameter of the shells. Finally, it would be useful to obtain constraints on the hydrogen contents of the hot ionized absorption shells, perhaps from ultraviolet observations. Ultraviolet observations may also help in determining the location of origin of the optical/ultraviolet flux.
Acknowledgments
This work is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). SRON is supported financially by NWO, the Netherlands Organization for Scientific Research. We also acknowledge financial support from the Faculty of the European Space Astronomy Centre. We also thank the referee for important suggestions, which improved the quality of the paper.
References
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Greiner, J., Hasinger, G., & Kahabka, P. 1991, A&A, 246, L17 [NASA ADS] [Google Scholar]
- Hachisu, I., & Kato, M. 2009, ApJ, 694, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, H. W., & Heise, J. 1997, A&A, 322, 591 [NASA ADS] [Google Scholar]
- Heise, J., van Teeseling, A., & Kahabka, P. 1994, A&A, 288, L45 [NASA ADS] [Google Scholar]
- Helton, L. A., Woodward, C. E., Vanlandingham, K., & Schwarz, G. J. 2008, Central Bureau Electronic Telegrams, 1379, 1 [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2010, A&A, 523, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2011, A&A, 533, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, eds. K. Yamashita, & T. Watanabe (Tokyo: Univ. Ac. Press), 411 [Google Scholar]
- Kahabka, P., & van den Heuvel, E. P. J. 1997, ARA&A, 35, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 1989, ApJ, 346, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Kovetz, A., Prialnik, D., & Shara, M. M. 1987, Ap&SS, 131, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., & Palme, H. 2009, Met. Plan. Sci. Suppl., 72, 5154 [Google Scholar]
- Lynch, D. K., Russell, R. W., Rudy, R. J., Woodward, C. E., & Schwarz, G. J. 2008, IAU Circ., 8935, 1 [NASA ADS] [Google Scholar]
- Munari, U., Siviero, A., Dallaporta, S., et al. 2011, New Astron., 16, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Naik, S., Banerjee, D. P. K., & Ashok, N. M. 2009, MNRAS, 394, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, S., Beize, J., Jin, Z., et al. 2008, IAU Circ., 8934, 1 [NASA ADS] [Google Scholar]
- Nauenberg, M. 1972, ApJ, 175, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, J.-U., Osborne, J. P., Dobrotka, A., et al. 2011, ApJ, 733, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Oegelman, H., Beuermann, K., & Krautter, J. 1984, ApJ, 287, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Oegelman, H., Orio, M., Krautter, J., & Starrfield, S. 1993, Nature, 361, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M., Covington, J., & Ögelman, H. 2001, A&A, 373, 542 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paerels, F., Brinkman, A. C., van der Meer, R. L. J., et al. 2001, ApJ, 546, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Osborne, J. P., Evans, P. A., et al. 2010, MNRAS, 401, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Petz, A., Hauschildt, P. H., Ness, J.-U., & Starrfield, S. 2005, A&A, 431, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietsch, W., Fliri, J., Freyberg, M. J., et al. 2005, A&A, 442, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinto, C., Kaastra, J. S., Costantini, E., & Verbunt, F. 2010, A&A, 521, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 293, 889 [NASA ADS] [Google Scholar]
- Provencal, J. L., Shipman, H. L., Koester, D., Wesemael, F., & Bergeron, P. 2002, ApJ, 568, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, T., & Werner, K. 2010, Astron. Nachr., 331, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Rudy, R. J., Lynch, D. K., Russell, R. W., Woodward, C. E., & Covey, K. 2008, IAUC, 8938, 2 [NASA ADS] [Google Scholar]
- Smith, N., & Owocki, S. P. 2006, ApJ, 645, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J., Hasinger, G., Aschenbach, B., et al. 1991, Nature, 349, 579 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Best fit to the first observation A.1 (see also Table 1). The rest-frame wavelengths of all main transitions are displayed. |
| In the text | |
 |
Fig. 2 Best fit to the second observation A.2. |
| In the text | |
 |
Fig. 3 Best fit to the third observation A.3. |
| In the text | |
 |
Fig. 4 Best fit to the fourth observation B. |
| In the text | |
 |
Fig. 5 Unabsorbed SED used for V2491 Cyg (solid line and data points). We also show the unabsorbed blackbody emission (blue dashed-dotted line) and the observed absorbed fluxes (red dotted line). |
| In the text | |
 |
Fig. 6 Absorption measure distribution (see also Table 2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


