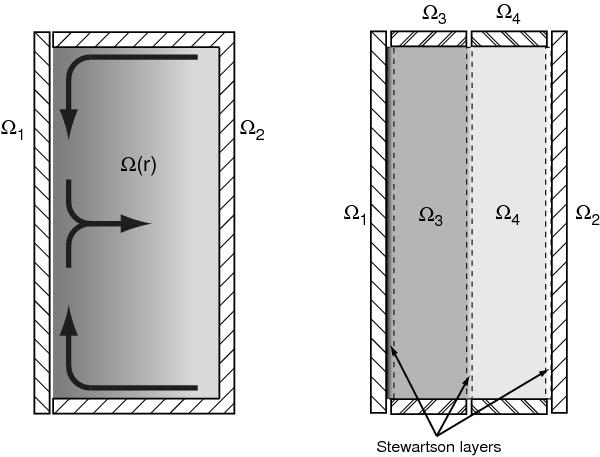
End cap effects which were predicted to distort significantly the mean profile of v_θ from the ideal Couette solution. Left: in the bulk flow the velocity profile is supported by the radial pressure gradient, 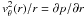. The pressure is approximately uniform vertically, but at the end caps the non-slip boundary condition requires v_θ = rΩ₂. This imbalance at the end cap drives the radial Ekman circulation, when Ω₂ < Ω₁ the flow is directed inward. When the Ekman flow reaches the inner cylinder it transitions to an axial flow. In a small aspect-ratio device such as the Princeton MRI Experiment (Kageyama et al. 2004) predict that the Ekman circulations would meet at the midplane and form a radial jet. Right: with independent end rings, the strength of the Ekman pumping can be reduced by minimizing the velocity difference between the rings and the bulk flow. The simulations of Kageyama et al. (2004) showed that two rings provided an effective trade off between mechanical complexity and reduced Ekman pumping. A simulation of the two-ring design by Hollerbach & Fournier (2004) predicted the formation of Stewartson layers at the boundaries between the components. The ideal Couette profile would then be replaced by two annuli in solid body rotation with the end rings.