| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | L23 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201219392 | |
| Published online | 24 May 2012 | |
HS Hydrae about to turn off its eclipses
1 Astronomical Institute, Faculty of Mathematics and Physics, Charles University Prague, 18000 Praha 8, V Holešovičkách 2, Czech Republic
e-mail: zasche@sirrah.troja.mff.cuni.cz
2 Weierstr 30, 8630 Rueti, Switzerland
Received: 12 April 2012
Accepted: 30 April 2012
Aims. We aim to perform the first long-term analysis of the system HS Hya.
Methods. We performed an analysis of the long-term evolution of the light curves of the detached eclipsing system HS Hya. Collecting all available photometric data since its discovery, the light curves were analyzed with a special focus on the evolution of system’s inclination.
Results. We find that the system undergoes a rapid change of inclination. Since its discovery until today the system’s inclination changed by more than 15°. The shape of the light curve changes, and now the eclipses are almost undetectable. The third distant component of the system is causing the precession of the close orbit, and the nodal period is about 631 yr.
Conclusions. New precise observations are desperately needed, preferably this year, because the amplitude of variations is decreasing rapidly every year. We know only 10 such systems on the whole sky at present.
Key words: binaries: eclipsing / stars: individual: HS Hydrae / stars: fundamental parameters / stars: solar-type
© ESO, 2012
1. Introduction
Eclipsing binaries are astronomical objects of high importance, especially owing to the possibility of deriving the basic physical properties of these stars with high precision. This is mostly because one can easily calculate the individual masses, semimajor axis, etc. if one knows the inclination of the system and the radial velocity curves. However, in some systems the plane of the orbit is moving slowly, and the radial velocity data have to be obtained at the same time as the data for the light curve solution. Otherwise, the method yields incorrect results.
At present, we know only a few systems where the orbital plane is moving and the eclipsing light curve had different shapes in different epochs. Six such systems were summarized by Mayer (2005). Moreover, three more systems show changes of minima depths, therefore they are also suspected to undergo a precession of the orbits, these are V685 Cen (Mayer et al. 2004), AH Cep (Drechsel et al. 1989), and V699 Cyg (Azimov & Zakirov 1991).
2. The system HS Hya
The eclipsing binary system HS Hya was discovered to be variable by Strohmeier et al. (1965), who also classified the system as an Algol-type, but the orbital period given is incorrect. Popper (1971) measured the radial velocities (hereafter RV) of the system, and analyzed the RV curves. The spectral type was derived to be F3-4, the correct orbital period is given to be about 1.568024 days, and the mass ratio is about 0.96. However, the RV data were obtained over a period of five years, from 1966 to 1970. Later, the complete light curve (hereafter LC) was obtained in the Strömgren uvby system by Gyldenkerne et al. (1975). These data were measured in 1972. The authors used the RV results from Popper (1971) and their inclination of about 85.3°, which yielded a reliable picture of the system.
However, Torres et al. (1997) published a new finding about HS Hya. The analysis was based on older data from photometry, RVs by Popper, but also Torres and coworker’s own new RV data, revealing that one more distant component is orbiting around the eclipsing pair. The period of this body is about 190 days, and it is probably of the spectral type M0. Its light contribution is quite low (below 1%), but the RV residuals obtained by a cross-correlation clearly show periodic modulation.
3. The change of inclination
The star has also been observed by the Hipparcos satellite (Perryman et al. 1997). During its three-year mission both minima were observed, but the coverage is only poor. However, after transformation from Hp to V magnitude (Harmanec & Božić 2001), it is clear that the depths of both minima are much lower than in the LCs obtained 20 yr ago. We solved the Hipparcos LC with the same parameters as given in Torres et al. (1997). The Phoebe program (Prša & Zwitter 2005) was used, which is based on the Wilson-Devinney code, Wilson & Devinney (1971). All relevant parameters were fixed except for the inclination, see Table 1. The value of the third light was fixed at a value of 0.4% only, in agreement with the finding published by Torres et al. (1997).
Inclination as obtained from various light curves.
 |
Fig. 1 Available light curves of HS Hya in the V filter. The changing depth of both minima is clearly visible. The three bottom figures were plotted with the same range in the y-axis. |
The star was also included into the photometric survey ASAS (Pojmanski 2002). We divided the whole data set into three parts and separately solved the light curves in 2002, 2005, and 2008. The procedure of LC fitting was the same as for the Hipparcos data, and the results are given in Table 1. As one can see from Fig. 1, the depths of the minima are still decreasing.
Unfortunately, it is not easy to find other reliable photometry to do a similar analysis in different time epochs. One of the limiting problems is the role of the filter, because the entire abovementioned photometry can easily be transformed into the standard V magnitudes. The photometry from the automatic survey called “Pi of the sky” (Burd et al. 2005) is another possibility, but this photometry is unfiltered, and therefore it is problematic to solve its light curve. Moreover, it has fairly high scatter and covers a similar time span as the ASAS data.
We also tried to use the data from the discovery paper (Strohmeier et al. 1965), but these are only the photographic data and were not obtained in any standard photometric filter. Another problem is that the original data are not available, only the phase plot, but this was constructed with incorrect ephemerides. As one can see from the LCs published in Gyldenkerne et al. (1975), the individual depths in different filters are quite similar to each other. Moreover, fixing the other relevant parameters during the fitting process, we were able to construct a plot of minima depth versus inclination. Using the eight dimmed data points from Strohmeier et al. (1965), we were able to roughly derive the inclination from these data obtained in 1964, see Table 1.
 |
Fig. 2 Inclination of the eclipsing binary with respect to the time. |
The data from Table 1 were used to construct the plot given in Fig. 2. Fitting these data points with a linear curve, one sees that the change of inclination is about 0.3° during one year. Therefore, the amplitude of photometric variations is decreasing rapidly every year.
Known eclipsing binaries with changing minima depths.
4. The nodal period
The precession effect of the close pair’s orbit due to the distant third body was described elsewhere, e.g. Söderhjelm (1975). The nodal period can be computed from the equation
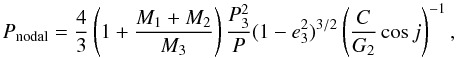 where subscripts 1 and 2 stand for the eclipsing binary components, while 3 stands for the third distant body. The term G2 stands for the angular momentum of the wide orbit, and the C is the total angular momentum of the system. However, the problem of the unknown inclination of the wide orbit (which is included in the last term in brackets) led us to use a different approach. Drechsel et al. (1994) analyzed the system IU Aur, where a similar problem arose, hence one can also fit the term cosi with a sinusoidal fit, following the equation
where subscripts 1 and 2 stand for the eclipsing binary components, while 3 stands for the third distant body. The term G2 stands for the angular momentum of the wide orbit, and the C is the total angular momentum of the system. However, the problem of the unknown inclination of the wide orbit (which is included in the last term in brackets) led us to use a different approach. Drechsel et al. (1994) analyzed the system IU Aur, where a similar problem arose, hence one can also fit the term cosi with a sinusoidal fit, following the equation
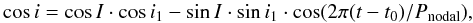 where I is the inclination of the invariant plane against the observer’s celestial plane, i is the inclination of the eclipsing binary, while i1 is the inclination between the invariant plane and the orbital plane of the eclipsing binary.
where I is the inclination of the invariant plane against the observer’s celestial plane, i is the inclination of the eclipsing binary, while i1 is the inclination between the invariant plane and the orbital plane of the eclipsing binary.
 |
Fig. 3 Fitting the cos(i) with the sinus term on available data, the confidence level of 95% is shown with the dash-dotted line. |
A similar analysis was performed (see Fig. 3), but regrettably only a small part of the nodal period is covered with data points nowadays. Fitting a sinusoidal curve, the nodal period is about 631 yr, of which only about 1/14 is covered. The other two adjustable quantities were only poorly constrained. New precise observations are urgently needed.
5. Observational consequences
HS Hya belongs to a group of unique systems, and therefore more observations are needed to confirm our hypothesis with higher confidence and to study its other physical properties. The amplitude of eclipses is lower than 0.015 mag in V filter at present, and is still decreasing. However, the ellipsoidal variations outside the eclipse will remain even when the photometric eclipses disappear. According to our model the photometric eclipses will stop in about 2022. Nevertheless, detecting these shallow eclipses is problematic, especially from the northern hemisphere, owing to the low declination of the star.
Concerning the third body period, one can ask why the 190-day orbit was not discovered earlier via analyzing the minima times via period variations. There exists a huge database of minima observations (more than 100), but no variation was detected. This is because of the short period of the third body and its low mass. This amplitude (see Irwin 1959) resulted in about 1 min only, which is comparable with the precision of individual times of minima observations.
6. Discussion and conclusions
Assembling all available systems with changing minima depths (see Table 2), one can see how unique these systems are. We know only 10 such systems today and the nodal period was derived in only four of them. Moreover, it seems that this effect was preferably observed in early type systems (B and A spectral types), and HS Hya is the first exception.
Our hypothesis of changing inclination would also slightly shift the physical parameters of components as presented in Torres et al. (1997). These authors assumed constant inclination and used light curve and radial velocity data from different epochs. However, the time gap of more than 20 years between photometry and spectroscopy yields a difference in inclination of about 7.8°. This difference is able to shift the true stellar masses as computed from the term m·sin3(i). The inclination in 1968 (when the RV data were obtained by Popper 1971) was about 87.15°, while in 1992 (roughly the middle of the time interval of radial velocities used in Torres et al. 1997) was about 79.3°. Using these values, the masses resulted in the values presented in Table 3.
Masses as derived from different data sets/methods.
These values agree much better with the predicted stellar masses of F4+F5 spectral types (i.e. with the temperatures) for normal metallicity. Hence, the errors of masses as presented by Torres et al. (1997) of about 0.007 M⊙ are too optimistic, because they neglect the systematic effect described above. Torres et al. (1997) presented a perfect fit of the derived values of log M, log T, and log g on the model isochrones. Likely an adjustment of metallicity or age will be required to accommodate the new mass determinations.
The plot presented in Fig. 3 needs to be spread in the next years. However, deriving the inclination of HS Hya when it stops having eclipses will be hard, because the ellipsoidal variations have only low amplitude. On the other hand, the interferometry of the close pair would solve this problem. Detecting the two eclipsing components via interferometry is difficult, but worth trying. The system itself is relatively bright and the two eclipsing components have a similar luminosity (i.e. magnitude difference close to zero). The computed angular separation of the two eclipsing components is about 0.4 mas.
Acknowledgments
Pavel Mayer is acknowledged for a useful discussion and valuable advice. This work was supported by the Czech Science Foundation grant No. P209/10/0715, by the grant UNCE 12 of the Charles University in Prague, and also by the Research Programme MSM0021620860 of the Czech Ministry of Education. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Bibliographic Services.
References
- Azimov, A. A., & Zakirov, M. M. 1991, IBVS, 3667, 1 [NASA ADS] [Google Scholar]
- Burd, A., Cwiok, M., Czyrkowski, H., et al. 2005, New Astron., 10, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Drechsel, H., Lorenz, R., & Mayer, P. 1989, A&A, 221, 49 [NASA ADS] [Google Scholar]
- Drechsel, H., Haas, S., Lorenz, R., & Mayer, P. 1994, A&A, 284, 853 [NASA ADS] [Google Scholar]
- Guilbault, P. R., Lloyd, C., & Paschke, A. 2001, IBVS, 5090, 1 [NASA ADS] [Google Scholar]
- Gyldenkerne, K., Jørgensen, H. E., & Carstensen, E. 1975, A&A, 42, 303 [NASA ADS] [Google Scholar]
- Harmanec, P., & Božić, H. 2001, A&A, 369, 1140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, C. H. S., Helt, B. E., & Vaz, L. P. R. 1999, AJ, 117, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, P. 2005, Ap&SS, 296, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, P., Pribulla, T., & Chochol, D. 2004, IBVS, 5563, 1 [NASA ADS] [Google Scholar]
- Olson, E. C., Schaefer, B. E., Fried, R. E., Lines, R., & Lines, H. 1992, AJ, 103, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Özdemir, S., Mayer, P., Drechsel, H., Demircan, O., & Ak, H. 2003, A&A, 403, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Pojmanski, G. 2002, AcA, 52, 397 [Google Scholar]
- Popper, D. M. 1971, ApJ, 166, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Söderhjelm, S. 1975, A&A, 42, 229 [NASA ADS] [Google Scholar]
- Strohmeier, W., Knigge, R., & Ott, H. 1965, IBVS, 107, 1 [NASA ADS] [Google Scholar]
- Torres, G. 2001, AJ, 121, 2227 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Stefanik, R. P., Andersen, J., et al. 1997, AJ, 114, 2764 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Available light curves of HS Hya in the V filter. The changing depth of both minima is clearly visible. The three bottom figures were plotted with the same range in the y-axis. |
| In the text | |
 |
Fig. 2 Inclination of the eclipsing binary with respect to the time. |
| In the text | |
 |
Fig. 3 Fitting the cos(i) with the sinus term on available data, the confidence level of 95% is shown with the dash-dotted line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


