| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201118630 | |
| Published online | 19 June 2012 | |
Non-linear simple relativistic Alfvén waves in astrophysical plasmas
1 LUTH, Observatoire de Paris, CNRS, Unversité Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
e-mail: thierry.lehner@obspm.fr; fabrice.mottez@obspm.fr
2 Observatoire Astronomique, Université de Strasbourg, 11 rue de l’Université, 67000 Strasbourg, France
e-mail: jean.heyvaerts@astro.unistra.fr
Received: 12 December 2011
Accepted: 7 April 2012
Aims. Large amplitude MHD perturbations are generated in magnetized tenuous relativistically moving plasmas, such as winds emitted by compact stellar objects or galactic nuclei, when a rapid change occurs at their boundaries or when an obstacle is present in them. These perturbations may involve relativistic motions in the rest-frame of the unperturbed plasma. In this paper, we calculate the characteristics and the structure of relativistic non-linear Alfvén waves.
Methods. We establish these properties for special-relativistic perturbations occurring in a particular type of non-linear waves, the simple waves.
Results. We derive the conditions applicable to Alfvénic perturbations in a cold flow. We calculate the characteristics of these perturbations and the structure of wave trains of finite extent in the propagation direction of these characteristics, as observed in the unperturbed fluid proper frame. We determine the velocity of the characteristics with respect to any observer. This velocity is found to be a first integral, constant in time and space. This implies that relativistic Alfvénic perturbations are channeled, in the unperturbed fluid proper frame, by the unperturbed magnetic field and travel along this field neither steepening nor breaking into shocks. For finite wave trains, the Lorentz factor is found to be limited by some maximum value that we calculate and that depends on the ratio of proper magnetic energy density to material energy density in the unperturbed fluid.
Key words: magnetohydrodynamics (MHD) / waves / relativistic processes / planet-star interactions
© ESO, 2012
1. Introduction
Obstacles moving in classical MHD winds create disturbances in different propagation modes, among them Alfvénic perturbations that are known to be channeled by the magnetic field and are associated with similarly propagating current systems forming a so-called Alfvénic wake. It is this channeling property, which avoids the progressive spreading of the currents, that makes Alfvénic disturbances of particular interest. The wake created by the motion of the satellite Io in Jupiter’s magnetosphere leads to Io-associated jovian radio emissions. Mottez & Heyvaerts (2011a) considered whether a small body embedded in a pulsar relativistic wind could develop a similar wake and demonstrated that the associated current system would have significant dynamical effects on small enough bodies (Mottez & Heyvaerts 2011b). Dense ejecta thrown at relativistic speeds into a tenuous magnetized environment would involve shock perturbations as well as Alfvénic ones. Such situations could be met, for example, in the cannon ball model of gamma-ray bursts (Dado et al. 2002) or in three-dimensional versions of the model developed by Daigne & Mochkovitch (1998). The generation of Alfvénic perturbations in relativistically moving tenuous flows is likely to be an ubiquitous phenomenon from which a number of observable phenomena may originate, caused by the associated electric currents, provided they remain channeled by the field. When these currents become either unstable or dissipative, particle acceleration is expected to occur and radio or possibly more energetic radiation is emitted.
It is unknown whether, as classical Alfvén waves, relativistic Alfvénic perturbations travel along the unperturbed magnetic field without steepening. This is because relativistic waves are compressive, owing to the Lorentz contraction, and fluid inertia in the observer’s frame varies with the Lorentz factor of the fluid motion. The magnetic field intensity and direction also vary with the fluid motion. This leads to question whether relativistic non-linear Alfvénic waves may experience a different propagation regime than non-relativistic ones, possibly steepening or escaping channeled propagation. These are the main questions considered in this paper.
Growing attention is given to MHD processes in tenuous highly magnetized plasma, where the magnetic energy density is comparable to or higher than the rest mass energy density and the classically-defined Alfvén speed (9) is higher than the speed of light. For example Lyubarsky (2005) studied the dynamics of reconnection under these circumstances and Mazur & Heyl (2011) analyzed the propagation of non-linear electromagnetic waves in the magnetospheres of magnetars, and found that some types of non-linear perturbations propagate without breaking into shocks. A number of relativistic-theoretical works have considered a covariant formulation of both MHD and MHD wave propagation (Pham Mau Quan 1965; Lukacevic 1968). In this paper, we adopt the conventional, but nevertheless Lorentz-invariant, 3+1 formulation in which space and time appear in the equations on a different footing.
In connection with the non-relativistic wake of Io in Jupiter’s magnetosphere, Neubauer (1980) showed that on each branch of the wake, where waves propagate in an unique sense, a certain vectorial quantity is constant in space and time. The existence of this first integral makes it possible, knowing the potential drop across the wake, to calculate the electric current that the wake supports (Neubauer 1980). Discussing the interaction of small bodies with a pulsar wind, Mottez & Heyvaerts (2011a) extended this result to linear perturbations on a relativistic flow.
In this paper, we consider fully non-linear, but special, Alfvénic perturbations that we refer to as simple waves.
2. Simple waves
Methods to study non-linear waves have been described in a number of textbooks, such as Jeffrey & Taniuti (1964) or Zel’dovitch & Raizer (1966). The structure of so-called simple waves is assumed to be such that all variables generated in the perturbation at a point r and time t of a certain reference frame are functions of only one quantity characterizing the perturbation, u(r,t), which we refer to as the master variable. This often-used assumption (Zel’dovitch & Raizer 1966; Broer & Sarluy 1964; Jeffrey 1976) selects non-linear perturbations propagating in a unique direction. The master variable determines all physical quantities Xi(r,t), regardless of whether they are scalar or vectorial. They depend on r,t indirectly through u(r,t) 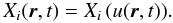 (1)The master variable u may be, but need not be, one particular physical variable of the perturbation. Its nature need not even be specified, provided it parametrically determines all the physical variables in terms of relations such as Eq. (1). In sound waves, it could be chosen to be either the local density or the local pressure. The choice is less straightforward for MHD waves.
(1)The master variable u may be, but need not be, one particular physical variable of the perturbation. Its nature need not even be specified, provided it parametrically determines all the physical variables in terms of relations such as Eq. (1). In sound waves, it could be chosen to be either the local density or the local pressure. The choice is less straightforward for MHD waves.
Non-linear simple waves are well-known in the hydrodynamical regime, such as for example acoustic waves propagating in an isentropic gas (Zel’dovitch & Raizer 1966). When they become non-linear, acoustic waves, as well as waves of many other modes such as compressive MHD waves, steepen and then eventually break, forming shocks in a finite time. Jeffrey & Taniuti (1964) looked for solutions that are static in some frame moving at a given propagation speed V. They illustrate their method by considering waves depending on only one spatial coordinate x. Such planar solutions are simple waves in the sense defined by Eq. (1), the master variable being (x − V t). Their approach, which excludes the possibility of wave steepening, is less general than the one developed by Zel’dovitch & Raizer (1966), in which the dependence of the master variable on space and time remain unspecified.
The ansatz given in Eq. (1) could a priori describe a number of different wave geometries. We show however in Appendix B that when Eq. (1) also applies to vectorial quantities, simple Alfvén waves should be planar. Perturbations endowed with other types of symmetry, such as for example cylindrical symmetry, may also depend on only one variable, the distance to the symmetry axis in this case, but could be considered simple only in a generalized sense because vectorial quantities would then not be functions of only this master variable. The simple wave approach would also be useful as a local representation of quasi-planar structures in which the scale of the perturbation is much smaller in the direction of propagation than in some other direction.
We assume the unperturbed fluid to be homogeneous and in uniform, possibly relativistic, motion with respect to some arbitrary inertial rest-frame ℛ. The traveling perturbation is supposedly of finite extent along the direction of propagation, which implies that any given piece of the fluid has been, or will be, in an unperturbed state at some time.
The instantaneous rest-frame of a piece of fluid is its proper frame, denoted by ℛ0, and physical variables observed in this frame are proper variables, usually denoted by a subscript 0, as in ρ0. Physical quantities associated with the unperturbed fluid, as observed from the general frame ℛ, are denoted by a subscript r, as in ρr. The proper frame of the unperturbed fluid, the unperturbed fluid frame, is denoted by ℛr0.
In this paper, we only study non-linear relativistic simple waves of the Alfvénic type, which might form current-density-conserving (coherent) wakes, while compressive MHD waves of the fast mode type might not. We define the term Alfvénic in the non-linear context in Sect. 6.
The stability of our non-linear pure mode solutions should be assessed because when an instability develops, it may become inappropriate to consider a pure mode. We note that stability issues are not however discussed in this paper. It has been reported (Boynton & Torkelsson 1996; Fukuda & Hanawa 1999; Medvedev 1999; del Zanna et al. 2001; Folini et al. 2004) that classical non-linear MHD perturbations may suffer a parametric instability, regardless of whether they either reduce to Alfvén waves in the linear limit (though otherwise supporting magnetic pressure gradients) or are full-fledged non-linear Alfvén waves (with constant magnetic field moduli). The mother wave excites a compressive perturbation and generates a daughter Alfvén wave. Such instabilities develop in both the fluid and kinetic regimes.
3. Equations of perfect MHD in a tenuous medium
Special-relativistic MHD equations for a cold, perfectly conducting and inviscid plasma can be written in an arbitrary inertial frame ℛ (Birkinshaw 1996; Heyvaerts 2003) as ![\begin{eqnarray} \label{consmassrelat}&&\partial_t\left(\gamma \rho_0\right) + {\mathrm{div}} \, \gamma \rho_0 \vec{v} = 0 \\[0.5mm] \label{mouvrelat}&& \partial_t\left(\gamma^2 \rho_0 \, \vec{v}\right) + {\mathrm{div}} \left(\gamma^2 \rho_0 \, \tens{vv} \right) = \rho_{\rm e} \vec{E} + {\vec{j}} \times {\vec{B}} \\[0.5mm] \label{Faradayrelat}&& \partial_t\, {\vec{B}} = - {\mathrm{rot}}\, {\vec{E}} \\[0.5mm] \label{Ampererelat}&& {\mathrm{rot}} \left({\vec{B}}/\mu_0\right) = {\vec{j}} + \varepsilon_o \, \partial_t {\vec{E}} \\[0.5mm] \label{MHDparfaiterelat} &&{\vec{E}} + {\vec{v}} \times {\vec{B}} = 0 \\[0.5mm] && \varepsilon_0 \, {\mathrm{div}} {\vec{E}} = \rho_{\rm e} \label{coulombrelat}\\[0.5mm] \label{divBnulle} && {\mathrm{div}}\, {\vec{B}} = 0. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq18.png) An event is labeled in ℛ according to its position r and its time of occurence t. The electric and magnetic fields are denoted E and B. The fluid velocity is v and its associated Lorentz factor is γ. The variable ρ0 is the proper mass density, that is, the mass density measured in the instantaneous rest-frame ℛ0 of the fluid. Owing to Lorentz length contraction, the apparent mass density in ℛ is γρ0. The electric current density and the charge density in ℛ are j and ρe, respectively. We assume the fluid to be cold, so that no pressure gradient force appears in the equation of motion in Eq. (3). Our equations are written in the MKSA system of units, where the magnetic permeability of vacuum is μ0 and its electric permittivity is ε0.
An event is labeled in ℛ according to its position r and its time of occurence t. The electric and magnetic fields are denoted E and B. The fluid velocity is v and its associated Lorentz factor is γ. The variable ρ0 is the proper mass density, that is, the mass density measured in the instantaneous rest-frame ℛ0 of the fluid. Owing to Lorentz length contraction, the apparent mass density in ℛ is γρ0. The electric current density and the charge density in ℛ are j and ρe, respectively. We assume the fluid to be cold, so that no pressure gradient force appears in the equation of motion in Eq. (3). Our equations are written in the MKSA system of units, where the magnetic permeability of vacuum is μ0 and its electric permittivity is ε0.
The linear propagation of MHD waves involves the classical Alfvén speed 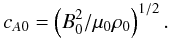 (9)In dense fluids, this velocity is much less than the speed of light c. Conversely, in tenuous fluids where the magnetic energy density is much higher than the rest-mass energy density, the classical Alfvén speed is much higher than c. Waves propagating in this regime are said to be relativistic MHD waves. It can be easily checked that the modulus vA0 of the propagation speed of linear relativistic Alfvén waves is related to the classical Alfvén speed cA0, defined in Eq. (9), by
(9)In dense fluids, this velocity is much less than the speed of light c. Conversely, in tenuous fluids where the magnetic energy density is much higher than the rest-mass energy density, the classical Alfvén speed is much higher than c. Waves propagating in this regime are said to be relativistic MHD waves. It can be easily checked that the modulus vA0 of the propagation speed of linear relativistic Alfvén waves is related to the classical Alfvén speed cA0, defined in Eq. (9), by 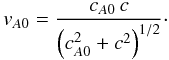 (10)This velocity is close to cA0 when cA0 ≪ c and close to the speed of light when cA0 ≫ c. In this latter case, the displacement current cannot be neglected in Ampère-Faraday’s Eq. (5). More generally, the charge density is not negligible in relativistically moving fluids and Coulomb’s Eq. (7) is needed to determine it. The shorthand notation ∂t designates the partial derivative with respect to the time t in ℛ. Similarly, ∇ is the space derivative with respect to position r in ℛ. The modulus of a vector A is denoted A. Second-rank tensors in a three-dimensional space are denoted by boldfaced script letters. The tensor product of two vectors is denoted similarly and U is the unit second rank tensor. The Lagrangian derivative with respect to time following the motion of velocity v is denoted dt
(10)This velocity is close to cA0 when cA0 ≪ c and close to the speed of light when cA0 ≫ c. In this latter case, the displacement current cannot be neglected in Ampère-Faraday’s Eq. (5). More generally, the charge density is not negligible in relativistically moving fluids and Coulomb’s Eq. (7) is needed to determine it. The shorthand notation ∂t designates the partial derivative with respect to the time t in ℛ. Similarly, ∇ is the space derivative with respect to position r in ℛ. The modulus of a vector A is denoted A. Second-rank tensors in a three-dimensional space are denoted by boldfaced script letters. The tensor product of two vectors is denoted similarly and U is the unit second rank tensor. The Lagrangian derivative with respect to time following the motion of velocity v is denoted dt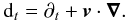 (11)Faraday’s equation in Eq. (4) implies that div B is a constant in time, and then vanishes because it initially vanished. The solenoidal equation in Eq. (8) is only needed to specify this initial condition. For this reason, it may be ignored in the following developments and only be used as a constraint of the structure of the magnetic field. The electric field can be eliminated from the system of equations in Eqs. (2) − (7) and expressed in terms of the velocity and the magnetic field using the perfect MHD relation in Eq. (6). The electromagnetic force density is first expressed in terms of the electric and magnetic fields E and B by using Ampère’s and Coulomb’s equations in Eqs. (5) and (7). This gives (Jackson 1975)
(11)Faraday’s equation in Eq. (4) implies that div B is a constant in time, and then vanishes because it initially vanished. The solenoidal equation in Eq. (8) is only needed to specify this initial condition. For this reason, it may be ignored in the following developments and only be used as a constraint of the structure of the magnetic field. The electric field can be eliminated from the system of equations in Eqs. (2) − (7) and expressed in terms of the velocity and the magnetic field using the perfect MHD relation in Eq. (6). The electromagnetic force density is first expressed in terms of the electric and magnetic fields E and B by using Ampère’s and Coulomb’s equations in Eqs. (5) and (7). This gives (Jackson 1975) ![\begin{eqnarray} \mu_0 c^2 \left(\rho_{\rm e} {\vec{E}} + {\vec{j}} \times {\vec{B}}\right) = - {\rm d}_t\, \left({\vec{E}}\times {\vec{B}} \right) + \left({\vec{v}} \cdot {\boldsymbol{\nabla}}\right) \left({\vec{E}}\times {\vec{B}}\right) \nonumber\\[0.5mm] ~~~~~~~~+ c^2 \, {\mathrm{div}} \left(\tens{BB} - \left(B^2/2\right)\, \tens{U} \right) + {\mathrm{div}} \left(\tens{EE} - \left(E^2/2\right) \, \tens{U} \right)\!. \label{forceEMPoyntingMaxwell} \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq45.png) (12)Equation (6) implies that
(12)Equation (6) implies that 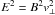 and E × B = B2v ⊥ . The subscripts ⊥ and ∥ respectively refer to components orthogonal or aligned with the direction of the local and instantaneous magnetic field such as, for example
and E × B = B2v ⊥ . The subscripts ⊥ and ∥ respectively refer to components orthogonal or aligned with the direction of the local and instantaneous magnetic field such as, for example  (13)Using Eq. (6), the force density in Eq. (12) is expressed only in terms of B and v. As a result, the set of Eqs. (2) − (7) reduces to the induction equation and the number and momentum conservation equations, involving only B, v, and ρ0
(13)Using Eq. (6), the force density in Eq. (12) is expressed only in terms of B and v. As a result, the set of Eqs. (2) − (7) reduces to the induction equation and the number and momentum conservation equations, involving only B, v, and ρ0![\begin{eqnarray} \label{consmassrelatsummary}&& {\rm d}_t \left(\gamma \rho_0\right) + \gamma \rho_0\, {\mathrm{div}}\, {\vec{v}} = 0 \\[0.5mm] &&\mu_0 \gamma \rho_0 c^2 \, {\rm d}_t\, (\gamma {\vec{v}}) + {\rm d}_t\! \left(B^2 {\vec{v}}_\perp \right) + B^2 {\vec{v}}_\perp \, {\mathrm{div}}\, {\vec{v}} + {\boldsymbol{\nabla}} \left(c^2 B^2/2\gamma^2\right) \nonumber \\[0.5mm] \label{mouvMHDparfaitsummary} &&\qquad\quad + {\boldsymbol{\nabla}} \left(\left({\vec{B}} \cdot {\vec{v}}\right)^2 / 2 \right) - \left({\vec{B}} \cdot {\boldsymbol{\nabla}}\right) \left(c^2{\vec{B}}/\gamma^2 + ({\vec{B}} \cdot {\vec{v}})\, {\vec{v}} \right) = 0\\[0.5mm] \label{inducrelatsummary} &&{\rm d}_t\, {\vec{B}} - \left({\vec{B}} \cdot {\boldsymbol{\nabla}}\right) {\vec{v}} + {\vec{B}} \ {\mathrm{div}}\, {\vec{v}} = 0. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq52.png)
4. Equations of simple waves
In a simple wave, all physical quantities observed in some rest frame ℛ are functions of the unique master variable u which depends on the position and time in this frame. Solving equations Eqs. (14) − (16) first amounts to determining this function u(r,t). This solution reveals the characteristics of the non-linear motion, which contain all the information that we need to know about non-linear wave propagation and steepening, if any. The functions that determine the physical quantities in terms of the master variable can then be found. Denoting by du the derivative with respect to u, the usual vector operators acting on a variable that depends on u(r,t) can be expressed as ![\begin{eqnarray} &&{\mathrm{div}}\, {\vec{A}} = {\boldsymbol{\nabla}}u \cdot {\rm d}_u {\vec{A}} \label{divAansatz}\\[0.5mm] &&({\vec{B}} \cdot {\boldsymbol{\nabla}}) \, {\vec{A}} = ({\vec{B}} \cdot {\boldsymbol{\nabla}} u) \, {\rm d}_u {\vec{A}} \\[0.5mm] && {\boldsymbol{\nabla}}F = {\boldsymbol{\nabla}} u \ {\rm d}_u F \\[0.5mm] \label{rotansatz} && {\mathrm{curl}}\, {\vec{A}} = {\boldsymbol{\nabla}} u \times {\rm d}_u {\vec{A}}. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq55.png) Under the simple wave ansatz, the system of Eqs. (14) − (16) becomes
Under the simple wave ansatz, the system of Eqs. (14) − (16) becomes ![\begin{eqnarray} \label{consmassansatz} &&{\rm d}_u\left(\ln\left(\gamma \rho_0\right)\right) \ {\rm d}_t u \ +\ {\rm d}_u{\vec{v}} \cdot {\boldsymbol{\nabla}}u = 0\\[0.5mm] &&\left(\mu_0\gamma \rho_0 c^2 \, {\rm d}_u\left(\gamma {\vec{v}}\right) + {\rm d}_u \left(B^2 {\vec{v}}_\perp \right)\ \right) \ \, {\rm d}_t u \nonumber \\[0.5mm] &&\qquad + B^2 {\vec{v}}_\perp \, \left({\rm d}_u {\vec{v}} \cdot {\boldsymbol{\nabla}} u\right) + {\rm d}_u \left(B^2/2 \gamma^2 + ({\vec{B}} \cdot {\vec{v}})^2 /2 \right) \ \, {\boldsymbol{\nabla}} u \nonumber \\[0.5mm] \label{mouvansatz}&&\qquad - \left({\rm d}_u \left(c^2 {\vec{B}}/\gamma^2 + ({\vec{B}} \cdot {\vec{v}}) \, {\vec{v}} \right)\, \right) \left({\vec{B}} \cdot {\boldsymbol{\nabla}} u\right) = 0 \\[0.5mm] \label{inducansatz} &&{\rm d}_u {\vec{B}} \ \, {\rm d}_t u - \left({\vec{B}} \cdot {\boldsymbol{\nabla}} u \right) \ {\rm d}_u {\vec{v}} + {\vec{B}} \, \left({\boldsymbol{\nabla}} u \cdot {\rm d}_u {\vec{v}} \right) = 0. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq56.png) The vectorial Eqs. (22) and (23) must be projected onto some set of basis vectors. A moving set based on the directions of the local and instantaneous magnetic field and plasma acceleration appears to be the most appropriate. We define the three projection vectors by
The vectorial Eqs. (22) and (23) must be projected onto some set of basis vectors. A moving set based on the directions of the local and instantaneous magnetic field and plasma acceleration appears to be the most appropriate. We define the three projection vectors by 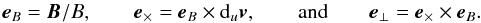 (24)These vectors are orthogonal to one another but, except for eB, they are neither unit vectors nor dimensionless when u is not assigned the dimension of a velocity. The vector e ⊥ is in fact the component of duv perpendicular to B
(24)These vectors are orthogonal to one another but, except for eB, they are neither unit vectors nor dimensionless when u is not assigned the dimension of a velocity. The vector e ⊥ is in fact the component of duv perpendicular to B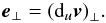 (25)However, e ⊥ is not the derivative with respect to u of v ⊥ . These basis vectors are local and vary with u, that is, with both position and time. The three projections of the induction equation given in Eq. (23) on these vectors are
(25)However, e ⊥ is not the derivative with respect to u of v ⊥ . These basis vectors are local and vary with u, that is, with both position and time. The three projections of the induction equation given in Eq. (23) on these vectors are ![\begin{eqnarray} \label{inducsur1} &&\left({\rm d}_u {\vec{v}} \right)_\perp \cdot \left(\left({\rm d}_u {\vec{B}} \right)_{\perp} \, {\rm d}_t u - \left({\rm d}_u {\vec{v}}\right)_{\perp} \ \left({\vec{B}} \cdot {\boldsymbol{\nabla}} u \right) \right) = 0 \\[0.5mm] \label{inducsur2} && \left({\vec{e}}_B \times \left({\rm d}_u{\vec{v}} \right)_\perp\right) \cdot \left({\rm d}_u {\vec{B}} \right)_\perp = 0 \\[0.5mm] \label{inducsur3} &&\left({\vec{e}}_B \cdot {\rm d}_u {\vec{B}}\right) \ {\rm d}_t u - \left({\vec{e}}_B \cdot {\rm d}_u {\vec{v}}\right) \left({\vec{B}} \cdot {\boldsymbol{\nabla}} u \right) + B\ {\boldsymbol{\nabla}} u \cdot {\rm d}_u{\vec{v}} = 0. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq63.png) Equation (28) can also be given in the form of the flux conservation equation
Equation (28) can also be given in the form of the flux conservation equation 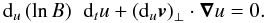 (29)The projections of the equation of motion in Eq. (22) on the vectors e ⊥ , e × , eB provide us with the three equations
(29)The projections of the equation of motion in Eq. (22) on the vectors e ⊥ , e × , eB provide us with the three equations ![\begin{eqnarray} && \left[\left(\mu_0 \gamma^2 \rho_0 c^2 \!+\! B^2 \right) {e}_{\perp}^2 + \left(\mu_0 \gamma \rho_0 c^2 {\rm d}_u\gamma + {\rm d}_u B^2/2\right) \left({\vec{v}} \cdot {\vec{e}}_\perp\right) \right] \ {\rm d}_t u \nonumber \\[0.5mm] && \quad - \left[ \left(c^2\!/\gamma^2\right)\! \left({\vec{e}}_{\perp}\! \cdot {\rm d}_u {\vec{B}}\right) \!+ \!2 ({\vec{B}} \cdot {\vec{v}}) \, {e}_\perp^2 \!+\! \left({\vec{v}} \cdot {\rm d}_u{\vec{B}}\right) \left({\vec{v}} \cdot {\vec{e}}_\perp\right) \right] \left({\vec{B}} \!\cdot\! {\boldsymbol{\nabla}} u\right) \nonumber \\[0.5mm] \label{mouvprojsure1recap} &&\quad + \left[{\rm d}_u \left(c^2 B^2/2 \gamma^2\right) + {\rm d}_u \left(\left({\vec{B}} \cdot {\vec{v}}\right)^2\!/2 \right) \right] \left({\vec{e}}_\perp \cdot {\boldsymbol{\nabla}} u \right) = 0 \\[0.5mm] && \left[ \left(\left({\vec{e}}_{\perp} \times {\vec{v}}_{\!\perp} \right) \cdot {\vec{e}}_B \right) \left(\mu_0 \gamma \rho_0 c^2 {\rm d}_u\gamma + {\rm d}_u B^2/2 \right)\right] \ \ {\rm d}_t u \nonumber \\[0.5mm] &&\quad - \left[\left(\left({\vec{e}}_{\perp} \times {\vec{v}}_{\!\perp} \right) \cdot {\vec{e}}_B\right) \ \left({\vec{v}} \cdot {\rm d}_u {\vec{B}} \right)\right] \left({\vec{B}} \cdot {\boldsymbol{\nabla}} u\right) \nonumber \\[0.5mm] \label{mouvprojsure2recap} &&\quad + \left[{\rm d}_u \left({B^2}/{2 \gamma^2} + ({\vec{B}} \cdot {\vec{v}})^2/2c^2 \right) \right] \left({\vec{e}}_\times \cdot {\boldsymbol{\nabla}} u \right) = 0 \\[0.5mm] \label{mouvprojsure3recap} && \left[{\vec{e}}_B \cdot \gamma \rho_0 \, {\rm d}_u\left(\gamma {\vec{v}}\right) \right] \ \ {\rm d}_t u \ = 0. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq66.png) The system of seven equations generated from Eqs. (21) − (23) by projecting onto the vectors eB, e ⊥ , and e × leads to Eqs. (21), (26), (27), (29) − (32). As a result of Eq. (27), the vectors (duv) ⊥ and (duB) ⊥ are parallel to each other and Eq. (26) effectively projects onto only one axis and can be written in the form of the scalar relation
The system of seven equations generated from Eqs. (21) − (23) by projecting onto the vectors eB, e ⊥ , and e × leads to Eqs. (21), (26), (27), (29) − (32). As a result of Eq. (27), the vectors (duv) ⊥ and (duB) ⊥ are parallel to each other and Eq. (26) effectively projects onto only one axis and can be written in the form of the scalar relation 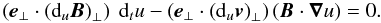 (33)Equation (27) can be replaced by Eq. (33), leaving us with six equations.
(33)Equation (27) can be replaced by Eq. (33), leaving us with six equations.
5. Alfvénic perturbations
The remaining six equations in Eqs. (21), (29), (33), (30), (31), and (32) can be regarded as a linear homogeneous system for the four unknowns dtu, (e ⊥ ·∇u), (e × ·∇u), and (eB·∇u). Since we wish to identify propagative solutions, dtu should not identically vanish, for otherwise the perturbation would simply be advected by the fluid. Since Eq. (32) involves only the unknown dtu, the factor of this variable should vanish. Equation (34) below results from substracting Eq. (29) from Eq. (21). With this slight change, Eqs. (21), (29), (33) (30), (31), and (32) can be respectively written as ![\begin{eqnarray} \label{masssurfluxSymbol}&& T_1 \, {\rm d}_t u - K_1 \left({\vec{e}}_B \cdot {\boldsymbol{\nabla}} u\right) = 0 \\[0.5mm] \label{fluxSymbol} && T_2 \, {\rm d}_t u + K_2 \, \left({\vec{e}}_\perp \cdot {\boldsymbol{\nabla}} u\right) = 0 \\[0.5mm] \label{dBdvSymbol} &&T_3 \, {\rm d}_t u - K_3 \, \left({\vec{e}}_B \cdot {\boldsymbol{\nabla}} u\right) = 0 \\[0.5mm] \label{mouvSymbolperp} &&T_4 \, {\rm d}_t u + A \, \left({\vec{e}}_\perp \cdot {\boldsymbol{\nabla}} u\right) - K_4 \, \left({\vec{e}}_B \cdot {\boldsymbol{\nabla}} u\right) = 0 \\[0.5mm] \label{mouvSymbolcroix} &&T_5 \, {\rm d}_t u + A \, \left({\vec{e}}_\times \cdot {\boldsymbol{\nabla}} u \right) - K_5 \, \left({\vec{e}}_B \cdot {\boldsymbol{\nabla}} u\right) = 0 \\[0.5mm] \label{projmouv3Symbol} && T_6 \, {\rm d}_t u =0 \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq75.png) where
where ![\begin{eqnarray} \label{T1K1} && T_1 = {\rm d}_u\!\left(\ln\left(B/\gamma \rho_0\right)\right) \qquad \qquad \ \, K_1 = {\vec{e}}_B \cdot {\rm d}_u{\vec{v}} \\[0.5mm] \label{T2B} && T_2 = {\rm d}_u \left(\ln\left(B\right)\right) \qquad \qquad \qquad \, K_2 = 1 \\[0.5mm] \label{T3K3} && T_3 = {\vec{e}}_\perp \cdot {\rm d}_u{\vec{B}} \qquad \qquad \qquad \quad K_3 = B \ {e}_\perp^2 \\[0.5mm] && T_4 = 2 \left(\mu_0 \gamma^2 \rho_0 \!+\! B^2/c^2 \right) {e}_\perp^2 \! \!+\! \left(\mu_0 \rho_0 \, {\rm d}_u\gamma^2 \!+ \!{\rm d}_u B^2\!/\!c^2 \right) \left({\vec{v}} \cdot {\vec{e}}_\perp\!\right) \\[0.5mm] && K_4 = \left(2 B/\gamma^2\right) \left({\vec{e}}_{\perp} \cdot {\rm d}_u {\vec{B}}\right) + \left(4B/c^2\right)\, ({\vec{B}} \cdot {\vec{v}}) \ {e}_\perp^2 \nonumber \\[0.5mm] &&\qquad \quad + \left(2B/c^2\right) \left({\vec{v}} \cdot {\rm d}_u{\vec{B}}\right) \ \left({\vec{v}}\! \cdot\! {\vec{e}}_\perp\! \right) \\[0.5mm] &&T_5 = \left(\left({\vec{e}}_{\perp} \times {\vec{v}}_{\perp} \right) \cdot {\vec{e}}_B\right) \left(\mu_0 \rho_0 c^2 {\rm d}_u\gamma^2 + {\rm d}_u B^2 \right) \\[0.5mm] &&K_5 = \left(\left({\vec{e}}_{\perp} \times {\vec{v}}_{\perp} \right) \cdot {\vec{e}}_B\right) \ 2 B \, \left({\vec{v}} \cdot {\rm d}_u {\vec{B}} \right) \\[0.5mm] &&T_6 = {\vec{e}}_B \cdot \ {\rm d}_u\!\left(\gamma {\vec{v}}\right) \\[0.5mm] \label{expressA} && A = {\rm d}_u \ \left(B^2/\gamma^2 + \left({\vec{B}} \cdot {\vec{v}}\right)^2\!/c^2 \right). \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq76.png) The system of equations in Eqs. (34) − (39) should have a non-obvious solution and be consistent with a non-identically-vanishing dtu. To achieve this, it is necessary that all the determinants of the (4 × 4) minors extracted from its (6 × 4) matrix in Eq. (49) vanish. If only a single one of them were to differ from 0, the corresponding homogeneous system of four equations for four unknowns would be a Cramer one, allowing only for the obvious solution. The rank r of the system is otherwise less than 4, which means that r column vectors, which we might consider to be the r first ones, form a linearly independent set, but that no larger set of column vectors does. Since any of the (r + 1)...n column vectors depend on the first r ones, any linear combination of the (r + 1)...n column vectors may be expanded on the basis formed by the r first ones. This means that the system has a solution for arbitrary values of the unknowns associated with columns (r + 1)...n and thus has non-obvious solutions. The matrix of the system (34) − (39) is
The system of equations in Eqs. (34) − (39) should have a non-obvious solution and be consistent with a non-identically-vanishing dtu. To achieve this, it is necessary that all the determinants of the (4 × 4) minors extracted from its (6 × 4) matrix in Eq. (49) vanish. If only a single one of them were to differ from 0, the corresponding homogeneous system of four equations for four unknowns would be a Cramer one, allowing only for the obvious solution. The rank r of the system is otherwise less than 4, which means that r column vectors, which we might consider to be the r first ones, form a linearly independent set, but that no larger set of column vectors does. Since any of the (r + 1)...n column vectors depend on the first r ones, any linear combination of the (r + 1)...n column vectors may be expanded on the basis formed by the r first ones. This means that the system has a solution for arbitrary values of the unknowns associated with columns (r + 1)...n and thus has non-obvious solutions. The matrix of the system (34) − (39) is ![\begin{equation} \left(\begin{array}{cccc} T_1 & \quad 0 & \quad 0 & \quad - K_1 \\[0.5mm] T_2 & \quad 1 & \quad 0 & \quad 0\\[0.5mm] T_3 & \quad 0 & \quad 0 & \quad - K_3 \\[0.5mm] T_4& \quad A & \quad 0 & \quad -K_4 \\[0.5mm] T_5 & \quad 0 & \quad A & \quad -K_5\\[0.5mm] T_6 & \quad 0 & \quad 0 & \quad 0\\ \end{array} \right). \label{matrixsystlin} \end{equation}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq81.png) (49)There are fifteen (4 × 4) minors, each of which is formed by suppressing two lines from the matrix in Eq. (49). The last line of this matrix represents Eq. (32). Since, for physical reasons explained above, dtu should not vanish, the vanishing of T6 is a necessary condition to obtain a propagating solution. We then demand that
(49)There are fifteen (4 × 4) minors, each of which is formed by suppressing two lines from the matrix in Eq. (49). The last line of this matrix represents Eq. (32). Since, for physical reasons explained above, dtu should not vanish, the vanishing of T6 is a necessary condition to obtain a propagating solution. We then demand that 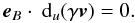 (50)We must now ensure that all 4 × 4 determinants extracted from the five first lines vanish. The determinant of the minor formed by the first four lines obviously does. In all other minors, the third column consists of zeroes except for the bottom line, where the element is A. These determinants are then all proportional to A and therefore
(50)We must now ensure that all 4 × 4 determinants extracted from the five first lines vanish. The determinant of the minor formed by the first four lines obviously does. In all other minors, the third column consists of zeroes except for the bottom line, where the element is A. These determinants are then all proportional to A and therefore 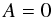 (51)is a sufficient condition for the system represented by the matrix in Eq. (49) to have non-obvious solutions. The condition in Eq. (51) is however not a necessary one. Other non-obvious solutions could be obtained by imposing conditions other than Eq. (51). They would describe MHD perturbations that are compressive, even in the classical limit. As explained in the introduction, no coherent electric current wake is expected to result from the propagation of these waves. We therefore concentrate on the solutions characterized by Eq. (51) which, for the reasons explained below, correspond to Alfvénic perturbations.
(51)is a sufficient condition for the system represented by the matrix in Eq. (49) to have non-obvious solutions. The condition in Eq. (51) is however not a necessary one. Other non-obvious solutions could be obtained by imposing conditions other than Eq. (51). They would describe MHD perturbations that are compressive, even in the classical limit. As explained in the introduction, no coherent electric current wake is expected to result from the propagation of these waves. We therefore concentrate on the solutions characterized by Eq. (51) which, for the reasons explained below, correspond to Alfvénic perturbations.
The condition in Eq. (51) is mathematically sufficient to find solutions of the equations represented by the five first lines of the matrix in Eq. (49) in which dtu, (e⊥·∇u), (e × ·∇u), and (eB·∇u) do not all vanish. However, this is physically insufficient, since it only warrants the existence of a solution to the five first equations in which the variable (e × ·∇u) could be given a non-zero value, all other variables possibly vanishing. However, as noted earlier in this section, the variable dtu should also have a non-vanishing value if the solution is to have the character of a propagating wave. Supplementary conditions, which we establish in Sect. 7, are necessary to achieve this. The system of the five first lines of Eq. (49) should then be of a rank strictly less than 3 to yield a physically meaningful solution. Having adopted the condition in Eq. (51), all the 3 × 3 minors extracted from the 5 × 3 matrix obtained by suppressing the third column and the last line in Eq. (49) should then also vanish. Since its second column has only one non-zero element, we need only demand that all 2 × 2 determinants extracted from the 4 × 2 matrix formed by the first and fourth column of Eq. (49) with the second and sixth lines suppressed should vanish. This amounts to demanding that the equations represented by the lines 1, 3, 4, and 5 of Eq. (49) with A = 0 be compatible.
6. Constancy of the proper field modulus
The condition in Eq. (51) defines solutions of the Alfvénic type, which is justified by the consideration of the classical limit c → ∞. Equation (48) shows that in this limit Eq. (51) simplifies to dB/du = 0, which is known to be the condition defining non-linear classical Alfvén waves (Neubauer 1980). In these waves, the modulus of the magnetic field is constant all over space and time. When motions are relativistic, as considered here, the field modulus is not constant in the chosen reference frame ℛ. Its structure is defined by Eq. (51), that is, from Eq. (48), by 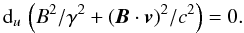 (52)We may however suspect that the proper field modulus (observed in the fluid’s instantaneous rest frame) should be constant because the frame of observation ℛ could always be chosen to coincide, at the considered time, with the instantaneous rest frame ℛ0 of some fluid element. In the vicinity of this fluid element, the motion is, for a while, non-relativistic. That the modulus B0 of the field in the instantaneous rest frame is constant can be shown formally by noting that under the perfect MHD condition in Eq. (6),
(52)We may however suspect that the proper field modulus (observed in the fluid’s instantaneous rest frame) should be constant because the frame of observation ℛ could always be chosen to coincide, at the considered time, with the instantaneous rest frame ℛ0 of some fluid element. In the vicinity of this fluid element, the motion is, for a while, non-relativistic. That the modulus B0 of the field in the instantaneous rest frame is constant can be shown formally by noting that under the perfect MHD condition in Eq. (6), 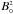 equals the relativistic invariant B2 − E2/c2 because E vanishes in ℛ0. This invariant is readily calculated in the observation frame because perfect MHD implies that E = B × v, hence
equals the relativistic invariant B2 − E2/c2 because E vanishes in ℛ0. This invariant is readily calculated in the observation frame because perfect MHD implies that E = B × v, hence 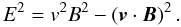 (53)The invariant B2 − E2/c2 then is
(53)The invariant B2 − E2/c2 then is 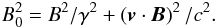 (54)From Eq. (52), this quantity is indeed seen to be constant with u, that is with space and time.
(54)From Eq. (52), this quantity is indeed seen to be constant with u, that is with space and time.
7. Structure of the perturbation
The vanishing of the mixed product in Eq. (27) indicates that the vectors (duv) ⊥ and (duB) ⊥ are parallel. Their ratio, q, is given by Eq. (26) 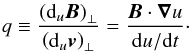 (55)We now establish the conditions ensuring that Eqs. (34), (36), (37), and (38) are indeed compatible, given Eqs. (51) and (50). These conditions constrain the relations between physical variables in a way that is specific to this particular type of perturbation. The reduction of Eqs. (34), (36), (37), and (38) to relations between physical variables is outlined in Appendix A.
(55)We now establish the conditions ensuring that Eqs. (34), (36), (37), and (38) are indeed compatible, given Eqs. (51) and (50). These conditions constrain the relations between physical variables in a way that is specific to this particular type of perturbation. The reduction of Eqs. (34), (36), (37), and (38) to relations between physical variables is outlined in Appendix A.
The ratio q defined in Eq. (55) describes the correlated variations in (duv) ⊥ and (duB) ⊥ . It is calculated in Appendix A. The solution yields the relation 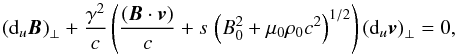 (56)where s is a sign related to the sense of propagation of the wave along the field. The velocity perturbation has a component aligned to the local and instantaneous magnetic field, which we represent by the variable
(56)where s is a sign related to the sense of propagation of the wave along the field. The velocity perturbation has a component aligned to the local and instantaneous magnetic field, which we represent by the variable 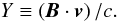 (57)A differential equation relating Y to the Lorentz factor γ of the perturbed flow is obtained in Appendix A. It can be written as
(57)A differential equation relating Y to the Lorentz factor γ of the perturbed flow is obtained in Appendix A. It can be written as 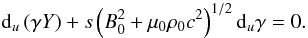 (58)Equation (34) describes the variations in the mass to flux ratio. In Appendix A, this equation is reduced to a relation between the proper mass density and the field-aligned velocity component, which eventually becomes the constancy of the proper mass density
(58)Equation (34) describes the variations in the mass to flux ratio. In Appendix A, this equation is reduced to a relation between the proper mass density and the field-aligned velocity component, which eventually becomes the constancy of the proper mass density 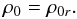 (59)To summarize, the rank of the global system of six equations represented by the matrix in Eq. (49) is 2 provided the relations in Eqs. (56), (58), (59), (51), and (50) are satisfied. The system of equations in Eq. (49) can be reduced to any one of the four equations that give, from Eq. (55), B·∇u in terms of dtu and Eq. (35), which gives e ⊥ ·∇u also in terms of dtu. The variables e × ·∇u and dtu can be fixed arbitrarily. A number of physical consequences on non-linear relativistic Alfvénic disturbances can be derived from these relations. In particular, we have already shown that the proper mass density and the modulus of the proper magnetic field are constant in these Alfvénic perturbations. Equation (58) can be integrated into
(59)To summarize, the rank of the global system of six equations represented by the matrix in Eq. (49) is 2 provided the relations in Eqs. (56), (58), (59), (51), and (50) are satisfied. The system of equations in Eq. (49) can be reduced to any one of the four equations that give, from Eq. (55), B·∇u in terms of dtu and Eq. (35), which gives e ⊥ ·∇u also in terms of dtu. The variables e × ·∇u and dtu can be fixed arbitrarily. A number of physical consequences on non-linear relativistic Alfvénic disturbances can be derived from these relations. In particular, we have already shown that the proper mass density and the modulus of the proper magnetic field are constant in these Alfvénic perturbations. Equation (58) can be integrated into 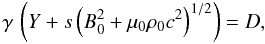 (60)where D is some integration constant. The proper choice of this constant is subtle because, for a given value of D, the solution is not defined for all values of γ from 1 to infinity. The integration constant should be chosen such that the relation (60) applies to the unperturbed state, which must definitely be in the range of the physically meaningful solution if, as assumed here, any fluid element is, at some time, in the unperturbed state. We note that this would not be so in an infinite wave train. We define vr to be the velocity of the fluid in this unperturbed state, γr the corresponding Lorentz factor, and Br the unperturbed magnetic field, all of which are observed in the chosen reference frame ℛ. Equation (60) then becomes
(60)where D is some integration constant. The proper choice of this constant is subtle because, for a given value of D, the solution is not defined for all values of γ from 1 to infinity. The integration constant should be chosen such that the relation (60) applies to the unperturbed state, which must definitely be in the range of the physically meaningful solution if, as assumed here, any fluid element is, at some time, in the unperturbed state. We note that this would not be so in an infinite wave train. We define vr to be the velocity of the fluid in this unperturbed state, γr the corresponding Lorentz factor, and Br the unperturbed magnetic field, all of which are observed in the chosen reference frame ℛ. Equation (60) then becomes 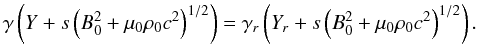 (61)The modulus B of the apparent field (i.e. the field seen in the rest frame ℛ) can then be calculated as a function of the change in the Lorentz factor, δ = γ − γr, from Eq. (61) by using Eqs. (54) and (57)
(61)The modulus B of the apparent field (i.e. the field seen in the rest frame ℛ) can then be calculated as a function of the change in the Lorentz factor, δ = γ − γr, from Eq. (61) by using Eqs. (54) and (57) 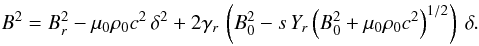 (62)The right hand side of Eq. (62) is not positive for any value of δ, which limits the set of physically acceptable values of γ. Moreover, the conservation of flux imposes that the modulus of the magnetic field remains larger than some strictly positive value, implying that this provides a more stringent constraint than merely the positivity of B2. This can be seen by considering the solenoidal Eq. (8), which, according to Eq. (17), transforms under the simple wave ansatz into
(62)The right hand side of Eq. (62) is not positive for any value of δ, which limits the set of physically acceptable values of γ. Moreover, the conservation of flux imposes that the modulus of the magnetic field remains larger than some strictly positive value, implying that this provides a more stringent constraint than merely the positivity of B2. This can be seen by considering the solenoidal Eq. (8), which, according to Eq. (17), transforms under the simple wave ansatz into 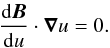 (63)Equation (63) implies that B·∇u/ | ∇u | is a constant if the direction of ∇u is independent of u, that is if the geometry of the perturbation is planar. It is shown in Appendix B that this is indeed so. The constraints on the values of γ as observed in the unperturbed fluid frame are discussed in Sect. 9.
(63)Equation (63) implies that B·∇u/ | ∇u | is a constant if the direction of ∇u is independent of u, that is if the geometry of the perturbation is planar. It is shown in Appendix B that this is indeed so. The constraints on the values of γ as observed in the unperturbed fluid frame are discussed in Sect. 9.
8. An explicit solution
The relations between physical variables in Alfvénic perturbations result from Eqs. (56), (58), (59), (54), and (50). To be specific, we set the observer’s frame to the unperturbed fluid frame ℛr0. The writing of these relations is simplified by introducing 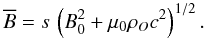 (64)In the frame ℛr0, Eq. (61) reduces to
(64)In the frame ℛr0, Eq. (61) reduces to 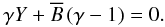 (65)In Eq. (56), the perpendicular direction refers to the local and instantaneous field. A fixed reference frame is preferable. We define it such that its unit vector en is aligned with the common direction of the normal to the phase planes, the planes of constant u (Appendix B). The projection of the unperturbed field onto a phase plane defines another unit vector e2. A third vector e1 forms with e2 and en a direct orthonormal frame of unit vectors, in which the unperturbed field can be written as B0 = B0sinθ e2 + B0cosθ en. In this frame, the perturbed magnetic field is written as B = B1 e1 + B2 e2 + Bn en, where, from Eq. (63), Bn = B0cosθ is constant. The velocity field is similarly expanded as v = v1 e1 + v2 e2 + vn en. It is a simple matter to express Eqs. (56), (65), and (50) in terms of the variables v1(u), v2(u), vn(u), B1(u), and B2(u). It appears that the Lorentz factor γ of the flow, or the modulus v of the fluid velocity, could be chosen as the master variable, wherever they vary monotonically. After some algebra, we obtain the system
(65)In Eq. (56), the perpendicular direction refers to the local and instantaneous field. A fixed reference frame is preferable. We define it such that its unit vector en is aligned with the common direction of the normal to the phase planes, the planes of constant u (Appendix B). The projection of the unperturbed field onto a phase plane defines another unit vector e2. A third vector e1 forms with e2 and en a direct orthonormal frame of unit vectors, in which the unperturbed field can be written as B0 = B0sinθ e2 + B0cosθ en. In this frame, the perturbed magnetic field is written as B = B1 e1 + B2 e2 + Bn en, where, from Eq. (63), Bn = B0cosθ is constant. The velocity field is similarly expanded as v = v1 e1 + v2 e2 + vn en. It is a simple matter to express Eqs. (56), (65), and (50) in terms of the variables v1(u), v2(u), vn(u), B1(u), and B2(u). It appears that the Lorentz factor γ of the flow, or the modulus v of the fluid velocity, could be chosen as the master variable, wherever they vary monotonically. After some algebra, we obtain the system ![\begin{eqnarray} \label{eqB1}&& c \frac{{\rm d} B_1}{{\rm d}v} - \frac{\gamma^2 v}{c} \, B_1 + \gamma {\overline{B}} \ \frac{{\rm d} v_1}{{\rm d}v} = 0 \\[0.5mm] \label{eqB2} && c \frac{{\rm d} B_2}{{\rm d}v} - \frac{\gamma^2 v}{c} \, B_2 + \gamma {\overline{B}} \ \frac{{\rm d} v_2}{{\rm d}v} = 0 \\[0.5mm] \label{eqvn} && \gamma {\overline{B}} \ \frac{{\rm d} v_n}{{\rm d}v} = B_0 \cos \theta \, \frac{\gamma^2 v}{c}\\[0.5mm] \label{eqY} && B_1 v_1 + B_2 v_2 + B_n v_n + c \, {\overline{B}} \ \frac{\gamma -1}{\gamma} = 0 \\[0.5mm] \label{eqforcenormale} && v_1 \frac{{\rm d} B_1}{{\rm d}v} + v_2 \frac{{\rm d} B_2}{{\rm d}v} + {\overline{B}} \ \frac{v \, \gamma^2}{c} = 0. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq145.png) The initial conditions that apply when v = 0 are v1 = v2 = vn = B1 = 0 , B2 = B0sinθ. This again assumes that the perturbation forms a finite wave train. Equations (66) − (68) can then be straightforwardly integrated, giving B1, B2, and vn in terms of v1, v2, and γ(v). These expressions of B1 and B2 are then inserted into Eqs. (69) − (70). The former gives v2 in terms of
The initial conditions that apply when v = 0 are v1 = v2 = vn = B1 = 0 , B2 = B0sinθ. This again assumes that the perturbation forms a finite wave train. Equations (66) − (68) can then be straightforwardly integrated, giving B1, B2, and vn in terms of v1, v2, and γ(v). These expressions of B1 and B2 are then inserted into Eqs. (69) − (70). The former gives v2 in terms of 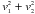 and γ and the latter then becomes a differential equation for
and γ and the latter then becomes a differential equation for 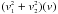 that can be integrated. From this solution, v2 and
that can be integrated. From this solution, v2 and 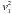 can be expressed in terms of γ. This gives
can be expressed in terms of γ. This gives ![\begin{eqnarray} \label{B1v1NL} && B_1 = -\, {\overline {B}} \, \gamma \, \frac{v_1}{c} \\[0.5mm] \label{B2v2NL}&& B_2 = \gamma \, \left(B_0 \sin\theta - {\overline {B}} \, \frac{v_2}{c}\right) \\[0.5mm] &&v_n = c\, \frac{B_0 \cos \theta}{ {\overline{B}}} \, \left(\frac{\gamma - 1}{\gamma}\right) \label{v_nNL} \\[0.5mm] \label{v2solo}&& v_2 = c \ \frac{B_0^2 \sin^2 \theta + \mu_0 \rho_0 c^2}{ B_0\, {\overline{B}} \, \sin \theta } \ \left(\frac{\gamma -1}{\gamma}\right) \\[0.5mm] &&v_1^2 = c^2 \, \frac{(\gamma -1) }{\gamma^2} \, \frac{1}{{\overline{B}}^2 B_0^2 \sin^2 \theta} \cdots \nonumber \\[0.5mm] \label{v1carresolo} &&\quad \cdots \left[ 2\, B_0^2 \, {\overline{B}}^2 \!\sin^2\! \theta - (\gamma -1) \left({\overline{B}}^2 - B_0^2\right) \left({\overline{B}}^2 - B_0^2 \cos^2\! \theta\right) \right]\!. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq158.png) In the linear approximation, vn, v2, and B2 − B0sinθ are negligible, while v1 = ± v. In the non-linear relativistic regime, the ratio v1/B1 is smaller by a factor γ than in the linear regime. Velocity components in the en and e2 directions are caused by non-linear effects and scale similarly with γ. In the limit B2 ≫ μ0ρ0c2, these two components of the velocity add up vectorially such that the sum is almost parallel to the unperturbed magnetic field.
In the linear approximation, vn, v2, and B2 − B0sinθ are negligible, while v1 = ± v. In the non-linear relativistic regime, the ratio v1/B1 is smaller by a factor γ than in the linear regime. Velocity components in the en and e2 directions are caused by non-linear effects and scale similarly with γ. In the limit B2 ≫ μ0ρ0c2, these two components of the velocity add up vectorially such that the sum is almost parallel to the unperturbed magnetic field.
In the classical limit, Eqs. (74) and (75) become approximately ![\begin{eqnarray} &&v_{\scriptscriptstyle{2}} = s v^{\scriptscriptstyle{2}}/\left(2 \sin \theta c_{\scriptscriptstyle{A0}}\right) \\[0.5mm] &&v_{\scriptscriptstyle{1}}^{\scriptscriptstyle{2}} = v^{\scriptscriptstyle{2}} \left(1 - v^{\scriptscriptstyle{2}}/ \left(4 \sin^2\theta c_{\scriptscriptstyle{A0}}^{\scriptscriptstyle{2}}\right)\right)\!. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq165.png) In the linear regime, when v is much smaller than vMV = 2sinθ cA0, the polarization of the wave is in the e1 direction. However, when the modulus v of the velocity builds up, the polarization rotates progressively toward the e2 direction. This transfer of polarization only becomes complete when v reaches the limit velocity vMV. Otherwise, the polarization change reverses when v starts diminishing. Since in this non-relativistic regime both Bn and B are conserved, the non-linear wave exhibits arc-polarization (Barnes & Hollweg 1974; Sonnerup et al. 2010).
In the linear regime, when v is much smaller than vMV = 2sinθ cA0, the polarization of the wave is in the e1 direction. However, when the modulus v of the velocity builds up, the polarization rotates progressively toward the e2 direction. This transfer of polarization only becomes complete when v reaches the limit velocity vMV. Otherwise, the polarization change reverses when v starts diminishing. Since in this non-relativistic regime both Bn and B are conserved, the non-linear wave exhibits arc-polarization (Barnes & Hollweg 1974; Sonnerup et al. 2010).
9. Constraints on the fluid’s Lorentz factor
Equation (62) is most simply expressed in the proper frame of the unperturbed fluid, ℛr0, where Yr0 = 0, γr0 = 1, and Br0 = B0. It becomes in this frame 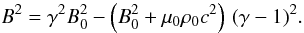 (78)To each value of B corresponds one value of γ, which is the largest root of Eq. (78).
(78)To each value of B corresponds one value of γ, which is the largest root of Eq. (78).
As mentioned in Sect. 7, the normal component Bn of the magnetic field is constant over space and time. In the frame ℛr0 its value is B0cosθ, where θ is the angle between ∇u and B0. Thus, the square of the field modulus remains bounded from below by 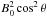 . Considering Eq. (78), this implies that the Lorentz factor γ should, in that frame, remain less than some upper limit γMB, namely
. Considering Eq. (78), this implies that the Lorentz factor γ should, in that frame, remain less than some upper limit γMB, namely 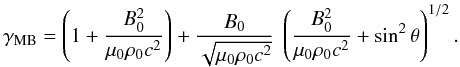 (79)For ultrarelativistic Alfvén waves
(79)For ultrarelativistic Alfvén waves 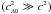 , this is a large limit, equal to
, this is a large limit, equal to 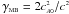 . For classical waves
. For classical waves 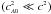 and a large enough angle, such that
and a large enough angle, such that 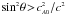 , this corresponds to a large maximum speed, which is approximately equal to vMB ≈ (2sinθ c cA0)1/2. For a very small angle θ, such that
, this corresponds to a large maximum speed, which is approximately equal to vMB ≈ (2sinθ c cA0)1/2. For a very small angle θ, such that 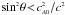 , the modulus of the fluid velocity is constrained to remain bounded by vMB ≈ 2cA0.
, the modulus of the fluid velocity is constrained to remain bounded by vMB ≈ 2cA0.
The solution is also constrained by the condition that 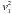 , given by Eq. (75), be positive. This is so provided that γ does not exceed a limit γMV given by
, given by Eq. (75), be positive. This is so provided that γ does not exceed a limit γMV given by 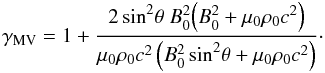 (80)In the regime when
(80)In the regime when 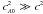 , and when sin2θ is not too small, γMV is approximately
, and when sin2θ is not too small, γMV is approximately 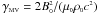 , which coincides with the limit γMB imposed by the fact that the modulus of the field should remain larger than B0sinθ. In the opposite classical regime, the constraint in Eq. (80) limits the fluid velocity to vMV = 2cA0sinθ.
, which coincides with the limit γMB imposed by the fact that the modulus of the field should remain larger than B0sinθ. In the opposite classical regime, the constraint in Eq. (80) limits the fluid velocity to vMV = 2cA0sinθ.
In the classical regime, the constraint v < vMV is more stringent than the constraint v < vMB and in the small θ limit it becomes very tight, since the condition v < 2cA0sinθ implies that v must effectively vanish. This can be readily understood by noting that in this regime B = B0, while Bn = B0cosθ is conserved. For vanishing θ, this prevents any magnetic perturbation from developing, since it implies that the components B1 and B2 should vanish. We note that this constraint specifically applies to wave trains that are of finite extent in the propagation direction of the characteristics. Infinite wave trains would not leave the fluid anywhere in its unperturbed state. As a result, different integration constants from those we used to derive the solution in this section would be involved, resulting in different constraints on both the velocity and Lorentz factor.
10. Characteristics
We now consider the propagation properties of these perturbations. Associating Eq. (55) and the explicit expression (A.5) of the ratio q, the master variable u(r,t) is found to satisfy the advection equation 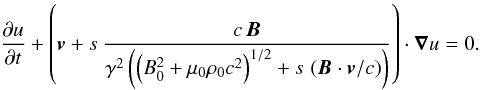 (81)Thus, u propagates at the characteristic’s speed
(81)Thus, u propagates at the characteristic’s speed 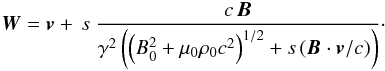 (82)The sign s characterizes the sense of the propagation of the perturbations along the field. In the instantaneous proper frame of some fluid element, the velocity of caracteristics reduces to
(82)The sign s characterizes the sense of the propagation of the perturbations along the field. In the instantaneous proper frame of some fluid element, the velocity of caracteristics reduces to 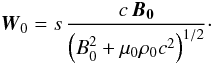 (83)The field B0 is the proper instantaneous perturbed magnetic field, which has the same modulus as the proper unperturbed field, but may have a different direction. The linear propagation velocity vA0 of relativistic Alfvén waves within a field B0 in a plasma of proper mass density ρ0 is given by Eq. (10). Its modulus is the same as that of the non-linear propagation velocity W0 given by Eq. (83). It can be checked that the velocity of characteristics in Eq. (82) can be obtained from the velocity (83) by Lorentz transforming this velocity and the magnetic field from the instantaneous rest frame ℛ0 to the actual reference frame ℛ.
(83)The field B0 is the proper instantaneous perturbed magnetic field, which has the same modulus as the proper unperturbed field, but may have a different direction. The linear propagation velocity vA0 of relativistic Alfvén waves within a field B0 in a plasma of proper mass density ρ0 is given by Eq. (10). Its modulus is the same as that of the non-linear propagation velocity W0 given by Eq. (83). It can be checked that the velocity of characteristics in Eq. (82) can be obtained from the velocity (83) by Lorentz transforming this velocity and the magnetic field from the instantaneous rest frame ℛ0 to the actual reference frame ℛ.
In the particular case of non-relativistic Alfvén waves, Eqs. (56) and (A.5) simplify in that only the second term subsists in the square root parenthesis because the classical Alfvén speed (9) is in this case meant to be much less than the speed of light. Under non-relativistic conditions, the square root term in Eq. (A.5) then reduces to c(μ0ρ0)1/2, while the ratio of the first term to this term is on the order of cA0v/c2, which is negligible in the Galilean approximation because both v and cA0 are meant to be much less than c. In contrast, (B·v)/c remains in general in the relation Eq. (A.5) when applied to relativistic Alfvén waves and depends on the master variable u. Under classical conditions, the velocity of characteristics reduces to 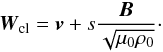 (84)It is known that in a non-relativistic situation the right-hand-side of Eq. (84) is a first integral of the motion, which in the unperturbed fluid rest-frame is aligned with the unperturbed magnetic field (Neubauer 1980). This results in the velocity of characteristics being independent of the amplitude of the perturbation and parallel to the unperturbed magnetic field. At this point, we do not know yet whether a similar first integral exists for relativistic Alfvén waves. This is the subject of Sect. 11. In the ultrarelativistic limit
(84)It is known that in a non-relativistic situation the right-hand-side of Eq. (84) is a first integral of the motion, which in the unperturbed fluid rest-frame is aligned with the unperturbed magnetic field (Neubauer 1980). This results in the velocity of characteristics being independent of the amplitude of the perturbation and parallel to the unperturbed magnetic field. At this point, we do not know yet whether a similar first integral exists for relativistic Alfvén waves. This is the subject of Sect. 11. In the ultrarelativistic limit  , the modulus of the velocity of characteristics in the instantaneous fluid rest-frame approaches the velocity of light.
, the modulus of the velocity of characteristics in the instantaneous fluid rest-frame approaches the velocity of light.
11. A relativistic first integral
The solution in Eq. (61) for Y may be used in Eq. (82) to obtain a revised expression for the velocity of the characteristics 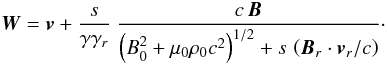 (85)We now show that the velocity W is a first integral of the Alfvénic motion, analogous to Neubauer’s non-relativistic first integral (Neubauer 1980). We consider a change in the state of the motion of a fluid element, in which the velocity changes by dv and the magnetic field by dB. The corresponding change in the velocity W is
(85)We now show that the velocity W is a first integral of the Alfvénic motion, analogous to Neubauer’s non-relativistic first integral (Neubauer 1980). We consider a change in the state of the motion of a fluid element, in which the velocity changes by dv and the magnetic field by dB. The corresponding change in the velocity W is 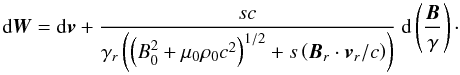 (86)There is no component of B perpendicular to itself. The perpendicular part of dW then is
(86)There is no component of B perpendicular to itself. The perpendicular part of dW then is 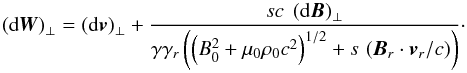 (87)The relations in Eqs. (55) and (56), combined with the alternative expression of the velocity of the characteristic’s in Eq. (85), imply that (dW) ⊥ = 0. The field-aligned component of dW is proportional to
(87)The relations in Eqs. (55) and (56), combined with the alternative expression of the velocity of the characteristic’s in Eq. (85), imply that (dW) ⊥ = 0. The field-aligned component of dW is proportional to 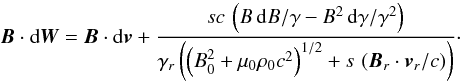 (88)Equation (50) gives an expression for B·dv and B2 is expressed by Eq. (54) in terms of γ and Y, the latter being itself a function of γ given by Eq. (61). Using these relations in Eq. (88), a short calculation shows that B·dW vanishes.
(88)Equation (50) gives an expression for B·dv and B2 is expressed by Eq. (54) in terms of γ and Y, the latter being itself a function of γ given by Eq. (61). Using these relations in Eq. (88), a short calculation shows that B·dW vanishes.
Therefore, W appears to be independent of the state of motion of the fluid element, or equivalently independent of the master variable u. It is a first integral, that is constant everywhere and at all times. Since we assumed that any fluid element has been, or will be at some time, in the undisturbed state, the value of W, which is the velocity of Alfvénic characteristics (85), can be calculated from this particular state. This gives 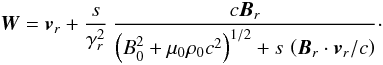 (89)The proper field modulus B0 is related to the unperturbed field Br observed in the chosen reference frame ℛ by the relation in Eq. (54), expressed for unperturbed conditions. In addition, ρ0 is the proper mass density, not the apparent unperturbed density in ℛ, which is γr ρ0. In the unperturbed fluid frame ℛr0, where vr = 0 and Br = B0r, the velocity of the characteristics (89) is simply
(89)The proper field modulus B0 is related to the unperturbed field Br observed in the chosen reference frame ℛ by the relation in Eq. (54), expressed for unperturbed conditions. In addition, ρ0 is the proper mass density, not the apparent unperturbed density in ℛ, which is γr ρ0. In the unperturbed fluid frame ℛr0, where vr = 0 and Br = B0r, the velocity of the characteristics (89) is simply 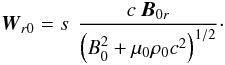 (90)The velocity of the characteristics in ℛr0 is then the linear propagation speed (83) of relativistic Alfvén waves. The relativistic expression in Eq. (85) of the first integral agrees with the linear result of Mottez & Heyvaerts (2011a). In the non-relativistic limit, the denominator in Eq. (89) reduces to c(μ0ρ0)1/2 because, as noted above, its other term is of relative order cA0v/c2. We then recover Neubauer’s classical first integral
(90)The velocity of the characteristics in ℛr0 is then the linear propagation speed (83) of relativistic Alfvén waves. The relativistic expression in Eq. (85) of the first integral agrees with the linear result of Mottez & Heyvaerts (2011a). In the non-relativistic limit, the denominator in Eq. (89) reduces to c(μ0ρ0)1/2 because, as noted above, its other term is of relative order cA0v/c2. We then recover Neubauer’s classical first integral 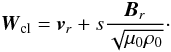 (91)
(91)
12. Conclusion
As in the case of classical propagation, we have found that the velocity of the characteristics of non-linear Alfvénic perturbations follows, in the unperturbed fluid frame, the unperturbed magnetic field and is independent of the amplitude of the perturbation. Thus, as in the non-relativistic regime, non-linear Alfvénic signals are channeled by the unperturbed magnetic field in this frame and do not spread in space. Since the velocity of the characteristics is independent of the amplitude of the perturbation, the Alfvénic perturbations neither steepen nor break. The relations among the physical variables in an Alfvénic perturbation, as observed from the unperturbed fluid frame, have been derived in Sect. 8 when the normal to the phase planes is at a sufficient angle from the unperturbed magnetic field. As discussed in Sects. 7 and 8 the Lorentz factor of the fluid in non-linear Alfvénic perturbations forming a finite wave train is limited to a value that depends on the ratio of the proper unperturbed magnetic to rest mass energy densities.
Acknowledgments
We thank Dr Silvano Bonazzola for useful discussions.
References
- Barnes, A., & Hollweg, J. V. J. 1974, Geophys. Res., 79, 2302 [Google Scholar]
- Boynton, G. C., & Torkelsson, U. 1996, A&A, 308, 299 [NASA ADS] [Google Scholar]
- Birkinshaw, M. 1996, Ap&SS, 242, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Broer, L. J. F., & Sarluy, P. A. H. 1964, Physica, 30, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Dado, S., Dar, A., & de Rújula, A. 2002, A&A, 388, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daigne, F., & Mochkovitch, R. 1998, MNRAS, 296, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, L., Velli, M., & Londrillo, P. 2001, A&A, 367, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Folini, D., Heyvaerts, J., & Walder, R. 2004, A&A, 414, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukuda, N., & Hanawa, T. 1999, AJ, 517, 226 [Google Scholar]
- Heyvaerts, J. 2003, in Accretion disks, jets and high energy phenomena in astrophysics, Les Houches school series, session LXXVIII, ed. V. Beskin, G. Henri, F. Menard, & G. Pelletier (EDP-Science and Springer Verlag) [Google Scholar]
- Jackson, J. D. 1975, Classical Electrodynamics, 2nd edn. (John Wiley & sons) [Google Scholar]
- Jeffrey, A. 1976, Quasilinear hyperbolic systems and waves, Res. Notes Math. (London: Pitman) [Google Scholar]
- Jeffrey, A., & Taniuti, T. 1964, Non-linear wave propagation with applications to physics and magnetohydrodynamics, Math. Sci. Eng. Ser. (Academic Press), 9 [Google Scholar]
- Lukacevic, I. 1968, Ann. IHP Sect. A, 3, 217 [Google Scholar]
- Lyubarsky, Y. E. 2005, MNRAS, 358, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Mazur, D., & Heyl, J. 2011, MNRAS, 412, 1381 [NASA ADS] [Google Scholar]
- Medvedev, M. V. 1999, Phys. Plasmas, 6, 2191 [NASA ADS] [CrossRef] [Google Scholar]
- Mottez, F., & Heyvaerts, J. 2011, A&A, 532, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mottez, F., & Heyvaerts, J. 2011, A&A, 532, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neubauer, F. M. 1980, JGR, 85, 1171 [Google Scholar]
- Pham Mau Quan 1965, Ann. IHP Sect. A, 2, 151 [Google Scholar]
- Sonnerup, B. U. Ö., Haaland, S. E., & Paschmann, G. 2010, Ann. Geophys., 28, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Zel’dovitch, Y. B., & Raizer, Y. P. 1966, Physics of Shock waves and High-Temperature Phenomena (Academic Press) [Google Scholar]
Appendix A: Compatibility relations
We first substract 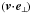 times the Eq. (38) from Eq. (37) multiplied by c2. Accounting for A = 0, this changes Eq. (37) into
times the Eq. (38) from Eq. (37) multiplied by c2. Accounting for A = 0, this changes Eq. (37) into ![\appendix \setcounter{section}{1} \begin{eqnarray} &&T'_4 \, {\rm d}_t u - K'_4 \, \left({\vec{e}}_B \cdot {\boldsymbol{\nabla}} u\right) = 0 \label{mouvSymbolperpprim}\\[0.5mm] &&T'_4 = 2\, \left(\mu_0 \rho_0 c^2 \gamma^2 + B^2 \right) \, {e}_\perp^2 \\[0.5mm] &&K'_4 = 2\, \left(Bc^2/\gamma^2\right)\left({\vec{e}}_{\perp} \cdot {\rm d}_u {\vec{B}}\right) + 4B\ \left({\vec{B}} \cdot {\vec{v}}\right) \ {e}_\perp^2. \end{eqnarray}](/articles/aa/full_html/2012/06/aa18630-11/aa18630-11-eq230.png) Equation (A.1) provides us with another expression of q, which should be compatible with either Eqs. (33), (36), or (55). Noting that
Equation (A.1) provides us with another expression of q, which should be compatible with either Eqs. (33), (36), or (55). Noting that 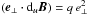 and using (55), Eq. (A.1) can be changed to
and using (55), Eq. (A.1) can be changed to 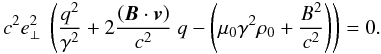 (A.4)This is a quadratic equation for q, the solutions of which, accounting for Eq. (54), can be written, with s = ± 1, as
(A.4)This is a quadratic equation for q, the solutions of which, accounting for Eq. (54), can be written, with s = ± 1, as 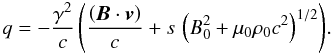 (A.5)This expression of q should be compatible with Eq. (55), providing us with our first compatibility relation in Eq. (56). The second compatibility condition is obtained from Eqs. (38) and (A.1). Equation (38) can be written in terms of q as
(A.5)This expression of q should be compatible with Eq. (55), providing us with our first compatibility relation in Eq. (56). The second compatibility condition is obtained from Eqs. (38) and (A.1). Equation (38) can be written in terms of q as 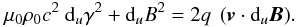 (A.6)The expression in Eq. (A.5) for q, which results from Eq. (A.1), is introduced in Eq. (A.6), and the field-aligned velocity component is expressed in terms of the variable Y defined by Eq. (57). Using Eq. (50), v·duB is written as
(A.6)The expression in Eq. (A.5) for q, which results from Eq. (A.1), is introduced in Eq. (A.6), and the field-aligned velocity component is expressed in terms of the variable Y defined by Eq. (57). Using Eq. (50), v·duB is written as 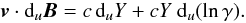 (A.7)We then take account of Eq. (52). Equation (A.6) eventually transforms into Eq. (58), which ensures that Eqs. (38) and (A.1) are compatible. The third compatibility relation stems from Eq. (34), which can be written in terms of q as
(A.7)We then take account of Eq. (52). Equation (A.6) eventually transforms into Eq. (58), which ensures that Eqs. (38) and (A.1) are compatible. The third compatibility relation stems from Eq. (34), which can be written in terms of q as 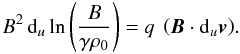 (A.8)The scalar product B·duv is obtained from Eq. (50) and use is again made of Eq. (52). The ratio q that appears in Eq. (A.8) is expressed in the form of Eq. (A.5). Equation (A.8) then transforms into
(A.8)The scalar product B·duv is obtained from Eq. (50) and use is again made of Eq. (52). The ratio q that appears in Eq. (A.8) is expressed in the form of Eq. (A.5). Equation (A.8) then transforms into 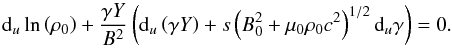 (A.9)Equation (58) however shows that the parenthesis in Eq. (A.9) vanishes, which establishes that the proper mass density is constant, and of course equal to its unperturbed value ρ0r (Eq. (59)). This result was expected because the mass density is known to be constant in non-relativistic Alfvénic motions. It would have been possible to establish the constancy of the proper mass density by choosing our reference frame ℛ to coincide with the proper rest frame ℛ0 of some fluid element, in which the motion is, for a while, classical. The constancy of the proper mass density expresses the compatibility between Eqs. (34) and either Eq. (38) or (A.6).
(A.9)Equation (58) however shows that the parenthesis in Eq. (A.9) vanishes, which establishes that the proper mass density is constant, and of course equal to its unperturbed value ρ0r (Eq. (59)). This result was expected because the mass density is known to be constant in non-relativistic Alfvénic motions. It would have been possible to establish the constancy of the proper mass density by choosing our reference frame ℛ to coincide with the proper rest frame ℛ0 of some fluid element, in which the motion is, for a while, classical. The constancy of the proper mass density expresses the compatibility between Eqs. (34) and either Eq. (38) or (A.6).
Appendix B: Simple MHD waves are planar
Equation (63) has interesting consequences for the geometry of the perturbation. It shows that ∇u is perpendicular to duB. Since B is a function of u, so also is duB. This vector is therefore constant over the entire surface of constant u, which is a phase surface. According to Eq. (63), it is in the tangent plane to this surface. We now consider Ampere’s Eq. (5). Using Eq. (20), it can be written under the ansatz (1) as 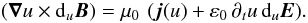 (B.1)The time-derivative of u is related to its space-derivatives by the advection Eq. (81), which indicates that u propagates at the velocity W. According to Eq. (82), this velocity is a vectorial function of u because it consists of vectors depending only on u. We establish in Sect. 11 that W is really a constant vector, but it is enough for our purposes to recognize that it may depend only on u. Substituting (W·∇u) for − ∂tu in Eq. (B.1), then dotting it by ∇u, it is found that
(B.1)The time-derivative of u is related to its space-derivatives by the advection Eq. (81), which indicates that u propagates at the velocity W. According to Eq. (82), this velocity is a vectorial function of u because it consists of vectors depending only on u. We establish in Sect. 11 that W is really a constant vector, but it is enough for our purposes to recognize that it may depend only on u. Substituting (W·∇u) for − ∂tu in Eq. (B.1), then dotting it by ∇u, it is found that 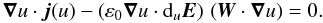 (B.2)Poisson’s Eq. (7) and Eq. (17) imply that ε0∇u·duE is the charge density ρe(u) so that Eq. (B.2) becomes
(B.2)Poisson’s Eq. (7) and Eq. (17) imply that ε0∇u·duE is the charge density ρe(u) so that Eq. (B.2) becomes 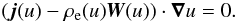 (B.3)Thus, ∇u is perpendicular to the vector j − ρeW, which depends only on u and is then constant over all the phase surface. This vector generally differs from duB, which also depends only on u and to which ∇u is also perpendicular (Eq. (63)). The normal to a phase surface is perpendicular to these two vectors, both of them being constant over the entire surface. The normal vector
(B.3)Thus, ∇u is perpendicular to the vector j − ρeW, which depends only on u and is then constant over all the phase surface. This vector generally differs from duB, which also depends only on u and to which ∇u is also perpendicular (Eq. (63)). The normal to a phase surface is perpendicular to these two vectors, both of them being constant over the entire surface. The normal vector
therefore has a unique direction over any phase surface that must then be a plane. Different phase planes must be parallel to each other since they cannot intersect if they refer to different values of the master variable u. This shows that simple Alfvénic waves must have a planar geometry.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


