| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117151 | |
| Published online | 14 June 2012 | |
Rotational splittings for slow to moderate rotators
Latitudinal dependence or higher order effects in Ω?
LESIA, UMR8109, Université Pierre et Marie Curie, Université Denis Diderot, Observatoire de Paris, 92195 Meudon Cedex, France
e-mail: rhita-maria.ouazzani@obspm.fr
Received: 28 April 2011
Accepted: 14 March 2012
Context. The unprecedented photometric quality reached by the CoRoT and Kepler space missions opens new prospects for studying stellar rotation. Information about the rotation rate is contained on the one hand in the low frequency part of the power spectra, where signatures of nonuniform surface rotation are expected, and on the other hand in the frequency splittings induced by the internal rotation rate.
Aims. We wish to figure out whether the differences between the seismic rotation period determined by a mean rotational splitting, and the rotation period measured from the low frequency peak in the Fourier spectrum – observed for some of CoRoT’s targets – can provide constraints on the rotation profile.
Methods. For uniform moderate rotators,perturbative corrections to second and third order in terms of the rotation angular velocity Ω, must not be neglected. These effects, in particular, may mimic differential rotation. We apply our perturbation method to evaluate mode frequencies that are accurate up to Ω3 for uniform rotation. The effects of latitudinal dependence are calculated in the linear approximation. Numerical results were obtained for selected models of the upper and lower parts of the main sequence. For the latitudinal dependence, we adopt two types of rotation profile: one with rotation uniform in depth, and one with a solar-like tachocline.
Results. Deviations from the first-order splitting for a uniformly rotating star can be due to both cubic-order effects of rotation and latitudinal differential rotation. In models of β Cephei pulsators, which represent upper main sequence stars, third order effects become comparable to that of a horizontal shear similar to the solar one at rotation rates well below the breakup values. These nonlinear effects are strongly mode-dependent. We show how a clean signature of the latitudinal shear may be extracted. Our models of two CoRoT target HD 181906 and HD 181420, which are solar-like pulsators, represent lower main sequence objects. These are slow rotators and nonlinear effects in splittings are accordingly small. We use data for one low frequency peak and one splitting of a dipolar mode to constrain the rotation profile in HD 181420 and HD 181906.
Conclusions. The relative influences of the two effects strongly depend on the type of oscillation modes excited in the star and the magnitude of the rotation rate. Given the mean rotational splitting and the frequency of a spot signature, it is possible to distinguish between the two hypotheses. In the case of differential rotation in latitude, we propose a method to determine the type of rotation profile and a range of values for the shear.
Key words: asteroseismology / stars: oscillations / stars: rotation
© ESO, 2012
1. Introduction
The CoRoT and Kepler space-borne missions with their uninterrupted observations spanning a long time interval promise a wealth of data suitable for studying stellar rotation. Information about internal rotation is contained in the characteristic spacings (known as the rotational splittings), which appear in the power spectra of light curves. Mean values of the rotational splitting have already been determined for a number of stars, namely HD 181420 (Barban et al. 2009), HD 49933 (Benomar et al. 2009), V1449 Aql (Belkacem et al. 2009), and HD 181906 (García et al. 2009), observed by CoRoT. These values yield some information about the average rotation rates sampled by modes detected in these objects. Since all the data concern p-modes, the mean values mostly reflect the rotation rate in the outer layers. To probe deeper layers, we need splittings for gravity modes. In three Fourier spectra analyzed so far (HD 181420, HD 181906 and V1449 Aql), low frequency peaks were found but were attributed to the effects of spots on the rotating stellar surfaces (for a complete review on spot modeling, see Collier Cameron 2002; Mosser et al. 2009). Rotation periods deduced this way were found to be different from those determined from the splittings. This is not surprising. The spots only give access to the surface rotation rate at the latitude of their location, whereas the splittings yield a mode-dependent mean value of the interior profile.
The linear relation between the splittings and the rotation rate, Ω, follows from the first-order perturbative treatment of the Coriolis acceleration (Ledoux 1945). At moderate rotation rates, the perturbative formalism may still be applicable but we have to go beyond the first order (Reese et al. 2006; Ouazzani et al. 2009; Suárez et al. 2010; Burke et al. 2011). Saio (1981), Gough & Thompson (1990), and Dziembowski & Goode (1992, hereafter DG92) derived oscillation frequencies including second order corrections in Ω. Such corrections arise from the higher order effects of the Coriolis acceleration and the lowest order effects of the centrifugal acceleration, which causes a distortion of the stellar structure. The oscillation frequencies no longer depend on Ω in a linear way but the linear rotational splittings may still be recovered from the frequency differences between prograde and retrograde modes of the same degree and order. This simple property is lost when rotation couples modes with frequencies close in value. The formalism must then be modified (DG92, Soufi et al. 1998) and the recovery is more difficult. The cubic-order effects in Ω even complicate this recovery. The resulting difference between prograde and retrograde modes becomes dependent on the mode’s azimuthal order, m, in such a way that it may be misinterpreted as the effects of a latitudinal dependence of the rotation rate.
The question arises of whether in the presence of significant nonlinear effects it is still possible to extract the values of linear splittings, which provide integral constraints on differential rotation in the interior. The next question that we ask in this paper is what may be learnt by combining these constraints with data on low frequency peaks that are attributed to spots and yield information on the surface rotation rate. We expect that the answers depend on the type of pulsator, and the characteristics of its observed modes. Here, we specifically consider two very different types of main sequence objects, β Cephei, and solar-like pulsators. In the first case, we study a massive star whose low order p- and g-modes are unstable, and in the second case two low-mass stars whose high order p-modes are damped but stochastically driven.
The paper is organized as follows. Section 2 gives the basic theoretical framework for this study. In Sect. 3, we focus on the effects of cubic order and near degeneracy contributions to pulsation frequencies and present numerical results for a selected model of a β Cephei star. Explicit expressions for the rotational splitting in the case of latitude dependent rotation profile are given in Sect. 4. Departures from a linear dependence on m are then compared with those connected to the nonlinear effects in Ω. Prospects for disentangling these two effects are discussed in Sect. 5, using the case of a β Cephei star as an example. Section 6 is devoted to two CoRoT targets, the solar-type stars HD 181906 and HD 181420, for which we combine the splitting with the low frequency peak and make some inference about the rotation profiles. Section 7 is dedicated to our conclusions.
2. Perturbational treatment of uniform rotation: effects on pulsation frequencies
In the presence of rotation, both centrifugal and Coriolis accelerations come into play. The centrifugal force affects the structure of the star and distorts its shape. The resonant cavity changes and with it the oscillation frequencies. The Coriolis force enters the equation of motion and affects the motion of the waves, hence the frequencies of normal modes. As rotation breaks the spherical symmetry, it lifts the frequency degeneracy, introducing a dependence on the azimuthal order, m. Without rotation, mode frequencies depend only on the radial order, n, and the angular degree, ℓ, and are 2ℓ + 1-fold degenerated.
To first order in the rotation rate, Ω, the normal mode frequencies in the inertial frame are given by ωn,ℓ,m = ωn,ℓ,0 + m Ω βn,ℓ. The explicit form of the last coefficient is provided in Eq. (B.5). Here, we only note that Cn,ℓ = 1 − βn,ℓ is known as the Ledoux constant (Ledoux 1945).
Characteristic spacings appear in the spectrum, such as the rotational splitting that we define here as 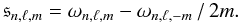 (1)This provides the basis for determining the rotation rate. From now on, we drop the subscripts (n,ℓ,m) for ω and the splitting, unless there is an ambiguity. We also use σ = ω/Ωk (where
(1)This provides the basis for determining the rotation rate. From now on, we drop the subscripts (n,ℓ,m) for ω and the splitting, unless there is an ambiguity. We also use σ = ω/Ωk (where 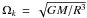 is the break-up frequency) instead of ω.
is the break-up frequency) instead of ω.
2.1. Equilibrium configuration
We consider here the case of uniform rotation. The stationary equation of motion in an inertial frame of reference is 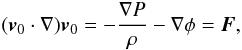 (2)where in the left hand side v0 = Ω ∧ r = Ω0 r sinθ eφ in the spherical basis is the velocity field due to rotation at the angular velocity Ω0, θ being the colatitude (see e.g. Unno et al. 1989) and P, ρ, and φ are the pressure, density, and gravitational potential, respectively. For a rotating star, the left hand side corresponds to the centrifugal acceleration F = −Ω × (Ω × r), whose effect on the equilibrium structure is twofold, on the one hand, producing a spherically symmetric perturbation,which mainly modifies the gravity, and on the other, θ-dependent perturbations, which are responsible for oblateness. Hence, all the equilibrium quantities, X, are well-approximated by
(2)where in the left hand side v0 = Ω ∧ r = Ω0 r sinθ eφ in the spherical basis is the velocity field due to rotation at the angular velocity Ω0, θ being the colatitude (see e.g. Unno et al. 1989) and P, ρ, and φ are the pressure, density, and gravitational potential, respectively. For a rotating star, the left hand side corresponds to the centrifugal acceleration F = −Ω × (Ω × r), whose effect on the equilibrium structure is twofold, on the one hand, producing a spherically symmetric perturbation,which mainly modifies the gravity, and on the other, θ-dependent perturbations, which are responsible for oblateness. Hence, all the equilibrium quantities, X, are well-approximated by 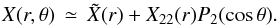 (3)The spherically symmetric part is then obtained by (see for example Kippenhahn & Weigert 1994)
(3)The spherically symmetric part is then obtained by (see for example Kippenhahn & Weigert 1994) 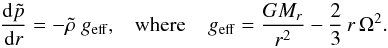 The non-spherically symmetric part is obtained by (see DG92)
The non-spherically symmetric part is obtained by (see DG92) 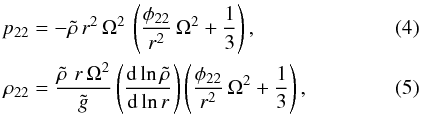 where
where 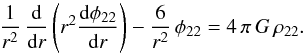 (6)The boundary conditions can be found in Soufi et al. (1998, hereafter S98).
(6)The boundary conditions can be found in Soufi et al. (1998, hereafter S98).
2.2. Oscillation frequencies up to cubic order in Ω
Using expansions of the type given in Eq. (3) for the oscillation quantities, i.e., 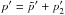 , the oscillation system is then expanded up to the cubic order. According to S98 (see also Karami 2008), the oscillation equation then becomes
, the oscillation system is then expanded up to the cubic order. According to S98 (see also Karami 2008), the oscillation equation then becomes 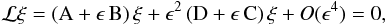 (7)ϵ being equal to Ω/Ωk, where
(7)ϵ being equal to Ω/Ωk, where 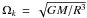 is the break-up frequency. The operator A represents the basic linear oscillation operator including the spherically symmetric perturbation caused by rotation (through geff). The operators B and D, respectively, contain the effects of the Coriolis force and the non-spherically symmetric distortion. The operator C shows that a coupling between the non-spherically symmetric distortion and the Coriolis force exists.
is the break-up frequency. The operator A represents the basic linear oscillation operator including the spherically symmetric perturbation caused by rotation (through geff). The operators B and D, respectively, contain the effects of the Coriolis force and the non-spherically symmetric distortion. The operator C shows that a coupling between the non-spherically symmetric distortion and the Coriolis force exists.
As in S98 and Karami (2008), parts of the Coriolis and centrifugal distortion effects are included in the pseudo-zeroth-order eigenvalue system. In this way, we are able to solve the eigenvalue problem up to cubic order without having to solve the successive equations for the eigenfunctions at each order. The solution yields eigenfrequencies σ0, which include parts of the frequency shifts induced by rotation. To single out the various contributions and emphasize the m-dependence, we write σ0 in the form 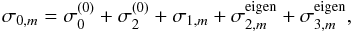 (8)where
(8)where 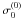 is the classical zeroth order frequency ignoring all effects of rotation,
is the classical zeroth order frequency ignoring all effects of rotation, 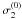 is the correction resulting from the spherically symmetric part of the centrifugal distortion, and the next three terms give the contributions of consecutive orders in Ω resulting from the Coriolis acceleration. The linear term, σ1,m = m Ω βΩk, is complete. The higher order terms only include the parts resulting from the poloidal component of ξ. The remaining contributions to frequency shifts to
is the correction resulting from the spherically symmetric part of the centrifugal distortion, and the next three terms give the contributions of consecutive orders in Ω resulting from the Coriolis acceleration. The linear term, σ1,m = m Ω βΩk, is complete. The higher order terms only include the parts resulting from the poloidal component of ξ. The remaining contributions to frequency shifts to 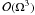 are calculated as integrals involving the eigenvectors ξ0 (see S98). To this accuracy, the complete expression for eigenfrequencies in uniformly rotating star is given by
are calculated as integrals involving the eigenvectors ξ0 (see S98). To this accuracy, the complete expression for eigenfrequencies in uniformly rotating star is given by 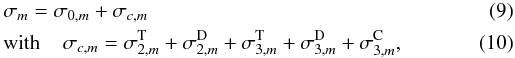 where the exponent T denotes the contributions from the Coriolis force acting on the toroidal component of ξ, the exponent D those arising from the non-spherically symmetric distortion, and C those resulting from the coupling of the two effects.
where the exponent T denotes the contributions from the Coriolis force acting on the toroidal component of ξ, the exponent D those arising from the non-spherically symmetric distortion, and C those resulting from the coupling of the two effects.
2.3. Near degeneracy
The standard perturbation approach is invalid if rotation couples modes with close frequencies. The treatment of these cases requires modification, which in the context of stellar pulsations was first used by Chandrasekhar & Lebovitz (1962) and developed later by DG92. In the case of latitude-independent rotation profiles, only modes with the same m and ℓs of the same parity are coupled. In the present work, we study the coupling of two resonant modes denoted kj for (nj,ℓj,m), j = 1,2 with frequencies σ1 ≥ σ2. For the range of stellar models we are interested in, our calculations reveal that near degeneracy occurs for quite a large number of modes.
Near degeneracy is taken into account by searching for solutions to Eq. (7) in the form 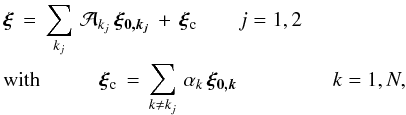 where the eigenfunction correction ξc is composed of all non-resonant modes. The standard procedure leads to a linear system of equations for
where the eigenfunction correction ξc is composed of all non-resonant modes. The standard procedure leads to a linear system of equations for 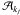 and the following condition for a non-zero solution
and the following condition for a non-zero solution 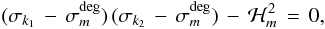 (11)where the frequencies σk1 and σk2 are given by Eq. (9). The coupling term ℋm corresponds to integrals containing second and third order contributions (see S98 for more details). The solutions of Eq. (11), denoted by σdeg, provide the desired eigenfrequencies
(11)where the frequencies σk1 and σk2 are given by Eq. (9). The coupling term ℋm corresponds to integrals containing second and third order contributions (see S98 for more details). The solutions of Eq. (11), denoted by σdeg, provide the desired eigenfrequencies 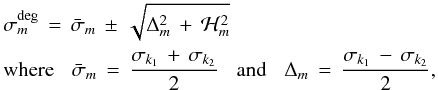 (12)where the sign + (resp.-) corresponds to mode k1 (resp. k2). Note that if | ℋm | ≪ | Δm | , the effects of coupling are small and mode frequencies are approximately described by Eq. (9).
(12)where the sign + (resp.-) corresponds to mode k1 (resp. k2). Note that if | ℋm | ≪ | Δm | , the effects of coupling are small and mode frequencies are approximately described by Eq. (9).
3. Relative magnitude of the different contributions for uniform rotators
As an example, we adopt a stellar model with a simple equilibrium structure for which uniform rotation in depth is assumed. All the results presented in this section were performed for an 8.5 M⊙ ZAMS stellar model described in Table 1 rotating at Ω ≃ 15% Ωk (vΩ = R Ω = 95 km s-1), which is representative of this type of star (Stankov & Handler 2005).
Stellar parameters of the ZAMS model (Sects. 2 and 3).
Stellar models and adiabatic oscillation frequencies are computed with the evolution code CESAM2k (Morel 1997; Morel & Lebreton 2008) and the WarM (Warsaw Meudon) oscillation code, respectively (see S98). All numerical results presented here and in the rest of this paper concern dipolar (ℓ = 1) modes.
3.1. Frequency contributions up to cubic order
 |
Fig. 1 Contributions of different approximation orders to l = 1,m = 0 mode frequencies: σ2eigen (σ3eigen) represent the implicit second (third respectively) order contribution to the eigenfrequency; σ2T and σ3T denote second and third order frequency corrections due to the Coriolis acceleration; σ2D and σ3D represent 2nd and 3rd order frequency corrections due to the centrifugal distorsion; σ3C comes from the coupling of the distorsion and Coriolis effects. The contributions are plotted as a function of the radial order n for an 8.5 M⊙ ZAMS model rotating uniformly at 15% Ωk, i.e. around 95 km s-1 (see stellar parameters in Table 1). The frequencies are scaled by |
Here we quantify the implicit contributions ( and
and 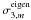 from Eq. (8)), and compare them with the corrective terms of the same orders given in Eq. (10). To extract these implicit contributions from the pseudo-zeroth-order eigenfrequencies, we make use of their symmetry properties in m. Thus, we get
from Eq. (8)), and compare them with the corrective terms of the same orders given in Eq. (10). To extract these implicit contributions from the pseudo-zeroth-order eigenfrequencies, we make use of their symmetry properties in m. Thus, we get 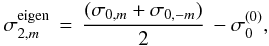 (13)and
(13)and 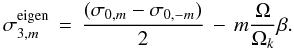 (14)Figure 1 shows all the contributions of different orders to the rotational frequency corrections for g-modes (g14 to g1) and p-modes (p1 to p16). We note the significantly different pattern for p- and g-modes. In the latter case, the second order correction due to the Coriolis acceleration dominates over the rest. It grows linearly with the radial order (in absolute value) as was already stated in Ballot et al. (2010) for polytropic models. The Coriolis effect remains dominant at the third order, whereas distortion seems to have no effect. The coupling between the Coriolis accelaration and distortion (σ3C) is negative, thereby reducing the impact of the former.
(14)Figure 1 shows all the contributions of different orders to the rotational frequency corrections for g-modes (g14 to g1) and p-modes (p1 to p16). We note the significantly different pattern for p- and g-modes. In the latter case, the second order correction due to the Coriolis acceleration dominates over the rest. It grows linearly with the radial order (in absolute value) as was already stated in Ballot et al. (2010) for polytropic models. The Coriolis effect remains dominant at the third order, whereas distortion seems to have no effect. The coupling between the Coriolis accelaration and distortion (σ3C) is negative, thereby reducing the impact of the former.
For p-modes, the dominant second-order term is 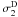 , as could be expected for modes that are mostly confined to superficial layers where the role of centrifugal acceleration is highest. In this case too, the dominant term grows linearly with the radial order, as noted in Goupil (2009) and Reese et al. (2006) for polytropic models. To third order,
, as could be expected for modes that are mostly confined to superficial layers where the role of centrifugal acceleration is highest. In this case too, the dominant term grows linearly with the radial order, as noted in Goupil (2009) and Reese et al. (2006) for polytropic models. To third order, 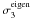 and
and 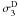 are of the same magnitude but opposite signs, canceling each other to some extent.
are of the same magnitude but opposite signs, canceling each other to some extent.
To sum up, as expected, for g-modes the most important contributions are those related to the effects of the Coriolis acceleration, whereas for p-modes we must take into account both the implicit eigenfrequency terms (related to the part of Coriolis force included in the pseudo-zeroth eigen-system) and the effects of centrifugal distortion. In Table D.3, numerical values of the different contributions are listed.
3.2. Near degeneracy corrections
Here we consider the same sequence of ℓ = 1 modes as in the previous section but we now take into account the coupling of each mode with the nearest ℓ = 3 partner. The coupled pairs must be of the same azimuthal order m. We use Eq. (12) here to calculate the frequency shift caused by such a coupling.
To compare the magnitude of this near degeneracy effect with the second and third order contributions shown in Fig. 1, we depict in Fig. 2 the frequency differences between computations with and without near degeneracy being accounted for. Figure 2 shows that near degeneracy primarily affects the p-modes (n > 0). This is not surprising as they are more sensitive to the outer regions that are more affected by distortion, a dominant factor in the coupling coefficient ℋ. Moreover, this correction is found to be of the same magnitude as the other second-order corrections (see Fig. 1) but of an opposite sign. Hence, the overall effect of the distortion is reduced. However, this is not a universal property. As we may see in Eq. (12), the coupling always causes an increase in the frequency separation between modes but the sign of the shift is mode-dependent. In any case, rotational mode coupling is an important effect, especially for p-modes. Taking it into account (as shown in Suárez et al. 2010) extends the validity domain of perturbative methods.
 |
Fig. 2 Frequency differences between degenerate σdeg and non-degenerate σno deg solutions scaled by |
Finally, we note that the sectorial components of the ℓ = 1 triplet are modified by roughly the same amount, which implies that the rotational splitting should not be strongly affected by near degeneracy (see Sect. 4.2). This is expected because in this case it enters as a third order effect.
 |
Fig. 3 Scaled contributions to the splittings due to the implicit third-order terms in the eigenfrequencies |
4. Rotational splitting for uniform rotators
The rotational splitting can be defined as Sm = (σm − σ0)/m. One also uses Sm = σm − σm − 1. In this work, we use a scaled expression of the rotational splitting given in Eq. (1) 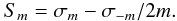 (15)These various definitions are equivalent only to first order in the rotation rate, Ω, and equal to the linear splitting
(15)These various definitions are equivalent only to first order in the rotation rate, Ω, and equal to the linear splitting 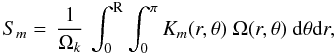 (16)where the analytical expression for the kernels Km is given in Goupil (2011) and references therein. At higher orders in terms of Ω, the two first definitions are contaminated by the effect of asphericity, which introduces an antisymmetric component in the frequency as a function of m. We choose to remove this second order contribution using the splitting expressed in Eq. (15).
(16)where the analytical expression for the kernels Km is given in Goupil (2011) and references therein. At higher orders in terms of Ω, the two first definitions are contaminated by the effect of asphericity, which introduces an antisymmetric component in the frequency as a function of m. We choose to remove this second order contribution using the splitting expressed in Eq. (15).
4.1. Cubic-order effects on the splitting
Assuming a uniform rotation Ω = Ω0, the splitting including the frequency corrections to cubic order is given by: 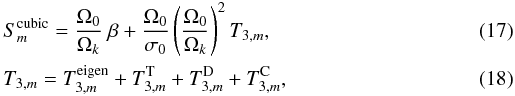 where σ0 = ω0/Ωk is the normalized frequency of the corresponding axisymmetric mode, Ω0 is the uniform rotation rate, and β is the integral of the kernel Km over the star (see Appendix B, Eq. (B.5)).
where σ0 = ω0/Ωk is the normalized frequency of the corresponding axisymmetric mode, Ω0 is the uniform rotation rate, and β is the integral of the kernel Km over the star (see Appendix B, Eq. (B.5)).
The term T3,m incorporates the implicit third-order contribution as well as the effects of the Coriolis acceleration, the distorsion, and the coupling of the two. From now on, we define the departure from a linear splitting as follows 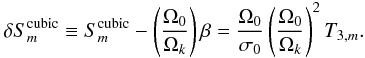 (19)
(19)
4.2. Near degeneracy correction
According to the formalism explained in Sect. 2.3, if we consider the coupling of the ℓ = 1 and ℓ = 3 modes, we define the degenerate frequency of ℓ = 1 modes by 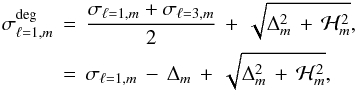 (20)where σℓ = 1,m and σℓ = 3,m are non-degenerate frequencies given by Eq. (9), and Δm is defined in Eq. (12). The splitting accounting for near degeneracy is then given by
(20)where σℓ = 1,m and σℓ = 3,m are non-degenerate frequencies given by Eq. (9), and Δm is defined in Eq. (12). The splitting accounting for near degeneracy is then given by ![\begin{eqnarray} S_{\ell=1,m=1}^{\rm deg} \, &=& \, S_{\ell=1,m=1}^{\rm ND} \, - \frac{1}{2}(\Delta_{1}\, - \, \Delta_{-1} ) \nonumber \\[3mm] &&+ \, \frac{1}{2} \Bigl(\sqrt{\Delta_1^2 \,+ \, \mathcal{H}_1^2} \, - \, \sqrt{\Delta_{-1}^2 \,+ \, \mathcal{H}_{-1}^2}\Bigr), \label{NDsplit} \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq127.png) (21)where
(21)where 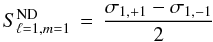 (22)with ND standing for non-degenerate. We note that
(22)with ND standing for non-degenerate. We note that 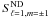 contains cubic-order contributions mentioned in the previous section. The contribution of near degeneracy to the splitting is then given by
contains cubic-order contributions mentioned in the previous section. The contribution of near degeneracy to the splitting is then given by 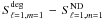 .
.
It is worth recalling that neglecting all cubic-order contributions in Eqs. (9), (10), and (12) results in Δ1 = Δ-1 and ℋ1 = ℋ-1. In that particular case, degeneracy does not contribute to the rotational splitting, and the rotational splitting is linear in Ω up to second order, satisfying 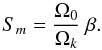 (23)
(23)
4.3. Sensitivity to the nature of the eigenmode
Figure 3 displays the near degenerate contributions to the splitting of p- and g-modes together with the cubic ones for a ZAMS stellar model (Table 1). The values of these different contributions are given mode by mode in Table D.2.
In Fig. 3 (left), the Coriolis correction 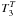 dominates for g-modes (by roughly a factor of 102 over other contributions) and decreases with the radial order to a roughly constant value for low | n | . The scale is too large in this figure to see the behavior of
dominates for g-modes (by roughly a factor of 102 over other contributions) and decreases with the radial order to a roughly constant value for low | n | . The scale is too large in this figure to see the behavior of 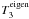 ,
, 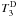 and
and 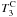 , and the near degeneracy contribution to the splitting, but we refer to Table D.1, where it is shown that there is no asymptotic behavior for these four contributions. Near degeneracy is fully negligible for all g-modes except for the n = −1 mode that is actually a mixed mode. The g-mode spectrum is much denser than the p-mode one but as shown in Fig. C.2 of Appendix C, the coupling term Hm is much smaller than Δm. This is because the distorsion effects are small for g-modes and therefore the overall (second and third order) contribution to Hm remains small.
, and the near degeneracy contribution to the splitting, but we refer to Table D.1, where it is shown that there is no asymptotic behavior for these four contributions. Near degeneracy is fully negligible for all g-modes except for the n = −1 mode that is actually a mixed mode. The g-mode spectrum is much denser than the p-mode one but as shown in Fig. C.2 of Appendix C, the coupling term Hm is much smaller than Δm. This is because the distorsion effects are small for g-modes and therefore the overall (second and third order) contribution to Hm remains small.
To emphasize possible asymptotic behavior, the contributions to p-modes have been divided by 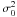 . In Fig. 3 (right), the implicit cubic order and the near-degenerate contributions dominate for p-modes but with opposite signs and therefore roughly compensate each other. Hence, as in the case of the pulsation frequencies, the near degeneracy correction tends to reduce the over-estimated contributions to rotational splittings. The contributions dominated by centrifugal distorsion, and in particular the near degeneracy one, scale as
. In Fig. 3 (right), the implicit cubic order and the near-degenerate contributions dominate for p-modes but with opposite signs and therefore roughly compensate each other. Hence, as in the case of the pulsation frequencies, the near degeneracy correction tends to reduce the over-estimated contributions to rotational splittings. The contributions dominated by centrifugal distorsion, and in particular the near degeneracy one, scale as 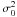 . In Appendix A, it is shown that near degeneracy contributes to the rotational splitting only if third order effects are taken into account (see Eq. (A.5)). However, it is also shown that second order effects (ℋ2) – dominated by distorsion (ℋ2) for p modes – are involved. This explains why the near degeneracy frequency variation follows a
. In Appendix A, it is shown that near degeneracy contributes to the rotational splitting only if third order effects are taken into account (see Eq. (A.5)). However, it is also shown that second order effects (ℋ2) – dominated by distorsion (ℋ2) for p modes – are involved. This explains why the near degeneracy frequency variation follows a 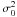 behavior for p-modes.
behavior for p-modes.
Similar conclusions for more evolved models with more complex structures are found for pure p-modes and pure g-modes. However, these complex structures also give rise to mixed modes for which all effects contribute equally, and a precise investigation, mode by mode, has to be done for each equilibrium model. This is investigated in detail in Sect. 6.
5. Effects of latitudinal shear on the splitting
 |
Fig. 4 Behavior of left: the scaled integrals β and γ (Eq. (27)), right: the scaled contributions to the splitting, as a function of the radial order n (Eqs. (31) to (33)). Computations were made for an 8.5 M⊙ ZAMS model uniformly rotating at 15% Ωk, i.e. 95 km s-1 (see stellar parameters in Table 1). |
Hansen et al. (1977) derived the expression for the rotational splitting of adiabatic nonradial oscillations for slow differential (steady, axially symmetric) rotation Ω(r,θ) and applied it to numerical models of white dwarfs and massive main sequence stars assuming a cylindrically symmetric rotation law. In the solar case, the effects of latitudinal differential rotation on theoretical frequencies were investigated by Gough & Thompson (1990), Dziembowski & Goode (1991), and Dziembowski & Goode (1992).
To be able to compute the splittings from Eq. (16), one must specify a rotation law. It is convenient to assume the form 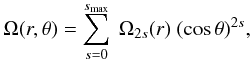 (24)where θ is the colatitude. The surface rotation rate at the equator is Ω(r = R,θ = π/2) = Ω0(r = R).
(24)where θ is the colatitude. The surface rotation rate at the equator is Ω(r = R,θ = π/2) = Ω0(r = R).
We note that in the solar case, Ω2 and Ω4 are negative and the equator rotates faster than the poles.
For the splitting, inserting Eqs. (24) into (16) yields the expression: 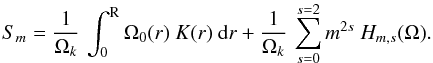 (25)The expression for Hm,s(Ω) can be found in Appendix B.
(25)The expression for Hm,s(Ω) can be found in Appendix B.
5.1. Latitudinally differential rotation only Ω(θ)
In this case, for which rotation is assumed to be uniform in depth, the splitting becomes: (Goupil 2011) 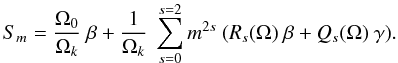 (26)Expressions for Rs and Qs can be found in Appendix B. Both β and γ depend on the radial and horizontal components of the mode
(26)Expressions for Rs and Qs can be found in Appendix B. Both β and γ depend on the radial and horizontal components of the mode ![\begin{eqnarray} && \beta = \frac{1}{I} \int_0^{\rm R} \left[ \xi_{r}^2-2 \xi_{r} \xi_{\rm h} + (\Lambda -1) \xi_{\rm h}^2 \right] \rho_0 r^2 {\rm d} r, \label{eq_integ}\\ && \gamma = - {1 / I}\int_0^{\rm R} ~ \xi^2_{\rm h} ~ \rho_0 r^2 ~ {\rm d} r, \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq157.png) I being the inertia of the mode
I being the inertia of the mode 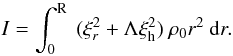 (29)For the sake of simplicity, we restrict our study to s = 1 in Eq. (25). The rotation law can then be expressed as
(29)For the sake of simplicity, we restrict our study to s = 1 in Eq. (25). The rotation law can then be expressed as 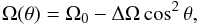 (30)where Ω0 = Ω(r = R,θ = π/2), Ω2 = −ΔΩ and Ω4 = 0. After some calculations provided in Appendix B, we are able to express the splittings of several (ℓ,m) combinations:
(30)where Ω0 = Ω(r = R,θ = π/2), Ω2 = −ΔΩ and Ω4 = 0. After some calculations provided in Appendix B, we are able to express the splittings of several (ℓ,m) combinations:
![\begin{eqnarray} S^{\rm lat}_{\ell=1, m=1} \approx \, \frac{\Omega_{0}}{\Omega_k} ~ \left[ 1+ \frac{1}{5} \left( {\Omega_2/ \Omega_{0}} + {3/ 7} ~ {\Omega_{4}/\Omega_{0}}\right) \right]. \label{S112} \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq175.png) (34)With Ω2/Ω0 = −0.127, Ω4/Ω0 = −0.159, one obtains a departure of | S1/Ω0 − 1 | ≃ 0.04 from a linear splitting, i.e. a 4% change in the solar case.
(34)With Ω2/Ω0 = −0.127, Ω4/Ω0 = −0.159, one obtains a departure of | S1/Ω0 − 1 | ≃ 0.04 from a linear splitting, i.e. a 4% change in the solar case.
For upper main sequence stars, excited modes are around the fundamental radial mode and may be mixed modes with | β | ~ | γ | ~ 1/2. This leads for instance to | S1,1/Ω0 − 1 | ~ 1% for Ω2/Ω0 and Ω4/Ω0 equal to a half of the solar values. We recall that for the stars treated in this article, we have taken Ω2 = −ΔΩ and Ω4 = 0.
As shown in Eqs. (26) to (29), the additional term due to the latitudinal shear strongly depends on the eigenfunction of the mode, through the radial and horizontal components of the displacement, therefore, we investigate the scaled contributions for different types of modes. The plots presented in Fig. 4 were again generated for an 8.5 M⊙, 4 R⊙ ZAMS model, rotating at Ω ≃ 15% Ωk (vΩ = R Ω = 95 km s-1). Once again, computations for more evolved stellar models give similar results – except for mixed modes around n = 1 – even for highier rotation rates.
Figure 4 shows the dependence of the β and γ integrals on the p or g nature of the mode. Globally, for g-modes, at a given rotation rate, we expect a small contribution of the latitudinal shear to the splittings, smaller for S1,1 than for S2,1 and S2,2, whereas for p-modes, the contribution is quite important for S2,1.
For the sake of simplicity, we focus from now on on ℓ = 1 splittings. We note that the investigations presented in the next two sections have also been addressed for ℓ = 2 splittings and led to the same conclusions.
5.2. A tachocline-like rotation profile: Ω(r,θ)
We refine the modeling of the rotation profile, assuming a rotation profile in depth as in the solar case. The rotation is uniform (Ω = Ω0) in the inner layers and differential latitudinally – as expressed in Eq. (30) – in the convective envelope. The rotation profile can be written in the form 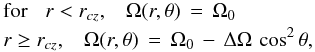 (35)where rcz is the radius of the inner stable layer. Therefore, after some calculations similar to those presented in Appendix B, Eq. (40) is no longer relevant, and should be replaced by
(35)where rcz is the radius of the inner stable layer. Therefore, after some calculations similar to those presented in Appendix B, Eq. (40) is no longer relevant, and should be replaced by ![\begin{eqnarray} \label{split_lat_bz} && S_{\ell=1,m= 1}^{\rm lat} \, = \,\frac{\Omega_0 }{\Omega_k} \, \left( \beta \, - \, \frac{\Delta \Omega}{\Omega_0} \, \frac{1}{5} \, \beta_{cz}\right) \\ && \hbox{where} \hspace{0.3cm} \beta_{cz}\, = \, \frac{1}{I} \int_{r_{cz}}^{\rm R} \left[ \xi_{r}^2-2 \xi_{r} \xi_{\rm h} + (\Lambda -1) \xi_{\rm h}^2 \right] \rho_0 r^2 {\rm d} r. \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq193.png) We note that for p modes for instance, βcz is smaller than β within the whole star – βcz ~ 0.45, whereas β ~ 1 − . Therefore, in the case of a tachocline-like profile, the effect of a same latitudinal shear ΔΩ is smaller than in the case where rotation is uniform in depth.
We note that for p modes for instance, βcz is smaller than β within the whole star – βcz ~ 0.45, whereas β ~ 1 − . Therefore, in the case of a tachocline-like profile, the effect of a same latitudinal shear ΔΩ is smaller than in the case where rotation is uniform in depth.
6. The case of a β Cephei on the main sequence
Massive stars on the main sequence are usually rapid rotators and their fast rotation affects their internal structure as well as their evolution. The rotation of β Cephei stars extends from slow rotational velocities (v < 50 km s-1) to extremely rapid ones (v > 250 km s-1) (Stankov & Handler 2005). These stars usually have a radiative envelope, which may or may not be in latitudinal differential rotation. For these rapid rotators, one can wonder whether cubic order or near degeneracy contributions dominate over the effects of latitudinal shear.
 |
Fig. 5 Departure from linear splitting for (ℓ = 1,m = 1) triplets. Left: for Ω = 20% Ωk. Right: for Ω = 30% Ωk, as a function of the radial order. Different contributions result from: cubic-order effects (dark blue), cubic-order effects with near degeneracy (purple, these two contributions overlap for all g-modes), and latitudinally differential rotation with ΔΩ/Ω = 0.127 (light blue), 0.2 (in green), 0.3 (in orange), and 0.4 (in red). These results were computed for the uniformly rotating evolved 8.5 M⊙β Cephei model described in Sect. 5.1 (Table 2). |
 |
Fig. 6 Departure from linear splitting for (ℓ = 1,m = 1) triplets due to cubic-order effects (dark blue), to cubic-order effects including near-degeneracy corrections (purple, these two contributions overlap for g5 and g2) and to latitudinally differential rotation with ΔΩ/Ω = 0.127 (light blue), 0.2 (green), 0.3 (orange), and 0.4 (red). These departures are plotted as a function of the rotation rate for a g5 mode (left), a g2 mode (center), and a p1 mode (right). These results were computed for the uniformly rotating evolved 8.5 M⊙β Cephei model described in Sect. 5.1 (Table 2). |
Here we investigate the importance of deviations from a linear splitting for an evolved main sequence model of an 8.5 M⊙ star with a 5.07 R⊙ radius (see Table 2 for the stellar parameters of the model).
Stellar parameters of the β Cephei model in Sect. 5.
6.1. Departure from linear splitting as a function of frequency
According to the region to which a mode belongs, very different types of behavior are observed for the different contributions to the splitting, as illustrated in Fig. 5.
Figure 5 displays the departure from a linear splitting caused by cubic-order effects with and without near degeneracy corrections, and to latitudinal differential rotation (uniform in depth). It has been computed for ℓ = 1 modes with radial orders ranging from −10 to 5. The parameters of the stellar model considered here are given in Table 2. It rotates at 20% Ωk (left) and 30% Ωk (right). In these plots, we can distinguish three regions for the behavior of δSℓ,m.
In the g-mode region (n ≤ −2), as the cubic-order effect is proportional to 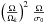 (see Eq. (19)), the lower the frequency, the higher cubic-order terms, and this effect increases with the rotation rate. In this region, cubic-order effects overtake those from latitudinally differential rotation.
(see Eq. (19)), the lower the frequency, the higher cubic-order terms, and this effect increases with the rotation rate. In this region, cubic-order effects overtake those from latitudinally differential rotation.
In the p-mode region (n > 2), latitudinal shear effects are larger than for the g-modes. Cubic-order effects are of the same order of magnitude as the contribution from latitudinally differential rotation with a shear of only 12.7%.
In between, in the mixed mode region, cubic-order effects with degeneracy corrections are of the same order of magnitude as effects from latitudinally differential rotation for all the considered shears.
To get a clearer understanding of these different types of behavior, one can look at Fig. C.1 in Appendix C. Figure C.1 displays mode inertia (defined in Eq. (29)) as a function of the radial order, for the model described in Table 2, that rotates uniformly at 30% Ωk. From this figure, the three frequency domains related to the nature of modes are clearly visible: below g3 (n ∈ [−10, −3]) are pure g-modes, above p2 are pure p-modes, and in between we find the mixed mode region.
Figure C.2, which has been computed for the model described in Table 2, that rotates uniformly at 30% Ωk, shows that near degeneracy has a very small effect on g-mode splittings. Although the frequency differences (Δm) between the ℓ = 1 and ℓ = 3 modes are small for g-modes (the y axis is in a logarithmic scale), near degeneracy is more or less negligible, since ℋm (which quantifies near degeneracy) is dominated by second order terms (due to distorsion) and takes small values.
In the mixed mode region, although ℋm increases, the frequency differences between the ℓ = 1 and ℓ = 3 modes Δm also increase. Consequently, near degeneracy should also be negligible in this range either. Once again, as mixed modes are very sensitive to the evolutionary stage, it is diffucult to make general statements for all the stellar models.
In the p-mode domain, Δm decreases, while ℋm increases causing the near degeneracy contribution to the splitting to increase. The near degeneracy effect is therefore larger in the pure p-mode region. This causes the departure from a linear splitting due to cubic-order effects including near degeneracy to be of the same order of magnitude as the latitudinal shear contribution (Fig. 5).
6.2. Departure from a linear splitting as a function of the rotation rate
We studied the relative values of the third order, near degeneracy, and latitudinal shear contributions to the splitting as a function of the rotation rate mode by mode. Figure 6 shows three different cases:
-
The mode g5 illustrates the case of high order g-modes (or pure g-modes) where the cubic-order contribution overtakes the latitudinal shear contribution as soon as the mean rotation rate exceeds 15% Ωk (which corresponds to a rotation velocity of around 80 km s1).
-
The mode g2 is located in the mixed mode region where cubic-order effects are larger than latitudinal differential rotation ones.
-
The mode p1 is still a mixed mode but with a nature closer to a pure p-mode for which near degeneracy is no longer negligible. As a result, the total cubic contribution including degeneracy is of the same order as a latitudinal shear of 12.7%.
6.3. How do we distinguish between the two effects?
 |
Fig. 7 Sℓ,m(p1) versus Sℓ,m(g2) due to cubic-order effects and near degeneracy (purple), and to a latitudinal shear (green), for ℓ = 1 modes in an evolved 8.5 M⊙ model (see Table 2). The rotation rate increases from left to right: from 18% Ωk to 34% Ωk. The error bars for V1449 Aquilae have been taken from Degroote et al. (2009). |
In the previous subsection, we have shown that for a massive star on the main sequence, in the frequency range where we expect pulsation modes, it is not easy to conclude whether a departure from a linear splitting is due to latitudinally differential rotation or cubic-order effects. Here we propose a method for disentangling the two effects.
We consider the two modes g2 and p1 to be representative of a mixed mode close to the g-modes and a mixed mode close to the p-modes, respectively, as seen in the previous section. In Fig. 7, S1(p1) versus S1(g2) is plotted for the two different assumptions (latitudinal shear or cubic-order effects with near degeneracy corrections) for different rotation rates (Ω ≤ 35% Ωk). We note that for g-modes, β is roughly equal to one-half, and for p-modes β approaches one. Accordingly, the ratio of 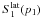 to
to 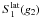 does not depend on ΔΩ and is approximatively equal to 2. On the other hand, the curve S1(p1) as a function of S1(g2) for splittings including cubic-order effects with near degeneracy corrections starts to deviate from a slope of two when the rotation rate is high enough. The deviation increases with the rotation rate as expected.
does not depend on ΔΩ and is approximatively equal to 2. On the other hand, the curve S1(p1) as a function of S1(g2) for splittings including cubic-order effects with near degeneracy corrections starts to deviate from a slope of two when the rotation rate is high enough. The deviation increases with the rotation rate as expected.
We now define 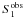 as the observed splittings for l = 1 modes for a rapid rotator with a uniform rotation profile
as the observed splittings for l = 1 modes for a rapid rotator with a uniform rotation profile 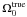 . Their values are then assumed to be given by
. Their values are then assumed to be given by 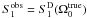 (Eq. (21)) i.e. rotational splittings computed up to cubic order, including near degeneracy corrections.
(Eq. (21)) i.e. rotational splittings computed up to cubic order, including near degeneracy corrections.
If one misinterprets 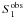 as being caused by a latitudinal shear,
as being caused by a latitudinal shear, 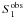 is assumed to obey Eq. (31). The point representing
is assumed to obey Eq. (31). The point representing 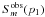 as a function of
as a function of 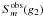 ought to lie on the straight line of slope 2 in Fig. 7. We represent this point by the splittings
ought to lie on the straight line of slope 2 in Fig. 7. We represent this point by the splittings 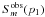 and
and 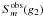 computed according to Eq. (21) assuming a rotation rate of 15% Ωk, v = 80 km s-1. As the observed point is not located on the straight line given by
computed according to Eq. (21) assuming a rotation rate of 15% Ωk, v = 80 km s-1. As the observed point is not located on the straight line given by 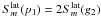 , we can then conclude that the deviation from a linear splitting is not due to a latitudinal shear.
, we can then conclude that the deviation from a linear splitting is not due to a latitudinal shear.
In the case of massive stars on the main sequence, the effects of latitudinal differential rotation and cubic order or near degeneracy are of the same order of magnitude in the frequency domain where we expect to observe oscillation modes. This is mostly caused by the mixed nature of modes around the fundamental frequency, and should therefore depend on the evolutionary stage of the star. However if two individual rotational splittings are available (one g-mode under the mixed mode region, and one p-mode above it), this method helps us to determine whether a departure from a linear splitting is due to cubic-order contributions including accidental degeneracy, or latitudinal shear.
7. The case of solar type stars
 |
Fig. 8 Departure from a linear splitting as a function of the radial order for (ℓ = 1,m = 1) triplets. Left: for Ω = 3.7% Ωk. Right: Ω = 7.4% Ωk – due to cubic-order effects (blue), cubic-order effects with near degeneracy (purple, the two of them overlap for most of the modes except g2) and to a latitudinally differential rotation of 12.7% (light blue) and 20% (green). Computations were made for a model of HD 181420 (M = 1.36 M⊙, see Table 3). |
Low-mass main sequence stars are known to be slow rotators. Owing to their outer convection zone, they undergo magnetic braking during their evolution (Kawaler 1988). Observational evidence has been found of surface latitudinal differential rotation (coming from stellar spots occurring again in their outer convection zone). Hence, for these stars, the average surface rotation rate Ω is much lower then for more massive stars, such as β Cephei stars, and ΔΩ = Ωequa − Ωpole, the difference between the rotation rates at the equator and the poles, can be large (25% for the Sun, between 1% and 45% for a star like Procyon, Bonanno et al. 2007). One therefore expects latitudinal corrections to the splittings to dominate over cubic-order effects, which are negligible. As illustrative examples, we studied the case of HD 181906 and HD 181420, which are two solar-like stars observed by CoRoT during the first long run, and which lightcurves have been analyzed by García et al. (2009) and Barban et al. (2009) respectively.
Before comparing the different contributions to the rotational splitting, one might wonder whether a perturbative approach up to the cubic order accounting for near degeneracy effects is valid for interpretation of seismic observations of this type of star. To answer this issue, we rely on the validity study of Suárez et al. (2010), which performed for a polytropic model of 1.3 M⊙, representative of HD 181420. We therefore consider this study adaptedto determine the validity of our approach for computing high-order pressure pulsation modes that propagate in the outer layers of a solar-like star. Suárez et al. (2010) show that for rotational velocities under approximately 40 km s-1, the structures of the frequency spectra computed with a non-perturbative and their perturbative method are very similar. Here, we study the rotational splitting, which is a frequency difference that removes some of the second-order effects, by adopting a cubic-order perturbative approach accounting for the effect of near degeneracy. We then consider our approach as valid for the rotation velocities at stake in the stars we study in this article.
7.1. Competition between the three effects
Here we investigate the order of magnitude of deviations from Eq. (23) for an M = 1.36 M⊙, R = 1.63 R⊙ main sequence stellar model (see Table 3 for the stellar parameters taken as a model representative of HD 181420).
Stellar parameters of the model of HD 181420 (Sect. 6).
In Fig. 8, we plot the three kinds of contributions, i.e. cubic order, cubic order with near degeneracy, and latitudinal shear, for (ℓ = 1, ± 1) splittings as a function of the central mode frequency for two different rotational angular velocities (3.7% Ωk and 7.4% Ωk, which correspond to 15 km s-1 and 30 km s-1, respectively, for the model described in Table 3). Once again, these contributions show a peculiar behavior in the mixed mode region, where the two types of contributions can be of the same order. We focus here on higher frequencies, since the oscillation modes of HD 181420 are detected in the 1.5−2 mHz frequency range (Barban et al. 2009). Therefore, these plots show that even for rotation rates that are high for this type of star (7.4% Ωk), cubic-order contributions (with or without near degeneracy) can be neglected compared to additional terms related to latitudinal shear. This leads to the conclusion that for HD 181420 in particular – as we expect for solar-like stars in general – the cubic-order contributions to the splitting can safely be neglected in comparison with potential latitudinal shear contributions. We have performed the same computations for a 1.2 M⊙ 1.4 R⊙ stellar model representative of HD 181906, and derive the same conclusions.
7.2. Determination of a latitudinal shear from seismic observations
The results of the seismic analysis provided in Barban et al. (2009) and García et al. (2009) both find significantly different values for the low frequency peak in the Fourier spectrum and what is interpreted as the rotational splitting. If a uniform surface rotation is assumed, it is impossible to reproduce these differences between these observables.
We assume a rotation profile of the form 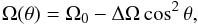 (38)where Ω0 is the rotation surface angular velocity at the equator, Ωequator, and ΔΩ = Ωequator − Ωpole. The rotation frequency is then given by
(38)where Ω0 is the rotation surface angular velocity at the equator, Ωequator, and ΔΩ = Ωequator − Ωpole. The rotation frequency is then given by 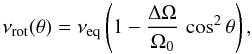 (39)where νeq and νrot correspond to the equatorial rotation rate (i.e. Ω0) and the rotation frequency at the colatitude θ in μHz, respectively.
(39)where νeq and νrot correspond to the equatorial rotation rate (i.e. Ω0) and the rotation frequency at the colatitude θ in μHz, respectively.
Using again the rotation law Eq. (38) to derive the rotational splitting from Eq. (26) we obtain for ℓ = 1,m = ± 1 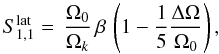 (40)which can be written in the form
(40)which can be written in the form 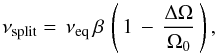 (41)where νsplit corresponds to S1,1.
(41)where νsplit corresponds to S1,1.
Equations (39) and (41) are then two equations with three unknowns: νeq, cosθ, and ΔΩ/Ω0. Dividing Eqs. (41) by (39) leads to 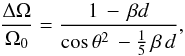 (42)where we have introduced the parameter
(42)where we have introduced the parameter 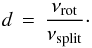 (43)We then determine ΔΩ/Ω0 as a function of cosθ, along with the constraints
(43)We then determine ΔΩ/Ω0 as a function of cosθ, along with the constraints ![\begin{eqnarray} && \theta \, \in \, \left[0;\frac{\pi}{2}\right] \, \Rightarrow \, \cos \theta \, \in \, \left[ 0;1 \right], \\ && \frac{\Delta \Omega}{\Omega_0} \, \in \, \left[ -1;1\right]. \label{contraintes} \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq291.png)
 |
Fig. 9 Possible values for ΔΩ/Ω0, depending on the parameter d in Eq. (43) and the value of the integral β Eq. (B.5). The line colors corresponds to the value of (d × β), which ranges here from 0.3 (in blue) to 1.5 (in red). In gray, we indicate the acceptable domain of values for the latitudinal gradient (Eq. (45)). This plot was produced for high order p modes. |
As illustrated in Fig. 9, the latitudinal shear is a hyperbolic function of cosθ, centered on 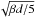 . Depending of the values of the product βd of the observational parameter d and the integral β, we find graphically different possible ranges of values for ΔΩ/Ω0 and cosθ.
. Depending of the values of the product βd of the observational parameter d and the integral β, we find graphically different possible ranges of values for ΔΩ/Ω0 and cosθ.
7.3. The case of HD 181906
HD 181906 is an F8 dwarf for which fundamental parameters have been determined by Bruntt (2009), considering the presence of a background star: mv = 7.65, L/L⊙ = 3.32 ± 0.45, Teff = (6300 ± 150) K, [Fe/H] = −0.11 ± 0.14, M/M⊙ = 1.144 ± 0.119, vsini = (10 ± 1) km s-1. Note that Nordström et al. (2004) had found vsini = (16 ± 1) km s-1 considering HD 181906 as single, with no background star. It has been observed during the first long run of CoRoT, and its light curve has been analyzed by García et al. (2009). They find two possible interpretations for the mode identification, as listed in Table 4.
Results concerning rotation from the analysis of HD 181906 performed in García et al. (2009).
Considering the uncertainties attached to the seismic observables, the result obtained for the latitudinal shear is presented in Table 5. These results show that the hypothesis of latitudinal differential rotation is consistent with the available observables. Therefore, the latitudinal differential rotation profile is a reliable assumption concerning HD 181906. Moreover, The results define a range of possible values for different characteristics of the rotation profile: the latitudinal shear, the rotation surface velocity at the equator, as well the inclination angle. The correspondant error bars are discussed in Sect. 7.5. Both scenarii give the same conclusionsvery similar results.
Latitudinal shear, equatorial velocity and inclination angle obtained for HD 181906, using models with rotation uniform in depth.
7.4. Solar or anti-solar latitudinal shear for HD 181420?
HD 181420 is an F2 main sequence star whose fundamental parameters were determined by Bruntt (2009) to be mv = 6.57, L/L⊙ = 4.28 ± 0.28, Teff = (6580 ± 105) K, [Fe/H] = 0.00 ± 0.06, M/M⊙ = 1.31 ± 0.063 and vsini = (18 ± 1) km s-1. The star was observed during the first long run of CoRoT, and its light curve has been analyzed by Barban et al. (2009). They found two possible interpretations depending on the mode identification, as listed in Table 6. Later Bedding & Kjeldsen (2010) used some empirical scaling method that seemed to favor scenario 1.
Concerning HD 181420, our model gives unexpected results: in both scenarii, the latitudinal shear is found to be negative, i.e. the pole rotates faster than the equator, which is the opposite of what is known for the Sun. To appreciate the reliability of this result, one should refer to the work of Käpylä et al. (2011), who study the impact of rotation on both the turbulent angular momentum and heat transport in the convective zone of solar-like stars, by mean of direct numerical simulations of turbulent convection in spherical geometry. According to the authors, the rotation profile varies from an anti-solar profile (equator rotates slower than poles) for low Coriolis numbers to a solar profile (equator rotates faster), with a transition around Co = 3. The Coriolis number, which measures the impact of rotation on turbulent motion is given by 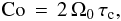 (46)Where τc is the convective overturning timescale, computed in the stellar evolution code CESAM (Morel & Lebreton 2008), and Ω0 is taken as the angular velocity at the equator. For HD 181420, when rotation is supposed to be uniform in depth, the Coriolis number is (3.2 ± 0.5) for scenario 1 and (4.0 ± 0.3), i.e. both values are only slightly above the transition threshold between anti-solar and solar surface rotation (see Fig. 17 of Käpylä et al. 2011). Therefore, it is difficult to confirm that the physics at stake in the convective envelope of HD 181420 can lead to an anti-solar rotation profile for HD 181420.
(46)Where τc is the convective overturning timescale, computed in the stellar evolution code CESAM (Morel & Lebreton 2008), and Ω0 is taken as the angular velocity at the equator. For HD 181420, when rotation is supposed to be uniform in depth, the Coriolis number is (3.2 ± 0.5) for scenario 1 and (4.0 ± 0.3), i.e. both values are only slightly above the transition threshold between anti-solar and solar surface rotation (see Fig. 17 of Käpylä et al. 2011). Therefore, it is difficult to confirm that the physics at stake in the convective envelope of HD 181420 can lead to an anti-solar rotation profile for HD 181420.
We refine the modeling of HD 181420 by taking a tachocline-like profile. As explained in Sect. 5.2, this profile consists in assuming uniform rotation (Ω = Ω0) in the inner layers, and latitudinal differential rotation (Ω(θ)) in the convective envelope. The rotational splitting given by Eq. (40) is no longer relevant, and should be replaced by Eq. (36).
In this case, we found different values for Ω0 than in the former case, as a consequence, the Coriolis number reaches (8.9 ± 1.7) for scenario 1 and (11.8 ± 0.7) for scenario 2, i.e. high above the transition limit between the anti-solar and solar rotational shears. The integral βcz reaches a constant value of 0.45 for high order p-modes, which changes the relationship between the colatitude of the spot and the latitudinal shear (42), and as a consequence changes the domain of possible shear. Positive latitudinal shear corresponding to solar-type latitudinal rotation is predicted for the two scenarii, which is this time fully consistent with the Coriolis number values. The results obtained with this tachocline-like model are listed in Table 7.
Results concerning rotation from the analysis of HD 181420 performed in Barban et al. (2009).
Latitudinal shear, equatorial velocity, and inclination angle obtained for HD 181420, using models with a tachocline-like rotation profile.
The case of HD 181420 is particularly interesting as a simple model of rotation uniform in depth and differential in latitude leads to non-physical latitudinal shear. Only a little more sophisticated model, where rotation varies in depth according to a tachocline-like profile, is fully coherent with the physics of the convective zone as well as the observables. We also give a range of possible values for the rotation profile parameters: the latitudinal shear in the convective zone, the rotation surface velocity at the equator, and the incination angle. To conclude, for this star, we find that rotation profile inside the star is likely to be a tachocline-like profile, with a solar-type latitudinal differential rotation. Moreover, these results, when compared to those of Mosser et al. (2009), seem to favor scenario 1 since the rotational frequency at the equator in the hypothesis of scenario 1 of (5.14 ± 0.07) × 10-6 rad s-1 is closest to the one found in Mosser et al. (2009) by spot modeling.
7.5. Discussion
As mentioned at the beginning of this section, Suárez et al. (2010) found that second order perturbative methods including near-degenaracy corrections are valid for rotation velocities up to approximately 40 km s-1. In this study, third order perturbative methods have been used for the computation of rotational splittings in Sect. 7.1. In Sect. 7.2, we provide a simple recipe that allows us to compute the latitudinal shear given the seismic observables. This formulation relies on the validity of the third-order perturbative method, but the only quantities provided by the modeling are β (Eq. (B.5)) and βcz, i.e. quantities computed from first-order eigenfunctions. The question is then: do eigenfunctions vary suffitiently widely with rotation rate (under 60 km s-1 i.e. 15% Ωk), to impact the value of β? After verifications, it appears that for high-order acoustic modes in moderately rotating stars (under 15% Ωk) β ≃ 1, and βcz ≃ 0.45 are satisfying evaluations. Therefore, the recipe is valid for the rotation rates at stake in Sects. 7.3 and 7.4. We note the convenience of the proposed recipe, which requires only seismic observables and the values of β.
The large error bars obtained in particular for the values of latitudinal shears (Tables 5, 7) is not only due to the observational uncertainties, but can also be attributed to the simplicity of the spot model used. This model does not account for spot parameters, such as for example a spot lifetime, or the spot distribution on the observed stellar disc (for more sophisticated modeling, see Mosser et al. 2009). We only consider a unique spot of infinite lifetime. Note that the use of a more complicated model would require more observational constraints than only one spot rotation signature. When only mean values of rotationnal splittings are available, and the observational error bars on the low frequency signature of a spot rotation are large (Barban et al. 2009), we are able to give general conclusions concerning the rotation profile – i.e. uniform in depth or tachocline-like, solar, or anti-solar − , but no reliable numerical values characterising it.
8. Conclusions
With the help of the perturbative approach established in Soufi et al. (1998), we have investigated the second and third-order contributions of the Coriolis and the centrifugal accelerations to the p and g-mode frequencies, as well as near degeneracy effects on the rotational splittings. Their effects were then compared with those of a latitudinal shear. We have studied two types of oscillating stars.
For an evolved model of a β Cephei, the effects of near degeneracy, cubic-order perturbations, and latitudinal shear are of the same order of magnitude in the frequency range, relevant to these stars – i.e. low order p- and g-modes – and for reasonable rotation rates ranging from 15% Ωk to 30% Ωk. Nevertheless, when two individual splittings for modes of a different nature (for example a pure g and a mixed mode) are available, a method is proposed to distinguish between a latitudinal shear and other effects.
For solar-like stars such as HD 181420 and HD 181906, which are mostly moderate rotators and oscillate with high-order p modes, cubic-order effects on frequency splittings are shown to be small compared to the effects of latitudinally differential rotation. Therefore, given a splitting and a rotation period signature, it is possible to infer a range for the latitudinal shear coefficient ΔΩ/Ω0. Although no precise determination of latitudinal shear is possible unless the spot latitude is fully determined, we have been able to determine the most reliable rotation profile for each of the two stars. Moreover, the determination of the latitudinal shear by our seismic method can be taken as a constraint to be added to other observational constraints, such as those coming from spectropolarimetric results (e.g. Donati et al. 2010) or spot modeling (e.g. Mosser et al. 2009).
Acknowledgments
We thank the referee for relevant remarks, which helped to improve this article. We are indebted to W. D. Dziembowski for his helpful comments, and to D. Reese for his careful reading of the manuscript. We also thank Stéphane Mathis for helpful discussions about the transport of angular momentum in the convective envelope of solar-like stars.
References
- Ballot, J., Lignières, F., Reese, D. R., & Rieutord, M. 2010, A&A, 518, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barban, C., Deheuvels, S., Baudin, F., et al. 2009, A&A, 506, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedding, T. R., & Kjeldsen, H. 2010, Commun. Asteroseismol., 161, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Belkacem, K., Samadi, R., Goupil, M.-J., et al. 2009, Science, 324, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Benomar, O., Baudin, F., Campante, T. L., et al. 2009, A&A, 507, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanno, A., Küker, M., & Paternò, L. 2007, A&A, 462, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H. 2009, A&A, 506, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burke, K. D., Reese, D. R., & Thompson, M. J. 2011, MNRAS, 414, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A. 2002, Astron. Nachr., 323, 336 [Google Scholar]
- Degroote, P., Briquet, M., Catala, C., et al. 2009, A&A, 506, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., Skelly, M. B., Bouvier, J., et al. 2010, MNRAS, 409, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 1989, ApJ, 347, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 1991, Solar interior and atmosphere (A92-36201 14-92) (Tucson, AZ: University of Arizona Press), 501 [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 1992, ApJ, 394, 670 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Régulo, C., Samadi, R., et al. 2009, A&A, 506, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gough, D. O., & Thompson, M. J. 1990, MNRAS, 242, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Goupil, M. J. 2009, Lecture Notes in Physics (Berlin: Springer Verlag), 765, 45 [Google Scholar]
- Goupil, M. 2011, Lect. Notes Phys., 832, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., Cox, J. P., & van Horn, H. M. 1977, ApJ, 217, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Jerzykiewicz, M., Handler, G., Shobbrook, R. R., et al. 2005, MNRAS, 360, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Guerrero, G., Brandenburg, A., & Chatterjee, P. 2011, A&A, 531, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karami, K. 2008, Chin. J. Astron. Astrophys., 8, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1994, Stellar Structure and Evolution, XVI (Berlin, Heidelberg, New York: Springer-Verlag), Also Astron. Astrophys. Libr., 468, 192 [NASA ADS] [Google Scholar]
- Ledoux, P. 1945, ApJ, 102, 143 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mosser, B., Baudin, F., Lanza, A. F., et al. 2009, A&A, 506, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouazzani, R.-M., Goupil, M.-J., Dupret, M.-A., & Reese, D. 2009, Commun. Asteroseismol., 158, 283 [NASA ADS] [Google Scholar]
- Ouazzani, R. M., Goupil, M. J., Dupret, M. A., & Reese, D. 2010, Ap&SS, 64 [Google Scholar]
- Reese, D., Lignières, F., & Rieutord, M. 2006, A&A, 455, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D. 2006, Ph.D. Thesis [Google Scholar]
- Saio, H. 1981, ApJ, 244, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Soufi, F., Goupil, M. J., & Dziembowski, W. A. 1998, A&A, 334, 911 [NASA ADS] [Google Scholar]
- Stankov, A., & Handler, G. 2005, VizieR Online Data Catalog, 215, 80193 [NASA ADS] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez, J. C., Moya, A., Amado, P. J., et al. 2009, ApJ, 690, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez, J. C., Goupil, M. J., Reese, D. R., et al. 2010, ApJ, 721, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars (Tokyo: University of Tokyo Press), 2nd edn. [Google Scholar]
Appendix A: Near degeneracy corrections to the splittings of high order p-modes
This section is dedicated to a qualitative estimation of the near degeneracy corrections to rotational splittings 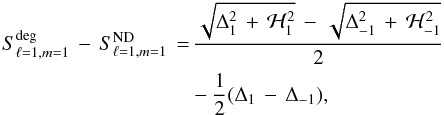 (A.1)where Δ1 and ℋ1 are normalized by the break-up frequency Ωk. The oscillation frequency given in Eq. (8) can be rewritten in the generic form
(A.1)where Δ1 and ℋ1 are normalized by the break-up frequency Ωk. The oscillation frequency given in Eq. (8) can be rewritten in the generic form 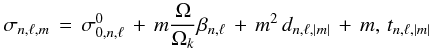 where dn,ℓ, | m | and tn,ℓ, | m | represent the second and third order contributions. Thus the term Δ1 and Δ-1 appearing in Eq. (21), for the coupling of an ℓ = 1,n and an ℓ = 3,n′ mode, can be written as:
where dn,ℓ, | m | and tn,ℓ, | m | represent the second and third order contributions. Thus the term Δ1 and Δ-1 appearing in Eq. (21), for the coupling of an ℓ = 1,n and an ℓ = 3,n′ mode, can be written as: 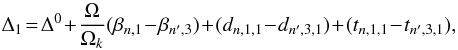 (A.2)where Δ0 stands for
(A.2)where Δ0 stands for 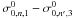 , the difference between the eigenfrequencies without rotation.
, the difference between the eigenfrequencies without rotation.
For high frequency p-modes, the radial contributions are concentrated in the outer layers and are then nearly the same for (n,ℓ = 1) and (n′,ℓ = 3). It is then legitimate to neglect the differences in their radial contributions. We then omit the radial order subscripts n,n′. For the same reason, the Ledoux constants are also quite similar β1 ~ β3. We then find that 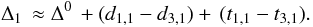 Similarly,
Similarly, 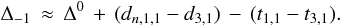 Hence, the quantity (Δ1 − Δ-1) in Eq. (A.1)
Hence, the quantity (Δ1 − Δ-1) in Eq. (A.1)  (A.3)is of third order. One can then approximate Δ-1 ~ Δ1 in the square root of Eq. (A.1), and the correction of near degeneracy is given by
(A.3)is of third order. One can then approximate Δ-1 ~ Δ1 in the square root of Eq. (A.1), and the correction of near degeneracy is given by ![\appendix \setcounter{section}{1} \begin{eqnarray} S_{\ell=1}^{\rm deg} \, - \, S_{\ell=1}^{\rm ND} \, &\approx & \, \, (t_{1,1}- t_{3,1}) \nonumber \\[3mm] &&+ \, \frac{ \sqrt{\Delta_1^2 \,+ \, \mathcal{H}_1^2} \, - \, \sqrt{\Delta_{1}^2 \,+ \, \mathcal{H}_{-1}^2} }{2}\cdot \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq403.png) (A.4)For the coupling term, one can separate the second ℋ2 and third ℋ3 order terms as ℋm = ℋ2 + m ℋ3. Thus, ℋ1 = ℋ2 + ℋ3, and ℋ-1 = ℋ2 − ℋ3. With | ℋ3 | ≪ | ℋ2 | , the near degeneracy correction to the splitting becomes
(A.4)For the coupling term, one can separate the second ℋ2 and third ℋ3 order terms as ℋm = ℋ2 + m ℋ3. Thus, ℋ1 = ℋ2 + ℋ3, and ℋ-1 = ℋ2 − ℋ3. With | ℋ3 | ≪ | ℋ2 | , the near degeneracy correction to the splitting becomes 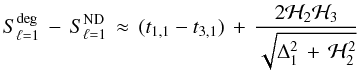 (A.5)which shows that for slow rotators, such as HD 181420, when cubic-order effects are neglected, the near degeneracy contribution is zero, and the splitting is a linear function of rotation. If cubic-order effects are included, then near degeneracy corrections affect the splitting, and the departure from a linear splitting is dominated by distorsion (predominantly in ℋ2).
(A.5)which shows that for slow rotators, such as HD 181420, when cubic-order effects are neglected, the near degeneracy contribution is zero, and the splitting is a linear function of rotation. If cubic-order effects are included, then near degeneracy corrections affect the splitting, and the departure from a linear splitting is dominated by distorsion (predominantly in ℋ2).
Appendix B: Contribution of the latitudinal shear to the splittings
To be able to compute the splittings from Eqs. (1) and (16), one must specify a rotation law. It is convenient to assume the form 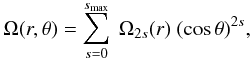 (B.1)where θ is the colatitude and we have limited our investigation to smax = 1. The surface rotation rate at the equator is Ω(r = R,θ = π/2) = Ω0(r = R).
(B.1)where θ is the colatitude and we have limited our investigation to smax = 1. The surface rotation rate at the equator is Ω(r = R,θ = π/2) = Ω0(r = R).
Inserting Eqs. (24) into (16) yields the expression for the generalized splitting 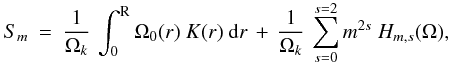 (B.2)where (see Goupil 2011),
(B.2)where (see Goupil 2011), ![\appendix \setcounter{section}{2} \begin{equation} H_{m,s} (\Omega) = - {1 / \rm I} \int_0^{\rm R} \Bigl[R_{s} ~\Bigl(\xi^2_{r} -2\xi_{r} \xi_{\rm h}+ \xi^2_{\rm h} (\Lambda-1)\Bigr) + Q_{s} ~ \xi^2_{\rm h}\Bigr) \Bigr] \rho_0 r^2 {\rm d}r \nonumber \end{equation}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq414.png) and Rs and Qs depend on Ω2,Ω4 and Λ = ℓ(ℓ + 1).
and Rs and Qs depend on Ω2,Ω4 and Λ = ℓ(ℓ + 1).
For example, if shellular rotation is expected, then Ω(r,θ) = Ω0(r) and smax = 0. Moreover, Ω2, Ω4 = 0, i.e. Rj = Qj = 0 for j = 0,2, and ![\appendix \setcounter{section}{2} \begin{eqnarray} S_{m} &=& - {1 / I} \int_0^{\rm R} ~ \frac{\Omega_{0}(r)}{\Omega_k}~ \Bigl[ \Bigr. \xi_{r}^2 - 2\xi_{r} \xi_{\rm h} + \Lambda ~ \xi_{\rm h}^2 \Bigl. \Bigr] ~\rho_0 r^2 {\rm d}r. \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq422.png) (B.3)If we consider latitudinally differential rotation only, Ω2j, j = 0,2 are depth independent, Ω0 = Ωequator, Ω2 = −ΔΩ, and Ω4 = 0. Rs and Qs are constant and
(B.3)If we consider latitudinally differential rotation only, Ω2j, j = 0,2 are depth independent, Ω0 = Ωequator, Ω2 = −ΔΩ, and Ω4 = 0. Rs and Qs are constant and 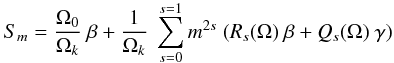 (B.4)where β and γ are defined as
(B.4)where β and γ are defined as ![\appendix \setcounter{section}{2} \begin{eqnarray} && \beta = \frac{1}{I} \int_0^{\rm R} \left[ \xi_{r}^2-2 \xi_{r} \xi_{\rm h} + (\Lambda -1) \xi_{\rm h}^2 \right] \rho_0 r^2 {\rm d}r \label{def_beta}\\[3mm] && \gamma= - \frac{1}{I} \int_0^{\rm R} ~ \xi^2_{\rm h} ~ \rho_0 r^2 ~{\rm d}r \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq427.png) and I is the inertia of the mode
and I is the inertia of the mode 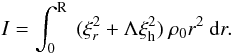 (B.7)The rotational splitting of a { n,ℓ,m } mode is then given by
(B.7)The rotational splitting of a { n,ℓ,m } mode is then given by ![\appendix \setcounter{section}{2} \begin{equation} S_{\ell,m}=\frac{1}{\Omega_k}\, \left[ \Omega_{0} \, \beta + R_0^{\ell} \, \beta + Q_0^{\ell} \, \gamma + m^2 \left( R_1^{\ell} \, \beta + Q_1^{\ell} \, \gamma \right)\right]. \end{equation}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq430.png) (B.8)In Goupil (2011), Qs and Rs are given for s = 0,1,2
(B.8)In Goupil (2011), Qs and Rs are given for s = 0,1,2 ![\appendix \setcounter{section}{2} \begin{eqnarray} R_0^{\ell} &=& - \frac{\Delta \Omega}{\Omega_0} ~ \frac{2 \Lambda-1}{4 \Lambda -3}, \\[3mm] R_1^{\ell} &=& \, \frac{\Delta \Omega}{\Omega_0} ~ \frac{2}{4 \Lambda -3}, \\[3mm] Q_0^{\ell} &=& -\frac{\Delta \Omega }{\Omega_0} ~ \frac{2 (1-3\Lambda)}{4 \Lambda -3}, \\[3mm] Q_1^{\ell} &=& -\frac{\Delta \Omega}{\Omega_0} ~ \frac{10}{4 \Lambda -3}\cdot \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq432.png) For ℓ = 1 and ℓ = 2 modes, this yields:
For ℓ = 1 and ℓ = 2 modes, this yields:
- (1)
- (2)
- (3)
Appendix C: Conditions for significant near degeneracy
As already mentionned, near degeneracy between two modes occurs whenever their frequencies are close, their azimuthal numbers are equal, and their angular degrees differ by 2. However, the magnitude of the near-degenerate corrections for both frequencies also depends on the magnitude of the coupling term Hm. In turn, the magnitude of Hm depends on the nature of the involved modes, namely whether they are g-modes, p-modes or mixed modes with a dominant p or g nature.
The g-mode spectrum is much denser than the p-mode one. Hence, as shown in Fig. C.2, Δm is much smaller than for the p-modes. This ought to favor near degeneracy. However, the coupling term Hm for g-modes is much smaller than for p-modes. This is because distorsion effects are small for g-modes and therefore the overall (second and third order) contribution to Hm remains small. As a result, the coupling term is much smaller than Δm for g-modes, which are then hardly coupled.
 |
Fig. C.1 Inertia of axisymmetric ℓ = 1 modes as a function of the radial order, n, for an evolved 8.5 M⊙β Cephei model, uniformly rotating at 30% Ωk, i.e. 160 km s-1 (see Table 2, Sect. 4.1). |
 |
Fig. C.2 The terms Δm and ℋm involved in near degeneracy corrections (see Eq. (12)) for ℓ = 1 modes computed for the same β Cephei model as in Fig. C.1. A logscale is used for the y axis. |
Appendix D: Values for third order contributions to the frequencies and to the splittings
Scaled contributions to the splittings of ℓ = 1 g-modes due to: implicit third order terms in the eigenfrequency (Teigen), Coriolis effects (TT), distorsion (TD), and coupling of the two (TC).
Scaled contributions to the splittings of ℓ = 1 p-modes due to third order effects divided by the square of the central mode frequency.
Different order contributions to the mode frequencies for various radial orders, n. All contributions are scaled by Ωk.
All Tables
Results concerning rotation from the analysis of HD 181906 performed in García et al. (2009).
Latitudinal shear, equatorial velocity and inclination angle obtained for HD 181906, using models with rotation uniform in depth.
Results concerning rotation from the analysis of HD 181420 performed in Barban et al. (2009).
Latitudinal shear, equatorial velocity, and inclination angle obtained for HD 181420, using models with a tachocline-like rotation profile.
Scaled contributions to the splittings of ℓ = 1 g-modes due to: implicit third order terms in the eigenfrequency (Teigen), Coriolis effects (TT), distorsion (TD), and coupling of the two (TC).
Scaled contributions to the splittings of ℓ = 1 p-modes due to third order effects divided by the square of the central mode frequency.
Different order contributions to the mode frequencies for various radial orders, n. All contributions are scaled by Ωk.
All Figures
 |
Fig. 1 Contributions of different approximation orders to l = 1,m = 0 mode frequencies: σ2eigen (σ3eigen) represent the implicit second (third respectively) order contribution to the eigenfrequency; σ2T and σ3T denote second and third order frequency corrections due to the Coriolis acceleration; σ2D and σ3D represent 2nd and 3rd order frequency corrections due to the centrifugal distorsion; σ3C comes from the coupling of the distorsion and Coriolis effects. The contributions are plotted as a function of the radial order n for an 8.5 M⊙ ZAMS model rotating uniformly at 15% Ωk, i.e. around 95 km s-1 (see stellar parameters in Table 1). The frequencies are scaled by |
| In the text | |
 |
Fig. 2 Frequency differences between degenerate σdeg and non-degenerate σno deg solutions scaled by |
| In the text | |
 |
Fig. 3 Scaled contributions to the splittings due to the implicit third-order terms in the eigenfrequencies |
| In the text | |
 |
Fig. 4 Behavior of left: the scaled integrals β and γ (Eq. (27)), right: the scaled contributions to the splitting, as a function of the radial order n (Eqs. (31) to (33)). Computations were made for an 8.5 M⊙ ZAMS model uniformly rotating at 15% Ωk, i.e. 95 km s-1 (see stellar parameters in Table 1). |
| In the text | |
 |
Fig. 5 Departure from linear splitting for (ℓ = 1,m = 1) triplets. Left: for Ω = 20% Ωk. Right: for Ω = 30% Ωk, as a function of the radial order. Different contributions result from: cubic-order effects (dark blue), cubic-order effects with near degeneracy (purple, these two contributions overlap for all g-modes), and latitudinally differential rotation with ΔΩ/Ω = 0.127 (light blue), 0.2 (in green), 0.3 (in orange), and 0.4 (in red). These results were computed for the uniformly rotating evolved 8.5 M⊙β Cephei model described in Sect. 5.1 (Table 2). |
| In the text | |
 |
Fig. 6 Departure from linear splitting for (ℓ = 1,m = 1) triplets due to cubic-order effects (dark blue), to cubic-order effects including near-degeneracy corrections (purple, these two contributions overlap for g5 and g2) and to latitudinally differential rotation with ΔΩ/Ω = 0.127 (light blue), 0.2 (green), 0.3 (orange), and 0.4 (red). These departures are plotted as a function of the rotation rate for a g5 mode (left), a g2 mode (center), and a p1 mode (right). These results were computed for the uniformly rotating evolved 8.5 M⊙β Cephei model described in Sect. 5.1 (Table 2). |
| In the text | |
 |
Fig. 7 Sℓ,m(p1) versus Sℓ,m(g2) due to cubic-order effects and near degeneracy (purple), and to a latitudinal shear (green), for ℓ = 1 modes in an evolved 8.5 M⊙ model (see Table 2). The rotation rate increases from left to right: from 18% Ωk to 34% Ωk. The error bars for V1449 Aquilae have been taken from Degroote et al. (2009). |
| In the text | |
 |
Fig. 8 Departure from a linear splitting as a function of the radial order for (ℓ = 1,m = 1) triplets. Left: for Ω = 3.7% Ωk. Right: Ω = 7.4% Ωk – due to cubic-order effects (blue), cubic-order effects with near degeneracy (purple, the two of them overlap for most of the modes except g2) and to a latitudinally differential rotation of 12.7% (light blue) and 20% (green). Computations were made for a model of HD 181420 (M = 1.36 M⊙, see Table 3). |
| In the text | |
 |
Fig. 9 Possible values for ΔΩ/Ω0, depending on the parameter d in Eq. (43) and the value of the integral β Eq. (B.5). The line colors corresponds to the value of (d × β), which ranges here from 0.3 (in blue) to 1.5 (in red). In gray, we indicate the acceptable domain of values for the latitudinal gradient (Eq. (45)). This plot was produced for high order p modes. |
| In the text | |
 |
Fig. C.1 Inertia of axisymmetric ℓ = 1 modes as a function of the radial order, n, for an evolved 8.5 M⊙β Cephei model, uniformly rotating at 30% Ωk, i.e. 160 km s-1 (see Table 2, Sect. 4.1). |
| In the text | |
 |
Fig. C.2 The terms Δm and ℋm involved in near degeneracy corrections (see Eq. (12)) for ℓ = 1 modes computed for the same β Cephei model as in Fig. C.1. A logscale is used for the y axis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



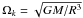
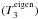
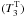
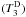

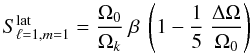
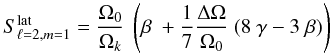
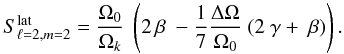
![\appendix \setcounter{section}{2} \begin{eqnarray} S_{1,1} = \, \frac{\Omega_{0}}{\Omega_k} ~ \beta ~ \left[ 1 - \frac{1}{5}~ \frac{\Delta \Omega}{\Omega_{0}} \right] \label{S11_app} \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq435.png)
![\appendix \setcounter{section}{2} \begin{eqnarray} S_{2,1} = \, \frac{\Omega_{0}}{\Omega_k} ~ \left[\beta ~ + \,\frac{1}{7}\, \frac{\Delta \Omega}{\Omega_{0}} ~ ( 8 ~ \gamma - 3 ~ \beta) \right] \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq438.png)
![\appendix \setcounter{section}{2} \begin{eqnarray} S_{2,2} = \, \frac{\Omega_{0}}{\Omega_k} \, \left[ 2~ \beta ~ - \frac{1}{7}\, \frac{\Delta \Omega}{\Omega_{0}} ~ ( 2 ~ \gamma +~ \beta)\right]. \label{S21_app} \end{eqnarray}](/articles/aa/full_html/2012/06/aa17151-11/aa17151-11-eq440.png)