| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219102 | |
| Published online | 04 May 2012 | |
Mean angular diameters, distances, and pulsation modes of the classical Cepheids FF Aquilae and T Vulpeculae
CHARA/FLUOR near-infrared interferometric observations
1
LESIA, Observatoire de Paris, CNRS UMR 8109, UPMC, Université Paris
Diderot,
5 place Jules Janssen,
92195
Meudon,
France
e-mail: alexandre.gallenne@obspm.fr
2
European Southern Observatory, Alonso de Córdova 3107, Casilla 19001,
Santiago 19,
Chile
3
Center for High Angular Resolution Astronomy, Georgia State
University, PO Box
3965, Atlanta,
Georgia
30302-3965,
USA
Received: 23 February 2012
Accepted: 21 March 2012
We report the first angular diameter measurements of two classical Cepheids, FF Aql and T Vul, that we obtain using observations with the FLUOR instrument installed at the CHARA interferometric array. We derive average limb-darkened angular diameters of θLD = 0.878 ± 0.013 mas and θLD = 0.629 ± 0.013 mas, respectively, for FF Aql and T Vul. Combining these angular diameters with the HST-FGS trigonometric parallaxes leads to linear radii R = 33.6 ± 2.2 R⊙ and R = 35.6 ± 4.4 R⊙, respectively. The comparison with empirical and theoretical period–radius relations leads to the conclusion that these Cepheids are pulsating in their fundamental mode. The knowledge of this pulsation mode is of prime importance to calibrating the period–luminosity relation with a uniform sample of fundamental mode Cepheids.
Key words: techniques: interferometric / techniques: high angular resolution / stars: variables: Cepheids / stars: distances / stars: oscillations
© ESO, 2012
1. Introduction
The direct detection of angular diameter variations in a pulsating star using optical interferometers has now been achieved for many stars (see e.g. Lane et al. 2002; Kervella et al. 2004; Mérand et al. 2006b; Davis et al. 2009; Lacour et al. 2009). The combination of angular diameters with radial velocity measurements allows us to accurately estimate their distances in a quasi-geometrical way. This independent distance determination is essential to calibrate the period-luminosity (P–L) and period-radius (P–R) relations of Cepheids. Direct radius measurements also enable us to compare theoretical (e.g. Neilson et al. 2010) and indirect radius estimates (e.g. Groenewegen 2007).
Having directly determined the diameter, we can also establish whether a Cepheid belongs to the fundamental mode group, because its average linear diameter should depart from the classical P–R relation. As different modes yield different relations, it is essential to know the pulsation mode in order to calibrate the P–L relation using a homogeneous sample of Cepheids.
We present here the first interferometric observations of the Cepheids FF Aql and T Vul. The former has a small amplitude (less than 0.5 mag in V), a sinusoidal-like light curve, and is therefore generally designated as a s-Cepheid. The s-Cepheids are suspected to be first overtone pulsators (see e.g. Bohm-Vitense 1988). T Vul has the same pulsation period as FF Aql but is expected to pulsate in the fundamental mode.
These Cepheids also belong to binary systems with hotter companions. From IUE spectra, Evans et al. (1990) detected around FF Aql a companion with a spectral type between A9 V and F3 V. This corresponds to a magnitude difference with respect to the Cepheid ΔK ~ 6.1–6.5 mag. Evans (1992) found that the companion of T Vul is a A0.8 V star, also estimated from IUE spectra, and corresponds to a magnitude difference ΔK ~ 5.2 mag.
In this paper, we focus on determining the distance and radius of these Cepheids using the interferometric Baade-Wesselink method (IBWM). We also compare the linear radii with both those in the literature and published P–R relations in order to reveal the pulsation mode.
2. Interferometric observations
The observations were performed in June 2010 and August 2011 at the CHARA Array (ten Brummelaar et al. 2005) in the near-infrared K′ band (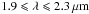 ) with the Fiber Linked Unit for Optical Recombination (FLUOR; Coudé du Foresto et al. 2003; Mérand et al. 2006a). For these observations, we used baselines longer than 200 m in order to resolve sufficiently well the two targets. The journal of the observations is presented in Table 1.
) with the Fiber Linked Unit for Optical Recombination (FLUOR; Coudé du Foresto et al. 2003; Mérand et al. 2006a). For these observations, we used baselines longer than 200 m in order to resolve sufficiently well the two targets. The journal of the observations is presented in Table 1.
Calibrated squared visibility measurements of FF Aql.
Calibrators used for the observations.
The squared visibility of the fringes was estimated from the raw data using the FLUOR data reduction software (Coudé du Foresto et al. 1997; Mérand et al. 2006a), based on the integration of the fringe power spectrum. The raw squared visibilities were then calibrated using resolved calibrator stars, chosen from the catalogue of Mérand et al. (2005a), using criteria defined to minimize the calibration bias and maximize the signal-to-noise ratio. The calibrators used for these observations are listed in Table 2. They were observed immediately before and/or after the Cepheid in order to monitor the interferometric transfer function of the instrument. The error introduced by the uncertainty in each calibrator’s estimated angular diameter was propagated using the formalism developed by Perrin (2003). The final uncertainty in the calibrated squared visibility includes statistical (from the dispersion in the raw squared visibilities obtained during the observations) and systematic errors (from the error bars on the calibrators).
For each night that we observed a Cepheid, we determined a uniform disk diameter based on one or several squared visibility measurements (Table 1). Each night was assigned a unique pulsation phase established using the average date of observation and the Samus et al. (2009) ephemeris: P = 4.470916 days and T0 = 2 441 576.4280 for FF Aql, and P = 4.435462 days and T0 = 2 441 705.1210 for T Vul.
3. The interferometric Baade-Wesselink method
The IBWM makes use of radial velocity and angular diameter measurements of the star during its pulsation cycle. This involves a good phase coverage and the highest possible angular resolution. The integral over time of the radial velocity is then directly linked to the angular diameter variation.
The presence of a companion can falsify the results if its magnitude is close to the one of the Cepheid, and if the orbital effect is detectable in the spectroscopic measurements. In our case, these main sequence companions are faint compared to the Cepheids, and do not affect the photometric signals. Only the radial velocities are affected by the presence of the companions and have to be corrected.
3.1. Radial velocity integrations
Among the published radial velocity data of FF Aql, we chose Evans et al. (1990) for two reasons. First, the orbital motion caused by the presence of the companion had already been removed from measurements, leaving only the displacement due to the pulsating photosphere. Secondly, the radial velocities were extracted using the cross-correlation method. As shown by Nardetto et al. (2004), the method used can affect the distance determination via the choice of the projection factor (hereafter p-factor), which we introduce in Sect. 3.2. For T Vul, we use the radial velocities of Bersier et al. (1994), also from the cross-correlation method. The amplitude of the orbital motion was not detected with this data so we did not apply any corrections for the presence of the companion. For both Cepheids, we redetermined the pulsation phases using the ephemeris presented previously.
The radial velocities, which were derived from data acquired at irregular phases, must be numerically integrated to get the radial displacement. The best way to achieve a robust integration and avoid noisy data is to interpolate the data before integration. For this purpose, the radial velocities were smoothly interpolated using a periodic cubic-spline function, defined by floating nodes. This method had already been used by Mérand et al. (2007) and we refer the reader to this paper for a detailed explanation. The interpolated curves for our two Cepheids are presented in Fig. 1. The dispersion of the residuals are σ = 61 m s-1 and σ = 68 m s-1, respectively, for T Vul and FF Aql.
 |
Fig. 1 Radial velocity data of FF Aql and T Vul. The solid line is the periodic cubic-spline function defined with four adjustable floating nodes (large black dots). The lower panel displays the residuals of the fit. |
 |
Fig. 2 Uniform disk angular-diameter variation of FF Aql and T Vul. The solid line is the integration of the radial velocity curve with the distance, average angular diameter, and period change as fitted parameters. The dashed line includes the period change. The lower panel displays the residuals of the fit. |
3.2. Distance determination
Our angular diameter measurements were then fitted to the radial displacements to get the distance d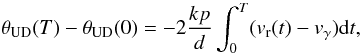 (1)where p is the so-called p-factor, defined as the ratio of the pulsation velocity to the radial velocity (measured by spectroscopy), θUD the interferometric angular diameter for a uniform disk model, k the ratio of the uniform to the limb-darkened stellar diameter, and vγ the systemic velocity.
(1)where p is the so-called p-factor, defined as the ratio of the pulsation velocity to the radial velocity (measured by spectroscopy), θUD the interferometric angular diameter for a uniform disk model, k the ratio of the uniform to the limb-darkened stellar diameter, and vγ the systemic velocity.
The parameters of the fit are the average angular diameter θUD(0), the quantity d/kp, and a possible variation in the pulsation period between interferometric and spectroscopic observations.
The p-factor depends on the detailed modelling of the stellar atmosphere, but such models are only available for a few Cepheids and we conventionally choose a multiplicative constant factor. Nardetto et al. (2004) showed that the choice of a constant factor instead of a time-dependent ones gives a systematic error in the final distance of ~0.2%, which is below the highest relative precision of current distance estimates. Mérand et al. (2005b) presented the unique measured value p = 1.27 ± 0.06 for δ Cep. Although there is no agreement in the literature about the optimum value of the p-factor, it is clear that it depends on each Cepheid. Different authors use either constant p-factor values (ranging from 1.27 to 1.5), or a dependence on the pulsation period. The period dependence is likely to reflect the dependence on the limb darkening. For this work, we chose the latest p-factor relation p = 1.550 ± 0.04−0.186 ± 0.06 log P of Storm et al. (2011), because this is an empirical relation based on the largest sample of Cepheids, covering the widest range of periods. We have for both stars p = 1.43 ± 0.06.
The k parameter is generally determined assuming a limb-darkened disk model and is expected to vary with the pulsation phase. However, in the near-IR, Marengo et al. (2003) showed from hydrodynamic models in spherical geometry that k is constant with the pulsation at a level of 0.2%. From hydrostatic models, Mérand (2008) found a variation in k of the order of 0.4%. Our interferometric measurements are insensitive to this variation and we therefore assumed a constant limb-darkening coefficient. The hydrostatic model computed from Claret coefficients (Claret 2000), with the average stellar parameters Teff = 6000 K,log g = 2, Fe/H = 0.0, and Vt = 4 km s-1 from Luck et al. (2008) for FF Aql and Andrievsky et al. (2005) for T Vul, corresponds to k = 0.985. The IBWM fit yields for FF Aql a distance d = 363 ± 73 pc and an average angular uniform-disk diameter θUD = 0.865 ± 0.013 mas, with a total reduced χ2 of 0.4. For T Vul, we obtain d = 415 ± 100 pc and θUD = 0.620 ± 0.012 mas, with a total reduced χ2 of 2.5. These results are summarized in Table 3 and the angular diameter variations are plotted in Fig. 2. We also allowed a change in the period for FF Aql and T Vul of ~14 s and ~−26 s, respectively.
Cepheid average angular diameters and distances determined by applying the interferometric BW method.
3.3. Linear radius
We transformed the uniform disk diameters to limb-darkened disk diameters using the value of k previously chosen, deriving θLD = 0.878 ± 0.013 mas for FF Aql and θLD = 0.629 ± 0.013 mas for T Vul. These measured values, which have an accuracy ~1.5%, are in good agreement with those predicted from the IR surface brightness method (e.g. Moskalik & Gorynya 2005; Groenewegen 2007). The fitted distance of FF Aql is also consistent with the derived value d = 356 ± 23 pc from the HST-FGS parallax of Benedict et al. (2007). The same authors give for T Vul d = 526 ± 64 pc, which is ~27% larger than our value, but within 1.1σ. As the values of Benedict et al. (2007) are more accurate and do not depend on a p-factor assumption (compared to our fitted distances), we preferred to use them to evaluate the linear radius. We therefore used the HST-FGS distances in the BW fit and obtained R = 33.6 ± 2.2 R⊙ and R = 35.6 ± 4.4 R⊙, respectively, for FF Aql and T Vul.
In our analysis, we did not take into account a possible circumstellar envelope (CSE) emission, which could lead to an overestimate of the angular diameter. From the spectral energy distribution of FF Aql given by Gallenne et al. (2012), the infrared excess caused by the CSE appears around 10 μm, while it is negligible at 2.2 μm. We assumed that this is also the case for T Vul.
3.4. p-factor
We used the HST-FGS distances in Eq. (1) to directly fit the p-factor, as previously done by Mérand et al. (2005b) for δ Cep. We obtained p = 1.40 ± 0.28 and p = 1.81 ± 0.44, for FF Aql and T Vul, respectively. These estimates can be compared with the empirical and theoretical p–P relations, respectively, of Storm et al. (2011) and Nardetto et al. (2009). For FF Aql, the p-factor is compatible with the value derived from the empirical relation, while the estimate of T Vul is within 1σ. Although at odds with the theoretical relation, our estimates are not accurate enough to constrain it.
A direct determination of the p-factor is a powerful constraint of the numerical atmosphere models of Cepheids, although our work does not contain enough measurements to accurately estimate this parameter for these stars.
4. Period–radius relation
The estimated linear radii can be compared with empirical and theoretical period–radius (P–R) relations, which are of the form log R = a log P + b. We chose the theoretical calculations of Neilson et al. (2010), who used a pulsation-driven mass-loss model. We also selected the results of Groenewegen (2007), who used Cepheids with known distances and angular diameters to derive an empirical P–R relation. These two relations are valid only for fundamental mode Cepheids.
In principle, the position of a Cepheid in the P–R diagram can reveal its pulsation mode, if the estimated radius is sufficiently accurate. In Fig. 3, we have plotted the P–R relations (thick curves) and our estimated linear radii. The intrinsic dispersion in each relation is represented by thinner curves (of the same colour and symbol). We note that both Cepheids are consistent (within the intrinsic dispersion) with stars pulsating in a fundamental mode. We have also plotted with triangles the radii assuming an overtone pulsation, using the ratio of the overtone period P1 to the fundamental period P0 given by P1/P0 = 0.720−0.027 log P0 (Alcock et al. 1995). In addition, we represented with squares the radii of the star assuming first overtone radii, by using the theoretical first overtone P–R relation of Bono et al. (2001). The overtone mode does not seem compatible with the P–R relations, and therefore suggest that FF Aql and T Vul are pulsating in the fundamental mode.
 |
Fig. 3 Period–radius relation for fundamental mode Cepheids. The colour curves represent the empirical and theoretical P–R relations from the literature. Each P–R intrinsic dispersion is plotted with a thinner curve, of the same colour and symbol. The dots are our estimated linear radii, the triangles are radii converted for first overtone pulsation, and the squares represent the theoretical first overtone radii. |
5. Conclusions and discussion
We have reported the first interferometric observations of two classical Cepheids, FF Aql and T Vul, with the CHARA/FLUOR instrument. The angular diameter variations were monitored over the pulsation cycle and combined with previously published radial velocity measurements to get independent estimates of the distance and mean angular diameter. The precision achieved is ~2% in their average angular diameter estimates.
We have found for FF Aql good agreement (0.3σ) between our fitted distance and the HST-FGS estimate (Benedict et al. 2007). For T Vul, a discrepancy is found between the two estimates, our value being ~27% smaller, but within 1.1σ. The main source of bias in the use of the BW method is the choice of the p-factor, which could explain the discrepancy encountered. We also note that additional interferometric measurements, of higher accuracy, would also help to reduce this discrepancy. To avoid a possible bias in the distance due to the p-factor assumption, we coupled our angular diameters with existing trigonometric parallaxes to evaluate the linear radii.
When we compared the linear radii with empirical and theoretical P–R relations, we were able to demonstrate that these two short-period Cepheids are pulsating in their fundamental mode. Our work confirms the pulsation mode of T Vul, which as been flagged as a fundamental pulsator by several authors (e.g. Groenewegen 2000, and references therein). However, this is not the case for FF Aql. This s-Cepheid, which has a small light-curve amplitude and practically sinusoidal light curve, is usually assumes to be pulsating in the first overtone (e.g. Sachkov 1997). As the pulsation mode is generally identified using the Fourier decomposition of either the light curve or the radial velocity curve, the presence of a companion around FF Aql could lead to an error in the determination of the pulsation mode. If the difference between the magnitude of the Cepheid and that of its companion is small, the apparent magnitude of the Cepheid will be falsified. The radial velocity measurements can also be altered because of the orbital effect.
The knowledge of the pulsation mode is of prime importance to calibrating the P–L relation with an uniform sample of fundamental mode Cepheids, since different modes will yield different relations.
Acknowledgments
The authors would like to thank the CHARA Array and Mount Wilson Observatory staff for their support. Research conducted at the CHARA Array is funded by the National Science Foundation through NSF grant AST-0908253, by Georgia State University, the W. M. Keck Foundation, the Packard Foundation, and the NASA Exoplanet Science Institute. We received the support of PHASE, the high angular resolution partnership between ONERA, Observatoire de Paris, CNRS, and University Denis Diderot Paris 7. This work made use of the SIMBAD and VIZIER astrophysical database from CDS, Strasbourg, France and the bibliographic informations from the NASA Astrophysics Data System. Data processing for this work have been done using the Yorick language which is freely available at http://yorick.sourceforge.net/.
References
- Alcock, C., Allsman, R. A., Axelrod, T. S., et al. 1995, AJ, 109, 1653 [NASA ADS] [CrossRef] [Google Scholar]
- Andrievsky, S. M., Luck, R. E., & Kovtyukh, V. V. 2005, AJ, 130, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Feast, M. W., et al. 2007, AJ, 133, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Bersier, D., Burki, G., Mayor, M., & Duquennoy, A. 1994, A&AS, 108, 25 [NASA ADS] [Google Scholar]
- Bohm-Vitense, E. 1988, ApJ, 324, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Bono, G., Caputo, F., & Marconi, M. 2001, MNRAS, 325, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Coudé du Foresto, V., Ridgway, S., & Mariotti, J. 1997, A&AS, 121, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coudé du Foresto, V., Borde, P. J., Merand, A., et al. 2003, in SPIE Conf. Ser. 4838, ed. W. A. Traub, 280 [Google Scholar]
- Davis, J., Jacob, A. P., Robertson, J. G., et al. 2009, MNRAS, 394, 1620 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. R. 1992, AJ, 104, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. R., Welch, D. L., Scarfe, C. D., & Teays, T. J. 1990, AJ, 99, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- Gallenne, A., Kervella, P., & Mérand, A. 2012, A&A, 538, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2000, A&A, 363, 901 [NASA ADS] [Google Scholar]
- Groenewegen, M. A. T. 2007, A&A, 474, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Nardetto, N., Bersier, D., Mourard, D., & Coudé du Foresto, V. 2004, A&A, 416, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Thiébaut, E., Perrin, G., et al. 2009, ApJ, 707, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, B. F., Creech-Eakman, M. J., & Nordgren, T. E. 2002, ApJ, 573, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., Andrievsky, S. M., Fokin, A., & Kovtyukh, V. V. 2008, AJ, 136, 98 [Google Scholar]
- Marengo, M., Karovska, M., Sasselov, D. D., et al. 2003, ApJ, 589, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A. 2008, in EAS Publ. Ser. 28, ed. S. Wolf, F. Allard, & P. Stee, 53 [Google Scholar]
- Mérand, A., Bordé, P., & Coudé Du Foresto, V. 2005a, A&A, 433, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Kervella, P., Coudé du Foresto, V., et al. 2005b, A&A, 438, L9 [Google Scholar]
- Mérand, A., Coudé du Foresto, V., Kellerer, A., et al. 2006a, in SPIE Conf. Ser., 6268, 46 [Google Scholar]
- Mérand, A., Kervella, P., Coudé du Foresto, V., ten Brummelaar, T., & McAlister, H. 2006b, MSAI, 77, 231 [NASA ADS] [Google Scholar]
- Mérand, A., Aufdenberg, J. P., Kervella, P., et al. 2007, ApJ, 664, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Moskalik, P., & Gorynya, N. A. 2005, Acta Astron., 55, 247 [NASA ADS] [Google Scholar]
- Nardetto, N., Fokin, A., Mourard, D., et al. 2004, A&A, 428, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Gieren, W., Kervella, P., et al. 2009, A&A, 502, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., Ngeow, C., Kanbur, S. M., & Lester, J. B. 2010, ApJ, 716, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, G. 2003, A&A, 400, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sachkov, M. E. 1997, Inform. Bull. Variable Stars, 4522, 1 [NASA ADS] [Google Scholar]
- Samus, N. N., Durlevich, O. V., et al. 2009, VizieR Online Data Catalog: B/gcvs, Originally published in: Institute of Astronomy of Russian Academy of Sciences and Sternberg, State Astronomical Institute of the Moscow State University, 1, 2025 [Google Scholar]
- Storm, J., Gieren, W., Fouqué, P., et al. 2011, A&A, 534, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Cepheid average angular diameters and distances determined by applying the interferometric BW method.
All Figures
 |
Fig. 1 Radial velocity data of FF Aql and T Vul. The solid line is the periodic cubic-spline function defined with four adjustable floating nodes (large black dots). The lower panel displays the residuals of the fit. |
| In the text | |
 |
Fig. 2 Uniform disk angular-diameter variation of FF Aql and T Vul. The solid line is the integration of the radial velocity curve with the distance, average angular diameter, and period change as fitted parameters. The dashed line includes the period change. The lower panel displays the residuals of the fit. |
| In the text | |
 |
Fig. 3 Period–radius relation for fundamental mode Cepheids. The colour curves represent the empirical and theoretical P–R relations from the literature. Each P–R intrinsic dispersion is plotted with a thinner curve, of the same colour and symbol. The dots are our estimated linear radii, the triangles are radii converted for first overtone pulsation, and the squares represent the theoretical first overtone radii. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


