| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 6 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201218992 | |
| Published online | 27 April 2012 | |
Breit-Pauli oscillator strengths and electron excitation collision strengths for Si VIII⋆
Department of Physics, Clark Atlanta University, Atlanta, GA 30314, USA
e-mail: stayal@cau.edu
Received: 8 February 2012
Accepted: 19 March 2012
Aims. Oscillator strengths and electron impact excitation collision strengths for transitions between the 68 fine-structure levels of the 2s22p3, 2s2p4, 2p5, 2s22p23s, 2s22p23p, 2s22p23d and 2s2p33s configurations in Si VIII are calculated. Thermally averaged collision strengths are presented as a function of electron temperature for application to solar and other astrophysical plasmas.
Methods. The collision strengths have been calculated using the B-splineBreit-Pauli R-matrixmethod for allowed and forbidden transitions in Si VIII. The relativistic effects have been incorporated through mass, Darwin and spin-orbit one-body operators in the Breit-Pauli Hamiltonian in the scattering calculation, while in the calculation of oscillator strengths the one-body and two-body relativistic operators are included. Flexible non-orthogonal sets of spectroscopic and correlation radial functions are used to obtain accurate description of Si VIII levels and to represent the scattering functions. The 68 fine-structure levels of the 2s22p3, 2s2p4, 2p5, 2s22p23s, 2s22p23p, 2s22p23d and 2s2p33s configurations have been considered in both the radiative and scattering calculations. The present scattering calculations are more extensive than previous ones, leading to a total 2278 transitions between fine-structure levels.
Results. The calculated excitation energies are in excellent agreement with experiment and represent an improvement over the previous calculations. The present collision strengths show reasonable agreement with the previously available R-matrix and distorted-wave calculations. The oscillator strengths for E1 transitions normally compare very well with previous calculations. The effective collision strengths are obtained by integrating total resonant and non-resonant collision strengths over a Maxwellian distribution of electron energies and these are presented over a wide temperature range from 104 to 4.0 × 106 K.
Key words: atomic processes / atomic data / Sun: corona / Sun: transition region
Tables 1–4 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/541/A61
© ESO, 2012
1. Introduction
Emission lines of silicon ions have been observed in different astrophysical objects for many years, and the knowledge of the radiative and collision atomic data of silicon ions in different ionization stages is crucial in modeling and understanding of processes occurring in the solar corona, nebulae and stellar atmospheres. The Si VIII forbidden lines are detected at 944.38, 949.22, 1440.49 and 1445.00 Å in the spectra of solar corona by SOHO/SUMER instrument. In addition to forbidden lines, Kink et al. (1999) identified lines of N-like Si VIII due to high-excitation 2s22p23s–2s22p23p and 2s22p23p–2s22p23d transitions in the solar coronal spectrum obtained by the SUMER. Spectral lines of N-like Mg VI and Si VIII due to 2s22p3–2s2p4 transitions have been observed with SERTS in the EUV spectrum of solar active region (Thomas & Neupert 1994). The Si VIII lines of the 2s22p3 4So–2s2p4 4P transitions occur at 314−320 Å in SERTS spectra, and line ratios of the 2s22p3 2Do–2s2p4 2D lines to the 2s22p3 4So–2s2p4 4P lines are density sensitive over the density range 108–1012 cm-3. The forbidden lines of Si VIII have been used to determine electron density in the solar atmosphere (Feldman et al. 1978). The N-like ions can provide some of the best density diagnostics, but the line blending and inconsistencies in the currently available atomic data has hampered their potential (Young & Thomas 1998). The line intensity ratios of the N-like ions forbidden lines from the ground configuration to the high-excitation lines are temperature sensitive (Kink et al. 1999) and can be used as plasma temperature diagnostics over a wide temperature range of the solar corona. However, the potential of these diagnostics is currently limited due to the lack of accurate atomic data. There are inconsistencies between the observed and theoretical predictions for line intensities of N-like Mg VI and Si VIII ions due to the atomic data for these ions (Bhatia & Landi 2003).
The excitation energy levels, oscillator strengths and electron excitation collision strengths for transitions in Si VIII have been studied both theoretically and experimentally. However, there is very little experimental work available on Si VIII spectral lines. The observed spectral wavelengths data have been compiled by Martin & Zalubas (1983) and Podobedova et al. (2004). The NIST Atomic Spectra Database reported energy level data for 60 Si VIII levels and Podobedova et al. (2004) reported data in the wavelength region 25–170 Å for astrophysical applications to Chandra X-ray Observatory. The Si VIII lines were identified in the solar coronal spectrum by the analysis of solar spectra combined with the laboratory spectra obtained using the beam-foil technique (Kink et al. 1999). The absolute wavelengths for 14 Si VIII spectral lines were determined by a calibration polynomial using in-beam reference lines of other silicon ions. In astrophysical plasma applications, the majority of required radiative decay rates and collisional rate coefficients are derived from calculations. In the present paper we present oscillator strengths, electron impact collision strengths and effective collision strengths for fine-structure transitions among the lowest 68 levels over a temperature range that is suitable for astrophysical plasma modeling calculations.
The reliable theoretical study of low-energy electron collisions with Si VIII ion requires an accurate target description and a sufficient number of target states in the close-coupling expansion to achieve convergence for the transitions of interest. The accurate description of Si VIII target wave functions includes a proper account of the strong term dependence of the valence orbitals and an adequate treatment of significant correlation corrections and relaxation effects. The purpose of the work reported here is to provide a set of accurate oscillator strengths and collision strengths for electron excitation of Si VIII for applications to astrophysical plasmas. Our scattering calculations are performed by using highly accurate target wave functions and by including fine-structure effects in the close-coupling expansions directly to make sure that the relativistic effects are adequately accounted in the scattering calculation. The present calculations were carried out with the B-spline Breit-Pauli R-matrix (BSR) approach (Zatsarinny & Tayal 2001; Zatsarinny 2006). One of the distinct features of the present method is the use of term-dependent non-orthogonal orbital sets in the description of the target states. This allows us to optimize the atomic wave functions for different states independently, resulting in a more accurate target description than those used in previous collision calculations.
2. Excitation energies, oscillator strengths and lifetimes
We have constructed Si VIII state wave functions from non-orthogonal orbitals to describe term dependence of valence orbitals as well as correlation and relaxation effects. A set of orthogonal orbitals is optimized for each atomic state separately. However, the different sets of orthogonal orbitals thus obtained for different states are not orthogonal to each other. The non-orthogonal orbitals provide much greater flexibility in the choice of wave functions than the orthogonal orbitals and also allow to include correlation with a reasonable number of configurations and correlated orbitals (Zatsarinny & Tayal 2001). Our calculations are performed using the multi-configuration Hartree-Fock (MCHF) method (Froese Fischer 1991; Zatsarinny & Froese Fischer 2000). In the MCHF approach the atomic state is represented by an atomic state function 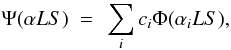 (1)where the configuration state functions (CSFs) Φ(αiLS) are constructed from one-electron functions and αi defines the coupling of angular momenta of the electrons. The J-dependent atomic state functions are written as a sum over different LS values which couple to give the total angular momentum J
(1)where the configuration state functions (CSFs) Φ(αiLS) are constructed from one-electron functions and αi defines the coupling of angular momenta of the electrons. The J-dependent atomic state functions are written as a sum over different LS values which couple to give the total angular momentum J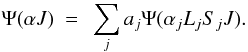 (2)The 2s22p3, 2s2p4, 2p5, 2s22p23l (l = 0−2) and 2s2p33s configurations define the low-lying states of Si VIII that we have considered in our work. These states show different correlation pattern. We began with the Hartee-Fock (HF) calculation for the 1s, 2s and 2p orbitals for the ground 2s22p3
(2)The 2s22p3, 2s2p4, 2p5, 2s22p23l (l = 0−2) and 2s2p33s configurations define the low-lying states of Si VIII that we have considered in our work. These states show different correlation pattern. We began with the Hartee-Fock (HF) calculation for the 1s, 2s and 2p orbitals for the ground 2s22p3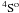 state and then determined separate sets of 2s, 2p, 3s, 3p and 3d orbitals by optimization on different states. Three separate sets of s, p, d, f and g correlation orbitals are also obtained by optimization on the 2s22p3
state and then determined separate sets of 2s, 2p, 3s, 3p and 3d orbitals by optimization on different states. Three separate sets of s, p, d, f and g correlation orbitals are also obtained by optimization on the 2s22p3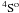 , 2s22p23s 4P and 2s22p23s 2P states. The correlation corrections for Si VIII are significant. The term dependence of the 3s, 3p and 3d valence orbitals is due to both the intermediate term and the final total term. We used a total of 61 orbitals in our calculations.
, 2s22p23s 4P and 2s22p23s 2P states. The correlation corrections for Si VIII are significant. The term dependence of the 3s, 3p and 3d valence orbitals is due to both the intermediate term and the final total term. We used a total of 61 orbitals in our calculations.
The spectroscopic and correlation functions are used to construct configuration-interaction (CI) expansions for different atomic states by allowing one-electron and two-electron excitations from all the main configurations mentioned above. In the construction of CI expansions for fine-structure levels with various J and π we used CSFs generated in this excitation scheme for the atomic LS states and with insignificant CSFs omitted from the expansions. We retained 2040 and 1475 CSFs for even and odd parity levels respectively in our calculations of oscillator strengths. We further omitted configurations with weights less than 0.005 in calculation for the description of target wave functions to make the subsequent scattering calculations computationally feasible. In our scattering calculations a total of 1076 CSFs were used to describe the target states of both even parity and odd parity. The calculated excitation energies from the latter calculation are listed in Table 1 together with the calculation of Bhatia & Landi (2003) and experimental energies. The present calculation represents an improvement over the calculation of Bhatia & Landi (2003) who used a set of the same orthogonal one-electron orbitals to represent all target states. They calculated energy levels, oscillator strengths and radiative rates by using the Superstructure program of Eissner & Nussbaumer (1974) in intermediate coupling. Bell et al. (2001) and Ramsbottom et al. (2003) calculated target state energies in LS coupling only. Our calculation is normally well within 2% of the measurement. An excellent agreement with measured values establishes a good quality of target wave functions used in our scattering calculations. We believe that our wave functions correctly represent the main correlation corrections, the interactions between different Rydberg series and term dependence effects. The theoretical lifetimes calculated in length form for various fine-structure levels are also displayed in last column of Table 1.
The oscillator strengths and transition probabilities for some dipole transitions E1 from the ground 2s22p3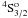 and excited metastable
and excited metastable 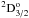 and
and 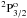 levels have been compared with the CI calculations of Bhatia & Landi (2003) and Tachiev & Froese Fischer (2002) in Table 2. The initial and final levels of a transition are given in Cols. 1 and 2 and in Cols. 3 and 4 we have listed the corresponding (2J + 1) values of the initial and final levels. We have presented our length values of oscillator strengths and transition probabilities in Table 2. We have used experimental energies in the calculations of oscillator strengths and radiative rates. A rather reasonable agreement between different calculations is noted. Our calculation shows somewhat better agreement with the results of Tachiev & Froese Fischer (2002). We present oscillator strengths and transition probabilities for allowed and intercombination lines between the 68 fine-structure levels in Table 3. The relativistic effects were included through the spin-orbit, spin-other-orbit, spin-spin, mass and Darwin Breit-Pauli operators. We have presented oscillator strengths in both length and velocity formulations and transition probabilities in length form in Table 3. We have also listed wavelengths in this table. The values of oscillator strengths for intercombination lines are usually much smaller than those for the allowed transitions. The intercombination lines are induced by the spin-orbit interaction by causing mixing between different LS symmetries with the same set of quantum numbers J and π. The agreement between the length and velocity forms of oscillator strengths may to some extent indicate the accuracy of wave functions and convergence of CI expansions. However, it is not a sufficient condition for the accuracy of results. The convergence of results is an important accuracy criterion. There is normally a very good agreement between the present length and velocity forms of oscillator strengths, particularly for transitions with significant strengths.
levels have been compared with the CI calculations of Bhatia & Landi (2003) and Tachiev & Froese Fischer (2002) in Table 2. The initial and final levels of a transition are given in Cols. 1 and 2 and in Cols. 3 and 4 we have listed the corresponding (2J + 1) values of the initial and final levels. We have presented our length values of oscillator strengths and transition probabilities in Table 2. We have used experimental energies in the calculations of oscillator strengths and radiative rates. A rather reasonable agreement between different calculations is noted. Our calculation shows somewhat better agreement with the results of Tachiev & Froese Fischer (2002). We present oscillator strengths and transition probabilities for allowed and intercombination lines between the 68 fine-structure levels in Table 3. The relativistic effects were included through the spin-orbit, spin-other-orbit, spin-spin, mass and Darwin Breit-Pauli operators. We have presented oscillator strengths in both length and velocity formulations and transition probabilities in length form in Table 3. We have also listed wavelengths in this table. The values of oscillator strengths for intercombination lines are usually much smaller than those for the allowed transitions. The intercombination lines are induced by the spin-orbit interaction by causing mixing between different LS symmetries with the same set of quantum numbers J and π. The agreement between the length and velocity forms of oscillator strengths may to some extent indicate the accuracy of wave functions and convergence of CI expansions. However, it is not a sufficient condition for the accuracy of results. The convergence of results is an important accuracy criterion. There is normally a very good agreement between the present length and velocity forms of oscillator strengths, particularly for transitions with significant strengths.
3. Collision calculation
We used B-spline basis for the description of continuum functions and did not impose any orthogonality constraint between continuum functions and the valence spectroscopic and correlated atomic orbitals (Zatsarinny & Tayal 2001; Zatsarinny 2006). This allowed us to avoid potential inconsistencies between the continuum and bound parts of the close-coupling expansion. We included 68 fine-structure levels arising from the lowest 32 LS target terms of the 2s22p3, 2s2p4, 2p5, 2s22p23l (l = 0−2) and 2s2p33s configurations in the close-coupling expansion. The inclusion of these levels in the expansion ensures channel coupling effects reasonably well up to the excited 2s22p2(1D)3d 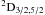 levels around 15.4 Ryd. The theoretical approach and codes used in the calculation of collision strengths have been described by Zatsarinny (2006), and here we present a brief outline. The wave function describing the total e+Si VIII system in the internal region is expanded in terms of energy-independent functions
levels around 15.4 Ryd. The theoretical approach and codes used in the calculation of collision strengths have been described by Zatsarinny (2006), and here we present a brief outline. The wave function describing the total e+Si VIII system in the internal region is expanded in terms of energy-independent functions 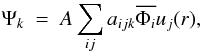 (3)where
(3)where 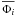 are channel functions formed from the multi-configurational functions of the 68 target levels and uj are the radial basis functions describing the motion of the scattering electron. The operator A antisymmetrizes the wave function and expansion coefficients aijk are determined by diagonalizing the (N + 1)-electron Hamiltonian. In our calculation, the radial functions uj are expanded in the B-spline basis as
are channel functions formed from the multi-configurational functions of the 68 target levels and uj are the radial basis functions describing the motion of the scattering electron. The operator A antisymmetrizes the wave function and expansion coefficients aijk are determined by diagonalizing the (N + 1)-electron Hamiltonian. In our calculation, the radial functions uj are expanded in the B-spline basis as 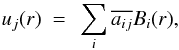 (4)and the coefficients
(4)and the coefficients 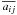 (which now replace aijk in Eq. (3)) are determined by diagonalizing the (N + 1)-electron Hamiltonian inside the R-matrix box that contained all bound atomic orbitals used for the description of Si VIII levels. The relativistic effects in the scattering calculations have been incorporated in the Breit-Pauli Hamiltonian through the use of the Darwin, mass correction and spin-orbit operators. The radius of the R-matrix box was chosen to be 6.2a0 and 54 B-splines were used for the expansion of continuum orbitals. These parameters were sufficient to obtain converged results for a wide energy range up to about 100.0 Ryd. The scattering parameters are found by matching the inner solution at r = a with asymptotic solutions in the outer region. The Seaton’s STGF program as extended by Badnell (1999) has been employed to find the asymptotic solutions and collision parameters. The B-spline R-matrix calculations were carried out for partial waves up to J = 35. These partial waves were estimated normally to give converged cross sections for forbidden transitions. For the dipole allowed transitions a top-up procedure based on the Coulomb-Bethe approximation (Burgess & Sheorey 1974) was employed to estimate the contributions for J larger than 35. The top-up contributions for the non-dipole transitions have been estimated by assuming that the collision strengths form a geometric progression in J.
(which now replace aijk in Eq. (3)) are determined by diagonalizing the (N + 1)-electron Hamiltonian inside the R-matrix box that contained all bound atomic orbitals used for the description of Si VIII levels. The relativistic effects in the scattering calculations have been incorporated in the Breit-Pauli Hamiltonian through the use of the Darwin, mass correction and spin-orbit operators. The radius of the R-matrix box was chosen to be 6.2a0 and 54 B-splines were used for the expansion of continuum orbitals. These parameters were sufficient to obtain converged results for a wide energy range up to about 100.0 Ryd. The scattering parameters are found by matching the inner solution at r = a with asymptotic solutions in the outer region. The Seaton’s STGF program as extended by Badnell (1999) has been employed to find the asymptotic solutions and collision parameters. The B-spline R-matrix calculations were carried out for partial waves up to J = 35. These partial waves were estimated normally to give converged cross sections for forbidden transitions. For the dipole allowed transitions a top-up procedure based on the Coulomb-Bethe approximation (Burgess & Sheorey 1974) was employed to estimate the contributions for J larger than 35. The top-up contributions for the non-dipole transitions have been estimated by assuming that the collision strengths form a geometric progression in J.
In many astrophysical applications it is convenient to use excitation rate coefficients or thermally averaged collision strengths as a function of electron temperature. The excitation rates are obtained by averaging collision strengths over a Maxwellian distribution of electron energies. The excitation rate coefficient for a transition from state i to state f at electron temperature Te is given by 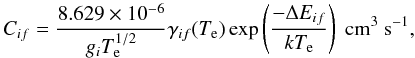 (5)where gi is the statistical weight of the lower level i, ΔEif = Ef − Ei is the excitation energy, and γif is a dimensionless quantity called effective collision strength given by
(5)where gi is the statistical weight of the lower level i, ΔEif = Ef − Ei is the excitation energy, and γif is a dimensionless quantity called effective collision strength given by 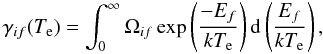 (6)where Ef is the energy of incident electron with respect to the upper level f. If the collision strength is assumed to be independent of the incident electron energy, we have γif = Ωif. The effective collision strengths are calculated by integrating collision strengths for fine-structure levels over a Maxwellian distribution of electron energies. The integration in Eq. (6) should be carried out using energy dependent collision strengths from threshold to infinity. The collision strengths at higher energies are particularly important for the allowed transitions. The energy dependence of collision strengths for allowed transitions can be properly accounted by using extrapolation technique. In the asymptotic region, the collision strengths follow a high energy limiting behavior for the dipole-allowed transitions
(6)where Ef is the energy of incident electron with respect to the upper level f. If the collision strength is assumed to be independent of the incident electron energy, we have γif = Ωif. The effective collision strengths are calculated by integrating collision strengths for fine-structure levels over a Maxwellian distribution of electron energies. The integration in Eq. (6) should be carried out using energy dependent collision strengths from threshold to infinity. The collision strengths at higher energies are particularly important for the allowed transitions. The energy dependence of collision strengths for allowed transitions can be properly accounted by using extrapolation technique. In the asymptotic region, the collision strengths follow a high energy limiting behavior for the dipole-allowed transitions 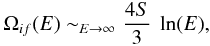 (7)where S is the line strength. The collision strengths vary smoothly in the high energy region and exhibit an increasing trend for dipole-allowed transitions. The collision strength increases more rapidly for the stronger dipole-allowed transitions than the weaker transitions. In the case of the non-dipole transitions such as electric quadrupole or magnetic-dipole transitions the high energy limiting behavior is given by
(7)where S is the line strength. The collision strengths vary smoothly in the high energy region and exhibit an increasing trend for dipole-allowed transitions. The collision strength increases more rapidly for the stronger dipole-allowed transitions than the weaker transitions. In the case of the non-dipole transitions such as electric quadrupole or magnetic-dipole transitions the high energy limiting behavior is given by 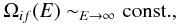 (8)where the value of constant can be obtained from the Born approximation.
(8)where the value of constant can be obtained from the Born approximation.
 |
Fig. 1 Collision strengths for the forbidden 2s22p3 |
 |
Fig. 2 Collision strengths for the forbidden 2s22p3 |
 |
Fig. 3 Collision strengths for the forbidden 2s22p3 |
4. Collision strengths
The collision strengths are determined by matching the inner solution at r = a to the asymptotic solutions in the outer region. We chose a fine-energy grid of 2 × 10-4 Ryd in the closed-channel energy region up to the 2s2p4 2P1/2 threshold and a grid of 3.5 × 10-2 Ryd up to the 2p2(1D)3d 2D5/2 threshold. This allowed us to delineate important resonance structures in the collision strengths. At higher energies where all channels are open and there are no resonances, the collision strengths show smooth behavior and we use an energy grid of 0.4 Ryd. The collision strengths for the forbidden 2s22p3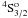 –
–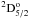 (1–3), 2s22p3
(1–3), 2s22p3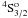 –
–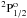 (1–4) and 2s22p3
(1–4) and 2s22p3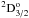 –
–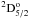 (2–3) transitions have been displayed in Figs. 1–3 as a function of incident electron energy. The collision strengths have been displayed from excitation threshold to the 2s22p2(1D)3d
(2–3) transitions have been displayed in Figs. 1–3 as a function of incident electron energy. The collision strengths have been displayed from excitation threshold to the 2s22p2(1D)3d 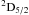 threshold at 15.45 Ryd. The resonance structures are almost completely resolved with a very fine energy mesh in our calculation. The resonance structures are very complex and quite dense due to many overlapping Rydberg series converging to various thresholds. The background collision strengths away from resonances are small for the forbidden transitions, and the resonances make substantial contributions to collision strengths. The resonances make substantial enhancements in collision strengths for many other transitions. Our calculation adequately account for the short-range electron correlation to ensure correct position of resonances in the low energy region.
threshold at 15.45 Ryd. The resonance structures are almost completely resolved with a very fine energy mesh in our calculation. The resonance structures are very complex and quite dense due to many overlapping Rydberg series converging to various thresholds. The background collision strengths away from resonances are small for the forbidden transitions, and the resonances make substantial contributions to collision strengths. The resonances make substantial enhancements in collision strengths for many other transitions. Our calculation adequately account for the short-range electron correlation to ensure correct position of resonances in the low energy region.
 |
Fig. 4 Collision strengths for the forbidden 2s22p3 |
We have plotted collision strength for the forbidden 2s22p3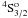 –
–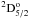 (1–3) in Fig. 4 in the energy region of all open channels and compared the present results with the distorted-wave calculation of Bhatia & Landi (2003) who have reported collision strengths at four incident electron energies 20, 40, 60 and 80 Ryd. There is a reasonable agreement between the two calculations for the forbidden transition; our results being larger than the calculation of Bhatia & Landi (2003) at all energies. The discrepancies appear to be caused by the differences in target wave functions used in two calculations. The collision strengths show smooth variation in this energy region as expected. The collision strengths for the dipole allowed 2s22p3
(1–3) in Fig. 4 in the energy region of all open channels and compared the present results with the distorted-wave calculation of Bhatia & Landi (2003) who have reported collision strengths at four incident electron energies 20, 40, 60 and 80 Ryd. There is a reasonable agreement between the two calculations for the forbidden transition; our results being larger than the calculation of Bhatia & Landi (2003) at all energies. The discrepancies appear to be caused by the differences in target wave functions used in two calculations. The collision strengths show smooth variation in this energy region as expected. The collision strengths for the dipole allowed 2s22p3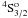 –2s2p4
–2s2p4 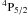 (1 − 6) and 2s22p3
(1 − 6) and 2s22p3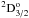 –2s2p4
–2s2p4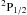 (2 − 13) transitions have been shown in Figs. 5, 6 as a function of incident electron energy. The collision strength in Fig. 5 has been shown from threshold to 100 Ryd and in Fig. 6 from 16 to 100 Ryd. Our results have been compared with the calculation of Bhatia & Landi (2003). These energies are above the highest excitation threshold at 2.066 Ryd where collision strength varies smoothly with incident electron energies. The results of Bhatia & Landi (2003) are larger than the present results at all four incident electron energies. The differences are mostly caused by the wave functions used in target descriptions and by the scattering models. It may be noted that the oscillator strengths from the work of Bhatia & Landi (2003) for the two dipole-allowed transitions plotted in Figs. 5, 6 are also larger than our results (Table 2). The collision strengths for different types of transitions generally show expected energy behavior in the higher energy region. The collision strengths for intercombination transitions fall-off rapidly with increasing energy. The non-resonant background collision strengths for the allowed transitions are normally larger than for the forbidden and intercombination transitions, while the resonance enhancement in collision strengths for the forbidden and intercombination transitions are generally larger compared to allowed transitions.
(2 − 13) transitions have been shown in Figs. 5, 6 as a function of incident electron energy. The collision strength in Fig. 5 has been shown from threshold to 100 Ryd and in Fig. 6 from 16 to 100 Ryd. Our results have been compared with the calculation of Bhatia & Landi (2003). These energies are above the highest excitation threshold at 2.066 Ryd where collision strength varies smoothly with incident electron energies. The results of Bhatia & Landi (2003) are larger than the present results at all four incident electron energies. The differences are mostly caused by the wave functions used in target descriptions and by the scattering models. It may be noted that the oscillator strengths from the work of Bhatia & Landi (2003) for the two dipole-allowed transitions plotted in Figs. 5, 6 are also larger than our results (Table 2). The collision strengths for different types of transitions generally show expected energy behavior in the higher energy region. The collision strengths for intercombination transitions fall-off rapidly with increasing energy. The non-resonant background collision strengths for the allowed transitions are normally larger than for the forbidden and intercombination transitions, while the resonance enhancement in collision strengths for the forbidden and intercombination transitions are generally larger compared to allowed transitions.
 |
Fig. 5 Collision strengths for the allowed 2s22p3 |
 |
Fig. 6 Collision strengths for the allowed 2s22p3 |
5. Effective collision strengths
We have calculated effective collision strengths by integrating the collision strengths over a Maxwellian distribution of electron energies. We have presented effective collision strengths for all transitions between the lowest 68 fine-structure levels considered in our work in Table 4. The indices of lower and upper levels of a transition are given in Table 1. The results are presented at 14 temperatures in the range T = 104 − 4.0 × 106 K suitable for modeling of astrophysical plasmas. The results for transitions to higher excitation levels may be somewhat uncertain because of the neglect of coupling with exciting levels above level 68. The effective collision strength for the stronger allowed transitions increases with increasing temperature and the effective collision strength for the intercombination transitions decreases with increasing temperature in the high-temperature regime. The intercombination transitions can occur only through electron exchange. The increasing trend for some very weak allowed transitions may occur at very high temperature than considered in Table 4.
 |
Fig. 7 Effective collision strengths for the forbidden 2s22p3 |
 |
Fig. 8 Effective collision strengths for the forbidden 2s22p3 |
We have plotted effective collision strengths for the forbidden 2s22p3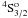 –
–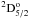 (1–3) and 2s22p3
(1–3) and 2s22p3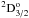 –
–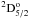 (2–3) transitions in Figs. 7, 8 and for the allowed 2s22p3
(2–3) transitions in Figs. 7, 8 and for the allowed 2s22p3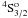 –2s2p4
–2s2p4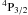 (1–7) transition in Fig. 9 as a function of electron temperature in the range Log10 T = 4.0 − 6.5 K. We have compared our results with the previously available effective collision strengths of Ramsbottom et al. (2003). A reasonable agreement in effective collision strengths for the forbidden 2s22p3
(1–7) transition in Fig. 9 as a function of electron temperature in the range Log10 T = 4.0 − 6.5 K. We have compared our results with the previously available effective collision strengths of Ramsbottom et al. (2003). A reasonable agreement in effective collision strengths for the forbidden 2s22p3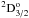 –
–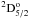 (2–3) and diploe allowed 2s22p3
(2–3) and diploe allowed 2s22p3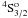 –2s2p4
–2s2p4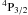 (1–7) transitions can be noted from Figs. 8 and 9 respectively. However, there is significant discrepancy in the effective collision strengths for the forbidden 2s22p3
(1–7) transitions can be noted from Figs. 8 and 9 respectively. However, there is significant discrepancy in the effective collision strengths for the forbidden 2s22p3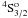 –
–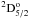 (1–3) transition at lower temperatures, but the two calculations approaches each other at higher temperatures. Our result at Log10 T = 4.0 K is higher by about 25% than the calculation of Ramsbottom et al. (2003). The differences at lower temperature may be caused by the omission of some significant resonances from the calculation of Ramsbottom et al. (2003). We have used a fine energy mesh to resolve resonances and included a large number of target levels in the close-coupling expansion to achieve convergence. Our results include directly the fine-structure splitting both for the N-electron target states and for (N + 1)-electron resonances in the close-coupling expansions, while Ramsbottom et al. (2003) carried out a non-relativistic R-matrix calculation and obtained collision strengths for fine-structure transitions by using algebraic transformation. The high quality wave functions that take adequate account of the term dependence of valence orbitals and of relaxation effects have been used in our calculation.
(1–3) transition at lower temperatures, but the two calculations approaches each other at higher temperatures. Our result at Log10 T = 4.0 K is higher by about 25% than the calculation of Ramsbottom et al. (2003). The differences at lower temperature may be caused by the omission of some significant resonances from the calculation of Ramsbottom et al. (2003). We have used a fine energy mesh to resolve resonances and included a large number of target levels in the close-coupling expansion to achieve convergence. Our results include directly the fine-structure splitting both for the N-electron target states and for (N + 1)-electron resonances in the close-coupling expansions, while Ramsbottom et al. (2003) carried out a non-relativistic R-matrix calculation and obtained collision strengths for fine-structure transitions by using algebraic transformation. The high quality wave functions that take adequate account of the term dependence of valence orbitals and of relaxation effects have been used in our calculation.
 |
Fig. 9 Effective collision strengths for the allowed 2s22p3 |
6. Discussion and conclusions
The target description and convergence of close-coupling expansion are generally two major sources of error in any close-coupling scattering calculation. Based on a comparison of calculated excitation energies and oscillator strengths with experiments and other reliable calculations as well as the fact that we used a well tested sound approach, our wave functions appear to be of high quality to yield an accurate target description. The excitation energies of the target levels shown in Table 1 demonstrate that our theory deviates from experiment by less than 2% for most levels. The excitation energies depend to first order on the accuracy of wave functions, while oscillator strengths depend to second order and thus can provide a better test of the wave functions. A comparison of oscillator strengths from the ground 2s22p3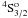 and excited metastable
and excited metastable 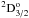 and
and 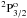 levels with the calculations of Bhatia & Landi (2003) and Tachiev & Froese Fischer (2002) shows good agreement. There is normally also a very good agreement between length and velocity values of oscillator strengths, particularly for transitions with significant strengths. Our target description is estimated to be accurate to about 5% or better.
levels with the calculations of Bhatia & Landi (2003) and Tachiev & Froese Fischer (2002) shows good agreement. There is normally also a very good agreement between length and velocity values of oscillator strengths, particularly for transitions with significant strengths. Our target description is estimated to be accurate to about 5% or better.
A sufficient number of target states in the close-coupling expansion are required to achieve convergence for the transitions of interest. This factor may introduce varied amount of uncertainties in different transitions. The collision strengths for transitions between the low-lying levels up to 2s22p2(1S)3p 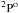 appear to
appear to
be well converged in our calculation. For higher levels of the 2s22p23d configuration there may be significant coupling effects from higher autoionizing and continuum states and thus our results may be less accurate for transitions involving these levels. We have presented effective collision strengths for all transitions among the 68 LSJ levels of Si VIII. Systematic comparisons with other available calculations have been made. The overall agreement with previous R-matrix calculations of Bell et al. (2001) and Ramsbottom et al. (2003) and distorted wave calculation of Bhatia & Landi (2003) is very reasonable and some discrepancies can be explained on the basis of more accurate target wave functions and fine energy mesh used in our calculations. The accuracy for the transitions among low lying levels is estimated to be within 10%. Overall, our results are estimated to be accurate to ~ 20% or better for most of the transitions
In conclusion, we have presented accurate oscillator strengths and effective collision strengths for Si VIII lines among the 68 fine-structure levels. We used non-orthogonal orbitals for the construction of CI wave functions for target levels and for the representation of scattering functions. The checks on excitation energies and oscillator strengths provide us confidence that our target wave functions are likely to be accurate to yield reliable collision strengths from the B-spline Breit-Pauli R-matrix scattering calculations. The present target wave functions contain both the electron correlation and relaxation effects. We have attempted to account for important physical effects such as electron correlation, relativistic, and channel coupling effects. The Rydberg series of resonances converging to several excited levels are found to enhance collision strengths substantially. The effective collision strengths are presented over a wide range of electron temperatures suitable for use in astrophysical plasmas modeling. We have also reported accurate radiative rates for E1 transitions using non-orthogonal wave functions in multiconfiguration Hartree-Fock approach which are of considerable interest in astrophysical applications.
Acknowledgments
This research work is supported by NASA grant NNX11AB62G from the Solar and Heliophysics program.
References
- Badnell, N. R. 1999, J. Phys. B, 32, 5583 [Google Scholar]
- Bell, K. L., Mathews, A., & Ramsbottom, C. A. 2001, MNRAS, 322, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatia, A. K., & Landi, E. 2003, At. Data Nucl. Data Tables, 85, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A., & Sheorey, V. B. 1974, J. Phys. B, 7, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Eissner, W. J. M., & Nussbaumer, H. 1974, Comput. Phys. Commun., 8, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Doschek, G. A., Mariska, J. T., Bhatia, A. K., & Mason, H. E. 1978, ApJ, 226, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Froese Fischer, C. 1991, Comput. Phys. Commun., 64, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Kink, I., Engstrom, L., & Feldman, U. 1999, ApJ, 512, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, W. C., & Zalubas, R. 1983, J. Phys. Chem. Ref. Data, 12, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Podobedova, L. I. K. D. E., Reader, J., & Wiese, W. L. 2004, J. Phys. Chem. Ref. Data, 33, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsbottom, C. A., Bell, K. L., Keenan, F. P., & Mathews, A. 2003, At. Data Nucl. Data Tables, 85, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Tachiev, G. I., & Froese Fischer, C. 2002, A&A, 385, 716 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, R. J., & Neupert, W. M. 1994, ApJS, 91, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R. L. E., & Thomas, R. J. 1998, A&A, 329, 291 [NASA ADS] [Google Scholar]
- Zatsarinny, O. 2006, Comput. Phys. Commun., 174, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Zatsarinny, O., & Froese Fischer, C. 2000, Comput. Phys. Commun., 124, 247 [Google Scholar]
- Zatsarinny, O., & Tayal, S. S. 2001, J. Phys. B, 34, 1299 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Collision strengths for the forbidden 2s22p3 |
| In the text | |
 |
Fig. 2 Collision strengths for the forbidden 2s22p3 |
| In the text | |
 |
Fig. 3 Collision strengths for the forbidden 2s22p3 |
| In the text | |
 |
Fig. 4 Collision strengths for the forbidden 2s22p3 |
| In the text | |
 |
Fig. 5 Collision strengths for the allowed 2s22p3 |
| In the text | |
 |
Fig. 6 Collision strengths for the allowed 2s22p3 |
| In the text | |
 |
Fig. 7 Effective collision strengths for the forbidden 2s22p3 |
| In the text | |
 |
Fig. 8 Effective collision strengths for the forbidden 2s22p3 |
| In the text | |
 |
Fig. 9 Effective collision strengths for the allowed 2s22p3 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


