| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201118636 | |
| Published online | 26 April 2012 | |
Manganese in dwarf spheroidal galaxies⋆,⋆⋆
1 Laboratoire d’astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
e-mail: pierre.north@epfl.ch
2 Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
3 GEPI, Observatoire de Paris, CNRS, Université de Paris Diderot, 92195 Meudon Cedex, France
4 Laboratoire Lagrange, UMR 7293, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300 Nice, France
5 McDonald Observatory, University of Texas, Fort Davis, TX 79734, USA
6 South African Astronomical Observatory, PO Box 9, 7935 Observatory, South Africa
7 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700AV Groningen, The Netherlands
8 Dept. of Physics & Astronomy, University of Victoria, 3800 Finerty Road, Victoria, BC V8P 1A1, Canada
9 European Southern Observatory, Karl-Schwarzschild-str. 2, 85748 Garching by München, Germany
10 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
Received: 13 December 2011
Accepted: 1 March 2012
We provide manganese abundances (corrected for the effect of the hyperfine structure) for a large number of stars in the dwarf spheroidal galaxies Sculptor and Fornax, and for a smaller number in the Carina and Sextans dSph galaxies. Abundances had already been determined for a number of other elements in these galaxies, including α and iron-peak ones, which allowed us to build [Mn/Fe] and [Mn/α] versus [Fe/H] diagrams. The Mn abundances imply sub-solar [Mn/Fe] ratios for the stars in all four galaxies examined. In Sculptor, [Mn/Fe] stays roughly constant between [Fe/H] ~ −1.8 and −1.4 and decreases at higher iron abundance. In Fornax, [Mn/Fe] does not vary in any significant way with [Fe/H]. The relation between [Mn/α] and [Fe/H] for the dSph galaxies is clearly systematically offset from that for the Milky Way, which reflects the different star formation histories of the respective galaxies. The [Mn/α] behavior can be interpreted as a result of the metal-dependent Mn yields of Type II and Type Ia supernovae. We also computed chemical evolution models for star formation histories matching those determined empirically for Sculptor, Fornax, and Carina, and for the Mn yields of SNe Ia, which were assumed to be either constant or variable with metallicity. The observed [Mn/Fe] versus [Fe/H] relation in Sculptor, Fornax, and Carina can be reproduced only by the chemical evolution models that include a metallicity-dependent Mn yield from the SNe Ia.
Key words: stars: abundances / galaxies: dwarf / galaxies: stellar content / galaxies: evolution / galaxies: formation
Based on observations made with the FLAMES-GIRAFFE multi-object spectrograph mounted on the Kuyen VLT telescope at ESO-Paranal Observatory (programs 171.B-0588, 074.B-0415 and 076.B-0146).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Manganese (Mn) is an iron-peak element that can be produced by both Type II and Type Ia supernovae (SNe). Theoretical works indicate that the SNe II yields of Mn should increase with metallicity (Woosley & Weaver 1995), which is supported by observations such as the rise in [Mn/O] with [O/H] increasing from −0.5 to 0.0 (e.g., Feltzing et al. 2007). Conversely, the question of the metal dependence of the SNe Ia yields remains a matter of debate. Shetrone et al. (2003) suggested that the SNe Ia yields of both Cu and Mn increase with metallicity, and McWilliam et al. (2003) brought additional arguments in favor of this hypothesis by comparing the Mn abundances in the Milky Way bulge, the solar neighborhood, and the Sagittarius dSph galaxy. These arguments in favor of a metallicity-dependent Mn yield by SNe Ia were however challenged by Carretta et al. (2004), who judge that the observational results gathered so far are too complex to allow a clear-cut conclusion to be drawn. Nevertheless, Cescutti et al. (2008), with their chemical evolution model, and Badenes et al. (2008), with their new method for measuring the metallicity of Type Ia supernovae, independently found additional evidence of the metal-dependence of the SNe Ia Mn yields, which was also suggested by theoreticians such as Ohkubo et al. (2006).
Badenes et al. (2008) suggest the following explanation of the phenomenon: during the late evolution of the supernova (SN) Ia progenitor, the 14N produced by the CNO cycle is converted into 18F (before being finally transformed into 22Ne), which is transformed into 18O through β+ decay. This increases the number of neutrons in the stellar core, which is the future white dwarf. The neutron excess η is proportional to the metallicity Z and is essentially preserved until the supernova explosion. Although this neutron excess leaves the production of the most abundant species (e.g. Fe) unaffected, the formation of elements with a larger number of neutrons than protons is favored at high Z during the SN Ia explosion. 55Mn, with its 25 protons and 30 neutrons, is the most abundant of them; it is produced during incomplete Si burning (first as 55Co, which then decays into 55Mn). When compared with the abundance of an element insensitive to the neutron excess (especially Cr, which is also built during incomplete Si burning), the resulting Mn abundance can be expected to be an efficient tracer of the progenitor metallicity.
To shed light on the production mechanisms of Mn, we clearly require to investigate its abundances in a variety of galaxies, with different star formation histories. To date the number of systems in which this information is available is small and the number of stars is very limited: besides the Milky Way, about two dozens of stars have been analyzed in Sagittarius (Bonifacio et al. 2000; McWilliam et al. 2003; Sbordone et al. 2007), nine stars in Sculptor (Shetrone et al. 2003; Geisler et al. 2005; Tafelmeyer et al. 2010), and up to a maximum of five stars per galaxy in Draco (Shetrone et al. 2001), Sextans (Shetrone et al. 2003; Tafelmeyer et al. 2010), Carina (Shetrone et al. 2003), Fornax (Shetrone et al. 2003; Tafelmeyer et al. 2010), and LeoI (Shetrone et al. 2003).
DART, the Dwarf galaxy Abundance and Radial-velocities Team, allows a real step forward for Sculptor, Fornax, Carina, and Sextans. This ESO large program based on the FLAMES/GIRAFFE spectrograph at the VLT can encompass stellar samples of up to 80 stars per galaxy with optical spectra at relatively high resolution (R ~ 20 000). The abundances of most elements with measurable lines have already been published, except for manganese: the equivalent widths of this element are available, but the abundance determination is more complicated. Since manganese has an odd atomic number (Z = 25), it has a significant hyperfine structure (hereafter HFS), which broadens the spectral lines. This can lead to desaturation of the lines, which cannot be neglected as soon as the equivalent widths exceed a few tens of mÅ. Therefore, reliable abundances cannot be obtained by just using the equivalent width and total oscillator strength of a given line. All components of the hyperfine structure have to be taken into account. This work provides Mn abundances (with HFS taken into account) in the three Local Group dwarf spheroidal galaxies for an unprecedentedly large number of stars. This constitutes by far the largest sets of Mn abundances in any galaxy other than the Milky Way, and the size of our sample is comparable to e.g. the samples of stars in the thin and thick disks of our Galaxy considered by Feltzing et al. (2007).
This paper is organized as follows. Section 2 introduces our sample of stars. Section 3 describes how we derived Mn HFS-corrected abundances, while Sect. 4 discusses the results. Section 5 presents chemical evolution models that reproduce the observations. Finally, Sect. 6 summarizes our results.
2. Observational material and analysis
In the following, we analyze five different samples. For four of them, the FLAMES/GIRAFFE HR10, HR13, and HR14 grisms were used, respectively, centered on 5488, 6273, and 6515 Å (see Tolstoy et al. 2006). The full abundance analysis papers of the DART FLAMES/GIRAFFE in Sextans and Sculptor are being written up. Surveys of the Fornax, Sculptor, and Sextans galaxies have already been been performed to search for extremely metal-poor stars (Tafelmeyer et al. 2010). The results for the Mn abundances of these stars, which were previously corrected for HFS, are incorporated in the present work. The results of the analysis of all elemental abundances besides Mn are published in Letarte et al. (2010) for Fornax and in Lemasle et al. (2012) for Carina. In a companion work, Venn et al. (2012) presented the chemical composition of 23 elements in nine bright Carina red giant branch stars observed with either the FLAMES/UVES fibers or the Magellan/MIKE spectrograph. Their Mn abundances were corrected for HFS structure and their sample complements ours. In summary, all necessary data, such as equivalent widths and stellar parameters, were available for the present analysis of manganese.
2.1. Galaxy and stellar sample
• The Fornax dSph galaxy was studied by Letarte et al. (2010), who provided and discussed the abundances of a large number of elements. There are 72 stars with at least one measurable Mn line, 60 of which have three reliable Mn lines.
• In Sculptor, 76 stars have at least one measurable Mn line, 50 of which have a reliable average Mn abundance based on three lines (Hill et al., in prep.).
• Twenty-one stars constitute the stellar magnitude-limited sample (I < 18) in Sextans (Jablonka et al., in prep.). However, only 5 stars have reliable Mn equivalent widths.
• In Carina, 17 stars have at least one Mn line (Lemasle et al. 2012), but only 6 have detectable Mn i λ5407 Å and λ5420 Å lines, which were finally selected to compute the average Mn abundance.
The detailed analysis of the Mn lines and the composition of the final sample of stars is performed in Sect. 3.
2.2. Stellar atmosphere models and HFS corrections
The abundance analysis was performed with two codes, calrai on the one hand, and moog on the other, both used with the new MARCS1 spherical models of stellar atmospheres (Gustafsson et al. 2003, 2008), under the LTE approximation (for Sculptor, the calrai abundances were determined using plane-parallel MARCS models). The computation of the radiative transfer was still done in a plane-parallel geometry.
The stellar effective temperatures, gravities, and turbulence velocities were adopted from the DART general analyses of each galaxy. Temperatures and gravities were determined from photometric data for Fornax, Sextans and Carina, and from spectroscopic data in the case of Sculptor.
In principle, equivalent widths were measurable for up to four Mn lines. All of these lines belong to the wavelength range of the HR10 FLAMES/GIRAFFE setup. One line, Mn i λ5432, belongs to the multiplet No. 1 and is a resonance line, while the other three belong to the multiplet No. 4. All four lines were significantly broadened by the hyperfine structure.
Parameters of the four Mn i lines used in this work and of their hyperfine components, taken from Kurucz’ database.
The Mn HFS-corrected abundances were derived in two steps:
-
⊳
First, the uncorrected Mn abundances werecomputed with calrai. The code was initially developed bySpite (1967) (see also the atomic part descriptionin Cayrelet al. 1991), and has beencontinuously updated over the years. calrai was used to analyzeall DART data sets. The DART results were partly summarized inTolstoy et al. (2009). Thehomogeneity of these analyses allows us to perform robustcomparisons of the chemical patterns for all metallicity rangesand between galaxies.
-
⊳
Second, an HFS correction was computed with the August 2010 version of Chris Sneden’s moog code2. On the one hand, for each line we computed the uncorrected Mn abundance (i.e. neglecting the hyperfine structure), using the abfind driver and the total log (gf) value of the lines, taken from the Kurucz file gfhy0600.1003. The resulting abundances are very close to those given by calrai (see the appendix for a comparison between the moog and calrai Mn abundances). On the other hand, we computed the abundances with the hyperfine structure, using the blends driver of moog and introducing all hyperfine components listed in the above Kurucz file.
Finally, the HFS correction Δhfs for each line was defined as the difference between the two above abundances. The line parameters and hyperfine components are given in Table 1.
As an example, the HFS corrections for the 72 stars in the Fornax dSph galaxy are shown in Fig. 1 as a function of equivalent width, for the four available lines (for 71 stars only in the case of the λ5516 Å line). The behavior of the correction for the strongest line, Mn i λ5432 Å, is especially noteworthy: the correction becomes increasingly negative as the equivalent width increases, then turns upward beyond 220 mÅ. This behavior reflects the curve of growth: the minimum correction (or maximum of its absolute value) coincides with the plateau of the curve of growth, while the desaturation effect of the hyperfine structure becomes unimportant in the linear part on the one hand, and on the strongly saturated part on the other. The scatter in the HFS corrections at a given equivalent width is due to the variety of stellar parameter values, especially for the micro-turbulent velocities. In Sculptor, the behavior of the HFS correction is similar, except that the rising branch (for the Mn i λ5432 Å line) is much shorter, because of the lower metallicity. In Sextans, the HFS corrections are never larger than 0.35 dex, this maximum being reached for the λ5432 Å line, which is the strongest. In Carina, the HFS corrections are smaller than 0.3 dex for the λ5407 Å and λ5516 Å lines, and smaller than 0.6 dex for the other two lines.
We note that the amplitude of the HFS correction may reach 1.6 dex; Fig. 1 illustrates how inescapable this correction is.
 |
Fig. 1 Hyperfine structure correction (defined as the abundance with HFS correction versus abundance without it) as a function of equivalent width for the Mn i lines λ5407, λ5420, λ5432, and λ5516 Å for red giants in the Fornax dSph galaxy. The λ5432 line was finally discarded (see text). |
3. Mn final abundances
3.1. Final line-by-line abundances
The final Mn abundances were obtained by adding Δhfs to the initial abundances derived with calrai. For Carina, whose data was included later, we used only moog to determine the Mn abundance, because the results of this code perfectly match those of calrai, as shown in Fig. A.1, where we used the same spherical atmosphere models as for the abundance determination of Fe and other elements.
Figure 2 displays [Mn/Fe] versus (vs.) [Fe/H] for the Sculptor, Fornax, Sextans, and Carina galaxies, for each of the four Mn i lines. The three lines λ5407 Å, λ5420 Å, and λ5516 Å follow very similar trends, while the λ5432 Å line behaves in a clearly different way.
While for the Sculptor dSph, the λ5432 Å line leads to differences in [Mn/Fe] of only a few tenths of a dex compared to the other ones, for the Fornax dSph, both the mean [Mn/Fe] level and the variation with [Fe/H] are affected. The Giraffe sample of stars at the center of the Fornax dSph is indeed more metal-rich than those at the center of the Sculptor dSph. Therefore, the equivalent widths of the λ5432 Å line are larger in Fornax than in Sculptor and above 200 mÅ for most stars. The λ5432 Å line is the most sensitive to non-local thermodynamic equilibrium (NLTE) effects because of its low excitation potential. Furthermore, it is so strong that its profile departs significantly from a Gaussian, thereby severely biasing the equivalent width estimated by the daospec code, which indeed assumes a Gaussian profile. As a consequence, we discarded the λ5432 Å line in the computation of the average Mn abundances.
The λ5407 Å line in Fornax also behaves in a slightly different way, with respect to the λ5420 Å and λ5516 Å lines. As for the λ5432 Å line, this is probably due to the large equivalent widths of the most metal-rich stars of this galaxy, which may greatly exceed 200 mÅ. Therefore, we excluded all lines with EW > 230 mÅ (for the λ5407 Å one, but also the two others) from the Fornax sample when computing the average Mn abundances. The safer and more stringent criterion of EW > 200 mÅ would have left only 25 stars with an average Mn abundance based on three lines. Including stars with 200 < EW < 230 mÅ raises the average [Mn/Fe] ratio by no more than 0.1 dex, without biasing too substantially the distribution of stars in terms of metallicity, hence this trade-off was deemed to be acceptable.
The line-by-line [Mn/H] and [Mn/Fe] abundances are listed in Tables A.1 and A.2 for the Fornax dSph, in Tables A.3 and A.4 for the Sculptor dSph, in Table A.5 for the Sextans dSph, and in Table A.6 for the Carina dSph.
 |
Fig. 2 Final Mn abundances for each of the four lines available for the stars in the Sculptor (blue), Fornax (red), Sextans (green), and Carina (dark green) dSph galaxies. The black horizontal line indicates the zero value; the dashed lines are the weighted averages for their respective galaxies. Note the strongly discrepant behavior of the λ5432 line. |
3.2. Average abundances and compilation of the [Mn/Fe] vs. [Fe/H] diagram
To compute the final abundances, we used an average weighted by the inverse variances of the abundances obtained from the individual lines; these variances were propagated from the estimated errors in the corresponding equivalent widths.
⊳ In Fornax, the average abundances were computed from the three lines λ5407 Å, λ5420 Å, and λ5516 Å. Since some stars lack one or more of these lines, or the equivalent width of some of the lines is larger than 230 Å, only 60 stars are left out of the initial 72 ones. ⊳ In Sculptor, the average abundances could be computed from the same three lines as in Fornax, for a final sample of 50 stars. ⊳ In Sextans, keeping only those stars with three reliable lines would have resulted in only one single object. Therefore, all 5 stars (in addition to the EMP stars of Tafelmeyer et al. 2010) were included in the final sample, even though the average abundances are based on fewer than three lines in most cases. ⊳ In Carina, the initial sample of 17 stars shrinks to 6 objects having at least the two Mn lines λ5407 Å, λ5420 Å. The average Mn abundances are based on these two lines.
The average Mn abundances are computed from three lines in both Sculptor and Fornax but from only two lines in Carina, which might cause a zero-point problem, when our results for the three galaxies are compared. However, Fig. 2 shows that the λ5516 Å line, which was not included in the average [Mn/Fe] values of Carina, yields [Mn/Fe] ratios that are in-between those derived using the two other lines (see e.g. the averages for Sculptor), such that neglecting the line does not change the average values by more than a few hundredths of dex at most. Another kind of zero-point problem does, however, arise between some published values and those of this work because of the different solar abundances adopted. We adopt log (NMn) + 12 = 5.39 and log (NFe) + 12 = 7.50, Sobeck et al. (2006) adopt 5.39 and 7.52 respectively, and Venn et al. (2012) adopt 5.43 and 7.50. This difference of a few hundredths of dex remains smaller than the uncertainties and was therefore neglected.
All points corresponding to fewer than two Mn lines were ignored in Fig. 3, except for a few stars in Sextans. Figure 3 is discussed further in Sect. 4.
 |
Fig. 3 The relation between [Mn/Fe] and [Fe/H]. Data: each dSph galaxy is shown with a different color: blue stands for Sculptor, red for Fornax, green for Sextans, dark green for Carina, and dark turquoise for Leo I. The two green triangles identify the Sextans stars S05-010 and S08-038, whose Mn abundances are based on the λ5432 line only. The colored filled circles identify the samples analyzed in this work; the open symbols stand for previous published analyzes. The four open pentagons at [Fe/H] ≲ −2.9 are from Tafelmeyer et al. (2010) and are corrected for the HFS. The attached arrows gives an idea of the NLTE correction that they likely need, + 0.44, as computed by Bergemann & Gehren (2008) for the halo giant HD 122563. The results of Shetrone et al. (2003) for Sculptor, Fornax, and Leo I are displayed with open circles, and for Carina with open triangles. The dark green open squares are the Carina results of Venn et al. (2012). The dark gray open and filled circles represent the Feltzing et al. (2007) Milky Way thin and thick disk stars, respectively. The Sobeck et al. (2006) Milky Way cluster and field halo stars are shown with full gray squares; gray dots are very metal poor stars in the Milky Way halo from Cayrel et al. (2004). The vertical blue and green downward arrows indicate the “knee”, where [Mg/Fe] starts to decrease with increasing [Fe/H], in the Sculptor and Sextans dSphs (DART). Models: the chemical evolutions of the Sculptor (model A in cyan and model B in blue, see text), Fornax (model C in magenta and model D in orange, see text), and Carina (model E in dark green) dSphs are followed. The continuous lines show models with metallicity-dependent SNe Ia Mn yields as in Cescutti et al. (2008). The dashed lines follow the evolution of [Mn/Fe] for the same SFHs, but with metal-independent SNe Ia Mn yields. |
3.3. Discussion of possible NLTE effects
Whilst we took the line HFS into account, our abundances may still suffer from NLTE effects. Very few studies address this problem for the manganese lines. Bergemann & Gehren (2007) examined the solar atmosphere for a total of 39 lines belonging to ten multiplets, and their line list includes the four Mn i lines we use here. They showed that the NLTE correction (defined as ΔX = log εNLTE − log εLTE, where ε is the ratio of the number densities of Mn to H) is at most on the order of 0.1 dex in absolute value. The maximum correction, ΔX = +0.11, applies to the λ5432 Å line, closely followed by the other three (+0.09 for λ5420 Å, and +0.085 for λ5407 Å, and λ5516 Å). Unfortunately, these corrections cannot be applied directly to our case, because the surface gravities and metallicities of our sample are very different from solar. Bergemann & Gehren (2008) computed the NLTE abundances of 14 stars, all of which but one are metal-deficient, down to [Fe/H] ~ −2.5. Unfortunately, all but one are main sequence or subgiant stars, the only exception being a giant star with log g ~ 1.5 and [Fe/H] = −2.51. In this case, the NLTE correction to [Mn/Fe] is on the order of +0.44. However, it is difficult to infer what the NLTE correction should really be for our stars. Bergemann & Gehren (2008) consider 18 lines from λ4018 Å to λ6021 Å but none of them coincide with the lines used here. Nevertheless, the possibility remains, that our [Mn/Fe] values might increase by as much as 0.2 dex when corrected for NLTE effects.
On the observational side, Feltzing et al. (2007) argued that the excitation balance is unaffected by departure from LTE in their sample, based on the identical behavior of lines with different excitation potentials, when plotting the abundance as a function of Teff, log g, and [Fe/H]. However, they did not exclude possible departures from ionization balance. In addition, all their stars are either on the main sequence or the subgiant branch, and none have [Fe/H] < −1. Furthermore, we have only one line in common with Feltzing et al. (2007), Mn i λ5432, which, as argued above, we chose to discard because it is probably the most sensitive to NLTE effects and its equivalent width is biased owing to its large strength. Therefore, the conclusion reached by Feltzing et al. (2007) cannot be generalized to our sample.
Sobeck et al. (2006) determined Mn abundances for 200 stars in 19 globular clusters and for a comparable number of field stars with similar stellar parameters. They also neglected the NLTE effects, on the grounds that they should be small when considering [Mn/Fe], which involves two neutral species (Ivans et al. 2001). Interestingly, they found an average constant value ⟨ [Mn/Fe] ⟩ = −0.36 for their halo field stars, which is about 0.15 dex lower than the value found by Feltzing et al. (2007) for their most metal-poor stars ([Fe/H] ≈ −1) in the thick disk. In the range −1 < [Fe/H] < + 0.4, where [Mn/Fe] increases to values above solar for the thick disk stars of Feltzing et al. (2007), the [Mn/Fe] values of Sobeck et al. (2006) show the same trend but systematically lower by about 0.1 dex. One possible explanation of this difference is a bias produced by there being only one line, Mn i λ6013 Å, in common to Sobeck et al. (2006). Another explanation might be an NLTE correction that would be 0.15 dex larger for giants than for less evolved stars4, but this remains to be confirmed on theoretical grounds.
4. Discussion of the observational results
4.1. The [Mn/Fe] versus [Fe/H] diagram
4.1.1. Description
The main results of the present study are summarized in Fig. 3. Our comparison sample is composed of the results of i) Sobeck et al. (2006) for the Milky Way globular clusters and field halo stars, ii) Cayrel et al. (2004) for field halo stars, and iii) Feltzing et al. (2007) for the Milky Way thin and thick disk stars. We also display the extremely metal-poor (EMP) stars found by Tafelmeyer et al. (2010) in Sculptor, Fornax, and Sextans, and the nine stars of Venn et al. (2012) in Carina. Finally, we show the stars studied by Shetrone et al. (2003) in the Sculptor, Fornax, Sextans, Carina, and Leo I dSph galaxies.
4.1.2. The extremely metal-poor (EMP) stars
Tafelmeyer et al. (2010) noted that the manganese abundances of their Sextans members, S11-04 and S24-72, were based on only one line, Mn i λ4823.52 Å which differs from the lines we used. In spite of this difference, their [Mn/Fe] values are in good agreement with those of other Sextans stars of higher metallicity. They also agree with the values found in the Milky Way halo (Sobeck et al. 2006) and our results in Fornax and Sculptor. The Mn abundance of the most extreme EMP star, Scl07-50, was obtained from the three resonance lines of the triplet at λ ~ 4030 Å, while that of Fnx05-42 (which is only slightly less iron-poor but has the lowest [Mn/Fe] ratio) was obtained from two lines of the same triplet. These resonance lines are expected to be strongly affected by NLTE. Hence, we drew an upward arrow at the position of the two most iron-poor stars, with an amplitude of 0.44 dex matching the NLTE correction of Bergemann & Gehren (2008) for the metal-poor giant HD 122563. These arrows, however, have to be considered only as a qualitative indication, because the true NLTE correction might be very different (possibly larger), with respect to the extremely low [Fe/H].
4.1.3. [Mn/Fe] trends with [Fe/H] in Sculptor and Fornax: are they real?
In a broad sense, the [Mn/Fe] vs [Fe/H] relations for the three Local Group dSphs of this study agree rather well with the trends found for the Galaxy by both Feltzing et al. (2007) in the thick disk and Sobeck et al. (2006) in the halo and globular clusters. This agreement can only be considered qualitative, owing to the zero point issues raised earlier and the different kind of stars considered (dwarfs instead of giants) in the case of Feltzing et al. (2007).
A closer look reveals some interesting features. In Fornax (red dots in Fig. 3), there seems to be a very slight correlation between [Mn/Fe] and [Fe/H], but the trend is essentially due to the small group of 4 stars near [Fe/H] = −1.4. Pearson’s correlation coefficient is only 0.17 (for 60 stars), the more robust Spearman correlation coefficient is 0.05, and the Student-t test is 0.38. The relatively large difference between the two correlation coefficients is due to the small group of 4 stars around [Fe/H] ~ −1.4, which lie rather far away from the bulk of the data and cause the large value of Pearson’s coefficient. In conclusion, even though future observations might confirm the trend suggested here in Fornax, we can only tell for the time being that it is not statistically significant. [Mn/Fe] might thus be considered constant with [Fe/H], with an average value ⟨ [Mn/Fe] ⟩ = −0.32 ± 0.02. Any cosmic dispersion must be smaller than about 0.09 dex, because the scatter in the [Mn/Fe] values around the mean amounts to ~0.12 dex, while their average error is ~0.07 dex.
Conversely, the 50 Sculptor stars display a global negative trend } = -0.299\, \mathrm{[Fe/H]} - 0.679\mathrm{,}~~~\mathrm{rms} =0.085 ~\mathrm{dex,} \end{equation*}](/articles/aa/full_html/2012/05/aa18636-11/aa18636-11-eq123.png) where Pearson’s correlation coefficient is − 0.569, Spearman’s coefficient is − 0.546, and the Student-t test is − 4.51 (for 50 stars). This is clearly significant because the null hypothesis has a probability well below one percent. Zooming into Sculptor in Fig. 3, the relation does not appear, however, to be a precisely monotically declining line, but rather like a plateau followed by a decreasing linear function (Fig. 4). If real, a “knee” appears between [Fe/H] = − 1.5 and − 1.3.
where Pearson’s correlation coefficient is − 0.569, Spearman’s coefficient is − 0.546, and the Student-t test is − 4.51 (for 50 stars). This is clearly significant because the null hypothesis has a probability well below one percent. Zooming into Sculptor in Fig. 3, the relation does not appear, however, to be a precisely monotically declining line, but rather like a plateau followed by a decreasing linear function (Fig. 4). If real, a “knee” appears between [Fe/H] = − 1.5 and − 1.3.
 |
Fig. 4 Same as Fig. 3, but for Sculptor only (blue dots), showing a plateau followed by a decreasing trend rather than a monotonic decrease in [Mn/Fe]. Results for the globular cluster ω Centauri are also shown as red circles (Cunha et al. 2010) and red dots (Pancino et al. 2011). |
The contrasting behaviors of [Mn/Fe] in Fornax and Sculptor seem difficult to explain entirely in terms of NLTE effects, primarily because the average surface gravities are the same (~0.7 dex) in both cases. Moreover, while one would expect NLTE effects alone to produce in all galaxies the same monotonic relation with metallicity as seen in the Milky Way, the observed trends instead differ for each galaxy. An alternative explanation could be a systematic error in the HFS components (splitting, oscillator strengths), because on average, the lower the [Fe/H], the smaller the HFS correction.
We conducted two different tests to explore the possibility of erroneous HFS corrections:
-
First, we excluded from the sample all Sculptorstars with HFS corrections larger than a given limit.Limiting the sample to the 45 stars with|Δhfs| ≤ 1 for the three lines at 5407 Å, 5420 Å, and 5516 Å still provides a Spearman rank correlation coefficient of −0.5 and a t-test of −3.75, implying a probability well below one percent that the correlation is random. Limiting ourselves further to |Δhfs| ≤ 0.3 (24 stars), the correlation remains, with a probability of random occurrence being well below five percent. This suggests that only a very large relative error in Δhfs, on the order of 50%, could account for the trend we see in Sculptor, which spans almost ~0.2 dex in [Mn/Fe]. This seems unlikely.
-
Second, instead of using the Kurucz line list, we extracted from Tables 1, 5, and 6 of Vitas & Vince (2003) the HFS components of the 5420 Å and 5432 Å lines, which are based on the laboratory measurements of Booth et al. (1983). We retained the uncorrected wavelength and oscillator strength values (the “λ′” and “log (gf)′” ones). We computed the HFS correction for these data again for the seven Sculptor stars for which the original HFS corrections ranged from −0.10 to −1.60 for the 5420 Å line, and from −0.34 to −1.07 for the 5432 Å line. For the 5420 Å line, we obtained the same Δhfs values as for the Kurucz components within 0.02 dex. For the 5432 Å line, Δhfs was recovered within 0.01 dex for six stars, and within 0.03 for the last one.
Therefore, the HFS corrections appear to be very robust, especially as the uncorrected log (gf)′ values listed in the paper of Vitas & Vince (2003) differ only slightly from Kurucz’ ones (the total log (gf) value is −1.492 instead of −1.462 for the 5420 Å line, and −3.740 instead of −3.795 for the 5432 Å line).
In summary, the variation in [Mn/Fe] can probably be taken at face value and genuinely related to the nucleosynthesis of Mn. The decreasing trend in [Mn/Fe] with increasing [Fe/H] seen in Sculptor had been observed nowhere else, except for giants and subgiants in the globular cluster ω Centauri (Cunha et al. 2010; Pancino et al. 2011), where the anti-correlation is even more pronounced (see Fig. 4). Romano et al. (2011) attempted to interpret these last sets of results, but unsuccessfully, although they also found that a metallicity-dependent yield of SNe Ia would be more realistic than a constant yield.
4.2. Manganese and the α elements
Since the α-elements are mostly produced in massive stars while Mn can be produced by both SNe II and SNe Ia, the ratio of Mn to some of the α-elements may reveal at which point manganese is produced by one or the other nucleosynthetic route. Figure 5 displays the cases of Mg and Ca, two α-elements with slightly different nucleosynthetic origins: Mg is produced in a hydrostatic phase of the evolution of massive stars, while Ca is instead produced during a Type II supernova explosion (Woosley et al. 2002).
Figure 5 clearly shows that the position in [Fe/H] of the rising branch of [Mn/α] depends on the galaxy star formation history, similarly to the “knee” in [α/Fe]. Tolstoy et al. (2009) report a decrease in [Mg/Fe] for Sculptor from ~+0.5 to ~−0.2 dex for [Fe/H] between ~−2.4 and ~−1, while [Ca/Fe] decreases from ~+0.3 to ~0.0. Unfortunately, most of the −2.4 < [Fe/H] < −1.8 stars in our sample do not have reliable equivalent widths for the Mn lines. Nevertheless, we have a dozen stars between [Fe/H] ~ −1.8 and ~ −1.4, where the slope of the relation between [Mg/Fe] and [Fe/H] is strongly negative. After an initial increase in [Mn/α] with metallicity [Fe/H], both [Mn/Mg] and [Mn/Ca] are constant at [Fe/H] > −1.4. The [Mn/Ca] mean level is higher in Fornax than Sculptor stars as a consequence of the lower [Ca/Fe] abundance ratio in Fornax. The dispersions around the mean are similar for both galaxies. In Carina, the 20 stars (6 from Lemasle et al. 2012; 9 from Venn et al. 2012; and 5 from Shetrone et al. 2003) lie close to the sequence defined by the Sculptor stars. However, the star at [Fe/H] = −1.4 lies outside the general trend defined by the sample of Lemasle et al. (2012), and the stars of Shetrone et al. (2003) do not show any trend. Our 5 Sextans stars define an increasing trend similar to that of Sculptor and possibly steeper, which needs confirmation by further observations.
In Sculptor, the variation in [Mn/Mg], from ~−0.8 to ~−0.3, with [Fe/H], reflects i) the plateau at [Mn/Fe] for [Fe/H] below − 1.4 (see Fig. 4), and ii) the decrease in [Mg/Fe] due to SNe Ia, as can be most clearly seen at [Fe/H] > −1.6. The differential behavior of Mn and the α-elements can be attributed to their different nucleosynthetic paths: Mn is produced ever more in increasingly metal-rich core-collapse supernovae, and definitely more than in the metal-poor Type Ia supernovae (McWilliam et al. 2003). To further investigate the relative roles of SNe II and SNe Ia, we introduce simple models of chemical evolution in the next section.
 |
Fig. 5 [Mn/α] versus [Fe/H] for each of the α elements Mg and Ca, for the Sculptor (blue dots), Fornax (red dots), Carina (dark green symbols), and Sextans (green symbols) galaxies. The key to the symbols is the same as in Fig. 3. For comparison, we provide results for field Milky Way stars, gathered from the literature: the open and full black dots are the thin and thick, respectively, disk dwarf stars measured by Bensby et al. (2003), Bensby et al. (2005), and Feltzing et al. (2007). The full grey symbols are from Cayrel et al. (2004) (round dots), and Gratton et al. (2003) (squares). |
5. The nucleosynthesis of Mn
We now discuss the chemical evolution of the three galaxies of our sample with the largest number of stars, Sculptor, Fornax, and Carina, adopting a differential approach in which we compare models with and without metal-dependent SNe Ia Mn yields.
5.1. Models of chemical evolution
Figure 6 presents the evolution of the star formation rate (SFR) with time for our five different models. They are based on the observed star formation histories (SFHs) of de Boer et al. (2011) for Sculptor, Coleman & de Jong (2008) for Fornax, and Rizzi et al. (2003) for Carina.
Models A, C, and E are set up to follow the observations as closely as possible, whereas models B and D are extreme cases, with which we intend to test the influence of the choice of SFH on the results. These five models attempt to describe the extremes of the possible SFH for these galaxies, the true one lying somewhere within these boundaries. Their main characteristics are summarized in Table 2.
Parameters of our models.
Models A and B refer to the Sculptor dSph. In model A, the SFR is a decreasing exponential function on a timescale of 1 Gyr. In model B, the SFR is also a decreasing exponential function, although on a shorter timescale of 100 Myr. Both models have a low star formation rate tail of 5 × 10-5 M⊙/yr, stopping 5 Gyr ago. They both form a similar total mass of stars on the order of ~1.5 × 106 M⊙, from a total initial mass of gas of 2 × 107 M⊙.
Models C and D refer to the Fornax dSph. Model C assumes an exponentially decreasing SFR on a long timescale of 10 Gyr, whereas model D, with an exponentially decreasing SFR on a short timescale of 100 Myr, has an extended tail with a star formation rate of 3 × 10-3 M⊙/yr. The evolution of the models was stopped 1 Gyr ago and has an amplitude of star formation that is ten times higher than for the Sculptor models. Both Fornax models form a total mass of stars of ~4.5 × 107 M⊙, from a total initial mass of gas of 3 × 108 M⊙.
Model E refers to the Carina dSph. The star formation (SF) history is modeled by three Gaussian functions, with σ = 500 Myr. These three Gaussian functions are centered at look-back times of 4, 7, and 14.5 Gyr, with respective peak values of ~10-4 M⊙ yr-1, ~4 × 10-4 M⊙ yr-1, and ~10-4 M⊙ yr-1. The Carina model forms a total mass of stars of ~0.5 × 106 M⊙, out of a 13 × 106 M⊙ total initial mass of gas.
For all these models, we used the initial mass function (IMF) of Kroupa (2001), in addition to the chemical evolution parameters, such as stellar lifetimes and SNe Ia scheme, of Cescutti et al. (2007).
For the SN Ia rate, which is a key component of our analysis, we underline that it was computed following Matteucci & Greggio (1986), hence expressed as: ![\begin{equation} R_{\rm SNe Ia}=A\int\limits^{M_{\rm BM}}_{M_{\rm Bm}}\phi(M_{\rm B}) \left[\int\limits^{0.5}_{\mu_{\rm m}}f(\mu)\,\psi(t-\tau_{M_{2}})\,{\rm d}\mu\right] {\rm d}M_{\rm B}\,\mathrm{,} \end{equation}](/articles/aa/full_html/2012/05/aa18636-11/aa18636-11-eq190.png) (1)where ψ(t) is the SFR, M2 is the mass of the secondary, MB is the total mass of the binary system, μ = M2/MB, μm = max[M(t)2/MB,(MB − 0.5MBM)/MB], MBm = 3 M⊙, and MBM = 16 M⊙. The IMF is represented by φ(MB) and refers to the total mass of the binary system when computing the SNe Ia rate, f(μ) is the distribution function for the mass fraction of the secondary
(1)where ψ(t) is the SFR, M2 is the mass of the secondary, MB is the total mass of the binary system, μ = M2/MB, μm = max[M(t)2/MB,(MB − 0.5MBM)/MB], MBm = 3 M⊙, and MBM = 16 M⊙. The IMF is represented by φ(MB) and refers to the total mass of the binary system when computing the SNe Ia rate, f(μ) is the distribution function for the mass fraction of the secondary 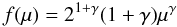 (2)with γ = 2 and A is the fraction of systems in the appropriate mass range that can give rise to SNe Ia events. This quantity is fixed to 0.05 by reproducing the observed SNe Ia rate at the present time (Cappellaro et al. 1999).
(2)with γ = 2 and A is the fraction of systems in the appropriate mass range that can give rise to SNe Ia events. This quantity is fixed to 0.05 by reproducing the observed SNe Ia rate at the present time (Cappellaro et al. 1999).
The metal-dependent yields of Fe and Mn for SNe II are taken from Woosley & Weaver (1995), with the difference that we halved the iron yields for SNe II, as suggested by Romano et al. (2010). These yields are represented by the red curve in Fig. 7 for SNe II with a 15 M⊙ progenitor, which is taken as representative of the majority of the core-collapse SNe. We first implemented the hypothesis of Cescutti et al. (2008) that the metal dependence of the Mn SNe Ia yields is y ∝ (Z/Z⊙)0.65 (see the black line in Fig. 7), which led to the five models A1, B1, C1, D1, and E1. We then considered the Iwamoto et al. (1999) metal-independent Mn yields for a solar metallicity, taking the SNe Ia yields for iron from Iwamoto et al. (1999). This led to the five additional models A2, B2, C2, D2, and E2.
 |
Fig. 6 The SF histories for the analyzed models. In cyan model A and in blue model B, for Sculptor. In magenta model C and in orange model D, for Fornax. In dark green, model E for Carina. |
 |
Fig. 7 Metallicity-dependent Mn yield of SNe Ia according to the prescription of Cescutti et al. (2008) (black line), and of SNe II with 15 M⊙ progenitors (red line) according to Woosley & Weaver (1995). |
5.2. Does the Mn yield depend on metallicity?
Figure 3 unambiguously demonstrates that regardless of the galaxy and the assumed SFH, models for which there is no metallicity dependence for the Mn SNe Ia yields (dashed lines) predict a far too high [Mn/Fe]. In contrast, all five models with a metal-dependence (solid lines) do pass through the observed data points.
 |
Fig. 8 Same as Fig. 3 but for models only, showing the respective contributions of the SNe II and Ia to the Mn synthesis. Only the models A1 and B1 for Sculptor (continuous cyan and blue lines respectively), and C1 and D1 for Fornax (continuous magenta and orange lines) are shown. The dotted lines show the evolution of [Mn/Fe] assuming no Mn is produced by the SNe Ia, in contrast to Fe and all other elements. The dashed lines indicate the same evolution, but assuming that no Mn is produced by the SNe II. |
Figure 8 indicates the respective contributions of the SNe II and SNe Ia to the Mn abundance. The plain lines show the total contribution of both types of SNe, similarly to Fig. 3. The dotted lines show the contribution to Mn of the SNe II only. In other words, the Mn yields of the SNe Ia are switched off, but not the yield of Fe. Finally, the dashed curves show how [Mn/Fe] evolves when only the SNe Ia contribute to the Mn abundance.
Below [Fe/H] ~ −2.5, [Mn/Fe] is set by the SNe II up to an average level of −0.2 dex. The SNe II Mn ejecta are also metal-dependent and increase with [Fe/H]. At [Fe/H] ~ −2.5, the exploding SNe Ia produce [Mn/Fe]SNeIa < [Mn/Fe]SNeII. This situation holds up to [Fe/H] ~ −1, when our nucleosynthesis predicts for the progenitors of SNe Ia that [Mn/Fe]SNeIa ~ [Mn/Fe]SNeII. This explains the decreasing trend for [Mn/Fe] vs. [Fe/H] in the metallicity range −2.5 < [Fe/H] < −1 for Sculptor and Fornax.
The Sculptor model A1, which has the closest SFH to the observations, results in a shallower decline of [Mn/Fe] with [Fe/H] than observed. This may well indicate that the form of the assumed metal-dependence of the SNe Ia yields is not fully correct. We did not try any fine-tuning at this stage, since our relatively simple models imply clearly enough that metal-poor SNe Ia should produce less Mn than metal-rich ones.
Unfortunately, the data for Fornax only span a narrow range of [Fe/H], making it more difficult to check the suitability of the models. The model C1 shows an increase in [Mn/Fe] above [Fe/H] ~ −1 after an initial decrease as in the case of Sculptor. While the origin of the first drop is the same as in the case of Sculptor, the increase for [Fe/H] > −1 is due to metal-rich SNe Ia progenitors, which are a consequence of the longer SFH.
As in Fornax, the data in Carina span a narrow range of metallicities, except for the three stars with [Fe/H] < 2.0 published by Venn et al. (2012). We see that the model E1 reproduces the observations quite satisfactorily. It is interesting to see the consequence of the bursty Carina SFH. [Mn/Fe] decreases between the first and the second star formation peaks (−3.5 < [Fe/H] < −2.2), because of the very low production of Mn by metal-poor SNe Ia. The second decrease in [Mn/Fe] (−1.6 < [Fe/H] < −1.4), at the end of the intermediate age peak of star formation, is shallower owing to the higher metallicity of the SNe Ia at that time.
5.3. Comparison with Lanfranchi’s models
The chemical evolution models adopted here are very similar to the ones computed by Lanfranchi et al. (2003, 2008), although there are two major differences: we do not consider galactic winds and our SFHs are quite different. While we adopt SFHs initially derived from color-magnitude diagrams, Lanfranchi et al. adjust their SF efficiency until the observations are reproduced.
Galactic winds or any other dynamical effects such as tidal and ram pressure stripping must have removed the gas in these dSphs, because none is detected. Moreover, as shown by Lanfranchi et al., the galactic winds can influence the chemical evolution at the end of the evolution of these galaxies, if one considers differential winds, i.e., that different elements can be expelled with different wind efficiencies. Nevertheless, to keep our models as simple as possible, galactic winds were not an option in our analysis. This does not affect our conclusions. Indeed the evidence that SN Ia Mn yields depend on metallicity does not arise from the latest stages of the galaxy chemical evolution, when winds would play a role, but much earlier. Moreover, given that Lanfranchi’s wind efficiency is essentially the same for Fe and Mn, [Mn/Fe] is definitely not expected to change.
6. Conclusion
On the basis of the three Mn i lines at λ5407, 5420, and 5516 Å, we have derived the stellar abundances of manganese in three dSph galaxies, Sculptor (50 stars), Fornax (60 stars), and Carina (6 stars); Mn abundances in a fourth dSph galaxy, Sextans (5 stars), was based on only one to three Mn lines. These Mn abundances are corrected for HFSs, the correction reaching 1.6 dex for strong lines (EW ~ 200 mÅ).
Our analysis of the relation between the [Mn/Fe] and [Mn/α] abundance ratios and [Fe/H] has highlighted the following features:
-
The Mn abundances lead to sub-solar [Mn/Fe]ratios for all stars in all four of the studied galaxies, as expectedfrom their low metallicity.
-
The variation in [Mn/Fe] with [Fe/H] in Sculptor has two phases: a plateau at [Fe/H] < − 1.4, followed by a ~0.3 dex decrease at higher metallicity. This decreasing trend of [Mn/Fe] with [Fe/H] had only been observed previously in the globular cluster ω Centauri. In Fornax, there is a marginal suggestion of an increasing trend, but without any statistical significance.
-
Our datasets in four different galaxies, and their comparison with the case of the Milky Way clearly demonstrates that the evolution of [Mn/α] as a function of [Fe/H] depends on the galaxy SFH. The variation in [Mn/α] can be interpreted in terms of the balance between the metal-dependent yields of Type II and Type Ia supernovae.
-
Three simple chemical evolution models for Sculptor, Fornax, and Carina have been developed. The impacts of the Type II and Type Ia Mn yields, with and without any metal-dependence, have been investigated. They unambiguously demonstrate that the reproduction of the observations requires SNe Ia metal-dependent yields. The successive increase and decrease in [Mn/Fe] as a function of [Fe/H], as well as the amplitude of these variations, are the result of the increasing SNe II Mn yields with [Fe/H], combined with initially low SNe Ia yields that subsequently augment with metallicity.
Online material
Appendix A: Comparison between MOOG and CALRAI abundances
The abundances of Mn that were uncorrected for the HFS were computed with both codes calrai and moog for the same atmosphere models. Therefore, it is possible to compare the results and check the consistency between the two codes.
For Fornax, the raw (i.e. uncorrected for HFS) Mn abundances given by the two codes prove to be perfectly consistent (Fig. A.1).
 |
Fig. A.1 Comparison between the Mn abundances (not corrected for HFS) obtained for the Fornax dSph galaxy using the moog code, and the ones obtained using the calrai code, for each of the 4 lines Mn i λ5407, λ5420, λ5432, and λ5516. In both cases, the abundances were determined using spherical atmosphere models. |
For Sculptor, however, there is a systematic shift of about 0.1 to 0.2 dex, in the sense that the moog abundances are lower than the calrai ones for all four lines. The slopes are very close to 1, but tend to be slightly above unity.
The reason why the systematic zero-point shift is much larger in Sculptor than Fornax lies in the atmosphere models used. While spherical models were used in connection with the moog spectral synthesis code for both galaxies, plane-parallel models were used in connection with the calrai code in the case of Sculptor, leading to the overestimated abundances seen in Fig. A.2.
 |
Fig. A.2 Same as Fig. A.1, but for the Sculptor dSph galaxy. Here the calrai abundances were determined using plane-parallel atmosphere models, while the moog abundances are based on spherical models. |
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407 and λ5420 lines observed for the stars of the Fornax dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5432 and λ5516 lines observed for the stars of the Fornax dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407 and λ5420 lines observed for the stars of the Sculptor dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5432 and λ5516 lines observed for the stars of the Sculptor dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407, λ5420, λ5432, and λ5516 lines observed for the stars of the Sextans dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407, λ5420, λ5432, and λ5516 lines observed for the stars of the Carina dSph galaxy.
Available at http://kurucz.harvard.edu/linelist.html
Note that Feltzing et al. (2007) see no difference between dwarf and giant stars in the [Mn/O] vs. [O/H] diagram, which contradicts this explanation, unless Fe alone is responsible for the difference.
Acknowledgments
P.J., P.N., and G.C. gratefully acknowledge support from the Swiss National Science Foundation. The work greatly benefited from the International Space Science Institute (ISSI) in Bern, thanks to the funding of the team “Defining the full life-cycle of dwarf galaxy evolution: the Local Universe as a template”.
References
- Aoki, W., Honda, S., Beers, T. C., et al. 2005, ApJ, 632, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Bravo, E., & Hughes, J. P. 2008, ApJ, 680, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., & Gehren, T. 2007, A&A, 473, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., & Gehren, T. 2008, A&A, 492, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Hill, V., Molaro, P., et al. 2000, A&A, 359, 663 [NASA ADS] [Google Scholar]
- Booth, A. J., Shallis, M. J., & Wells, M. 1983, MNRAS, 205, 191 [NASA ADS] [Google Scholar]
- Cappellaro, E., Evans, R., & Turatto, M. 1999, A&A, 351, 459 [NASA ADS] [Google Scholar]
- Carretta, E., Gratton, R. G., Bragaglia, A., Bonifacio, P., & Pasquini, L. 2004, A&A, 416, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel, R., Perrin, M., Barbuy, B., & Buser, R. 1991, A&A, 247, 108 [NASA ADS] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Matteucci, F., François, P., & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Matteucci, F., Lanfranchi, G. A., & McWilliam, A. 2008, A&A, 491, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coleman, M. G., & de Jong, J. T. A. 2008, ApJ, 685, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Smith, V. V., Bergemann, M., Suntzeff, N. B., & Lambert, D. L. 2010, ApJ, 717, 333 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, T. J. L., Tolstoy, E., Saha, A., & Olsen, K. 2011, in EAS Pub. Ser., 48, ed. M. Koleva, P. Prugniel, & I. Vauglin, 79 [Google Scholar]
- Feltzing, S., Fohlman, M., & Bensby, T. 2007, A&A, 467, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geisler, D., Smith, V. V., Wallerstein, G., Gonzalez, G., & Charbonnel, C. 2005, AJ, 129, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., Claudi, R., Lucatello, S., & Barbieri, M. 2003, A&A, 404, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2003, in Stellar Atmosphere Modeling, ed. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 331 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivans, I. I., Kraft, R. P., Sneden, C., et al. 2001, AJ, 122, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lanfranchi, G. A., & Matteucci, F. 2003, MNRAS, 345, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Lanfranchi, G. A., Matteucci, F., & Cescutti, G. 2008, A&A, 481, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemasle, B., Hill, V., Tolstoy, E., et al. 2012, A&A, 538, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Letarte, B., Hill, V., Tolstoy, E., et al. 2010, A&A, 523, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
- McWilliam, A., Rich, R. M., & Smecker-Hane, T. A. 2003, ApJ, 592, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Ohkubo, T., Umeda, H., Nomoto, K., & Yoshida, T. 2006, in Origin of Matter and Evolution of Galaxies, ed. S. Kubono, W. Aoki, T. Kajino, T. Motobayashi, & K. Nomoto, AIP Conf. Ser., 847, 458 [Google Scholar]
- Pancino, E., Mucciarelli, A., Sbordone, L., et al. 2011, A&A, 527, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rizzi, L., Held, E. V., Bertelli, G., & Saviane, I. 2003, ApJ, 589, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Cescutti, G., & Matteucci, F. 2011, MNRAS, 418, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L., Bonifacio, P., Buonanno, R., et al. 2007, A&A, 465, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shetrone, M. D., Côté, P., & Sargent, W. L. W. 2001, ApJ, 548, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M., Venn, K. A., Tolstoy, E., et al. 2003, AJ, 125, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Sobeck, J. S., Ivans, I. I., Simmerer, J. A., et al. 2006, AJ, 131, 2949 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M. 1967, Annales d’Astrophysique, 30, 211 [NASA ADS] [Google Scholar]
- Tafelmeyer, M., Jablonka, P., Hill, V., et al. 2010, A&A, 524, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tolstoy, E., Hill, V., Irwin, M., et al. 2006, The Messenger, 123, 33 [NASA ADS] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Venn, K. A., Shetrone, M. D., Irwin, M. J., et al. 2012, ApJ, submitted [Google Scholar]
- Vitas, N., & Vince, I. 2003, Serbian Astron. J., 167, 35 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters of the four Mn i lines used in this work and of their hyperfine components, taken from Kurucz’ database.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407 and λ5420 lines observed for the stars of the Fornax dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5432 and λ5516 lines observed for the stars of the Fornax dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407 and λ5420 lines observed for the stars of the Sculptor dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5432 and λ5516 lines observed for the stars of the Sculptor dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407, λ5420, λ5432, and λ5516 lines observed for the stars of the Sextans dSph galaxy.
Equivalent widths, HFS corrections (labeled “HFS” on top of the respective columns), and Mn abundance for the Mn i λ5407, λ5420, λ5432, and λ5516 lines observed for the stars of the Carina dSph galaxy.
All Figures
 |
Fig. 1 Hyperfine structure correction (defined as the abundance with HFS correction versus abundance without it) as a function of equivalent width for the Mn i lines λ5407, λ5420, λ5432, and λ5516 Å for red giants in the Fornax dSph galaxy. The λ5432 line was finally discarded (see text). |
| In the text | |
 |
Fig. 2 Final Mn abundances for each of the four lines available for the stars in the Sculptor (blue), Fornax (red), Sextans (green), and Carina (dark green) dSph galaxies. The black horizontal line indicates the zero value; the dashed lines are the weighted averages for their respective galaxies. Note the strongly discrepant behavior of the λ5432 line. |
| In the text | |
 |
Fig. 3 The relation between [Mn/Fe] and [Fe/H]. Data: each dSph galaxy is shown with a different color: blue stands for Sculptor, red for Fornax, green for Sextans, dark green for Carina, and dark turquoise for Leo I. The two green triangles identify the Sextans stars S05-010 and S08-038, whose Mn abundances are based on the λ5432 line only. The colored filled circles identify the samples analyzed in this work; the open symbols stand for previous published analyzes. The four open pentagons at [Fe/H] ≲ −2.9 are from Tafelmeyer et al. (2010) and are corrected for the HFS. The attached arrows gives an idea of the NLTE correction that they likely need, + 0.44, as computed by Bergemann & Gehren (2008) for the halo giant HD 122563. The results of Shetrone et al. (2003) for Sculptor, Fornax, and Leo I are displayed with open circles, and for Carina with open triangles. The dark green open squares are the Carina results of Venn et al. (2012). The dark gray open and filled circles represent the Feltzing et al. (2007) Milky Way thin and thick disk stars, respectively. The Sobeck et al. (2006) Milky Way cluster and field halo stars are shown with full gray squares; gray dots are very metal poor stars in the Milky Way halo from Cayrel et al. (2004). The vertical blue and green downward arrows indicate the “knee”, where [Mg/Fe] starts to decrease with increasing [Fe/H], in the Sculptor and Sextans dSphs (DART). Models: the chemical evolutions of the Sculptor (model A in cyan and model B in blue, see text), Fornax (model C in magenta and model D in orange, see text), and Carina (model E in dark green) dSphs are followed. The continuous lines show models with metallicity-dependent SNe Ia Mn yields as in Cescutti et al. (2008). The dashed lines follow the evolution of [Mn/Fe] for the same SFHs, but with metal-independent SNe Ia Mn yields. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for Sculptor only (blue dots), showing a plateau followed by a decreasing trend rather than a monotonic decrease in [Mn/Fe]. Results for the globular cluster ω Centauri are also shown as red circles (Cunha et al. 2010) and red dots (Pancino et al. 2011). |
| In the text | |
 |
Fig. 5 [Mn/α] versus [Fe/H] for each of the α elements Mg and Ca, for the Sculptor (blue dots), Fornax (red dots), Carina (dark green symbols), and Sextans (green symbols) galaxies. The key to the symbols is the same as in Fig. 3. For comparison, we provide results for field Milky Way stars, gathered from the literature: the open and full black dots are the thin and thick, respectively, disk dwarf stars measured by Bensby et al. (2003), Bensby et al. (2005), and Feltzing et al. (2007). The full grey symbols are from Cayrel et al. (2004) (round dots), and Gratton et al. (2003) (squares). |
| In the text | |
 |
Fig. 6 The SF histories for the analyzed models. In cyan model A and in blue model B, for Sculptor. In magenta model C and in orange model D, for Fornax. In dark green, model E for Carina. |
| In the text | |
 |
Fig. 7 Metallicity-dependent Mn yield of SNe Ia according to the prescription of Cescutti et al. (2008) (black line), and of SNe II with 15 M⊙ progenitors (red line) according to Woosley & Weaver (1995). |
| In the text | |
 |
Fig. 8 Same as Fig. 3 but for models only, showing the respective contributions of the SNe II and Ia to the Mn synthesis. Only the models A1 and B1 for Sculptor (continuous cyan and blue lines respectively), and C1 and D1 for Fornax (continuous magenta and orange lines) are shown. The dotted lines show the evolution of [Mn/Fe] assuming no Mn is produced by the SNe Ia, in contrast to Fe and all other elements. The dashed lines indicate the same evolution, but assuming that no Mn is produced by the SNe II. |
| In the text | |
 |
Fig. A.1 Comparison between the Mn abundances (not corrected for HFS) obtained for the Fornax dSph galaxy using the moog code, and the ones obtained using the calrai code, for each of the 4 lines Mn i λ5407, λ5420, λ5432, and λ5516. In both cases, the abundances were determined using spherical atmosphere models. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but for the Sculptor dSph galaxy. Here the calrai abundances were determined using plane-parallel atmosphere models, while the moog abundances are based on spherical models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


