| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118502 | |
| Published online | 10 May 2012 | |
Constraining cosmic rays and magnetic fields in the Perseus galaxy cluster with TeV observations by the MAGIC telescopes
1 IFAE, Edifici Cn., Campus UAB, 08193 Bellaterra, Spain
2 Universidad Complutense, 28040 Madrid, Spain
3 INAF National Institute for Astrophysics, 00136 Rome, Italy
4 Università di Siena, and INFN Pisa, 53100 Siena, Italy
5 Technische Universität Dortmund, 44221 Dortmund, Germany
6 Max-Planck-Institut für Physik, 80805 München, Germany
7 Università di Padova and INFN, 35131 Padova, Italy
8 Inst. de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
9 Depto. de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Spain
10 University of Łódź, 90236 Lodz, Poland
11 Tuorla Observatory, University of Turku, 21500 Piikkiö, Finland
12 Deutsches Elektronen-Synchrotron (DESY), 15738 Zeuthen, Germany
13 ETH Zurich, 8093 Zurich, Switzerland
14 Universität Würzburg, 97074 Würzburg, Germany
15 Universitat de Barcelona (ICC/IEEC), 08028 Barcelona, Spain
16 Università di Udine, and INFN Trieste, 33100 Udine, Italy
17 Institut de Ciències de l’Espai (IEEC-CSIC), 08193 Bellaterra, Spain
18 Inst. de Astrofísica de Andalucía (CSIC), 18080 Granada, Spain
19 Croatian MAGIC Consortium, Rudjer Boskovic Institute, University of Rijeka and University of Split, 10000 Zagreb, Croatia
20 Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
21 Inst. for Nucl. Research and Nucl. Energy, 1784 Sofia, Bulgaria
22 INAF/Osservatorio Astronomico and INFN, 34143 Trieste, Italy
23 Università dell’Insubria, Como, 22100 Como, Italy
24 Università di Pisa, and INFN Pisa, 56126 Pisa, Italy
25 ICREA, 08010 Barcelona, Spain
26 Now at École polytechnique fédérale de Lausanne (EPFL), Lausanne, Switzerland
27 Supported by INFN Padova
28 Now at: Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
29 Now at: Finnish Centre for Astronomy with ESO (FINCA), University of Turku, Finland
30 HITS, Schloss-Wolfsbrunnenweg 33, 69118 Heidelberg, Germany
31 UC Santa Barbara, CA 93106, Santa Barbara, USA
Received: 22 November 2011
Accepted: 6 March 2012
Galaxy clusters are being assembled today in the most energetic phase of hierarchical structure formation which manifests itself in powerful shocks that contribute to a substantial energy density of cosmic rays (CRs). Hence, clusters are expected to be luminous gamma-ray emitters since they also act as energy reservoirs for additional CR sources, such as active galactic nuclei and supernova-driven galactic winds. To detect the gamma-ray emission from CR interactions with the ambient cluster gas, we conducted the deepest to date observational campaign targeting a galaxy cluster at very high-energy gamma-rays and observed the Perseus cluster with the MAGIC Cherenkov telescopes for a total of ~85 h of effective observing time. This campaign resulted in the detection of the central radio galaxy NGC 1275 at energies E > 100 GeV with a very steep energy spectrum. Here, we restrict our analysis to energies E > 630 GeV and detect no significant gamma-ray excess. This constrains the average CR-to-thermal pressure ratio to be ≲1–2%, depending on assumptions and the model for CR emission. Comparing these gamma-ray upper limits to models inferred from cosmological cluster simulations that include CRs constrains the maximum CR acceleration efficiency at structure formation shocks to be <50%.Alternatively, this may argue for non-negligible CR transport processes such as CR streaming and diffusion into the outer cluster regions. Finally, we derive lower limits on the magnetic field distribution assuming that the Perseus radio mini-halo is generated by secondary electrons/positrons that are created in hadronic CR interactions: assuming a spectrum of E-2.2 around TeV energies as implied by cluster simulations, we limit the central magnetic field to be >4–9 μG, depending on the rate of decline of the magnetic field strength toward larger radii. This range is well below field strengths inferred from Faraday rotation measurements in cool cores. Hence, the hadronic model remains a plausible explanation of the Perseus radio mini-halo.
Key words: gamma rays: galaxies: clusters / acceleration of particles / galaxies: clusters: individual: Perseus
© ESO, 2012
1. Introduction
In the hierarchical model of structure formation, clusters of galaxies are presently forming through mergers of smaller galaxy groups, and assembling masses up to a few times 1015 M⊙. During these merger events, enormous amounts of energy – of the order of the final gas binding energy Ebind ~ 3 × (1061–1063) erg – are released through collisionless shocks and turbulence. This energy is dissipated on a dynamical timescale of τdyn ~ 1 Gyr (see Voit 2005, for a review). Hence, the corresponding energy dissipation rates are L ~ (1045–1047) erg s-1. If only a small fraction of this energy were converted into non-thermal particle populations, the associated emission should be detectable in the gamma-ray regime and can potentially be used to decipher the short- and long-term history of structure formation.
Many galaxy clusters show large scale diffuse synchrotron radio emission in the form of so-called radio (mini-)halos which proves the existence of magnetic fields and relativistic electrons permeating the intra-cluster medium (ICM) (e.g., Kempner et al. 2004; Feretti et al. 2004). Through this synchrotron emission we can identify the sites of acceleration and injection of the relativistic electrons into the ICM: (1) merger shocks propagating toward the cluster outskirts, observed as giant radio relics; (2) active galactic nuclei (AGN) in clusters, observed through radio jets and bubbles; and (3) galactic winds and ram pressure stripping are often accompanied by synchrotron emission. In analogy with shocks within our Galaxy, such as those in supernova remnants, galaxy clusters should also be acceleration sites for relativistic protons and heavier relativistic nuclei. Due to their higher masses compared with the electrons, protons and nuclei are accelerated more efficiently to relativistic energies and are expected to show a ratio of the spectral energy flux of cosmic ray (CR) protons to CR electrons above 1 GeV of about 100 (as it is observed in our Galaxy between 1–10 GeV, see Schlickeiser 2002). CR protons also have radiative cooling times that are larger than the corresponding cooling times of CR electrons by the square of the mass ratio, (mp/me)2, and hence can accumulate for the Hubble time in a galaxy cluster (Völk et al. 1996). For gas densities in galaxy clusters, n, the radiative cooling time of CR protons is much longer relative to the hadronic timescale, τpp ≃ 30 Gyr × (n/10-3 cm-3)-1, on which CR protons collide inelastically with ambient gas protons of the ICM. This is the process in which we are primarily interested here as it produces pions that successively decay into synchrotron emitting electrons/positrons (so-called secondaries) and gamma-rays.
There are two principal models that explain radio (mini-)halos. In the “hadronic model” the radio emitting electrons are produced in inelastic CR proton-proton (p-p) interactions (Dennison 1980; Vestrand 1982; Enßlin et al. 1997; Blasi & Colafrancesco 1999; Dolag & Enßlin 2000; Miniati et al. 2001; Miniati 2003; Pfrommer & Enßlin 2003, 2004a,b; Blasi et al. 2007; Pfrommer et al. 2008; Pfrommer 2008; Kushnir et al. 2009; Donnert et al. 2010a,b; Keshet & Loeb 2010; Keshet 2010; Enßlin et al. 2011; Fujita & Ohira 2012) requiring only a very modest fraction of a few percent of CR-to-thermal pressure. Some clusters, known as cool-core clusters, e.g., the Perseus cluster studied here, are characterized by a central temperature decrease and a correspondingly enhanced central ICM density (Fabian 1994; Hudson et al. 2010). These cool cores provide high target densities for hadronic CR interactions, increasing the resulting gamma-ray flux. This is the main reason for a larger expected flux from Perseus in comparison to other nearby clusters (Pinzke & Pfrommer 2010; Pinzke et al. 2011). Another alternative is the “re-acceleration model”: during states of powerful ICM turbulence, e.g., after a cluster merger, re-acceleration might be efficient enough to accelerate CR electrons to high enough energies (~10 GeV) that they produce observable radio emission (Schlickeiser et al. 1987; Giovannini et al. 1993; Gitti et al. 2002; Brunetti & Blasi 2005; Brunetti & Lazarian 2007, 2011; Brunetti et al. 2009). This, however, requires a sufficiently long-lived CR ICM electron population at energies around 100 MeV which might be maintained by re-acceleration processes by particle-plasma wave interactions at a rate faster than the cooling processes. We refer the reader to Enßlin et al. (2011) for a discussion on the strengths and weaknesses of each of the models. That magnetic fields with central field strengths ranging between B ~ (1−20) μG are ubiquitous in galaxy clusters and permeate the ICM is suggested by Faraday rotation measurements (RM; Kim et al. 1991; Clarke et al. 2001; Carilli & Taylor 2002; Vogt & Enßlin 2005; Kuchar & Enßlin 2011). Combining the diffuse synchrotron radio emission with detections of galaxy clusters in hard X-rays can also be used to constrain the intra-cluster magnetic field if the hard X-ray emission is due to inverse Compton up-scattering of cosmic microwave photons by CR electrons (see Rephaeli et al. 2008 for a recent review). The derived magnetic field strengths, typically 0.1 μG, are in direct conflict with the much stronger field strengths estimated from Faraday RM analyses. However, more sensitive observations by Swift/BAT have not found evidence of a hard power-law tail above the thermal emission. With the potential exception of the Bullet Cluster (i.e., 1E 0657-558), the emission is compatible with a multi-temperature plasma (Ajello et al. 2009, 2010; Wik et al. 2011), disputing earlier claims of the existence of a nonthermal component. Combining hadronically-induced synchrotron emission by secondaries from CR interactions with the associated pion-decay gamma-ray emission would yield significant information on cluster magnetic fields (e.g., Pfrommer & Enßlin 2004b; Pfrommer 2008; Jeltema & Profumo 2011). Limits on the gamma-ray emission provide limits on the intra-cluster magnetic field if the hadronic model is applicable to the radio (mini-)halo emission.
Very high-energy (VHE, E > 100 GeV) gamma-ray observations are very important for delimiting the CR pressure. A substantial CR pressure contribution can bias hydrostatic equilibrium cluster masses as well as the total Comptonization parameter due to the Sunyaev-Zel’dovich effect which is proportional to the thermal energy of a galaxy cluster (e.g., see Pfrommer et al. 2007). This would at least complicate, if not render it impossible, to use these methods for estimating cosmological parameters with galaxy clusters. There are two ways to assess the bias due to nonthermal pressure contributions from CRs, magnetic fields or turbulence. At the cluster center a comparison of X-ray and optically-inferred gravitational potential profiles yields an upper limit of 0.2–0.3 for the ratio of nonthermal pressure to the thermal gas pressure (Churazov et al. 2008, 2010). On large scales, there are indications that hydrostatic mass estimates can be biased by up to ~ 20% relative to weak gravitational lensing masses at R500 – the radius of a sphere enclosing a mean density that is 500 times the critical density of the Universe (Mahdavi et al. 2008). While this could be due to nonthermal pressure, weak lensing mass estimates must be interpreted with caution since they are intrinsically biased: cluster mass (shear) profiles at large radii attain systematic modifications due to substructure and halo triaxiality (Becker & Kravtsov 2011). VHE gamma-ray emission is a complementary method for constraining the pressure contribution of CRs that is most sensitive to the cluster core region. Multi-frequency constraints limited the CR pressure component to be below a few percent of the thermal pressure in the best cases (e.g., Pfrommer & Enßlin 2004a; Reimer et al. 2004; Ackermann et al. 2010a; Pinzke et al. 2011). However, this approach assumes that the CR component is fully mixed with the ICM and is almost insensitive to a two-phase structure of CRs and the thermal ICM. In addition to this cosmological motivation, constraining the CR pressure contribution in clusters in combination with cosmological hydrodynamical simulations provides limits on the average acceleration efficiency at strong formation shocks, the CR transport properties (Enßlin et al. 2011) and the impact of the cluster’s dynamical state on the CR population.
Following up on earlier high-energy gamma-ray observations of galaxy clusters, in this work we present the deepest yet VHE gamma-ray observation of a galaxy cluster (for space-based cluster observations in the GeV-band, see Reimer et al. 2003; Ackermann et al. 2010a,b; for ground-based observations in the energy band > 100 GeV, see Perkins et al. 2006; Perkins 2008; Aharonian et al. 2009a,b; Domainko et al. 2009; Galante et al. 2009; Kiuchi et al. 2009; Acciari et al. 2009; Aleksić et al. 2010a). We are able to constrain simulation-based models for the CR induced gamma-ray emission and the cluster magnetic field in the hadronic model for radio (mini-)halos.
The MAGIC Telescopes observed the Perseus cluster in stereoscopic mode from October 2009 to February 2011 for a total of ~85 h of effective observation time. This campaign produced the VHE detection of the head-tail radio galaxy IC 310, which lies in the field of view of the Perseus observation (Aleksić et al. 2010b), and of the central radio galaxy NGC 1275 (Aleksić et al. 2012a). Here, we focus on the CR induced gamma-ray emission from the cluster itself. Galaxy clusters are also very promising targets for constraining the dark matter annihilation cross section or decay rate (Colafrancesco et al. 2006; Pinzke et al. 2009; Jeltema et al. 2009; Cuesta et al. 2011; Dugger et al. 2010; Sánchez-Conde et al. 2011; Pinzke et al. 2011; Gao et al. 2012). We defer any such analysis to future work. The presence of a central gamma-ray emitting source at energies <600 GeV, combined with the expected flat dark matter annihilation emission profile out to the virial radius owing to the substructures that dominate the cluster emission (Sánchez-Conde et al. 2011; Pinzke et al. 2011; Gao et al. 2012), calls for novel analysis techniques that are beyond the scope of the present study.
This work has two companion papers. One is dedicated to the NGC 1275 detection using the August 2010–February 2011 campaign data (Aleksić et al. 2012a), while the other will address the NGC 1275 multi-wavelength emission from radio to VHE and give a comprehensive interpretations of all collected data (MAGIC Collaboration, in prep.). The paper is organized as follows. In Sect. 2, we explain and present our target selection and put the observation of the cool-core cluster Perseus into the broader context of nonthermal cluster radio emission. Specifically, we compare Perseus to the expected TeV characteristics of a merging cluster, namely Coma. In Sect. 3, we describe the MAGIC telescopes, present the observations, and detail the data analysis and results. These data are used to constrain the CR population in the Perseus cluster and the magnetic field distribution in the hadronic model of the radio mini-halo (Sect. 4). Finally, in Sect. 5, we summarize our findings. All quantities are scaled to the currently favored value of Hubble’s constant H0 = 70 km s-1 Mpc-1.
2. Target selection: comparing the nonthermal emission of cool-core versus merging clusters
The Perseus cluster was selected for the MAGIC observations as it is the most promising target for the detection of gamma-rays coming from neutral pion decay resulting from hadronic CR interactions with the ICM (Aleksić et al. 2010a; Pinzke & Pfrommer 2010; Pinzke et al. 2011). This cluster of galaxies (also known as Abell 426), at a distance of 77.7 Mpc (z = 0.018), is the brightest X-ray cluster with a luminosity in the soft X-ray band (ranging from 0.1−2.4 keV), LX,0.1−2.4 = 8.3 × 1044 erg s-1 (Reiprich & Böhringer 2002). It contains a massive cool core with high central gas densities of about 0.05 cm-3 (Churazov et al. 2003). The cluster also contains a luminous radio mini-halo with an extension of 200 kpc (Pedlar et al. 1990). More details on possible VHE gamma-ray emission in galaxy clusters can be found in the first MAGIC paper about the Perseus cluster observation with a single telescope (Aleksić et al. 2010a).
 |
Fig. 1 Left panel: significance skymap of the Perseus cluster above 150 GeV. The positions of NGC 1275 (white cross), which coincides with the cluster center, and the head-tail radio galaxy IC 310 (black cross) are marked. Right panel: significance skymap of the Perseus cluster region above 630 GeV. The central white circle marks the 0.15° region used to derive constraints (see main text for details). The quoted energy thresholds are obtained assuming a spectral index of 4 as observed in NGC 1275. |
One of the most important questions in studies of nonthermal cluster emission is the origin of giant radio halos in merging clusters and radio mini-halos in cool-core clusters and whether they have a common physical origin. Hence it is instructive to compare the prospects for detecting VHE gamma-ray emission from two representative clusters of each model class, namely Coma and Perseus. First, assuming universality of the gamma-ray spectrum, Coma is expected to be fainter than Perseus by approximately a factor of 3.4. This is mainly because of the lower central gas density in Coma (Pinzke et al. 2011). Second, the Coma X-ray emission is more extended than in Perseus by the ratio of the half-flux radii of 0.18°/0.11° = 1.6 (Pinzke & Pfrommer 2010). Since the sensitivity of Imaging Atmospheric Cherenkov Telescopes (IACTs) drops almost linearly with source extension for the angular scales considered here, this makes it even more challenging to detect the Coma cluster. Third, the CR spectral index is expected to steepen due to CR transport processes such as streaming and momentum-dependent diffusion (Enßlin et al. 2011). The authors of that paper indicate that these mechanisms alleviate some tension between the hadronic model of radio halos and their observations, such as Coma. The following line of arguments shows that this third point slightly favors Coma as a target source, but the sum of all points clearly favors Perseus:
-
Coma should have a central magnetic field strength of
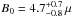 G according to Faraday RM studies (e.g., Bonafede et al. 2010). While GHz-radio observations probe 2.5 GeV electrons that are produced in hadronic interactions of 40 GeV CR protons, gamma-rays at 200 GeV are from 1.6 TeV CRs: hence, for Coma, we have to extrapolate a factor of 50 in energy to connect the CRs probed by radio halo observations with those probed by IACTs and we expect a weak bias due to possible CR spectral steepening.
G according to Faraday RM studies (e.g., Bonafede et al. 2010). While GHz-radio observations probe 2.5 GeV electrons that are produced in hadronic interactions of 40 GeV CR protons, gamma-rays at 200 GeV are from 1.6 TeV CRs: hence, for Coma, we have to extrapolate a factor of 50 in energy to connect the CRs probed by radio halo observations with those probed by IACTs and we expect a weak bias due to possible CR spectral steepening. -
For Perseus, we expect a stronger central magnetic field (~20 μG, see discussion in Sect. 4.4) from adiabatic magnetic field compression during the formation of the cool core. While GHz-radio observations probe 1.2 GeV electrons and the 20 GeV CR protons that generate those electrons hadronically, the MAGIC gamma-ray constraints at 1 TeV correspond to 8 TeV CR protons (since the detection of VHE gamma-ray emission from the central AGN, NGC 1275, renders it difficult to observe diffuse emission at lower energies). Hence the CRs probed by the radio observations and those probed by MAGIC are a factor of 400 different in energy. A possible CR spectral steepening due to, e.g., momentum-dependent CR diffusion would induce a larger bias in the CR pressure and magnetic field constraints. Assuming a change in the spectral index by 0.2 between 20 GeV and 8 TeV implies a decrease of the VHE gamma-ray flux by a factor of 3.3−1.6 times larger than the corresponding decrease of flux for Coma (over the eight times smaller energy range).
In summary, it appears that Perseus is the most promising target for detecting CR-induced gamma-ray emission and hence we chose this cluster for our deep VHE gamma-ray campaign. Assuming that the energy dependence of the CR transport and the associated spectral steepening is representative for clusters, we would need ten times longer integrations to detect gamma-ray emission from Coma in comparison to Perseus. However we stress that cool-core and non-cool core clusters are complementary and equally deep or deeper observations of merging clusters that host giant radio halos – such as Coma – are needed. We also emphasize the need to theoretically model how the variation of the CR spectral index due to energy dependent CR transport processes, e.g., CR diffusion, depends on the mass and dynamical state of the cluster. This will be critical for modeling the gamma-ray brightness of clusters and how to interpret the underlying CR physics.
3. MAGIC observations, analysis, and results
The MAGIC telescopes are two 17 m dish IACTs located at the Roque de los Muchachos observatory (28.8°N, 17.8°W, 2200 m a.s.l.), on the Canary Island of La Palma. Since the end of 2009 the telescopes are working together in stereoscopic mode which ensures a sensitivity of ~0.7% of the Crab Nebula flux above approximately 600 GeV in 50 h of observations (Aleksić et al. 2012b). For the energies of interest here (i.e., above 600 GeV), the point spread function (PSF), defined as a 2-dimensional Gaussian, has a σ ≃ 0.06°.
The Perseus cluster region was observed by the MAGIC telescopes from October 2009 to February 2011 for a total of about 99 h. During the October 2009–February 2010 campaign (45.3 h), the data were taken in the so called soft-stereo trigger mode with the first telescope (MAGIC-I) trigger working in single mode and the second telescope (MAGIC-II) recording only events triggered by both telescopes. The soft-stereo trigger mode may result in slightly degraded performance at the lowest energies with respect to Aleksić et al. (2012b), but has a negligible impact at the energies of interest here. During the August 2010–February 2011 campaign (53.6 h), data were taken in the standard full-stereo trigger mode (where events are triggered simultaneously by both telescopes). Observations were performed in wobble mode (Fomin et al. 1994) tracking positions 0.4° from the cluster center, at zenith angles ranging from 12° to 36°.
The selected data sample consists of 84.5 h of effective observation time. The data quality check resulted in the rejection of about 14.4 h of data, mainly due to non-optimal atmospheric conditions. The standard MAGIC stereo analysis chain was used for calibration and image cleaning (see Aleksić et al. 2012b, for details). In order to combine data taken with different trigger modes, we applied a high cut on the shower image size (total signal inside the image). Only events with image size above 150 photo-electrons in both telescopes were kept (the standard analysis uses 50 photo-electrons cuts). With this cut, the rate and image parameter distributions of the background events are compatible between the two samples.
The left panel of Fig. 1 shows the significance skymap obtained with this analysis with an energy threshold of 150 GeV. The two AGNs detected during the campaign can clearly be seen (NGC 1275 in the center and IC 310 in the lower-right part).
In this work we limit our attention to pion-decay gamma-ray emission resulting from hadronic CR interactions with thermal protons of the ICM. Cosmological simulations of Pinzke & Pfrommer (2010) suggest that the spectral energy distribution of gamma-rays follows a power-law, F ∝ E − α, with a spectral index of α = 2.2 at the energies of interest here (Aleksić et al. 2010a). The simulated signal is extended with approximately 60% of the emission coming from a region centered on NGC 1275 with a radius of 0.15° (see Fig. 13 of Pinzke & Pfrommer 2010). The emission from NGC 1275 is dominant below about 600 GeV and with a spectral index of about 4 (Aleksić et al. 2012a). Therefore, since the expected CR-induced signal is much harder than the measured NGC 1275 spectrum, we expect it to appear at higher energies with no break or cut-off in the energy range covered by MAGIC. Hence, we limit the data analysis to energies >630 GeV for which the NGC 1275 signal vanishes (Aleksić et al. 2012a). The right panel of Fig. 1 shows the significance skymap above 630 GeV. In contrast to NGC 1275, the spectrum of IC 310 is very hard and remains detectable above 600 GeV (Aleksić et al. 2010b). IC 310 is ~0.6° (≃10 PSF) away from the cluster center, far enough so that its emission does not leak into the signal region. However, if not explicitly accounted for, it could affect the estimated background. Here, the background is measured with three off-source positions at 0.4° from the the camera center and >0.28° away from IC 310. This distance guarantees that there is no contamination from IC 310.
 |
Fig. 2 θ2 distribution above 630 GeV of the signal (data points) and background (gray filled region) at the cluster center. The dashed line represents the signal region cut within which the excess event number is estimated. Here it corresponds to 0.02 deg2. The quoted energy threshold is obtained assuming a spectral index of 4 as observed in NGC 1275. |
In Fig. 2, we show the θ2 distribution1 of the signal and background at the cluster center for energies above 630 GeV. Since the emission is expected to be more extended than the MAGIC PSF we must optimize the cut in the θ2 distribution which defines the signal region. We take the following approach. First, we estimate the θ2 distribution of the expected signal considering the simulated surface brightness of the Perseus cluster emission smoothed with the MAGIC PSF. Second, we estimate the background level from our data. Finally, we calculate the significance for signal detection (according to the Eq. (17) in Li & Ma 1983) as a function of the θ2 cut. The derived optimal θ2 cut was close to 0.02 deg2. As shown in Fig. 2, we find no significant excess within 0.02 deg2.
Since we did not detect a signal, we derived integral flux upper limits (ULs) for several energy thresholds. The effective area of MAGIC is calculated using point-like source Monte Carlo simulation and the ULs have to be corrected to take into account the expected source extension. To calculate this correction factor, we compare the fraction of the total events inside the signal region for a point-like source and for the expected CR induced signal. Therefore, the presented ULs can be compared with the theoretical expectations for the region within a radius of 0.15°. The UL estimation is performed using the Rolke method (Rolke et al. 2005) as in Aleksić et al. (2011) with a confidence level of 95% and a total systematic uncertainty of 30%. In Table 1, we present the integral flux ULs above specified energy thresholds calculated for a spectral index of 2.2. We also give the point-like ULs, significance and ULs in number of events. The integral ULs for energies above Eth = 1 TeV corresponds to the best sensitivity for sources with spectral index 2.2 and it is the most constraining value; for this reason we will adopt this UL for the discussion. For purposes that will be clear in the following, we also recalculate the 0.15° integral flux UL above 1 TeV for spectral indexes of 2.1, 2.3 and 2.5 which are 1.37, 1.38 and 1.39 × 10-13 cm-2 s-1, respectively.
Integral flux ULs.
4. Implications for cosmic rays and magnetic fields
We follow different approaches in constraining the CR pressure distribution in the Perseus cluster with the MAGIC ULs. This enables us to explore the underlying plasma physics that produce the CR distribution and hence reflect the Bayesian priors in the models (see Pinzke et al. 2011, for a discussion). Our approaches include (1) a simplified analytical approach that assumes a constant CR-to-thermal pressure and a momentum power-law spectrum (Sect. 4.1); (2) an analytic model of CRs derived from cosmological hydrodynamical simulations of the formation of galaxy clusters (Sect. 4.2); and (3) the use of the observed luminosity and surface brightness profile of the radio mini-halo in Perseus to place a lower limit on the expected gamma-ray flux in the hadronic model of radio mini-halos – where the radio-emitting electrons are secondaries from CR interactions (Sect. 4.3). This provides a minimum CR pressure which, using tight gamma-ray limits/detections, checks the hadronic model of the formation of radio mini-halos; (4) alternatively, by constructing a CR distribution that is just allowed by the flux ULs, and requiring the model to match the observed radio mini-halo data, we can derive a lower limit on the magnetic field strength (Sect. 4.4). Note, however, that this limit assumes that the observed synchrotron emission is produced by secondary electrons resulting from hadronic CR interactions.
4.1. Simplified analytical CR model
Here, we adopt a simplified analytical model that assumes a power-law CR momentum spectrum, f ∝ p − α, and a constant CR-to-thermal pressure ratio, i.e., we adopt the isobaric model of CRs following the approach of Pfrommer & Enßlin (2004a). To facilitate comparison with earlier analytical work in the literature, we do not impose a low-momentum cutoff on the CR distribution function, i.e., we adopt q = 0 (this assumption can be easily generalized to an arbitrary q using e.g., Fig. 1 of Pfrommer & Enßlin 2004a). Since a priori the CR spectral index2, α, is unconstrained, we vary it within a plausible range of 2.1 < α < 2.5. The central value of this spectral range is compatible with the radio spectral index in the core of the Perseus radio mini-halo of αν = α/2 ~ 1.25 (Sijbring 1993)3: assuming a central magnetic field strength of 20 μG, appropriate for cool-core clusters, the CR protons responsible for the GHz radio emitting electrons have an energy of ~20 GeV and are ~400 times less energetic than the CR protons with an energy of 8 TeV that are responsible for gamma-ray emission at 1 TeV. This is consistent with the concavity in the universal CR spectrum that connects the steep-spectrum low-energy CR population around GeV energies (α ≃ 2.5) with the harder CR population at TeV energies (α ≃ 2.2) (Pinzke & Pfrommer 2010). To model the thermal pressure, we adopt the measured electron temperature and density profiles for the Perseus cluster (Churazov et al. 2003). The temperature profile has a dip in the central cool core region and otherwise a constant temperature of kT = 7 keV. The density profile is hybrid in the sense that it combines Einstein X-ray observations on large scales with high-resolution XMM-Newton observations of the cluster core (Churazov et al. 2003).
Table 2 shows the resulting constraints on the CR-to-thermal pressure ratio, XCR = ⟨PCR⟩/⟨Pth⟩, averaged within the virial radius, Rvir = 2 Mpc, that we define as the radius of a sphere enclosing a mean density that is 200 times the critical density of the Universe. The inferred constraints on XCR strongly depend on α due to the comparably large lever arm from GeV-CR energies (that dominate the CR pressure) to CR energies at 8 TeV. Using the integral flux UL above 1 TeV, we constrain XCR to be between 0.77% and 11.6% (for α varying between 2.1 and 2.5). For a spectral index of 2.2, favored by the simulation-based model of Pinzke & Pfrommer (2010) at energies > 1 TeV, we obtain XCR < 1.1%.
Constraints on CR-to-thermal pressure ratio.
4.2. Simulation-inspired CR model
For a more realistic approach, we turn to cosmological hydrodynamical simulations. These have considerable predictive power, e.g., they calculate the CR spectrum self-consistently rather than leaving it as a free parameter, and permit tests of various assumptions about the underlying CR physics. We adopt the universal spectral and spatial CR model developed by Pinzke & Pfrommer (2010) that uses only a density profile as input which can be inferred from cosmological simulations or X-ray observations. This analytic approach models the CR distribution, and the associated radiative emission processes from hadronic interactions with gas protons, from radio to the gamma-ray band. The gamma-ray emission from decaying neutral pions dominates over the IC emission from primary and secondary electrons above 100 MeV in clusters (e.g., Pfrommer 2008). This analytic formalism was derived from high-resolution simulations of clusters that included radiative hydrodynamics, star formation, supernova feedback, and followed CR physics spectrally and spatially by tracing the most important injection and loss processes self-consistently while accounting for the CR pressure in the equation of motion (Pfrommer et al. 2006; Enßlin et al. 2007; Jubelgas et al. 2008). The results are consistent with earlier numerical results within their range of applicability regarding the overall characteristics of the CR distribution and the associated radiative emission processes (Dolag & Enßlin 2000; Miniati et al. 2001; Miniati 2003; Pfrommer et al. 2007, 2008; Pfrommer 2008).
There are (at least) two major uncertainties in modeling the CR physics that significantly affect the resulting spatial and spectral CR distribution (and may impact the universality of the CR populations across different cluster masses): the CR acceleration efficiency and the microscopic CR transport relative to the thermal plasma. We will discuss each process separately. The overall normalization of the CR and gamma-ray distribution scales with the maximum acceleration efficiency at structure formation shocks. Following recent observations (Helder et al. 2009) and theoretical studies (Kang & Jones 2005) of supernova remnants, we adopt an optimistic but realistic value of this parameter and assume that 50% of the dissipated energy at strong shocks is injected into CRs while this efficiency rapidly decreases for weaker shocks. The vast majority of internal formation shocks (merger and flow shocks) are weak with Mach numbers M ≲ 3 (e.g., Ryu et al. 2003; Pfrommer et al. 2006) which we presume have low CR acceleration efficiencies and do not contribute significantly to the CR population in clusters. Instead, strong shocks during the cluster formation epoch and strong accretion shocks at the present time (at the boundary of voids and filaments/super-cluster regions) dominate the injection of CRs which are adiabatically transported throughout the cluster. These models provide a plausible UL for the CR contribution from structure formation shocks in galaxy clusters which can be scaled with the effective acceleration efficiency. Other possible CR sources, such as starburst-driven galactic winds and AGNs, could increase the expected gamma-ray yield, but have been neglected4.
These cosmological simulations only consider advective transport of CRs by turbulent gas motions which produces a centrally enhanced profile. However, active CR transport such as CR diffusion and streaming flattens the CR radial profile, producing a spatially constant CR number density in the limiting case. Although the CR streaming velocity is larger than typical advection velocities in a galaxy cluster, it becomes comparable to or lower than this only for periods with trans- and supersonic cluster turbulence during a cluster merger. As a consequence a bimodality of the CR spatial distribution results with merging (relaxed) clusters showing a centrally concentrated (flat) CR energy density profile (Enßlin et al. 2011). This produces a bimodality of the diffuse radio and gamma-ray emission of clusters, since more centrally concentrated CRs will find higher target densities for hadronic CR proton interactions (Enßlin et al. 2011). Thus, relaxed clusters could have a reduced gamma-ray luminosity by up to a factor of five. The goal of this and future searches for gamma-ray emission from clusters is to constrain the acceleration physics and transport properties of CRs.
In the following, we use two different CR models. In our optimistic CR model (simulation-based analytics with galaxies), we calculated the cluster total gamma-ray flux within a given solid angle. In contrast, we cut the emission from individual galaxies and compact galactic-sized objects in our more conservative model (simulation-based analytics without galaxies). In short, the ICM is a multiphase medium consisting of a hot phase which attained its entropy through structure formation shock waves dissipating gravitational energy associated with hierarchical clustering into thermal energy. The dense, cold phase consists of the true interstellar medium within galaxies (which is modelled with an effective equation of state following Springel & Hernquist 2003) and at the cluster center as well as the ram-pressure stripped interstellar medium. These cold dense gas clumps dissociate incompletely in the ICM due to insufficient numerical resolution as well as so far incompletely understood physical properties of the cluster plasma. All of these phases contribute to the gamma-ray emission from a cluster. To assess the bias associated with this issue, we performed our analysis with both limiting cases bracketing the realistic case.
 |
Fig. 3 Integral flux ULs of the single telescope observations (point-like ULs, upper arrows; Aleksić et al. 2010a) and of this work (solid arrows; Table 1) are shown. We compare ULs with the simulated integrated spectra of the gamma-ray emission from decaying neutral pions that result from hadronic CR interactions with the ICM in the Perseus cluster coming from within a radius of 0.15° around the center. The conservative model without galaxies (solid line) is shown together with the model with galaxies (dotted line). The flux UL at 1 TeV is a factor of 1.25 below the conservative model and hence constrains a combination of CR shock acceleration efficiency and CR transport processes. We also show the minimum gamma-ray flux estimates for the hadronic model of the Perseus radio mini-halo (dashed line with minimum flux arrows) using the universal gamma-ray spectrum resulting from pion decay (Pinzke & Pfrommer 2010) and adopting the spectral index, 2.2, of this spectrum around TeV energies. |
We again adopt the hybrid electron density and temperature profile from X-ray observations of the Perseus cluster (Churazov et al. 2003)5, modifying the temperature profile in the outer cluster regions beyond 0.2 R200 ≃ 400 kpc. This produces the characteristic decline toward the cluster periphery in accord with a fit to the universal profile derived from cosmological cluster simulations (Pinzke & Pfrommer 2010; Pfrommer et al. 2007) that also follows the behavior of a nearby sample of deep Chandra cluster data (Vikhlinin et al. 2005). While this modification has little influence on the expected gamma-ray emission (in projection onto the core region) as the densities drop considerably in these regions, the resulting profiles for the CR-to-thermal pressure ratio are changed as we will discuss below. We estimate the spatial and spectral distribution of CRs using the model by Pinzke & Pfrommer (2010). Figure 3 shows the expected spectrum for Perseus within an aperture of radius 0.15°. The MAGIC limit for Eγ > 1 TeV falls below the flux level of the conservative model (that does not take into account the emission from galaxies6) by 20%; thereby constraining assumptions about the adopted CR physics in the simulations and the resulting CR pressure.
Figure 4 shows the CR-to-thermal pressure ratio, XCR = ⟨PCR⟩/⟨Pth⟩ as a function of radial distance from the Perseus cluster center, in units of the virial radius, Rvir. To compute PCR, we assume a low-momentum cutoff of the CR distribution of q = 0.8 mpc found in cosmological simulations by Pinzke & Pfrommer (2010). This cutoff derives from the high cooling rates for low energy CRs due to Coulomb interactions with the thermal plasma. The ratio XCRrises toward the outer regions because of the higher CR acceleration efficiency in the peripheral strong accretion shocks compared to the weak central flow shocks. Adiabatic compression of a mixture of CRs and thermal gas reduces the CR pressure relative to the thermal pressure due to the softer CR equation of state. The strong increase of XCR toward the core is a remnant of the formation of the cool core in Perseus. During this transition, the mixed gas of CRs and thermal particles has been adiabatically compressed. While the thermal gas radiates on a comparatively fast thermal bremsstrahlung timescale, the long hadronic interaction time scale for energetic CRs ensures an accumulation of this population, thus diminishing the thermal pressure support relative to that in CRs.
 |
Fig. 4 CR-to-thermal pressure ratio, XCR = ⟨PCR⟩/⟨Pth⟩ at the radial distance from the Perseus cluster center, R/Rvir (red lines), and integrated up to R/Rvir (blue lines), using the simulation-based analytical model of CRs (Pinzke & Pfrommer 2010). The simulation model (dashed) is contrasted to a model that has been scaled by the MAGIC constraints obtained in this work (solid). |
The MAGIC flux limits constrain XCR of the simulation-based analytical model to be less than 1.6% within 0.15° (200 kpc). Assuming this spatial CR profile yields a CR-to-thermal pressure ratio < 1.7% within Rvir ≃ 2 Mpc and < 5% within 20 kpc. When scaling the XCR profile to the flux ULs, we used the conservative model of Pinzke & Pfrommer (2010) that neglects the contribution of cluster galaxies since those increase only the gamma-ray yield but do not contribute to the CR pressure within the ICM. The XCR-limit within the virial radius is larger by a factor of 1.5 than a pure power-law spectrum (see Sect. 4.1) because the concave curvature of the simulated spectrum accumulates additional pressure toward GeV energies relative to a pure power-law.
With these gamma-ray flux ULs, we constrain the CR physics in galaxy clusters: this either limits the maximum acceleration efficiency of CRs at strong structure formation shocks to < 50% or indicates possible CR streaming and diffusion out of the cluster core region. The latter populates the peripheral cluster regions and XCR increases toward the cluster periphery at the expense of a decrease of the central XCR (Enßlin et al. 2011) compared to the simulation model. The X-ray morphology of the central region in Perseus shows spiral structure in the density and temperature maps with an anti-correlation of both quantities (Fabian et al. 2011). This resembles sloshing motions after a past merger event, suggesting that Perseus is currently relaxing. This interpretation is supported by recent magnetohydrodynamical simulations (ZuHone et al. 2011) which argue that magnetic fields are draped at the contact discontinuity of the remnant cool core (Lyutikov 2006; Dursi & Pfrommer 2008; Pfrommer & Dursi 2010) that is sloshing in the potential of the parent halo. The abrupt drop in the radio surface brightness map outside the spiral pattern (see Fig. 8 in Fabian et al. 2011) may then be produced by a strong decrease of magnetic field strengths outside the sloshing core. If CR streaming and diffusion out of the central core region is indeed correlated with a dynamical relaxation of a cluster after a merger event as suggested by Enßlin et al. (2011), this would render CR transport more plausible for explaining the smaller gamma-ray flux relative to the simulation model. By the same token, it may argue for a more extended gamma-ray emission signature than that seen in the radio, further justifying the larger source extension, 0.15°, that we adopted in this work (which is twice that of the largest radial extend of the mini-halo of 0.075°).
4.3. Minimum gamma-ray flux
For clusters with radio (mini-)halos we can derive a minimum gamma-ray flux in the hadronic model of radio (mini-)halos. A stationary distribution of CR electrons loses all its energy to synchrotron radiation for strong magnetic fields (B ≫ BCMB ≃ 3.2 μG, where BCMB is the equivalent magnetic field strength of the cosmic microwave background (CMB) so that 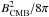 equals the CMB energy density). Hence the ratio of gamma-ray to synchrotron flux becomes independent of the spatial distribution of CRs and thermal gas (Völk 1989; Pohl 1994; Pfrommer 2008), particularly with the observed synchrotron spectral index αν = α/2 ≃ 1. This can be easily seen by considering the pion-decay induced gamma-ray luminosity, Lγ, and the synchrotron luminosity, Lν, of a steady state distribution of CR electrons that has been generated by hadronic CR interactions,
equals the CMB energy density). Hence the ratio of gamma-ray to synchrotron flux becomes independent of the spatial distribution of CRs and thermal gas (Völk 1989; Pohl 1994; Pfrommer 2008), particularly with the observed synchrotron spectral index αν = α/2 ≃ 1. This can be easily seen by considering the pion-decay induced gamma-ray luminosity, Lγ, and the synchrotron luminosity, Lν, of a steady state distribution of CR electrons that has been generated by hadronic CR interactions,  Here, εB and εCMB denote the energy density of the magnetic field and the CMB, respectively, Aγ and Aν are dimensional constants that depend on the hadronic physics of the interaction (Pfrommer et al. 2008; Pfrommer 2008). Hence we can derive a minimum gamma-ray flux in the hadronic model:
Here, εB and εCMB denote the energy density of the magnetic field and the CMB, respectively, Aγ and Aν are dimensional constants that depend on the hadronic physics of the interaction (Pfrommer et al. 2008; Pfrommer 2008). Hence we can derive a minimum gamma-ray flux in the hadronic model: 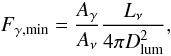 (4)where Lν is the observed luminosity of the radio mini-halo and Dlum = 77 Mpc denotes the luminosity distance to Perseus. Lowering the magnetic field strength would require increasing the CR electron energy density to reproduce the observed synchrotron luminosity and thus increases the associated gamma-ray flux. The maximum emission radius of the radio mini-halo of 100 kpc corresponds to an angular size of 0.075°, well within the MAGIC PSF; hence Lν does not need to be cut to match the angular region tested by the MAGIC ULs.
(4)where Lν is the observed luminosity of the radio mini-halo and Dlum = 77 Mpc denotes the luminosity distance to Perseus. Lowering the magnetic field strength would require increasing the CR electron energy density to reproduce the observed synchrotron luminosity and thus increases the associated gamma-ray flux. The maximum emission radius of the radio mini-halo of 100 kpc corresponds to an angular size of 0.075°, well within the MAGIC PSF; hence Lν does not need to be cut to match the angular region tested by the MAGIC ULs.
Hence in this section, we assume B ≫ BCMB everywhere in the radio-emitting region, and (in order to obtain this minimum gamma-ray flux) require a considerable drop in the CR distribution outside the radio (mini-)halo. While we do not make any assumptions on how to realize such a scenario, we discuss possible physical processes that could be causing it. The large magnetic field can be realized by adiabatically compressing the magnetic field during the formation of the cool core. The edge of the radio emitting region can be caused by a region of predominantly toroidal magnetic field which efficiently confines CRs to the central region. Such a magnetic field configuration could be arranged by magnetic draping at the sloshing core (Lyutikov 2006; Dursi & Pfrommer 2008; Pfrommer & Dursi 2010) or the saturated (non-linear) state of the heat-flux driven buoyancy instability (Quataert 2008; Parrish & Quataert 2008). The drop in CR number density outside this region can be realized by CR streaming to the peripheral cluster regions with substantially lower target densities that would imply a negligible contribution to the gamma-ray flux outside the radio mini-halo (Enßlin et al. 2011). The next generation of cluster simulations that couple CR physics self-consistently to magnetic fields and account for anisotropic transport processes of the thermal gas as well as CRs will be needed to scrutinize such a presented scenario.
In contrast to our previous analysis in Aleksić et al. (2010a), we derive here the absolute minimum gamma-ray flux rather than the “physical” minimum gamma-ray flux that depends on the assumed magnetic field distribution and requires an uncertain extrapolation into the outer regions of the cluster. The density and pressure profile of Perseus as derived from X-ray observations can both be described by double-beta profiles with an inner core radius of 57 and 47 kpc, respectively (Churazov et al. 2003; Pfrommer et al. 2005). Hence, there is only a small interval between ~50 and ~100 kpc, the maximum radius of the radio mini-halo, that is sensitive to the outer CR and magnetic field profile. Only the extrapolation of that behavior well beyond the radio mini-halo to the virial radius will determine whether the energy density in the magnetic field becomes implausibly large in comparison to that of the thermal gas, thereby possibly violating the energy conditions.
The results for the minimum gamma-ray flux Fγ,min(>1 TeV) and the minimum CR-to-thermal pressure ratio, XCR, min = XCRFγ,min/Fγ,iso are presented in Table 2 and Fig. 3 (assuming α = 2.2). Here, Fγ,iso is the gamma-ray flux in the isobaric model of CRs introduced in Sect. 4.1. The ratio of the maximum to minimum CR pressures, XCR,max/XCR,min, varies between 1.8 and 17.3 for a spectral index between 2.1 ≤ α ≤ 2.5. For the spectral index α = 2.2 of the universal gamma-ray spectrum around TeV energies, the ratio is XCR,max/XCR,min = 3.2. This puts the long-sought gamma-ray detection of clusters, in particular for Perseus, within the reach of deeper campaigns with the possibility of scrutinizing the hadronic emission model of radio (mini-)halos.
4.4. Implications for the cluster magnetic field
As shown in Sect. 4.3, an absolute lower limit on the hadronic model gamma-ray emission comes from assuming high magnetic field strengths, B ≫ BCMB, everywhere in the radio-emitting region. Using our UL on the gamma-ray emission (and on PCR) we can turn the argument in Sect. 4.3 around to derive a lower limit on the magnetic field strength needed to explain the observed diffuse radio emission within the hadronic model (Pfrommer & Enßlin 2004b). Lowering the gamma-ray limit will tighten (increase) the magnetic field limit. If this conflicts with magnetic field measurements by means of other methods, e.g., Faraday RM, this would challenge the hadronic model of radio (mini-)halos. The method that we use to constrain the magnetic field, B, depends on the assumed spatial structure of B that we parametrize by 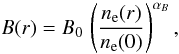 (5)as suggested by a cosmological MHD simulation of a cool core cluster (Dubois & Teyssier 2008), which demonstrates a tight correlation of the magnetic field with the ICM gas density and highlights the importance of cooling processes in amplifying the magnetic field in the core of galaxy clusters up to one order of magnitude above the typical amplification obtained for a purely adiabatic evolution. Moreover, such a parametrization is favored by Faraday RM studies (Bonafede et al. 2010; Kuchar & Enßlin 2011, and references therein).
(5)as suggested by a cosmological MHD simulation of a cool core cluster (Dubois & Teyssier 2008), which demonstrates a tight correlation of the magnetic field with the ICM gas density and highlights the importance of cooling processes in amplifying the magnetic field in the core of galaxy clusters up to one order of magnitude above the typical amplification obtained for a purely adiabatic evolution. Moreover, such a parametrization is favored by Faraday RM studies (Bonafede et al. 2010; Kuchar & Enßlin 2011, and references therein).
Generally, Faraday RM determinations of the magnetic field strength, for instance using background sources seen through clusters, depend intrinsically on the magnetic correlation length. Recent Faraday RM studies yield estimates for the central magnetic field of typically 5 μG for merging clusters (Bonafede et al. 2010, for Coma) and significantly higher values in cool core clusters of around 16 μG (Kuchar & Enßlin 2011, for Hydra A). For the Perseus cluster, Faraday RMs are available only on very small scales (Taylor et al. 2006), i.e., a few tens of pc. The RM estimates are ~7000 rad m-2 implying magnetic field strengths of ~25 μG. This assumes that the Faraday screen is situated within the ICM. This location is not, however, certain since variations of 10% in the RM are observed on pc-scales (Taylor et al. 2002), while ICM magnetic fields are expected to be ordered on scales of a few kpc (Taylor et al. 2006; Vogt & Enßlin 2005).
To proceed, we derived a deprojected radio emissivity profile. We fit the point-source subtracted, azimuthally averaged surface brightness profile at 1.38 GHz (Pedlar et al. 1990) with a β-model, ![\begin{equation} \label{beta} S_{\nu} (r_{\bot})= S_{0} \left[ 1 + \left( \frac{r_{\bot}}{r_{\rmn{c}}}\right)^{2}\right]^{-3\beta + 1/2}, \end{equation}](/articles/aa/full_html/2012/05/aa18502-11/aa18502-11-eq128.png) (6)where S0 = 2.3 × 10-1 Jy arcmin-2, rc = 30 kpc, and β = 0.55. This profile is valid within a maximum emission radius of 100 kpc. An Abel integral deprojection then provides the radio emissivity distribution (see Appendix of Pfrommer & Enßlin 2004a),
(6)where S0 = 2.3 × 10-1 Jy arcmin-2, rc = 30 kpc, and β = 0.55. This profile is valid within a maximum emission radius of 100 kpc. An Abel integral deprojection then provides the radio emissivity distribution (see Appendix of Pfrommer & Enßlin 2004a), 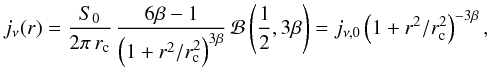 (7)where ℬ denotes the beta function. To constrain the magnetic field, we proceed as follows:
(7)where ℬ denotes the beta function. To constrain the magnetic field, we proceed as follows:
-
1.
Given a model for the magnetic field characterized byαB and an initial guess for B0, we determine the profile of XCR(r) such that the hadronically produced synchrotron emission matches the observed radio mini-halo emission over the entire extent.
-
2.
For this XCR(r) profile, we compute the pion-decay gamma-ray surface brightness profile, integrate the flux within a radius of 0.15°, and scale the CR profile o match the corresponding MAGIC UL. This scaling factor, XCR,0, depends on the CR spectral index, α, (assuming a power-law CR population for simplicity), the radial decline of the magnetic field, αB, and the initial guess for B0.
-
3.
We then solve for B0 requiring that it matches the observed synchrotron profile while fixing the profile of XCR(r) determined in the previous two steps. Note that for B0 ≫ BCMB and a radio spectral index of αν = 1, the solution is degenerate, as can be seen from Eq. (2).
-
4.
Inverse Compton cooling of CR electrons on CMB photons introduces a scale that depends on the CMB-equivalent magnetic field strength, BCMB ≃ 3.2 μG; if magnetic field values are close to this value, the resulting synchrotron emission depends non-linearly on the inferred magnetic field strengths. Hence, we iterate, repeating the previous steps until convergence for the minimum magnetic field B0.
Table 3 gives the resulting lower limits for B0 that depend sensitively on the assumptions of α and αB. Its behavior can be understood as follows. (1) The hardest CR spectral indices correspond to the tightest limits on B0. This is because for an UL for CR energies of around 8 TeV (as probed by 1 TeV gamma-rays) and a CR population with a softer spectral index (larger α) there is a comparably larger fraction of CRs at 25 GeV available which produce more radio-emitting electrons. Thus, lower magnetic field strengths can be accommodated while still matching the observed synchrotron flux; (2) for a steeper magnetic decline (larger αB), the CR number density must be higher to match the observed radio emission profiles. This would yield a higher gamma-ray flux so the ULs are more constraining. This implies tighter lower limits for B0.
Constraints on magnetic fields in the hadronic model.
The inferred values for the minimum magnetic field strengths in Table 3 range from 2–13 μG for the values of α and αB used in this study and suggested by radio observations. These are much lower than the thermal equipartition value in the center of Perseus, Beq,0 ≃ 80 μG or magnetic field estimates from the Faraday RM values on small scales (Taylor et al. 2006). In Table 3, we additionally give the corresponding values for the CR-to-thermal pressure ratio (at the largest emission radius at 100 kpc) such that the model reproduces the observed radio surface brightness profile7. Since they are derived from flux upper limits they are also ULs on the CR-to-thermal pressure ratio. The corresponding values for XCR in the cluster center are lower than 5% for the entire parameter space probed in this study. We conclude that there is still considerable leeway for the hadronic model as an explanation of the radio mini-halo emission.
5. Conclusions
MAGIC observed the Perseus cluster for a total of ~85 h of high quality data between October 2009 and February 2011. This campaign resulted in the detection of the head-tail radio galaxy IC 310 (Aleksić et al. 2010b) and the detection of the central radio galaxy NGC 1275 (Aleksić et al. 2012a). No significant excess of gamma-rays was detected from the cluster central region at energies above 630 GeV where the NGC 1275 emission vanishes. The flux UL for the CR-induced emission above 1 TeV, for a region of radius of 0.15° around the cluster center, corresponds to 1.38 × 10-13 cm-2 s-1.
We constrain the CR population and the magnetic field strength in Perseus using contrasting models that differ in their assumptions and are constructed to circumvent our lack of knowledge of the true distributions. (1) We use a simplified “isobaric CR model” with constant CR-to-thermal pressure fraction and power-law momentum spectrum – a model that has been widely used in the literature; (2) this is complemented by an analytical approach based on cosmological hydrodynamical simulations (Pinzke & Pfrommer 2010) that provide a CR distribution, combined with the observed density profile; (3) we finally use a pragmatic approach that models the CR and magnetic field distributions to reproduce the observed emission profile of the Perseus radio mini-halo.
Within the simplified analytical approach we can constrain the CR-to-thermal pressure, XCR < 0.8% and 12% (for a CR or gamma-ray spectral index, α, varying between 2.1 and 2.5). For the spectral index at TeV energies of α = 2.2, favored by simulations, we find that XCR < 1.1%. The simulation-based approach gives XCR < 1.7%. This latter value is a factor of 1.5 less constraining because of the concave curvature of the simulated spectrum that has higher partial pressure toward GeV energies relative to a pure power-law spectrum. This constraint is a factor of 1.25 below the simulation model and – for the first time – limiting the underlying physics of the simulation. This could either indicate that the maximum acceleration efficiency of CRs relative to the total dissipated energy at strong structure formation shocks is <50% (i.e., smaller than the value assumed in the simulations) or may point to CR streaming and diffusion out of the cluster core region that lowers the central XCR values (Enßlin et al. 2011). The observed spiral X-ray structure in the central cluster region suggests that Perseus is currently in a relaxation state following a past merging event. If a net outward CR transport is indeed correlated with a dynamical relaxation state of a cluster, this would render CR transport a plausible agent that lowers the gamma-ray flux in comparison to the simulation model that neglects this mechanism.
Our third, pragmatic, approach employed two different assumptions. First, adopting a strong magnetic field everywhere in the radio-emitting region (B ≫ BCMB) yields the minimum gamma-ray flux, Fγ,min, in the hadronic model of radio mini-halos. We find Fγ,min to be a factor of 2 to 18 below the MAGIC ULs for spectral indices varying between 2.1 and 2.5. For α = 2.2, following the universal CR model, the minimum gamma-ray flux is a factor of 3.2 lower than the MAGIC ULs. Second, by matching the radio emission profile (i.e., fixing the radial CR profile for a given magnetic field model) and by requiring the pion-decay gamma-ray flux to match the MAGIC flux ULs (i.e., fixing the normalization of the CR distribution) we obtain lower limits on the magnetic field distribution under consideration. Recall that we employ a parametrization of the magnetic field of B = B0 (n/n0)αB. The inferred values range from 2 μG ≤ B0,min ≤ 13 μG for the parameter space spanned by the magnetic field strength radial index, αB, and CR spectral index, α. Since B0,min is smaller than recent field strengths estimates through Faraday RM studies in cool core clusters (e.g., Kuchar & Enßlin 2011), this argues that the hadronic model is an interesting possibility in explaining the radio mini-halo emission. This displays the potential of future gamma-ray observations of Perseus to further refine the parameters of the hadronic model and for eventually assessing its validity in explaining radio (mini-)halos. This is true for the currently operating Cherenkov telescopes and for the future planned Cherenkov Telescope Array whose sensitivity is planned to be about an order of magnitude higher than current instruments.
The θ2 is the squared angular distance between the arrival direction of events and the nominal source positions (see e.g. Daum et al. 1997).
The reported radial spectral steepening of the radio mini-halo emission (Gitti et al. 2002) could be an observational artifact owing to a poor signal-to-noise ratio in the outer core of the cluster and the ambiguity in determining the large scale Fourier components owing to nonuniform coverage of the Fourier plane and missing short-baseline information: the so-called “missing zero spacing”-problem of interferometric radio observations. By comparing the spectral index distribution of the three radio maps (at 92 cm, 49 cm, and 21 cm, Sijbring 1993), radial spectral flattening depending on the chosen radial direction seems possible.
Adiabatic CR losses during the expansion phase of the galactic winds imply a negligible contribution to the CR energy density of the ICM today (Aleksić et al. 2010a) but integrated over cluster history, they may contribute an interesting seed population that however needs to be re-accelerated. It is currently unclear whether AGN jets are powered by the Poynting flux or by the kinetic energy of hadrons (e.g., Celotti et al. 1998; Hirotani et al. 1998; Sikora & Madejski 2000). Even if there was a non-negligible CR ion component, it would probably be confined to dilute radio lobes that rise almost unperturbed in the cluster atmosphere to the less dense outer cluster regions (McNamara & Nulsen 2007) where these lobes may be destroyed by shocks and dissolved within the ICM (Enßlin & Brüggen 2002; Pfrommer & Jones 2011). Since the CRs are then released into an ambient ICM with a small density, this implies a negligible contribution to the cluster gamma-ray emission due to pion decay.
While the X-ray data show a complicated ICM structure including cavities blown by the central AGN, the use of deprojected, spherically averaged gas density and temperature profiles can be justified as follows. The inhomogeneities of the ICM can be quantified statistically using a clumping factor 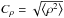 /⟨ρ⟩ that estimates the relative bias factor to true density profile. However, since we are interested in the CR-induced gamma-ray emissivity which also scales with the square of the gas density (modulo a dimensionless CR-to-gas ratio that we quantify by using CR simulations) our modeling should inherit exactly the same bias as in X-ray-inferred density profiles. We emphasize that the overall X-ray emission is smooth with fluctuations on the level < 20−25% (Fabian et al. 2011). Those substructures are only amplified by unsharp mask imaging. Moreover, the X-ray cavities (interpreted as AGN bubbles) do not correlate with structures in the radio mini-halo and only make up a small fraction of the radio-emitting volume (<10-3, since they only subtend a linear scale of <10% relative to the radio emission, Fabian et al. 2011), justifying our procedure.
/⟨ρ⟩ that estimates the relative bias factor to true density profile. However, since we are interested in the CR-induced gamma-ray emissivity which also scales with the square of the gas density (modulo a dimensionless CR-to-gas ratio that we quantify by using CR simulations) our modeling should inherit exactly the same bias as in X-ray-inferred density profiles. We emphasize that the overall X-ray emission is smooth with fluctuations on the level < 20−25% (Fabian et al. 2011). Those substructures are only amplified by unsharp mask imaging. Moreover, the X-ray cavities (interpreted as AGN bubbles) do not correlate with structures in the radio mini-halo and only make up a small fraction of the radio-emitting volume (<10-3, since they only subtend a linear scale of <10% relative to the radio emission, Fabian et al. 2011), justifying our procedure.
Note that the models “with galaxies” and “without galaxies” differ from those used in the first MAGIC paper on Perseus observations with a single telescope (Aleksić et al. 2010a). Previously, the models were based on the simulated cool core cluster g51 (which is similar in morphology to Perseus) while here we use the universal CR model – which is based on high-resolution simulations of 14 galaxy clusters that span almost two decades in mass – to compute the expected pion decay emission (Pinzke & Pfrommer 2010). The spectral normalization (between the two models) therefore increased from 1.5 to 2.4 and the gamma-ray flux in the model “without galaxies” used here differs by 10%.
Note that in this section, radial profiles of XCR are uniquely determined by the adopted model for the magnetic field and the observed synchrotron surface brightness profile of the radio mini-halo. This differs from the simplified analytical CR model where XCR = const. (Sect. 4.1) and contrasts with the simulation-based model where XCR(r) is derived from cosmological cluster simulations (Sect. 4.2). For most of the cases studied here, the CR-to-thermal pressure ratio profiles vary within a factor of two, and flat profiles of both the relative magnetic and CR pressure profiles are able to reproduce the observed radio surface brightness profile (see Fig. 2 of Pfrommer & Enßlin 2004b).
Acknowledgments
We thank the anonymous referee for valuable comments. We would like to thank Andrey Kravtsov for the useful comments on the paper. We would like to thank the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. The support of the German BMBF and MPG, the Italian INFN, the Swiss National Fund SNF, and the Spanish MICINN is gratefully acknowledged. This work was also supported by the Marie Curie program, by the CPAN CSD2007-00042 and MultiDark CSD2009-00064 projects of the Spanish Consolider-Ingenio 2010 programme, by grant DO02-353 of the Bulgarian NSF, by grant 127740 of the Academy of Finland, by the YIP of the Helmholtz Gemeinschaft, by the DFG Cluster of Excellence “Origin and Structure of the Universe”, by the DFG Collaborative Research Centers SFB823/C4 and SFB876/C3, and by the Polish MNiSzW grant 745/N-HESS-MAGIC/2010/0. C.P. gratefully acknowledges financial support of the Klaus Tschira Foundation. A.P. acknowledges NSF grant AST 0908480 for support.
References
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 706, L275 [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2010a, ApJ, 717, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2010b, JCAP, 5, 25 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009a, A&A, 495, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009b, A&A, 502, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2009, ApJ, 690, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2010, ApJ, 725, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2010a, ApJ, 710, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2010b, ApJ, 723, L207 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2011, J. Cosmol. Astropart. Phys., 6, 35 [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012a, A&A, 539, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012b, Astropart. Phys., 35, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, M. R., & Kravtsov, A. V. 2011, ApJ, 740, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., & Colafrancesco, S. 1999, Astropart. Phys., 12, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Gabici, S., & Brunetti, G. 2007, Inter. J. Mod. Phys. A, 22, 681 [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunetti, G., & Blasi, P. 2005, MNRAS, 363, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Lazarian, A. 2007, MNRAS, 378, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Lazarian, A. 2011, MNRAS, 410, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Cassano, R., Dolag, K., & Setti, G. 2009, A&A, 507, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., Kuncic, Z., Rees, M. J., & Wardle, J. F. C. 1998, MNRAS, 293, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Forman, W., Jones, C., & Böhringer, H. 2003, ApJ, 590, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Forman, W., Vikhlinin, A., et al. 2008, MNRAS, 388, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Tremaine, S., Forman, W., et al. 2010, MNRAS, 404, 1165 [NASA ADS] [Google Scholar]
- Clarke, T. E., Kronberg, P. P., & Böhringer, H. 2001, ApJ, 547, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Colafrancesco, S., Profumo, S., & Ullio, P. 2006, A&A, 455, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuesta, A. J., Jeltema, T. E., Zandanel, F., et al. 2011, ApJ, 726, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Daum, A., Hermann, G., Hess, M., et al. 1997, Astropart. Phys., 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dennison, B. 1980, ApJ, 239, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., & Enßlin, T. A. 2000, A&A, 362, 151 [NASA ADS] [Google Scholar]
- Domainko, W., Nedbal, D., Hinton, J. A., & Martineau-Huynh, O. 2009, Int. J. Mod. Phys. D, 18, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Brunetti, G., Cassano, R., & Bonafede, A. 2010a, MNRAS, 401, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Cassano, R., & Brunetti, G. 2010b, MNRAS, 407, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2008, A&A, 482, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dugger, L., Jeltema, T. E., & Profumo, S. 2010, J. Cosmology Astropart. Phys., 12, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Dursi, L. J., & Pfrommer, C. 2008, ApJ, 677, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., & Brüggen, M. 2002, MNRAS, 331, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., Biermann, P. L., Kronberg, P. P., & Wu, X.-P. 1997, ApJ, 477, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., Pfrommer, C., Springel, V., & Jubelgas, M. 2007, A&A, 473, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enßlin, T., Pfrommer, C., Miniati, F., & Subramanian, K. 2011, A&A, 527, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C. 1994, ARA&A, 32, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Allen, S. W., et al. 2011, MNRAS, 418, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Burigana, C., & Enßlin, T. A. 2004, New Astron. Rev., 48, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Fomin, V. P., Stepanian, A. A., Lamb, R. C., et al. 1994, Astropart. Phys., 2, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., & Ohira, Y. 2012, ApJ, 746, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Galante, N., Acciari, V. A., Aliu, E., et al. 2009, 31nd Int. Cosmic Ray Conference, Lodz, Poland [arXiv:0907.5000] [Google Scholar]
- Gao, L., Frenk, C. S., Jenkins, A., Springel, V., & White, S. D. M. 2012, MNRAS, 419, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Feretti, L., Venturi, T., Kim, K. T., & Kronberg, P. P. 1993, ApJ, 406, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Gitti, M., Brunetti, G., & Setti, G. 2002, A&A, 386, 456 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helder, E. A., Vink, J., Bassa, C. G., et al. 2009, Science, 325, 719 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hirotani, K., Iguchi, S., Kimura, M., & Wajima, K. 1998, in Abstracts of the 19th Texas Symposium on Relativistic Astrophysics and Cosmology, held in Paris, France, ed. J. Paul, T. Montmerle, & E. Aubourg (CEA Saclay) [Google Scholar]
- Hudson, D. S., Mittal, R., Reiprich, T. H., et al. 2010, A&A, 513, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeltema, T. E., & Profumo, S. 2011, ApJ, 728, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Jeltema, T. E., Kehayias, J., & Profumo, S. 2009, Phys. Rev. D, 80, 023005 [NASA ADS] [CrossRef] [Google Scholar]
- Jubelgas, M., Springel, V., Enßlin, T., & Pfrommer, C. 2008, A&A, 481, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kang, H., & Jones, T. W. 2005, ApJ, 620, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kempner, J. C., Blanton, E. L., Clarke, T. E., et al. 2004, in The Riddle of Cooling Flows in Galaxies and Clusters of galaxies [Google Scholar]
- Keshet, U. 2010 [arXiv:1011.0729] [Google Scholar]
- Keshet, U., & Loeb, A. 2010, ApJ, 722, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, K.-T., Kronberg, P. P., & Tribble, P. C. 1991, ApJ, 379, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Kiuchi, R., Mori, M., Bicknell, G. V., et al. 2009, ApJ, 704, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchar, P., & Enßlin, T. A. 2011, A&A, 529, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kushnir, D., Katz, B., & Waxman, E. 2009, J. Cosmol. Astropart. Phys., 9, 24 [Google Scholar]
- Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M. 2006, MNRAS, 373, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., & Henry, J. P. 2008, MNRAS, 384, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Miniati, F. 2003, MNRAS, 342, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F., Ryu, D., Kang, H., & Jones, T. W. 2001, ApJ, 559, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Parrish, I. J., & Quataert, E. 2008, ApJ, 677, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Pedlar, A., Ghataure, H. S., Davies, R. D., et al. 1990, MNRAS, 246, 477 [NASA ADS] [Google Scholar]
- Perkins, J. S. 2008, in AIP Conf. Ser. 1085, ed. F. A. Aharonian, W. Hofmann, & F. Rieger, 569 [Google Scholar]
- Perkins, J. S., Badran, H. M., Blaylock, G., et al. 2006, ApJ, 644, 148 [Google Scholar]
- Pfrommer, C. 2008, MNRAS, 385, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., & Dursi, L. J. 2010, Nat. Phys., 6, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., & Enßlin, T. A. 2003, A&A, 407, L73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., & Enßlin, T. A. 2004a, A&A, 413, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., & Enßlin, T. A. 2004b, MNRAS, 352, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., Pfrommer, C., & Bergström, L. 2011, Phys. Rev. D, 84, 123509 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., & Jones, T. W. 2011, ApJ, 730, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., Enßlin, T. A., & Sarazin, C. L. 2005, A&A, 430, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., Springel, V., Enßlin, T. A., & Jubelgas, M. 2006, MNRAS, 367, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., Enßlin, T. A., Springel, V., Jubelgas, M., & Dolag, K. 2007, MNRAS, 378, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., Enßlin, T. A., & Springel, V. 2008, MNRAS, 385, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., & Pfrommer, C. 2010, MNRAS, 409, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., Pfrommer, C., & Bergström, L. 2009, Phys. Rev. Lett., 103, 181302 [NASA ADS] [CrossRef] [Google Scholar]
- Pohl, M. 1994, A&A, 287, 453 [NASA ADS] [Google Scholar]
- Quataert, E. 2008, ApJ, 673, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Reimer, A., Reimer, O., Schlickeiser, R., & Iyudin, A. 2004, A&A, 424, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reimer, O., Pohl, M., Sreekumar, P., & Mattox, J. R. 2003, ApJ, 588, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Nevalainen, J., Ohashi, T., & Bykov, A. M. 2008, Space Sci. Rev., 134, 71 [Google Scholar]
- Rolke, W. A., López, A. M., & Conrad, J. 2005, Nucl. Instrum. Meth. Phys. Res. A, 551, 493 [Google Scholar]
- Ryu, D., Kang, H., Hallman, E., & Jones, T. W. 2003, ApJ, 593, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Conde, M. A., Cannoni, M., Zandanel, F., Gómez, M. E., & Prada, F. 2011, J. Cosmology Astropart. Phys., 12, 11 [Google Scholar]
- Schlickeiser, R. 2002, Cosmic ray astrophysics (Springer) [Google Scholar]
- Schlickeiser, R., Sievers, A., & Thiemann, H. 1987, A&A, 182, 21 [NASA ADS] [Google Scholar]
- Sijbring, L. G. 1993, Ph.D. Thesis, Groningen University [Google Scholar]
- Sikora, M., & Madejski, G. 2000, ApJ, 534, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
- Taylor, G. B., Fabian, A. C., & Allen, S. W. 2002, MNRAS, 334, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, G. B., Gugliucci, N. E., Fabian, A. C., et al. 2006, MNRAS, 368, 1500 [NASA ADS] [CrossRef] [Google Scholar]
- Vestrand, W. T. 1982, AJ, 87, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Markevitch, M., Murray, S. S., et al. 2005, ApJ, 628, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, C., & Enßlin, T. A. 2005, A&A, 434, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J. 1989, A&A, 218, 67 [NASA ADS] [Google Scholar]
- Völk, H. J., Aharonian, F. A., & Breitschwerdt, D. 1996, Space Sci. Rev., 75, 279 [Google Scholar]
- Wik, D. R., Sarazin, C. L., Finoguenov, A., et al. 2011, ApJ, 727, 119 [NASA ADS] [CrossRef] [Google Scholar]
- ZuHone, J. A., Markevitch, M., & Lee, D. 2011, ApJ, 743, 16 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left panel: significance skymap of the Perseus cluster above 150 GeV. The positions of NGC 1275 (white cross), which coincides with the cluster center, and the head-tail radio galaxy IC 310 (black cross) are marked. Right panel: significance skymap of the Perseus cluster region above 630 GeV. The central white circle marks the 0.15° region used to derive constraints (see main text for details). The quoted energy thresholds are obtained assuming a spectral index of 4 as observed in NGC 1275. |
| In the text | |
 |
Fig. 2 θ2 distribution above 630 GeV of the signal (data points) and background (gray filled region) at the cluster center. The dashed line represents the signal region cut within which the excess event number is estimated. Here it corresponds to 0.02 deg2. The quoted energy threshold is obtained assuming a spectral index of 4 as observed in NGC 1275. |
| In the text | |
 |
Fig. 3 Integral flux ULs of the single telescope observations (point-like ULs, upper arrows; Aleksić et al. 2010a) and of this work (solid arrows; Table 1) are shown. We compare ULs with the simulated integrated spectra of the gamma-ray emission from decaying neutral pions that result from hadronic CR interactions with the ICM in the Perseus cluster coming from within a radius of 0.15° around the center. The conservative model without galaxies (solid line) is shown together with the model with galaxies (dotted line). The flux UL at 1 TeV is a factor of 1.25 below the conservative model and hence constrains a combination of CR shock acceleration efficiency and CR transport processes. We also show the minimum gamma-ray flux estimates for the hadronic model of the Perseus radio mini-halo (dashed line with minimum flux arrows) using the universal gamma-ray spectrum resulting from pion decay (Pinzke & Pfrommer 2010) and adopting the spectral index, 2.2, of this spectrum around TeV energies. |
| In the text | |
 |
Fig. 4 CR-to-thermal pressure ratio, XCR = ⟨PCR⟩/⟨Pth⟩ at the radial distance from the Perseus cluster center, R/Rvir (red lines), and integrated up to R/Rvir (blue lines), using the simulation-based analytical model of CRs (Pinzke & Pfrommer 2010). The simulation model (dashed) is contrasted to a model that has been scaled by the MAGIC constraints obtained in this work (solid). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


