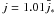| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201118380 | |
| Published online | 11 April 2012 | |
Particle acceleration in the polar cap region of an oscillating neutron star
1 Laboratory of Applied Mathematics, University of Trento, via Mesiano 77, 38100 Trento, Italy
e-mail: olindo.zanotti@gmail.com
2 Max-Planck-Institut für Gravitationsphysik, Albert Einstein Institut, 14476 Golm, Germany
3 Institute of Nuclear Physics, Ulughbek, 100214 Tashkent, Uzbekistan
4 Ulugh Beg Astronomical Institute, Astronomicheskaya 33, 100052 Tashkent, Uzbekistan
5 ZARM, University Bremen, Am Fallturm, 28359 Bremen, Germany
Received: 2 November 2011
Accepted: 8 February 2012
Aims. We revisit particle acceleration in the polar cap region of a neutron star by taking into account both general relativistic effects and the presence of toroidal oscillations at the star surface. In particular, we address the question of whether toroidal oscillations at the stellar surface can affect the acceleration properties in the polar cap.
Methods. We solve numerically the relativistic electrodynamics equations in the stationary regime, focusing on the computation of the Lorentz factor of a space-charge-limited electron flow accelerated in the polar cap region of a rotating and oscillating pulsar. To this extent, we adopt the correct expression of the general relativistic Goldreich-Julian charge density in the presence of toroidal oscillations.
Results. Depending on the ratio of the actual charge density of the pulsar magnetosphere to the Goldreich-Julian charge density, we distinguish two different regimes of the Lorentz factor of the particle flow, namely an oscillatory regime produced for sub-GJ current density configurations, which does not produce an efficient acceleration, and a true accelerating regime for super-GJ current density configurations. We find that star oscillations may be responsible for a significant asymmetry in the pulse profile that depends on the orientation of the oscillations with respect to the pulsar magnetic field. In particular, significant enhancements of the Lorentz factor are produced by stellar oscillations in the super-GJ current density regime.
Key words: magnetic fields / relativistic processes / stars: neutron / pulsars: general
© ESO, 2012
1. Introduction
Understanding the physical mechanism behind particle acceleration, and hence electromagnetic emission, in the magnetospheres of neutron stars remains an unsolved topic of pulsar physics, more than forty five years after their discovery. A completely force-free (FF) magnetosphere with no parallel component of the electric field along the magnetic field lines clearly does not allow for the acceleration of particles, and local violations to the FF condition are therefore expected (Kalapotharakos et al. 2012). This was first noticed by Sturrock (1971), who proposed that the acceleration of particles occurs in a small vacuum gap, where E·B ≠ 0, that is confined to the polar region above the star surface, the so-called polar cap, whose edge is defined by the locus of the last closed magnetic field line. This seminal idea was developed and investigated by several authors over the years, both in flat spacetime (Ruderman & Sutherland 1975; Fawley et al. 1977; Scharlemann et al. 1978; Arons & Scharlemann 1979; Cheng & Ruderman 1980; Daugherty & Harding 1982; Shibata 1997) and in a general relativistic framework (Muslimov & Tsygan 1992; Muslimov & Harding 1997; Harding & Muslimov 1998; Sakai & Shibata 2003; Morozova et al. 2008).
A relevant result obtained by these works is that the particle motion can show an oscillatory behavior depending on the charge current density. This behavior has been indirectly confirmed by numerical simulations. By performing time-dependent particle-in-cell simulations of electrons extracted from the star surface, Barzilay (2011) found that the Lorentz factor of the accelerated electrons reaches the analytical estimates of 106 and follows an oscillatory pattern that increases with the distance from the stellar surface. Although these numerical analyses are very promising, numerical simulations of neutron star magnetospheres have not yet entered a mature enough stage where physical mechanisms such as plasma effects, non-ideal magnetohydrodynamics, pair-creation, and radiation processes can be properly taken into account. As a result, analytical investigations continue to play a crucial role in elucidating the physics of pulsar magnetospheres.
Among the physical effects deserving particular attention is the possibility that neutron star oscillations, most likely excited during a glitch phenomenon (i.e. a sudden change in the rotational period), propagate into the magnetosphere, thus affecting the acceleration properties in the polar cap region. The idea that neutron star oscillations may induce high energy emission in neutron star magnetospheres was developed in a series of papers by Timokhin and collaborators (Timokhin et al. 2000; Timokhin 2007; Timokhin et al. 2008), after the first pioneering investigations by McDermott et al. (1984), Muslimov & Tsygan (1986), and Rezzolla & Ahmedov (2004), who considered the case of an oscillating neutron star in a vacuum. A few years ago we initiated a program aimed at assessing the impact of toroidal oscillations of the star surface on the properties of the external magnetosphere, with general relativistic effects properly taken into account. Starting from Abdikamalov et al. (2009), where the theoretical basis of our approach was developed, we showed in Morozova et al. (2010) that the electromagnetic energy losses from the polar cap region of a rotating neutron star can be significantly enhanced if oscillations are also present, and, for the mode (l,m) = (2,1), these electromagnetic losses turned out to be a factor ~ 8 larger than the rotational energy losses, even for a velocity oscillation amplitude at the star surface as small as 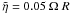 , where Ω and R are the angular velocity and the radius of the neutron star, respectively. In Morozova et al. (2012), on the other hand, we considered the conditions for radio emission in magnetars and we found that, when oscillations of the magnetar are taken into account, radio emission from the magnetosphere is generally favored. The major effect of oscillations is to amplify the scalar potential in the polar cap region of the magnetar magnetosphere, which implies that the death-line in the P − Ṗ diagram shifts downward1.
, where Ω and R are the angular velocity and the radius of the neutron star, respectively. In Morozova et al. (2012), on the other hand, we considered the conditions for radio emission in magnetars and we found that, when oscillations of the magnetar are taken into account, radio emission from the magnetosphere is generally favored. The major effect of oscillations is to amplify the scalar potential in the polar cap region of the magnetar magnetosphere, which implies that the death-line in the P − Ṗ diagram shifts downward1.
As a natural follow-up of our investigations, we address in this paper the question of whether toroidal oscillations at the star surface can affect the acceleration properties in the polar cap region. We rely on our results presented in Morozova et al. (2010) revisiting some of the conclusions found by Sakai & Shibata (2003). In particular, we expect that an oscillating magnetosphere can alter the parallel component of the electric field that is responsible for particle acceleration just above the star surface. The size of oscillation amplitude necessary to produce significant physical effects is still a matter of debate. Timokhin et al. (2008), for example, argue that noticeable effects in the spectra of soft gamma repeater giant flares can be produced when the amplitude of the neutron star surface oscillations is of the order of ~ 1% of the star radius. As we show in the paper, on the other hand, significant effects on the Lorentz factor are visible even with (normalized) velocity oscillation amplitudes 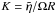 as low as 0.02. Since the range of oscillation frequencies is quite broad, typically between 18 Hz and 1800 Hz (Steiner & Watts 2009), such low values of K can be obtained, for example, by adopting an oscillation frequency that is 20 times higher than the stellar rotation frequency Ω, and a spatial oscillation amplitude that is only 0.001R. We anticipate, therefore, that the effects of an oscillating magnetosphere on the acceleration of particles close to the stellar surface become important, even for very small oscillation amplitudes.
as low as 0.02. Since the range of oscillation frequencies is quite broad, typically between 18 Hz and 1800 Hz (Steiner & Watts 2009), such low values of K can be obtained, for example, by adopting an oscillation frequency that is 20 times higher than the stellar rotation frequency Ω, and a spatial oscillation amplitude that is only 0.001R. We anticipate, therefore, that the effects of an oscillating magnetosphere on the acceleration of particles close to the stellar surface become important, even for very small oscillation amplitudes.
The plan of the paper is the following. In Sect. 2, we describe the basic features of the physical model, while Sect. 3 is devoted to the presentation and discussion of the results. Section 4 contains the conclusions of our work. In addition to the Gauss units for the magnetic field, we set c = G = 1. In this way, any quantity, including the magnetic field, is geometrized, namely there is only one unit of measure, which is the gravitational radius rg = GM/c2. We keep c and G in an explicit form in those expressions of particular physical interest. Appendix A describes the extended geometrized system of units adopted in the numerical solution of Eqs. (8) and (9).
2. The physical model
2.1. Particle dynamics in the pulsar polar cap
We assume that the space-time outside a representative neutron star of mass M, radius R, and angular velocity Ω is given by the Hartle & Thorne metric in the slow-rotation limit (Hartle & Thorne 1968), i.e. 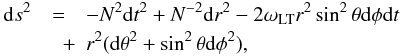 (1)where
(1)where 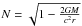 is the lapse function,
is the lapse function, 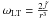 is the Lense-Thirring angular velocity, and
is the Lense-Thirring angular velocity, and 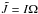 is the total angular momentum of the neutron star measured from infinity, with I being the moment of inertia. The frozen dipole-like magnetic field of the pulsar has the following orthonormal components in spherical coordinates (r,θ,φ) (see, for instance, Ginzburg & Ozernoi 1965; Wasserman & Shapiro 1983; Rezzolla et al. 2001)
is the total angular momentum of the neutron star measured from infinity, with I being the moment of inertia. The frozen dipole-like magnetic field of the pulsar has the following orthonormal components in spherical coordinates (r,θ,φ) (see, for instance, Ginzburg & Ozernoi 1965; Wasserman & Shapiro 1983; Rezzolla et al. 2001) ![\begin{eqnarray} \label{Br} B_{\hat{r}}&=&B_0 \frac{f(\eta)}{f(1)}\frac{1}{\eta^3}\cos\theta , \\ \label{Btheta} B_{\hat{\theta}}&=&\frac{1}{2}B_0 N\left[-2\frac{f(\eta)}{f(1)}+\frac{3}{\left(1-\frac{\varepsilon}{\eta}\right)f(1)}\right] \frac{1}{\eta^3} \sin\theta , \end{eqnarray}](/articles/aa/full_html/2012/04/aa18380-11/aa18380-11-eq28.png) where
where ![\begin{equation} \label{f} f(\eta)=-3\left(\frac{\eta}{\varepsilon}\right)^3\left[\ln\left(1-\frac{\varepsilon}{\eta}\right)+\frac{\varepsilon}{\eta} \left(1+\frac{\varepsilon}{2\eta}\right)\right]\cdot \end{equation}](/articles/aa/full_html/2012/04/aa18380-11/aa18380-11-eq29.png) (4)In the expressions above, η = r/R is the normalized radius, ε = 2M/R is the compactness parameter of the neutron star, and B0 is the value of the magnetic field at the pole of the star, which is of the order of 1012 G for a typical pulsar. Over the years, a series of fundamental works (see, among others, Goldreich & Julian 1969; Ruderman & Sutherland 1975; Arons & Scharlemann 1979; Mestel et al. 1985; Fitzpatrick & Mestel 1988; Michel 1991; Muslimov & Harding 1997; Beskin 2010) have helped to reveal the mechanism behind the pulsar magnetosphere generation. A strong surface magnetic field and a relatively rapidly rotating pulsar lead to the generation of an electric field in the vicinity of the pulsar. In the framework of a space-charge-limited-flow accelerator that we assume here, the parallel component of the electric field E|| at the stellar surface is zero (Becker 2009). Therefore, if the surface temperature is higher than the thermionic emission temperature, particles can leave the star, but with non-relativistic speeds. Once above the star surface, electrons are accelerated to ultra-relativistic velocities on a short distance scale by the non-zero E||. This first generation of electrons, called primary electrons, emit curvature γ-quanta, which, in turn, create electron-positron pairs, initiating the cascade process that forms the pulsar magnetosphere.
(4)In the expressions above, η = r/R is the normalized radius, ε = 2M/R is the compactness parameter of the neutron star, and B0 is the value of the magnetic field at the pole of the star, which is of the order of 1012 G for a typical pulsar. Over the years, a series of fundamental works (see, among others, Goldreich & Julian 1969; Ruderman & Sutherland 1975; Arons & Scharlemann 1979; Mestel et al. 1985; Fitzpatrick & Mestel 1988; Michel 1991; Muslimov & Harding 1997; Beskin 2010) have helped to reveal the mechanism behind the pulsar magnetosphere generation. A strong surface magnetic field and a relatively rapidly rotating pulsar lead to the generation of an electric field in the vicinity of the pulsar. In the framework of a space-charge-limited-flow accelerator that we assume here, the parallel component of the electric field E|| at the stellar surface is zero (Becker 2009). Therefore, if the surface temperature is higher than the thermionic emission temperature, particles can leave the star, but with non-relativistic speeds. Once above the star surface, electrons are accelerated to ultra-relativistic velocities on a short distance scale by the non-zero E||. This first generation of electrons, called primary electrons, emit curvature γ-quanta, which, in turn, create electron-positron pairs, initiating the cascade process that forms the pulsar magnetosphere.
The charge density of the pulsar magnetosphere, which is required in order to completely screen the electric field component parallel to the magnetic field of the pulsar, is called the Goldreich-Julian charge density. The actual charge density ρ of the pulsar magnetosphere slightly deviates from the Goldreich-Julian charge density and the deviation can be roughly estimated from the one-dimensional equation (Beskin 2010) 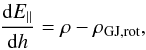 (5)where h is the distance from the star surface. The expression for the Goldreich-Julian charge density of the pulsar, corrected for general relativistic effects, was obtained by Muslimov & Tsygan (1992) and is given by
(5)where h is the distance from the star surface. The expression for the Goldreich-Julian charge density of the pulsar, corrected for general relativistic effects, was obtained by Muslimov & Tsygan (1992) and is given by ![\begin{eqnarray} \label{inclined_rho} && \rho_{\rm GJ, rot}= \nonumber \\ && \quad -\frac{\Omega B_0}{2\pi c}\frac{1}{N\eta^3}\frac{f(\eta)}{f(1)}\left[\left(1-\frac{\kappa}{\eta^3}\right)\cos\chi +\frac{3}{2}H(\eta)\theta\sin\chi\cos\phi\right]\ , \end{eqnarray}](/articles/aa/full_html/2012/04/aa18380-11/aa18380-11-eq39.png) (6)where
(6)where ![\begin{equation} \label{H} H(\eta)=\frac{1}{\eta}\left(\varepsilon-\frac{\kappa}{\eta^2}\right)+ \left(1-\frac{3\varepsilon}{2\eta}+\frac{\kappa}{2\eta^3}\right)\left[f(\eta)\left(1-\frac{\varepsilon}{\eta}\right)\right]^{-1}\ , \end{equation}](/articles/aa/full_html/2012/04/aa18380-11/aa18380-11-eq40.png) (7)while χ is the inclination angle between the axis of rotation of the pulsar and the magnetic moment of the dipole. Moreover, κ ≡ εβ = (ωLT)∗/Ω, where the asterisk denotes a value at the surface of the star, and β = I/I0 is the normalized moment of inertia, where I0 = MR2. Since the polar cap is located in the vicinity of the magnetic pole, in Eq. (6) the polar axis of the spherical coordinates (r,θ,φ) is chosen to be directed along the magnetic dipole axis, which also explains why the angle χ does not appear in the expressions for the magnetic field components given in Eqs. (2) and (3).
(7)while χ is the inclination angle between the axis of rotation of the pulsar and the magnetic moment of the dipole. Moreover, κ ≡ εβ = (ωLT)∗/Ω, where the asterisk denotes a value at the surface of the star, and β = I/I0 is the normalized moment of inertia, where I0 = MR2. Since the polar cap is located in the vicinity of the magnetic pole, in Eq. (6) the polar axis of the spherical coordinates (r,θ,φ) is chosen to be directed along the magnetic dipole axis, which also explains why the angle χ does not appear in the expressions for the magnetic field components given in Eqs. (2) and (3).
Within this framework, it is possible to solve the equations of motion of the electron accelerated in the vicinity of the polar cap. Under the assumption that the charge flow reaches a stationary configuration, Shibata (1997) and Sakai & Shibata (2003) formulated this problem in the form 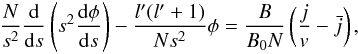 (8)
(8)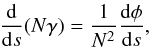 (9)where
(9)where 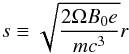 (10)is a normalized radial coordinate, while v is the velocity of the electron. In Eqs. (8) and (9), additional normalizations are performed as
(10)is a normalized radial coordinate, while v is the velocity of the electron. In Eqs. (8) and (9), additional normalizations are performed as 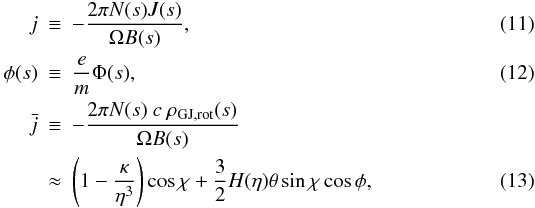 where J is the current density in the pulsar magnetosphere, Φ is the scalar electric potential, m and e are the mass and the charge of the electron, respectively, γ is the Lorentz factor of the accelerated electrons and
where J is the current density in the pulsar magnetosphere, Φ is the scalar electric potential, m and e are the mass and the charge of the electron, respectively, γ is the Lorentz factor of the accelerated electrons and 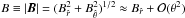 . Moreover, we stress that, in order to derive Eq. (8) from the relativistic Poisson equation, the scalar potential Φ has been expanded in the angular directions as
. Moreover, we stress that, in order to derive Eq. (8) from the relativistic Poisson equation, the scalar potential Φ has been expanded in the angular directions as 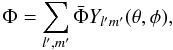 (14)where the spherical orthonormal functions Ylm(θ,φ) are the eigenfunctions of the Laplacian operator in spherical coordinates. Only modes of the polar cap scale have been considered, with l′ ≈ π/Θ0, where
(14)where the spherical orthonormal functions Ylm(θ,φ) are the eigenfunctions of the Laplacian operator in spherical coordinates. Only modes of the polar cap scale have been considered, with l′ ≈ π/Θ0, where ![\begin{equation} \Theta_0=\arcsin\left[\frac{R}{R_{\rm LC}f(1)}\right]^{1/2} \end{equation}](/articles/aa/full_html/2012/04/aa18380-11/aa18380-11-eq58.png) (15)is the polar angle of the last open magnetic field line at the surface of the star (Muslimov & Tsygan 1992), while RLC = c/Ω is the radius of the light cylinder. In our computations, for typical values of Θ0 in the range ≈ [2°,3°] , we have l′ ≈ [60,90] . The polar trajectory of the accelerated particles is described by the curve
(15)is the polar angle of the last open magnetic field line at the surface of the star (Muslimov & Tsygan 1992), while RLC = c/Ω is the radius of the light cylinder. In our computations, for typical values of Θ0 in the range ≈ [2°,3°] , we have l′ ≈ [60,90] . The polar trajectory of the accelerated particles is described by the curve 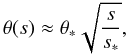 (16)and remains bounded by the polar angle of the last open magnetic field line (Morozova et al. 2010), i.e.
(16)and remains bounded by the polar angle of the last open magnetic field line (Morozova et al. 2010), i.e. ![\begin{equation} \theta(s)\leq \Theta\cong\arcsin\left\{\left[\eta\frac{f(1)}{f(\eta)}\right]^{1/2}\sin\Theta_0\right\}. \end{equation}](/articles/aa/full_html/2012/04/aa18380-11/aa18380-11-eq64.png) (17)
(17)
2.2. The effects of pulsar oscillations
In our analysis, we also consider the case when the rotating pulsar is subject to toroidal oscillations, with the orthonormal velocity field given by (Unno et al. 1989) 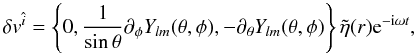 (18)where ω is the real part of the oscillation frequency and
(18)where ω is the real part of the oscillation frequency and 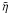 is the radial eigenfunction expressing the amplitude of the oscillations. We assume that the oscillations of the stellar crust can induce oscillations in the plasma magnetosphere, at least in the close vicinity of the surface, which is our main region of interest. As a result, in the rest of our analysis we neglect the radial dependence of the oscillation amplitude, i.e. we assume
is the radial eigenfunction expressing the amplitude of the oscillations. We assume that the oscillations of the stellar crust can induce oscillations in the plasma magnetosphere, at least in the close vicinity of the surface, which is our main region of interest. As a result, in the rest of our analysis we neglect the radial dependence of the oscillation amplitude, i.e. we assume 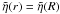 .
.
In principle, an additional degree of freedom should be introduced, related to the possible uncertainty in the orientation of the oscillations with respect to both the axis of rotation and the pulsar magnetic field. However, we adopted here a simplified approach and, as implied by Eq. (18), oriented the oscillation mode axis along the z-axis of the magnetic dipole, while the rotational axis is inclined.
The Goldreich-Julian charge density of a rotating and oscillating pulsar was obtained by Morozova et al. (2010) and is given by2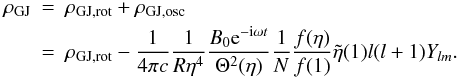 (19)After using the expression above, one can easily obtain the current
(19)After using the expression above, one can easily obtain the current 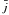 in the presence of both rotation and oscillations as
in the presence of both rotation and oscillations as 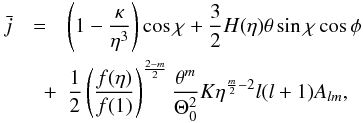 (20)where the amplitude of the oscillation has been parametrized in terms of the small number
(20)where the amplitude of the oscillation has been parametrized in terms of the small number 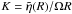 , giving the ratio of the velocity of oscillations to the linear rotational velocity of neutron star. For any particular mode (l,m), we used the approximation Ylm(θ,φ) ≈ Alm(φ)θm, which is valid in the limit of small polar angles θ, where the terms Alm(φ) appearing in Eq. (20) have real parts given by
, giving the ratio of the velocity of oscillations to the linear rotational velocity of neutron star. For any particular mode (l,m), we used the approximation Ylm(θ,φ) ≈ Alm(φ)θm, which is valid in the limit of small polar angles θ, where the terms Alm(φ) appearing in Eq. (20) have real parts given by 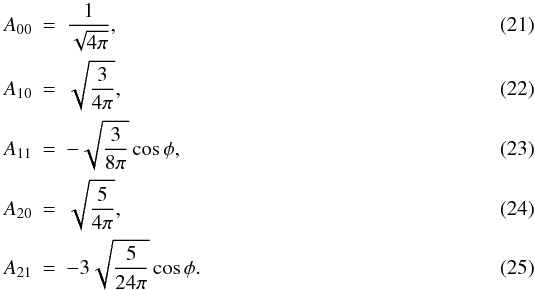 We note that in all our analysis we only consider constant ratios
We note that in all our analysis we only consider constant ratios 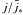 , namely we assume that the ratio of actual charge density to the Goldreich-Julian charge density is constant. This should be regarded as a very good approximation as long as the acceleration mechanism is confined to a short distance from the stellar surface.
, namely we assume that the ratio of actual charge density to the Goldreich-Julian charge density is constant. This should be regarded as a very good approximation as long as the acceleration mechanism is confined to a short distance from the stellar surface.
We stress that the two most plausible models of pulsar magnetosphere, namely those of Mestel (1981) and Arons & Scharlemann (1979), predict different distributions of the charge density in the polar cap region, and hence different conditions for pair creation. In the model of Mestel, a super-GJ charge density is formed along the magnetic field lines that curve away from the rotational axis, while along the field lines curving towards the rotational axis a perfect screening of the accelerating electric field component can be achieved and the charge density is equal to the Goldreich-Julian charge density. In contrast, in the model of Arons, the region where magnetic field lines curve towards the rotational axis has a super-GJ charge density near the star surface, and a sub-GJ charge density away from it3. One of the main differences between the two models, which is responsible for different predictions about the charge density in the pulsar magnetosphere, lies in the boundary conditions of the problem: in the model of Mestel, in particular, the charge density is taken to be equal to the Goldreich-Julian charge density at the surface of the star, while Arons suggests that E∥ = 0 far away from the surface.
However, the present lack of a fully self-consistent model of pulsar magnetospheres motivates a pragmatic approach, according to which the charge density can be treated as a free parameter.
3. Results
In a first series of calculations, we have solved the system of equations given by Eqs. (8), (9) for the case of a rotating but non-oscillating pulsar. The two equations Eqs. (8) and (9) have been reduced to a system of three ODEs in the unknowns φ, dφ/ds, and Nγ, which has been solved with a standard fourth-order Runge-Kutta method. The main parameters of our fiducial pulsar model are R = 10 km, M = 1.4 M⊙, Ω = 2π/(0.1 s), B0 = 1.0 × 1012 G, κ = 0.1, and χ = 30°. We note that, by selecting κ = 0.1, the moment of inertia of the pulsar is given by I/I0 ≈ 0.24. The initial value of the Lorentz factor at the star surface is γ∗ = 1.01, while the initial θ∗ is bounded by Θ0, namely is 0 ≤ θ∗ ≤ Θ0.
Figure 1 reports the Lorentz factor as a function of the normalized radial coordinate r/R − 1 for different values of the ratio 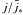 . Fig. 1 essentially confirms the results of Sakai & Shibata (2003), which were originally predicted by Mestel et al. (1985), namely the existence of two different acceleration regimes. When
. Fig. 1 essentially confirms the results of Sakai & Shibata (2003), which were originally predicted by Mestel et al. (1985), namely the existence of two different acceleration regimes. When 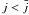 , small values of the velocity v can make the right-hand side of Eq. (8) positive, thus producing an increasing potential and an increasing Lorentz factor. As soon as the velocity reaches a critical value, given by the initial ratio
, small values of the velocity v can make the right-hand side of Eq. (8) positive, thus producing an increasing potential and an increasing Lorentz factor. As soon as the velocity reaches a critical value, given by the initial ratio 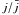 , the right-hand side of Eq. (8) becomes negative and the potential, as well as the velocity, starts to decrease. As a result, the case
, the right-hand side of Eq. (8) becomes negative and the potential, as well as the velocity, starts to decrease. As a result, the case 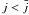 is responsible for the occurrence of an oscillatory regime, with the oscillation frequency (in the spatial domain) that is strongly dependent on the ratio
is responsible for the occurrence of an oscillatory regime, with the oscillation frequency (in the spatial domain) that is strongly dependent on the ratio 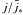 . As shown by Mestel et al. (1985) and Shibata (1997), this situation corresponds to the case where the effective charge density ρ − ρGJ,rot changes sign. When ρ − ρGJ,rot > 0, the electron flow decelerates to increase the charge density; in contrast, when ρ − ρGJ,rot < 0, the flow accelerates to reduce the charge density. A rather different behavior is instead encountered when
. As shown by Mestel et al. (1985) and Shibata (1997), this situation corresponds to the case where the effective charge density ρ − ρGJ,rot changes sign. When ρ − ρGJ,rot > 0, the electron flow decelerates to increase the charge density; in contrast, when ρ − ρGJ,rot < 0, the flow accelerates to reduce the charge density. A rather different behavior is instead encountered when 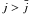 . In this case, the effective charge density is always negative, the right hand side of Eq. (8) is always positive, and the potential as well as the velocity can only grow.
. In this case, the effective charge density is always negative, the right hand side of Eq. (8) is always positive, and the potential as well as the velocity can only grow.
 |
Fig. 1 Dependence of the Lorentz factor on the ratio |
 |
Fig. 2 Lorentz factor dependence on the intensity of the magnetic field for a neutron star with M = 1.4 M⊙, R = 10 km, P = 0.1 s, χ = 30°, θ∗ = 0°, Θ0 = 2°, γ∗ = 1.01. Top panel: |
 |
Fig. 3 Lorentz factor dependence on the inclination angle χ for a neutron star with M = 1.4 M⊙, R = 10 km, and P = 0.1 s, |
Sakai & Shibata (2003) erroneously attributed the abrupt interruption of the oscillatory pattern, which is manifested by some models (see the bottom panel of their Fig. 1), to a purely general relativistic effect. In contrast and as we have verified, this effect is purely numerical and caused by v2 possibly becoming negative during the integration of the system of Eqs. (8)–(9). For instance, this is also true for the long-dashed blue curve in Fig. 1, where the Lorentz factor decays to unity at r/R − 1 ≈ 0.003 after having reached a value of γmax ~ 4100. The pathology of the ODE system that we have demonstrated could not be solved even when resorting to stiff solvers. As a result, the behavior of the Lorentz factor after v2 becomes negative cannot be trusted and is not reported in our figures. We also note that a value of r/R − 1 = 0.006 corresponds to a distance of 60 m above the star surface, which is smaller than the radius of the polar cap rpc ≈ R Θ0 ≈ 350 m as inferred by the polar cap model of Ruderman & Sutherland (1975).
On the other hand, Fig. 2 illustrates the dependence of the Lorentz factor of the accelerated particles on the intensity of the magnetic field. We note that both the accelerating electric field E∥ and the difference ρ − ρGJ,rot are directly proportional to the magnetic field (see Eq. (56) by Muslimov & Tsygan 1992). Therefore, if 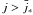 , corresponding to the case when the effective charge density is always negative, the Lorentz factor increases with the magnetic field, as shown in the bottom panel of Fig. 2. On the other hand, if
, corresponding to the case when the effective charge density is always negative, the Lorentz factor increases with the magnetic field, as shown in the bottom panel of Fig. 2. On the other hand, if 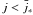 , corresponding to the case when the effective charge density changes sign, the charge density jump |ρ − ρGJ,rot| increases with the magnetic field, producing a pattern with a higher frequency of oscillation (see Eq. (23) by Shibata 1997). This effect is reported in the top panel of Fig. 2.
, corresponding to the case when the effective charge density changes sign, the charge density jump |ρ − ρGJ,rot| increases with the magnetic field, producing a pattern with a higher frequency of oscillation (see Eq. (23) by Shibata 1997). This effect is reported in the top panel of Fig. 2.
 |
Fig. 4 Lorentz factor dependence on the normalized amplitude of the stellar oscillations K for the mode of oscillations (l,m) = (1,1) with θ∗ = 2°, Θ0 = 3°, γ∗ = 1.015, and B0 = 1.0 × 1012 G. The two top panels correspond to the case |
 |
Fig. 5 Lorentz factor dependence on the normalized amplitude of the stellar oscillations K for the mode of oscillations (l,m) = (2,1) with θ∗ = 2°, Θ0 = 3°, γ∗ = 1.015, and B0 = 1.0 × 1012 G. The two panels correspond to the case |
 |
Fig. 6 Lorentz factor as a function of radial distance and azimuthal angle φ for a model with stellar oscillations K = 0.02, (l,m) = (1,1), θ∗ = 2°, Θ0 = 3°, γ∗ = 1.015, and B0 = 1.0 × 1012 G. Left panel: |
The dependence of the Lorentz factor on the inclination angle χ is shown in Fig. 3. When 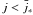 , namely when the oscillatory pattern is produced, the Lorentz factor is insignificantly affected by variations in χ and the results are not reported here. In contrast, when
, namely when the oscillatory pattern is produced, the Lorentz factor is insignificantly affected by variations in χ and the results are not reported here. In contrast, when 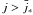 , the results are more interesting and show that smaller Lorentz factors are obtained for larger inclination angles χ, although this effect becomes significant only for very inclined configurations.
, the results are more interesting and show that smaller Lorentz factors are obtained for larger inclination angles χ, although this effect becomes significant only for very inclined configurations.
In a second series of calculations, we have considered the effects of stellar oscillations on the Lorentz-factor of the accelerated particles by adopting the prescription given in Eq. (20). Figures 4 and 5 show the solutions for the modes of oscillations (l,m) = (1,1) and (2,1), respectively. As is apparent from the two top panels of Fig. 4, the presence of stellar oscillations does not affect the amplitude of the Lorentz factor of the particle for 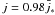 and (l,m) = (1,1). On the other hand, the frequency of the velocity oscillation is smaller for larger K at φ = 0° (left-top panel), while it is larger for larger K at φ = 180° (right-top-panel). As long as the velocity of oscillations for the considered modes is proportional to cosφ, the effect will be the opposite when cosφ changes sign. The same qualitative behavior was also encountered for the mode (l,m) = (2,1), and we conclude that it is typical of the case
and (l,m) = (1,1). On the other hand, the frequency of the velocity oscillation is smaller for larger K at φ = 0° (left-top panel), while it is larger for larger K at φ = 180° (right-top-panel). As long as the velocity of oscillations for the considered modes is proportional to cosφ, the effect will be the opposite when cosφ changes sign. The same qualitative behavior was also encountered for the mode (l,m) = (2,1), and we conclude that it is typical of the case 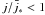 .
.
The case 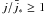 is reported in the two bottom panels of Fig. 4 for the mode (l,m) = (1,1) and in Fig. 5 for the mode (l,m) = (2,1), and illustrate that star oscillations can significantly affect the Lorentz factor. We note that the influence of the stellar oscillations on the acceleration of the particle strongly depends on the azimuthal angle φ. In particular, owing to the modulation produced by the term cosφ, larger oscillation amplitudes K become responsible for a net decelerating effect at angles φ ~ 0, while they produce a net accelerating effect at angles φ ~ π. Moreover, a strong dependence on the ratio
is reported in the two bottom panels of Fig. 4 for the mode (l,m) = (1,1) and in Fig. 5 for the mode (l,m) = (2,1), and illustrate that star oscillations can significantly affect the Lorentz factor. We note that the influence of the stellar oscillations on the acceleration of the particle strongly depends on the azimuthal angle φ. In particular, owing to the modulation produced by the term cosφ, larger oscillation amplitudes K become responsible for a net decelerating effect at angles φ ~ 0, while they produce a net accelerating effect at angles φ ~ π. Moreover, a strong dependence on the ratio 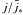 is also encountered, as is clearly evident from the two panels of Fig. 6, which show the modulation of the Lorentz factor with the angle φ for the mode (l,m) = (1,1) in a representative model with K = 0.02. The left panel refers to the case
is also encountered, as is clearly evident from the two panels of Fig. 6, which show the modulation of the Lorentz factor with the angle φ for the mode (l,m) = (1,1) in a representative model with K = 0.02. The left panel refers to the case 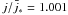 , while the right panel has
, while the right panel has 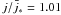 . Interestingly, Morozova et al. (2010) found that the oscillation modes with m = 1 considerably increase the electromagnetic energy losses from the polar cap region of the neutron star, losses that can be several times larger than in the case when no oscillations are present. A more efficient particle acceleration typically corresponds to higher energy losses from the neutron star magnetosphere (Osmanov & Rieger 2009). As a result, we conclude that, at least for the modes (l,m) = (1,1) and (l,m) = (2,1) that we have considered here, larger oscillation amplitudes at the stellar surface may be responsible for both stronger accelerations and higher luminosities, provided that the current density in the magnetosphere is higher than the Goldreich-Julian current density.
. Interestingly, Morozova et al. (2010) found that the oscillation modes with m = 1 considerably increase the electromagnetic energy losses from the polar cap region of the neutron star, losses that can be several times larger than in the case when no oscillations are present. A more efficient particle acceleration typically corresponds to higher energy losses from the neutron star magnetosphere (Osmanov & Rieger 2009). As a result, we conclude that, at least for the modes (l,m) = (1,1) and (l,m) = (2,1) that we have considered here, larger oscillation amplitudes at the stellar surface may be responsible for both stronger accelerations and higher luminosities, provided that the current density in the magnetosphere is higher than the Goldreich-Julian current density.
At least in the case of small inclination angles, a noticeable influence of stellar oscillations on the conditions for particle acceleration can be intuitively understood as follows. The acceleration of charged particles extracted from the surface of the pulsar in the polar cap region is determined by the electric field, which is generated by the combined effect of strong magnetic fields and the motion of the star surface. When stellar oscillations are added to the pure rigid rotation, a given velocity distribution at the star surface is produced. The rotation velocity in the polar cap region is proportional to the small polar angle θ, is exactly equal to zero on the axis of rotation, and increases with distance away from the axis. In contrast, the velocity of oscillations, which is given by Eq. (18), in the case m = 1 does not depend on the small polar angle θ and is effectively constant across the polar cap region of the star. This explains why for these modes even small oscillation velocities may have a noticeable effect on the accelerating component of the electric field.
4. Conclusions
By numerically solving the relativistic electrodynamics equations in the stationary regime of a space-charge-limited-flow accelerator, we have computed the Lorentz factor of electrons accelerated in the polar cap region of a rotating and oscillating pulsar magnetosphere. Our results confirm some of the fundamental findings of Sakai & Shibata (2003), namely the existence of two different regimes: an oscillatory one, which is produced for sub-GJ current density configurations, (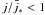 ) and does not produce an efficient acceleration, and a truly accelerating one, which is produced for super-GJ current density configurations (
) and does not produce an efficient acceleration, and a truly accelerating one, which is produced for super-GJ current density configurations (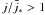 ). We have also clarified the numerical origin of a stopping effect on the velocity of the electron, which has nothing to do with general relativistic effects. Stellar oscillations, on the other hand, can affect both the absolute value of the Lorentz factor gained by the electron and the frequency of the oscillatory patterns, when the latter is present. Owing to the modulation produced by the term cosφ in the equations, where φ is the azimuthal angle, the way in which each mode of oscillation affects the dynamics is different at different azimuthal positions on the polar cap surface, and, in particular, it follows the periodicity of cosφ. These results are overall consistent with those obtained by Morozova et al. (2010), who showed that oscillations are responsible for an extra term in the total energy losses from the system, because the electromagnetic energy losses are determined by the integrated absolute value of the current, flowing in the magnetosphere. At least for the modes (l,m) = (1,1) and (l,m) = (2,1), larger oscillation amplitudes at the star surface may produce both higher accelerations and higher luminosities, provided that the magnetosphere has a super-GJ current density configuration. However, these results also suggest that pulsar oscillations may become responsible for a significant asymmetry in the pulse profile, which will depend on the orientation of the oscillations with respect to the pulsar magnetic field.
). We have also clarified the numerical origin of a stopping effect on the velocity of the electron, which has nothing to do with general relativistic effects. Stellar oscillations, on the other hand, can affect both the absolute value of the Lorentz factor gained by the electron and the frequency of the oscillatory patterns, when the latter is present. Owing to the modulation produced by the term cosφ in the equations, where φ is the azimuthal angle, the way in which each mode of oscillation affects the dynamics is different at different azimuthal positions on the polar cap surface, and, in particular, it follows the periodicity of cosφ. These results are overall consistent with those obtained by Morozova et al. (2010), who showed that oscillations are responsible for an extra term in the total energy losses from the system, because the electromagnetic energy losses are determined by the integrated absolute value of the current, flowing in the magnetosphere. At least for the modes (l,m) = (1,1) and (l,m) = (2,1), larger oscillation amplitudes at the star surface may produce both higher accelerations and higher luminosities, provided that the magnetosphere has a super-GJ current density configuration. However, these results also suggest that pulsar oscillations may become responsible for a significant asymmetry in the pulse profile, which will depend on the orientation of the oscillations with respect to the pulsar magnetic field.
Finally, we stress that some recent investigations have tried to connect the models of stellar oscillations with the observational data available for pulsars (Rosen & Clemens 2008; Rosen & Demorest 2011; Rosen et al. 2011). The scenario that is emerging from these studies is that the presence of stellar oscillations creates different kinds of “noise” in the clock-like picture of pulses, i.e. changes in the pulse shape, changes in the spin-down rate, and the switching between different regimes of pulsar emission. van Leeuwen & Timokhin (2012), in particular, revisited the issue of drifting subpulses in the pulsar profiles, reaching the important conclusion that the rate of subpulse drift is proportional to the latitudinal derivative of the scalar potential across the pulsar polar cap and not to the absolute value of the scalar potential, as had been generally assumed. This provides a wide range of opportunities for comparing the observational data on pulsar profiles with the results presented here and in our previous investigations of oscillating magnetopsheres. Stellar oscillations, indeed, affect the scalar potential in the polar cap region and are expected to have a significant effect on the character of the subpulse drift. We plan to devote our future research to a closer analysis of the observational aspects of these ideas.
Acknowledgments
V. Morozova would like to acknowledge the support of the German Academic Exchange Service DAAD for supporting her stay at ZARM.
References
- Abdikamalov, E. B., Ahmedov, B. J., & Miller, J. C. 2009, MNRAS, 395, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Arons, J., & Scharlemann, E. T. 1979, ApJ, 231, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Barzilay, Y. 2011, ApJ, 732, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, W. 2009, Neutron Stars and Pulsars, Astrophys. Space Sci. Lib., 357 [Google Scholar]
- Beskin V. S. 2010, MHD Flows in Compact Astrophysical Objects: Accretion, Winds and Jets. (Berlin: Springer-Verlag) [Google Scholar]
- Cheng, A. F., & Ruderman, M. A. 1980, ApJ, 235, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, I., Kazanas, D., & Fendt, C., 1999, ApJ, 511, 351 [Google Scholar]
- Daugherty, J. K., & Harding, A. K. 1982, ApJ, 252, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Fawley, W. M., Arons, J., & Scharlemann, E. T. 1977, ApJ, 217, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, R., & Mestel, L. 1988, MNRAS, 232, 277 [NASA ADS] [Google Scholar]
- Ginzburg, V. L., & Ozernoi, L. M. 1965, Soviet Phys.-JETP, 20, 689 [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gruzinov, A. 2005, Phys. Rev. Lett., 94, 021101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Harding, A. K., & Muslimov, A. G. 1998, ApJ, 508, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Hartle, J. B., & Thorne, K. S. 1968, ApJ, 153, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Kalapotharakos, C., Kazanas, D., Harding, A., & Contopoulos, I. 2012, ApJ, 749, 2 [Google Scholar]
- McDermott, P. N., Savedoff, M. P., van Horn, H. M., Zweibel, E. G., & Hansen, C. J. 1984, ApJ, 281, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1981, in Pulsars, Proc. ed. W. Sieber, R. Wielebinski (Dordrecht: Reidel), IAU Symp., 95, 9 [Google Scholar]
- Mestel, L., Robertson, J. A., Wang, Y.-M., & Westfold, K. C. 1985, MNRAS, 217, 443 [NASA ADS] [Google Scholar]
- Michel, F. C. 1991, Theory of Neutron Star Magnetospheres (Chicago: Univ. Chicago Press) [Google Scholar]
- Morozova, V. S., Ahmedov, B. J., & Kagramanova, V. G. 2008, ApJ, 684, 1359 [NASA ADS] [CrossRef] [Google Scholar]
- Morozova, V. S., Ahmedov, B. J., & Zanotti, O. 2010, MNRAS, 408, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Morozova, V. S., Ahmedov, B. J., & Zanotti, O. 2012, MNRAS, 419, 2147 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A., & Harding, A. K. 1997, ApJ, 485, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Tsygan, A. I. 1986, Ap&SS, 120, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Tsygan, A. I. 1992, MNRAS, 255, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Osmanov, Z., & Rieger, F. M. 2009, A&A, 502, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezzolla, L., & Ahmedov, B. 2004, MNRAS, 352, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Ahmedov, B. J., & Miller, J. C. 2001, MNRAS, 322, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, R., & Clemens, J. C., 2008, ApJ, 680, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, R., & Demorest, P. 2011, ApJ, 728, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, R., McLaughlin, M. A., & Thompson, S. E. 2011, ApJ, 728, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, N., & Shibata, S. 2003, ApJ, 584, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Scharlemann, E. T., Arons, J., & Fawley, W. M. 1978, ApJ, 222, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, S. 1997, MNRAS, 287, 262 [NASA ADS] [Google Scholar]
- Steiner, A. W., & Watts, A. L. 2009, Phys. Rev. Lett., 103, 181101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sturrock, P. A. 1971, ApJ, 164, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N. 2007, Astropys. Space Sci., 308, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., Bisnovatyi-Kogan, G. S., & Spruit, H. C. 2000, MNRAS, 316, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., Eichler, D., & Lyubarsky, Y. 2008, ApJ, 680, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi H. 1989, Nonradial Oscillations of Stars (Tokyo: Univ. Tokyo Press) [Google Scholar]
- van Leeuwen, J., & Timokhin, A. N. 2012, ApJ, submitted [arXiv:1201.3647] [Google Scholar]
- Wasserman, I., & Shapiro, S. L. 1983, ApJ, 265, 1036 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Extended geometrized system of units
We recall that the definition of geometric units of time and lengths is obtained by setting the speed of light c and the gravitational constant G to pure numbers. This implies that seconds and grams of the cgs system can be written as 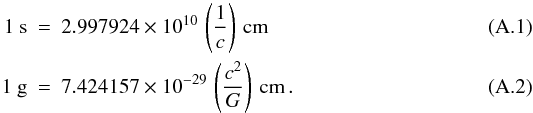 Within this general setup, a convenient unit of space is still required. The cm is of course a bad choice in a gravitational framework and the gravitational radius rg = GM/c2 is instead chosen. In order for this new unit to be more convenient than the centimeter, the mass M of the system has to be sufficiently high. From the physical value of the solar mass and Eq. (A.2), we find the relations between the cgs units and the new unit of length rg
Within this general setup, a convenient unit of space is still required. The cm is of course a bad choice in a gravitational framework and the gravitational radius rg = GM/c2 is instead chosen. In order for this new unit to be more convenient than the centimeter, the mass M of the system has to be sufficiently high. From the physical value of the solar mass and Eq. (A.2), we find the relations between the cgs units and the new unit of length rg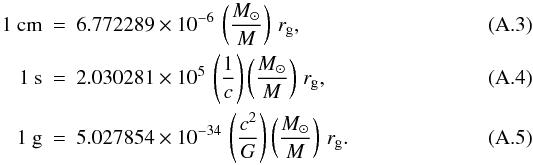 In the traditional geometrized system c and G are set equal to unity. Equations (A.3)–(A.5) allow us to perform the geometrization of any dynamical quantities. Quantities involving the charge, on the other hand, are naturally geometrized within the Gauss system of units, which we adopt here in addition to the choice c = G = 1. In Gauss units, the unit of measure of the magnetic induction, the Gauss G, is given by
In the traditional geometrized system c and G are set equal to unity. Equations (A.3)–(A.5) allow us to perform the geometrization of any dynamical quantities. Quantities involving the charge, on the other hand, are naturally geometrized within the Gauss system of units, which we adopt here in addition to the choice c = G = 1. In Gauss units, the unit of measure of the magnetic induction, the Gauss G, is given by 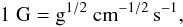 (A.6)which, by virtue of (A.3)–(A.5), provides
(A.6)which, by virtue of (A.3)–(A.5), provides 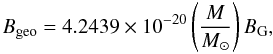 (A.7)where BG and Bgeo are the pure numbers expressing the intensity of the magnetic field in Gauss units and the geometrized system, respectively. We note that in these units the charge-to-mass ratio is a pure number, and, in the case of electrons, is given by
(A.7)where BG and Bgeo are the pure numbers expressing the intensity of the magnetic field in Gauss units and the geometrized system, respectively. We note that in these units the charge-to-mass ratio is a pure number, and, in the case of electrons, is given by 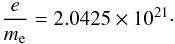 (A.8)
(A.8)
All Figures
 |
Fig. 1 Dependence of the Lorentz factor on the ratio |
| In the text | |
 |
Fig. 2 Lorentz factor dependence on the intensity of the magnetic field for a neutron star with M = 1.4 M⊙, R = 10 km, P = 0.1 s, χ = 30°, θ∗ = 0°, Θ0 = 2°, γ∗ = 1.01. Top panel: |
| In the text | |
 |
Fig. 3 Lorentz factor dependence on the inclination angle χ for a neutron star with M = 1.4 M⊙, R = 10 km, and P = 0.1 s, |
| In the text | |
 |
Fig. 4 Lorentz factor dependence on the normalized amplitude of the stellar oscillations K for the mode of oscillations (l,m) = (1,1) with θ∗ = 2°, Θ0 = 3°, γ∗ = 1.015, and B0 = 1.0 × 1012 G. The two top panels correspond to the case |
| In the text | |
 |
Fig. 5 Lorentz factor dependence on the normalized amplitude of the stellar oscillations K for the mode of oscillations (l,m) = (2,1) with θ∗ = 2°, Θ0 = 3°, γ∗ = 1.015, and B0 = 1.0 × 1012 G. The two panels correspond to the case |
| In the text | |
 |
Fig. 6 Lorentz factor as a function of radial distance and azimuthal angle φ for a model with stellar oscillations K = 0.02, (l,m) = (1,1), θ∗ = 2°, Θ0 = 3°, γ∗ = 1.015, and B0 = 1.0 × 1012 G. Left panel: |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.