| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118355 | |
| Published online | 13 April 2012 | |
The extinction law from photometric data: linear regression methods⋆
1 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
e-mail: jascenso@eso.org
2 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
3 Centro de Astrofisica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
4 University of Milan, Department of Physics, via Celoria 16, 20133 Milan, Italy
5 University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
Received: 28 October 2011
Accepted: 14 February 2012
Context. The properties of dust grains, in particular their size distribution, are expected to differ from the interstellar medium to the high-density regions within molecular clouds. Since the extinction at near-infrared wavelengths is caused by dust, the extinction law in cores should depart from that found in low-density environments if the dust grains have different properties.
Aims. We explore methods to measure the near-infrared extinction law produced by dense material in molecular cloud cores from photometric data.
Methods. Using controlled sets of synthetic and semi-synthetic data, we test several methods for linear regression applied to the specific problem of deriving the extinction law from photometric data. We cover the parameter space appropriate to this type of observations.
Results. We find that many of the common linear-regression methods produce biased results when applied to the extinction law from photometric colors. We propose and validate a new method, LinES, as the most reliable for this effect. We explore the use of this method to detect whether or not the extinction law of a given reddened population has a break at some value of extinction.
Key words: methods: data analysis / ISM: clouds / dust, extinction / stars: formation
© ESO, 2012
1. Introduction
The properties of interestellar dust appear to be fairly constant throughout the interstellar medium (ISM) of the Galaxy (Rieke & Lebofsky 1985; Kenyon et al. 1998; Lombardi et al. 2006; Jones & Hyland 1980; Martin & Whittet 1990), reflecting the homogeneous physical conditions that characterize it. In the cold molecular cores, however, under lower temperatures and higher densities, the dust grains are believed to change, namely grow by coalescence and/or develop ice mantles (e.g., Whittet et al. 1988; Ossenkopf 1993; Whittet et al. 2001; Draine 2003; Román-Zúñiga et al. 2007; Steinacker et al. 2010). Measuring these differences using methods other than detailed spectral analysis has proved somewhat challenging, but the advent of larger and more sensitive telescopes has started to reveal extinction laws toward these regions that depart from the ISM typical curves, particularly in the near- and mid-infrared regime1, putting forward the extinction law as a good indicator of grain properties.
Whereas the extinction law in low-density regions and the ISM is well characterized by a power-law (Aλ ∝ λ − β) of index β ~ 1.8, several authors have found a pronounced flattening of the extinction law in high density regions. Lutz et al. (1996) and Lutz (1999) first noted a flat extinction law toward the Galactic center in this wavelength range using spectroscopy of hydrogen recombination lines. Nishiyama et al. (2006) confirmed a flat extinction law toward the Galactic center using the colors of red clump stars, later confirmed independently by Fritz et al. (2011). Another example was found by Indebetouw et al. (2005), using a different method based on Spitzer photometry, in the direction of and around the star forming region RCW 49. A number of other studies on the extinction law using Spitzer followed, namely Flaherty et al. (2007), Chapman et al. (2009) and McClure (2009), who found a gray extinction law for star forming regions and molecular clouds; Chapman & Mundy (2009) and Román-Zúñiga et al. (2007), who found a gray extinction law for cloud cores; and Nishiyama et al. (2009), who found a similar law for the Galactic center. Chapman & Mundy (2009), Chapman et al. (2009) and McClure (2009) go a step further by analyzing the dependence of the extinction law with extinction, finding that the extinction law becomes grayer at higher extinction regimes. More recently, Cambrésy et al. (2011) measured an actual change of the extinction law within the same region for a threshold of AV = 20 mag in the Trifid Nebula.
In this paper we address the issue of determining the extinction law from photometric data alone and the biases inherent to some of the fitting methods used frequently in the literature. We begin by defining the mathematical problem and the possible methods to extract a linear fit (Sect. 2), validating each method with synthetic data (Sect. 3). In Sect. 4 we address the issue of detecting a flattening of the extinction law with extinction.
This is the first paper in a series of two. The following paper (Ascenso et al., in prep.) will apply the results reported here to actual observations of cores in the Pipe Nebula.
2. The extinction law from photometric data
2.1. Defining the problem
The problem of deriving the extinction law from photometric data is one of linear regression: the goal is to determine the slope of the line that best fits the reddening-displaced positions of the stars in a color–color diagram. This slope, β, is the ratio of two color excesses that compose the color–color diagram, e.g., β = Eλ − K/EH − K in a λ − K vs. H − K diagram, and is, in this case, related to the extinction law Aλ/AK by: 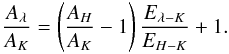 (1)Linear regression, however, is not a simple science. The presence of errors in both coordinates, that they vary as a function of the quantities being analyzed (heteroscedasticity), that they may be correlated, and the presence of intrinsic scatter, make the required linear regression analysis far more complex than the typical chi-squared minimization of residuals. Problems of this nature, in particular applied to astronomical analysis, have been debated in the literature for over 50 years (Seares 1944; Trumpler & Weaver 1953), although every specific case seems to require a careful consideration of the methods to use.
(1)Linear regression, however, is not a simple science. The presence of errors in both coordinates, that they vary as a function of the quantities being analyzed (heteroscedasticity), that they may be correlated, and the presence of intrinsic scatter, make the required linear regression analysis far more complex than the typical chi-squared minimization of residuals. Problems of this nature, in particular applied to astronomical analysis, have been debated in the literature for over 50 years (Seares 1944; Trumpler & Weaver 1953), although every specific case seems to require a careful consideration of the methods to use.
The particular distribution to which we presently wish to fit a linear function has the following characteristics:
-
The X and Y variables are photometric colors, obtained by subtracting the magnitudes of a star in two bands. Both variables are therefore subject to photometric errors that increase with magnitude but not in an entirely predictable way with color.
-
Because we observe (parts of) non-homogeneous clouds, the amount of extinction is not the same for all stars, and since most of the area is at low extinction, the distribution of points in a color–color diagram is denser in the bluer end, and scarcer in the redder end.
-
The X and Y colors will usually have one band in common (e.g., J − H and H − K), which causes the errors to be correlated (anti-correlated in the example).
-
Because we observe the colors of a random sample of stars background to the cloud, the data will have intrinsic scatter caused by the range in spectral types of the stars. The intrinsic scatter is unrelated to extinction.
To summarize, the position of each datapoint in the color–color diagram is determined by three factors: the intrinsic scatter from the dispersion in spectral types of field stars, the reddening caused by dust extinction, and the measurement (photometric) error. The first alone would trace the loci occupied by the unreddened colors of the population of stars in the field, mostly giant and main-sequence stars; the effect of extinction is to (dim the objects and) move each point along the line whose slope we want to determine; and the photometric errors scatter the points in an ellipse around the intrinsic, reddened position (not a circle because the errors are correlated). A proper method to measure the slope of this distribution should be robust enough to disentangle these effects and return the single slope of the reddening vector.
2.2. Methods for linear regression
In this paper we test the following methods for linear regression applied to the problem described in the previous section.
2.2.1. Least squares fitting
The ordinary least-squares (OLS) fit is the simplest approach to linear regression. It works by minimizing the vertical distance of all data points to successive lines in the 2-D (slope and intercept) parameter space. Formally, it is equivalent to finding αOLS and βOLS that minimize the quantity: 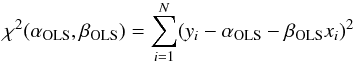 (2)where (xi,yi) is the ith data point, and α and β are the intercept and the slope one is trying to find. This method treats all data points the same, even though the position of some points will be more uncertain than that of others. The knowledge of the measurement errors for each data point can be used to attribute different weights to the different data points, thus optimizing the fit, which is equivalent to finding αWLS and βWLS that minimize the quantity:
(2)where (xi,yi) is the ith data point, and α and β are the intercept and the slope one is trying to find. This method treats all data points the same, even though the position of some points will be more uncertain than that of others. The knowledge of the measurement errors for each data point can be used to attribute different weights to the different data points, thus optimizing the fit, which is equivalent to finding αWLS and βWLS that minimize the quantity: 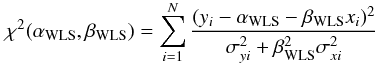 (3)where σxi and σyi are the measurement errors of the ith data point. This method is called the weighed least squares (WLS) method.
(3)where σxi and σyi are the measurement errors of the ith data point. This method is called the weighed least squares (WLS) method.
2.2.2. Symmetrical methods
Applications of the least squares method have been suggested to be most appropriate when the intrinsic scatter in the data dominates over the measurement errors (see Isobe et al. 1990, for a detailed discussion and formal description). As opposed to the method described above, these treat both variables symmetrically, in such a way that it is no longer meaningful to speak of dependent and independent variables.
Two of these methods are based on calculating the OLS slope of the Y vs. X distribution,  OLS(Y|X) following the notation of Isobe et al. (1990), and that of the X vs. Y distribution,
OLS(Y|X) following the notation of Isobe et al. (1990), and that of the X vs. Y distribution, 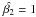 /OLS(X|Y). The best fit is the line that bisects the OLS(Y|X) and the OLS(X|Y) in the bisector method (Eq. (4)), or the geometric mean of the OLS(Y|X) and OLS(X|Y) slopes in the geometric mean method (Eq. (5)). A third method, orthogonal regression (Eq. (6)), minimizes the distances of the points to a model line, but perpendicularly to the line instead of vertically as the regular least-squares method. Isobe et al. (1990) clearly state that these three methods do not produce the same or equivalent solutions. The plus or minus in the equations below refer to the sign of the covariance of the two variables – positive if they are correlated, negative if anti-correlated.
/OLS(X|Y). The best fit is the line that bisects the OLS(Y|X) and the OLS(X|Y) in the bisector method (Eq. (4)), or the geometric mean of the OLS(Y|X) and OLS(X|Y) slopes in the geometric mean method (Eq. (5)). A third method, orthogonal regression (Eq. (6)), minimizes the distances of the points to a model line, but perpendicularly to the line instead of vertically as the regular least-squares method. Isobe et al. (1990) clearly state that these three methods do not produce the same or equivalent solutions. The plus or minus in the equations below refer to the sign of the covariance of the two variables – positive if they are correlated, negative if anti-correlated. 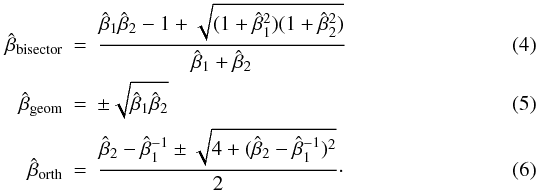
2.2.3. Binning
Binning data always causes loss of information, but, sometimes, what is lost in information, is gained in simplicity of analysis and results. In their studies of extinction by molecular clouds, Lombardi et al. (2006) developed a method to determine the extinction law that consisted in binning the colors in both axes and fitting the bins using the weighed least-squares fitting described in Sect. 2.2.1. The characterization of the data changes entirely, because (1) the data points are no longer measurements but the weighed average of many measurements, (2) the errors are no longer measurement errors but the dispersion of colors within each bin, and (3) the fewer high extinction points are given more weight than before as they are represented by a bin with the same weight as those bins containing more points. The latter point implies, although with the potential of introducing small number statistics issues, that the weight of any extinction range is the same, regardless of where the majority of datapoints lie. In this way, instead of the fit being weighed by the more abundant points at low extinction, as is the case for the fit to all datapoints, it is equally weighed by a much larger range of extinction thus allowing a better constrain of the extinction law. It also implies that part of the intrinsic scatter problem is eliminated as the high extinction population will be dominated by giants whose range in intrinsic colors is much narrower.
For the purpose of these experiments we have binned the data in two ways: (1) along the color in the X-axis in bins of color and (2) iteratively along an assumed reddening vector in bins of AV following the method described by Lombardi et al. (2006).
2.2.4. BCES method
The standard BCES method (Akritas & Bershady 1996) starts from the simple observation that the slope β that minimizes the standard OLS Eq. (1) can be alternatively written as 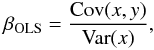 (7)where Cov(x,y) is the observed covariance between the data { xi } and { yi } , and Var(x) is the variance of { xi } . These two quantities can be evaluated from the usual equations
(7)where Cov(x,y) is the observed covariance between the data { xi } and { yi } , and Var(x) is the variance of { xi } . These two quantities can be evaluated from the usual equations 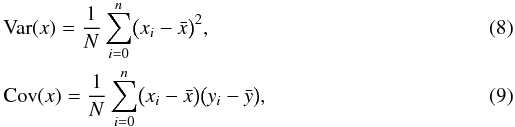 where the bar indicates the average values. Note that for the specific purposes of the BCES method the variance and covariance of the data should be evaluated using N in the denominator (instead of the more common N − 1, used when estimating the variance and the mean from the same dataset).
where the bar indicates the average values. Note that for the specific purposes of the BCES method the variance and covariance of the data should be evaluated using N in the denominator (instead of the more common N − 1, used when estimating the variance and the mean from the same dataset).
The equation for β above suggests that we can easily take into account the presence of measurement errors on both x and y by simply subtracting their effect from the estimates of the covariance and variance. To this purpose, suppose that each point (xi,yi) in our dataset is affected by a statistical error, so that the measured values 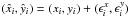 . The quantities
. The quantities 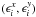 represent the errors, and are drawn from some distribution; the errors on x and y are not assumed to be uncorrelated here. The presence of the errors changes the covariance and variance in the expression of β above as follows
represent the errors, and are drawn from some distribution; the errors on x and y are not assumed to be uncorrelated here. The presence of the errors changes the covariance and variance in the expression of β above as follows 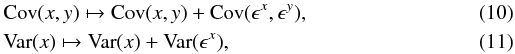 where we have introduced the variance and covariance of the errors measurements. Since the true, original variance and covariance is relevant for the estimate of β, the equations above suggest that in presence of measurement errors, we can replace the equation above with
where we have introduced the variance and covariance of the errors measurements. Since the true, original variance and covariance is relevant for the estimate of β, the equations above suggest that in presence of measurement errors, we can replace the equation above with 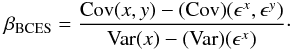 (12)Note that, in contrast to (x,y), the variance and covariance of the measurement errors is assumed to be known and cannot be derived from the data alone. For example, in our case, if (x,y) are two colors, say x = H − K and y = J − H, we will have
(12)Note that, in contrast to (x,y), the variance and covariance of the measurement errors is assumed to be known and cannot be derived from the data alone. For example, in our case, if (x,y) are two colors, say x = H − K and y = J − H, we will have  where σH and σK are the mean photometric error in the H and K bands, respectively.
where σH and σK are the mean photometric error in the H and K bands, respectively.
2.2.5. A new method for linear regression: LinES
The standard BCES methods is very simple to implement, but, although, in principle, it should be able to work in presence of an intrinsic scatter, in practice, at least in the original version presented by Akritas & Bershady (1996), it is does not. The authors do mention the possibility of accounting for intrinsic scatter in the data, but only when x is measured without error, which is not applicable to the case of the extinction law. Additionally, in the situations that they consider, the amount of intrinsic scatter is taken to be unknown. In our case, however, we can estimate this quantity directly from a control field with no extinction: the variance and covariance of the colors there is just the sum of the variance and covariance due to the intrinsic scatter in color of stars, and by the photometric errors for the control field. This way we can derive the slope using the following expression: 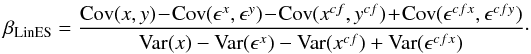 (15)We call this estimate the LinES method (Linear regression with Errors and Scatter)2. As shown in Sect. 3.4.7, this method is robust against the presence of correlated errors in both variables, and against the presence of intrinsic scatter.
(15)We call this estimate the LinES method (Linear regression with Errors and Scatter)2. As shown in Sect. 3.4.7, this method is robust against the presence of correlated errors in both variables, and against the presence of intrinsic scatter.
3. Method validation
We tested the methods described above using controlled sets of synthetic data. The following sections discuss these data, and the effects of varying the data parameters on the results produced by each method.
3.1. Synthetic data
We constructed a set of simulations meant as controlled, realistic datasets comparable to the observed data for the Pipe Nebula cores (Lombardi et al. 2006; Alves et al. 2007). The simulated data consisted of a number of points (stars) characterized by brightnesses in three bands – arbitrarily J, H and K – affected by a value of extinction that obeys a predetermined extinction law. We simulated three sets of data to test the different aspects of each method.
 |
Fig. 1 Observed J-band luminosity function of a control field, used as a model distribution for the unreddened J luminosities of the synthetic data. |
For all sets, the J brightnesses were drawn randomly from the distribution of J luminosities from an observed unreddened control field toward the galactic bulge (Fig. 1).
 |
Fig. 2 Log-normal model distribution of extinction AV for a generic cloud. The dotted line corresponds to AV = 2.5 mag, the median extinction of the Pipe Nebula. |
The synthetic extinction profile was defined as a lognormal distribution (Eq. (16)) centered at μ = log (2.5), the logarithm of the median extinction of the Pipe, and with a width of σ = 0.46, chosen so that the number of stars at high extinctions approximately matches that for the observed data of the Pipe cores (Fig. 2) 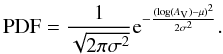 (16)Because the probability distribution function (PDF) for the extinction is a lognormal, there will be many stars at low extinction and progressively fewer stars at high extinction.
(16)Because the probability distribution function (PDF) for the extinction is a lognormal, there will be many stars at low extinction and progressively fewer stars at high extinction.
AK was then calculated from the relation AK/AV = 0.112 (Rieke & Lebofsky 1985) and the values of extinction drawn from Eq. (16)were applied to the J, H and K brightnesses using the extinction law characterized by:  The second equation, derived from Eq. (1)for a (J − H) vs. (H − K) diagram, defines β = E(J − H)/E(H − K), which means the reddening vector has a slope of β in a (J − H) vs. (H − K) color–color diagram. AH/AK = 1.55 is adopted from Indebetouw et al. (2005).
The second equation, derived from Eq. (1)for a (J − H) vs. (H − K) diagram, defines β = E(J − H)/E(H − K), which means the reddening vector has a slope of β in a (J − H) vs. (H − K) color–color diagram. AH/AK = 1.55 is adopted from Indebetouw et al. (2005).
3.1.1. Set 1: Homoscedastic data, no intrinsic scatter
For the first set, the H and K brightnesses were derived from J assuming that all stars have the typical intrinsic color of giants (J − H = 0.7 and H − K = 0.15, Bessell & Brett 1988)3. Each star was then assigned a value of extinction drawn randomly from the extinction profile (Eqs. (16), (18), Fig. 2).
In addition to reddening, each star was assigned errors in J, H and K, to simulate the photometric errors inherent to real data. The errors were first applied in the simplest possible way: independently of brightness. The magnitudes of the errors were drawn randomly and independently for J, H and K, from a normal distribution with μ = 0 and σ = 0.05, so that 95% of the stars will have errors below 0.1 mag, the typical acceptable errors for photometry. A random value from these distributions was then added to the magnitudes of each star in all bands independently. The synthetic data produced in this way will henceforth be referred to as Set 1, or homoscedastic dataset, since the errors do not scale with the variables.
3.1.2. Set 2: Heteroscedastic data, no intrinsic scatter
A second approach was designed to reproduce the fact that the error in real observations does in fact increase with magnitude. We modeled this dependence using an error distribution in the form of a power-law S(m) = Cmx, where S is the typical error associated with magnitude m (Fig. 3). The normalization constant C was set so that 90% of the 25th magnitude stars have an error up to 0.3 mag, and the index x, that defines how rapidly the errors increase with magnitude, was set to 4. Both parameters were empirically chosen to produce a curve that resembles a typical error distribution of the NIR data, but other combinations around these values would also be good representations of the general distribution of photometric errors in a sample, and do not change the results. This function was then used to determine the width of the Gaussian from which the errors for each star were drawn according to its magnitude, the error for the bright stars being drawn from a narrow Gaussian, and that for the faint stars being drawn from a wider Gaussian (see the insets in Fig. 3). The synthetic data produced in this way will hereafter be referred to as Set 2, or heteroscedastic data, since the errors do scale with magnitude.
 |
Fig. 3 Width of the error distribution as a function of magnitude used to generate the “photometric errors”. The insets show the actual error distribution for stars of magnitude 15 (left) and 25 (right). |
Figure 4 shows the construction of the synthetic data in the color–color diagrams for a given realization of heteroscedastic data without intrinsic scatter.
3.1.3. Set 3: Heteroscedastic data with intrinsic scatter
The final experiment was meant to represent the fact that the stars being observed through the cloud do not have a single color, but are rather distributed along the main-sequence and giant stars loci according to their individual masses and ages. This intrinsic “scatter” about a single color was modeled by assuming a fraction f of main-sequence-to-giant stars, and randomly populating the loci accordingly, regardless of the stars’ brightnesses. This does not produce a completely realistic set of data because the position of the stars would depend on their brightness (Sect. 3.2), but our goal is to test how the presence of a generic, non-symmetrical intrinsic scatter affects the measurement of the slope of the extinction law.
In this dataset there are then three contributions to the distribution of points in the color–color diagram: the distribution of intrinsic colors of stars background to the cloud, that spread the stars along the main-sequence and giant loci; the extinction, that moves each point from its intrinsic position along a line whose slope is determined by the properties of the dust; and the magnitude-dependent photometric error, that, in a color–color diagram, is equivalent to each point being drawn from an ellipse around each intrinsic and reddened point, whose dimensions depend on the observed brightness of the corresponding star.
The data produced in this way will be referred to Set 3, or heteroscedastic data with intrinsic scatter.
3.1.4. Synthetic control fields
For each set intended to pose as science data, we generated a corresponding set intended to pose as data from a control field. For Sets 1 and 2 the synthetic control fields had equivalent homoscedastic or heteroscedastic errors, respectively, drawn randomly but independently from the same distributions as the errors for the synthetic “science” fields. For Set 3, apart from the heteroscedastic errors, the control field simulation also included an amount of intrinsic scatter equivalent to that of the synthetic “science” field. Neither of the synthetic control fields included extinction, as they are meant to represent the population background to the cloud that is causing the reddening on the “science” field stars.
 |
Fig. 4 Example of the generation of synthetic heteroscedastic data without scatter. From left to right: all synthetic stars have the same intrinsic color; they are reddened according to the log-normal distribution of AV; photometric error that depends on magnitude is added; and finally a magnitude cut is implemented, reducing the size of the sample and the coverage in AV. |
 |
Fig. 5 (J − H) vs. (H − K) color–color diagrams for the disk dataset. Left: all stars in the dataset. Middle: 450 stars chosen randomly from the dataset, representing the “control field”. Right: 450 stars chosen randomly from the dataset, and reddened to represent the “science field”. |
 |
Fig. 6 (J − H) vs. (H − K) color–color diagrams for the bulge dataset. Left: all stars in the dataset. Middle: 800 stars chosen randomly from the dataset, representing the “control field”. Right: 800 stars chosen randomly from the dataset, and reddened to represent the “science field”. |
3.2. “Real” data
There is one aspect of real observations that we cannot test with the synthetic datasets described above: whereas at low extinction both main-sequence and giants can be observed, at high extinction the main-sequence stars are more efficiently dimmed below the detection limit, leaving a population dominated by the intrinsically brighter giants at redder colors. In our definitions for the synthetic data, this means that f should change with extinction, being larger at low extinctions and progressively smaller at high extinctions. As already hinted in Sect. 3.1.3, in set 3 of our synthetic data we do simulate intrinsic scatter, but the brightness of each star does not scale with its spectral type, which translates into having a constant f throughout the entire extinction range. To test the effect of a varying amount of intrinsic scatter with extinction on the methods we applied them to actual observations of control fields (courtesy of C. Róman-Zúñiga), which we reddened in the same way as we did the synthetic data. We refer to these datasets as “real”, keeping the quotes to make clear that the actual observed data were then artificially modified.
The first dataset contains data taken with the SOFI instrument at ESO’s New Technology Telescope, in the direction of the galactic disk (10h38m12s, − 59°12′02′′, J2000.0), on the night of March 31st, 2006. This dataset, which we refer to as “disk dataset”, contains 548 stars with PSF photometry in the J, H and Ks filters. This is not the ideal dataset for two reasons: first, it contains few stars, and second, since this is a field in the galactic disk, it already has some extinction.
The second dataset contains data also taken with the SOFI instrument at ESO’s New Technology Telescope on the night of June 22nd, 2002, but in the direction of the galactic bulge (17h08m10s, − 28°03′03′′, J2000.0). This dataset, which we refer to as “bulge dataset”, contains 1071 stars with PSF photometry in the J, H and Ks filters.
5000 “science” subsets were drawn randomly from each of these datasets, and extinction was applied to each star from the extinction distribution (Eq. (1), Fig. 2). Similarly, 5000 “control field” subsets were drawn randomly from each dataset, and used as they were. 450 and 800 stars were drawn from the disk and the bulge datasets, respectively, in order to keep the possibility of the “control” and “science” subsets being made of different stars.
For the effects of these experiments, the two sets differ in three aspects: the bulge dataset contains more stars, does not have extinction, and is made up mostly of giant stars, whereas the disk dataset contains fewer stars, has already some extinction, and is more likely to have a higher fraction of main-sequence objects. The (J − H) vs. (H − K) color–color diagrams of the two datasets are shown in Figs. 5 and 6, and illustrates these differences. In both figures, the left panels are the original datasets, and the middle and right panels show one realization of the extracted “control field” and “science” subsets used for the tests, respectively.
The only caveat regarding these datasets is that, when reddening the stars to pose as science subsets, their magnitudes change, so their associated errors should change accordingly. However, since these are real observations and given the statistical nature of the errors, that adjustment is not possible. In practice, this means that there will be stars at high extinction with an underestimated associated error, but for the effect of our tests this is not critical, since there continues to be no clear dependence of the error with extinction, as is the case in real data subject to extinction.
3.3. Parameters
To test the robustness of the methods, the synthetic datasets were generated using a range of parameters, namely input slopes of the reddening vector, amount of intrinsic scatter, size of the sample, and other specific parameters only relevant to some of the methods.
Input slope.
Each set was generated with seven values of input slope β in the range [ − 1.0,3.0] to cover the range expected for an extinction law in the near- and mid-infrared. The methods were tested under ideal conditions of number of stars and AV coverage to test only the ability of the methods to deal with different values of β. The input slope was varied to guarantee that our conclusions are not only valid for one specific value of β. While varying the remaining parameters the input slope was fixed at 1.8.
Magnitude limit.
The magnitude limit was parameterized by mc. It corresponds to setting a brightness limit in real data, and it was applied identically in J, H and K such that all the synthetic stars fainter than mc in any band after applying the extinction, are discarded from the fit (see rightmost panel in Fig. 4). A magnitude limit is naturally set in real data (detection limit), but is also something one might consider doing artificially to eliminate those stars with the largest photometric errors.
Decreasing mc is equivalent to reducing the size of the sample, both in number and in range of extinction (the stars at high extinction will likely be fainter), while simultaneously reducing the range of errors in Sets 2 and 3 (fainter stars will have larger errors). By construction, a value of mc = 25 corresponds to allowing the largest errors to be 0.3 mag (see Sect. 3.1.2).
Effective number of stars as a function of magnitude cut.
Table 1 shows the average4 number of stars from Set 3 that survive each magnitude cut (effective number of stars,  ) from an initial sample of NS = 5000 synthetic stars. The ratio
) from an initial sample of NS = 5000 synthetic stars. The ratio 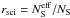 reflects the functional form of the model distributions and, as such, would be the same for any other input number of stars NS for each magnitude cut. The table also shows the average H − K color of the most heavily reddened datapoint attained for each magnitude cut, illustrating the loss in AV coverage with magnitude limitation. The same magnitude cuts were applied to the control field, but because the control field does not have extinction, the effect of the cut in the effective number of stars is much more subtle. The ratio of effective to initial number of stars for the control field is 1.00 for mc ≤ 21 mag, and drops to 0.90 and 0.25 for mc of 19 mag and 17 mag, respectively.
reflects the functional form of the model distributions and, as such, would be the same for any other input number of stars NS for each magnitude cut. The table also shows the average H − K color of the most heavily reddened datapoint attained for each magnitude cut, illustrating the loss in AV coverage with magnitude limitation. The same magnitude cuts were applied to the control field, but because the control field does not have extinction, the effect of the cut in the effective number of stars is much more subtle. The ratio of effective to initial number of stars for the control field is 1.00 for mc ≤ 21 mag, and drops to 0.90 and 0.25 for mc of 19 mag and 17 mag, respectively.
Number of stars.
Generating fewer stars in the first place also changes the size of the sample. The (subtle) difference with respect to implementing magnitude cuts is that the sample with fewer stars and no magnitude cut will most likely have a broader range of AV than would a richer sample with magnitude cut, as some of the fewer stars that are generated and kept may still be faint and heavily extincted from the random drawing process. In real observations, generating fewer stars without imposing magnitude cuts would be comparable to observing a sparse region of the sky where the faint and highly reddened stars can be detected. Imposing a magnitude limit, on the other hand, would correspond to having shallow observations regardless of the richness of the observed field; in this case, the fainter and more reddened stars would not be detected.
We tested the methods against varying number of stars in the range [100,5000] , both in the science and the control field.
Amount of intrinsic scatter.
The amount of intrinsic scatter for Set 3 was parametrized by f, the fraction of stars in the main-sequence locus with respect to those in the giant locus, taking values of 0.01, 0.15 and 0.50. Given the shape of the loci, a larger scatter is obtained for larger values of f, although the giant locus alone still produces some intrinsic scatter. Larger values of f would correspond to a large fraction of the stars behind the cloud being main-sequence in real data, as opposed to having mainly giants. When varying the remaining parameters, f is fixed at 0.15 for Set 3 (f is not a parameter in Sets 1 and 2).
Number of control-field stars.
The synthetic control field is only used for the LinES method, as the other methods rely solely on the science data. Unless explicitly stated, the control field was generated with the same number of stars and was subject to the same magnitude cuts as the synthetic “science” datasets. This means that, after applying a given magnitude cut, there will effectively be more stars in the control field sample than in the science sample, since a fraction of the stars in the science dataset will have been dimmed below the magnitude cut by the effect of extinction. This mimics real observations in that the control field should be obtained from a region of comparable background stellar density (same number of stars generated in the simulations) and using the same instrumental setup (same magnitude cut in the simulations) as the science field. To test the effect of a less than ideal control field, we tested the LinES method against varying numbers of stars also in the control-field datasets.
3.4. Results from synthetic data
Each method was applied to 5000 realizations of the synthetic data, producing an average value  , and a dispersion
, and a dispersion 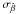 around the average for each parameter within sets 1, 2, and 3. We define bias b as the difference between
around the average for each parameter within sets 1, 2, and 3. We define bias b as the difference between  and the input value of the slope (
and the input value of the slope (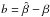 ), and consider a method unbiased if it produces an estimate within the 1-σ dispersion of the input value (i.e.,
), and consider a method unbiased if it produces an estimate within the 1-σ dispersion of the input value (i.e., 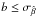 ).
).
We note that the quoted absolute values of the biases are formally only valid for the conditions of these simulations, namely for the magnitude of the error and the functional form of the error distribution with magnitude.
The results are summarized below. Figures 7 through 13 show the bias as a function of varied parameters.
 |
Fig. 7 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the ordinary least squares (OLS) method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
 |
Fig. 8 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the weighed least squares (WLS) method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
3.4.1. Ordinary least-squares
The OLS method has long been known to be biased when there are errors in both coordinates. This was observed also in our simulations (Fig. 7), with the method failing to recover the right value of the slope in the majority of the tests performed. It did provide an unbiased result for the following combinations of input slopes and datasets: β = −0.5 for Set 1, β = −1.0 and β = −0.5 for Set 2, and β = 1.0 for Set 3, making this method unsuitable if one is trying to find precisely β.
This method is also not robust against variations in mc, the bias and the dispersion both increasing for brighter mc in the heteroscedastic sample, except for the brightest magnitude cut considered, where the bias is suddenly reduced. It also reacts, although to a lesser extent, to changes in the amount of intrinsic scatter in the heteroscedastic sample (Set 3), the bias increasing with f.
This method is extremely robust against variations in the number of stars within the same magnitude cut, although the dispersion in the slope increases for fewer stars as would be expected from poor statistics, and the absolute value is biased.
Overall, this method is not a reliable estimator of the extinction law.
3.4.2. Weighed least-squares
The WLS method performs well in homoscedastic or heteroscedastic data without intrinsic scatter (Fig. 8), suggesting that, under these conditions, the method can deal properly with the presence of errors in both coordinates, and with them being correlated. For these samples the dispersion in the slope is remarkably small, making it a very accurate estimator. In the presence of intrinsic scatter, however, the method systematically fails to recover the input slope whatever its value in the range [ − 1.0,3.0] , although it does come close around β = 2.5. The bias as a function of input slope plot for this method and dataset (Fig. 8, blue line) suggests that there could be another unbiased value of β between − 0.5 and 0.5, but tests suggest that there is instead a discontinuity around β = 0.
Although biased for Set 3, this method is robust against variations in the number of stars to within 1.5% in the considered range, but the dispersion increases steadily for fewer stars.
Biased in the presence of even a small intrinsic scatter, this method is not a reliable estimator of the extinction law.
 |
Fig. 9 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the symmetrical methods: the bisector method in the top four panels, the geometric mean method in the middle panels, and the orthogonal regression method in the bottom panels. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
 |
Fig. 10 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the binning in (H − K) method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
 |
Fig. 11 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the binning in AV method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
 |
Fig. 12 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the BCES method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
3.4.3. Symmetrical methods
The three symmetrical methods returned biased results for all tests (Fig. 9), except for input slopes of − 1.0 and 1.0 in datasets 1 and 2 (without intrinsic scatter). The bisector and geometric mean methods produce very similar results. The orthogonal regression method presents the largest biases of the three.
Besides being biased, neither method is robust against variations in mc or f in the presence of intrinsic scatter, the bias increasing for bright magnitude cuts and more intrinsic scatter. The methods are highly robust to variations in the number of stars, the dispersion increasing steadily for fewer stars.
These methods are not reliable estimators of the extinction law.
3.4.4. Binning in (H − K)
This method is biased for most datasets and parameters tested; the exceptions are for Set 3 with the brightest magnitude cut (mc = 17 mag) or for β = 0.5 and 1.0, and for β = −0.5 and no intrinsic scatter (Fig. 10).
The slope in mostly underestimated for all datasets, with the bias increasing for brighter mc for Set 1, and keeping relatively stable against varying mc for Sets 2 and 3. For Set 3 the bias slightly increases with f, as does the dispersion. This method reacts to the number of stars for a given magnitude cut, the bias increasing toward fewer stars. Overall, this is not a reliable estimator of the extinction law.
3.4.5. Binning in Av
This method is formally unbiased for all tested values of β when applied to the three datasets (Fig. 11). However, whereas the bias is always close to zero for the datasets without intrinsic scatter, it becomes slightly large for most values of β when intrinsic scatter is introduced.
The method is robust against variations in the amount of intrinsic scatter within the considered range, and it is stable against variations in magnitude cut, except for the brightest value of mc for Set 3, where the smaller number of stars and range in AV result in very few bins for the fit. The dispersion increases toward brighter magnitude cuts and amount of intrinsic scatter. Because it is based on binning, this method reacts significantly to the number of stars within the same magnitude cut, the bias and the dispersion increasing for fewer stars.
Small variations occur when the size of the bin is varied, with the slope being increasingly overestimated for smaller bins, but the method continues to be unbiased within the dispersion.
This method is a reliable estimator of the extinction law.
3.4.6. BCES method
This method is highly reliable and unbiased for homoscedastic data and for heteroscedastic data without intrinsic scatter (Sets 1 and 2). However, in the presence of intrinsic scatter (Set 3), it becomes biased for all input slope values except for β = 2.1 (Fig. 12) for f = 0.15. Since the other parameters were tested using an input slope of 1.8 (very close to 2.1), the bias seems small in the mc, Nstars and f plots, but we can nevertheless analyze the sensitivity of the method to these parameters. For Set 3, the bias is mildly sensitive to mc, robust against variations in the number of stars, and only minimally sensitive to variations in the amount of intrinsic scatter f.
Since real data will be similar, in essence, to Set 3, we do not consider this method a reliable estimator in the specific case of the extinction law.
 |
Fig. 13 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the LinES method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
3.4.7. LinES
This method is the most unbiased and robust of all presented here for homoscedastic or heteroscedastic data, with or without intrinsic scatter, for all tested values of the input slope (Fig. 13).
The method is robust against variations in mc and f, number of stars in the science field, and number of stars in the control field, although the dispersion follows the same tendency as before: increases for brighter magnitude cuts, slightly increases with f, and decreases with number of science and/or control field stars. The bias is larger when there are simultaneously very few science and control field stars, and small AV coverage, but is nevertheless better than any of the other methods for the same conditions. The dispersion is significantly smaller than the next least unbiased method, the binning in AV, in all cases, granting it more precision.
Since LinES relies on the characterization of the data through the properties of a control field, we tested the stability of the method against variations in the number of stars in the control field. Given a reasonable number of stars in the science field, the method is robust against variations in the number of control field stars. However, if the science field itself does not have enough stars or AV coverage, the bias increases further for few control field stars. Invariably, the dispersion increases toward fewer control field stars. This method has proven to be robust as long as the control field is a good representation of the underlying population on the science field, even if containing a smaller number of stars.
The excellent performance of this method while varying all relevant parameters validates the LinES method for our case study. In general, it will provide accurate results for observations of cores with either rich or poor background populations, regardless of their spread in spectral types, even for relatively shallow observations, as long as there is a reasonable spread in extinction and the control field is a good representation of the reddened, background population.
Limitations.
The simulations show that LinES is not reliable for distributions that do not cover a wide enough range of extinction, if the errors are too large. For reasonable errors, like those described for the simulations, LinES starts overestimating the slope by more than 10% for ranges in x-color (i.e., the color plotted on the x-axis) smaller than 0.25 to 0.45 mag for slopes between 0.6 and 3.0, respectively, and underestimating the slope by more than 10% for the same ranges in x-color for slopes between 0.3 and 0.5. This method should therefore not be applied to data that span less than these values in x-color.
Error estimation.
We used the bootstrap method (e.g., Wall & Jenkins 2003) to estimate the uncertainty in the slope derived by LinES. This method consists in randomly dividing each sample in two equal-number subsets, and measuring the slope of the extinction law in each subset. This produces two values of β from which we derive the standard deviation σβi. This was repeated N = 1000 times and the uncertainty in the slope was defined as: 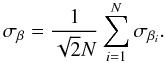 (19)We applied this method on the synthetic data and compared the results with the dispersion
(19)We applied this method on the synthetic data and compared the results with the dispersion 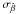 from the simulations. We found that the bootstrap uncertainty is typically 80% of
from the simulations. We found that the bootstrap uncertainty is typically 80% of 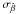 , the dispersion from the synthetic data, and the value we believe is a better estimate of the actual dispersion expected for real data. Given the consistency of the results against the variation of the different parameters, we take the uncertainty on the LinES result of our case study to be 1.25 times the uncertainty derived by the bootstrap method described above.
, the dispersion from the synthetic data, and the value we believe is a better estimate of the actual dispersion expected for real data. Given the consistency of the results against the variation of the different parameters, we take the uncertainty on the LinES result of our case study to be 1.25 times the uncertainty derived by the bootstrap method described above.
 |
Fig. 14 Bias in the slope as a function of the input slope for the bulge (blue line) and disk (red line) datasets, for all the methods tested. The error bars correspond to the 1-σ dispersion of the 5000 realizations. |
 |
Fig. 15 Bias in the slope as a function of the magnitude cut for the bulge (blue line) and disk (red line) datasets, for all the methods tested. The error bars correspond to the 1-σ dispersion of the 5000 realizations. |
3.5. Results from “real” data
Figures 14 and 15 show the bias of each method vs. varying input slope and varying magnitude cut, respectively, for the “real” datasets described in Sect. 3.2. Except for the cases described below, these results follow those from the synthetic data, maintaining the same behavior and changing only the magnitude of the bias. The methods that deserve some further consideration are the binning in AV method, the BCES, and LinES.
The BCES (bottom-middle panel in the figures) applied to these datasets shows the same type of behavior as with the synthetic data against varying magnitude cuts (Fig. 15). The bias is slightly larger than before because there are fewer stars and more dispersion. For varying input slopes, however, the bias is considerably larger, showing that the method is severely biased for some ranges of β when applied to less than ideal data.
The binning in AV method, which we concluded was reasonably unbiased when applied to the synthetic data, shows a severe bias also for some values of the input slope β, in particular for the disk dataset (bottom-left panel in the figures). However, this happens because this dataset has very few stars, and a very limited range in AV (see Fig. 5), which translates into too few AV bins to constrain the extinction vector slope adequately. This presents a limitation of the method, away from which it can be used with relatively good precision.
In the “real” datasets, LinES continues to perform beautifully. Except for the first point in Fig. 15 (bottom-right panel), where the magnitude cut is such that limits the AV to a very narrow range, the bias is consistent with zero for all other magnitude cuts and for all values of the input slope we tested.
4. Detecting a break in the extinction law
Grain growth at high densities has been proposed by a number of studies (see references in Sect. 1). If it does occur, then in dense cores the extinction law will become grayer toward higher extinctions, which should translate into a variation of the slope of the reddening vector with extinction, either smooth or abrupt depending on the nature of the transition between grain sizes. This break was detected and measured in the Trifid Nebula for an extinction of AV = 20 mag by Cambrésy et al. (2011). We used the synthetic and “real” datasets to test whether we could detect such a break in the extinction law using LinES. The data was generated using the exact same method as described above for Set 3 with f = 0.15 and for the “real” dataset (see Sects. 3.1.3, 3.2), but the reddening vector was made flatter at some value of AV, or conversely, at some value of (H − K) color, since the color scales linearly with AV. This produced color–color diagrams similar to that of Fig. 16, where the break is more or less obvious depending on the difference between the two slopes.
For each realization, we divided the sample into low-extinction ((H − K) less than a value (H − K)limit), and high-extinction ((H − K) > (H − K)limit), and determined the best fits to the reddening vector in the two groups using the LinES method, obtaining two slopes  and
and  . This was done for increasing values of (H − K)limit in steps of 0.2, and starting at (H − K)limit = 0.4.
. This was done for increasing values of (H − K)limit in steps of 0.2, and starting at (H − K)limit = 0.4.
Figures 17 and 18 show the behavior of  (black) and
(black) and  (red) as a function of (H − K)limit for the synthetic dataset 3 and the “real” bulge dataset, respectively, when applied to 5000 realizations. The solid lines show the median curves, and the shaded regions represent the 1 − σ scatter from the 5000 realizations. The upper panels are for a single-slope reddening vector with slopes 1.0 (left) and 1.5 (right). The bottom panels show the same distributions but for broken extinction laws, with slopes of 1.5 at low-extinction and 1.0 and high-extinction, and breaks located around AK = 0.4 mag (left) and AK = 1.5 mag (right). For completeness, we find the same results using the disk dataset, albeit with a larger dispersion.
(red) as a function of (H − K)limit for the synthetic dataset 3 and the “real” bulge dataset, respectively, when applied to 5000 realizations. The solid lines show the median curves, and the shaded regions represent the 1 − σ scatter from the 5000 realizations. The upper panels are for a single-slope reddening vector with slopes 1.0 (left) and 1.5 (right). The bottom panels show the same distributions but for broken extinction laws, with slopes of 1.5 at low-extinction and 1.0 and high-extinction, and breaks located around AK = 0.4 mag (left) and AK = 1.5 mag (right). For completeness, we find the same results using the disk dataset, albeit with a larger dispersion.
In the absence of a break, the two curves are indistinguishable except for the lowest and highest values of (H − K)limit; this is because the subsets used for the fits in these two extremes contain too narrow ranges in (H − K) to constrain the LinES method. When a break does exist, however, the two curves separate distinguishably, even if the break is at low extinction. This then provides a simple method to test whether the same extinction law applies to the full AV range of a given dataset, or if it would rather best be described as a two-segment law. Unfortunately this method does not allow for the determination of the actual value of the break, but the figures show that the slope of the extinction vector at high extinction can be determined with reasonable accuracy. In particular, the procedure of measuring the slopes in the low-AV and high-AV regimes provides a much better handle on the extinction law at high extinction (red line in the figures) than measuring the slope of the entire dataset as a whole (blue line in the figures).
5. Summary
We tested several methods of linear regression associated with the problem of measuring the extinction law from photometric data. We found that many of the commonly used methods provide biased results caused by the presence of errors in both coordinates (which are colors), by the fact that they are correlated, and by the presence of scatter intrinsic to the underlying distribution.
We adapted the BCES method of Akritas & Bershady (1996) to allow a compensation for intrinsic scatter, using a control field to characterize the background, unreddened population. We called this method LinES (Linear regression with Errors and Scatter). Using synthetic data, we showed this method provides unbiased and correct results, and that it is robust against the variation of all relevant parameters (at least) within reasonable limits, such as size of sample, range of extinction, and amount of intrinsic scatter.
 |
Fig. 16 Example of a color–color diagram of a synthetic stellar population reddened with a reddening vector with slope 1.5 up to (H − K) ~ 1.0 mag, and with slope 1.0 for higher (H − K). |
 |
Fig. 17
|
 |
Fig. 18
|
We found that dividing any subset in sliding values of AV and measuring the slopes of each subset can robustly differentiate between an extinction law characterized by a single slope and one with a break.
These results can be applied to observations of background stars seen through dense cores of molecular clouds, or through regions that span a reasonable range of dust density. The characterization of the extinction law through deep, photometric data is a very useful tool to probe the properties of the dust grains in these regions, and a “cheap” one when compared with, for example, spectral analysis of many individual sources.
Acknowledgments
We thank C. Róman-Zúñiga for kindly providing the SOFI data, and the referee, L. Cambresy, for helpful comments that contributed to making the paper more robust. J. Ascenso acknowledges financial support from FCT grant number SFRH/BPD/62983/2009. The research leading to these results has received funding from the European Community’s Seventh Framework Programme (/FP7/2007-2013/) under grant agreement No. 229517. Support for this work was also provided by NASA through an award issued by JPL/Caltech, contract 1279166.
References
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Cambrésy, L., Rho, J., Marshall, D. J., & Reach, W. T. 2011, A&A, 527, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapman, N. L., & Mundy, L. G. 2009, ApJ, 699, 1866 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, N. L., Mundy, L. G., Lai, S., & Evans, N. J. 2009, ApJ, 690, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Pipher, J. L., Megeath, S. T., et al. 2007, ApJ, 663, 1069 [CrossRef] [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, T. J., & Hyland, A. R. 1980, MNRAS, 192, 359 [NASA ADS] [Google Scholar]
- Kenyon, S. J., Lada, E. A., & Barsony, M. 1998, AJ, 115, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2006a, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, D. 1999, in The Universe as Seen by ISO, ed. P. Cox, & M. Kessler, ESA SP, 427, 623 [Google Scholar]
- Lutz, D., Feuchtgruber, H., Genzel, R., et al. 1996, A&A, 315, L269 [NASA ADS] [Google Scholar]
- Martin, P. G., & Whittet, D. C. B. 1990, ApJ, 357, 113 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, M. 2009, ApJ, 693, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V. 1993, A&A, 280, 617 [NASA ADS] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Román-Zúñiga, C. G., Lada, C. J., Muench, A., & Alves, J. F. 2007, ApJ, 664, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Seares, F. H. 1944, ApJ, 100, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Steinacker, J., Pagani, L., Bacmann, A., & Guieu, S. 2010, A&A, 511, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trumpler, R. J., & Weaver, H. F. 1953, Statistical astronomy (Berkeley: University of Calfiornia Press) [Google Scholar]
- Wall, J. V., & Jenkins, C. R. 2003, Practical Statistics for Astronomers, ed. J. V. Wall, & C. R. Jenkins [Google Scholar]
- Whittet, D. C. B., Bode, M. F., Longmore, A. J., et al. 1988, MNRAS, 233, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Gerakines, P. A., Hough, J. H., & Shenoy, S. S. 2001, ApJ, 547, 872 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Observed J-band luminosity function of a control field, used as a model distribution for the unreddened J luminosities of the synthetic data. |
| In the text | |
 |
Fig. 2 Log-normal model distribution of extinction AV for a generic cloud. The dotted line corresponds to AV = 2.5 mag, the median extinction of the Pipe Nebula. |
| In the text | |
 |
Fig. 3 Width of the error distribution as a function of magnitude used to generate the “photometric errors”. The insets show the actual error distribution for stars of magnitude 15 (left) and 25 (right). |
| In the text | |
 |
Fig. 4 Example of the generation of synthetic heteroscedastic data without scatter. From left to right: all synthetic stars have the same intrinsic color; they are reddened according to the log-normal distribution of AV; photometric error that depends on magnitude is added; and finally a magnitude cut is implemented, reducing the size of the sample and the coverage in AV. |
| In the text | |
 |
Fig. 5 (J − H) vs. (H − K) color–color diagrams for the disk dataset. Left: all stars in the dataset. Middle: 450 stars chosen randomly from the dataset, representing the “control field”. Right: 450 stars chosen randomly from the dataset, and reddened to represent the “science field”. |
| In the text | |
 |
Fig. 6 (J − H) vs. (H − K) color–color diagrams for the bulge dataset. Left: all stars in the dataset. Middle: 800 stars chosen randomly from the dataset, representing the “control field”. Right: 800 stars chosen randomly from the dataset, and reddened to represent the “science field”. |
| In the text | |
 |
Fig. 7 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the ordinary least squares (OLS) method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
| In the text | |
 |
Fig. 8 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the weighed least squares (WLS) method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
| In the text | |
 |
Fig. 9 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the symmetrical methods: the bisector method in the top four panels, the geometric mean method in the middle panels, and the orthogonal regression method in the bottom panels. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
| In the text | |
 |
Fig. 10 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the binning in (H − K) method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
| In the text | |
 |
Fig. 11 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the binning in AV method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
| In the text | |
 |
Fig. 12 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the BCES method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
| In the text | |
 |
Fig. 13 From left to right, bias in the slope as a function of the magnitude cut, input slope, number of stars in the science field, and intrinsic scatter for the LinES method. The black, red and blue lines represent the results for the 5000 realizations of Sets 1, 2 and 3, respectively. The error bars correspond to the 1-σ dispersion in the results. |
| In the text | |
 |
Fig. 14 Bias in the slope as a function of the input slope for the bulge (blue line) and disk (red line) datasets, for all the methods tested. The error bars correspond to the 1-σ dispersion of the 5000 realizations. |
| In the text | |
 |
Fig. 15 Bias in the slope as a function of the magnitude cut for the bulge (blue line) and disk (red line) datasets, for all the methods tested. The error bars correspond to the 1-σ dispersion of the 5000 realizations. |
| In the text | |
 |
Fig. 16 Example of a color–color diagram of a synthetic stellar population reddened with a reddening vector with slope 1.5 up to (H − K) ~ 1.0 mag, and with slope 1.0 for higher (H − K). |
| In the text | |
 |
Fig. 17
|
| In the text | |
 |
Fig. 18
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


