| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 9 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201117534 | |
| Published online | 16 March 2012 | |
The Quintuplet cluster
III. Hertzsprung-Russell diagram and cluster age
1 Max-Planck Institut für Radioastronomie, 53121 Bonn, Germany
e-mail: liermann@mpifr-bonn.mpg.de
2 Universität Potsdam, Institut für Physik und Astronomie, 14476 Potsdam, Germany
Received: 21 June 2011
Accepted: 2 February 2012
The Quintuplet, one of three massive stellar clusters in the Galactic center (GC), is located about 30 pc in projection from Sagittarius A∗. We aim at the construction of the Hertzsprung-Russell diagram (HRD) of the cluster to study its evolution and to constrain its star-formation history. For this purpose we use the most complete spectral catalog of the Quintuplet stars. Based on the K-band spectra we determine stellar temperatures and luminosities for all stars in the catalog under the assumption of a uniform reddening towards the cluster. We find two groups in the resulting HRD: early-type OB stars and late-type KM stars, well separated from each other. By comparison with Geneva stellar evolution models we derive initial masses exceeding 8 M⊙ for the OB stars. In the HRD these stars are located along an isochrone corresponding to an age of about 4 Myr. This confirms previous considerations, where a similar age estimate was based on the presence of evolved Wolf-Rayet stars in the cluster. We derive number ratios for the various spectral subtype groups (e.g. NWR/NO, NWC/NWN) and compare them with predictions of population synthesis models. We find that an instantaneous burst of star formation at about 3.3 to 3.6 Myr ago is the most likely scenario to form the Quintuplet cluster. Furthermore, we apply a mass-luminosity relation to construct the initial mass function (IMF) of the cluster. We find indications for a slightly top-heavy IMF. The late-type stars in the LHO catalog are red giant branch (RGB) stars or red supergiants (RSGs) according to their spectral signatures. Under the assumption that they are located at about the distance of the Galactic center we can derive their luminosities. The comparison with stellar evolution models reveals that the initial masses of these stars are lower than 15 M⊙ implying that they needed about 15 Myr (RSG) or even more than 30 Myr (RGB) to evolve into their present stage. It might be suspected that these late-type stars do not physically belong to the Quintuplet cluster. Indeed, most of them disqualify as cluster members because their radial velocities differ too much from the cluster average. Nevertheless, five of the brightest RGB/RSG stars from the LHO catalog share the mean radial velocity of the Quintuplet, and thus remain highly suspect for being gravitationally bound members. If so, this would challenge the cluster formation and evolution scenario.
Key words: stars: late-type / Hertzsprung-Russell and C-M diagrams / infrared: stars / stars: early-type / open cluster and associations: individual: Quintuplet
© ESO, 2012
1. Introduction
Stellar clusters are unique objects to study stellar populations and their evolution, as they are supposed to represent a single coeval stellar population. The Quintuplet cluster is one of the massive young stellar clusters in the Galactic center region. Located at about 30 pc projected distance from the Galactic Center, its age has been estimated to be about 4 Myr (Figer et al. 1999a) from the evolved massive stars in their Wolf-Rayet (WR) phase, i.e. stars displaying CNO-processed (WN stars) or helium burning products (WC stars) in their spectra. The WN stars were analyzed in detail by Liermann et al. (2010) who found from comparison with stellar evolution models ages of about 3 Myr that agree quite well with the previously assumed cluster age.
Despite the young cluster age, Glass et al. (1990) reported the presence of one red supergiant (RSG) in the cluster. A few other Galactic clusters are known to show the coexistence of evolved stars like WR stars and RSGs, e.g. Westerlund 1 (Crowther et al. 2006), but it seems quite puzzling for a young cluster like the Quintuplet. Liermann et al. (2009) presented the so far most complete spectral catalog of the Quintuplet stars. From this catalog the Hertzsprung-Russell diagram (HRD) can be constructed, and the results can be compared to stellar evolution models and isochrones. This will allow to put more stringent constrains on the age of the Quintuplet cluster. The comparison of number ratios with population synthesis models will help to confine the cluster age further and allows a statement about the formation history to be made. Especially, the apparent existence of RSGs in the cluster needs to be addressed.
The paper is organized as follows. In Sect. 2 we introduce the spectra and the sample of stars, Sect. 3 explains the methods to derive a cluster HRD. Finally, the results are discussed in the context of stellar and cluster evolution in Sect. 4.
2. Observations
The analysis in this paper is based on observations of the Quintuplet cluster with the ESO Very Large Telescope’s integral-field spectrograph SINFONI, that cover K-band spectra with a resolution of about R ≈ 4000, complete to a photometric magnitude of about Ks = 13 mag. The data were published in a catalog by Liermann et al. (2009, hereafter LHO catalog), listing 85 early-type and 62 late-type stars with their spectral classification and individual radial velocity (RV). A field of view of about 40′′ × 40 ′′ is covered in total. Please refer to the LHO catalog for more detailed information about observational strategy and data reduction.
3. Analysis
3.1. Sample stars
The LHO catalog gives a mean cluster radial velocity of RV = 113 ± 37 km s-1 and a first approximation for the velocity dispersion σ = 17 km s-1 within the Quintuplet cluster, under the assumption of a virialized cluster. The cluster membership was rejected for stars with a radial velocity that differs from the cluster mean by more than 3σ ( ± 51 km s-1). However, field stars in the vicinity of the Quintuplet may participate in a similar Galactocentric rotation and thus show a similar RV, albeit not being bound to the cluster. Moreover, RVs can be affected by the orbital motion for stars in close binary systems. In these cases the periodic variation of the RVs can only be detected from time series of spectra, which are not (yet) available for the Quintuplet stars.
 |
Fig. 1 Histogram of the distribution of RVs of all LHO stars (light gray). Overplotted is the distribution for the late-type KM stars (dark/red). Solid and dashed lines indicate the cluster RV of 113 km s-1 and the 1σ and 3σ intervals, respectively. |
The number distributions of the radial velocities of the late-type and early-type stars are shown in Figs. 1 and 2. While we find a very pronounced peak in the distribution for the early-type stars in the RV range assumed to indicate cluster membership, the late-type KM stars seem to be distributed more homogeneously with a somewhat lower peak within the 3σ interval around the mean cluster RV. To estimate the number of stars, late-type stars in particular, along a line-of-sight towards the Galactic center, we would need to observe control fields around the Quintuplet. The lack of those requires a more careful interpretation of Fig. 1: from the rather flat distribution, we could assume a median number of five stars per velocity bin to possibly be field stars.
Additionally, the question of foreground stars has to be regarded under the aspect that the high visual extinction towards the Galactic center is overcome in the near-IR range. This in return makes it more difficult to distinguish between foreground and background objects relative to the cluster. As can be seen from Fig. 3 there is no clear distinction in magnitude between bright foreground or faint background objects, but a wide distribution of the K-band magnitudes over the RV range. The photometric completeness of the LHO catalog at Ks = 13 mag hardly alters the distribution.
We set the following criteria to assess the possible cluster membership: stars within the 1σ interval of the cluster RV and brighter than the photometric completeness limit, i.e. Ks < 13 mag, will be considered as very likely cluster members. We will refer to this sample of stars as the corrected sample in the following in comparison to the complete LHO sample1.
3.2. Stellar luminosities and the HRD
The HRD is a useful tool to characterize a stellar cluster; to establish it we need to know the effective temperatures and stellar luminosities for the Quintuplet stars.
 |
Fig. 2 Same as Fig. 1, but overplotted with the RV distribution of early-type OB stars (dark/blue). Both distributions peak within the intervals assumed for cluster membership, albeit more pronounced for the early-type stars. |
 |
Fig. 3 Distribution of Ks magnitudes over radial velocity for all stars in the LHO catalog (circles for early-type stars, triangles for late types). The completeness limit at Ks = 13 mag is indicated by the horizontal line, while the vertical lines refer to the different RV intervals as in Fig. 1. |
The effective temperature is defined via the Stefan-Boltzmann law, and thus follow from the stellar luminosity and radius. This reference radius is a matter of definition. Usually one refers the stellar radius to a Rosseland optical depth of 2/3. In stars with a well defined photosphere the precise definition does not matter. In WR atmospheres, however, τ = 2/3 is often reached already in moving layers, i.e. in the wind. Therefore it became standard to define the “stellar radius” R∗ of WR stars at a Rosseland optical depth of 20. In most models, this point lies at subsonic velocities, i.e. in nearly hydrostatic layers. The effective temperature related to R∗ is termed the “stellar temperature” T∗, and this value is quoted for the WN stars as the result from the spectral analyses from Liermann et al. (2010).
The motivation for using the radius of the hydrostatic part is the hope that R∗ can be identified with the stellar radius from stellar evolution models. However, our empirical R∗ is in fact based on an inward extrapolation of the stellar wind’s velocity law into optically thick, i.e. un-observable layers. In the case of our Quintuplet WN stars, this is not critical because R∗ is only slightly smaller than the radius where τ = 2/3 – only in very thick WR winds, the difference becomes significant. Nevertheless, there is evidence that most WR stars have very extended subphotospheric layers which make R∗ much bigger (and thus T∗ much lower) than current models of the stellar structure predict.
For the WC stars in the Quintuplet the analysis is in progress. All of them are classified as WC8-9 and their majority produces dust (van der Hucht 2006, Liermann et al. 2009). This dust production is considered to arise from colliding winds in high-mass binaries, as has been confirmed already for some of the Quintuplet WC stars by Tuthill et al. (2006, “pinwheel stars”). Therefore, the WC stars will be excluded from the present considerations of the cluster HRD, as they need to be analyzed and discussed with respect to the special scenarios of binary evolution.
For the late-type KM stars, we determine the effective temperatures (Teff) according to their spectral classification in the LHO catalog. Those were based on the equivalent widths measured from the first overtone CO absorption band at 2.3 μm (see González-Fernández et al. 2008). The Teff are then applied to obtain the bolometric correction for the K-band magnitude, BCK, adopting the relation 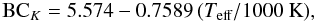 (1)derived by Levesque et al. (2005) for red supergiants. We apply the same relation for our red giant branch stars (RGBs) as well, thus neglecting effects of the luminosity class on the spectral energy distribution.
(1)derived by Levesque et al. (2005) for red supergiants. We apply the same relation for our red giant branch stars (RGBs) as well, thus neglecting effects of the luminosity class on the spectral energy distribution.
The effective temperatures for the early-type OB type stars were determined from their spectral (sub-)types according to the spectral-type-temperature calibration of Martins et al. (2005, Tables 2, 3, 5, and 6) and applied for their bolometric corrections 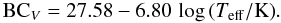 (2)These BCs are valid only for the visual spectral range as indicated by the index and a correcting term for the K-band BCs is necessary. From a previous model analysis of O stars (Oskinova et al. 2006) we can estimate an average MV − MK = ( − 0.98 ± 0.04) mag for their sample stars. That sample contained spectral types O3 to O7 with luminosity classes I to V, therefore the term is considered to be robust and applicable for the correction BCK = BCV − (MV − MK).
(2)These BCs are valid only for the visual spectral range as indicated by the index and a correcting term for the K-band BCs is necessary. From a previous model analysis of O stars (Oskinova et al. 2006) we can estimate an average MV − MK = ( − 0.98 ± 0.04) mag for their sample stars. That sample contained spectral types O3 to O7 with luminosity classes I to V, therefore the term is considered to be robust and applicable for the correction BCK = BCV − (MV − MK).
Absolute stellar magnitudes MK were derived from the Ks given in the LHO catalog with the mean cluster extinction AK = 3.1 ± 0.5 mag derived from the analyses of the WN stars (Liermann et al. 2010) together with the corresponding BCs. For the cluster distance we adopt the distance to the GC of 8 kpc (Reid 1993).
The absolute magnitudes are transformed to stellar luminosities 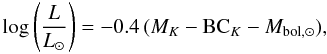 (3)with Mbol, ⊙ = 4.74 mag for the bolometric luminosity of the Sun. The resulting HRD of the Quintuplet cluster is shown in Fig. 4.
(3)with Mbol, ⊙ = 4.74 mag for the bolometric luminosity of the Sun. The resulting HRD of the Quintuplet cluster is shown in Fig. 4.
 |
Fig. 4 Hertzsprung-Russell diagram of the Quintuplet. Circles (blue) represent the early-type OB stars, triangles (red) the late-type KM stars, filled symbols refer to stars of the corrected sample (see text). The ZAMS and stellar evolution tracks with rotation (solid lines) and without rotation (dashed lines) for different initial masses are from Meynet & Maeder (2003). |
The errors on the temperature and luminosity of the WN stars are taken from Liermann et al. (2010).
For the late-type KM stars, the error on Teff is of the order of 200 K (González-Fernández et al. 2008). For those stars the error bars vanish within the stars’ symbol sizes.
For the early-type OB stars the error on Teff reflects the range in the spectral classification in the LHO catalog as an upper and lower temperature according to the spectral-type-temperature calibration. This error is usually quite large and could be minimized by tailored modeling of the individual stars, which is out of scope for the work presented here.
For both late- and early-type stars we estimate the error on the luminosity from the combined errors of the K-band magnitude, extinction, and bolometric corrections. The error is dominated by the error of the mean cluster extinction determined from the WN star analysis (0.5 mag). The error on the K-band magnitudes from the LHO catalog is given with 0.2 mag. For the BCs Levesque et al. (2005) list an error of 0.01 mag for late-type stars and Martins et al. (2005) give 0.05 mag for early-type stars. We had to correct the BCs for the early-type stars from the visual to the K-band with a correcting term for with we estimate an error of 0.04 mag (see above). In total, the combined error on the luminosity amounts to about 0.3 dex for both the late- and early-type stars.
4. Discussion
4.1. Stellar evolution and cluster age
As can be clearly seen from Fig. 4, two distinct groups are found in the HRD. The OB stars are located more or less along a main sequence, while the KM stars line up in the low-temperature regime with Teff < 5000 K over an extended luminosity range. It seems that a number of OB stars are found to the left of the zero-age main sequence (ZAMS). On one hand, this can be attributed to the rather large error bars in temperature, i.e. uncertainty of the star’s spectral type, and luminosity. However, it might also reflect the fact that the assumed homogeneous reddening towards the cluster is not correct. And with the presence of dusty WC stars an additional intrinsic reddening might have to be considered for the different regions of the cluster.
Stellar evolution tracks including the effects of rotation (solid lines) and without rotation (dashed lines) for initial masses of 9, 15, 25 and 60 M⊙ (Meynet & Maeder 2003) show that the OB stars are massive stars in the classical definition, i.e. Minit > 8 M⊙. We omit the tracks for higher masses as they overlap with the track for 60 M⊙ in case of the 85 M⊙ track or don’t extend into the cooler temperature range in case of the 120 M⊙ track. The difference in stellar evolution between models with rotation and without is stronger from 25 M⊙ upwards, i.e. the high-mass stars potentially evolving to WR stars, and is less important for the majority of stars in the current sample.
 |
Fig. 5 Same as Fig. 4 but with theoretical isochrones for different cluster ages. The isochrones, shown with alternating line styles, were constructed by Lejeune & Schaerer (2001). The majority of the population of OB stars in the Quintuplet follows the 4 Myr isochrone, while most KM stars would need more than 30 Myr to evolve. |
 |
Fig. 6 Same as Fig. 5 but with theoretical isochrones based on Girardi et al. (2002). Again, the majority of OB stars falls on the 4 Myr isochrone, while most KM stars evolve on timescales with more than 30 Myr. |
Number ratios for the Quintuplet stars in comparison to other Galactic center clusters.
Concerning their position in the HRD below the 9 M⊙ track and off the main sequence, the late-type KM stars would have to be considered evolved low- and intermediate stars. This is confirmed by the presence of 13CO absorption in their spectra which led to the classification as (super-) giants (LHO catalog). However, a few late-type stars extend to the regime of massive stars touching the 9 to 15 M⊙ tracks. Their potential status as red supergiant (RSG) will be discussed separately (see below).
In Fig. 5 the HRD with isochrones compiled by Lejeune & Schaerer (2001, based on Geneva stellar evolution models) is shown for different cluster ages. For comparison we show the isochrones from Girardi et al. (2002, “Padova isochrones” in the following) in Fig. 6. In both cases, the assumed cluster main sequence of OB stars corresponds well with the 4 Myr isochrone with the 3 and 5 Myr isochrone forming an “age envelope”.
In case of the WN stars, two stars (WR 102d and WR 102i) seem to follow the Geneva 2 Myr isochrone, while the 2 Myr isochrone from Padova is below any WN star position (Fig. 6). In addition, both of these isochrones don’t extend far enough into the cooler region of the HRD to cover all WN stars. Interestingly, the Padova isochrones for 3, 4 and 5 Myr loop backwards in the hotter region of the HRD, and especially the 3 Myr isochrone corresponds very well to the position of all the evolved WN stars. A detailed comparison of the WN stellar parameters with the Geneva stellar evolution models (Meynet & Maeder 2003) revealed ages of about 2.1 to 3.6 Myr for the Quintuplet WN stars (Liermann et al. 2010, 2011); an age of 3 Myr seems to be confirmed by the Padova isochrone. The presence of WC stars in the Quintuplet cluster speaks neither in favor of a much older nor a younger cluster age, since they may originate from binary evolution as explained above.
The same argument holds for the luminous blue variables (LBVs) in the Quintuplet, the Pistol star and qF 362. From high-mass single star evolution the LBV phase can be estimated to start at about 4 Myr, which was also used as age criterion for the Quintuplet (Figer et al. 1999a, Geballe et al. 2000). However, recent interferometric studies indicate that the Pistol star, just like the LBV prototype η Car, might be a binary and thus evolved through the binary channel (Martayan et al. 2011).
A similar spread in age between O stars and WR stars was reported by Martins et al. (2008) for the Arches cluster. They found ages of 2 to 3 Myr for the most luminous WN stars, while the O stars cover a range of 2 to 4 Myr. They conclude that this might be due to the fact that the most massive stars have formed last in the cluster, to prevent their feedback on the ongoing star formation. In the end they determine a cluster age of 2.5 ± 0.5 Myr. Similar arguments can be applied for the difference in age of the OB and WN stars in the Quintuplet. Thus we conclude that a cluster age of 3.5 ± 0.5 Myr is likely.
Both sets of isochrones suggest that the KM stars, if they were cluster members, would need about 15 Myr to evolve to RSGs for Mini > 9 M⊙ and more than 30 Myr for Mini < 9 M⊙ to become red giants, respectively. The detected 13CO gives spectroscopic evidence that these stars are evolved giants or supergiants (Liermann et al. 2009). It appears that for the majority of these stars it might not be justified to assume that they are located at a distance of 8 kpc. They can be foreground objects and/or physically unrelated to the Quintuplet cluster. This conclusion seems to be supported by the radial velocities of most of these stars which are off the limits of the corrected sample for the cluster. However, we are left with a group of eight evolved KM stars that might be physical members of the Quintuplet (see below).
A priori the coexistence of RSGs, main sequence OB stars, and WR stars is not expected under the assumption of a coeval evolution. However, Hunter et al. (2000) discuss the possibility of an extended star formation event lasting over a few million years, which could explain the simultaneous presence of WR stars and RSGs. We find an age range of about 4 Myr (OB stars) to 15 to 30 Myr (KM stars) for the two populations. Could such a spread in age be called an “extended” star formation event? Or is it more likely that one star formation event was responsible for the WR and OB stars while the evolved KM stars might represent an older population that is unrelated to the cluster?
4.2. Number ratios and the binary effect
In Table 1 we list stellar number ratios for some prominent clusters and the Milky Way in total. These numbers are only approximates. The ratios can suffer from systematic observational errors, incomplete samples used in the different references, or from unknown/unconfirmed binary stars in the samples. For example, among the general results of van der Hucht (2001) for the Galactic WR star population, they give a NWC/NWN ratio of 1.5 and a binary frequency for the WR stars of 39%. These numbers are based on a stellar subsample limited to WR stars within 2.5 kpc; presumably a complete sample. On the other hand, their total catalog numbers would result in a different NWC/NWN ratio of 0.7, which might lead to biased estimates of the WR subclasses. Hamann et al. (2006) selected only putatevely single stars from the WR star catalog (van der Hucht 2001) for their study of the ratio between different spectral subclasses. The binarity status of invidual objects may have been revised in the meantime, and thus affect the number ratios.
For the Arches and the Central Parsec cluster the situation is similar, depending on the study, their field of view or the available stellar subsample, the numbers in the different columns of Table 1 may differ from those listed in van der Hucht (2006).
With these uncertainties in mind, we compare the number ratios NWR/NO and NWC/NWN with the predictions of population synthesis models as presented in the figures by Leitherer et al. (1999), Vázquez & Leitherer (2005, starburst. The models account for solar metallicity and single star evolution. From Leitherer et al. (1999, Figs. 39 to 42), we find lower limits for the age of the Quintuplet cluster of 3.3 to 3.6 Myr in the scenario of instantaneous burst star formation. This agrees very well with the above HRD and isochrones. Although we cannot exclude a past supernova in the Quintuplet, the determined age would also be conform with the predictions of Leitherer et al. (1999, Fig. 43) in terms of first supernovae taking place only at about 3.5 Myr in the star burst scenarios.
One issue with the Quintuplet stellar population is obvious: All WN-type stars in the Quintuplet have been classified as WNL, i. e. they still contain hydrogen in their atmosphere (Liermann et al. 2009, 2010). WNE stars (hydrogen-free WN stars) are significantly missing, although the number ratio NWC/NWR is compatible with the value found by van der Hucht (2001) for the Milky Way. From the regular Milky Way WR population we would expect a slightly higher number of WNE stars than WNL stars (Hamann et al. 2006). WR 102c, which lies outside the LHO field of view in the Sickle nebula, was classified by Figer et al. (1999a) as WN6 type star and thus belongs to an “early” subtype (WNE). But Barniske et al. (2008) found from comparison with model spectra that the stellar atmosphere still contains up to 20% hydrogen, making it a “WNL” star in the evolutionary sense. Interestingly, WNE stars seem to be missing in the other clusters in the Galactic center region as well (see Liermann et al. 2010,and Table 1). From the Geneva models we know that hydrogen burning lifetimes and WNL lifetimes are increased when the effects of rotation are included, while WNE lifetimes are hardly affected. This might skew the number ratios in favor of WNL stars. Liermann et al. (2010) noticed that evolutionary models without rotation represent the Quintuplet WNL stars better than those with rotation. This might imply that the initial rotational velocity of 300 km s-1 in the models is too much. Or, as pointed out by Vanbeveren et al. (2007), the mismatch between evolution tracks and observations for massive stars may be due to inappropriate assumptions of the mass loss in the RSG stage.
So far we have only considered single star evolution, but what about binaries? The most promising indications for binarity seem to be present among the WR stars, so we will focus on those in the following. In the Milky Way about a quarter of all WN stars and half of all WC stars are in binaries (van der Hucht 2001, see also Table 1). As noted by several authors (e.g. van der Hucht 2006, Crowther et al. 2006, Liermann et al. 2009), K-band spectra that show an increasing continuum with wavelength (IR excess) can be interpreted as being colliding wind binaries in which dust is formed (Williams et al. 1987). The majority of WC stars in current catalogs and surveys are binary candidates on this “dust” argument alone.
With no time series of spectral observations available, the LHO spectra allow only indirect conclusions about binarity to be drawn. Among the WC stars in the Quintuplet are nine stars classified as WCd, i.e. dust producing colliding wind binary candidates. Five of those, the enigmatic Quintuplet pinwheels, can be considered confirmed binaries as they were partially or fully spatially resolved by interferometry by Tuthill et al. (2006). Two further WC stars, LHO 76 and 79, have been classified in the LHO catalog as potential binaries on the basis of a “dusty” spectrum. So, the number of WC binaries might even be higher.
Among five WN stars in the LHO catalog, we find only one binary candidate: LHO 110. Liermann et al. (2010) found small absorption lines in the spectrum which might belong to an O-type companion. This is corroborated by its high measured radio flux. One further WC and one WN star are listed by van der Hucht (2006) as binary candidate. But for these, WR 102f (WC8+?) and WR 102i (WN9+?), the LHO spectra look unsuspicious, which is why the classification as binary candidates was dropped. The number of unconfirmed binaries makes it difficult to compare the binary fraction with other Galactic center clusters and the Milky Way (see Table 1). But it seems that the binary fraction of the Quintuplet WN and WC stars resembles roughly the one for the Milky Way in general.
Vanbeveren et al. (1998) argue that taking binaries into account is required to get correct NWR/NO and NWC/NWN ratios. Their population synthesis suggests that, especially for the inner Milky Way, a NWR/NO ratio of the order of 0.2, a value similar to the one found for the Quintuplet, cannot be explained with a continuous star formation scenario. It could rather be explained with an enhanced star formation or star burst. In addition, according to those models a star burst that includes binaries encounters the effect of rejuvenation, i.e. mass transfer which takes place in massive close binaries leads to a population of young O-type stars mimicking a much younger age. This is supposed to happen after about 4 Myr, and would manifest in a group of blue young stars above the main sequence turn-off of the main population. We don’t see a prominent group of such O-type stars in the HRD of the Quintuplet, which eliminates a cluster age of ≥ 6 Myr according to Vanbeveren et al. (1998, Fig. 11B). Given the error bars in our empirical Teff and log L (Fig. 4), and comparing this to the spread in Vanbeveren et al. (1998, Fig. 11A), we can furthermore limit the cluster age to ≤ 4 Myr. This is within the range we estimate from the main sequence of OB and WR stars and the isochrones.
From the good agreement with the overall numbers ratios (van der Hucht 2001) and the age limits inferred from single and/or binary star evolution (Vanbeveren et al. 1998; Leitherer et al. 1999) it seems secure to conclude that the formation of the Quintuplet cluster most likely needed a star burst event about 3.5 ± 0.5 Myr ago.
4.3. Late-type stars in the Quintuplet?
According to Vanbeveren et al. (1998) almost one third of all Galactic open cluster and stellar aggregates host WR stars and RSGs simultaneously. In the majority of them the total numbers are rather small, of the order of one or two, and in all cases the number of WR stars exceeds those of RSGs.
In terms of abundance of these special stars, Westerlund 1 (Wd 1) is the most prominent Galactic open cluster known to simultaneously contain evolved early-type stars, such as luminous blue variables (LBVs), yellow hypergiants (YHGs), WR stars, and RSGs. Based on single star evolution, Crowther et al. (2006) concluded from an number ratio of NRSG + YHG/NWR = 8:24 a cluster age of 4.5–5 Myr for Wd 1. Mengel & Tacconi-Garman (2007) list four RSGs plus six YHGs found by Clark et al. (2005) which changes the number ratio slightly (see Table 1). Vanbeveren et al. (1998) argue on basis of single star lifetimes that WRs and RSGs can be present simultaneously only in a very limited time span of 4 to 5 Myr. Too early no RSG would be present and too late the WR stars would be already gone.
We already noted that in the Geneva models with rotation the WNL lifetime is increased. In addition, Hirschi et al. (2004) found that in the rotating models the RSG phase could be reached even before helium ignites in the stars, much earlier than in non-rotating models, and that the RSGs become more luminous. Similar effects were found for the WNL stars. Both WNL and RSGs can appear spectra-wise as evolved stars, while they are still core-hydrogen burning. This might twist the number ratios towards more WNL than WNE stars plus the simultaneous presence of RSGs even at young cluster ages.
For the Quintuplet cluster, eight late-type stars in the regime of log (L/L⊙) > 3.4 are found (see Fig. 7). Including stellar evolution tracks from Bressan et al. (1993), most stars below log (L/L⊙) < 4 could also be regarded as intermediate-mass stars (tracks with Mini ≈ 6 to 7 M⊙). However, only five out of eight of these stars are from the corrected sample of late-type stars, i.e. potential cluster members, due to their RV. This would result in a number ratio NRSG + YHG/NWR of 5:21 similar as for Wd 1 (see Table 1) and could imply that the Quintuplet cluster is slightly older than just 4 Myr.
The stars LHO 006, LHO 036, LHO 053, and LHO 063 have not yet been studied in detail. The remaining stars are discussed individually in the following:
 |
Fig. 7 Detail of Fig. 4 with focus on the late-type stars with log (L/L⊙) > 3.4 that might be Quintuplet RSG candidates. Tracks show stellar evolution models from Meynet & Maeder (2003) with and without rotation (solid and dashed lines, respectively) and from Bressan et al. (1993, solid line with circles for Mini = 6 and 7 M⊙. |
LHO 007
– alias GMM 7 (Q 7), qF 192. Glass et al. (1990) mentioned this prominent and bright source as a late-type star in the Quintuplet region. Moneti et al. (1994) found the star to be an M-type supergiant with K = 7.36 mag, and Glass et al. (1999b) consider the star to be not variable. The stellar parameters from a detailed study by Blum et al. (2003) are compared with our results in Table 2. Similar K-band magnitudes but slightly different effective temperatures put the star at the highest luminosity within our group of late-type stars. A number of studies also focused on the chemical composition of the star (e.g. Ramírez et al. 2003, Cunha et al. 2007, Davies et al. 2009), finding iron abundances to be nearly consistent with solar values but slightly enhanced α elements. Most authors agree that LHO 007 is an evolved star with an initial mass likely between 15 and 20 M⊙ depending on the stellar evolution model. From our results we find that all stellar evolution models (with and without rotation, from Geneva and Padova) imply an initial mass of 15 M⊙ (Fig. 7). The star’s membership to the Quintuplet cluster was debated in terms of extinction issues (Glass et al. 1990, Moneti et al. 1994, Glass et al. 1999b). According to its RV = 124 km s-1 it may belong to the Quintuplet cluster.
Comparison of stellar parameters for LHO 007.
LHO 108
– alias [NWS90] A, [GMC99] D 322, qF 269. This star is considered to be a foreground star by Nagata et al. (1990). In contrast, Glass et al. (1999b) list the star in the group of probable cluster members. Its RV = 127 km s-1 puts it in our corrected sample. Figer et al. (1999a) list the star in their Quintuplet sample, with a spectral classification as OBI and a luminosity of log (L/L⊙) = 5.54. But the LHO spectrum definitely shows CO bands classifying it as late-type star (see LHO catalog spectra). Thus we derive a much smaller luminosity of log (L/L⊙) = 3.51. It places the star at the lower end of the group in vicinity to the non-rotating 9 M⊙ track from Geneva or the 6 to 7 M⊙ tracks from Padova (see Fig. 7).
LHO 115
– alias GMM 5 (Q 5), MGM 5-5, qF 270N. This star is one of the five from which the Quintuplet cluster derived its name. Its K-band magnitude is 8.71 mag (Glass et al. 1990). Later works give a range of values: K = 9.1 mag (Moneti et al. 1992), K = 8.78 mag (Moneti et al. 1994), K = 7.81 mag (Figer et al. 1999a, spectral type “late”). Glass et al. (1999b) list the star in their sample of long-period variables in the Quintuplet with an average K = 8.62 mag and a 680 d photometric variability of 1.5 mag. They attribute the variability to the star being a Mira variable and argue on basis of stellar evolution that the star would then be too old to be a Quintuplet member. However, according to its photometric colors (Moneti et al. 1994) and its apparent magnitude being in the range expected for Miras in the GC region (Glass et al. 1999a), the cluster membership might still be likely.
From our K = 8.6 mag we derive a luminosity of log (L/L⊙) = 4.38, which makes the star the second most luminous in this group of RSG candidates. Its position in the HRD (Fig. 7) puts it at the stellar evolution track for a star with an initial mass of 9 M⊙. With the RV = 137 km s-1 it dropped out of the corrected sample, but still is within the 3σ interval of possible cluster membership.
LHO 156
– alias [GMC99] D 307. Glass et al. (1999b) list this star with K = 10.83 mag in the sample of probable Quintuplet members and show a slightly variable light curve. However, no firm conclusion about a possible variability is drawn. We find K = 10.4 mag in the LHO catalog. It’s derived luminosity log (L/L⊙) = 3.72 puts it on the non-rotating 9 M⊙ track from Geneva or the tracks from Padua with 6 to 7 M⊙ initial mass. However, with RV = 169 km s-1 the star is outside the limits for the corrected sample and even outside of the 3σ cluster RV.
Summarizing, there are a few KM stars in the Quintuplet field which share the radial velocity of the cluster. One of them, LHO 007 alias Q 7, has supergiant luminosity. Other ones are red-giant branch stars, assuming Galactic center distance. One can exclude that they are foreground KM dwarfs, because of their radial velocity and because of the 13CO signature in their spectra that is indicative for giants and supergiants. It would be very puzzling if these relatively old (>30 Myr) stars would be gravitationally bound to the Quintuplet cluster. Otherwise, they may belong to an old field population in the Galactic center region.
It seems that the assessment of the cluster membership, e.g. from proper motion studies (Hußmann et al. 2011), is needed to settle the question if older stars belong to the Quintuplet. As discussed in the previous section, binary evolution (Vanbeveren et al. 1998) and stellar evolution with rotation (Hirschi et al. 2004) may explain the coexistence of RSG and WR stars in a cluster of about 4 Myr, as the likely age of the Quintuplet. Alternatively, if none of these scenarios works, the conclusion would become inevitable that the cluster contains a second, older population of stars.
 |
Fig. 8 Luminosity function of the Quintuplet cluster for all stars in the LHO catalog (dashed line) and for the corrected sample (solid line). The photometric completeness at Ks = 13 mag is indicated by the vertical dashed line. The linear fits to both distributions are indicated by the slope coefficient α. |
4.4. Luminosity function and mass function
To further exploit the LHO data of the Quintuplet cluster, we establish the luminosity function by counting the number of stars per magnitude bin in our total cluster field of view; in addition we apply a normalization factor to account for the cluster area. The resulting distribution is shown in Fig. 8. A power law with an exponent α = 0.24 ± 0.06 can be fitted to the distribution of the corrected sample. Figer et al. (1999b) argue that such kind of shallow distribution is expected for young coeval clusters. Harayama et al. (2008) found for example α = 0.27 for the young massive star-forming region NGC 3606.
 |
Fig. 9 IMF for the early-type OB stars in the corrected sample of the LHO catalog plus the WN stars. The distribution shown has variable mass range bins with a constant number of stars per bin to avoid numerical biases according to Maíz Apellániz & Úbeda (2005); the linear fit gives a slope coefficient as indicated in the plot. |
For a young coeval cluster it is expected that the mass distribution in the stellar population still resembles the initial mass distribution. However, the evolved WR stars (WN and WC subtypes) and the presence of RSG candidates clearly show that some stars have already undergone significant mass-loss. On the other hand, we found that the majority of early-type stars form a main sequence around a 4 Myr isochrone. Thus, we assume the OB stars to have formed during one star formation event and omit the evolved WR stars and late-type stars for this moment from the further discussion.
From the Geneva 4 Myr isochrone a mass-luminosity relation is constructed and applied. Our completeness limit of Ks = 13 mag translates to a minimum mass of Mini = 10 M⊙ for an OB star. Thus we obtain initial masses in the range of 10 to 78 M⊙, with most stars concentrating in the 10 to 30 M⊙ range and much fewer stars for higher mass bins. The error bars are estimated on the basis of the uncertainty of the luminosity propagating through to the derived masses.
To determine the IMF we follow Maíz Apellániz & Úbeda (2005) and use bins with a variable mass range but a constant number of stars per bin to be robust against numerical biases. In Fig. 9 we show the resulting distribution for the OB stars in the corrected sample plus the WN stars with their masses as determined by Liermann et al. (2011). A linear fit of the form log (dN/dM) ~ γ × log M gives a power law with γ = −1.23 ± 0.51. The fit for the OB stars only gives a slightly steeper result of γ = −1.66 ± 0.51 as the WN stars basically populate the very high-mass bins. Both scenarios suggest a slightly top-heavy IMF in comparison to the canonical Salpeter-IMF (Salpeter 1955, γ = −2.35).
Tests with the Padova 4 Myr isochrone give similar results.
Top-heavy IMFs are discussed for massive stellar cluster throughout the Galaxy and especially for the Galactic center region. For example, Maness et al. (2007) find γ = −0.85 for the Central Parsec cluster assuming continuous star formation, albeit Paumard et al. (2006) favor a star burst scenario for this cluster. The Arches cluster was analyzed by Stolte et al. (2005) who discuss a flat present-day mass function with γ = −1.9 to −2.1, but Portegies Zwart et al. (2002) do not exclude a regular Salpeter-IMF for that cluster when mass segregation is taken into account. Our results on the Quintuplet cluster seem to be in agreement with the findings of a recent study by Hußmann et al. (2011).
5. Summary
In this paper we have used the K-band spectra of the LHO catalog to obtain stellar temperatures and luminosities for all early- and late-type stars in the Quintuplet cluster. Furthermore, we used the LHO catalog to obtain number ratios for the different stellar subclasses. As result we present a cluster HRD that is compared with stellar evolution tracks and isochrones; the main findings are the following:
-
1.
The early-type OB stars in the Quintuplet are high-mass stars with initial masses > 8 M⊙. They form a main sequence population of massive stars around an isochrone of about 4 million years.
-
2.
For the WN stars we determine an age of 3 million years from the isochrones which is consistent with the ages found by Liermann et al. (2010). A possible interpretation for the slight difference to the age of the OB stars is that the most massive stars might have formed late in the cluster formation process.
-
3.
Alternatively, if all WR stars in the Quintuplet evolved as secondary stars in binary systems, they might have been rejuvenated by mass transfer while being originally older.
-
4.
Considering different number ratios (e.g. NWR/NO, NWC/NWN) in the Quintuplet we find best agreement from comparison with population synthesis models for a star burst that formed the Quintuplet cluster about 3.5 ± 0.5 million years ago.
-
5.
The late-type KM stars need much longer to evolve to their present stage. According to their radial velocities the majority of them cannot be considered as cluster members. Five of the KM stars, however, share the radial velocity of the Quintuplet cluster. One of them (LHO 007 alias Q 7) is a supergiant, the others are less luminous. They may represent an older field population in the Galactic center region.
-
6.
If LHO 007 really is a physical member of the Quintuplet cluster, this would have interesting implications. With standard single-star evolution, the simultaneous presence of WR stars and a RSG of initially about 15 M⊙ is only expected for clusters of much older age.
-
7.
Recent stellar evolution models which take the effects of rotation into account, as well as considering binary evolution channels, may help to explain the coexistence of WR stars and RSGs in a cluster of only about 4 million years.
-
8.
We derive the luminosity function of the Quintuplet cluster with a power-law slope of α = 0.24 ± 0.06. This is consistent with a young coeval cluster and confirms the star burst scenario for the formation of the Quintuplet.
-
9.
For the subgroup of the high-mass stars we derive a mass-luminosity relation from the 4 million year isochrone and apply it to obtain the IMF. The result is a power law with a slope that suggest a slightly top-heavy IMF compared to the Salpeter-IMF. If we include the WN stars the effect is more pronounced.
In summary, the Quintuplet cluster seems to have an intermediate age of 3.5 ± 0.5 million years compared to the other Galactic center clusters, the Arches (2.5 ± 0.5 million years, Martins et al. 2008) and the Central cluster (6 ± 2 million years, Paumard et al. 2006). As recently discussed by Böker et al. (2008), an age gradient of young stellar clusters in extragalactic nuclei can be explained in a scenario of almost continuous star formation by over-density regions in a circum-nuclear ring (CNR) in a galaxy. This would lead to a burst-like release of stellar clusters in regular time steps like “pearls on a string” in the central zone. From radio data we know the existence of the Milky Way’s CNR and the active high-mass star formation region Sgr B2 (e.g. Morris & Serabyn 1996). Thus, if the star formation in the inner Milky Way is interpreted in the way described above, this would explain the observed age sequence in the three Galactic center clusters.
Acknowledgments
We thank the anonymous referee for the suggestions to improve the manuscript. The authors are very thankful to B. Davies who kindly shared his knowledge about red supergiant stars. Furthermore discussions with A. Stolte and B. Hußmann about the cluster membership and cluster age were of great value. We thank J. Groh for comments that helped to improve the manuscript. The work was supported in its early phase by the Deutsche Forschungsgemeinschaft (DFG) with grant HA 1455/19.
References
- Barniske, A., Oskinova, L. M., & Hamann, W.-R. 2008, A&A, 486, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, R. D., Ramírez, S. V., Sellgren, K., & Olsen, K. 2003, ApJ, 597, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Böker, T., Falcón-Barroso, J., Schinnerer, E., Knapen, J. H., & Ryder, S. 2008, AJ, 135, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Fagotto, F., Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647 [NASA ADS] [Google Scholar]
- Clark, J. S., Negueruela, I., Crowther, P. A., & Goodwin, S. P. 2005, A&A, 434, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cotera, A. S., Simpson, J. P., Erickson, E. F., et al. 1999, ApJ, 510, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Hadfield, L. J., Clark, J. S., Negueruela, I., & Vacca, W. D. 2006, MNRAS, 372, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Sellgren, K., Smith, V. V., et al. 2007, ApJ, 669, 1011 [Google Scholar]
- Davies, B., Origlia, L., Kudritzki, R.-P., et al. 2009, ApJ, 694, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., McLean, I. S., & Morris, M. 1999a, ApJ, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., Morris, M., Kim, S. S., & Serabyn, E. 1999b, in The Central Parsecs of the Galaxy, ed. H. Falcke, A. Cotera, W. J. Duschl, F. Melia, & M. J. Rieke (ASP: San Fransisco), ASP Conf. Ser., 186, 329 [Google Scholar]
- Geballe, T. R., Najarro, F., & Figer, D. F. 2000, ApJ, 530, L97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glass, I. S., Moneti, A., & Moorwood, A. F. M. 1990, MNRAS, 242, 55P [Google Scholar]
- Glass, I. S., Matsumoto, S., Carter, B. S., & Sekiguchi, K. 1999a, in Asymptotic Giant Branch Stars, ed. T. Le Bertre, A. Lebre, & C. Waelkens (Cambridge: Cambridge University Press), IAU Symp., 191, 523 [Google Scholar]
- Glass, I. S., Matsumoto, S., Carter, B. S., & Sekiguchi, K. 1999b, MNRAS, 304, L10 [NASA ADS] [CrossRef] [Google Scholar]
- González-Fernández, C., Cabrera-Lavers, A., Hammersley, P. L., & Garzón, F. 2008, A&A, 479, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., Gräfener, G., & Liermann, A. 2006, A&A, 457, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harayama, Y., Eisenhauer, F., & Martins, F. 2008, ApJ, 675, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2004, A&A, 425, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, D. A., O’Connell, R. W., Gallagher, J. S., & Smecker-Hane, T. A. 2000, AJ, 120, 2383 [NASA ADS] [CrossRef] [Google Scholar]
- Hußmann, B., Stolte, A., Brandner, W., Gennaro, M., & Liermann, A. 2011, A&A, in press, DOI: 10.1051/0004-6361/201117637 [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lejeune, T., & Schaerer, D. 2001, A&A, 366, 538 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Liermann, A., Hamann, W.-R., & Oskinova, L. M. 2009, A&A, 494, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liermann, A., Hamann, W., Oskinova, L. M., Todt, H., & Butler, K. 2010, A&A, 524, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liermann, A., Hamann, W., Oskinova, L. M., & Todt, H. 2011, Bull. Soc. Roy. Sci. Liege, 80, 160 [NASA ADS] [Google Scholar]
- Maíz Apellániz, J., & Úbeda, L. 2005, ApJ, 629, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Maness, H., Martins, F., Trippe, S., et al. 2007, ApJ, 669, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Martayan, C., Blomme, R., Le Bouquin, J.-B., et al. 2011, Bull. Soc. Roy. Sci. Liege, 80, 400 [NASA ADS] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Trippe, S., Paumard, T., et al. 2006, ApJ, 649, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Hillier, D. J., Paumard, T., et al. 2008, A&A, 478, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mengel, S., & Tacconi-Garman, L. E. 2007, A&A, 466, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Moneti, A., Glass, I., & Moorwood, A. 1992, MNRAS, 258, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Moneti, A., Glass, I. S., & Moorwood, A. F. M. 1994, MNRAS, 268, 194 [NASA ADS] [Google Scholar]
- Nagata, T., Woodward, C. E., Shure, M., Pipher, J. L., & Okuda, H. 1990, ApJ, 351, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Negueruela, I., Clark, J. S., & Ritchie, B. W. 2010, A&A, 516, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Hamann, W.-R. 2006, MNRAS, 372, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Paumard, T., Genzel, R., Martins, F., et al. 2006, ApJ, 643, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., Makino, J., McMillan, S. L. W., & Hut, P. 2002, ApJ, 565, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., Sellgren, K., Blum, R., & Terndrup, D. M. 2003, Astron. Nachr. Suppl., 324, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J. 1993, ARA&A, 31, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Stolte, A., Brandner, W., Grebel, E. K., Lenzen, R., & Lagrange, A.-M. 2005, ApJ, 628, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Tuthill, P., Monnier, J., Tanner, A., et al. 2006, Science, 313, 935 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Hucht, K. A. 2001, New Astron. Rev., 45, 135 [NASA ADS] [CrossRef] [Google Scholar]
- van der Hucht, K. A. 2006, A&A, 458, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanbeveren, D., De Donder, E., van Bever, J., van Rensbergen, W., & De Loore, C. 1998, New Astron., 3, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Vanbeveren, D., Van Bever, J., & Belkus, H. 2007, ApJ, 662, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez, G. A., & Leitherer, C. 2005, ApJ, 621, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. M., van der Hucht, K. A., & The, P. S. 1987, A&A, 182, 91 [NASA ADS] [Google Scholar]
All Tables
Number ratios for the Quintuplet stars in comparison to other Galactic center clusters.
All Figures
 |
Fig. 1 Histogram of the distribution of RVs of all LHO stars (light gray). Overplotted is the distribution for the late-type KM stars (dark/red). Solid and dashed lines indicate the cluster RV of 113 km s-1 and the 1σ and 3σ intervals, respectively. |
| In the text | |
 |
Fig. 2 Same as Fig. 1, but overplotted with the RV distribution of early-type OB stars (dark/blue). Both distributions peak within the intervals assumed for cluster membership, albeit more pronounced for the early-type stars. |
| In the text | |
 |
Fig. 3 Distribution of Ks magnitudes over radial velocity for all stars in the LHO catalog (circles for early-type stars, triangles for late types). The completeness limit at Ks = 13 mag is indicated by the horizontal line, while the vertical lines refer to the different RV intervals as in Fig. 1. |
| In the text | |
 |
Fig. 4 Hertzsprung-Russell diagram of the Quintuplet. Circles (blue) represent the early-type OB stars, triangles (red) the late-type KM stars, filled symbols refer to stars of the corrected sample (see text). The ZAMS and stellar evolution tracks with rotation (solid lines) and without rotation (dashed lines) for different initial masses are from Meynet & Maeder (2003). |
| In the text | |
 |
Fig. 5 Same as Fig. 4 but with theoretical isochrones for different cluster ages. The isochrones, shown with alternating line styles, were constructed by Lejeune & Schaerer (2001). The majority of the population of OB stars in the Quintuplet follows the 4 Myr isochrone, while most KM stars would need more than 30 Myr to evolve. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but with theoretical isochrones based on Girardi et al. (2002). Again, the majority of OB stars falls on the 4 Myr isochrone, while most KM stars evolve on timescales with more than 30 Myr. |
| In the text | |
 |
Fig. 7 Detail of Fig. 4 with focus on the late-type stars with log (L/L⊙) > 3.4 that might be Quintuplet RSG candidates. Tracks show stellar evolution models from Meynet & Maeder (2003) with and without rotation (solid and dashed lines, respectively) and from Bressan et al. (1993, solid line with circles for Mini = 6 and 7 M⊙. |
| In the text | |
 |
Fig. 8 Luminosity function of the Quintuplet cluster for all stars in the LHO catalog (dashed line) and for the corrected sample (solid line). The photometric completeness at Ks = 13 mag is indicated by the vertical dashed line. The linear fits to both distributions are indicated by the slope coefficient α. |
| In the text | |
 |
Fig. 9 IMF for the early-type OB stars in the corrected sample of the LHO catalog plus the WN stars. The distribution shown has variable mass range bins with a constant number of stars per bin to avoid numerical biases according to Maíz Apellániz & Úbeda (2005); the linear fit gives a slope coefficient as indicated in the plot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


