| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116524 | |
| Published online | 04 April 2012 | |
Testing the accretion-induced field-decay and spin-up model for recycled pulsars
1 Institute of Astronomy, National Tsing Hua University, 30013 Hsinchu, Taiwan
e-mail: jwang@mx.nthu.edu.tw
2 National Astronomical Observatories, Chinese Academy of Sciences, 100012 Beijing, PR China
3 Department of Physics, National Tsing Hua University, 30013 Hsinchu, Taiwan
Received: 16 January 2011
Accepted: 6 February 2012
Millisecond radio pulsars have long been proposed to form from a spin-up recycling process in a binary system. In this paper, we demonstrate that the accretion-induced field-decay and spin-up model for recycled pulsars can indeed produce these millisecond pulsars with relatively weak magnetic fields of 108−109 G and short spin periods of a few milliseconds. Our results also suggest that the value of the currently observed highest spin frequency of millisecond pulsars may simply depend on the amount of mass available for accretion.
Key words: binaries: general / X-rays: binaries
© ESO, 2012
1. Introduction
Radio pulsars are found to be of two types, i.e., normal pulsars, with a magnetic field B ~ 1012 G and a spin period P ~ a few seconds, and millisecond pulsars (MSPs), which have low magnetic fields (B ~ 108 − 109 G) and short spin periods (P ≤ 20 ms, e.g. Bhattacharya & van den Heuvel 1991; Lorimer 2008). These bimodal distributions in magnetic fields and spin periods are shown, e.g., in Fig. 1 in Wang et al. (2011) and also Fig. 1 of this paper, which, with data taken from ATNF pulsar catalogue, shows a large population of normal pulsars and a smaller population of MSPs. These two populations are connected by a thin bridge of pulsars in binaries. Moreover, most MSPs are in binary systems. It has long been proposed that MSPs are formed by means of a recycling process in which neutron stars accrete material from their low-mass companions and are spun up by the angular momentum carried by the accreted material. During this phase, the magnetic field is buried by the accreted material and decays (Alpar et al. 1982; Taam & van den Heuvel 1986; Bhattacharya & van den Heuvel 1991; Radhakrishnan & Srinivasan 1982; Bhattacharya & Srinivasan 1995; van den Heuvel 2004). These objects are therefore called recycled MSPs (Taam & van den Heuvel 1986; Bhattacharya & van den Heuvel 1991; van den Heuvel 2004).
 |
Fig. 1 Magnetic fields and spin periods of observed pulsars, where data are taken from the ATNF pulsar catalogue. Black dots are normal pulsars. Red dots represent MSPs. Green triangles are pulsars in binaries. The “spin-up line” represents the minimum spin-period to which a spin-up process may proceed in an Eddington-limited accretion, while the “death-line” corresponds to a polar cap voltage below which the pulsar activity is likely to switch off (Bhattacharya & van den Heuvel 1991). |
The evolutionary precursors to recycled MSPs are widely believed to be pulsars in binaries with high magnetic fields (B ~ 1011 − 1013 G) and long spin periods (P ~ a few seconds, Bhattacharya & van den Heuvel 1991; Liu et al. 2007; Lorimer 2011). It is evident that the B and P of normal pulsars and recycled pulsars are correlated with the duration of the accretion phase and the total amount of accreted mass (Taam & van den Heuvel 1986; Shibazaki et al. 1989; Wijers 1997). If a neutron star accretes a small amount of mass from its companion, e.g. ~0.001 M⊙ − 0.01 M⊙, a recycled pulsar with a mildly weak field and short spin period (B ~ 1010 G, P ~ 50 ms) will be formed (e.g. Francischelli et al. 2002), such as PSR 1913+16 and PSR J0737–3039 (Lyne et al. 2004; Kramer 2006). Strong support for this recycling idea has been found in low mass X-ray binaries (LMXBs) containing accreting millisecond X-ray pulsars (AMXPs), e.g. SAX J 1808.4–3658 (Wijnands & van der Klis 1998), and in observing the transition link from an X-ray binary to a radio pulsar PSR J1023+0038 (Archibald et al. 2009). At the end of the accretion phase during which the accreted mass is greater than 0.2 M⊙, the neutron star magnetic field may arrive at a bottom value of about 108 − 109 G and its spin period may reach a minimum of about a few milliseconds. A millisecond pulsar is formed (van den Heuvel & Bitzaraki 1995a,b; Urpin et al. 1998). The accretion-induced field-decay and spin-up torque cause the magnetic field and spin period (Hobbs & Manchester 2004; Manchester et al. 2005) to change from B ~ 1011 − 1013 G and P ~ a few seconds to B ~ 108 − 109 G and P ~ a few milliseconds. It is the recycling process that leads to the bimodal distribution of radio pulsars.
In this paper, we examine the accretion-induced field-decay and spin-up model of Zhang & Kojima (2006) for these recycled pulsars. We investigate the differences in the model-predicted B and P distributions with different initial conditions. We also compare those distributions with currently observed ones. This paper is organized in the following way. Section 2 gives an overview of the model. We describe the input parameters necessary in the calculations of field and spin evolutions and analyze the results in Sect. 3. Section 4 contains a discussion and summary.
2. The model
2.1. The recycling process
A neutron star in a binary, with an initial magnetic field of about B0 ~ 1012 G and an initial spin period of about P0 ~ a few seconds, can accrete material from its companion to form an accretion disk. When the ram pressure of accretion material equals the magnetic pressure, a magnetosphere forms. As a result, a boundary layer appears between the innermost disk and magnetosphere, that is produced by the transition of the rotating velocity of plasma from Keplerian to the spin velocity of the neutron star (Inogamov & Sunyaev 1999). In this layer, the accreted matter is channeled onto the polar patches by the field lines, where the compressed accreted matter causes the expansion of magnetic polar zone in two directions, downward and equatorward (Zhang & Kojima 2006). Therefore, the magnetic flux in the polar zone is diluted, and more matter is accreted onto the polar cap and diffuses to the surface of the neutron star. Finally, the polar cap area expands and occupies the entire neutron-star surface, and the magnetic flux is buried in the equatorial area. The magnetosphere is then compressed onto the neutron star surface, leading to an object with weak fields on large scales (about ~ 108 G) and very strong fields on small scales (about ~1014 G). Meanwhile, the angular momentum carried by the accreted matter spins up the neutron star, forming a MSP with the spin period of a few milliseconds.
2.2. Magnetic field evolution
On the basis of the above accretion-induced field-decay and spin-up model, the accretion-induced field and spin evolution is obtained analytically (Zhang & Kojima 2006) ![\begin{equation} \label{bt} B(t) = \frac{B_{\rm f}}{(1 - [C\,{\rm e}^{-y}-1]^2)^{\frac{7}{4}}} , \end{equation}](/articles/aa/full_html/2012/04/aa16524-11/aa16524-11-eq20.png) (1)where we have
(1)where we have 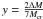 , the accreted mass ΔM = Ṁt, the crust mass Mcr ~ 0.2 M⊙, and
, the accreted mass ΔM = Ṁt, the crust mass Mcr ~ 0.2 M⊙, and 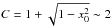 with
with 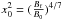 . The parameter B0 = B(t = 0) is the initial field strength and Bf is the bottom magnetic field, which is defined by the neutron-star magnetosphere radius matching the stellar radius, i.e., RM(Bf) = R, where RM = φRA and the Alfvén radius
. The parameter B0 = B(t = 0) is the initial field strength and Bf is the bottom magnetic field, which is defined by the neutron-star magnetosphere radius matching the stellar radius, i.e., RM(Bf) = R, where RM = φRA and the Alfvén radius 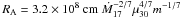 (Elsner & Lamb 1977; Ghosh & Lamb 1977). The model-dependent parameter φ is about 0.5 (Ghosh & Lamb 1979b; Shapiro & Teukolsky 1983; Frank et al. 2002), where Ṁ17 is the accretion rate in units of 1017 g/s and μ30 is the magnetic moment in units of 1030 G cm3. The mass m = M/M⊙ is in units of solar masses. According to this model, the bottom field of neutron stars is determined by the condition that the magnetosphere radius equals the neutron star radius (Zhang & Kojima 2006). Using the relation RM(Bf) = R, we can obtain the bottom field
(Elsner & Lamb 1977; Ghosh & Lamb 1977). The model-dependent parameter φ is about 0.5 (Ghosh & Lamb 1979b; Shapiro & Teukolsky 1983; Frank et al. 2002), where Ṁ17 is the accretion rate in units of 1017 g/s and μ30 is the magnetic moment in units of 1030 G cm3. The mass m = M/M⊙ is in units of solar masses. According to this model, the bottom field of neutron stars is determined by the condition that the magnetosphere radius equals the neutron star radius (Zhang & Kojima 2006). Using the relation RM(Bf) = R, we can obtain the bottom field 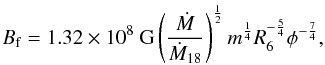 (2)where Ṁ18 = Ṁ/1018 g/s and R6 = R/106 cm.
(2)where Ṁ18 = Ṁ/1018 g/s and R6 = R/106 cm.
2.3. Spin evolution
During the accretion phase, the neutron star is spun up by the angular momentum carried by the accreted matter. The spin evolves according to the relation given by Gosh & Lamb (1979b) ![\begin{eqnarray} -\dot{P}&=&5.8 \times 10^{-5}\left[\left(\frac{M}{M_\odot}\right)^{-\frac{3}{7}} R^{\frac{12}{7}}_6 I_{45}^{-1}\right]\nonumber\\~& & \times B^{\frac{2}{7}}_{12} (PL^{\frac{3}{7}}_{37})^2n(\omega_{\rm s}) {\empty ~ ~ } {\rm s~yr}^{-1},\label{pdot} \end{eqnarray}](/articles/aa/full_html/2012/04/aa16524-11/aa16524-11-eq40.png) (3)where the parameters are the surface field B12 = B/1012 G, the moment of inertia I45 = I/1045 g cm2, and the X-ray brightness (L = GMṀ/R) L37 in units of 1037 erg/s, respectively. The dimensionless parameter n(ωs) is the fastness parameter, whose expression is given by Gosh & Lamb (1979b)
(3)where the parameters are the surface field B12 = B/1012 G, the moment of inertia I45 = I/1045 g cm2, and the X-ray brightness (L = GMṀ/R) L37 in units of 1037 erg/s, respectively. The dimensionless parameter n(ωs) is the fastness parameter, whose expression is given by Gosh & Lamb (1979b) 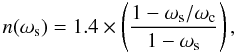 (4)where ωs is defined as
(4)where ωs is defined as ![\begin{equation} \omega_{\rm s}\equiv\frac{\Omega_{\rm s}}{\Omega_{\rm k}(R_{\rm M})} =1.35\left[\left(\frac{M}{M_\odot}\right)^{-2/7}R^{15/7}_6\right] B^{6/7}_{12} P^{-1}L^{-3/7}_{37} , \label{omega} \end{equation}](/articles/aa/full_html/2012/04/aa16524-11/aa16524-11-eq49.png) (5)with Ωs is the stellar spin frequency, Ωk is the Keplarian frequency, and ωs is the ratio parameter of the angular velocities, which describes the relative importance of stellar rotation and plays a significant role in our entire understanding of accretion onto the rotating magnetic neutron stars (Elsner & Lamb 1977; Ghosh & Lamb 1977; Li & Wang 1996, 1999; Shapiro & Teukolsky 1983). For a slowly rotating magnetic neutron star, ωs ≪ 1, where ωc depends on several properties of the system (Gosh & Lamb 1979b) and is taken to be 0.35 in this computation.
(5)with Ωs is the stellar spin frequency, Ωk is the Keplarian frequency, and ωs is the ratio parameter of the angular velocities, which describes the relative importance of stellar rotation and plays a significant role in our entire understanding of accretion onto the rotating magnetic neutron stars (Elsner & Lamb 1977; Ghosh & Lamb 1977; Li & Wang 1996, 1999; Shapiro & Teukolsky 1983). For a slowly rotating magnetic neutron star, ωs ≪ 1, where ωc depends on several properties of the system (Gosh & Lamb 1979b) and is taken to be 0.35 in this computation.
3. B and P distributions of MSPs
3.1. Input parameters
According to the accretion-induced field-decay and spin-up model of Zhang & Kojima (2006), a pulsar with a strong magnetic field (e.g. B ~ 1012 G) and slow rotation (P ~ a few seconds) in a binary system may be spun up to become a millisecond pulsar via accretion, and the magnetic field will decay to a minimum value of B ~ 108 − 109 G during this phase. The final state of a recycled system is characterized by the magnetic field and spin period, which are related to the initial magnetic field, initial spin period, accretion rate, accretion time, and the mass and radius of a neutron star. In computing the model predictions of B and P, we adopt these input parameters in the following way:
-
(1)
All precursors to recycled MSPs are assumed to be normal pulsars with magnetic fields of about B0 ~ 1012 G and a spin period of about a few seconds. According to the data taken from ATNF catalogue, the log B and log P distributions of normal pulsars can be well-described by a Gaussian function (see Wang et al. 2011). We therefore take lognormal distributions as the inputs to the initial magnetic fields and spin periods. The probability density function reads
![\begin{equation} p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{1}{2}\left[\frac{x-\mu}{\sigma}\right]^2\right),\label{Gaussian} \end{equation}](/articles/aa/full_html/2012/04/aa16524-11/aa16524-11-eq56.png) (6)where μ is the mean value of the distribution, and σ is the standard deviation. We take μ = log B(G) = 12 and σ = 0.5 for the B distribution (see e.g. Hartman et al. 1997; Hobbs et al. 2011; Kaspi 2010; Wang et al. 2011) and μ = log P(s) = 0 and σ = 0.4 for the P distribution (see e.g. Lorimer 2011, and references therein). The range of B and P to consider is taken as B0 = 1010.5 − 1014.0 G and P0 = 0.1 − 30 s, respectively.
(6)where μ is the mean value of the distribution, and σ is the standard deviation. We take μ = log B(G) = 12 and σ = 0.5 for the B distribution (see e.g. Hartman et al. 1997; Hobbs et al. 2011; Kaspi 2010; Wang et al. 2011) and μ = log P(s) = 0 and σ = 0.4 for the P distribution (see e.g. Lorimer 2011, and references therein). The range of B and P to consider is taken as B0 = 1010.5 − 1014.0 G and P0 = 0.1 − 30 s, respectively. -
(2)
The accretion rate is assumed to range from Ṁ = 1016 g/s to Ṁ = 1018 g/s (see e.g. Wijers 1997) and to be constant during the whole process. The duration of the accretion phase is in the range from Δt = 107 yr to Δt = 109 yr. Most systems may accrete 0.1 − 0.2 M⊙ at the end of the accretion phase (see Shapiro & Teukolsky 1983). However, in some binary systems, the maximum accretion mass can be 0.6 − 0.8 M⊙ (van den Heuvel 2011), depending on the intrinsic properties of the system. We adopt lognormal distributions (see Eq. (6)) for both the accretion rate and the accretion time. The mean values and standard deviations are μ = log Ṁ(g/s) = 17, σ = 0.1 for the accretion rate, and μ = log Δt(yr) = 8, σ = 0.4 for the accretion time, respectively.
-
(3)
According to recent statistics of neutron star masses (see Zhang et al. 2011), we consider a Gaussian mass distribution with the mean at 1.4 M⊙ and the standard deviation equal to 0.2 M⊙ within the range from 0.9 M⊙ to 2.2 M⊙.
-
(4)
It is widely believed that the neutron star radius is about 10 km. We consider a uniform distribution of radii from 10 km to 20 km.
3.2. Distribution of recycled MSPs
We calculated the final B and P according to the accretion-induced B and P evolution model described in Sect. 2. To produce the model-predicted distribution, we generated a large number of input parameter random samples from the input parameter distributions mentioned in Sect. 3.1. Different computation runs with 300, 3000, and 30 000 samples were performed to examine how many samples are needed to achieve a converged result. Figure 2 shows the B and P distributions of recycled MSPs obtained with 300, 3000 and 30 000 random samples, respectively. We can see that, with the initial conditions considered in Sect. 3.1, the Zhang & Kojima (2006) model indeed predicts that the magnetic fields of recycled MSPs are 108 − 109 G, and that their spin periods are a few milliseconds. We divided these distributions into histograms with a bin size of 0.1 and assessed their differences from each other using the Kolmogorov-Smirnov (K-S) test (Press et al. 1992). For the comparison of the B distributions between 300 and 3000 samples, the K-S statistic gives a 86.1% probability of the two being drawn from the same parent distribution. The same probability for the two distributions of 3000 and 30 000 samples is 100.0%. For the P distributions, the probability is 64.9% for the 300 and 3000 samples, and again reaches 100.0% for the 3000 and 30 000 samples. We are therefore content with the results obtained for 30 000 random samples.
Although the initial conditions, that is, input parameters, described in Sect. 3.1 are quite commonly adopted, we checked the sensitivity of the model predictions to the variation in the distribution of the input parameters. We used different input widths of the lognormal B and P distributions, which are 0.375 (instead of 0.5) for B and 0.2 (instead of 0.4) for P. The ranges exploited for the B and P distributions are the same as in Sect. 3.1. These input distributions and the corresponding computed final B and P distributions are shown in Fig. 3. On the basis of the K-S test, the similarity between the final distributions obtained with narrow and wide inputs is 100.0%, for both B and P distributions. These results are insensitive to the mild variations in their progenitor distributions.
 |
Fig. 2 The computed B and P distributions of recycled MSPs with different numbers of random input samples. The left (right) panel is the B (P) distribution. As discussed in the text, the computed distributions with 30 000 random samples are good enough and are those used for comparison with observations in this work. |
 |
Fig. 3 B and P input distributions with narrow and wide Gaussian widths (the upper panels) and their resultant final B and P distributions (the lower panels). |
Finally, we compared the model-predictions for the B and P distributions with currently observed distributions. The observed MSPs are usually defined as pulsars with spin periods shorter than 20 ms. Figure 4 shows the B and P distributions of observed MSPs. Owing to the wide ranges of the input parameters, some MSPs have longer computed spin periods (see Fig. 2). The comparison with observation is conducted for spin periods shorter than 20 ms, and the computed B and P distributions for these recycled pulsars are plotted in Fig. 5. Using the K-S test, we again found that the degree of similarity between the B distributions is 69.2% and between the P distributions is 73.6%. We also performed a χ2 test to check the consistency between the model predicted distributions and observed ones. The errors in the observed distributions were defined to be 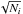 for each bin, where Ni is the number of observed recycled pulsars in the ith bin. The χ2 value is 22.8 (19 degrees of freedom) for the B distribution, which corresponds to a null hypothesis probability of 24.6%, and 16.6 (11 degrees of freedom) for the P distribution, which corresponds to a 12.0% null hypothesis probability. Both the K-S test and χ2 test indicate that the consistency between the currently observed distributions and the Zhang & Kojima (2006) model prediction is at roughly the so-called 1-σ level. In other words, although they do not share a high degree of similarity, they are not inconsistent with each other.
for each bin, where Ni is the number of observed recycled pulsars in the ith bin. The χ2 value is 22.8 (19 degrees of freedom) for the B distribution, which corresponds to a null hypothesis probability of 24.6%, and 16.6 (11 degrees of freedom) for the P distribution, which corresponds to a 12.0% null hypothesis probability. Both the K-S test and χ2 test indicate that the consistency between the currently observed distributions and the Zhang & Kojima (2006) model prediction is at roughly the so-called 1-σ level. In other words, although they do not share a high degree of similarity, they are not inconsistent with each other.
 |
Fig. 4 The B and P distributions of observed MSPs (data taken from the ATNF pulsar catalogue). |
 |
Fig. 5 The computed B and P distributions of recycled MSPs with spin periods shorter than 20 ms. |
3.3. B and P evolutions of recycled MSPs
Figure 6 displays the B and P evolutionary tracks during the accretion phase with initially slowly rotating and highly magnetized progenitors. In this calculation, we assumed the initial magnetic field to be B0 = 5 × 1012 G and the initial spin period to be P0 = 1 s. Accretion rates of 1018 g/s, 1017 g/s, and 1016 g/s were considered. These tracks were followed until the accreted mass reached 1 M⊙. The upper right panel in Fig. 6 shows that the magnetic field decays with the accumulation of the accreted material and that the weakest values of the magnetic fields correlate with the accretion rates. The lower left panel shows that the pulsar rotates faster and faster while accreting more and more mass and that the spin period is insensitive to the accretion rate after accreting about 0.001 M⊙ of mass.
 |
Fig. 6 B and P evolution in the recycling process. The upper left panel shows the joint evolution of B and P. The upper right and lower left panels are their evolution as a function of accreted mass ΔM. The solid, dashed, and dotted lines are the evolutionary tracks with the accretion rate of 1018 g/s, 1017 g/s, and 1016 g/s, respectively. The initial B and P are taken as B0 = 5 × 1012 G and P0 = 1 s. The lower right panel is a zoom-in view of the lower left panel in a linear scale for spin periods shorter than 5 ms. |
4. Discussion and summary
We have tested the accretion-induced field-decay and spin-up model for recycled MSPs (Zhang & Kojima 2006; Wang et al. 2011). In our computation, we have considered lognormal distributions of initial B and P in the range of B0 = 1010.5−1014 G and P0 = 0.1−30 s, a Gaussian neutron star mass distribution in the range of M = 0.9−2.2 M⊙, a uniform neutron-star radius distribution of R = 10−20 km, a lognormal distribution of the accretion rate of Ṁ = 1016 − 1018 g/s, and an accretion time of Δt = 107 − 109 yr. We found that the computed B and P distributions of recycled MSPs are insensitive to mild variations in the width of the initial distributions. On the basis of the K-S test and χ2 test, we have found that the Zhang & Kojima (2006) model prediction is consistent with observations at the 1-σ level.
The accretion-induced field-decay model is based on the idealized idea of the dilution of polar magnetic flux by accretion. We have ignored all the possible instabilities. In addition, we have assumed a constant accretion rate during the whole accretion process. There are, however, some special features of each system, such as the influence of both thermal and viscous instabilities in the accretion disk and the propeller effect on the mass transfer process. The orbital angular momentum loss of the system and its causes may also have some effect on the final B and P states. The numerous plasma instabilities, such as the Rayleigh-Taylor instability and the Kelvin-Helmholtz instability (Ghosh & Lamb 1979a), may result in the penetration of the magnetosphere, prying the field lines aside and azimuthally wrapping the field lines with the disk matter (e.g. Romanova 2008; Kulkarni & Romanova 2008), which in turn may modify the field strength evolution and then perturb the spin evolution. During the accretion, the accretion rate may change owing to variations in the system and some instabilities, which may cause the difference between the theoretical results and the actual values.
It is generally believed that there are two possible ways of forming MSPs, i.e. the standard accretion-induced field-decay and spin-up model and accretion-induced collapse of white dwarfs (AIC). Owing to the conservation of magnetic flux during the collapse of white dwarfs, the MSPs formed via AIC are expected to have high magnetic fields and short spin periods. Although the number of MSPs formed via AIC is no more than 20% (Zhang et al. 2011), this may also contribute to cause the observed B and P distributions of MSPs to somewhat differ from those of MSPs formed via only the standard mechanism.
Some selection effects should also be noted when comparing the model predictions with observations. For example, the spin-down energy loss rate, 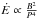 , is related to the radio power of a pulsar, hence MSPs with relatively stronger magnetic fields and shorter spin periods are easier to observe.
, is related to the radio power of a pulsar, hence MSPs with relatively stronger magnetic fields and shorter spin periods are easier to observe.
Owing to the ohmic dissipation, the buried field may re-emerge after accretion (e.g. Young & Chanmugam 1995; Bhattacharya 2008). In addition, if the magnetic field of recycled pulsars arrive at the bottom value at this stage and the accretion has not yet ended, the accumulation of material may spin up the recycled pulsar yet further. However, the magnetic field of neutron stars will not decay. The magnetic flux carried by the plasma accreted onto the neutron star surface may increase the neutron-star surface field strength.
We also plot the B and P evolutionary scenarios during the accretion process in Fig. 6. All of these plots show that the bottom magnetic field strength is different for different accretion rates and that the minimum period is insensitive to the accretion rate at the end of the accretion phase. After the pulsar has accreted 1 M⊙, its spin period reaches about 1 ms. If sufficient mass has been accreted (e.g. 1.2 M⊙), the spin period may become shorter than one millisecond, forming a submillisecond pulsar. The maximum accreted mass may be 0.8 M⊙ under the assumption of a 1 M⊙ companion star (van den Heuvel & Bitzaraki 1995a; Wijers 1997). From recent statistics for neutron stars/LMXB (Liu et al. 2007), most neutron stars/LMXBs have a companion mass of 0.7 M⊙. According to the accretion-induced field-decay and spin-up model, the spin period can reach 1.1–1.2 ms after accreting 0.7–0.8 M⊙. To date, the shortest observed period for MSPs is 1.4 ms (Hessels et al. 2006), and that for millisecond X-ray pulsars is 1.6 ms (e.g. Patruno 2010). The two spin frequencies, 716 Hz and 620 Hz, are both lower than than the most probable break-up spin frequency ~1000 Hz (e.g. Lattimer & Prakash 2004). Models capable of explaining the lack of submillisecond pulsars have been proposed, including magnetic spin equilibrium and angular momentum loss by means of gravitational radiation. A significant quadrupole moment may be produced in some oscillation modes or so-called “crustal mountains” and “magnetic deformation”, which lead to the emission of gravitational waves and the loss of angular momentum, in particularly owing to the strong dependence of the spin frequency to the fifth power (e.g. Bildsten 1998; Haskell & Patruno 2012; Patruno et al. 2012). On the other hand, however, the magnetic braking resulting from the action of the stellar wind indirectly carries away the angular momentum (Rappaport et al. 1983), the consequent removal of momentum being more efficient than gravitational radiation by about two orders of magnitude in some close systems (Kalogera et al. 1998). Furthermore, the magnetic spin equilibrium set by disk/magnetosphere coupling seems to be successful in explaining the lack of submillisecond pulsars (D’Angelo & Spruit 2011; Kajava et al. 2011). In addition to those efforts, the results of the accretion-induced field-decay and spin-up model presented in this paper suggest that the achievable minimum spin period produced by the recycling process may depend mainly on the amount of mass available for accretion, before the limiting shortest period, which depends on the magnetic spin equilibrium, is reached.
Acknowledgments
We greatly appreciate the valuable comments of anonymous referees, which significantly improved this paper. This work was partially supported by the National Natural Science Foundation of China (NSFC 10773034) and the National Basic Research Program of China (2012CB821800). It was also supported by the National Science Council of Taiwan under grant NSC 99-2112-M-007-017-MY3.
References
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., et al. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Archibald, A. M., Stairs, I. H., Ransom, S. M., et al. 2009, Science, 324, 1411 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bhattacharya, D. 2008, AIPC, 1068, 137 [NASA ADS] [Google Scholar]
- Bhattacharya, D., & Srinivasan, G. 1995, in X-ray Binaries, ed. W. H. G. Lewin, J. van Paradijs, & E. P. J. van den Heuvel (Cambridge University Press) [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L. 1998, ApJ, 501, L89 [Google Scholar]
- D’Angelo, C. R., & Spruit, H. C. 2011, MNRAS, 416, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Elsner, R. F., & Lamb, F. K. 1977, ApJ, 215, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Francischelli, G. J., Wijers, R. A. M. J., & Brown, G. E., 2002, ApJ, 565, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics, Cambridge, UK [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1977, ApJ, 217, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979a, ApJ, 232, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979b, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. W., Portegies Zwart, S., & Verbunt, F. 1997, 325, 1031 [Google Scholar]
- Haskell, B., & Patruno, A. 2011, ApJ, 738, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hobbs, G., & Manchester, R. 2004, ATNF Pulsar Catalogue, http://www.atnf.csiro.au/research/pulsar/psrcat/psrcat_help.html [Google Scholar]
- Hobbs, G., Miller, D., Manchester, R. N., et al. 2011, PASP, 28, 202 [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 1999, AstL, 25, 269 [Google Scholar]
- Kajava, J. J. E., Ibragimov, A., Annala, M., Patruno, A., & Poutanen, J. 2011, MNRAS, 417, 1454 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M. 2010, PNAS, 107, 7147 [Google Scholar]
- Kalogera, V., Kolb, U., & King, A. R. 1998, ApJ, 504, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, A. K., & Romanova, M. M. 2008, MNRAS, 386, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Stairs, I. H., Marchester, R. N., et al. 2006, Science, 314, 97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2004, Science, 304, 536 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, X. D., & Wang, Z. R. 1996, A&A, 307, L5 [NASA ADS] [Google Scholar]
- Li, X. D., & Wang, Z. R. 1999, ApJ, 513, 845 [Google Scholar]
- Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2007, A&A, 469, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorimer, D. R. 2008, Liv. Rev. Rel., 11, 8 [Google Scholar]
- Lorimer, D. R. 2011, in High-Energy Emission from Pulsars and their Systems, Astrophysics and Space Science Proceedings (Berlin Heidelberg: Springer-Verlag), 21 [Google Scholar]
- Lyne, A. G., Burgay, M., Kramer, M., et al. 2004, Science, 303, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Shibazaki, N., Murakami, T., Shaham, J., & Nomoto, K. 1989, Nature, 342, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs and Neutron Stars (New York: Wiley) [Google Scholar]
- Patruno, A. 2010, ApJ, 722, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Patruno, A., Haskell, B., & D’Angelo, C. 2012, ApJ, 746, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran 77 (London: Cambridge University Press) [Google Scholar]
- Radhakrishnan, V., & Srinivasan, G. 1982, Curr. Science, 51, 1096 [Google Scholar]
- Romanova, M. M., Kulkarni, A. K., & Lovelace, R. V. E. 2008, ApJ, 673, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., & van den Heuvel, E. P. J. 1986, ApJ, 305, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V., Geppert, U., & Konenkov, D. 1998, A&A, 331, 244 [NASA ADS] [Google Scholar]
- van den Heuvel, E. P. J. 2004, Science, 303, 1143 [CrossRef] [PubMed] [Google Scholar]
- van den Heuvel, E. P. J. 2011, BASI, 39, 1 [Google Scholar]
- van den Heuvel, E. P. J., & Bitzaraki, O. 1995a, A&A, 297, L41 [NASA ADS] [Google Scholar]
- van den Heuvel, E. P. J., & Bitzaraki, O. 1995b, in The Lives of the Neutron Stars (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Wang, J., Zhang, C. M., Zhao, Y. H., et al. 2011, A&A, 526, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Wijers, R. A. M. J. 1997, MNRAS, 287, 607 [NASA ADS] [Google Scholar]
- Young, E. J., & Chanmugam, G. 1995, ApJ, 442, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, C. M., & Kojima, Y. 2006, MNRAS, 366, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, C. M., Wang, J., Zhao, Y. H., et al. 2011, A&A, 527, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Magnetic fields and spin periods of observed pulsars, where data are taken from the ATNF pulsar catalogue. Black dots are normal pulsars. Red dots represent MSPs. Green triangles are pulsars in binaries. The “spin-up line” represents the minimum spin-period to which a spin-up process may proceed in an Eddington-limited accretion, while the “death-line” corresponds to a polar cap voltage below which the pulsar activity is likely to switch off (Bhattacharya & van den Heuvel 1991). |
| In the text | |
 |
Fig. 2 The computed B and P distributions of recycled MSPs with different numbers of random input samples. The left (right) panel is the B (P) distribution. As discussed in the text, the computed distributions with 30 000 random samples are good enough and are those used for comparison with observations in this work. |
| In the text | |
 |
Fig. 3 B and P input distributions with narrow and wide Gaussian widths (the upper panels) and their resultant final B and P distributions (the lower panels). |
| In the text | |
 |
Fig. 4 The B and P distributions of observed MSPs (data taken from the ATNF pulsar catalogue). |
| In the text | |
 |
Fig. 5 The computed B and P distributions of recycled MSPs with spin periods shorter than 20 ms. |
| In the text | |
 |
Fig. 6 B and P evolution in the recycling process. The upper left panel shows the joint evolution of B and P. The upper right and lower left panels are their evolution as a function of accreted mass ΔM. The solid, dashed, and dotted lines are the evolutionary tracks with the accretion rate of 1018 g/s, 1017 g/s, and 1016 g/s, respectively. The initial B and P are taken as B0 = 5 × 1012 G and P0 = 1 s. The lower right panel is a zoom-in view of the lower left panel in a linear scale for spin periods shorter than 5 ms. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


