| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201118215 | |
| Published online | 17 February 2012 | |
Center-to-limb variation of the area covered by magnetic bright points in the quiet Sun
1 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
e-mail: jab@iac.es
2 Departamento de Astrofísica, Universidad de La Laguna, Tenerife, Spain
3 Image Processing Laboratory, Universidad de Valencia, 46980 Paterna, Valencia, Spain
Received: 6 October 2011
Accepted: 9 December 2011
Context. The quiet Sun magnetic fields produce ubiquitous bright points (BPs) that cover a significant fraction of the solar surface. Their contribution to the total solar irradiance (TSI) is so-far unknown.
Aims. We aim at measuring the center-to-limb variation (CLV) of the fraction of solar surface covered by quiet Sun magnetic bright points. The fraction is referred to as the fraction of covered surface (FCS).
Methods. We count the area covered by BPs in G-band images obtained at various heliocentric angles with the 1-m Swedish Solar Telescope on La Palma. We restore the images to bring them close to the diffraction limit of the instrument (~0'.1).
Results. The FCS is largest at the disk center (≃1%), and then drops down to become ≃0.2% at μ ≃ 0.3 (where μ is the cosine of the heliocentric angle). The relationship has a large scatter, which we evaluate by comparing different subfields within our FOVs. We develop a toy-model to describe the observed CLV, which considers the BPs as depressions in the mean solar photosphere characterized by a depth, a width, and a spread in the inclinations. Although the model is poorly constrained by observations, it shows the BPs to be shallow structures (depth < width) with a large range of inclinations. We also estimate how different parts of the solar disk may contribute to the TSI variations, finding that 90% is contributed by BPs with μ > 0.5, and half of it is due to BPs with μ > 0.8.
Key words: magnetic fields / Sun: activity / Sun: photosphere / Sun: surface magnetism / Sun: granulation
© ESO, 2012
1. Introduction
Our understanding of the quiet Sun magnetic fields has drastically improved in the last decade (for reviews, see, e.g., de Wijn et al. 2009; Sánchez Almeida & Martínez González 2011). We have evolved from measuring magnetic signals present only at the network boundaries (e.g., Beckers 1977; Solanki 1993), to detecting ubiquitous polarization signals created by Hanle effect (e.g., Faurobert-Scholl 1993; Trujillo Bueno et al. 2004) and Zeeman effect (e.g., Lin & Rimmele 1999; Sánchez Almeida & Lites 2000; Domínguez Cerdeña et al. 2003; Harvey et al. 2007; Lites et al. 2008). The wealth of quiet Sun magnetic structures makes them potentially important to understanding the global magnetic properties of the Sun (Sánchez Almeida et al. 2003b; Trujillo Bueno et al. 2004), and also makes it unlikely that the quiet Sun magnetism results from the decay of active regions (e.g., Sánchez Almeida et al. 2003a). Theoretical arguments, corroborated by numerical experiments, favor a different production mechanism (Petrovay & Szakaly 1993; Cattaneo 1999; Vögler & Schüssler 2007; Pietarila Graham et al. 2010; Moll et al. 2011). An efficient turbulent dynamo transforms into magnetic fields part of the kinetic energy of the granular convection. It generates a complex magnetic field that evolves on short timescale (of a few min) and has small characteristic length-scales (<1 Mm).
In agreement with the turbulent dynamo scenario, quiet Sun magnetic fields come with strengths in the full range from almost zero to 2 kG (Sánchez Almeida & Lites 2000; Domínguez Cerdeña et al. 2006; Martínez González et al. 2008; Bommier et al. 2009; Viticchié et al. 2011). Even if they only fill a small fraction of the quiet photosphere, the part with strong kG fields may be particularly important for a number of reasons. Firstly, the magnetic flux and energy increase with field strength, hence, the energy and flux provided by kGs may surpass the contribution of the more common but weaker fields (Sánchez Almeida 2004). The need to consider kGs is illustrated by the numerical experiments set up by Cameron et al. (2011), where realistic granular convection redistribute initial hG fields such that daG, hG, and kG field strengths have the same energy despite their very different area covering. Magnetic concentrations with kG fields may also be important because buoyancy makes them vertical (e.g., Schüssler 1986) and so, they naturally provide a mechanical connection between the photosphere and the upper atmosphere (e.g., van Ballegooijen et al. 1998; Schrijver & Title 2003; Goodman 2004; Jendersie & Peter 2006; Sánchez Almeida et al. 2007). They can function as guides that sustain magneto-acoustic wave propagation, or be physical channels connecting plasmas of different atmospheric layers. Finally, kG magnetic concentrations are expected to be particularly bright owing to the so-called hot-wall effect1 (Spruit 1977; Carlsson et al. 2004; Keller et al. 2004). They produce bright points (BPs) that, depending on the variation across the solar disk and during the solar cycle, may even contribute to the total solar irradiance (TSI) variations, adding up to the contribution from network and plage magnetic fields (Lean 1997; Fröhlich & Lean 2004; Fröhlich 2011).
The discovery of BPs in the quiet Sun was immediately identified with the kG magnetic concentrations inferred from polarization measurements (Sánchez Almeida et al. 2004). The basic properties of BPs and their ubiquitous presence have been confirmed by a number of researchers (de Wijn et al. 2005, 2008; Bovelet & Wiehr 2008; Sánchez Almeida et al. 2007; Viticchié et al. 2009, 2010; Goode et al. 2010). They vary on timescales of minutes similar to that of granulation, and many BPs are at the resolution limit of the current instrumentation (some 0.1 Mm). They are extremely common, filling at least 1% of the solar surface and outnumbering granules (Sánchez Almeida et al. 2010).
Schnerr & Spruit (2011) estimate the excess of brightness produced by the quiet magnetic fields at the disk center, which was found to be of the order of 0.15%. Their contribution is larger than the 0.08% TSI variations associated with the cycle, although, determining the impact of these kG fields on TSI demands knowing their center-to-limb variation (CLV), as well as the variation of the quiet Sun magnetic fields with the solar cycle. These two properties, central to assessing the role of quiet Sun fields on TSI, are poorly known. As far as the variation during the cycle is concerned, the claims in the literature are of little variation if any (Sánchez Almeida 2003; Shchukina & Trujillo Bueno 2003; Harvey, priv. comm.). Unfortunately, the uncertainty in these claims can be as large as a factor of two (Faurobert et al. 2001). There have been several studies of the CLV of the polarization signals associated with the quiet Sun magnetic fields (e.g., Martínez González et al. 2008; Lites et al. 2008; Lites 2011). However, to the best of our knowledge, nothing is known about the CLV of the quiet Sun magnetic BPs. This is precisely the subject of our work, i.e., providing a first observational description of the CLV of the quiet Sun BPs. To be specific, we evaluate how the area covered by quiet Sun BPs varies with the position on the disk.
Two main difficulties hinder the analysis. First, one has to use images of sufficient spatial resolution and uniform quality, since the number of BPs depends critically on the spatial resolution of the observations (Title & Berger 1996; Sánchez Almeida et al. 2010). This problem is resolved using data from the 1-m Swedish Solar Telescope (SST, Scharmer et al. 2003) obtained in a single day during moments of excellent seeing, and then restored to get images with uniform resolution close to the diffraction limit of the instrument (van Noort et al. 2005). Second, the BPs can be misidentified with granule borders and other structures (e.g., Bovelet & Wiehr 2007), a problem particularly severe in near-limb images. This second problem is addressed resorting to the cumbersome method of eye-ball identification which, however, has been proven to be reliable for our purposes (Sánchez Almeida et al. 2010, and references therein).
The work is organized as follows. The observations are presented in Sect. 2. The actual CLV measurements are described in Sect. 3. In principle, these measurements have to be interpreted using realistic models of magneto-convection (such as those used for plages by Carlsson et al. 2004; or Keller et al. 2004), where the 3-dimensional geometry of the photosphere is considered consistently. This approach would require repeating the analyses carried out on the observed images using synthetic images from the simulations. The CLV produced by a comprehensive battery of numerical simulations should then be compared with the observations. This detailed realistic approach clearly exceeds the scope of the work. However, we attempt a toy-modeling which, despite its simplicity, considers the key ingredients that within the hot-wall paradigm determine the CLV (Sect. 4). The model is compared with the observed CLV in Sect. 4.2, which constrains some of the properties of the magnetic structures. The implications for TSI variations are analyzed in Sect. 5. These results are discussed and put into context in Sect. 6.
2. Observations and data reduction
 |
Fig. 1 Images to illustrate how the quiet Sun G-band BPs look at different heliocentric angles – top μ = 0.99, bottom μ = 0.53. They correspond to the reference images in the series number 6 and 8, respectively (Table 1). Axes have units of arcsecs from the lower left corner. |
Quiet Sun inter-network regions away from active areas were observed on August 7, 2006, with the 1-m SST (Roque de los Muchachos Observatory, La Palma; Scharmer et al. 2003, 2002). The data consist of time series of images taken at eight different heliocentric angles, θ, with μ( = cosθ) ranging from 0.34 to 1. The logbook, in Table 1, includes the heliocentric angle of each series as well as the UT of each observation.
Description of the data sets including the fraction of covered surface (FCS).
The seeing was variable, with periods of excellence. As we explain below, we select for analysis only the best snapshots.
Images were simultaneously recorded in three channels, two of them in G-continuum (λ 4363.9 Å; FWHM 11 Å), yielding pairs of simultaneous in-focus and out-of-focus images for post-facto application of phase diversity (Paxman et al. 1992). The third channel, in the G-band (λ 4305.6 Å; FWHM 10.8 Å), is the one used for our analysis. Each camera continuously gathered images at a rate of some 100 min-1. An additional fourth channel was devoted to CaII H (λ 3968.5 Å; FWHM 1.1 Å), which was used during observations to avoid active regions in the field of view (FOV). We employed two 10-bit Kodak Mega Plus 1536 × 1024 cameras for G-continuum, a 12-bit Redlake Mega Plus II 1536 × 1024 camera for G-band, and a 10-bit Kodak Mega Plus 2024 × 2048 camera for CaII H. The image scale was 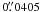 pix-1 in all cases.
pix-1 in all cases.
After dark-current subtraction, flatfielding, and elimination of spurious pixels and borders, the image restoration in the first three channels was performed simultaneously employing the multi-object multi-frame blind deconvolution method (MOMFBD; van Noort et al. 2005). Sets of ~30 images per channel (i.e., a total of ~3 × 30 images) were combined to produce a single pair of simultaneous G-band and G-continuum restored snapshots. Thus, we achieved two time series of restored images with a cadence of ~10 s, an effective FOV of 58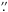 6 × 38
6 × 38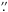 6, and an angular resolution close to the diffraction limit of the SST at the working wavelengths (~0
6, and an angular resolution close to the diffraction limit of the SST at the working wavelengths (~0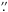 1). The images of these series were de-rotated to compensate diurnal field rotation, rigid-aligned, destretched to remove image distortion, and subsonic filtered to suppress p-modes and residual jitter stemming from destretching (Title et al. 1989).
1). The images of these series were de-rotated to compensate diurnal field rotation, rigid-aligned, destretched to remove image distortion, and subsonic filtered to suppress p-modes and residual jitter stemming from destretching (Title et al. 1989).
The final products of the reduction process were two time series (G-band and G-continuum) for each one of the eight heliocentric positions on the solar disk, with a duration ranging from 28 to 100 images (from 5 to 17 min) as summarized in Table 1. They represent a set with homogeneous angular resolution and covering a wide range of heliocentric angles. On the basis of their contrast, we selected the G-band image of the best quality around the middle of each time series. They are the reference images used in our CLV analysis. Examples of two of these images are shown in Fig. 1.
3. Center-to-limb variation of the solar surface occupied by bright points
We have measured the fraction of solar surface occupied by BPs in each one of the eight G-band reference images described in Sect. 2, which correspond to different heliocentric positions on the disk. From now we refer to this quantity as the fraction of covered surface (FCS).
The detection of BPs was performed by eye with the help of computer tools. The procedure was identical to that used by Sánchez Almeida et al. (2004, 2010), and can be briefly described as follows. The reference image of a particular time series is segmented with the algorithm by Strous (1994) that, based on the sign of the second derivative of the intensity at every image point, detects locally bright areas (i.e., areas brighter than their surroundings). The algorithm creates a binary mask with the pixels of the bright patches set to 1. Using an interactive program, we flick on the computer display the reference image and the binary mask, which allows us to identify coincidences between G-band BPs and small segmented patches. The BPs are selected one by one as those bright features fulfilling the following criteria: (1) matching a segmented patch in the binary mask; (2) overlying intergranular lanes; and (3) preserving identity in at least two frames around the reference image. We also select some faint bright features that are not clearly evident BPs in the reference image but which reveal themselves as such in the preceding or the following image. As a general policy doubtful structures are discarded. The procedure is carried out for two different saturation levels of the reference image on the computer display – low contrast to select the brightest and more evident BPs, and high contrast to identify weaker structures.
The area occupied by the BPs is calculated as the number of pixels corresponding to the selected BPs. The ratio of this area to the total number of pixels in the image provides the FCS. Thus, we get the FCS for every μ, as listed in Table 1. These values should be regarded as lower limits for three reasons: (1) we only include secure BPs; (2) the number of detections increases with the angular resolution, which is finite; and (3) the segmentation algorithm underestimates the area covered by the large BPs (Sánchez Almeida et al. 2010). As an argument for consistency, we point out that the FCSs at disk center are in agreement with that obtained from images of similar quality using the same method (Sánchez Almeida et al. 2010, ~0.9%), but are larger than those obtained from lower quality images (Sánchez Almeida et al. 2004, ~0.5%).
 |
Fig. 2 Measurements of the fraction of solar surface occupied by BPs, FCS, at eight heliocentric positions. Vertical bars represent the errors while horizontal bars show the range of heliocentric positions included in the finite extension of the FOV. The three different curves represent the three different solutions provided by our toy-model – the solid, the dashed, and the dot-dashed lines correspond to models a, b, and c in Table 2, respectively. |
The CLV of the FCS values are displayed in Fig. 2. Each symbol corresponds to one of the series, and includes error bars in both heliocentric angle and FCS. The horizontal error bars represent the range of μ in the FOVs. The vertical error bars have been estimated by dividing each full FOV into 24 non-overlapping subfields. They represent the standard deviation of the mean FCS, considering the various FCSs in the independent sub-fields. These error bars estimate the statistical error of the measurement. They do not account for the systematic errors stemming from the subjectivity of our BP identification.
4. Interpretation
4.1. A toy-model kG magnetic concentration
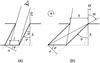 |
Fig. 3 a) Vertical section of the toy-model magnetic concentration used in the paper (the thick solid line). It represents a concentration of width a, tilted an angle ϕ with respect to the local vertical and observed at heliocentric angle θ. The symbols h and l are, respectively, the geometrical depth of the concentration and the portion of the bottom accessible to observation. b) For a given tilt angle ϕ, Θ and Θ′ represent the extreme inclination angles that allow us to observe the bottom of the magnetic concentration. The encircled plus symbol between the figures shows the positive sense of rotation used in our equations. |
In essence, a kG magnetic concentration represents a depression in the solar surface. Light comes from deeper photospheric layers that are usually hotter, and so the structure looks brighter. This basic idea, simplified to the extreme but retaining key ingredients, is considered in the 2-dimensional toy-model of magnetic concentration represented in Fig. 3a. It portrays the vertical section of a magnetic concentration of width a, which is located at an heliocentric angle θ. Owing to the evacuation, we see deeper through the magnetic concentration, and the difference in the geometrical depths with respect to the non-magnetic photosphere is denoted by h. The concentration can be inclined with respect to the local vertical, an inclination that we parameterize as ϕ. We assume that the magnetic concentration is bright only if our line-of-sight (LOS) reaches its bottom. In other words, the fraction of solar atmosphere that looks bright according to this model is proportional to l (see Fig. 3a). For a given configuration of the concentration (set by a,h, and ϕ), it appears only for a limited range of heliocentric angles, i.e., Θ′ < θ < Θ as illustrated in Fig. 3b. These extreme heliocentric angles are given by 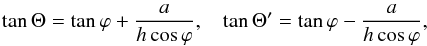 (1)with the natural constraints 0 < Θ < 90° and 0 ≤ Θ′ < Θ. Given an heliocentric angle θ within the proper interval (Θ′, Θ), the length of the concentration that is visible, l, turns out to be
(1)with the natural constraints 0 < Θ < 90° and 0 ≤ Θ′ < Θ. Given an heliocentric angle θ within the proper interval (Θ′, Θ), the length of the concentration that is visible, l, turns out to be 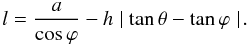 (2)The FOV contains a number of these idealized magnetic concentrations with different properties, therefore, within this toy-model, the FCS is proportional to the mean l averaged over the set of magnetic concentrations, ⟨ l ⟩
(2)The FOV contains a number of these idealized magnetic concentrations with different properties, therefore, within this toy-model, the FCS is proportional to the mean l averaged over the set of magnetic concentrations, ⟨ l ⟩ 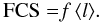 (3)The scaling factor f accounts for the number of concentrations per unit surface, the area of the individual concentrations, and possibly other factors of order unity associated with the fact that the magnetic concentrations do have a 3-dimensional structure not included in our 2-dimensional toy-model. In our case we additionally assume all concentrations to have the same a and h, but different inclinations2, with the tilt ϕ following a uniform distribution from − ϕ0 to + ϕ0 (ϕ0 < 90°). Consequently, our model for the CLV of FCS depends on three parameters, namely h/a,ϕ0, and af. It does not depend on h and a separately since the scaling factor af absorbs the dependence on a of l (see Eq. (3)). The closer to the limb, the higher in the photosphere we observe (e.g. Stix 1991), which does not contradict our assumption of h/a being independent of heliocentric angle. We assume that this systematic increase in altitude towards the limb affects the photosphere globally. In other words, both the magnetic concentrations and their surroundings are uplifted by the same amount, leaving unchanged the relative depth of the concentration h.
(3)The scaling factor f accounts for the number of concentrations per unit surface, the area of the individual concentrations, and possibly other factors of order unity associated with the fact that the magnetic concentrations do have a 3-dimensional structure not included in our 2-dimensional toy-model. In our case we additionally assume all concentrations to have the same a and h, but different inclinations2, with the tilt ϕ following a uniform distribution from − ϕ0 to + ϕ0 (ϕ0 < 90°). Consequently, our model for the CLV of FCS depends on three parameters, namely h/a,ϕ0, and af. It does not depend on h and a separately since the scaling factor af absorbs the dependence on a of l (see Eq. (3)). The closer to the limb, the higher in the photosphere we observe (e.g. Stix 1991), which does not contradict our assumption of h/a being independent of heliocentric angle. We assume that this systematic increase in altitude towards the limb affects the photosphere globally. In other words, both the magnetic concentrations and their surroundings are uplifted by the same amount, leaving unchanged the relative depth of the concentration h.
Parameters of the best fitting toy-model considering the eight heliocentric angles.
It is obviously difficult to justify the use of our toy-model based on its realism. The Sun is not 2-dimensional, the magnetic concentrations are not slabs, their walls are also bright, the non-magnetic background is not uniform, several concentrations may contribute along a single LOS, the depth h depends on the field strength, and so on and so forth. However, the model considers the basic physical ingredients responsible for the CLV of the FCS, i.e., the bright structures are depressed with respect to the mean photosphere, so that they may or may not be observed depending on their width, depth, and the relative orientation between their axes and the LOS. Moreover, the use of the proper 3-dimentional numerical models of magneto-convection is complicated, and clearly goes beyond the scope of the work (see Sect. 1). Using models that consider 3-dimensional magnetic flux-tubes fanning-out with height may be viewed as an intermediate alternative, but we disregarded this possibility from scratch since the analytic model becomes extremely complicated, and its realism remains way off that of the proper numerical simulations of magneto-convection (cf. Buente et al. 1993; with Carlsson et al. 2004; or Keller et al. 2004). The use of simplified models is also justified by the large scatter in the observed CLV (Fig. 2), provided that they only intend to explain general trends.
4.2. Results of the model
As we pointed out in the previous section, the CLV in our toy-model depends on only three independent parameters, that we choose to be h/a,ϕ0, and af. In order to determine which set of parameters reproduces the observation best, we carry out a least squares fit to determine the three free parameters. Since the model is non-linear, the fit has to be carried out using an iterative procedure for which we employ the standard Levenberg-Marquardt algorithm (e.g., Press et al. 1988). Non-linear least squares fits do not grant uniqueness. The algorithm seeks and finds local minima of the merit function (χ2), and if it has several, the best-fit parameters depend on the starting point. To get rid of this undesired dependence, we repeated the fit using 104 different initializations, where the starting h/a,ϕ0, and af were obtained from three independent uniform distributions spanning the full range of sensible values (0.2 ≤ h/a ≤ 4, 0° ≤ ϕ0 ≤ 89° and 5 × 10-4 ≤ af ≤ 5 × 10-1). The ensemble average needed to account the distribution of tilts from − ϕ0 to ϕ0 (see Sect. 4.1) was evaluated numerically from 104 samples drawn from a uniform distribution. The different initializations converge to essentially three different solutions. Table 2 summarizes the parameters characteristic of these three families – it gives the mean values among all solutions in the family plus the formal error bars provided by the χ2-minimization algorithm. The corresponding fits are plotted in Fig. 2. The most recurrent result (73% of the accepted solutions – a in Table 2) is also the most reliable since it represents the smallest χ2 close to 1 (Table 2). It corresponds to fairly shallow magnetic concentrations (aspect ratio h/a ≈ 3/5) with a large range of tilts (ϕ0 ≈ 64°). The second most common solution (b in Table 2) also corresponds to shallow magnetic concentrations (h/a ≈ 3/10) but they are vertical. Its χ2 is slightly larger than that for solution a. The third case is intermediate between a and b.
According to the model and its assumptions, one just sees as BPs a portion l of the surface, which is only a fraction of the true surface occupied by magnetic structures A – see Fig. 3. The two quantities agree when the LOS coincides with the axis of the concentration, but in general A ≥ l. In our toy-model the fraction of true surface that is observed as BP turns out to be ⟨ l ⟩ / ⟨ A ⟩ , where the brackets mean that we consider an ensemble of magnetic concentrations. The variation with heliocentric angle of this fraction is represented in Fig. 4. As one approaches the limb, most of the magnetic concentrations are no longer BPs – fewer than 20% of them at μ < 0.5. Figure 4 also shows how the solution with large range of magnetic field inclinations (a in Table 2, and the solid line in Fig. 2) hides a large fraction of the existing magnetic structures; only 60% of them are observed as BPs at the disk center.
 |
Fig. 4 Fraction of magnetized surface producing BPs. The three curves correspond to the predictions of our toy-model for the three solutions portrayed in Fig. 2. Note that magnetic structures no longer render BPs as one approaches the limb. |
 |
Fig. 5 Same as Fig. 2 but for fits to the six center-most data points describing the CLV. The solid line, the dashed line, the dot dashed line, and the triple-dot dashed line correspond to solutions d, e, f and g in Table 3, respectively. |
Parameters of the best fitting toy-model considering the six center-most fields.
The closer to the limb the more difficult the BP identification is (Sect. 2 and Fig. 1). To explore the effect of this uncertainty, we repeated the fits removing the two FOVs closest to the limb (μ = 0.34 and 0.53). The results are shown in Table 3 and Fig. 5. Table 3 reflects the presence of four families of solutions, all of them with similar χ2. The third most frequent result (f in Table 3 –17% of cases) depicts a shallow flux tube h/a ≈ 3/5 with a significant tilting range ϕ0 ≈ 46°, i.e., it looks quite similar to the main solution a in Table 2. However, the most common solution (40 % of cases – d in Table 3) represents a much deeper tube, h/a > 3, although with a similar tilting range (ϕ0 ≈ 52°). Finally, the solution e in Table 3 closely resembles that reported as solution c in Table 2. Removing the two most uncertain FCSs yields solutions similar to the full case, but it also introduces another possibility of rather slim magnetic concentrations (d in Table 3).
In short, the large scatter in the observations makes it easy to reproduce the CLV with our toy-model. The most favored solution corresponds to BPs being rather shallow structures with a large spread in vertical inclinations. This solution is not unique, and the model also allows for predominantly vertical structures and for narrow concentrations.
5. Fraction of solar disk covered by BPs
The function FCS(μ) describes the fraction of surface covered by BPs at each location on the Sun. Once FCS(μ) is known, the fraction of the solar disk covered by BPs can be determined by integration. The fraction of solar disk with a heliocentric angle between μ and μ + dμ is 2μ dμ (e.g., Foukal et al. 1991), hence, 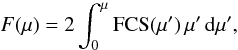 (4)provides the fraction of surface with BPs from the limb to μ. Obviously, F(1) represents the fraction covering the full Sun. The function F(μ) is given in Fig. 6b for the three solutions in Fig. 2. The three functions are very similar with F(1) ≃ 0.005, i.e., some 0.5% of the solar disk is covered by BPs. The disk center is the maximum contributor to this BP covering – 90% of the coverage is due to BPs at μ > 0.5, and half of it is associated with BPs at μ > 0.8 (Fig. 6b). Even though the above conclusions use the CLV of our toy-model, it is important to emphasize that they are independent of the assumptions upon which the model is based. The model CLVs are used here as smooth continuous approximations to describe the actual observations.
(4)provides the fraction of surface with BPs from the limb to μ. Obviously, F(1) represents the fraction covering the full Sun. The function F(μ) is given in Fig. 6b for the three solutions in Fig. 2. The three functions are very similar with F(1) ≃ 0.005, i.e., some 0.5% of the solar disk is covered by BPs. The disk center is the maximum contributor to this BP covering – 90% of the coverage is due to BPs at μ > 0.5, and half of it is associated with BPs at μ > 0.8 (Fig. 6b). Even though the above conclusions use the CLV of our toy-model, it is important to emphasize that they are independent of the assumptions upon which the model is based. The model CLVs are used here as smooth continuous approximations to describe the actual observations.
As we argue in the previous paragraph, most of the area occupied by BPs is at the disk center. It seems that any potential contribution of the quiet Sun magnetic fields to the TSI cannot come from the solar limb. To make this statement more quantitative, we follow the equations derived by Foukal et al. (1991) to write down the contribution of the BPs to the TSI, 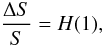 where
where ![\begin{equation} H(\mu)=\frac{1}{2}\int_0^\mu{\rm FCS}(\mu')\,\big[C(\mu')-1\big]\, (3\mu'+2)\,\mu'\,{\rm d}\mu'. \label{irrad} \end{equation}](/articles/aa/full_html/2012/03/aa18215-11/aa18215-11-eq119.png) (5)The symbol ΔS represents the change in the solar irradiance S produced by the quiet Sun BPs. The previous equation assumes an Eddington limb-darkening for the quiet Sun intensity. The parameter C(μ) is the contrast of the BPs relative to the mean intensity averaged over all wavelengths. (To clarify the meaning of ΔS/S, if BPs twice as bright as the mean photosphere fully cover the disk, i.e. C = 2 ∀ μ, then ΔS/S = 1.) As we explained above, the part of the integrand of Eq. (5) involving FCS is strongly biased towards the disk center. The only parameter that may counter-balance this effect is C. If C increases too rapidly with μ it may dominate the integrand, and hence the TSI. We ignore how C varies from center to limb, however, as an educated-guess to evaluate H(μ), we have assumed C to scale as the intensity variation we measure in the G-band. This CLV of the contrast in the G-band is given in Table 1 and corresponds to the symbols represented in Fig. 6a. Two smooth curves fitted to the observed points are also included in the figure – they consider the two extreme scenarios of the contrast remaining constant at the limb (the dotted line) or dropping down significantly (the triple-dot dashed line).
(5)The symbol ΔS represents the change in the solar irradiance S produced by the quiet Sun BPs. The previous equation assumes an Eddington limb-darkening for the quiet Sun intensity. The parameter C(μ) is the contrast of the BPs relative to the mean intensity averaged over all wavelengths. (To clarify the meaning of ΔS/S, if BPs twice as bright as the mean photosphere fully cover the disk, i.e. C = 2 ∀ μ, then ΔS/S = 1.) As we explained above, the part of the integrand of Eq. (5) involving FCS is strongly biased towards the disk center. The only parameter that may counter-balance this effect is C. If C increases too rapidly with μ it may dominate the integrand, and hence the TSI. We ignore how C varies from center to limb, however, as an educated-guess to evaluate H(μ), we have assumed C to scale as the intensity variation we measure in the G-band. This CLV of the contrast in the G-band is given in Table 1 and corresponds to the symbols represented in Fig. 6a. Two smooth curves fitted to the observed points are also included in the figure – they consider the two extreme scenarios of the contrast remaining constant at the limb (the dotted line) or dropping down significantly (the triple-dot dashed line).
 |
Fig. 6 a) Contrast of the BPs in the G-band as observed in our fields, C. The different smooth fits to the observed CLV. b) Fraction of total solar disk covered by BPs from the solar limb to a particular μ – F in Eq. (4). The three different types of line correspond to the three curves in Fig. 2. c) Fraction of TSI contributed by the quiet Sun BPs – H in Eq. (5). The three different types of thin lines correspond to the three curves in Fig. 2, with the contrast given by the triple-dot dashed line in a). The thick solid line is equivalent to the thin solid line except that the contrast is taken as the dotted line in a). |
Figure 6c displays H(μ) for the three solutions in Fig. 2 when we assume that the contrast decreases at the limb. They are very similar showing in all cases that the irradiance is strongly biased towards the disk center. This result is independent of whether the CLV of C has or not the drop at the limb – the thick solid line in Fig. 6c is equivalent to the thin solid line except that the used C maintains a constant value at the limb (the dotted line in Fig. 6a). From H(μ) in Fig. 6c one finds that 90% of the TSI originates in BPs with μ > 0.5, and some half of it is due to BPs with μ > 0.8.
The peak value of H is about 0.07% (Fig. 6c). It can be reproduced with the observed disk coverage of some 0.5% (Fig. 6b), assuming BPs with a typical contrast on the order of 1.15. This figure for the contribution of the quiet Sun magnetic fields to TSI is similar to the estimate in Schnerr & Spruit (2011) mentioned in Sect. 1. Actually, it is a factor of two smaller, but their estimate refers to the disk center observed at a different wavelength. In view of the uncertainties involved in this type of work, the coincidence is worth pointing out. The two estimates are completely different and yet provide consistent results.
6. Discussion and conclusions
We have measured the center-to-limb variation (CLV) of the area covered by G-band bright points (BPs) in the quiet Sun (FCS). This is a difficult parameter to determine because the detection of BPs critically depends on the angular resolution of the observation (Sect. 1). We employ several time series taken over two hours during moments of excellent seeing with the SST. The images were post-processed using MOMFBD (see Sect. 2), which provides a homogeneous set of images adequate for these subtle measurements. They were restored to provide an angular resolution close to the diffraction limit of the instrument at the working wavelength (some 0 1 at the G-band).
1 at the G-band).
We have found that the FCS reaches its largest value at disk center ( ≃ 1%), and then it drops down at μ ≃ 0.3 to become ≃ 0.2%. The relationship has a large scatter, which we managed to estimate by comparing different subfields within our FOVs (see the error bars in Fig. 2 and Table 1). The value obtained at the disk center agrees with previous estimates based on data of similar quality.
We have developed a toy-model to describe the observed CLV. The model assumes that the magnetic bright points are depressions in the mean solar photosphere, characterized by a depth, a width, and a range of inclinations. It is only an exploratory modeling that, nevertheless, includes the physical ingredients that seem to be responsible for the kG magnetic concentrations to show as bright features on the solar disk. The solutions offered by our toy-model are poorly constrained, but they seem to show that the BPs are shallow structures3 (ratio depth to width ≃ 0.7 ± 0.2) with a large spread of inclinations ( ≃ ± 70°).
Among others, the FCS is of interest because it determines the impact that quiet Sun magnetic fields may have on TSI variations, an influence so far unknown. Since the measured FCS is so peaked towards the disk center, any role that quiet Sun magnetic fields may have in changing the TSI will be due to the center of the disk. According to our estimate, 90% of the TSI is contributed by BPs with μ > 0.5, and half of it is due to BPs with μ > 0.8 (Sect. 5). This estimate is based on assuming that the CLV of the BP (wavelength-integrated) flux scales as the observed G-band intensity. It is an ad-hoc assumption adopted for lack of a better one which, however, has allowed us to provide a first constraint on the effect of quiet Sun BPs on TSI.
We stress that the FCS has been measured in the G-band because the magnetic concentrations are particularly conspicuous at this wavelengths. We then implicitly assume throughout the work that the FCS is the same at all wavelengths, i.e., that the area covered by magnetic concentration does not change with wavelength. (The G-band BPs are brighter but not bigger.) This assumption remains to be proven, but seems for the time being to be a reasonable working hypothesis.
Our toy-model suggests the BPs to be shallow structures with varied inclinations. One could test these predictions by observing polarization signals of quiet Sun BPs at the disk center. On the one hand, the polarization signals provide magnetic field inclinations by means of Stokes inversion (e.g., Socas-Navarro et al. 2008). On the other hand, assuming the magnetic concentrations to be in mechanical balance, one can infer their depths (e.g., Sánchez Almeida & Lites 2000). These inferences require low-noise spectro-polarimetry with an angular resolution similar to that of our G-band images. They represent a technical challenge, but these observations seem to be doable in the near future (see, e.g., Lagg et al. 2010). As we mentioned in the introduction, the existing numerical simulations of magneto-convection predict that the BPs are depressed with respect to the mean photosphere (e.g., Vögler et al. 2005; Vögler & Schüssler 2007). Whether the faint BPs observed in quiet Sun are predicted to be superficial or deep remains to be worked out. However, the existing simulations of plage magnetic concentrations suggest that the continuum intensity originates in a rather shallow region (Keller et al. 2004; Carlsson et al. 2004).
This result is not inconsistent with the magnetic concentrations producing BPs being modeled as a compactly packed ensemble of narrow magnetic concentrations arranged in a micro-structured magnetic atmosphere MISMA fashion (Sanchez Almeida et al. 1996; Sánchez Almeida 2000; Sánchez Almeida et al. 2001). The CLV of the FCS is sensitive to the global scale of the ensemble, whereas the MISMA accounts for the smallest scales responsible, among others, for the asymmetries of the spectral lines formed in the atmosphere.
Acknowledgments
This work has been partially funded by the Spanish Ministry of Science and Innovation through projects AYA2010–18029, ESP2006-13030-C06, ESP2003-07735-C04-04, and AYA2009-14105-C06. Financial support by the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484) is gratefully acknowledged. The SST is operated in the Spanish Observatorio del Roque de los Muchachos by the Institute for Solar Physics of the Royal Swedish Academy of Sciences.
References
- Beckers, J. M. 1977, in Illustrated Glossary for Solar and Solar-Terrestrial Physics, ed. A. Bruzek, & C. J. Durrant (Dordrecht: Reidel), 21 [Google Scholar]
- Bommier, V., Martínez González, M., Bianda, M., et al. 2009, A&A, 506, 1415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovelet, B., & Wiehr, E. 2007, Sol. Phys., 243, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Bovelet, B., & Wiehr, E. 2008, A&A, 488, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buente, M., Solanki, S. K., & Steiner, O. 1993, A&A, 268, 736 [NASA ADS] [Google Scholar]
- Cameron, R., Voegler, A., & Schuessler, M. 2011, A&A, 533, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., Stein, R. F., Nordlund, Å., & Scharmer, G. B. 2004, ApJ, 610, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, F. 1999, in Motions in the Solar Atmosphere, ed. A. Hanslmeier, & M. Messerotti, (Dordrecht: Kluwer), ASSL, 239, 119 [Google Scholar]
- de Wijn, A. G., Rutten, R. J., Haverkamp, E. M. W. P., & Sütterlin, P. 2005, A&A, 441, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Wijn, A. G., Lites, B. W., Berger, T. E., et al. 2008, ApJ, 684, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijn, A. G., Stenflo, J. O., Solanki, S. K., & Tsuneta, S. 2009, Space Sci. Rev., 144, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez Cerdeña, I., Kneer, F., & Sánchez Almeida, J. 2003, ApJ, 582, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez Cerdeña, I., Sánchez Almeida, J., & Kneer, F. 2006, ApJ, 636, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Faurobert, M., Arnaud, J., Vigneau, J., & Frish, H. 2001, A&A, 378, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faurobert-Scholl, M. 1993, A&A, 268, 765 [NASA ADS] [Google Scholar]
- Foukal, P., Harvey, K., & Hill, F. 1991, ApJ, 383, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, C. 2011, Space Sci. Rev., 133 [Google Scholar]
- Fröhlich, C., & Lean, J. 2004, A&ARv, 12, 273 [Google Scholar]
- Goode, P. R., Yurchyshyn, V., Cao, W., et al. 2010, ApJ, 714, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, M. L. 2004, A&A, 424, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harvey, J. W., Branston, D., Henney, C. J., & Keller, C. U. 2007, ApJ, 659, L177 [NASA ADS] [CrossRef] [Google Scholar]
- Jendersie, S., & Peter, H. 2006, A&A, 460, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keller, C. U., Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ, 607, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Lagg, A., Solanki, S. K., Riethmüller, T. L., et al. 2010, ApJ, 723, L164 [NASA ADS] [CrossRef] [Google Scholar]
- Lean, J. 1997, ARA&A, 35, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H., & Rimmele, T. 1999, ApJ, 514, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 2011, ApJ, 737, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, ApJ, 672, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Beck, C. 2008, A&A, 477, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moll, R., Pietarila Graham, J., Pratt, J., et al. 2011, ApJ, 736, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Paxman, R. G., Schulz, T. J., & Fienup, J. R. 1992, J. Opt. Soc. Am. A, 9, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovay, K., & Szakaly, G. 1993, A&A, 274, 543 [Google Scholar]
- Pietarila Graham, J., Cameron, R., & Schuessler, M. 2010, ApJ, 714, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1988, Numerical Recipes (Cambridge: Cambridge University Press) [Google Scholar]
- Sánchez Almeida, J. 2000, ApJ, 544, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J. 2003, A&A, 411, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Almeida, J. 2004, in The Solar-B Mission and the Forefront of Solar Physics, ed. T. Sakurai & T. Sekii (San Francisco: ASP), ASP Conf. Ser., 325, 115 [Google Scholar]
- Sánchez Almeida, J., & Lites, B. W. 2000, ApJ, 532, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., & Martínez González, M. 2011, in Solar Polarization 6, ed. J. R. Kuhn, D. M. Harrington, H. Lin, et al., ASP Conf. Ser., 437, 451 [Google Scholar]
- Sanchez Almeida, J., Landi Degl’Innocenti, E., Martinez Pillet, V., & Lites, B. W. 1996, ApJ, 466, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Asensio Ramos, A., Trujillo Bueno, J., & Cernicharo, J. 2001, ApJ, 555, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Emonet, T., & Cattaneo, F. 2003a, in Solar Polarization 3, ed. J. Trujillo-Bueno, & J. Sánchez Almeida (San Francisco: ASP), ASP Conf. Ser., 307, 293 [Google Scholar]
- Sánchez Almeida, J., Emonet, T., & Cattaneo, F. 2003b, ApJ, 585, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Márquez, I., Bonet, J. A., Domínguez Cerdeña, I., & Muller, R. 2004, ApJ, 609, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Teriaca, L., Sütterlin, P., et al. 2007, A&A, 475, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Almeida, J., Bonet, J. A., Viticchié, B., & Del Moro, D. 2010, ApJ, 715, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., Gudiksen, B. V., Kiselman, D., Löfdahl, M. G., & Rouppe van der Voort, L. H. M. 2002, Nature, 420, 151 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scharmer, G. B., Bjelksjo, K., Korhonen, T. K., Lindberg, B., & Petterson, B. 2003, in SPIE Conf. Ser., 4853, ed. S. L. Keil, & S. V. Avakyan, 341 [Google Scholar]
- Schnerr, R. S., & Spruit, H. C. 2011, A&A, 532, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2003, ApJ, 597, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M. 1986, in Small Scale Magnetic Flux Concentrations in the Solar Photosphere, ed. W. Deinzer, M. Knölker, & H. H. Voigt (Göttingen: Vandenhoeck & Ruprecht), 103 [Google Scholar]
- Shchukina, N. G., & Trujillo Bueno, J. 2003, in Solar Polarization Workshop 3, ed. J. Trujillo-Bueno, & J. Sánchez Almeida (San Francisco: ASP), ASP Conf. Ser., 307, 336 [Google Scholar]
- Socas-Navarro, H., Borrero, J. M., Asensio Ramos, A., et al. 2008, ApJ, 674, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 1993, Space Sci. Rev., 63, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1977, Sol. Phys., 55, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Stix, M. 1991, The Sun (Berlin: Springer-Verlag) [Google Scholar]
- Strous, L. H. 1994, Ph.D. Thesis, Utrecht University [Google Scholar]
- Title, A. M., & Berger, T. E. 1996, ApJ, 463, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Title, A. M., Tarbell, T. D., Topka, K. P., et al. 1989, ApJ, 336, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N. G., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Ballegooijen, A. A., Nisenson, P., Noyes, R. W., et al. 1998, ApJ, 509, 435 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Viticchié, B., Del Moro, D., Berrilli, F., Bellot Rubio, L., & Tritschler, A. 2009, ApJ, 700, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Viticchié, B., Del Moro, D., Criscuoli, S., & Berrilli, F. 2010, ApJ, 723, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Viticchié, B., Sánchez Almeida, J., Del Moro, D., & Berrilli, F. 2011, A&A, 526, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Parameters of the best fitting toy-model considering the eight heliocentric angles.
All Figures
 |
Fig. 1 Images to illustrate how the quiet Sun G-band BPs look at different heliocentric angles – top μ = 0.99, bottom μ = 0.53. They correspond to the reference images in the series number 6 and 8, respectively (Table 1). Axes have units of arcsecs from the lower left corner. |
| In the text | |
 |
Fig. 2 Measurements of the fraction of solar surface occupied by BPs, FCS, at eight heliocentric positions. Vertical bars represent the errors while horizontal bars show the range of heliocentric positions included in the finite extension of the FOV. The three different curves represent the three different solutions provided by our toy-model – the solid, the dashed, and the dot-dashed lines correspond to models a, b, and c in Table 2, respectively. |
| In the text | |
 |
Fig. 3 a) Vertical section of the toy-model magnetic concentration used in the paper (the thick solid line). It represents a concentration of width a, tilted an angle ϕ with respect to the local vertical and observed at heliocentric angle θ. The symbols h and l are, respectively, the geometrical depth of the concentration and the portion of the bottom accessible to observation. b) For a given tilt angle ϕ, Θ and Θ′ represent the extreme inclination angles that allow us to observe the bottom of the magnetic concentration. The encircled plus symbol between the figures shows the positive sense of rotation used in our equations. |
| In the text | |
 |
Fig. 4 Fraction of magnetized surface producing BPs. The three curves correspond to the predictions of our toy-model for the three solutions portrayed in Fig. 2. Note that magnetic structures no longer render BPs as one approaches the limb. |
| In the text | |
 |
Fig. 5 Same as Fig. 2 but for fits to the six center-most data points describing the CLV. The solid line, the dashed line, the dot dashed line, and the triple-dot dashed line correspond to solutions d, e, f and g in Table 3, respectively. |
| In the text | |
 |
Fig. 6 a) Contrast of the BPs in the G-band as observed in our fields, C. The different smooth fits to the observed CLV. b) Fraction of total solar disk covered by BPs from the solar limb to a particular μ – F in Eq. (4). The three different types of line correspond to the three curves in Fig. 2. c) Fraction of TSI contributed by the quiet Sun BPs – H in Eq. (5). The three different types of thin lines correspond to the three curves in Fig. 2, with the contrast given by the triple-dot dashed line in a). The thick solid line is equivalent to the thin solid line except that the contrast is taken as the dotted line in a). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


