| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117697 | |
| Published online | 21 February 2012 | |
Thermal stresses in small meteoroids
II. Effects of an insulating surface layer
1 Astronomical Institute of the Academy of Sciences, Fričova 298, 251 65 Ondřejov, Czech Republic
e-mail: capek@asu.cas.cz
2 Institute of Astronomy, Charles University, V Holešovičkách 2, 180 00 Prague 8, Czech Republic
e-mail: vokrouhl@cesnet.cz
Received: 14 July 2011
Accepted: 2 November 2011
Aims. We extend our previous analysis of thermal stresses in small, spherical and homogeneous meteoroids by taking into account the effects of a surface insulating layer.
Methods. Using analytical computations, we determine the temperature distribution in a spherical inhomogeneous body smaller than ~10 cm with a high-conductivity core and a low-conductivity surface layer. Our main approximation consists in (i) linearization of the surface energy-conservation constraint and (ii) omission of the seasonal effects in the Fourier spectrum of the incident solar radiation flux. Using the temperature solution, we analytically compute the mechanical (thermal) stress field in the core, neglecting its effects in the particulate surface layer. Conditions for material failure in the whole volume of the body are analyzed. In particular, we pay attention to whether the surface layer depth evolves toward an equilibrium situation.
Results. As the meteoroid approaches the Sun, the thermal stress first exceeds the material strength at the surface of meteoroid. If the fractured material is able to stay on meteoroid, a particulate shell begins to form. After one revolution about the Sun, this process is roughly completed. We determine the dependence of its thickness on perihelion distance, spin axis orientation with respect to the Sun, and the size of meteoroid. We estimate the distribution of the final depths of the surface layer for eight major meteoroid showers with perihelion distances smaller than 1 AU.
Key words: minor planets, asteroids: general / methods: analytical / meteorites, meteors, meteoroids
© ESO, 2012
1. Introduction
In a previous paper Čapek & Vokrouhlický (2010, CV1), we developed an analytic approach to determining the thermal stress field in a small, spherical, and homogeneous meteoroid. Since the coupling between the thermal and mechanical state of the body was only “unidirectional” in our approach, namely temperature gradients produce mechanical stress but the stresses themselves do not act as a source of thermal energy, we proceeded in two separate steps: (i) we first solved the temperature distribution in the whole volume of the body; and (ii) we then used this information to determine the mechanical stresses in the body, including those caused by thermal gradients and the related differential volume expansion effects. Both problems are solved as a continuum model with appropriate boundary conditions.
In CV1, we identified several restrictive assumptions, which represent the limitations of our theory when attempting to compare its predictions with the observations. For instance, we included the diurnal (rotational) variations of the solar flux for a given surface element, but neglected the seasonal effects caused by the heliocentric orbital motion. This makes the theory applicable to bodies smaller than several meters in size (see discussion in CV1 for details). Another important approximation of CV1 was that of the homogeneity of the body. Nevertheless, it was noted that the thermal stresses may first overcome the material failure threshold in the subsurface region and result in the formation of a damaged zone. This might have a regulatory, feedback effect on the whole process of mechanical damage because of the thermal stresses. The granular, particulate surface layer, which is characterized by a lower value of the thermal conductivity, may start to thermally shield the interior regions in the body, halting thus further propagation of the thermal damage.
In an attempt to understand these processes in more detail, we develop here a theory of thermal stresses in a small (size ≤ 10 cm), spherical but inhomogeneous body. To conserve the advantages of the analytical approach of CV1, we restrict our analysis to a simple model for the inhomogeneity, namely assuming two layers consisting of a core covered with a surface layer of spherical symmetry.
In Sect. 2, we first generalize our analytical model of the temperature field in a spherical body to the case of a core covered with a surface layer of different thermal properties. We also discuss how the results in CV1 might be straightforwardly used to determine the associated stress field. A description of our numerical experiments is given in Sect. 4 and our conclusions are summarized in Sect. 5.
2. Theory
2.1. Formulation of the problem
As in CV1, we assume that the body (meteoroid) has a simple spherical shape of radius R. We use spherical coordinates (r,θ,φ) with an origin at the center of the body and an angle θ measured from the rotation axis. The latter is assumed to be fixed in the inertial space and the body rotates with constant angular frequency ω = 2π f (where f is the spin frequency in Hz).
Unlike in CV1, we do not assume that the body is homogeneous, but that it is a compound of two homogeneous, but unequal parts: (i) a surface layer of a thickness h; and (ii) a core with radius RB = R − h. The particulate, granular surface layer is assumed to have different mechanical and thermal properties than the monolitic core. As we later show (Sect. 2.2), the fundamental parameter in our solution is 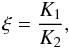 (1)where K1 and K2 is the thermal conductivity in the surface layer and the core. Owing to the nature of the composition assumptions, we always assume that ξ ≤ 1, with typical values between 0.1 and 1. At a given position on the heliocentric orbit, h is assumed to be constant, but overall its value may change as the body moves along the orbit responding to a mechanical damage of the subsurface region by thermal stresses. The characteristic timescale over which h grows is thus assumed to be longer than the rotation period of the body, but much shorter than the revolution period about the Sun.
(1)where K1 and K2 is the thermal conductivity in the surface layer and the core. Owing to the nature of the composition assumptions, we always assume that ξ ≤ 1, with typical values between 0.1 and 1. At a given position on the heliocentric orbit, h is assumed to be constant, but overall its value may change as the body moves along the orbit responding to a mechanical damage of the subsurface region by thermal stresses. The characteristic timescale over which h grows is thus assumed to be longer than the rotation period of the body, but much shorter than the revolution period about the Sun.
Since we assume that the surface layer consists of particulate material, we neglect the effects of mechanical stresses in this part of the body. Two extreme approaches can then be adopted: (i) the surface layer is never removed from the body, assuming that the electrostatic and molecular sticking of its particles is able to resist either centrifugal or tidal effects (e.g., Scheeres et al. 2010), and it only increases in size; or (ii) the surface layer, or its part, could be removed under some conditions by centrifugal or tidal accelerations. We deal with the first case and the second one is postponed to a forthcoming paper. Despite the mechanical stress field not beeing solved in the surface layer in our approach, we still need to solve the temperature field in this part of the body. This is because it can have an insulating influence and affect the temperature distribution, and thus the thermal stress field, in the core. The growth of the surface layer can thus play a very important regulatory effect on the mechanical integrity of the whole body.
In the same way as the depth h of the surface layer is assumed to be constant in our solution, the solar position with respect to the rotation axis of the body is also assumed to be constant. In other words, we neglect the orbital motion of the body about the Sun and solve its thermal, and mechanical, state at a given heliocentric position. This assumption has a subtle consequence related to the time variation in the solar flux at the surface of the body that means our theory is valid only for objects of a size smaller than several meters (more details are given in CV1). In the present study, we assume that bodies have dimensions ≤ 10 cm. As the body moves along a given orbit about the Sun, its mutual geometric configuration with respect to the spin axis of the body changes. However, we model this effect in a quasi-static way, assuming that diurnal thermal relaxation at a given point on the orbit is faster than the orbital drift to a consecutive point.
In the first step of our approach, we develop a general solution of the temperature distribution in both the core and the surface layer. The general concepts and the solution for the core are discussed in Sect. 2.2, while details and the solution for the surface layer are described in Appendix A. We then use the temperature field solution in the core to derive the associated mechanical stress in Sect. 2.3.
2.2. Temperature distribution
Neglecting volumic sources of energy, the distribution of temperature T(r,t) in the continuum is determined by the heat diffusion (Fourier) equation 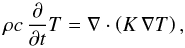 (2)complemented with appropriate boundary conditions. In our case of the two-layer body, we have a simpler form
(2)complemented with appropriate boundary conditions. In our case of the two-layer body, we have a simpler form 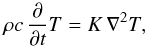 (3)in each of the volume parts where the thermal parameters, the conductivity K, the specific heat capacity c, and the bulk density ρ are all constant. The generic boundary conditions are (i) the regularity of the solution throughout the volume of the body (including the center); and (ii) the energy conservation at the surface. The latter can be expressed as
(3)in each of the volume parts where the thermal parameters, the conductivity K, the specific heat capacity c, and the bulk density ρ are all constant. The generic boundary conditions are (i) the regularity of the solution throughout the volume of the body (including the center); and (ii) the energy conservation at the surface. The latter can be expressed as 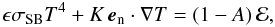 (4)where ϵ is the thermal emissivity, σSB = 5.67 × 10-8 W m-2 K-4 is the Stefan-Boltzmann constant, en is the unit outer normal to the surface, A represents the albedo value, and ℰ is the solar radiation flux. At the boundary layer ℬ between the two parts with different values of thermal parameters in the body, the solution must satisfy continuity of the temperature T and the heat flux eb·K∇T, where eb is the normal vector to ℬ. Denoting with [ ] ± the respective limits from the two sides of ℬ, we have
(4)where ϵ is the thermal emissivity, σSB = 5.67 × 10-8 W m-2 K-4 is the Stefan-Boltzmann constant, en is the unit outer normal to the surface, A represents the albedo value, and ℰ is the solar radiation flux. At the boundary layer ℬ between the two parts with different values of thermal parameters in the body, the solution must satisfy continuity of the temperature T and the heat flux eb·K∇T, where eb is the normal vector to ℬ. Denoting with [ ] ± the respective limits from the two sides of ℬ, we have ![\begin{eqnarray} \left[T\right]_- &=& \left[T\right]_+ \! , \label{bc2} \\ \left[K\vec{e}_\mathrm{b}\cdot \nabla T\right]_- &=& \left[K\vec{e}_\mathrm{b}\cdot \nabla T\right]_+ \! . \label{bc3} \end{eqnarray}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq36.png) Since we assume that the surface layer is a spherical shell with thickness h, ℬ is simply a sphere with radius RB. In this case, both vectors en and eb are equal to the radial unit vector er = ∂r/∂r, and er·∇T = ∂T/∂r for the boundary conditions given in Eqs. (4) and (6) above.
Since we assume that the surface layer is a spherical shell with thickness h, ℬ is simply a sphere with radius RB. In this case, both vectors en and eb are equal to the radial unit vector er = ∂r/∂r, and er·∇T = ∂T/∂r for the boundary conditions given in Eqs. (4) and (6) above.
As in CV1, we assume that the temperature T is always close to a properly chosen average value Tav, namely T = Tav + ΔT with ΔT ≪ Tav. This justifies the linearization of the troublesome fourth-order term 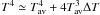 in the boundary condition given in Eq. (4) and enables an analytic solution of the problem. The average temperature is determined from
in the boundary condition given in Eq. (4) and enables an analytic solution of the problem. The average temperature is determined from 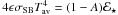 , where ℰ ⋆ is the solar flux at a given heliocentric distance (e.g., Vokrouhlický 1998).
, where ℰ ⋆ is the solar flux at a given heliocentric distance (e.g., Vokrouhlický 1998).
Adopting a parametrization of the surface elements using spherical angles (θ,φ), we have 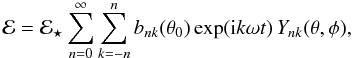 (7)where θ0 is the colatitude of the solar direction in the body-frame system (assumed constant in our model) and
(7)where θ0 is the colatitude of the solar direction in the body-frame system (assumed constant in our model) and 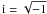 . The functions bnk(θ0) were given in CV1 and read (see also Vokrouhlický 2006)
. The functions bnk(θ0) were given in CV1 and read (see also Vokrouhlický 2006) 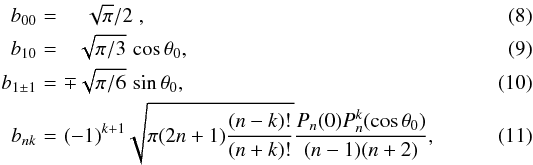 where the last row applies for n ≥ 2, and Pn and
where the last row applies for n ≥ 2, and Pn and 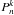 are Legendre polynomials and the associated Legendre functions respectively. We note that Pn(0) = 0 for n odd such that only even-degree terms appear in the insolation given in Eq. (7) for n ≥ 2.
are Legendre polynomials and the associated Legendre functions respectively. We note that Pn(0) = 0 for n odd such that only even-degree terms appear in the insolation given in Eq. (7) for n ≥ 2.
Similarly to the insolation term in Eq. (7), the temperature field can also be expressed using a mixed Fourier and spherical-harmonics expansion 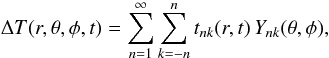 (12)where the Fourier part in the amplitude functions tnk(r,t) ∝ exp(ikωt). Some details of the solution are given in the Appendix A, while here we provide a solution for the temperature distribution in the solid core (i.e., for r < RB = R − h) that is relevant to determination of the thermal stress field.
(12)where the Fourier part in the amplitude functions tnk(r,t) ∝ exp(ikωt). Some details of the solution are given in the Appendix A, while here we provide a solution for the temperature distribution in the solid core (i.e., for r < RB = R − h) that is relevant to determination of the thermal stress field.
First, we discuss the zonal (axisymmetric) part of the solution with k = 0 (Vokrouhlický & Brož 1999). Since the isolation terms are time-independent in this case, the Fourier equation in Eq. (3) simplifies to the Laplace equation with the characteristic regular solution 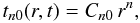 (13)(where we note that the time dependence is in fact a dummy here). The constants Cn0 are to be determined from the boundary conditions (see Appendix A). We obtain
(13)(where we note that the time dependence is in fact a dummy here). The constants Cn0 are to be determined from the boundary conditions (see Appendix A). We obtain ![\begin{equation} C_{n0} = \frac{T_\mathrm{av}}{R^n\Psi_n}\, \frac{b_{n0}(\theta_0)}{1+ \Lambda_1 n} \, \left[1-\frac{n\left(1-\xi\right)}{n+ \left(n+1\right)\xi}\right] , \label{cn0} \end{equation}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq63.png) (14)where
(14)where 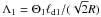 and
and 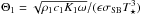 is the thermal parameter derived from the physical quantities (ρ1,c1,K1) of the surface layer and
is the thermal parameter derived from the physical quantities (ρ1,c1,K1) of the surface layer and 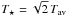 is the subsolar temperature. The scaling parameter
is the subsolar temperature. The scaling parameter 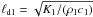 is called the penetration depth of the surface thermal wave, and the auxiliary function Ψn is defined to be
is called the penetration depth of the surface thermal wave, and the auxiliary function Ψn is defined to be 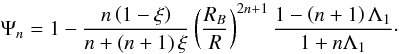 (15)The solution for the tesseral (non-axisymmetric) modes with k ≠ 0 is given by (see also CV1)
(15)The solution for the tesseral (non-axisymmetric) modes with k ≠ 0 is given by (see also CV1) 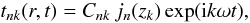 (16)jn(z) denoting the spherical Bessel function of the first kind with a complex argument
(16)jn(z) denoting the spherical Bessel function of the first kind with a complex argument 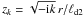 . We note, in particular, the scaling of the radial coordinate r by the penetration depth
. We note, in particular, the scaling of the radial coordinate r by the penetration depth 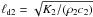 determined by the physical parameters (ρ2,c2,K2) of the core. The constants Cnk are again to be determined from the boundary conditions. A somewhat lengthy computation yields
determined by the physical parameters (ρ2,c2,K2) of the core. The constants Cnk are again to be determined from the boundary conditions. A somewhat lengthy computation yields 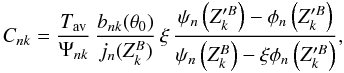 (17)where
(17)where  with yn(z) the spherical Bessel function of the second kind (sometimes also called the spherical Neumann function). Their arguments are computed at the boundary distance RB and scaled either by the thermal penetration depth ℓd1 in the surface layer,
with yn(z) the spherical Bessel function of the second kind (sometimes also called the spherical Neumann function). Their arguments are computed at the boundary distance RB and scaled either by the thermal penetration depth ℓd1 in the surface layer, 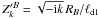 , or the thermal penetration depth ℓd2 in the core,
, or the thermal penetration depth ℓd2 in the core, 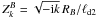 1. The Ψnk functions are then given by
1. The Ψnk functions are then given by ![\begin{eqnarray} \Psi_{nk} &=& \frac{j_n\left(Z^\prime_k\right)}{j_n\left(Z^{\prime B}_k\right)} \left[1+\Lambda_1\psi_n\left(Z^\prime_k\right)\right]\label{cpsink}\nonumber \\ & & -\frac{y_n\left(Z^\prime_k\right)}{y_n\left(Z^{\prime B}_k\right)} \frac{\psi_n\left(Z^B_k\right)-\xi\psi_n\left(Z^{\prime B}_k\right)} {\psi_n\left(Z^B_k\right)-\xi\phi_n\left(Z^{\prime B}_k\right)} \left[1+\Lambda_1\phi_n\left(Z^\prime_k\right)\right], \end{eqnarray}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq87.png) (20)where
(20)where 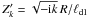 .
.
One can easily check the various limits of our general solution for the temperature distribution in the core, thus justifying its validity. For instance, with the same thermal parameters of the surface layer and the core we recover results from CV1 that are valid for a homogeneous body2. The same is true when taking the limit h → 0, namely shrinking the surface layer to zero. While this can be computed analytically3, the case of a small, but nonzero h/R value requires special attention in numerical applications. Another interesting limit is that of ξ → 0, namely of a very low conductivity surface layer. In this case, we note that both Cn0 and Cnk are proportional to ξ, thus the temperature field in the core vanishes or is significantly reduced. This confirms our intuition that the perfectly insulating surface layer should entirely shield the core region from temperature variations driven by solar irradiation. In this case both, the thermal gradients and the related mechanical stress field, would also be diminished.
2.3. Thermal stress field in the core
After developing an analytical solution to the temperature distribution in the core, we may now directly apply our results from Sects. 2.3 and 3.1 of CV1 to derive the associated thermal stress field, as described below. We recall that we assume a granular, particulate character for the surface layer that does not support mechanical stress and thus we may still use the boundary condition for a free, unloaded surface of the core (Eq. (19) in CV1). The analytical solution from CV1 is thus modified by taking (i) different expression for Cn0(θ0) and Cnk(θ0); and (ii) the boundary (surface) condition at different distance from the center, namely r = RB.
2.3.1. Time-independent part of the thermal stress tensor
First we provide explicit formulae for the stationary (zonal) part of the thermal stress. We use the auxiliary functions Fn(λ,μ) and Gn(r) from Eqs. (34) and (35) in CV1, and Cn0(θ0) from (14) above. Introducing the scaled radial coordinate x = r/R ≤ RB/R, the only non-zero components of the stationary stress tensor are ![\begin{eqnarray} \label{eqTSstat1} \tau_{\rm rr} &=& \bbigz{\bigz{\frac{R_B}{R}}^2-x^2} \sum_{n=2}^\infty n(n-1)\,G_n(r)\, Y_{n0}(\theta,\phi) , \\ \tau_{\rm r\theta} &=& \bbigz{\bigz{\frac{R_B}{R}}^2-x^2} \sum_{n=2}^\infty \,(n-1)\,G_n(r)\, \dth Y_{n0}(\theta,\phi) , \\ \tau_{\rm \theta\theta} &=& \sum_{n=2}^\infty G_n(r)\,\left\{n\left[ \bigz{\frac{R_B}{R}}^2-\left(2n+1\right)x^2\right]\,Y_{n0}(\theta, \phi)\right. \nonumber \\ & & \qquad\quad\quad\;\; \left.+\bbigz{\bigz{\frac{R_B}{R}}^2-3x^2}\, \parderii{}{\theta}Y_{n0}(\theta,\phi)\right\},\\ \tau_{\rm \phi\phi} &=& \sum_{n=2}^\infty G_n(r)\,\left\{n\left[\left(n+2\right) x^2-n\bigz{\frac{R_B}{R}}^2\right]\,Y_{n0}(\theta,\phi)\right. \nonumber \\ & & \qquad\quad\quad\;\; \left.-\bbigz{\bigz{\frac{R_B}{R}}^2-3x^2}\, \parderii{}{\theta}Y_{n0}(\theta,\phi)\right\}.\label{eqTSstat2} \end{eqnarray}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq99.png) For zero depth of the surface layer, we thus have RB = R, and these expressions become Eqs. (36)–(39) in CV1.
For zero depth of the surface layer, we thus have RB = R, and these expressions become Eqs. (36)–(39) in CV1.
2.3.2. Time-dependent part of the thermal stress tensor
The time-dependent (tesseral) part of the stress tensor cannot be expressed in a compact form similar to the time-independent part above. However, it can be obtained from a system of Eqs. (42) and (43) in CV1 (k ≠ 0) 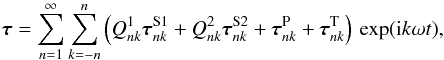 (25)where two independent spheroidal modes
(25)where two independent spheroidal modes 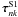 and
and 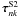 are given by Eqs. (44)–(55) in CV1. The stress corresponding to the particular solution
are given by Eqs. (44)–(55) in CV1. The stress corresponding to the particular solution 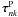 , and stress caused by volumetric expansion in the generalized Hook’s law
, and stress caused by volumetric expansion in the generalized Hook’s law 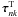 , can be computed from Eqs. (56)–(64) in CV1, where only the coefficient Cnk(θ0) is now given by Eq. (17) above. The coefficients
, can be computed from Eqs. (56)–(64) in CV1, where only the coefficient Cnk(θ0) is now given by Eq. (17) above. The coefficients 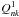 and
and 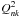 can be expressed using Eqs. (65)–(67) in CV1, but we have to substitute
can be expressed using Eqs. (65)–(67) in CV1, but we have to substitute 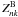 for Znk and RB for R.
for Znk and RB for R.
3. Summary of model parameters
To apply our theory either to specific bodies or their populations, such as known meteoroid streams, we must use specific values for a number of free parameters in the formulae outlined above. Since we do not aim to provide a complete analysis of this parameter space in this paper, we fixed values for many of them, thus testing the dependence of the results on a very restricted set of parameters. Interested readers may wish to change our fixed-parameter values and recompute our results for their particular applications.
We assume that the monolithic core has a composition of carbonaceous or ordinary chondrite materials with the same thermal properties (bulk density ρ, thermal conductivity K, heat capacity c) and mechanical properties (Lamé’s parameters λ and μ, linear coefficient of thermal expansion α an uniaxial tensile strength σt) as summarized in CV1, Sect. 2.5. While these parameters depend on temperature (Eqs. (22)–(32) in CV1), here we only recall their values for 300 K: ρ = 3560 kg m-3, K = 3.05 W m-1 K-1, c = 847 J K-1 m-1, λ = 36.2 GPa, μ = 29.1 GPa, α = 9.69 × 10-6 K-1and σt = −32 MPa for ordinary chondrite. Similarly, values of these parameters for carbonaceous chondrite are: ρ = 2260 kg m-3, K = 0.75 W m-1 K-1, λ = 17.2 GPa, μ = 17.6 GPa, σt = −2 MPa. Values of c and α are assumed to be the same as for the ordinary chondrites.
As described above, the particulate (granular) nature of the surface layer, makes it insensitive to the mechanical stress. To reduce the number of free parameters, we assume that the thermal parameters c and ρ in the core and the surface layer are identical. This assumption is partly justified because the thermal stress tensor is less sensitive to these parameters (which appear only in terms of the penetration depths ℓd1 and ℓd2), while the principal parameter is the ratio of the thermal conductivity in the surface layer to that in the core ξ = K1/K2 (Eq. (1)). We consider three test cases: (i) ξ = 1, which permits a comparison with the results in CV1 and thus a reference solution where effects studied in this paper are not included; (ii) ξ = 0.5; and (iii) ξ = 0.1, which correspond to an increasing level of thermal shielding of the core, presumably by a finer-grain surface layer. We find that these ratios are plausible, given the various laboratory measurements of granular and monolithic meteoritic samples (e.g., Yomogida & Matsui 1983; Beech et al. 2009; Opeil et al. 2010).
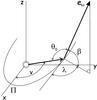 |
Fig. 1 Geometric parameters of our model: the orbital plane of meteoroid’s heliocentric motion defines the xy plane of our reference system with x-axis oriented toward the perihelion Π. Instantaneous position of the body along its orbit is given by the true anomaly v. The orientation of the spin axis eω is specified by longitude λ and latitude β; the solar colatitude in the body-frame, with the z′-axis along eω, is denoted θ0. |
Parameters related to the heliocentric motion of the body and orientation of its spin axes are shown in Fig. 1. For the sake of simplicity, we assume that the orbital plane coincides with the xy plane of the reference system and that the x axis is oriented toward the perihelion (Π) direction. The z axis is aligned along the orbital angular momentum and no restrictions on the semimajor axis and eccentricity are made. The direction of the spin axis eω is defined in our reference system by longitude λ ∈ ⟨ 0°,360°) and latitude β ∈ ⟨90°, −90°⟩. The solar colatitude θ0 ∈ ⟨0°,180°⟩ is the angle between spin axis and the direction to the Sun. Defining the true anomaly, v, as the polar angle of the position vector of the body in the xy plane, we thus have a simple relation 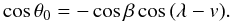 (26)The spin frequency f for all cases studied below is assumed to be inversely proportional to the size D, such that
(26)The spin frequency f for all cases studied below is assumed to be inversely proportional to the size D, such that 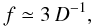 (27)where D is the diameter of the body in meters and f is the frequency in Hertz (see Eq. (68) in CV1). This relationship between f and D roughly matches the observations of centimeter to decimeter sized meteoroids reported by Beech & Brown (2000). With this value of f for D ≤ 10 cm meteoroids, the time-dependent part of the temperature and thermal stress tensor fields are pushed to a very narrow slab near the surface. The static parts of the fields thus approximate the total fields very well in most of the volume of the body. We nevertheless use the complete formulation in what follows.
(27)where D is the diameter of the body in meters and f is the frequency in Hertz (see Eq. (68) in CV1). This relationship between f and D roughly matches the observations of centimeter to decimeter sized meteoroids reported by Beech & Brown (2000). With this value of f for D ≤ 10 cm meteoroids, the time-dependent part of the temperature and thermal stress tensor fields are pushed to a very narrow slab near the surface. The static parts of the fields thus approximate the total fields very well in most of the volume of the body. We nevertheless use the complete formulation in what follows.
4. Results
In CV1, we assumed that the destruction of meteoroids caused by thermal stresses takes place when the Griffith criterion of the brittle fracture is fulfilled at the center of a homogeneous spherical meteoroid. For the given material parameters, we sought the heliocentric distance, meteoroid size, spin axis orientation, and rotation frequency for which a homogeneous and isotropic body cannot exist unfractured. However, the real process of destruction of the meteoroid by thermal stresses is more complicated. As the meteoroid approaches the Sun, thermal stresses first exceed the material strength near the surface. One may then consider two possible end-state situations:
-
The fractured material at the surface is immediately removed bythe transformation of elastic energy into kinetic energy during thecrack formation (e.g., Jewitt & Li 2010), or owing to centrifugal forces. In thiscase, the thermal stress results in erosion of the meteoroid,reducing its size. We plan to consider this possibility in moredetail in a forthcoming paper.
-
The fractured material remains at the surface, possibly owing to either molecular sticking (Scheeres et al. 2010) or an insufficiently interconnected system of fractures. This process leads to a gradual growth of the fractured volume near the surface, the physical and mechanical properties of which may be different from those of the core (interestingly, recent laboratory experiments have demonstrated that the thermal fatigue is able to disintegrate the surface of NEAs, producing a low-conductivity regolith layer, Delbo et al. 2011). The fractured part of a meteoroid propagates deeper into the body as it approaches the Sun. The meteoroid is no longer a homogeneous body and description of thermal stresses by the theory from CV1 is not self-consistent.
In this paper, we adopt the second possibility and explore its consequences by using the two-layer thermo-mechanical theory developed in Sect. 2. The assumption of an exactly spherical surface shell is obviously only a simplification given the non-spherical heating of the surface by solar radiation. As an example, Fig. 2 shows four snapshots of the thermal stress field in the meridional plane of a spherical, 10 cm size Geminid meteoroid during its approach to the perihelion. Unlike below, in this example we only use the theory of CV1 assuming a homogeneous body. The dashed regions denote areas where the brittle fracture criterion has been satisfied and fractures are being built. The top two panels show how the surface layer gradually grows. Neither of these cases are exactly spherical, but taking their deepest point near the rotational poles for h would provide a reasonable approximation. Closer to perihelion, as represented in bottom panels, the fractured domain is of a more complex shape. However, in the real situation the previously formed insulating surface layer may prevent the damage propagating to close to the center of the body. We adopt this more precise modeling in the following sections, thus taking a record of the thermo-mechanical state of the body along its approach to the pericenter. Performing a number of experiments, we found that our spherical-shell approximation only fails when θ0 is close to its extreme values of 0° or 180°, i.e. when the spin axis of the body is directly oriented toward the Sun. In this case, the brittle failure quickly propagates towards the center along the equatorial zone of the body and is not accurately represented by a spherical shell. Fortunately, these configurations represent only a minority of our studied cases.
 |
Fig. 2 Propagation of a damaged volume, where the thermal stress exceeds the material strength (dashed areas), inside a meteoroid approaching the Sun. We show here the situation in the meridional plane with the spin pole (λ = 0°, β = 45°) pointing up and use the homogeneous-body model from CV1 for simplicity (because the time-dependent part of the stress field is pushed to a very small surface shell, not seen in this resolution, the global stress field in the body is roughly axisymmetric and accurately approximated by the zonal part of the stress field). The 10-cm size meteoroid was placed on a Geminid-stream orbit and assumed to have the thermal and mechanical parameters of carbonaceous chondrites. At large heliocentric distance, the damaged zone first takes a shape of polar caps (top and left panel a)), which then propagate more deeply into the body. At a distance of 0.35 AU from the Sun, the fractured volume has a shape of a near-spherical shell, which is thicker at the poles (top and right panel b)). Closer to the perihelion, bottom panels, the damaged zone takes a more complex shape. However, when the previously developed surface insulating layer begins to thermally shield the core (used in Sects. 4.1 to 4.3), the damaged zone will stop propagating deeper to the center. The arrows indicate the direction toward the Sun. |
4.1. Surface layer depth for β = 90°
To obtain an indication of the protection role of the surface insulating layer, we first perform a simple numerical experiment. We consider meteoroids of different size D approaching the Sun at distance d along an elliptic orbit, but fixing their spin axis to be perpendicular to the orbital plane (thus β = 90°, implying also θ0 = 90°). During the solar approach, we study the depth h(D,d) of the surface layer to prevent any brittle fracture deeper in the core.
The method for determining h(D,d) is as follows. Selecting D in the range from 1 mm to 10 m4, we proceed from a large enough d value, such that the body does not suffer any thermal damage, to its smallest value 0.1 AU (as if the body was approaching the Sun). We start with a homogeneous model of CV1 and verify whether the thermal stresses in the whole volume of the body are smaller that the condition for brittle fracture. Proceeding toward smaller d values, we note the onset of the damage zone near the surface. From this value of d, we use our two-layer model from Sect. 2 and iteratively solve for a depth h, such that the core remains undamaged. We perform three different runs for three different values of the ξ = K1/K2 parameter discussed above. We then proceed toward the minimum value of d and record all of the h(d,D) values. For the sake of simplicity, we evaluate the ratio h(d,D)/R, i.e. scale the necessary surface layer depth by the radius of the body.
 |
Fig. 3 Depth of fractured surface layer h (isolines), expressed as a fraction of meteoroid’s radius R, which prevents propagation of the damage deeper into the core in the plane of heliocentric distance d (abscissa) and size D of the body (ordinate). The core has the thermal and mechanical properties of a carbonaceous chondrite and the spin axis is perpendicular to the orbital plane (β = 90°, implying also θ0 = 90°). Three values of the ratio ξ of the thermal conductivity in the surface layer K1 to that in the core K2 are tested: ξ = 1 (top panel), ξ = 0.5 (middle panel), and ξ = 0.1 (bottom panel). |
Our results are shown in Fig. 3. The onset of the surface layer formation, which is independent on the ξ value, is shown by the curve labeled “0.0”. The surface layer depth increases with (i) increasing size of the meteoroid, and (ii) decreasing heliocentric distance, owing to the stronger solar radiation flux. Most importantly, however, h(d,D)/R also depends on ξ. As expected, the lower the value of ξ, the smaller h(D,d) value is needed to protect the core from damage. In other words, less conductive surface layer results in smaller temperature gradients in the core and thus smaller thermal stress field. For instance, only a ~20% surface layer is able to protect meteoroids of all considered sizes down to ~0.15 AU heliocentric distance for ξ = 0.1, while a ~25−50% surface layer, depending on D, is needed for ξ = 0.5. We can also compare our results with Fig. 5c in CV1, which shows the value of the thermal stress and destruction at the center of a homogeneous meteoroid with the same spin axis orientation and the same material properties. We find that the formation of the surface layer starts when the value of the thermal stress at the center of the homogeneous body is still below 1 MPa. The destruction of the center of homogeneous meteoroid starts when the present model of two-layer body reaches h ≃ 0.36R for ξ = 1, h ≃ 0.3R for ξ = 0.5, and h ≃ 0.1R for ξ = 0.1, all three of these cases preventing material failure in the center. This implies that the ratio of the fractured volume to the whole volume Vdest/V in these cases is ≃74%, ≃66%, and ≃27%, respectively.
If the meteoroid material were ordinary chondritic, the formation of surface layer would occur only for bodies larger than ~1 cm at heliocentric distances smaller than ~0.1 AU.
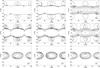 |
Fig. 4 Depth of fractured surface layer h (isolines), expressed as a fraction of meteoroid’s radius R, which prevents propagation of the damage deeper into the core shown here as a function of the spin axis orientation parameters, longitude λ (abscissa) and latitude β (ordinate). Three different size values, D = 10 cm (upper row), D = 1 cm (middle row), and D = 1 mm (bottom row), and three different values of the ξ parameter, ξ = 1 (left column), ξ = 0.5 (middle column), and ξ = 0.1 (right column) are considered. The core has the thermal and mechanical parameters of a carbonaceous chondrite, and minimum considered heliocentric distance along the orbit is 0.14 AU (that of the Geminid meteoroid stream). |
4.2. Surface layer depth for general spin axis orientation
For a general spin axis orientation, the solar colatitude θ0 changes in accordance with orbital motion of the meteoroid (Eq. (26)). As a result, the required depth h of the surface layer protecting the core from damage is no longer be a function of only D and d (and, obviously, ξ), but depends also on the parameters of the spin axis orientation, namely longitude λ and latitude β. We thus explore the dependence of the surface layer depth h on these two parameters. In particular, we determine the h(λ,β;D) that would develop for Geminid-orbit meteoroids, thus allowing d to decrease to a perihelion distance of 0.14 AU, for a different size D after one revolution about the Sun. To illustrate our results, we consider three sizes of D = 1 mm, D = 1 cm, and D = 10 cm, and three values of the ξ parameter, namely ξ = 1, ξ = 0.5, and ξ = 0.1 as before.
In practice, our procedure is as follows. For a given spin axis parameters and a pair D and ξ values from our matrix, we consider heliocentric distance starting from the aphelion of the Geminids’ orbit and decreasing with a small stepsize to the pericenter. At each step of this algorithm, we determine the surface layer depth h necessary to shield the core from damage by thermal stresses. This value is a seed for the iteration of the h value at the next step, namely a smaller heliocentric distance.
The results are shown in Fig. 4; the consecutive panels are for different sizes D and different values of the ξ parameter. As in Fig. 3, the labels of different isolines denote the surface layer depth at perihelion scaled by the radius of the meteoroid, h/R. We show the values only up to a maximum h/R = 0.5, since larger values of this parameter would perhaps be unrealistic (we note that for h/R = 0.5 approximately 88% of the body volume is represented by the damaged, surface layer). The results may be summarized in several conclusions:
-
While there is some dependence on spin axis longitudeλ, the value of the spin axis latitude β is far more important. The greatest damage to the body occurs when |β| ≤ 45° and, in particular, when the spin axis is in the orbital plane β = 0°. In contrast, values |β| ≥ 45° imply that there will be minimum damage to the body.
-
As expected, the smaller the ξ value, the smaller the damage to the meteoroids even for the largest meteoroid size (upper right panel). The ξ ≤ 0.5 value ensures that centimeter to decimeter size bodies survive the whole revolution about the Sun with reasonable thickness of the surface layer. For small enough bodies, such as the millimeter case in the bottom row of Fig. 4, meteoroids tend to survive for a wider range of ξ values.
-
As suggested by the analysis of β = 90° in Sect. 4.1, the largest bodies are more susceptible to thermal damage than small objects.
 |
Fig. 5 Cumulative number of meteoroids (ordinate) with a surface layer depth equal to or greater than h/R (abscissa), where R is the radius of the body. The data on the ordinate are given in percents of the total population initially released along the orbit of the stream. The spin axes were assumed to be isotropic and three sizes of meteoroids were used: (i) D = 10 cm (solid line); (ii) D = 1 cm (dotted line); and (iii) D = 1 mm (dashed line). When the dotted or dashed lines are not plotted, no insulating surface layer develops; ten-centimetre size meteoroids of the Southern δ-Aquariids stream (top and left panels) are all destroyed by the thermal stresses. Meteoroid showers, denoted by the IAU three-letter code, are SDA for Southern δ-Aquariids, GEM for Geminids, MON for Monocerotids, NTA for Northern Taurids, AMO for α-Monocerotids, ETA for η-Aquariids, CAP for α-Capricornids and DRA for (Oct.) Draconids. The panels from top to down and left to right are ordered according to the increasing perihelion distance, i.e., smallest for the Southern δ-Aquariids (top and left panel) and largest for the (Oct.) Draconids (bottom and right panel). |
Basic orbital data of the major meteoroid showers used in our study: semimajor axis a and perihelion distance q (e.g., Jenniskens 2006).
4.3. Distribution of surface layer depths for various meteoroid streams
In Sects. 4.1 and 4.2, we tested the dependence of our results for our new theory on various subset of parameters such as heliocentric distance, size, or spin axis orientation. Here, we attempt to use these parameters on a population scale, namely to evaluate the typical degree of the surface damage for meteoroids in several streams with perihelion distance smaller than 1 AU (Table 1). For the sake of simplicity, we assume an isotropic distribution of fixed spin axes, that the thermal and mechanical parameters of the core are those of carbonaceous chondrites, and fix the ratio of the surface layer to core conductivities to be ξ = 0.5. The association of these streams to either active or dormant comets (e.g., Jenniskens 2006) makes our choice of material parameters plausible. In a more detailed approach, one should however analyze the observational data of meteoroid strength for different streams and use it to refine these calculations. We leave this in-depth analysis to a forthcoming paper, giving here only an outline of the approach. We also use three representative meteoroid sizes, 1 mm, 1 cm, and 10 cm, while a more detailed study would need to consider a more finely sampled range of sizes.
Our procedure is as follows. We release 171 meteoroids of a given size and material parameters at the aphelion of the meteoroid stream orbit. Initially, all meteoroids are assumed to be homogeneous without a particulate surface layer. We give them the random orientation of spin axes in space, and use the techniques developed in the previous Sections to allow them approach the Sun along their orbit to the pericenter of their orbit. At each step, we consider the mechanical state of each of the bodies from the previous step and determine the thermal stress field in their volume. We observe whether the condition of brittle fracture has been satisfied anywhere in the homogeneous core, and if so, we iterate a new depth of the surface layer to prevent any further core damage. When particles return to the aphelion of their orbit, each of them has a certain depth of the surface layer, depending on the history of damage propagation. We then use this information to compute a cumulative distribution of meteoroids with surface layer depth larger than h/R (where R is the initial radius of the bodies and the distribution is normalized by the number of initially released particles). As above, we do not take into account any material loss from the surface.
Our results for all streams listed in Table 1 are shown in Fig. 5. We give the h/R value up to a 0.5 limit, because – as noted above – cases with larger values of this ratio should be effectively considered as disintegrated meteoroids. As expected, particles in streams with the smallest of perihelia distances are much more damaged than particles in streams with the largest perihelia distances. For instance, the formation of thick surface layer is the most important for southern δ-Aquariids, for which most of the centimeter- to decimeter- sized meteoroids would have been destroyed (or have h/R > 0.5). Even all 1 mm size meteoroids in this stream would have h/R > 0.2 and about ~60% of them would have h/R > 0.5. For Geminids, the second closest approaching stream, our results would predict the formation of significantly thick surface layer. All 10 cm meteoroids would have h/R > 0.35 and ~60% of them would have h/R > 0.5. These fraction values would decrease toward smaller particles, with none of 1 mm meteoroids having h/r > 0.4 and ~60% of them having h/R < 0.05. Small, 1 mm size particles in other streams would not suffer any damage by thermal stresses, and the 1 cm particles would be partly damaged for Monocerotids and Northern Taurids. The population of 10 cm sized meteoroids suffers partial damage for streams with more distant perihelion distances, but October Draconids with q ≃ 1 AU are basically intact.
Our results depend on the assumed ratio of the surface-layer to core thermal conductivity ξ. A smaller value of ξ would increase the survival rate of the meteoroids and vice versa.
5. Discussion and conclusions
We have developed an analytical theory for thermal stress in small ( ≤ 10 cm), spherical, and uniformly rotating meteoroid with a monolithic core and particulate surface layer. The thermal stress is caused by inhomogeneous temperature field induced by solar heating. This theory was used to provide a more realistic description of thermal stress influence on meteoroids in the solar vicinity. As the meteoroid approaches the Sun, these stresses first exceed the material strength at the surface and create a fractured layer. In this paper, we adopted a simplifying assumption that inter-molecular forces are able to retain the surface layer, despite the competing effects of thermal lifting and centrifugal forces. As a result, in one or a few revolutions, a particulate surface layer develops and is able to thermally shield the core, preventing any further damage by thermal stresses.
The depth of a particulate layer depends on body size, perihelion distance, spin axis orientation with respect to the Sun, and the material properties of the meteoroid. The dependence on material properties had never been studied in detail. We found that the depth of fractured surface layer increases with increasing body size, it increases with decreasing angle between the spin axis and the orbital plane, and decreases with decreasing ξ (ratio of thermal conductivity of the surface layer to the core). The surface layer depth also increases with decreasing perihelion distance. For example, the formation of fractured surface layer starts at ~0.12 AU for a 1 mm body, at ~0.27 AU for a 1 cm body and at ~0.6 AU for a 10 cm body with a spin axis perpendicular to the orbital plane.
In Sect. 4.3, we presented the expected population-averaged results for several major, low-perihelion streams. The most affected meteoroid streams seem to be δ-Aquariids, Geminids, and Monocerotids. More work is indeed needed to apply these results to observations.
The quantitative results given above are valid for carbonaceous chondrites with tensile strength 2 MPa at 300 K (see Sect. 3). The tensile strength of ordinary chondrite material can however be one order of magnitude higher (Medvedev et al. 1985), which would decrease the significance of the destruction of the surface by the thermal stress and shift its action closer to the Sun. However, the tensile strength of the parent material of cometary meteoroids is probably at least one order of magnitude smaller (e.g. Borovička 2006). The thermal stress is therefore more important for these bodies than for chondrites5. The thermal conductivity also affects our results – the higher the value, the smaller the temperature differences inside the meteoroid and therefore the smaller the thermal stresses. On the other hand, the value of the heat capacity does not affect our results significantly, at least when it remains in a reasonable range about the considered value (say within an order of magnitude).
The thermal stress weathering (which is caused by cyclic temperature variation) affects not only the surface of the Earth’s dry deserts, Mercury, or NEAs (Hall 1999; Molaro & Byrne 2011; Dombard et al. 2010). Despite the dependency of our quantitative results on poorly known material properties, our results indicate that thermal stresses generated by inhomogeneous temperature field are also able to damage the surface of small meteoroids6 at sufficiently small perihelion distances.
Here we list a number of problems that warrant closer inspection and a more extensive analysis in the future:
-
Our assumptions about the rotation state of meteoroidshave been very simplified and need to be revisited. Anisotropic distribution of fixed spin axes is an idealized onesince their orientation may evolve in time, for instance bymeans of radiation torques (e.g., Breiteret al. 2010). The same effectsmay also decelerate the rotation of a fraction of meteoroids in thestream. Many of our results do not directly depend on the adoptedrotation rate, but since the time-independent zonal part of thethermal stress field is usually dominant one, this may not be truefor particles that rotate slowly. In this case, the time-independenttesseral part of the stress field will play an important role and, asshown in CV1, the bodies would then experience much largerthermal gradients and thus stress.
-
Meteoroid streams may not be composed of particles of identical thermal and mechanical properties, but the ejected meteoroids from the parent comet may instead have material parameters spanning a certain range of values. In this way, thermal stresses may act as a selective process: for instance, weaker large meteoroids may be more likely to be removed than their stronger neighbors.
-
The surface layer was assumed to be stress-free, which applies only to highly particulate materials. Henceforth, our approach would need to be modified if the crack system of the surface, damaged layer were insufficiently interconnected. A more precise way of describing the evolution of the fractured volume would be a numerical modeling based on fracture mechanics.
-
While the retention of the surface layer by inter-molecular forces is plausible, it also requires an analysis. If the particulate surface layer were instead removed by either centrifugal forces or the elastic energy release that occurs during the the crack formation (e.g., Jewitt & Li 2010), results would be modified. In this approach, large particles would be eroded and transferred into smaller ones, directly modifying the size distribution of the meteoroid population.
-
The surface layer of particulate, poorly bound material on meteoroids that is able to form at Earth’s heliocentric distance on weak cometary meteoroids, would have implications for the erosion and fragmentation of these bodies during their flight through Earth’s atmosphere. A detailed analysis would be needed to verify whether they are in agreement with observational data.
All of the aforementioned topics would be interesting pathways to help us generalize our current model, and should be considered in the future.
Given possibly a low thermal conductivity value in the surface layer, our model is acceptable only for sizes smaller than ~ 10 cm, such that the estimate depth of the seasonal thermal wave is much larger than the size of the body. We, however, use a somewhat larger range to compare our results with those in CV1.
Acknowledgments
The work of D.Č. was supported by the Grant Agency of the Czech Republic under the contract 205/09/P455. The work of D.V. was supported by the Research Program MSM0021620860 of the Czech Ministry of Education.
References
- Beech, M., & Brown, P. 2000, Planet. Space Sci., 48, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Beech, M., Coulson, I. M., Nie, W., & McCausland, P. 2009, Planet. Space Sci., 57, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Borovička, J. 2006, in Asteroids, Comets, Meteors, ed. L. Daniela, M. Sylvio Ferraz, & F. J. Angel, IAU Symp., 229, 249 [Google Scholar]
- Breiter, S., Vokrouhlický, D., & Nesvorný, D. 2010, MNRAS, 401, 1933 [NASA ADS] [CrossRef] [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2010, A&A, 519, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delbo, M., Libourel, G., Ganino, C., Michel, P., & Verati, C. 2011, in EPSC-DPS Joint Meeting 2011, 2–7 October, Nantes [Google Scholar]
- Dombard, A. J., Barnouin, O. S., Prockter, L. M., & Thomas, P. C. 2010, Icarus, 210, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, K. 1999, Geomorphology, 31, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P. 2006, Meteor Showers and their Parent Comets, ed. P. Jenniskens [Google Scholar]
- Jewitt, D., & Li, J. 2010, AJ, 140, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, R. V., Gorbatsevich, F. I., & Zotkin, I. T. 1985, Meteoritika, 44, 105 [NASA ADS] [Google Scholar]
- Molaro, J. L., & Byrne, S. 2011, in Lunar and Planetary Inst. Technical Report, Lunar and Planetary Institute Science Conference Abstracts, 42, 1494 [NASA ADS] [Google Scholar]
- Opeil, C. P., Consolmagno, G. J., & Britt, D. T. 2010, Icarus, 208, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J., Hartzell, C. M., Sánchez, P., & Swift, M. 2010, Icarus, 210, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D. 1998, A&A, 335, 1093 [NASA ADS] [Google Scholar]
- Vokrouhlický, D. 2006, A&A, 459, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., & Brož, M. 1999, A&A, 350, 1079 [NASA ADS] [Google Scholar]
- Yomogida, K., & Matsui, T. 1983, J. Geophys. Res., 88, 9513 [Google Scholar]
Appendix A: Solution of the Fourier equation
Here we provide more details about the analytical solution of the temperature T distribution for a spherical body with a core of radius RB and a surface layer of thickness h (Sect. 2.2). Assuming that all thermal parameters are constant in each of the two parts of the body and the solution is periodic (with a period 2π/ω), we can derive a general solution of the heat diffusion (Fourier) Eq. (3) of the form: 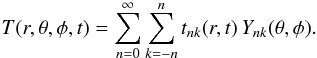 (A.1)The monopole part (n = 0) corresponds to the average temperature
(A.1)The monopole part (n = 0) corresponds to the average temperature 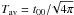 , and the terms from the dipole contribute to the temperature variations ΔT(r,θ,φ,t) in the body. The temperature gradients in the body ∇(ΔT) are of major importance to our work, because they directly provide the mechanical stress field in the body (e.g., CV1).
, and the terms from the dipole contribute to the temperature variations ΔT(r,θ,φ,t) in the body. The temperature gradients in the body ∇(ΔT) are of major importance to our work, because they directly provide the mechanical stress field in the body (e.g., CV1).
General solution of the Fourier equation.– In both of the two parts of the body, the temperature field can be developed in the series (A.1) given above. To distinguish the two solutions, we use 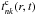 and
and 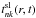 for the amplitude functions in the core and the surface layer. The linearity of the Fourier Eq. (3) grossly simplifies the solution of the t-functions with the following results:
for the amplitude functions in the core and the surface layer. The linearity of the Fourier Eq. (3) grossly simplifies the solution of the t-functions with the following results:
-
zonal terms with k = 0 are time-independent and given by
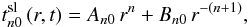 (A.2)and
(A.2)and 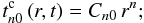 (A.3)
(A.3) -
tesseral terms with k ≠ 0 have frequency kω and read
![\appendix \setcounter{section}{1} \begin{equation} t^{\rm sl}_{nk}\left(r,t\right) = \left[A_{nk}\,j_n\left(z^\prime_k\right)+ B_{nk}\,y_n\left(z^\prime_k\right)\right]\,\exp\left({\rm i} k\omega t\right)\!, \label{Atnk1} \end{equation}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq210.png) (A.4)where
(A.4)where 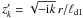 , and
, and 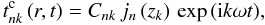 (A.5)where
(A.5)where 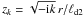 .
.
The 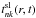 terms are the most general solution of the Fourier equation in spherical coordinates, while the
terms are the most general solution of the Fourier equation in spherical coordinates, while the 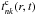 are reduced by eliminating the singular term at r = 0. We discuss the coefficients A, B, and C, that are determined by the boundary conditions.
are reduced by eliminating the singular term at r = 0. We discuss the coefficients A, B, and C, that are determined by the boundary conditions.
Boundary conditions.– Apart from the regularity of the solution that we previously took into account, we have to satisfy three additional boundary constraints (Sect. 2.2). The energy conservation condition in Eq. (4) is the most complicated of them, and troubles the analytic solution by the fourth-order emission term ϵσSBT4. As in CV1, we circumvent this problem by performing a linearization. Assuming ΔT ≪ Tav and retaining only terms of the first order in ΔT, Eq. (4) simplifies to ![\appendix \setcounter{section}{1} \begin{equation} \sqrt{2}\,t^{\rm sl}_{nk}\left(R,t\right)+\frac{K_1}{\epsilon\sigma_\mathrm{SB} T_\star^3}\,\left[\frac{\partial t^{\rm sl}_{nk}\left(r,t\right)}{\partial r} \right]_{r=R} = T_\star\,b_{nk}\left(\theta_0\right)\!. \label{bc1t} \end{equation}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq218.png) (A.6)The linearity of the resulting boundary condition prevents any mixing of the constraints on
(A.6)The linearity of the resulting boundary condition prevents any mixing of the constraints on 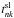 coefficients with different degree n and order k. The boundary conditions (5) and (6) at the boundary between the core and the surface layer are linear and thus provide the simple constraints
coefficients with different degree n and order k. The boundary conditions (5) and (6) at the boundary between the core and the surface layer are linear and thus provide the simple constraints 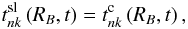 (A.7)and
(A.7)and ![\appendix \setcounter{section}{1} \begin{equation} K_1\,\left[\frac{\partial t^{\rm sl}_{nk}\left(r,t\right)}{\partial r} \right]_{r=R_B} = K_2\,\left[\frac{\partial t^{\rm c}_{nk}\left(r,t\right)} {\partial r}\right]_{r=R_B}, \label{bc3t} \end{equation}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq222.png) (A.8)
(A.8)
Equations for A, B and C.– We use now Eqs. (A.6) to (A.8) to derive the integration constants Ank, Bnk, and Cnk. Plugging in the solution (A.2) into Eq. (A.5), we obtain ![\appendix \setcounter{section}{1} \begin{eqnarray} \frac{b_{n0}(\theta_0)}{\sqrt{2}} &=& \phantom{+}A_{n0}\,\left(\frac{R} {\ell_\mathrm{d1}}\right)^n \left[1+n \Lambda_1\right] \label{abc1} \\ & & +B_{n0}\,\left(\frac{\ell_\mathrm{d1}}{R}\right)^{n+1} \left[1-\left(n+1\right) \Lambda_1\right], \nonumber \\ C_{n0}\,\left(\frac{R_B}{\ell_\mathrm{d2}}\right)^n &=& A_{n0}\,\left( \frac{R_B}{\ell_\mathrm{d1}}\right)^n+ B_{n0}\,\left(\frac{\ell_\mathrm{d1}} {R_B}\right)^{n+1}, \label{abc2} \\ n\, C_{n0}\,\left(\frac{R_B}{\ell_\mathrm{d2}}\right)^n &=& \xi\, \Bigl[n A_{n0}\,\left(\frac{R_B}{\ell_\mathrm{d1}}\right)^n \label{abc3} \\ & & \quad - \left(n+1\right) B_{n0}\,\left(\frac{\ell_\mathrm{d1}} {R_B}\right)^{n+1}\Bigr] \nonumber \end{eqnarray}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq225.png) for the zonal terms (k = 0), and
for the zonal terms (k = 0), and ![\appendix \setcounter{section}{1} \begin{eqnarray} \frac{b_{nk}(\theta_0)}{\sqrt{2}} &=& \phantom{+}A_{nk}\,j_n\left(Z^\prime_k\right) \left[1+\Lambda_1\psi_n\left(Z^\prime_k\right)\right] \label{abc4} \\ & & +B_{nk}\,y_n\left(Z^\prime_k\right)\left[1+\Lambda_1\phi_n \left(Z^\prime_k\right)\right], \nonumber \\ C_{nk}\,j_n\left(Z^B_k\right) &=& A_{nk}\,j_n\left(Z^{\prime B}_k\right)+B_{nk}\, y_n\left(Z^{\prime B}_k\right), \label{abc5} \\ C_{nk}\,\left[\frac{{\rm d}j_n}{{\rm d}z}\right]_{z=Z^B_k} &=& \xi\,\frac{\ell_\mathrm{d2}} {\ell_\mathrm{d1}}\left[A_{nk}\,\frac{{\rm d}j_n}{{\rm d}z}+B_{nk}\,\frac{{\rm d}y_n}{{\rm d}z} \right]_{z=Z^{\prime B}_k} \label{abc6} \end{eqnarray}](/articles/aa/full_html/2012/03/aa17697-11/aa17697-11-eq226.png) for the tesseral terms (k ≠ 0). In each of these systems of three equations, we may use the last two to eliminate Cn0 and Cnk, and then couple the resulting equation with the first one to solve (An0,Bn0) and (Ank,Bnk). Once knowing the A- and B-constants, we may finally solve the C-constant in either of the two cases. After some straightforward algebra, we obtain Eqs. (14) and (17) in Sect. 2.2.
for the tesseral terms (k ≠ 0). In each of these systems of three equations, we may use the last two to eliminate Cn0 and Cnk, and then couple the resulting equation with the first one to solve (An0,Bn0) and (Ank,Bnk). Once knowing the A- and B-constants, we may finally solve the C-constant in either of the two cases. After some straightforward algebra, we obtain Eqs. (14) and (17) in Sect. 2.2.
In principle, our method might be used to describe a more complicated case of the radial dependence of the thermal parameters. We would only have a larger set of spherical shells defined by the chose radial grid-points. In each of them, the solution would have a form given by Eqs. (A.2) and (A.4) with its own pair of A- and B-constants. These would be solved numerically by extending the set of conditions from Eq. (A.9) to Eq. (A.12), to an appropriate number of transition boundaries.
All Tables
Basic orbital data of the major meteoroid showers used in our study: semimajor axis a and perihelion distance q (e.g., Jenniskens 2006).
All Figures
 |
Fig. 1 Geometric parameters of our model: the orbital plane of meteoroid’s heliocentric motion defines the xy plane of our reference system with x-axis oriented toward the perihelion Π. Instantaneous position of the body along its orbit is given by the true anomaly v. The orientation of the spin axis eω is specified by longitude λ and latitude β; the solar colatitude in the body-frame, with the z′-axis along eω, is denoted θ0. |
| In the text | |
 |
Fig. 2 Propagation of a damaged volume, where the thermal stress exceeds the material strength (dashed areas), inside a meteoroid approaching the Sun. We show here the situation in the meridional plane with the spin pole (λ = 0°, β = 45°) pointing up and use the homogeneous-body model from CV1 for simplicity (because the time-dependent part of the stress field is pushed to a very small surface shell, not seen in this resolution, the global stress field in the body is roughly axisymmetric and accurately approximated by the zonal part of the stress field). The 10-cm size meteoroid was placed on a Geminid-stream orbit and assumed to have the thermal and mechanical parameters of carbonaceous chondrites. At large heliocentric distance, the damaged zone first takes a shape of polar caps (top and left panel a)), which then propagate more deeply into the body. At a distance of 0.35 AU from the Sun, the fractured volume has a shape of a near-spherical shell, which is thicker at the poles (top and right panel b)). Closer to the perihelion, bottom panels, the damaged zone takes a more complex shape. However, when the previously developed surface insulating layer begins to thermally shield the core (used in Sects. 4.1 to 4.3), the damaged zone will stop propagating deeper to the center. The arrows indicate the direction toward the Sun. |
| In the text | |
 |
Fig. 3 Depth of fractured surface layer h (isolines), expressed as a fraction of meteoroid’s radius R, which prevents propagation of the damage deeper into the core in the plane of heliocentric distance d (abscissa) and size D of the body (ordinate). The core has the thermal and mechanical properties of a carbonaceous chondrite and the spin axis is perpendicular to the orbital plane (β = 90°, implying also θ0 = 90°). Three values of the ratio ξ of the thermal conductivity in the surface layer K1 to that in the core K2 are tested: ξ = 1 (top panel), ξ = 0.5 (middle panel), and ξ = 0.1 (bottom panel). |
| In the text | |
 |
Fig. 4 Depth of fractured surface layer h (isolines), expressed as a fraction of meteoroid’s radius R, which prevents propagation of the damage deeper into the core shown here as a function of the spin axis orientation parameters, longitude λ (abscissa) and latitude β (ordinate). Three different size values, D = 10 cm (upper row), D = 1 cm (middle row), and D = 1 mm (bottom row), and three different values of the ξ parameter, ξ = 1 (left column), ξ = 0.5 (middle column), and ξ = 0.1 (right column) are considered. The core has the thermal and mechanical parameters of a carbonaceous chondrite, and minimum considered heliocentric distance along the orbit is 0.14 AU (that of the Geminid meteoroid stream). |
| In the text | |
 |
Fig. 5 Cumulative number of meteoroids (ordinate) with a surface layer depth equal to or greater than h/R (abscissa), where R is the radius of the body. The data on the ordinate are given in percents of the total population initially released along the orbit of the stream. The spin axes were assumed to be isotropic and three sizes of meteoroids were used: (i) D = 10 cm (solid line); (ii) D = 1 cm (dotted line); and (iii) D = 1 mm (dashed line). When the dotted or dashed lines are not plotted, no insulating surface layer develops; ten-centimetre size meteoroids of the Southern δ-Aquariids stream (top and left panels) are all destroyed by the thermal stresses. Meteoroid showers, denoted by the IAU three-letter code, are SDA for Southern δ-Aquariids, GEM for Geminids, MON for Monocerotids, NTA for Northern Taurids, AMO for α-Monocerotids, ETA for η-Aquariids, CAP for α-Capricornids and DRA for (Oct.) Draconids. The panels from top to down and left to right are ordered according to the increasing perihelion distance, i.e., smallest for the Southern δ-Aquariids (top and left panel) and largest for the (Oct.) Draconids (bottom and right panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


