| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913537 | |
| Published online | 23 February 2012 | |
Radiative equilibrium in solar prominences reconsidered
1 Astronomical Institute, Academy of Sciences of the Czech Republic, 25165 Ondřejov, Czech Republic
e-mail: pheinzel@asu.cas.cz
2 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85740 Garching, Germany
Received: 23 October 2009
Accepted: 17 December 2011
Aims. We reconsider the question which kinetic temperatures can lead to prominence configurations that are in radiative equilibrium. We compare these temperatures to those from other calculations.
Methods. For this purpose we solved the full non-LTE radiative-transfer problem for a gas consisting of hydrogen, helium and calcium. We used simple isobaric 1D slabs and began with isothermal models. Then we solved the radiative-relaxation problem and determined the radiative-equilibrium conditions within the whole slab.
Results. By adding the calcium radiative losses, we found that these equilibrium temperatures are considerably lower than those obtained for a pure hydrogen gas. This is because the newly calculated CaII line losses appear to play a significant role in the energy balance, similar to chromospheric conditions. The equilibrium temperatures obtained span the range between 4400−9500 K, depending on the gas pressure and slab thickness.
Key words: radiative transfer / Sun: filaments, prominences / line: formation
© ESO, 2012
1. Introduction
Solar quiescent prominences are cool structures in the solar atmosphere that are globally long-lived and fairly stationary. This requires the existence of a magneto-hydrostatic equilibrium and of an energy balance. We will not address the question of the mechanical equilibrium here, but instead concentrate on the energy problem. This energy-balance problem for prominences has been investigated over several decades, but the results obtained by various authors are still controversial. One of the earliest papers is that of Poland & Anzer (1971), who studied the radiative losses and the inflow of thermal energy by conduction for one-dimensional (1D) prominence slab models. These authors found that under certain circumstances a global energy balance can be obtained, but they did not consider the problem of the local energy equilibrium. Later, Heasley & Mihalas (1976) produced a set of 1D models, using the complete-linearization technique for solving the highly coupled set of equations of non-LTE radiative transfer, pressure and energy balance. These authors considered both isobaric models and models that are in magneto-hydrostatic equilibrium, as suggested by Kippenhahn & Schlüter (1957). They found that in all these models the central temperature consistent with the radiative equilibrium is very low, down to around 4600 K. Only when they included sufficiently strong mechanical heating, the temperatures could be increased up to 7700 K.
These low values for the radiative-equilibrium temperatures contrast with most of the typical prominence temperature determinations (see Engvold et al. 1990, where T = 7500 K is quoted as the most frequently observed value in the central parts) and thus suggests that some kind of heating input is necessary. The prominence plasma considered by Heasley & Mihalas (1976) is a mixture of hydrogen and helium and for these species the radiative losses were computed in detail. Note, however, that under prominence conditions, especially in the cool central parts, the helium contribution seems to be negligible.
In order to reinvestigate the problem of radiative equilibrium in prominence like structures, Gouttebroze (2007) considered a pure hydrogen plasma and constructed a set of isobaric models of 1D vertical cylinders representing loop-like or thread-like structures. His models cover an extensive range of gas pressures and cylinder radii. In the coolest central parts of these cylinders the author found radiative-equilibrium temperatures down to around 5700 K for thick cylinders with a diameter of 5000 km. However, for thinner cylinders with a diameter of only 200 km (which could represent the fine-structure threads), the central temperatures are higher than 6500 K. For low gas pressures, all these temperatures rise up to 9000 K or more. Note that a comparable range of equilibrium temperatures can be deduced from hydrogen radiative losses computed for similar models by Anzer & Heinzel (1999). These results therefore suggest that there is no need for any extra heating of the central regions of prominences, and there will be even less need in the fine-structure threads. However, one should consider these temperature values as upper limits for the radiative-equilibrium temperature, simply because the radiative losses of other species have been neglected in these calculations.
A consistent treatment of the radiative losses of other elements is quite a complex task. In several studies these losses have been considered as optically thin and were determined using various approximate ways (Kuin & Poland 1991; Fontenla et al. 1996; Anzer & Heinzel 1999). This approach works relatively well in hotter prominence-corona transition regions (PCTR), but is uncertain for the cool central parts. In these regions, optically-thin losses may dominate those of hydrogen and this naturally lowers the values of the radiative-equilibrium temperatures (see Anzer & Heinzel 1999). Fortunately there are only a few elements of which it is well known that they significantly contribute to the total losses under chromospheric conditions, and this might be also the case of quiescent prominences. Vernazza et al. (1981) have already shown that dominant chromospheric coolants are hydrogen, plus singly ionized calcium and magnesium. For prominences, calcium losses were computed by Zhang & Fang (1987), who found them to be negligible compared to hydrogen for some specific models. Because this contradicts the results found in the chromosphere, we recompute here the calcium losses in prominences, using the most up-to-date radiative transfer models (Gouttebroze & Heinzel 2002). Based on that, we reconsider the radiative-equilibrium conditions within the isobaric prominence structures of various sizes, following the the time-relaxation technique of Gouttebroze (2007).
In Sect. 2 we present our models, Sect. 3 gives the results and Sect. 4 contains the discussion and the conlusions.
2. Model calculations
Our models are represented by 1D isobaric plasma slabs standing vertically above the solar surface and illuminated symmetrically from both sides by the incident solar radiation. They represent the whole prominence with a geometrical thickness of a few thousand km, but they are also useful to investigate fine-structure elements that are much thinner. To compare our results with those of Gouttebroze (2007) (i.e. for pure hydrogen), we considered three sizes of the slab with the geometrical thickness D = 200, 1000 and 5000 km (the models of Gouttebroze 2007 represent vertical cylinders with the same values for the diameters). We used three values of the gas pressure, p = 0.01, 0.1 and 0.5 dyn cm-2, the same as in Gouttebroze (2007). All models have a constant microturbulent velocity of 5 km s-1. Helium is taken into account only for the density determination but not to contribute to the electron density at the low temperatures considered here – note that a helium contribution to the electron density was recently considered for cylinders by Gouttebroze & Labrosse (2009). We took the helium abundance to be equal to 0.1. The model with D = 1000 km and p = 0.1 dyn cm-2 is referred to as a “standard model” in Gouttebroze (2007), here we call it a “reference model” to demonstrate some reference (typical) characteristics. All models were computed for a prominence height 10 000 km, which determines the dilution factor for the incident radiation.
To determine the importance of CaII radiative losses for prominence plasmas, we computed the same 1D slab models, using our most recent versions of the non-LTE multilevel codes for hydrogen and calcium. The hydrogen code uses a five-level plus continuum model atom with partial frequency redistribution (PRD) in the Lα and Lβ lines and the hydrogen radiative losses/gains were computed with this code in the same way as in Anzer & Heinzel (1999). The calcium code previously used by Anzer & Heinzel (1999) was later substantially modified and extensively tested against the results of a similar code developed by Gouttebroze. As a result, a new hydrogen and calcium modeling of prominences was presented by Gouttebroze & Heinzel (2002). An important feature of the modified CaII code is the consistent treatment of the CaII ionization by the UV radiation of hydrogen Lyman lines and continuum. We used this new version of the calcium code to compute the CaII radiative losses. The CaII H and K lines are treated with partial frequency redistribution, the calcium abundance is taken to be 2.19 × 10-6.
Apart from hydrogen and calcium radiative losses, one should also consider the losses by resonance MgII lines h and k. However, the solar chromospheric modeling (Vernazza et al. 1981) suggests that the Mg II losses are considerably lower compared to those produced by CaII. Although some work has been done in the past regarding the non-LTE modeling of MgII lines in the frame of a two-level atom approximation (Vial 1982; Paletou et al. 1993), a more systematic study (including the ionization of magnesium) will be needed before one can firmly include these lines into the energy-balance modeling. Indeed, any additional losses will lower the radiative-equilibrium temperatures even more and thus neglecting MgII losses we just obtain an upper limit of these temperatures for a mixture of hydrogen and calcium.
The net radiative losses are computed as 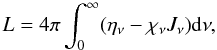 (1)where ην and χν are, respectively, the emissivity and opacity, and Jν is the mean intensity of the radiation field. For radiative equilibrium L must be equal to zero throughout the whole slab. We note that the losses are quite sensitive to the accuracy of converged atomic level populations and consequently well converged models are required. We therefore computed all atomic level populations and electron densities to a relative accuracy of 10-6. For the lines, an alternative expression to compute the net radiative losses is
(1)where ην and χν are, respectively, the emissivity and opacity, and Jν is the mean intensity of the radiation field. For radiative equilibrium L must be equal to zero throughout the whole slab. We note that the losses are quite sensitive to the accuracy of converged atomic level populations and consequently well converged models are required. We therefore computed all atomic level populations and electron densities to a relative accuracy of 10-6. For the lines, an alternative expression to compute the net radiative losses is ![\begin{equation} L=h\nu \left[n_j \left(A_{ji} + B_{ji} \overline{J}_{ij}\right) - n_i B_{ij} \overline{J}_{ij}\right] , \end{equation}](/articles/aa/full_html/2012/03/aa13537-09/aa13537-09-eq20.png) (2)where A and B are the Einstein coefficients for the line transition i − j, n are the atomic level populations, ν the line frequency, h the Planck constant and
(2)where A and B are the Einstein coefficients for the line transition i − j, n are the atomic level populations, ν the line frequency, h the Planck constant and 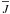 is the mean integrated intensity of the line radiation.
is the mean integrated intensity of the line radiation.
 |
Fig. 1 Lyman-continuum radiation temperatures. The crosses represent data used in our non-LTE models, while the full line was derived from SOHO/SUMER data (courtesy of P. Schwartz). |
It is well known that the radiation properties of solar prominences critically depend on the incident solar radiation in the respective lines and continua and therefore the incident radiation may strongly affect the internal energy balance. For hydrogen we used the data compiled by Gouttebroze et al. (1993), with certain updates made for Lyman lines as observed by SOHO/SUMER. Because the radiative equilibrium of the hydrogen plasma depends on the radiation temperatures of the hydrogen continua, we show in Fig. 1 the Lyman-continuum radiation temperatures Tr for the incident solar radiation (without geometrical dilution, which is taken into account in the non-LTE codes). The crosses represent previously compiled values used in our non-LTE modeling, while the full line shows the mean values obtained from recent SOHO/SUMER disk-center intensities. The value around 504 Å is a mean over the HeI photoionization jump. Note that Heasley & Mihalas (1976) as well as Gouttebroze (2007) used similar data. In all our models we use Tr from Table 2 of Gouttebroze et al. (1993), i.e. we expand the wavelength range down to about 100 Å. The wavelength dependence of Tr for the Lyman continuum is denoted below as f(λ). For the Balmer continuum and other subordinate continua we took Tr from Gouttebroze et al. (1993) and numerically integrated optically-thin losses according to Eq. (1). This gives the same results as using the approach of Rudawy & Heinzel (1992) with their radiation temperatures. For calcium we used the same incident radiation fields as in Gouttebroze & Heinzel (2002).
To compute the slab models in radiative equilibrium, we followed the approach of Gouttebroze (2007). For models with constant pressure (isobaric models), the radiative relaxation is governed by Eq. (30) of Gouttebroze (2007)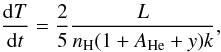 (3)where T is the temperature, t the time, nH the number density of hydrogen, AHe = 0.1 the helium abundance, y is the hydrogen ionization degree and k is the Boltzmann constant. We began from an isothermal slab and let the temperature evolve in time according to this equation, where the total radiative losses (i.e. hydrogen plus calcium) are computed from the fully converged non-LTE transfer problem at each time step. The relaxation properties have been found to be identical to those described by Gouttebroze (2007). The method is robust and the fact that the same solution is obtained irrespectively of the initially prescribed temperature distribution ensures its correctness. For all models we present here we found an optimum time step of 10 s, which requires several hundred or thousand steps to reach the relaxed solution, i.e. the radiative equilibrium within the whole slab. This relaxation method is very different from the complete-linearization technique previously used by Heasley & Mihalas (1976), but both approaches should lead to the same results. Note that the solution is sensitive to the incident radiation, as we will discuss below.
(3)where T is the temperature, t the time, nH the number density of hydrogen, AHe = 0.1 the helium abundance, y is the hydrogen ionization degree and k is the Boltzmann constant. We began from an isothermal slab and let the temperature evolve in time according to this equation, where the total radiative losses (i.e. hydrogen plus calcium) are computed from the fully converged non-LTE transfer problem at each time step. The relaxation properties have been found to be identical to those described by Gouttebroze (2007). The method is robust and the fact that the same solution is obtained irrespectively of the initially prescribed temperature distribution ensures its correctness. For all models we present here we found an optimum time step of 10 s, which requires several hundred or thousand steps to reach the relaxed solution, i.e. the radiative equilibrium within the whole slab. This relaxation method is very different from the complete-linearization technique previously used by Heasley & Mihalas (1976), but both approaches should lead to the same results. Note that the solution is sensitive to the incident radiation, as we will discuss below.
In the next section we present our results for a set of slab models computed under various conditions.
3. Model results
Radiative-equilibrium temperatures at slab center and slab surface (in parentheses).
 |
Fig. 2 Radiative-equilibrium temperatures in pure hydrogen slabs with D = 1000 km (full lines) are compared to those in cylinders of Gouttebroze (2007) (dashed lines). The gas pressures are 0.01, 0.1 and 0.5 dyn cm-2 from top to bottom of the plot, respectively. In both geometries, CRD in hydrogen lines was assumed. |
 |
Fig. 3 Radiative-equilibrium temperatures in pure hydrogen slabs with D = 1000 km, computed with PRD (full lines) and CRD (dashed lines) in Lα and Lβ. For all other hydrogen lines the CRD was assumed. The gas pressures are 0.01, 0.1 and 0.5 dyn cm-2 from top to bottom of the plot, respectively. |
Our pure hydrogen models have been constructed in the same way as those of Gouttebroze (2007). For the case of complete frequency redistribution (CRD) the only difference is the geometry (1D slabs versus 1D cylinders). The atomic parameters and all incident radiation fields have been set to be identical. In Fig. 2 we present a comparison between the slab and cylindrical models for D = 1000 km. The differences are relatively small, around 300 K at maximum, which represents less than 5% of the equilibrium temperatures. Similar results were also found for models with other thicknesses. We ascribe these fairly small differences mainly to distinct geometries, but no clear trend is evident from comparison plots. Some might be also due to different numerical codes used. However, these small differences are unimportant for the energy-balance modeling aimed at in this study and therefore we consider our models to be sufficiently accurate. Despite these differences, our results fully confirm the important conclusion of Gouttebroze (2007) that pure hydrogen models which are in radiative equilibrium (considering the incident radiation fields mentioned in the previous section) never have central temperatures as low as previously found by Heasley & Mihalas (1976).
All models of Gouttebroze (2007) have been constructed assuming the complete frequency redistribution in all hydrogen lines. However, it is now well established that the hydrogen Lyman lines, in particular Lα and partially also Lβ, are sensitive to the effects of partially-coherent scattering, namely for low-pressure and optically-thick prominence models (Heinzel et al. 1987). To demonstrate the effect of PRD on radiation-equilibrium models, we show in Fig. 3 a comparison between temperature structures of 1000 km thick slabs, computed with CRD and PRD. The PRD was used for the Lα and Lβ lines. While the synthetic line profiles significantly differ in both cases, the temperature structures are similar, indicating a rather small influence of PRD on the energy balance. This can be understood in the following way. The radiation fields in the line cores are similar for both CRD and PRD and only the wings (including peaks) are strongly affected by partially-coherent scattering. Because the integrated mean intensities 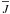 inside the slab are mainly determined by the line-core radiation field, the effect of PRD is less important for them. These mean integrated intensities, together with atomic level populations which they determine via the statistical equilibrium, give the line radiative losses according to Eq. (2). A similar effect was found for the CaII lines. But despite these small differences, we used the full PRD approach for the first two hydrogen Lyman lines and for the CaII H and K lines in all models discussed below. Our PRD results for pure hydrogen models are summarized in Table 1, first part.
inside the slab are mainly determined by the line-core radiation field, the effect of PRD is less important for them. These mean integrated intensities, together with atomic level populations which they determine via the statistical equilibrium, give the line radiative losses according to Eq. (2). A similar effect was found for the CaII lines. But despite these small differences, we used the full PRD approach for the first two hydrogen Lyman lines and for the CaII H and K lines in all models discussed below. Our PRD results for pure hydrogen models are summarized in Table 1, first part.
The rather high temperatures obtained for the lowest pressures are the result of an increasing radiation temperature of the incident Lyman-continuum radiation with decreasing wavelength (see Fig. 1). This can be easily demonstrated by considering just a constant Tr, which we set to the value at 912 Å, i.e. Tr = 6500 K. The results are shown in the second part of our Table 1 (for pure hydrogen models with PRD), where the radiative-equilibrium temperatures Tre at the lowest pressure are much lower. We also indicate the Lyman-continuum head optical thickness and see that at low pressures the optical thickness is small and going to lower wavelengths, it decreases as λ3. This allows the incident radiation at higher Tr to heat up the central parts of the slab. At higher pressures, where the optical thickness significantly grows, the Lyman-continuum Tr plays no longer any significant role and the results are similar to those for f(λ). But the fact that Tre saturates for the thickest models around 6500 K indicates a direct relation to Tr = 6500 K of the incident Lyman-continuum radiation. However, a closer inspection shows that this is not the case.
To demonstrate this we increased the incident Tr arbitrarily to 8000 K and found similar central Tre not much higher than 6500 K (for highest pressure) – see the third set of models in Table 1. Our calculations indicate that the central equilibrium temperature saturates at values around or slightly above 6500 K, independently of the intensity of the photoionizing Lyman continuum. Moreover, this value can hardly be explained by the role of the optically-thin Balmer continuum, which has a much lower Tr = 5500 K in our case (using data from Table IV of Rudawy & Heinzel 1992, at the height of 104 km). Heating caused by the Balmer continuum was suggested by Heasley & Mihalas (1976), who arrived at much lower central equilibrium temperatures, well below 5000 K. For the 1D cylinders of Gouttebroze (2007), the central Tre also saturates at 6500 K for D = 200 km, while for large D = 5000 km it saturates below 6000 K. The very low central temperatures obtained by Heasley & Mihalas (1976) have been explained by the authors as a consequence of the equilibrium with the optically-thin Balmer continuum radiation, which fully penetrates into the slab center and is determined by the photospheric intensity. However, our results point to a more complex scenario. Our Balmer-continuum has Tr = 5500 K, which gives even lower irradiation when the dilution factor is taken into account. Therefore, the central temperatures around 6500 K, found in this paper for dense hydrogen models, can hardly be explained by this photoionization equilibrium. We made several sensitivity tests and found that this particular central temperature results from both the excitation rate by the Lα radiation field, giving the hydrogen second-level population, and from the photoionization rate from that level, which corresponds to the Balmer continuum. For example, by changing the incident Lα radiation artificially, the central equilibrium temperature also changes. And because the Lα line is formed under PRD conditions, the resulting temperature will also somewhat depend on this (note that Heasley & Mihalas 1976, used CRD for the hydrogen lines).
Finally, in Figs. 4 − 6 and in Table 1 (last part) we show our new results for a mixture of hydrogen and calcium and compare them with those obtained for pure hydrogen slabs. All models use PRD in both hydrogen and CaII lines. For small D = 200 km and for the lowest pressures, the central Tre is similar to that obtained for pure hydrogen models, which indicates the negligible role of calcium losses. In other words, very small fine structures would need no additional heating provided that the gas pressure is on the order of 10-2 dyn cm-2 or lower. Such a situation seems to be possible under some conditions – see 2D fine-structure modeling of Berlicki et al. (2011) based on SOHO/SUMER observations. However, for higher pressures and thicknesses, the CaII losses start to be significant and they compensate for hydrogen gains at lower temperatures. As a result, much lower temperatures are obtained in comparison to a pure hydrogen plasma. For p = 0.5 dyn cm-2 and D = 5000 km we arrived at Tre as low as 4400 K.
 |
Fig. 4 Radiative-equilibrium models with D = 200 km. Three pressures are 0.01, 0.1 and 0.5 dyn cm-2 from top to bottom, respectively. Full lines: hydrogen plus CaII, dashed lines: pure hydrogen. |
The values of all central and surface equilibrium temperatures are summarized in Table 1. One can see the following general trends:
-
For all thicknesses considered the central temperature decreasesdrastically with increasing gas pressure; from around9500 K down to a minimum of4400 K.
-
There is also a weaker dependence on the slab thickness, with a decrease of temperature with increasing thickness.
-
From all our figures one clearly sees that large parts of all slabs have equilibrium temperatures that are close to the central values. This then means that the central temperatures are very useful when one compares the models with temperatures derived from prominence observations, unless the spectral line under consideration is sufficiently opaque so that one sees mainly the outer layers which have higher temperatures.
4. Discussion and conclusions
We have shown that the radiative losses caused by CaII are quite important for thick slabs with high pressures, while in the case of thin slabs at low pressures they are negligible. When included into the energy balance, these losses lead to much lower radiative-equilibrium temperatures as compared to the case of a pure hydrogen plasma. The effect is more pronounced at the slab center than at its surface. Although we have theoretically computed the radiative-equilibrium temperatures for various slab parameters, this paper is not aimed at determining real prominence temperatures, but rather to check whether the radiative equilibrium studied recently by Gouttebroze (2007) can give reasonable central values of the temperature. However, the range of possible (realistic) temperatures can be additionally constrained by taking into account the relevant prominence conditions. For example, the models with very low pressures have sufficiently high equilibrium temperatures so that no heating would be required. But since the pressure in the ambient corona is typically higher than this, these structures cannot be in pressure equilibrium. This implies that they would have to be completely shielded by the magnetic field as plasmoids. The other point is that such structures would have very small optical depths in Hα and therefore should be invisible, unless D is unreasonably large or very many fine-structure elements are aligned along the line of sight. We nevertheless include these models in our investigation for the sake of comparison with Gouttebroze’s results and also because they give us useful information on the relevance of the different radiation processes. On the other hand, the model with the highest pressure p = 0.5 dyn cm-2 and D = 5000 km leads to an unrealistically large column mass. One can obtain acceptable values for the equilibrium temperature if one considers fine-structures with D = 200 km, or 1000 km, together with a pressure of 0.1 dyn cm-2. However, for the thick single slab configurations with D = 5000 km some additional heating will be needed.
 |
Fig. 7 Radiative relaxation of the slab-center temperature is shown for the reference model. Full line corresponds to hydrogen-calcium mixture, dashed one is for pure hydrogen plasma. Both cases are treated in PRD and are therefore consistent with the results in Table 1 (note that the dashed line can be compared with the corresponding plot in Gouttebroze 2007, the differences are due to geometry and PRD/CRD). In both cases, the relaxation starts from an isothermal slab model with T = 10 000 K. |
An important question concerns the radiative relaxation times for various prominence structures. As shown by Gouttebroze (2007), they differ for constant-pressure and constant-volume models, but the radiative-equilibrium temperature structure is the same. To demonstrate their behavior, we show in Fig. 7 the radiative relaxation times for the reference isobaric model. Here the relaxation to a radiative equilibrium from starting temperature T = 10 000 K is initially quite fast and temperatures around 8000 K are reached within about two minutes for pure hydrogen and even one minute if CaII losses are added. This means that if the plasma is heated, it cools down to typically observed temperatures on time scales comparable to fine-structure life times. But to reach the radiative equilibrium, the reference model needs more than 1000 s for pure hydrogen and even longer – like one hour – for a mixture of hydrogen-calcium. We can therefore conclude that after some substantial heating, the fine structure will hardly reach the radiative equilibrium because its typical life time is too short (on the order of minutes, see very recent movies from Hinode/SOT). For very thick prominences having D = 10 000 km, the relaxation is much longer (up to days) and the whole prominence could thus be observed out of thermal equilibrium (Gouttebroze 2007).
In a following study we plan to extend this radiative-relaxation modeling to 2D multi-thread prominences that are in magneto-hydrostatic equilibrium (Heinzel & Anzer 2001; Gunár et al. 2008). We will also refine the radiative loss functions for prominence plasmas, taking into account that individual threads
are irradiated differently as compared to the case of the present single isolated slabs. At very low temperatures below 5000 K, neutral calcium may also play a role, which we neglected in this investigation. Finally, we have to understand the role of a PCTR, which is certainly not in radiative equilibrium.
Acknowledgments
We thank the anonymous referee for helpful comments and suggestions. P.H. and U.A. thank the MPA and the Ondřejov Observatory, respectively, for support and hospitality during their visits. This work was partially supported by the grants 209/10/1680 and 205/09/1705 of the Grant Agency of the Czech Republic. We thank P. Schwartz for providing the plot shown in our Fig. 1.
References
- Anzer, U., & Heinzel, P. 1999, A&A, 349, 974 [NASA ADS] [Google Scholar]
- Berlicki, A., Gunar, S., Heinzel, P., Schmieder, B., & Schwartz, P. 2011, A&A, 530, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engvold, O., Hirayama, T., Leroy, J.-L., Priest, E. R., & Tandberg-Hanssen, E. 1990, in Dynamics of Quiescent Prominences, ed. V. Ruždjak, & E. Tandberg-Hanssen, Proc. IAU Coll., 117, Lecture Notes in Physics, 363 (Berlin: Springer-Verlag), 294 [Google Scholar]
- Fontenla, J., Rovira, M., Vial, J.-C., & Gouttebroze, P. 1996, ApJ, 466, 496 [Google Scholar]
- Heasley, J. N., & Mihalas, D. 1976, ApJ, 205, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., & Anzer, U. 2001, A&A, 375, 1082 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Gouttebroze, P., & Vial, J.-C. 1987, A&A, 183, 351 [NASA ADS] [Google Scholar]
- Gouttebroze, P. 2007, A&A, 465, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gouttebroze, P., & Heinzel, P. 2002, A&A, 385, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gouttebroze, P., & Labrosse, N. 2009, A&A, 503, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gouttebroze, P., Heinzel, P., & Vial, J.-C. 1993, A&AS, 99, 513 [NASA ADS] [Google Scholar]
- Gunár, S., Heinzel, P., Anzer, U., & Schmieder, B. 2008, A&A, 490, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kippenhahn, R., & Schlüter, A. 1957, Z. Astrophys., 43, 36 [Google Scholar]
- Kuin, N. M. P., & Poland, A. I. 1991, ApJ, 370, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Paletou, F., Vial, J.-C., & Auer, L. H. 1993, A&A, 274, 571 [NASA ADS] [Google Scholar]
- Poland, A. I., & Anzer, U. 1971, Sol. Phys., 19, 401 [Google Scholar]
- Rudawy, P., & Heinzel, P. 1992, Sol. Phys., 138, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Vial, J.-C. 1982, ApJ, 254, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q. Z., & Fang, C. 1987, A&A, 175, 277 [NASA ADS] [Google Scholar]
All Tables
Radiative-equilibrium temperatures at slab center and slab surface (in parentheses).
All Figures
 |
Fig. 1 Lyman-continuum radiation temperatures. The crosses represent data used in our non-LTE models, while the full line was derived from SOHO/SUMER data (courtesy of P. Schwartz). |
| In the text | |
 |
Fig. 2 Radiative-equilibrium temperatures in pure hydrogen slabs with D = 1000 km (full lines) are compared to those in cylinders of Gouttebroze (2007) (dashed lines). The gas pressures are 0.01, 0.1 and 0.5 dyn cm-2 from top to bottom of the plot, respectively. In both geometries, CRD in hydrogen lines was assumed. |
| In the text | |
 |
Fig. 3 Radiative-equilibrium temperatures in pure hydrogen slabs with D = 1000 km, computed with PRD (full lines) and CRD (dashed lines) in Lα and Lβ. For all other hydrogen lines the CRD was assumed. The gas pressures are 0.01, 0.1 and 0.5 dyn cm-2 from top to bottom of the plot, respectively. |
| In the text | |
 |
Fig. 4 Radiative-equilibrium models with D = 200 km. Three pressures are 0.01, 0.1 and 0.5 dyn cm-2 from top to bottom, respectively. Full lines: hydrogen plus CaII, dashed lines: pure hydrogen. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for models with D = 1000 km. |
| In the text | |
 |
Fig. 6 Same as Fig. 4, but for models with D = 5000 km. |
| In the text | |
 |
Fig. 7 Radiative relaxation of the slab-center temperature is shown for the reference model. Full line corresponds to hydrogen-calcium mixture, dashed one is for pure hydrogen plasma. Both cases are treated in PRD and are therefore consistent with the results in Table 1 (note that the dashed line can be compared with the corresponding plot in Gouttebroze 2007, the differences are due to geometry and PRD/CRD). In both cases, the relaxation starts from an isothermal slab model with T = 10 000 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


