EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A103 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A103
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201118406
Published online 09 February 2012

© ESO, 2012

1. Introduction

The BL Lac object 1ES 0414 + 009 was first detected with the HEAO 1 satellite (Gursky et al. 1978) in the energy range 0.2 keV–10 MeV, and identified in Einstein Observatory X-ray images (Giacconi et al. 1979). On the basis of the original X-ray, optical and radio observations, it was identified as a probable BL Lac object by Ulmer et al. (1983). Located at a redshift of z = 0.287 (Halpern et al. 1991), 1ES 0414 + 009 harbours a super-massive black hole of mass  ~2 × 109 M⊙ (Falomo et al. 2003). The host galaxy is classified as elliptical, with absolute magnitude MR = −23.5 (Falomo et al. 2003). Polarization measurements by Impey & Tapia (1988) confirmed the classifications of this source as a BL Lac object. According to the classification scheme of Padovani & Giommi (1995), 1ES 0414 + 009 belongs to the class of high-frequency-peaked BL Lac (HBLs), objects with a synchrotron-emission peak located at UV/soft-X-ray frequencies, or equivalently, sources for which the X-ray emission is dominated by synchrotron radiation.

There are several archival measurements of the spectral properties of 1ES 0414 + 009 in X-rays taken using ASCA (Kubo et al. 1998), ROSAT (Brinkmann et al. 1995), and BeppoSAX (Beckmann et al. 2002). Observations with EXOSAT (Giommi et al. 1990; Sambruna et al. 1994) showed evidence of temporal variability and strong spectral variations, at times having an X-ray photon index of ΓX < 2. During these states 1ES 0414 + 009 is characterized by a SED typical of “extreme” BL Lac objects (i.e. objects with the synchrotron peak above a few keV, Costamante et al. 2001). In the VHE γ-ray domain, the data from the HEGRA experiment were used to derive an upper limit on the flux for this source corresponding to 13.5 × 10-12 cm-2 s-1 above 910 GeV (Aharonian et al. 2000). 1ES 0414 + 009 was considered a good candidate for VHE emission by Costamante & Ghisellini (2002), on the basis of a high X-ray and radio flux, and its detection was yet more likely after blazar γ-ray spectra indicated a low intensity of the diffuse EBL (Aharonian et al. 2006a).

Based on these VHE estimates, observations of 1ES 0414 + 009 with H.E.S.S. began in 2005 and continued until 2009, and significant observing time was dedicated to its detection, because its high redshift made this source a potentially interesting candidate for EBL studies. In Sect. 2 the analysis of the 5-year data set on 1ES 0414 + 009 collected by the H.E.S.S. collaboration is reported. In the high-energy γ-ray domain, emission from 1ES 0414 + 009 was first detected by the Large Area Telescope (LAT) on the Fermi γ-ray space telescope (Atwood et al. 2009). 1ES 0414 + 009 was detected with a significance of TS = 2Δlog ℒ > 25 in the first 11 months of the Fermi-LAT operation and is listed in the first year (Abdo et al. 2010a) and second year (Abdo et al. 2011) Fermi catalogues. In Sect. 3 the 20 month Fermi-LAT observation of 1ES 0414 + 009 is reported. The γ-ray observations have been complemented with measurements in X-ray and UV, carried out using the Swift/XRT and UVOT instruments (Burrows et al. 2005; Roming et al. 2005). These, together with the optical measurements from the ATOM telescope (Hauser et al. 2004) are presented. Constraints on the EBL are discussed in Sect. 4, and finally, the spectral energy distribution (SED) of 1ES 0414 + 009 is presented in Sect. 5.

In this paper the luminosity distance of the source, located at a redshift z = 0.287 is computed with the standard ΛCDM cosmological model (H0 = 71 km s-1 Mpc-1, ΩΛ = 0.73, ΩM = 0.27), yielding a luminosity distance DL = 1469.3 Mpc.

2. VHE γ-ray observations with H.E.S.S.

H.E.S.S. is an array of four imaging atmospheric Cherenkov telescopes situated in the Khomas highland of Namibia (23°16′18″ south, 16°30′00″ east), at an elevation of 1800 m above sea level (see Aharonian et al. 2006b). The H.E.S.S. array is sensitive to γ-rays above  ~100 GeV, and commonly achieves an event-by-event angular resolution of  ≲ 0.1° and a relative energy resolution of  ~15%.

Table 1

Summary of H.E.S.S. observations of 1ES 0414 + 009 for each year.

The BL Lac 1ES 0414 + 009 was observed every year between 2005 and 2009. After run-quality selection the data set comprises 73.7 h (live time) of observations, of which 67.5 h were taken with four telescopes. Observations have been carried out at zenith angles of 22° to 41° with a mean value of 26°. The pointing offset from 1ES 0414 + 009 was 0.5°. The data were analysed with the Model Analysis (de Naurois & Rolland 2009), in which shower images of all triggered telescopes are compared to a precalculated model by means of a log-likelihood minimisation. The analysis has been cross-checked with a multivariate analysis (Ohm et al. 2009) using an independent calibration, which yielded consistent results.

Two sets of cuts were used. For the source-detection analysis standard cuts were used, including a minimum image charge of 60 photoelectrons (energy threshold Eth = 220 GeV, defined here as the energy at which the effective area falls to 10% of its maximum value). Loose cuts, with a smaller charge cut of 40 photoelectrons, result in a decreased signal-to-background ratio but have the advantage of higher photon statistics and a lower threshold of 150 GeV. Since 1ES 0414 + 009 is a very faint and distant source, loose cuts were used for the spectral analysis and light curve generation1. Therefore, in this text all the fluxes and light curves shown are derived with loose cuts.

A significant excess of 224 events (7.8σ) from the direction of 1ES 0414 + 009 was found in the total data set using standard cuts. A year-by-year summary of the observations and of the corresponding results is shown in Table 1. The background subtracted distribution of the square of the angular difference between the reconstructed shower position and the nominal source position (θ2) is shown in Fig. 1. The reflected-region method (Berge et al. 2007) was used for the definition of the ON-source and OFF-source data regions. The θ2 distribution is consistent with that of a point-like source, as shown in Fig. 1.

The fit of the uncorrelated excess map with a two-dimensional point-like function convolved with the instrument point spread function PSF (68% containment radius of 0.064° for standard cuts) also indicates that the source is consistent with being point-like and is located at (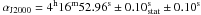, 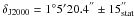). This position is consistent with the nominal position (αJ2000 = 4h16m52.8s, δJ2000 = 1°5′24′′) reported by Ulmer et al. (1983).

Figure 2 shows the differential energy spectrum of the VHE γ-ray emission above the energy threshold of  ~150 GeV using the  ~530 excess events obtained with loose cuts. The spectrum is obtained using a forward-folding maximum-likelihood method, described by Piron et al. (2001). The spectrum is compatible with a power-law distribution (dN/dE ~ E−Γ) with a photon index of ΓVHE = 3.45 ± 0.25stat ± 0.20syst; the differential flux at the decorrelation energy of 305 GeV is (5.70 ± 0.62stat)  × 10-12 cm-2 s-1 TeV-1. In Fig. 2 the confidence band of the power-law fit for 1ES 0414 + 009 is illustrated, clearly steep in appearance and affected by EBL absorption. The spectral points (with 1σ statistical errors) in the upper panel in Fig. 2 are derived from the residuals in the different energy bins shown in the bottom panel in the same figure. The integral flux above 200 GeV is F = (1.88 ± 0.20stat ± 0.38syst) × 10-12 cm-2 s-1 and it corresponds to  ~0.6% of the Crab Nebula flux above the same energy threshold (Aharonian et al. 2006b).

The light curves for E > 200 GeV with different time samplings have been derived with loose cuts, assuming the spectral index ΓVHE = 3.45 obtained by the maximum-likelihood fit (see the top panel in Fig. 3). No evidence of variability is found on different timescales. Accounting for both statistical and systematic (20%) uncertainties on the flux points, the fit of the night-by-night light curve with a constant value yields χ2 = 81.1 (for 79 degrees of freedom) with a corresponding probability P = 0.41 and a 99% confidence level upper limit on the fractional variability Fvar < 0.40 with Fvar defined as in Vaughan et al. (2003) (calculated with the method described in Feldman & Cousins 1998). The fit of the monthly light curve yields a χ2 = 18.73 for 12 degrees of freedom, with a corresponding probability of 0.1 and upper limit Fvar < 0.76. The same conclusion is found on a yearly timescale, with a probability of a constant flux P = 0.62 and 99% confidence level upper limit Fvar < 0.32.

Table 1 shows the measured integral flux for each year the source was observed. Also reported are the χ2 values for a fit of a constant when the flux is binned by nights within each year and by years within the total observation. As the χ2 probability for each fit is greater equal than 0.2 there is no evidence for variability in this data set.

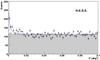thumbnail Fig. 1

The distribution of the squared angular distance (θ2) for the ON-source events (crosses) and the OFF-source events (shaded). The dashed blue line represents a PSF profile for a point-like source estimated by Monte Carlo simulations.

thumbnail Fig. 2

Differential energy spectrum of 1ES 0414 + 009. The shaded band corresponds to the range of the power-law fit (68% confidence level), taking into account statistical errors. The lower panel shows the residuals of the fit; the difference in each energy bin between the expected and observed number of excess events, normalized to the uncertainty on the latter. The 68% confidence level upper limit is calculated with the method of Feldman & Cousins (1998).

3. Multi-wavelength observations

3.1. Gamma-ray observations with the Fermi-LAT

The LAT is a pair-conversion telescope, and is the primary instrument of the Fermi satellite launched in June 2008. The Fermi-LAT instrument, described in detail in Atwood et al. (2009), detects γ rays with energies between 20 MeV and  >300 GeV. The bulk of the Fermi observational program is dedicated to a survey, in which the full γ-ray sky is covered every 3 h.

thumbnail Fig. 3

Overall light curve of the multi-wavelength observations of 1ES 0414 + 009 covering the period from 2005 to 2010. Night-wise (shaded) and year-wise (dark) light curves of 1ES 0414+009 by H.E.S.S. a) The Swift/XRT c), UVOT d), and ATOM e) observations have a night-wise binning, while the Fermi light curve b) has 32.5 day binning with 95% upper limits (black open circles) and 130 day binning (blue filled circles). Only statistical uncertainties of the flux points are shown.

The spectrum of 1ES 0414 + 009 in the 100 MeV to 100 GeV energy band2 was derived from LAT data taken between August 4, 2008 and May 17, 2010 (651 days). To minimize background contamination, only events with a high probability of being γ rays, known as “DIFFUSE” events, having an angle of less than 105° to the Zenith, were retained. The spectrum was evaluated using an unbinned maximum likelihood approach (Mattox et al. 1996) in which the events originating within a region of interst (ROI) of 10° around 1ES 0414 + 009 were modelled using diffuse Galactic and isotropic components and 17 point sources with power-law spectra. The diffuse components are tabulated in the standard files gll_iem_v02.fit and isotropic_iem_v02.txt, respectively; the overall normalization of each component was allowed to vary in the fit. The point sources include a test source at the location of 1ES 0414+009, all sources from the first Fermi catalogue (Abdo et al. 2010a) within 12° of 1ES 0414 + 009 and three additional sources found in a dedicated search for additional γ-ray emission in the ROI. These additional sources are weak, with detection significances between TS = 24 and TS = 42 (approximately 4σ to 5.6σ), and all lie relatively far from 1ES 0414 + 009 , the closest being separated by  >5.2°3. For the brighter background sources the power-law spectral assumption was tested by evaluating a log parabolic model, which was found not to significantly improve the fit. In total the model had 30 free parameters4. The maximum likelihood optimization was performed using the standard Fermi ScienceTools package (v9r19p0), using the P6_V3_DIFFUSE instrument response functions (IRFs).

Table 2

Spectral parameters and fluxes of the Swift data in the three epochs.

The null hypothesis, that no source is present at the location of 1ES 0414 + 009, is rejected with TS = 67.7 for 2 degrees of freedom, or approximately 7.9σ. The best-fit power law has an integral flux of (4.3 ± 2.2stat) × 10-9 cm-2 s-1 (100 MeV to 100 GeV) and an index of ΓHE = 1.85 ± 0.18. The differential flux at the decorrelation energy of 3.6 GeV is (5.0 ± 1.1) × 10-14 cm-2 s-1 MeV-1. The systematic errors on the index, estimated using the bracketing IRF method (Abdo et al. 2010b), in which the IRFs are modified to give the greatest change in the index of the best-fit power law, are .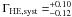

The most energetic photon detected within a region of 0.5° around the source was reconstructed with an energy of E = 19.7 GeV. The energy resolution is less than 10% for photons with E = 20 GeV.

Variability in the flux of γ rays on monthly timescales was evaluated by producing a light curve with 32.5 day bins (second panel of Fig. 3, see Abdo et al. 2010a, for details of methodology). Comparing the likelihood of a model in which the flux in each time bin is free, to one where it is assumed constant gives a difference of TSVAR = 2Δlog ℒ = 19.2 for 19 extra degrees of freedom (DOF). The probability of getting a value of TSVAR > 19.2 by chance is P = 0.44, assuming the theorem of Wilks (1938) is applicable, and we conclude that there is no evidence for variability on monthly timescales. Since there is a relatively large number of upper limits in the 32.5-day light curve, we rebinned the data to produce a 130-day light curve which is also shown in Fig. 3 (blue points). Applying the same variability test gives TSVAR = 1.44 for 4 DOF, with a chance probability of P = 0.84, again consistent with no variability.

3.2. X-ray observations with the Swift/XRT

Archival Swift observations within the timespan of the overall H.E.S.S. observing campaign were analysed. Swift performed three snapshot observations in 2006, on October 21 (1138 s), 22 (226 s) and 23 (553 s), and three in 2008, two on January 29 (1008 and 993 s) and one on February 4 (2227 s).

The XRT data were processed with standard procedures using the FTOOLS task XRTPIPELINE (version 0.12.4). Only data taken in photon counting (PC) mode were considered, given the low rate of the source (<0.5 counts/s in the 0.3–10 keV range) and because the exposures in Window Timing mode were extremely short. Source events were extracted in the 0.3−10 keV range within a circle with a radius of 20 pixels (47′′), while background events were extracted from both circular and annular regions around the source, free of other sources.

The spectra were fitted with a single power-law model with Galactic absorption NH fixed at 9.15 × 1020 cm-2, as obtained by dedicated 21 cm observations (Elvis et al. 1999). No significant flux or spectral variability was found within the 2006 or Jan. 2008 data sets (the fit with a constant gives χ2/ndf of 4.9/10 and 10.5/7, respectively, with a probability of 0.90 and 0.16). The corresponding exposures were thus summed, obtaining a total of three data sets for further analysis: the first covering the period October 21–23, 2006 (1916 s), the second for January 29 (2001 s), and the third for February 4, 2008 (2227 s).

To test the possible presence of spectral curvature, broken power-law and log-parabolic models were compared to the simple power-law hypothesis. The three spectra are well fitted by a single power law within the available statistics, with steep indices around 2.2–2.3 (see Table 2). Log-parabolic models do not significantly improve the χ2 (F-test  ~85–95%). Variations among the different epochs are modest: both flux and spectra are similar between October 2006 and January 2008, while on Feb. 4 the flux increases by  ~15%, but consistent within 1 sigma with other two epochs, with a slightly harder spectrum by ΔΓ ≃ 0.15 ± 0.10. The light curve for the XRT observations is shown in Fig. 3.

The Swift Burst Alert Telescope (BAT, Barthelmy et al. 2005) data from 2004 to 2010 were also analysed, following the procedure described in Ajello et al. (2008). The source presented only a marginal signal of 2.5σ in the 14–30 keV band. The corresponding 99% upper limit on the flux is reported in the SED in Fig. 4, for reference.

3.3. Optical and UV observations with the Swift/UVOT

The UVOT instrument (Roming et al. 2005) took exposures in different filters during the XRT pointings, namely V (547 nm), B (439 nm), and U (347 nm) in October 2006, UVM2 (225 nm) in January 2008 and U in February 2008 (the observations are summarised in Table 2). Photometry of the source was performed using the UVOT software in the HEAsoft 6.9 package. Counts were extracted from the standard aperture of 5′′ radius for all single exposures and all filters, while the background was carefully estimated from different positions more than 27′′ away from the source. Count rates were then converted to fluxes using the standard photometric zero points (Poole et al. 2008).

The fluxes were de-reddened for Galactic absorption using the extinction curve from Cardelli et al. (1989) with the updates from O’Donnell (1994), assuming RV [= AV/E(B − V)]  = 3.1. This is the average value for the Galactic diffuse interstellar medium. For the line of sight of 1ES 0414 + 009, a value of AB = 0.507 was used (Schlegel et al. 1998), with E(B − V) = 0.117 mag.

The host galaxy of 1ES 0414 + 009 is elliptical, of total R magnitude 17.49 and half-light radius 4.7″ ± 0.5″ (from HST snapshot observations, Scarpa et al. 2000). To isolate the flux of the active core the UVOT fluxes were corrected for the contribution of the host galaxy. The wavelength-dependent correction was determined using a template for elliptical galaxies (Silva et al. 1998), rescaled to the host-galaxy flux in the R band, and accounts for the given apertures.

As in the X-ray band, no significant variability was found in the UV band in October 2006, nor in January 2008 (see fourth panel in Fig. 3, where fluxes are reported without extinction correction). The individual frames were thus co-added, and the results are given in Table 2. A decrease by 0.5 mag can be noted between 2006 and February 2008, in the U filter (the only filter in common). This behaviour contradicts what observed in the X-ray band, where the corresponding XRT spectrum showed an increased flux and harder spectrum. This is indicative of a shift of the SED peak towards higher energies, which is confirmed by the simultaneous UVOT-XRT spectral fitting (see Sect. 4.1).

3.4. Optical observations with ATOM

The 75 cm optical telescope of the H.E.S.S. collaboration, ATOM, is located next to the Cherenkov telescopes at the H.E.S.S. site in Namibia. ATOM has been monitoring 1ES 0414 + 009 since Nov. 2006 with a sampling of  ≈2 observations per week during its visibility from July to March.

During the H.E.S.S. observations of 1ES 0414 + 009, the sampling was increased to obtain truly simultaneous data. The observations of this source were mostly carried out in B and R band (440 nm and 640 nm). On some of the nights, observations in V and I bands (550 nm and 790 nm) were also performed. The data analysis consists of debiassing, flat fielding and photometry using SExtractor (Bertin & Arnouts 1996) and was performed using the ATOM-specific pipeline processing (Hauser et al. 2004). The fluxes were determined using a 4′′ radius aperture and the flux scale was fixed on 7 nearby stars from the USNO catalogue (Fiorucci et al. 1998).

The night-by-night light curve of the ATOM observations with the R-filter is shown in the bottom panel of Fig. 3, where no Galactic extinction correction was considered. There is no strong variability in the light curve (the amplitude variations are less than 50% overall) but a long-term trend can be seen, with a minimum in 2008 with respect to the other years. No change in (B − R) colour was observed.

4. Combined spectral fits

4.1. UVOT and XRT spectral fits

To study the connection between the UV and X-ray components of the synchrotron emission, and to better estimate the position of its peak, a broad-band fit of the simultaneous UVOT and XRT data was performed in Xspec, using the UVOT response matrices in the calibration database. Only the B and UV filters were considered, to minimize the contamination from the host galaxy. In Xspec, Galactic reddening and X-ray absorption are taken into account using the models redden (updated with O’Donnell 1994) and wabs for the two bands, respectively.

The UV-to-X-ray broadband spectra in all three epochs are well represented by a single log-parabolic component (Table 2), with values of the curvature which are typical for HBLs: around 0.1–0.2 (Tramacere et al. 2007). The resulting estimate for the energy of the synchrotron peak is around 0.1 keV, overall, with a slight shift (at  ~3σ level) of the peak position from 0.07 to 0.17 keV between the 2006 and 2008 epochs. The corresponding flux at the synchrotron peak is steady around (1.25 ± 0.10)  ×  10-11 erg   cm-2   s-1 between 2006 and Jan. 2008, decreasing slightly to (1.01 ± 0.11)  × 10-11 erg   cm-2   s-1 on Feb. 4, 2008.

4.2. Fermi and H.E.S.S. spectral fits

By combining the Fermi and H.E.S.S. spectra it is possible to study the broadband properties of the γ-ray SED peak, once the effects of γ − γ interactions with photons of the diffuse EBL are taken into account. At z = 0.287, the intrinsic spectrum calculated from the VHE observations is strongly sensitive to the EBL density. Using the high EBL density given by direct estimates at 1–3 μm (~20 nW/m2 sr, see e.g. Aharonian et al. 2006a), the reconstructed spectrum is unrealistically hard (Γint ≤ 0.3), but it softens to Γint ≥ 1.5 for lower EBL densities.

Considered independently of other spectral information, therefore, the H.E.S.S. spectrum of 1ES 0414 + 009 further corroborates the upper limits on the EBL level previously derived from other HBLs (Aharonian et al. 2006a, 2007a,b), indicating a low density around  ~1–3 μm close to the lower bound given by galaxy counts (Aharonian et al. 2006a). However, the measured spectrum of 1ES 0414 + 009 does not improve those upper limits, nor their statistical uncertainty.

For example, comparing with 1ES 1101-232 (z = 0.186) and performing the same analysis described in Aharonian et al. (2006a), where a scaled EBL spectral shape was used, a higher EBL scaling factor P is required in this case as compared to 1ES 1101-232 (P0.58 vs. P0.55) in order to give the same estimated intrinsic spectral index. The higher redshift (z = 0.287 vs. z = 0.186) provides a longer path-length over which the effect of EBL absorption is integrated, thus giving a larger measurable effect of absorption of the intrinsic spectrum (i.e. a smaller difference in EBL flux ΔFEBL is sufficient to yield the same observed ΔΓ). This longer leverage, however, is not enough to compensate for the larger statistical error on the spectral slope (~0.35 vs.  ~0.15).

Therefore, the approach adopted here is to fix the EBL to the best current estimates (e.g. Franceschini et al. 2008; Dominguez et al. 2011), and to investigate the resulting SED properties. The EBL model assumed here (Franceschini et al. 2008) is close to the lower limits from galaxy counts and compatible with the limits from VHE observations (Aharonian et al. 2006a). With this model, both the Fermi and H.E.S.S. absorption-corrected spectra are harder than 2, indicating a high-energy peak above few TeV. Both spectra have the same index, within statistical errors (ΓHE ≃ 1.85 ± 0.18 vs. ΓVHE,int ≃ 1.87 ± 0.35), indicating that the spectral properties do not change significantly between the HE and VHE bands. The typical uncertainty on the VHE spectral index due to the residual EBL uncertainty can be estimated to be in the range [+0.15, 0.3], scaling the Franceschini template between the level of galaxy counts and the current upper limits. A single power-law model provides a good representation of the combined Fermi and H.E.S.S. spectra from 1 GeV to 2 TeV, with index 1.86 ± 0.06 and χ2/ndf = 4.7/7.

Because the H.E.S.S. observations overlap only partially in time with the Fermi data, variations in the flux could bias the combined spectral fitting of the average spectra towards harder or softer values. To quantify this, the Fermi average spectrum during the H.E.S.S. observing epochs (~3.6 months) was compared to the total (20 months).

The differences are negligible with respect to the statistical errors (<7%), and the confidence contours in the flux-index plane of the total data set are fully enclosed in the respective contours of the H.E.S.S. epoch. Thus, it is possible to conclude that no correction between the Fermi and H.E.S.S. spectra is necessary.

5. Discussion

The overall SED is shown in Fig. 4. Unfortunately, the X-ray pointings are not strictly simultaneous with the H.E.S.S. or Fermi observing epochs. (see Fig. 3). However, given the lack of strong variability in all the observed bands, it can be reasonably assumed that the ATOM, Swift, H.E.S.S. and Fermi data provide together a good representation of the average SED properties of the source over the time span of the observations.

thumbnail Fig. 4

Average SED of 1ES 0414 + 009 from the observations reported in Fig. 3 in the epoch 2005–2009. H.E.S.S.: black filled/open circles with/without EBL correction, respectively. Fermi: red full circles correspond to detections with TS > 9, red downward-pointing arrows to 95% upper limits. Swift/BAT in 5 yrs: magenta 99% upper limit. Swift/XRT&UVOT: green open squares (Oct. 2006), blue open triangles (Jan. 2008), and cyan crosses (Feb. 2008). ATOM: black triangle and blue inverted triangles corresponding to two different states, lower flux level in 2008 and higher in 2006, respectively, in the R and I bands. Gray points and butterflies are a collection of archival data from Costamante & Ghisellini (2002) and references therein.

These observations confirm 1ES 0414 + 009 as a typical HBL, with a synchrotron peak around 0.1 keV and where the X-ray band is dominated by the synchrotron emission of high-energy electrons. The higher-energy component, which is commonly interpreted as inverse Compton (IC) emission from the same population of electrons responsible for the synchrotron emission, was largely unexplored before the observations reported here. The combined data indicate that a single, hard power law fits the intrinsic spectrum over the combined HE-VHE γ-ray ranges, constraining the peak of the IC emission to lie at energies greater than  ~1–2 TeV. Thus, 1ES 0414 + 009 seems to belong to the subclass of HBLs characterized by Compton peak energies in the multi-TeV range, like 1ES 1101-232 (Aharonian et al. 2007b), 1ES 0347-121 (Aharonian et al. 2007a), 1ES 0229+200 (Aharonian et al. 2007c; Tavecchio et al. 2009), or 1ES 1218+304 (Acciari et al. 2009).

Such high energies for the IC peak are difficult to explain with a standard one-zone SSC model, due to the decrease in the scattering efficiency in the Klein-Nishina regime and the decrease in the energy density of the seed photons available for scatterings in the Thomson regime. Both these effects tend to steepen the emitted γ-ray spectrum at VHE. In principle it would be possible to avoid this steepening by assuming that the cooling of the electrons occurs only by IC scattering in the deep Klein-Nishina regime (for example, off a black-body-like spectrum of target photons, see Moderski et al. 2005). However, the resulting hardening of the electron distribution at high energies (because high-energy electrons would cool slower than those at lower energies) would necessarily imply a strong hardening of the synchrotron spectrum towards hard X-ray energies (Moderski et al. 2005). The Swift/XRT and BAT data do not seem to corroborate this hypothesis, though such an enhancement could in principle be located at even higher energies (>100 keV).

Therefore, to explain an SED such as that of 1ES 0414 + 009 (Fig. 4) in the context of a one-zone SSC model, one is drawn to consider a set of parameters for which the IC peak is obtained in the Thomson regime (γpeakhν′ ≤ mec2/4) (see Aharonian et al. 2008; Boettcher et al. 2008, for alternative scenarios). The branch of the electron distribution corresponding to the GeV–TeV band would then correspond to the optical-UV band of the synchrotron spectrum (i.e. electron energies γ < γpeak).

Adopting hνs = 0.1 keV and hνc = 2 TeV as the energies of the synchrotron and IC peaks respectively, the Lorentz factor of the electrons at the peak would be γp = (3νc/4νs)1/2 ≃ 1.2 × 105. The luminosity at these two energies can be estimated as Ls ~ 1045.5 and Lc ~ 1044.9 erg/s, respectively, from the log-parabolic fit to the synchrotron peak and the power-law fit to the γ-ray spectrum. Performing an analysis of the independent SSC constraints in the (log B–log δ) plane (see e.g. Tavecchio et al. 1998; Guy et al. 2000), with these parameters, a solution in the Thomson regime can be found for δ ≳ 50 and B ≲ 0.01 G, but only with a rather large emitting region (R ~ 1017 cm, vs. RS ~ 6 × 1014 cm, the Schwartzschild radius of the putative Black Hole). If this is the case, no variability faster than 1 day is expected, though this is below the sensitivity of current experiments at this source’s flux level. Assuming instead a more typical size of the emitting region for HBLs, around R ~ 1−2 × 1016 cm, rather extreme parameters would be required: δ > 200 and B < 0.002 G.

However, in both cases the synchrotron cooling is very slow, and the cooling time of the electrons at the synchrotron peak is much longer than the escape time (see e.g. Tavecchio et al. 1998, considering the electron escape velocity in the range 1–1/3c). The break in the electron spectrum corresponding to the SED peak, therefore, cannot be explained simply by radiative cooling (a “cooling break”) or by an equilibrium between cooling and escape from the source, as typically assumed for BL Lac objects with much lower Compton-peak energies, like PKS 2155-304, Mkn 421 or Mkn 501 (e.g. Tavecchio et al. 1998; Guy et al. 2000; Krawczynski et al. 2002; Ghisellini et al. 2002). Furthermore, the slow cooling requires the kinetic energy of the jet to be increased significantly in order to compensate for the low efficiency of the radiative emission. It should be noted that the Fermi and H.E.S.S. spectra provide only a lower limit on the energy and luminosity of the IC peak; if the true source values are actually higher, even more extreme parameters would be required. The problems just described are a general issue for the class of TeV BL Lac objects characterized by a hard TeV spectrum, an IC peak at very high energies and a large separation between synchrotron and IC peak frequencies. It might indicate either a fundamental difference in the physical jet conditions with respect to the other HBLs, or the need for an emission mechanism different from that of homogeneous SSC models.

As a final caveat, however, it should be noted that the statistical uncertainty on the γ-ray spectra is rather large, especially at VHE (ΓVHE,int = 1.87 ± 0.35). If the true VHE spectrum were  ≥ 1σ steeper than the H.E.S.S. measurement (i.e. ΓVHE,int = 2.2), the IC component would have a peak energy around 100–200 GeV, and a slightly lower luminosity. This would make the 1ES 0414 + 009 SED more similar to a typical HBL and would be easier to explain with standard SSC parameters.

6. Conclusion

The H.E.S.S. array of Cherenkov telescopes has been used to detect significant VHE γ-ray emission in the direction of 1ES 0414 + 009, a distant BL Lac objects of known redshift. The overall flux above 200 GeV from 2005 to 2009 shows no variability on any time-scale and is on average very low (around 0.6% Crab Nebula flux), making 1ES 0414 + 009 one of the faintest extra-galactic sources detected in the TeV domain. This source was detected with the Fermi-LAT in the first 20 months of its operation between 2008 and 2010 and was very faint in the HE domain too.

The VHE spectrum measured using H.E.S.S. is consistent with the current limit of the EBL and confirms the low level of EBL in the few μm range as derived from galaxy counts. The HE and VHE spectra (absorption corrected with an EBL model close to the lower limits) show a best-fit power law with an index harder than 2, indicating that 1ES 0414 + 009 can be classified as a hard-TeV BL Lac object. The overall SED of this source is averaged over five years with no strict simultaneity between the Swift and H.E.S.S. observations. With this caveat, the properties of the SED – in particular an IC peak energy above 1–2 TeV – are difficult to explain in the framework of a pure one-zone SSC model, unless using unusual values for the main parameters.

Future observations of 1ES 0414 + 009 are strongly motivated, in particular with the next generation of Cherenkov telescope arrays such as the Cherenkov Telescope Array (CTA, The CTA Consortium 2010). With a tenfold increase in sensitivity with respect to the current Cherenkov experiments, CTA will allow better measurements of the VHE spectrum of faint sources, especially at high energies, provide better constraints of the IC peak, and will help to address the physics issues posed by the hard-TeV BL Lac objects.

1

In this case the loose cuts almost double the number of excess events resulting in a poorer background rejection.

2

The analysis has been restricted to the energy range over which the response of the instrument is best understood.

3

These additional sources are not associated with any point sources in 2FGL, however one is approximately two degrees from a 2FGL source marked as confused. It seems likely that they are the result of deficits in the galactic diffuse model that were eliminated in the improved model use in 2FGL.

4

The spectral parameters for point sources formally outside the 10° ROI were fixed at their catalogue values (Abdo et al. 2010a). They were included in the model to account for the effects of the relatively large PSF at low energies.

Acknowledgments

The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. The Fermi-LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Energie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. This research has made use of data obtained from the High Energy Astrophysics Science Archive Research Center (HEASARC), provided by NASA’s Goddard Space Flight Center.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi Collaboration) 2010a, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi Collaboration) 2010b, ApJ, 708, 1254 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi Collaboration) 2011, ApJS, submitted [arXiv:1108.1435v1] [Google Scholar]
  4. Acciari, V. A., Aliu, E., Arlen, T., et al. (VERITAS Collaboration) 2009, ApJ, 695, 1370 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aharonian, F. A., Akhperjanian, A. G., Barrio, J. A., et al. 2000, A&A, 353, 847 [NASA ADS] [Google Scholar]
  6. Aharonian, F., Akhperjanian, A. G., Barrio, J. A., et al. (H.E.S.S. Collaboration) 2006a, Nature, 440, 1018 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (H.E.S.S. Collaboration) 2006b, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. (H.E.S.S. Collaboration) 2007a, A&A, 473, 25 [Google Scholar]
  9. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (H.E.S.S. Collaboration) 2007b, A&A, 470, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. (H.E.S.S. Collaboration) 2007c, A&A, 475, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Aharonian, F., Khangulyan, D., & Costamante, L. 2008, MNRAS, 387, 1206 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ajello, M., Rau, A., Greiner, J., et al. 2008, ApJ, 673, 96 [NASA ADS] [CrossRef] [Google Scholar]
  13. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. (Fermi Collaboration) 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  14. Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, SSRv, 120, 143 [Google Scholar]
  15. Beckmann, V., Wolter, A., Celotti, A., et al. 2002, A&A, 383, 410 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [Google Scholar]
  17. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Boettcher, M., Dermer, C. D., & Finke, J. D. 2008, ApJ, 679, L9 [NASA ADS] [CrossRef] [Google Scholar]
  19. Brinkmann, W., Siebert, J., Reich, W., et al. 1995, A&AS, 109, 147 [NASA ADS] [Google Scholar]
  20. Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, SSRv, 120, 165 [Google Scholar]
  21. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
  22. Costamante, L., & Ghisellini, G. 2002, A&A, 384, 56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Costamante, L., Ghisellini, G., Giommi, P., et al. 2001, A&A, 371, 512 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. The CTA Consortium 2010 [arXiv:1008.3703v2] [Google Scholar]
  25. Dominguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [NASA ADS] [CrossRef] [Google Scholar]
  26. Elvis, L. et al. 1999, NCSA Astronomy Digital Image Library [Google Scholar]
  27. Falomo, R., Carangelo, N., & Treves, A. 2003, MNRAS, 343, 505 [NASA ADS] [CrossRef] [Google Scholar]
  28. Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Feldman, G. J., & Cousins, R. D. 1998, Phys. Rev. D, 57, 3873 [Google Scholar]
  30. Fiorucci, M., Tosti, G., & Rizzi, N. 1998, PASP, 110, 105 [NASA ADS] [CrossRef] [Google Scholar]
  31. Giacconi, H., Branduardi, G., Briel, U., et al. 1979, ApJ, 230, 540 [NASA ADS] [CrossRef] [Google Scholar]
  32. Giommi, P., Barr, P., Pollock, A. M. T., Garilli, B., & Maccagni, D. 1990, ApJ, 356, 432 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ghisellini, G., Celotti, A., & Costamante, L. 2002, A&A, 386, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Gursky, H., Bradt, H., Doxsey, R., et al. 1978, ApJ, 223, 973 [NASA ADS] [CrossRef] [Google Scholar]
  35. Guy, J., Renault, C., Aharonian, F. A., Rivoal, M., & Tavernet, J.-P. 2000, A&A, 359, 419 [NASA ADS] [Google Scholar]
  36. Halpern, J. P., Chen, V. S., Madejski, G. M., & Chanan, G. A. 1991, AJ, 101, 818 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hauser, M., Möllenhof, C., Pühlhofer, G., et al. 2004, Astron. Nachr., 325, 659 [Google Scholar]
  38. Impey, C. D., & Tapia, S. 1988, ApJ, 333, 666 [NASA ADS] [CrossRef] [Google Scholar]
  39. Krawczynski, H., Coppi, P. S., & Aharonian, F. 2002, MNRAS, 336, 721 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kubo, H., Takahashi, T., Madejski, G., et al. 1998, ApJ, 504, 693 [NASA ADS] [CrossRef] [Google Scholar]
  41. Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
  42. Moderski, R., Sikora, M., Coppi, P. S., & Aharonian, F. 2005, MNRAS, 363, 954 [NASA ADS] [CrossRef] [Google Scholar]
  43. de Naurois, M., & Rolland, L. 2009, Astrop. Phys., 32, 231 [Google Scholar]
  44. O’Donnel, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ohm, S., van Eldik, C., & Egberts, K. 2009, Astrop. Phys., 31, 383 [Google Scholar]
  46. Padovani, P., & Giommi, P. 1995, MNRAS 427, 1477 [NASA ADS] [CrossRef] [Google Scholar]
  47. Piron, F., Djannati-Ataï, A., Punch, M., et al. 2001, A&A, 374, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Poole, T. S., Breeveld, A. A., Page, M. J., et al. 2008, MNRAS, 383, 627 [NASA ADS] [CrossRef] [Google Scholar]
  49. Roming, P. W. A., Kennedy, T. E., Mason, K. O, et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
  50. Sambruna, R. M., Barr, P., Giommi, P., et al. 1994, ApJS, 95, 371 [NASA ADS] [CrossRef] [Google Scholar]
  51. Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] [Google Scholar]
  52. Scarpa, R., Urry, C. M., Falomo, R., Pesce, J., & Treves, A. 2000, ApJ, 532, 740 [NASA ADS] [CrossRef] [Google Scholar]
  53. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  54. Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [NASA ADS] [CrossRef] [Google Scholar]
  55. Tavecchio, F., Ghisellini, G., Ghirlanda, G., Costamante, L., & Franceschini, A. 2009, MNRAS, 399, L59 [NASA ADS] [CrossRef] [Google Scholar]
  56. Tramacere, A., Giommi, P., Massaro, E., et al. 2007, A&A, 467, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Ulmer, M. P., Brown, R. L., Schwartz, D. A., Patterson, J., & Cruddace, R. G. 1983, ApJ, 270, L1 [NASA ADS] [CrossRef] [Google Scholar]
  58. Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
  59. Wilks, S. S. 1938, Ann. Math. Statist., 9, 1, 60 [CrossRef] [Google Scholar]

All Tables

Table 1

Summary of H.E.S.S. observations of 1ES 0414 + 009 for each year.

In the text
Table 2

Spectral parameters and fluxes of the Swift data in the three epochs.

In the text

All Figures

thumbnail Fig. 1

The distribution of the squared angular distance (θ2) for the ON-source events (crosses) and the OFF-source events (shaded). The dashed blue line represents a PSF profile for a point-like source estimated by Monte Carlo simulations.
In the text
thumbnail Fig. 2

Differential energy spectrum of 1ES 0414 + 009. The shaded band corresponds to the range of the power-law fit (68% confidence level), taking into account statistical errors. The lower panel shows the residuals of the fit; the difference in each energy bin between the expected and observed number of excess events, normalized to the uncertainty on the latter. The 68% confidence level upper limit is calculated with the method of Feldman & Cousins (1998).

In the text
thumbnail Fig. 3

Overall light curve of the multi-wavelength observations of 1ES 0414 + 009 covering the period from 2005 to 2010. Night-wise (shaded) and year-wise (dark) light curves of 1ES 0414+009 by H.E.S.S. a) The Swift/XRT c), UVOT d), and ATOM e) observations have a night-wise binning, while the Fermi light curve b) has 32.5 day binning with 95% upper limits (black open circles) and 130 day binning (blue filled circles). Only statistical uncertainties of the flux points are shown.
In the text
thumbnail Fig. 4

Average SED of 1ES 0414 + 009 from the observations reported in Fig. 3 in the epoch 2005–2009. H.E.S.S.: black filled/open circles with/without EBL correction, respectively. Fermi: red full circles correspond to detections with TS > 9, red downward-pointing arrows to 95% upper limits. Swift/BAT in 5 yrs: magenta 99% upper limit. Swift/XRT&UVOT: green open squares (Oct. 2006), blue open triangles (Jan. 2008), and cyan crosses (Feb. 2008). ATOM: black triangle and blue inverted triangles corresponding to two different states, lower flux level in 2008 and higher in 2006, respectively, in the R and I bands. Gray points and butterflies are a collection of archival data from Costamante & Ghisellini (2002) and references therein.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.