EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A100 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A100
Number of page(s) 17
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201118132
Published online 09 February 2012

© ESO, 2012

1. Introduction

The main advantage of nearby galaxies in the Local Group is that it is possible to study their resolved stellar populations. This means that stars of particular ages can be picked out of a colour–magnitude diagram (CMD) for a more detailed study of specific epochs in the evolution of a galaxy. An important and bright population of stars that trace the chemical evolution over almost the entire star formation history (SFH) of a galaxy are the red giant branch (RGB) stars (see Tolstoy et al. 2009, and references therein).

In the context of a Λ-CDM universe dwarf galaxies play a key role in galaxy formation (e.g. Kauffmann et al. 1993). The most simple scenario assumes that the small and unevolved dwarf spheroidal (dSph) galaxies that we see around the Milky Way should be related to the type of objects that originally merged to form the Milky Way. This suggests that the stellar populations at the ages when mergers occurred should be similar in small dSph galaxies and the Milky Way. The comparison of stellar abundances in dSph galaxies around the Milky Way and the stars in the Milky Way itself have shown that the merging of these nearby dwarf galaxies to create the Milky Way could only have happened at very early times, within the first Gyr of star formation occuring in either system (e.g. Unavane et al. 1996; Shetrone et al. 2001; Tolstoy et al. 2003; Venn et al. 2004; Tolstoy 2011). After this time the differences in α-element enrichment (the position of the “knee”) become too different between large and small systems.

The Carina dSph galaxy has long been known to have a most unusual and episodic SFH. The presence of RR Lyrae variable stars first indicated an ancient stellar population (Saha et al. 1986), and anomalous Cepheid variable stars (Mateo et al. 1998) showed that a young (<1 Gyr) population is also present. Anomalous Cepheids are believed to be metal-poor classical Cepheids (Bono et al. 1997), but they could also be the result of mass transfer and possibly coalescence in a low-mass binary systems (Zinn & Searle 1976). The Carina dSph is still the only galaxy where such distinct main sequence turnoffs can clearly be seen in deep CMDs (first shown by Smecker-Hane et al. 1996). This is the unequivocal signature of periods of active star formation separated by similarly long periods of no star formation at all.

There have been numerous analyses of the CMDs of the Carina dSph, including the distinct main sequence turn-offs, in a variety of filters, for different fields of view to determine the full SFH (e.g., Mighell 1997; Hurley-Keller et al. 1998; Dolphin 2002; Monelli et al. 2003; Rizzi et al. 2003; Bono et al. 2010). There is still quite some discrepancy between the SFHs obtained; specifically precisely when the different episodes of star formation occurred. These differences usually relate to the field of view of the observations modelled and thus how well different features in the CMD are populated (see Cignoni & Tosi 2010) and also the different methods used to determine the SFH. However, all studies agree that there were at least two major episodes of star formation in the Carina dSph which were separated by a long quiescent era. They also agree that the dominant stellar population (~70% of the stars) comes from an intermediate age episode of star formation.

Despite its complex SFH the Carina dSph has an extremely narrow RGB. This is a result of the age-metallicity degeneracy, where the metal-rich, young stars have almost the same colour as the metal-poor older stars. The thinness of the RGB is also a consequence of the dominant intermediate age population which formed over a relatively short time (a few Gyr) with only a small spread in [Fe/H]. The thin RGB has made reliable photometric determinations of the metallicity and its evolution challenging (e.g., Rizzi et al. 2003; Bono et al. 2010).

The first spectroscopic studies of the metallicities of individual stars in the Carina dSph came from the empirical calibration of the strong Ca II triplet (CaT) lines (Armandroff & Da Costa 1991; Da Costa 1994; Smecker-Hane et al. 1999). These studies typically reported a mean metallicity between [Fe/H] = −1.5 and –2.0 dex, with a small dispersion. The largest sample was  ~50 RGB stars. The advent of multi-fibre instruments like FLAMES at the VLT led to a dramatic increase in the sizes of these CaT samples (e.g., 437 stars from Koch et al. 2006), leading to a much better defined and statistically robust metallicity distribution function (Helmi et al. 2006; Starkenburg et al. 2010). The spread in iron (e.g., a FWHM of 0.92 dex derived from CaT by Koch et al. 2006) is much larger than the one suggested by photometric evidence.

The first detailed, high resolution, abundance study of a sample of five individual RGB stars in the Carina dSph used VLT/UVES (Shetrone et al. 2003). These results were analyzed in terms of galactic evolution with the help of both photometric ages and detailed spectroscopic abundances (Tolstoy et al. 2003). Recently a study of iron and α-element abundances from UVES spectra of a further 10 RGB stars has been made (Koch et al. 2008) and a study of a large range of elements in 9 stars with UVES and MIKE on Magellan spectra (Venn et al. 2011). As the total number of RGB stars studied in the Carina dSph has increased so has the apparent star to star scatter in the abundance ratios of most elements, although the dispersion in elemental ratios was already apparent from the start (Shetrone et al. 2003; Koch et al. 2008).

There have been several attempts to self-consistently model the SFH and the chemical evolution of the Carina dSph (e.g., Lanfranchi et al. 2003, 2004, 2006; Revaz et al. 2009). This is challenging mostly because the Carina dSph is so unusual compared to the other dSph in the Local Group. It is hard to find a unique explanation for the clear gaps seen in the SFH (e.g. Pasetto et al. 2011).

It is hoped that detailed chemical abundances of a large sample of individual RGB stars, with age estimates, in the Carina dSph will better define the effects of star formation on the chemical evolution. These large samples will also better quantify the scatter seen in the abundances of a variety of chemical elements.

This paper is organized as follows: in Sect. 2, we describe the sample selection, observations and data reduction. In Sect. 3, we explain how we derived the atmospheric parameters (Teff, log    g, vt and [Fe/H]) and the individual abundances. The abundances are discussed in detail in Sect. 4 and the ages in Sect. 5. They are interpreted in terms of the SFH of the Carina dSph in Sect. 6.

2. Sample selection, observations and data reduction

Table 1

Observing log.

Our program consists of high resolution spectroscopy of individual RGB stars in the Carina dSph galaxy. We used FLAMES (Pasquini et al. 2002) to obtain spectra simultaneously with both GIRAFFE (in high resolution mode) and UVES spectrographs (programs 074.B-0415 and 076.B-0146). This paper deals with the abundances determined from the FLAMES/GIRAFFE observations and the FLAMES/UVES results are described in a separate paper (Venn et al. 2011).

2.1. Sample selection and observations

Our targets consist of RGB stars located within a 25 arcmin diameter field of view close to the center of the Carina dSph. They were selected partly from ESO low resolution spectra (Helmi et al. 2006) and partly from a CMD. We cannot exclude that our sample contains some contamination from AGB stars.

Observations were carried out between 9 and 11 January 2005, 6 and 8 December 2005, and on 6 January, 2006. Due to bad weather conditions, only 12 out of 25 frames had a sufficient S/N to be useful. The observing log  is listed in Table 1.

We used GIRAFFE in the Medusa mode with 98 out of 132 fibres placed on targets over the 25 arcmin diameter field of view. The remaining 34 fibres were put on blank sky positions to provide for sky subtraction of the target spectra. Observations must provide not only a sufficient wavelength coverage for a canonical analysis (i.e., sufficient neutral and ionized iron lines), but also a good number of useful α-element and heavy element lines. To achieve this we observed three different wavelength settings with three different gratings, namely HR10, HR13 and HR14 (see Table 2). To increase the S/N, several exposures were taken with each HR setting. Due to bad weather conditions, only five HR10 frames, five HR13 frames and two HR14 frames could be used, resulting in the total exposure times given in Table 2. The large number of low S/N observations, which had to be rejected, obviously limited the total number of stars that could be analysed from the initial selection. In order to illustrate the data quality of our sample, we show in Fig. 1 the spectra of two stars (MKV0614, S/N = 22; MKV0900, S/N = 44) centered on the Mg line at 552.8 nm (HR10 grating).

Table 2

FLAMES-GIRAFFE gratings used.

2.2. Data reduction

We used the ESO pipeline to perform the basic data reduction, as well as the extraction and wavelength calibration of the spectra. For sky subtraction, we used a routine (from M. Irwin) that produces an average sky spectrum from the sky-dedicated fibers, which is then subtracted from each object spectrum after being rescaled to match the sky features in each fibre.

As spectra were taken at several different epochs, they need to be registered to the same rest frame. We computed the barycentric correction to radial velocity with the dopcor task and coadded individual spectra with the scombine task in IRAF. We used a flux weighted average, with median sigma clipping to remove cosmic rays.

2.3. Membership

We derived radial velocities from the reduced spectra with DAOSPEC (Stetson & Pancino 2008), which cross-correlates all the lines detected by the software with an input line list. The accuracy is in general better than  ± 2 km s-1. The radial velocity distribution is shown in Fig. 2a, where the systemic radial velocity peak of the Carina dSph stands out from the Galactic foreground contamination at 224.4 km s-1, which is consistent with previous determinations (Mateo et al. 1998; Majewski et al. 2005; Koch et al. 2006; Walker et al. 2007; Fabrizio et al. 2011). We also compared our velocites with those obtained in our low resolution CaT sample (Helmi et al. 2006), and this is shown in Fig. 2b. There is no systematic bias between the CaT and HR radial velocities and values agree within their error bars.

We considered as likely members those stars with a radial velocity within 2σ of the mean radial velocity, which means between 212 and 236 km s-1. We found that 26 out of our 98 targets have velocities that are inconsistent with membership of the Carina dSph. All of these are stars for which no radial velocity from CaT spectra was available before selection. An additional 37 stars had to be discarded because their spectra were too low S/N to perform an accurate abundance analysis. This depends on both the setting and the intrinsic metallicity of the star, so no S/N limit is specified. Our sample thus reduced to 35 stars which are likely members of the Carina dSph with sufficient S/N for an abundance analysis. They are shown in the I vs. (V − I) CMD in Fig. 3. Target coordinates, photometry and radial velocities of these stars are listed in Table 3.

3. Determination of stellar parameters and abundances

We measured the equivalent widths (EWs) of the absorption lines with DAOSPEC (Stetson & Pancino 2008), which is an automatic tool optimised for the characteristics of GIRAFFE HR spectra. Lines are fitted by saturated Gaussians because at the resolution of our data, the line profile is dominated by the instrumental effects and not astrophysical processes. All lines with EW > 200 mÅ are discarded as they will most likely depart from a Gaussian profile. The EWs determined by DAOSPEC for our sample are listed in Table 4.

We used the same line list as in the other DART (Dwarf Abundances and Radial velocity Team, Tolstoy et al. 2006) papers based on GIRAFFE medium resolution spectroscopy (Letarte et al. 2010; Hill et al., in prep.) It is based on the line list of Shetrone et al. (2003) with additional lines from Pompéia et al. (2008).

We used a grid of OSMARCS atmosphere models in spherical symmetry (Gustafsson et al. 2008) valid for Teff = [4000–5500] K, log    g = [0.0–3.5] dex, [Fe/H] = [–3.0 – +1.0] dex and [α/Fe] following the trend of increasing as [Fe/H] decreases. Abundances are derived with Calrai, a LTE spectrum synthesis code originally developped by Spite (1967) and continuously improved since then. Abundances were first computed for each individual line and the uncertainties on the EW measurements given by DAOSPEC are propagated into uncertainties on individual abundances. They are subsequently propagated into error estimates on the abundances for each element by weighting each line by 1/(σ2).

Stellar temperatures Teff and surface gravities log    g were determined from photometric data in the VIJHK bands. We have V and I bands from ESO-WFI for the whole sample and ESO-SOFI JHK magnitudes for  ≈60% of our sample (Gullieuszik, priv. comm.). The photometry is listed in Table 3.

thumbnail Fig. 1

Representative spectra of two stars of our sample, centered on the Mg line at 552.841 nm. (Top) MKV0900: S/N = 44, Vmag = 17.79; (bottom) MKV0614: S/N = 22, Vmag = 18.72. A ScII line (λ = 552.679 nm) is located on the left of the Mg line.

thumbnail Fig. 2

a) The distribution of heliocentric radial velocities for our whole FLAMES/GIRAFFE sample, including a Gaussian fit which gives Vc = 224.4 km s-1 ± 5.95 km s-1. b) Comparison between radial velocities derived from our data (HR) compared to CaT (Helmi et al. 2006).

thumbnail Fig. 3

I vs. (V − I) CMD: our FLAMES/GIRAFFE sample is shown in red dots and other Carina members (from CaT) are shown in grey dots.

When available, we averaged Teff given by the four different colours (V − I), (V − J), (V − H) and (V − K) to determine the photometric Teff, following the calibrations for giants from Ramìrez & Meléndez (2005). For those stars lacking IR photometry, we used the temperature determined from the (V − I) colour. In most cases, the temperatures from different colors are in very good agreement (see Table 5). We adopted the reddening law Av/E(B − V) = 3.24 with an extinction of 0.06 mag (Schlegel et al. 1998). A first evaluation of Teff was computed with the metallicities derived from the CaT, and when no CaT value was available the mean value [Fe/H] = −1.5 dex was assumed. These values were later updated with the final metallicities of the stars.

Using our temperature estimates together with a distance modulus of μ0 = 20.06 ± 0.12 mag (Mateo et al. 1998) and assuming an average stellar mass of 0.8 M⊙, the photometric surface gravities where computed using the bolometric correction from Alonso et al. (1999). Adopting a 1.0 M⊙ for the intermediate-age stars in our sample would increase log    g by 0.1 dex with no effect on Teff and, in turn, have a very small effect on the chemical abundances. The distance modulus from Mateo et al. (1998) was derived from the Period-Luminosity relation of the dwarf Cepheids found in the Carina dSph. It is in good agreement with more recent values also based on primary distance indicators (RR Lyrae, anomalous Cepheids, tip of the RGB), for example from Dall’Ora et al. (2003): μv = 20.19 ± 0.12 mag or Pietrzyński et al. (2009): 20.09 ± 0.03 ± 0.12 mag in the J band, 20.14 ± 0.04 ± 0.14 mag in the K band. Adopting a lower extinction value (for example, Monelli et al. 2003, proposed E(B − V) = 0.03 mag) leads to lower Teff by 40–60 K but has a negligible influence on log    g.

Table 5

The atmospheric parameters (derived from photometry) for stars in our sample.

As our [FeII/H] could only be computed from a handful of weak lines, we were not able to accurately determine the ionization balance. From Fig. 4b, it can be seen that [FeII/H] is rather uncertain with average errors up to  ≈± 0.25 dex. In comparison, [FeI/H] errors (Fig. 4a) do not exceed  ± 0.09 dex. This uncertainty on [FeII/H] translates to an uncertainty on log    g ≳ 0.3 dex. The same outcome applies for the TiI/TiII comparison, where both [TiI/H] and [TiII/H] are derived from only between 1 and 5 lines. We therefore decided to keep a common photometric log    g scale rather than using the uncertain ionization balance of iron or titanium lines to determine individual spectroscopic gravities. Surface gravity has a minor effect on our abundances derived from neutral ions: a variation of 0.5 dex in log    g results in a variation of  ≈0.1 dex in [FeI/H] and  ≈0.25 dex in [FeII/H].

The photometric Teff values were checked by ensuring that [FeI/H] does not depend on the excitation potential χex and indeed the slopes of [FeI/H] versus χex are small (see Fig. 4c). However, the HR analyses of Venn et al. (2011) and Koch et al. (2008) had to increase their photometric temperatures to reach the excitation balance, and Fig. 4c shows a systematic offset of  ≈0.05 which is in the same sense. This suggests a systematic bias between the photometric temperature and the excitation temperature. Following Venn et al. (2011), we tried to increase our Teff by 200 K and consequently adjusted the other atmospheric parameters. As a result, [Fe/H] increases by  ≃ 0.2–0.3 dex and [Mg/H] increases by  ≃ 0.05–0.15 dex. The FeI/FeII ionization balance is better satisfied but our [Fe/H] show a systematic offset of  ≈+0.3 dex with those derived from CaT. We decided not to apply any offset to our photometric parameters because there was no compelling reason to do so.

The relatively high Teff uncertainty quoted in Table 6 reflects a conservative error bar associated with this possible bias in the Teff scale.

The microturbulent velocity, vt, is determined with an iterative process, which imposes the requirement that [FeI/H] does not depend on EW, that is to say that the slope between [FeI/H] and EW is zero. Measuring the value of the slope around the correct value of vt shows that vt varies linearly and symmetrically as a function of the slope and it is therefore possible to use this relation to estimate the uncertainty on the slope between [FeI/H] and EW. Given that the error on the slope is lower than  ± 0.0016 dex/mÅ (see Fig. 4), the uncertainty on microturbulent velocity does not exceed 0.3 km s-1. We have used the theoretical EWs (computed from the atomic parameters of the line and the atmospheric parameters of the star) rather than the measured values in order to avoid systematic biases on vt caused by random errors on the EW measurements (Magain 1984). The stellar parameters can be found in Table 5.

thumbnail Fig. 4

The distribution of errors on the stellar atmospheric diagnostics for the stars in our sample: a) the error on the mean [FeI/H] and b) [FeII/H] which are measured from the dispersion around the mean divided by the square root of the number of lines measured; c) the slope of [FeI/H] versus the excitation potential χex; d) the propagated error on the measurement of the slope of [FeI/H] versus the line strength.

DAOSPEC returns an error estimate on the EW measurements that was propagated throughout the abundance determination. We also used the abundance dispersion σ(X) around the mean value, to take into account not only the uncertainties on the EW measurements but also the uncertainties on the atomic parameters of the lines. This dispersion is defined for a given element X as 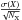where NX is the number of lines measured for this element. It can happen that the abundance dispersion is underestimated due to small number statistics when abundances are determined from a limited number of lines. We therefore do not allow that any abundance can be measured more accurately than [FeI/H] and set the [FeI/H] dispersion as a lower limit, leading to a lower limit for the error estimate of 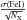. The maximum of these three values was adopted as the final error on [X/H]. It includes all the errors due to measurements and will be used throughout the rest of the paper. The errors on the abundance ratios [X/Fe] were subsequently computed as the quadratic sum of the errors on [X/H] and [Fe/H]. Averaged over the whole sample, they lead to representative error bars of 0.04 dex for [FeI/H], 0.19 dex for [Ba/Fe], 0.16 dex for [Ca/Fe] and 0.21 dex for [Mg/Fe].

The uncertainties resulting from the choice of the atmospheric parameters have been estimated by varying one by one these parameters by their uncertainties (ΔTeff =  ± 200 K, Δlog    g =  ± 0.5 dex, Δvt =  ± 0.3 km s-1) for the stars MKV0770 and MKV0900, and determining how this modification affects the nominal abundances. The overall uncertainties due to atmospheric parameters are then calculated as the quadratic sum of the individual uncertainties due to Teff, log    g and vt. By construction, this method ignores covariances between the atmospheric parameters and thus overestimates the total error (McWilliam et al. 1995). The uncertainties due to the determination of atmospheric parameters are given in Table 6.

The hyperfine structure (HFS) of a line tends to desaturate it, which can lead to an overestimate of the abundance of an element. Following Letarte et al. (2010), we applied a line-by-line HFS correction to La and Eu lines in the few cases where we managed to detect these elements. This correction only depends on the EW of the lines.

4. Results

We have determined the atmospheric parameters and detailed abundances for 35 RGB stars in the Carina dSph. These abundances are listed in Tables 7–9 and the abundance ratios can be found in Table 10. The solar abundances of Anders & Grevesse (1989) have been adopted in this study, except for Ti, Fe and La for which the values of Grevesse & Sauval (1998) have been chosen.

4.1. Iron and iron-peak elements

The metallicity distribution of our sample:

The iron abundances of our sample are determined from between 15 and 36 FeI lines (see Table 7) which are all in good agreement. Our sample spans a metallicity range from [Fe/H]  ≈ −1.2 dex to [Fe/H]  ≈ −2.5 dex. It is clearly biased towards higher metallicities, with 24 stars more metal-rich than the mean [Fe/H] of  ≈ −1.70 dex and only 6 stars with [Fe/H]  ≤  −2.0 dex. An obvious explanation for this bias is that at lower S/N, the analysis of metal-rich stars remains possible while the weaker lines of the more metal-poor stars are drowned in the noise.

A comparison with the calcium triplet MDF:

Table 6

Errors on abundances due to sensitivity on the stellar parameters, computed for MKV0770 and MKV0900.

thumbnail Fig. 5

The [Fe/H] distribution of our sample (in red) and the full HR sample showing the stronger effect of low S/N on more metal poor stars (in green). The larger set of CaT measurements (Starkenburg et al. 2010) is in gray for comparison.

Figure 5 shows the metallicity distribution of our sample, compared to the larger sample with low-resolution spectroscopy in the CaT region (from Starkenburg et al. 2010). The effect of our metallicity bias can clearly be seen. We also show our full sample and how metal-poor stars are preferentially excluded due to the weak lines being more sensitive to S/N.

For 29 out of the 35 stars in our sample, both the CaT metallicity and our high resolution determination of [Fe/H] are available. In general, they agree well, despite the presence of outliers (see Fig. 6). Some of these outliers are stars with large errors on [Fe/H], but we have carefully investigated all of them and found no obvious error in the high resolution analysis. To try to understand the origin of the differences we first consider [Ca/Fe], which was found to be the dominant factor driving the EW of the CaT lines (Starkenburg et al. 2010). Unfortunately we couldn’t measure Ca in the most distant outlier, MKV0577, that is also Mg-depleted, with [Mg/Fe]  ≈ −0.15 dex. As Mg is one of the main electron donors, a depletion in Mg lowers the H− concentration and hence affects the continuous opacity and the temperature structure of the star. Several other outliers also have extreme [Ca/Fe] and/or [Mg/Fe] ratios, that sometimes fall out of the range (+0.0  < [α/Fe]  < + 0.4 dex) of the stellar models used to calibrate the CaT vs. [Fe/H] relation e.g. MKV0743, MKV0925, MKV1061 (see Table 10). However, this cannot be considered as a general pattern as two stars (MKV0840, MKV0976) with a rather common chemical composition also don’t match very well and conversely the agreement between both methods is very good for two other stars (MKV0740, MKV0902) which are both strongly depleted in Mg and/or Ca.

Venn et al. (2011) report 2 stars with large under-abundances for all elements measured, except the iron-peak and proposed that these stars are iron enriched. Both of them also show discrepancies of the order of 0.5 dex between metallicities obtained from a classical analysis and those derived from the CaT. Shetrone et al. (2009) already suggested that the CaT calibration is sensitive to changes in the continuous opacity and hence related to the global budget of free electrons (mostly released by metals) rather than to any particular element. As a consequence, the CaT feature might not be such a good proxy for the iron abundance for stars with a peculiar chemical composition. For large samples of stars with more standard abundance patterns, the metallicity estimates from the CaT agree very well in the mean (within 0.1–0.2 dex over the range −2.5 < [Fe/H]  < −0.5) with high resolution spectroscopic determinations as shown in Battaglia et al. (2008).

thumbnail Fig. 6

For our sample of RGB stars in the Carina dSph, we show the comparison between [Fe/H] measured from our high resolution spectroscopy and from the CaT (Starkenburg et al. 2010). The solid line indicates where [Fe/H]CaT = [Fe/H]HR while the dashed lines indicate an uncertainty of  ± 0.2 dex.

Other iron peak elements: Sc, Cr, Co, Ni:

The iron peak elements are synthesized in small quantities during SNe II events, but mostly come from SNe Ia. We were able to measure Sc, Cr, Co and Ni for many stars in our sample (see Tables 8 and 9). Cr I (measured from 2 lines) is, as expected, underabundant for metal-poor stars and the Cr abundance increases with [Fe/H], with a handful of stars remaining underabundant at intermediate metallicities. Co (up to four lines) shows the same behaviour (see Table 8). The situation is more complex in the case of Ni, where the abundance is derived from only 1–2 lines (see Table 8). We find a global increase of [Ni/Fe] with [Fe/H], and the persistence of Ni-poor stars at intermediate metallicities. Our sample also harbours a group of Ni-rich (>+0.5 dex) stars. Sc, measured from one line, was detected in only two stars (see Table 9).

thumbnail Fig. 7

The distribution of [Mg/Fe] for our sample of RGB stars in the Carina dSph as pink filled circles. Also included in the plot are the 5 RGB stars in the Carina dSph from Shetrone et al. (2003): pink open triangles; the 9 RGB stars from Venn et al. (2011): pink open squares and 6 of the RGB stars from Koch et al. (2008): pink open diamonds. Stars in Sculptor are in green crosses ((Shetrone et al. 2003; Geisler et al. 2005); Hill et al., in prep.). Milky Way halo stars are in small grey dots (from Venn et al. 2004, and references therein). Individual error bars are given for some peculiar stars and a representative error bar for the rest is given in bottom right hand corner.

4.2. α-elements

The α-elements are named after their formation process, the capture of He nuclei during different stages of stellar evolution. They are mainly formed and released when high mass (>8 M⊙), short lived stars explode as type II supernovae (SNe II).

The change in slope of measurements in a [Mg/Fe] versus [Fe/H] plot is often called a “knee” (e.g. Matteucci & Brocato 1990; Matteucci 2003) whose position indicates the level of Fe-enrichment reached by a system when SNe Ia begin to influence the chemical evolution. We know from CMD analysis that Local Group dSphs experienced a range of different SFHs, and so we expect that the “knee” will occur at different [Fe/H] in different galaxies. At present, the only dSph for which the knee position is clear (at [Fe/H] = −1.8 dex) is Sculptor (Tolstoy et al. 2009; Hill et al., in prep.). In the case of the Fornax dSph, current data suggests that the knee should occur below [Fe/H]  < −1.5 dex, while in the case of Sagittarius it could be at [Fe/H]  < −1.0 dex. It might be expected that the Carina dSph will have more than one “knee” given the multiple star formation episodes separated in time (e.g., Gilmore & Wyse 1991).

We focus on Mg and Ca results, where we also add to our measurements literature samples (Shetrone et al. 2003; Koch et al. 2008; Venn et al. 2011). It consists of 5 stars for Shetrone et al. (2003), 10 stars Koch et al. (2008) and 9 stars for Venn et al. (2011), of which 4 are overlapping with Koch et al. (2008). We also have 1 star in common with Koch et al. (2008).

Magnesium: We can only determine [Mg/H] using a single, well defined line at λ = 5528.41   Å (see Table 7). Three stars lack Mg abundances because of an EW in excess of 200 mÅ. Most of the stars in our sample are Mg-rich, with [Mg/Fe]  ≈ 0.3 dex (see Fig. 7). However, seven stars have low or extremely low [Mg/Fe]. MKV0740 and MKV0743 have among the lowest [Mg/Fe] ever reported, although the errors on the abundances of these stars are fairly large. As can be seen in Fig. 7, the many RGB stars in the Carina dSph have [Mg/Fe] similar to Galactic halo stars at same [Fe/H]. The same feature can also be observed for similar metallicity stars in the Sculptor dSph, with about the same [Fe/H] limit (Tolstoy et al. 2009; Hill et al., in prep.).

There does appear to be a general downward trend of the mean [Mg/Fe] with increasing [Fe/H] for the Carina dSph stars in Fig. 7, but we need ages of the stars to disentangle the different star formation episodes. It is clear that the Carina dSph has not followed the same chemical enrichment path as the Sculptor dSph. The sparse numbers of low [Fe/H] stars measured in the Carina dSph have lower [Mg/Fe] than in the Sculptor dSph. There is an overlap of the majority of stars for the more [Fe/H] rich stars in the Carina dSph with those in Sculptor, but these stars have a much higher scatter in Carina, going down to extremely underabundant [Mg/Fe].

Calcium: For our sample, as many as eight lines can be used to determine [Ca/Fe] (see Table 7). As with Mg, our sample is mostly Ca-rich (see Fig. 8), but some stars have low [Ca/Fe]. The samples of Shetrone et al. (2003), Koch et al. (2008) and Venn et al. (2011) also include stars with similarly low [Ca/Fe]. Both the spread and the extremes are much less pronounced than for [Mg/Fe]. Magnesium (and oxygen) are produced during the hydrostatic He burning in massive stars, and therefore their yields are not predicted to be affected by the SNe II explosion. Conversely, Ca (and Si, Ti) are formed during the SNe II explosion itself and thus their yields depend sensitively on the energy of the SNe. However, explosion energies cover only a small energy range which leads to a small scatter in [Ca/Fe].

In Fig. 8, we see that [Ca/Fe] for the Carina dSph stars overlaps less markedly the halo stars of the Milky Way than [Mg/Fe] (in Fig. 7). This is also true for the Sculptor dSph measurements. The [Ca/Fe], like [Mg/Fe], for the Carina dSph stars does overlap the measurements of Sculptor stars, but as for [Mg/Fe] the scatter in the Carina measurements is larger, with a number of outliers with particularly low [Ca/Fe]. In most cases, stars with a low [Mg/Fe] also have a low [Ca/Fe].

thumbnail Fig. 8

The distribution of [Ca/Fe] for our sample of RGB stars in the Carina dSph. Additional data, definition of symbols and references are as in Fig. 7.

The [Ca/Fe] for the Carina dSph (Fig. 8) shows no obvious knee, but rather a shallow downward trend, with an increased scatter at intermediate metallicities. This could be due to the overlapping influence of both SNe Ia and SNe II from distinct episodes of star formation.

Titanium: We could measure both TiI (5 lines) and TiII (1–5 lines) but the abundances obtained do not agree well with each other (see Table 7). TiI is systematically lower than TiII. We expect this effect to be mainly due to NLTE effects, with a departure from ionization equilibrium affecting TiI. However, errors in the determination of Teff could also shift the ionization equilibrium in the same way. This is the same discrepancy already reported by Letarte et al. (2010), for the Fornax dSph, observed with the same FLAMES setup. Letarte et al. (2010) warns us that CaI could also be affected by NLTE effects in the same way as TiI, without any possibility to check since we cannot measure CaII lines in these stars.

Silicon: The available Si lines are very weak and could only be measured in three stars (see Table 9). Like the other α-elements, Si is over-abundant.

4.3. Neutron-capture elements

Elements with atomic number Z > 30 are neutron-capture elements. The two main ways to produce them are the slow s-process and the rapid r-process. For the s-process a longer period (with respect to the timescale for β− decay) elapses between successive neutron capture events. This process is thought to occur in thermally pulsating AGB stars, which are long-lived low or intermediate mass stars. The r-process in contrast, is where successive neutron captures occur on a very short timescale. The r-process divides into two different branches: the weak r-process, which forms the lighter n-capture elements (e.g. Sr, Y, Zr) and the main r-process, which forms the heavier n-capture elements. There remains significant uncertainty about exactly what is the origin of the r-process elements (e.g., Sneden et al. 2008). We can measure [Ba/Fe] for the majority of stars in our sample. A few stars have Y, La, Eu and Nd measurements as well.

Barium: Our analysis is based on 1–2 strong lines (see Table 8). The most metal-poor RGB stars in the Carina dSph have low [Ba/Fe] with a lot of scatter. Studies which could measure both [Ba/Fe] and [Eu/Fe] (Shetrone et al. 2003; Venn et al. 2011) suggest that the Ba in very metal-poor stars has an r-process-only origin. This scatter is also seen in the RGB stars measured in the Sculptor dSph (Hill et al., in prep.). Our sample, combined with Shetrone et al. (2003) and Venn et al. (2011) measurements, shows an increase of [Ba/Fe] with [Fe/H], once again similar to what is seen in Sculptor (Hill et al., in prep.). This can be interpreted as an increasing contribution of the s-process from AGB stars (Shetrone et al. 2001). A couple of the stars in the Carina dSph reach high Ba abundances at rather low [Fe/H], more similar to Fornax (Letarte et al. 2010).

Y, La, Eu, Nd: Only a handful of measurements could be made for these elements in our sample, and always in stars with an enhanced content in neutron-capture elements. [La/Fe] is consistent with [Ba/Fe], where stars with high [Ba/Fe] also have high [La/Fe] (see Tables 8 and 9).

4.4. Comparison with previous work

We have no stars in common with Shetrone et al. (2003) or Venn et al. (2011), and only one star in common with the UVES study of Koch et al. (2008), our MKV0948 is his LG04d_006628. Making a careful comparison we can see that the photometric Teff values agree, however Koch et al. (2008) chose to use the spectroscopic Teff in their study and so they had to increase the photometric estimate by  ≈450 K to reach the excitation equilibrium for this star. As a consequence, our log    g and vt are also different, though only slightly for vt. In addition, for the few lines in common in both linelists, our EWs are systematically lower (by  ≃ 15 mÅ) than those of Koch et al. (2008). Finding out why is not straightforward and seems to be more complicated than due only to a difference in continuum placement. Despite these differences, our abundances are in reasonably good agreement: [FeII/H] matches almost exactly and [FeI/H] differs by −0.25 dex (which is nearly within the error bars). [TiII/H] is also in good agreement, however [Ca/H] is strongly discrepant by  ~+0.4 dex.

5. Ages

Due to its distinct episodes of star formation, the age-metallicity relation for stars in the Carina dSph is not expected to be as straightforward as in more simple systems like the Sculptor dSph (e.g. de Boer et al., in prep.). Accurate ages would allow us to determine the speed of chemical enrichment of different elements and hence the relative importance of SNe II and SNe Ia at any given time.

5.1. Age determination

Combining measurements of [Fe/H] and [Mg/Fe] with accurate photometry we can estimate the ages of individual RGB stars using simple isochrone fitting. The age is determined by finding the isochrone with appropriate [Fe/H] and [α/Fe] abundances that best matches the position of the star in the CMD.

We first built a grid of metallicities by dividing the possible [Fe/H] range (given by the error-bars) into bins of 0.05 dex. We used [Mg/Fe] as a proxy for [α/Fe] (and [Ca/Fe] when [Mg/Fe] was not available). The isochrones do not sample the full [α/Fe] range, so we used the lowest value available to compute the ages of the α-poor stars. As a consequence, the accuracy of our ages will be reduced for these stars.

For each point on the metallicity grid, we generated isochrones using the Teramo/BaSTI stellar evolutionary models (Pietrinferni et al. 2004, 2006) for ages between 1 and 15 Gyr, with a spacing of 0.5 Gyr. Those isochrones which are consistent with the observed colours and magnitudes within the photometric error-bars were then used to build up a probability distribution function for ages. Figure 9a shows the age probability distribution for an intermediate age star (MKV0976, age = 2.61 ± 0.76 Gyr) while Fig. 9b shows the age probability distribution for a star (MKV0614) with a more uncertain age (6.80 ± 1.84 Gyr) but that probably still belongs to the intermediate age population. The age distribution is fit by a Gaussian where the mean is the likely age of the star and the standard deviation the error bar on the age. According to their colours, a few stars (7) are found to be older than 14 Gyr and hence inconsistent with the age of the Universe. It is likely that these are old stars, and so we set their age to 15 Gyr (without error-bar) to identify the larger than normal uncertainty in their true age.

We applied the same method to the RGB stars in the samples of Shetrone et al. (2003), Koch et al. (2008) and Venn et al. (2011), using homogeneous V and I magnitudes from ESO-WFI. The ages and their uncertainties of all the stars in the Carina dSph with HR abundances can be found in Table 10.

thumbnail Fig. 9

Age probability distributions built up from isochrone fitting and their Gaussian fits. We show here two examples: a) MKV0976, age = 2.61 ± 0.76 Gyr; and b) MKV0614, age = 6.80 ± 1.84 Gyr.

Table 10

Ages and abundance ratios for all the stars in the Carina dSph with detailed abundance measurements.

5.2. The age range: two populations

We noticed that the ages of the RGB stars in the Carina dSph (Table 10) fall broadly into two groups, as might be expected from the SFH (Smecker-Hane et al. 1996; Monelli et al. 2003; Rizzi et al. 2003; Bono et al. 2010). Because our ages have large error bars, our aim is simply to split our sample into an old population and an intermediate age population. Our abundances are of RGB stars, so we cannot observe stars from the very young population (<1 Gyr old). We chose 8 Gyr as the border between the old and intermediate age populations. Most of the photometric studies place the intermediate population in the 2–6 Gyr range, while the old population should be older than 10 Gyr. The majority of our stars fall naturally into these age groups, and only a few stars lie near the threshold value (see Fig. 10). Indeed, only 13 (out of 54) stars have ages between 6 and 10 Gyr, the rest are clearly younger or older than 8 Gyr. However it is still possible to attribute these 13 stars to either age group given their age probability distribution. The case of MKV0614 (see Fig. 9b) shows for example that it is probably an intermediate-age star, as most of the possible isochrones indicate an age  <8 Gyr, though we cannot exclude an older age for this star.

thumbnail Fig. 10

The ages (in Gyr) as a function of [Fe/H] (dex) for the RGB stars with high resolution abundances in the Carina dSph (see also Table 10). The shaded areas represent the expected age ranges of star formation as indicated by photometric studies.

Table 11

The median and median absolute deviation (mad) computed for 2 age groups (intermediate-age stars and old stars), either for the whole sample or for a more restricted sample in which all the stars whose age is betwen 6 and 10 Gyr have been removed.

To quantify the distribution of stars in both age groups, we computed the median and median absolute deviation (mad). The mad method is a robust estimate of the dispersion, much less sensitive to outliers than the standard deviation. This was done for two different samples: the whole sample of RGB stars in the Carina dSph with detailed abundances available; and a smaller sample in which all the stars whose age is between 6 and 10 Gyr (i.e., within  ± 2 Gyr from the border) have been removed. The results shown in Table 11 indicate that a more restricted sample has a negligible effect on the median and the mad for the intermediate age population. This is because they already had a narrower age distribution but also because only 4 stars have been removed. In the case of the older population, reducing the sample to those stars older than 10 Gyr only has a noticeable effect on the median age, that is shifted toward higher values by  ≈2 Gyr. This effect is not surprising as 9 stars are removed and they are preferentially among the youngest of the old sample.

thumbnail Fig. 11

The [Mg/Fe] distribution for the RGB stars from the Carina dSph separated into two ages groups: stars  >10 Gyr old are represented by red filled circles, stars  <10 Gyr old are represented by blue filled circles. Stars in the age range 6–10 Gyr are represented either by red open circles (8< age <10 Gyr) or by blue open circles (6< age <8 Gyr). Milky Way halo stars are shown as small grey dots.

6. Discussion

The Carina dSph has a particularly complex SFH, with at least two, and possibly three or four distinct bursts of star formation over its history as shown by multiple MSTOs in its CMD (e.g., Smecker-Hane et al. 1996; Hurley-Keller et al. 1998). The extremely narrow RGB shows the strong presence of an age-metallicity degeneracy. Spectroscopic abundances of stars with age estimates are required to determine how the chemical evolution progressed with the SFH. Our FLAMES study (35 stars) significantly enlarges the sample of RGB stars in the Carina dSph with accurate abundances, which was 15 stars (Shetrone et al. 2003; Koch et al. 2008, focusing only on α-elements). The Venn et al. (2011) sample looks at a smaller number of stars (9) but with the accuracy and wealth of chemical elements of UVES, whereas our sample contains more stars, but with fewer elements and larger uncertainties.

We would like to briefly mention that none of the values discussed ([Fe/H], [Mg/Fe], ages...]) correlates with the distance from the center of Carina. The GIRAFFE field of view (25′) does not cover the whole galaxy, but from CaT measurements that do (Koch et al. 2006), no obvious radial metallicity gradient was found. However, the shape of the MDF varies from the inner to the outer region, where the more metal-rich stars are more centrally concentrated than the metal-poor.

6.1. SFH and the [α/Fe] “clock”

One of the most obvious signs of chemical evolution in galaxies is the [α/Fe] “clock” (Tinsley 1979; Gilmore & Wyse 1991; Matteucci 2003). The traditional interpretation is that the α-elements are predominantly released into the interstellar medium (ISM) by SNe II explosions. As the progenitors of SNe II are high-mass stars with short lifetimes, the α-enrichment of the ISM starts soon after the beginning of star formation. Some Fe is also formed in SNe II, but it is mainly produced by explosive nucleosynthesis in SNe Ia. The progenitors of SNe Ia are long lived low-mass stars. The first SNe Ia explosions are believed to occur  ≈1 Gyr after the first SNe II and to be much less concentrated in time (Matteucci & Brocato 1990; Matteucci 2003). Their explosions cause a decrease in [α/Fe] if the SFR is constant with time. The variation of [α/Fe] allows us to trace the relative importance of SNe II and SNe Ia. For this purpose the α-element Mg is more suitable than Ca or Ti, as it is only produced in very small quantities by SNe Ia (Tsujimoto et al. 1995).

Figure 11 displays [Mg/Fe] against [Fe/H] for the RGB stars observed in the Carina dSph, with symbols identifying the two age groups and those stars with error bars that overlap the boundaries of the different age groups. The interpretation of both the large spread in [Mg/Fe] and the existence of an intermediate age, Mg-rich population, is extremely puzzling. [Ca/Fe] (see Fig. 12) shows a similar behaviour but with a smaller dispersion.

thumbnail Fig. 12

The [Ca/Fe] distribution with the RGB stars from the Carina dSph separated into two ages groups as described in Fig. 11.

6.2. The old population (>8 Gyr old)

We can use the [Fe/H] values provided in Fig. 10 to divide the oldest stellar population observed in Carina in two groups: very metal-poor, [Fe/H]  < −2.2 dex, and metal-poor, −2.2 <  [Fe/H]  < −1.0, stars.

6.2.1. Very metal-poor old stars

Our age estimates indicate that most of the low-metallicity RGB stars in the Carina dSph are very old (>13 Gyr) (see also Table 10 and Figs. 11, 12). These stars were probably formed at a time when the ISM was only enriched by α-elements from SNe II, which means during the first Gyr after star formation started in the Carina dSph. The low values and large scatter of [Ba/Fe] measurements (see Fig. 13) also support this. At the oldest ages Ba is expected to form, from pre-existing Fe-peak seeds, mainly through the r-process whose production sites are still debated but probably related to neutron-rich regions surrounding SNe (e.g., Sneden et al. 2008) Very metal-poor stars in our sample have low values of  [Ba/Fe]  < −0.5, which gradually decrease with decreasing [Fe/H] reaching the extreme value of  [Ba/Fe]  = −1.1 in the most metal-poor star.

In Fig. 11 we can see that [Mg/Fe] in very metal-poor stars in the Carina dSph are consistent with those measured in  [Fe/H]  < −2.2 Milky Way halo stars. This result may imply that at very early times the conditions for the chemical enrichment were the same. In particular, as the α-elements are mostly produced by massive stars exploding as SNe II, a similar [α/Fe] tells us that the IMF was most likely similar. Note that even though these stars are Ca-enhanced, they do not reach the high values found in very metal-poor stars in Sculptor or the Milky Way halo (see Fig. 8). This is usually attributed to a lower star formation rate (Matteucci 2003).

It is hard to establish if there is a “knee” associated with the first episode of star formation and what may be its position. Instead, one could also imagine that the low [α/Fe] ratios seen in Carina stars among the oldest stars is merely a large scatter, that might be due to inhomogeneous mixing (see Sect. 6.2.2 and Venn et al. 2011). However, Fig. 11 suggests that there may be a knee somewhere between [Fe/H]  ~ (−2.7,−2.3). A larger sample in this metallicity range is needed to confirm the reality and exact location of the knee. A low [Fe/H] value for the position of the knee is consistent with the Carina dSph only experiencing a modest chemical evolution before the onset of SNe Ia.

6.2.2. Metal-poor old stars

In Fig. 11 we can see that our sample includes a number of old metal-poor stars with a very large scatter in [Mg/Fe]. Although these stars are typically younger (≈3 ± 1 Gyr) than the Mg-rich, very metal-poor population (see Table 10), the interpretation of their abundances is not straightforward.

The most massive among the stars formed during the early episodes of star formation exploded as SNe II and their ejecta polluted the ISM. The subsequent generation of stars are then formed from an α- and Fe-enriched ISM. Hence, these new stars should have a similar [α/Fe] to those that formed in the first burst, but at higher [Fe/H]. Approximately 1 Gyr after the first SNe II explosion, SNe Ia are expected to contribute to the ISM enrichment, thus causing a decrease in [Mg/Fe] and an increase in [Fe/H].

In our sample of old metal-poor stars we find the presence of both Mg-rich and Mg-poor objects. Interestingly, three of the stars that seem to be old (MKV0612) or very old (car-5070 and MKV0902) have very low [Mg/Fe], [Ca/Fe] and [Ba/Fe], suggesting that they formed from SNe Ia-contaminated material, while SNe II seem to have played only a minor role for Fe. The presence of these stars, along with the existence of Mg-rich stars up to [Fe/H]  ~ −1.4, is extremely puzzling, and could be consistent with inhomogeneous mixing (see Venn et al. 2011, for more details).

6.3. Intermediate age stars (<8 Gyr old)

Stars with intermediate ages appear to span only a restricted range of [Fe/H] (from –1.8 to –1.2 dex), concentrated at [Fe/H]  ~ −1.5, (see Figs. 11 and  12). Unexpectedly, only 1–2 stars are depleted in [Mg/Fe], most of the others being Mg-rich stars which overlap with the old and metal-poor population described in Sect. 6.2.2. Therefore, most of the  <8 Gyr old stars in Carina, are presumably formed from gas that was apparently not strongly polluted by SNe Ia compared to SNe II. In Fig. 11 we can see that a couple of  ≈(5−6) Gyr old stars have extremely low  [Mg/Fe]  < −0.5 dex. Although these outliers have quite high error bars, it is not clear how to explain their properties.

There is no obvious second “knee” associated with the dominant intermediate age star formation episode. This may be partly because there is a large scatter in the abundances at higher [Fe/H]. It is also possible that due to significant errors in both ages and abundances stars from different star formation episodes may be misidentified, confusing the picture. As these results stand there is no knee and very little sign of chemical evolution in the intermediate age group of RGB stars in the currently observed stars in the Carina dSph.

The large spread in [Ba/Fe] at all ages seems to extend toward lower [Ba/Fe] than in the Milky Way halo stars, similar to what is observed in the Sculptor dSph (see Fig. 13). Unfortunately, we could measure [Eu/Fe] in only one of our stars and only upper limits could be determined for most of the high resolution sample of Venn et al. (2011), preventing us from commenting on relative weights of r- and s-processes for these stars.

thumbnail Fig. 13

The [Ba/Fe] distribution for the RGB stars from the Carina dSph separated into two ages groups: stars  >10 Gyr old are represented by red filled circles, stars  <10 Gyr old are represented by blue filled circles. Stars in the age range 6–10 Gyr are represented either by red open circles (8< age <10 Gyr) or by blue open circles (6< age <8 Gyr). Sculptor stars (Shetrone et al. 2003; Geisler et al. 2005; Hill et al., in prep.) are shown as small green dots and Milky Way halo stars as small grey dots.

6.4. The chemical evolution of the Carina dSph

Our observations, combined with additional abundances from other high resolution spectroscopic studies, confirm that the Carina dSph has had a complex chemical evolution. From the segregation of stars in two age groups we can try to disentangle the chemical properties of the gas driving these two star formation episodes. It can be seen that the oldest star formation episode (>10 Gyr old), suggests a fairly “normal” chemical evolution, from  [Fe/H]  ~ −3 to  −1.5, with [Mg/Fe] decreasing with time after a “knee” at  [Fe/H]  ~ −2.3, as SNe Ia start to contribute to enrichment of the ISM. The second episode of star formation (<6 Gyr old) does not appear to conform to the same pattern. There is a relatively small range in [Fe/H], with most of the stars at  [Fe/H]  ~ −1.5 ± 0.2 dex. This episode also appears to predominantly contain stars with high [Mg/Fe] (~+0.3 dex). There does not seem to be a significant contribution by SNe Ia to the chemical evolution during this episode of star formation.

There is always the chance, in such a complex situation, that the sample of stars which have been observed, which we know is biased to high metallicity stars, has missed the low metallicity tail of this intermediate age sample. Stars of low metallicity show very little spread in colour for different ages, so these stars may also be hard to identify with straight forward photometric age determinations. But even if we are missing the low metallicity tail, we still have to explain the apparent lack of a “knee” at any metallicity for this age group. It seems that, in the mean, the stars managed to form at roughly the same  [Fe/H] (~−1.5 dex) and  [Mg/Fe] (~+0.3 dex) for the entire star formation episode. It is not clear what happened to the SNe Ia products, which should have had time to contribute, if the length of the star formation episode determined from CMD analysis is to be believed. It may also be possible that this star formation episode was much shorter (and also much more intense) than current CMD analysis suggests, or consists of discontinuous star formation episodes. Recently Stetson et al. (2011) suggested a restricted age range of 2 Gyr for the intermediate-age (4–6 Gyr old) population. Short star formation episodes (<1 Gyr) could explain the lack of SNe Ia enrichment. Indeed, if SNe II are able to remove the ISM of a galaxy before the onset of SNe Ia, then the effectiveness of SNe Ia in enriching the ISM may be limited.

It seems that the chemical evolution does not run smoothly from the first star formation episode to the second. The [Fe/H] range overlaps between  [Fe/H]  ~ −2 and −1.4 dex. It is likely that we are more incomplete for metal poor stars in our sample (see Sect. 4.1) than the metal rich, which is only likely to increase the overlap. This overlap means that the most metal poor stars in the intermediate age group, are at lower [Fe/H] than the most metal rich stars in the old group. This requires that either star formation in this second episode started from scratch, with a new reservoir of gas (at  [Fe/H]  ≲ −2,  [Mg/Fe]  ~ + 0.3,  [Ba/Fe]  ~ 0) or additional more metal poor gas was added to gas that was enriched by the first star formation episode to be able to start forming stars at lower [Fe/H]. It is hard to imagine a scenario, in such a small system, where explaining the properties of these two very distinct episodes of star formation does not involve the addition of external gas.

6.5. Physical interpretation

We briefly consider what are the physical processes that may influence the evolution of a small dwarf galaxy like Carina and thus offer some hints as how to interpret the puzzling results we found namely: (i) the presence of numerous Mg-rich stars in the intermediate age population; and (ii) the absence of a knee associated to the second burst of star formation.

The cycle of forming stars, heating the ISM with supernovae explosions, and partially removing it thus decreasing the star formation, is generally called “feedback” (Larson 1974). This physical process mainly depends on the supernovae rate and on the binding energy of the galaxy. Therefore, it is likely to be a critically important factor driving the evolution of low mass galaxies (e.g., Dekel & Silk 1986; Mac Low & Ferrara 1999; Ferrara & Tolstoy 2000; Salvadori et al. 2008) like the Carina dSph, with Mtot = 6.1 ± 2.3 × 106   M⊙ within the half radius 241 ± 23 kpc (Walker et al. 2009). If the bursts of star formation observed in Carina are part of an ongoing cycle of heating and cooling of an initial gas reservoir (e.g., Stinson et al. 2007; Valcke et al. 2008), there should be a clear evolutionary path in the observed abundances, showing the influence of SNe Ia enrichment at increasing [Fe/H] values. On the other hand, if the ISM is removed after each burst of star formation then new gas is required to power the subsequent star formation activity. This gas will have to originate from external processes such as merging, or accretion from the intergalactic medium (IGM), and will thus most likely have chemically distinct properties. A high abundance of Mg over a large time range is perhaps a sign of this.

The reduced mixing of SN ejecta within the ISM of gas-poor galaxies may also play a role in the chemical enrichment of a small galaxy like Carina. Metal-enhanced winds (Vader 1986; Martin et al. 2002) are more efficient in actively star forming galaxies (Fujita et al. 2004), and may strongly reduce the effectiveness of both SNe II and SNe Ia in enriching the ISM. This may be especially apparent during the second burst of star formation, which is the most intense. An extremely slow chemical enrichment due to high wind losses may be able to explain the narrow [Fe/H] range of intermediate age stars along with the lack of a second knee for these stellar population. Of course, full calculations have to be made and complete models made to try to explain the complex age-metallicity relation of the relic stars observed.

The chemical evolution of the Carina dSph has been modelled several times (e.g. Lanfranchi et al. 2006; Revaz et al. 2009) and compared to the (then) observed abundance ratios (Shetrone et al. 2003; Koch et al. 2008). Interestingly, the N-body/tree-SPH simulations (Revaz et al. 2009) have successfully predicted the large scatter in α-abundances seen in our observations, including the very low [Mg/Fe] stars. However, the SFH is not a good match, with gaps in star formation predicted by the model shorter than those observed in Carina. This implies that the age-metallicity relation may be different to our observations. This discrepancy may be related to the fact that the model assumes that the dwarf galaxy was isolated with a fixed gas reservoir. In contrast the complicated star formation history of Carina is probably driven by external physical processes (e.g., Pasetto et al. 2011). Carina has currently a very small galactocentric velocity (vgalacto = 7 km s-1) which suggests that it is at apocentre, and has been orbiting the Milky Way environment for a considerable time (e.g., Piatek et al. 2003). Updated models are clearly needed, but Carina has always proved a complicated challenge.

7. Summary and conclusions

We determined detailed high resolution abundances for a variety of elements, including Mg, Ca and Ba, for most of our 35 RGB stars in the Carina dSph. This is a significant increase in the number of RGB stars analysed from previous studies. We confirm that the abundances of individual RGB stars, at a given [Fe/H] in the Carina dSph are typically more scattered than in the Milky Way or other dSph, as has already been noted by Koch et al. (2008). This scatter exists at all [Fe/H] and is clearly representative of the global properties of the Carina dSph.

We also determined ages for our sample of RGB stars and for  ~20 additional RGB stars in the Carina dSph with detailed abundances from the literature. This allows us for the first time to distinguish significant numbers of stars from different episodes of star formation in the Carina dSph. The ages we determined are broadly consistent with the two episodes of star formation expected from CMD analysis. Our ages are not accurate enough to do more than place our stars in one star formation episode or another.

As in other dSphs, Carina contains old metal-poor, alpha-rich stars, and among these stars there appears to be a general trend of decreasing [Mg/Fe] with increasing [Fe/H], which is presumably due to the onset of SNe Ia enrichment (although a stochastic star formation could also be invoked). This population of stars is associated to the oldest episode of star formation in the Carina dSph. We have also identified stars associated to a second episode of star formation. Their enrichment history is not so easy to interpret. The most metal poor stars in this later, longer lasting and more intense episode of star formation are somewhat more metal poor than the most metal rich stars in the oldest sample. This suggests that there has not been a simple chemical evolution path following from one episode to the next in a fixed reservoir of gas.

An important step would be to carry out a combined model of the detailed SFH and the abundances, as has been done for Sculptor (de Boer et al., in prep.), and of course to better populate the entire [Fe/H] range of Carina with accurate and detailed stellar abundances.

Despite a large increase in the number of RGB stars with accurate abundances in the Carina dSph, we still have not been able to fully disentangle the chemical evolution history.

Acknowledgments

The authors thank the anonymous referee for her/his comments and suggestions that helped to improve the paper. The authors thank ISSI (Bern) for support of the team “Defining the Life-Cycle of Dwarf Galaxy Evolution: the Local Universe as a Template” and M. Gullieuszik for sending the IR photometry for stars in our sample. B.L., E.T., T.d.B., and E.S. have been funded by The Netherlands Foundation for Scientific Research (NWO) through a VICI grant and S.S. through a NOVA fellowship. B.L. thanks the Leids Kerkhoven-Bosscha Fonds (LKBF) for financial support to attend the “A Universe of dwarf galaxies” conference, June 2010, Lyon and E. Tiesinga for his help in installing DAOSPEC on a 64-bit machine.

References

  1. Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
  3. Armandroff, T. E., & Da Costa, G. S. 1999, AJ, 101, 1329 [Google Scholar]
  4. Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008, MNRAS, 383, 183 [Google Scholar]
  5. Bono, G., Caputo, F., Santolamazza, P., Cassisi, S., & Piersimoni, A. 1997, AJ, 113, 2209 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bono, G., Stetson, P. B., Walker, A. R., et al. 2010, PASP, 122, 651 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cignoni, M., & Tosi, M. 2010, in Adv. Astron., article 158568 [Google Scholar]
  8. Da Costa, G. S. 1994, in ESO/OHP Workshop on Dwarf Galaxies, ed. G. Meylan, & P. Prugniel (Garching: ESO), 221 [Google Scholar]
  9. Dall’Ora, M., Ripepi, V., Caputo, F., et al. 2003, AJ, 126, 197 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dolphin, A. E. 2002, MNRAS, 332, 91 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fabrizio, M., Nonino, M., Bono, G., et al. 2011, PASP, 123, 384 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ferrara, A., & Tolstoy, E. 2000, MNRAS, 313, 291 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fujita, A., Mac Low, M.-M., Ferrara, A., & Meiksin, A. 2004, ApJ, 613, 159 [NASA ADS] [CrossRef] [Google Scholar]
  15. Geisler, D., Smith, V. V., Wallerstein, G., Gonzalez, G., & Charbonnel, C. 2005, AJ, 129, 1428 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gilmore, G., & Wyse, R. F. G. 1991, ApJ, 367, 55 [Google Scholar]
  17. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Helmi, A., Irwin, M. J., Tolstoy, E., et al. 2006, ApJ, 651, L121 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hurley-Keller, D., Mateo, M., & Nemec, J. 1998, AJ, 115, 1840 [NASA ADS] [CrossRef] [Google Scholar]
  21. Kauffmann, G., White, S. D. M., & Guiderdoni, B. 1993, MNRAS, 264, 201 [NASA ADS] [CrossRef] [Google Scholar]
  22. Koch, A., Grebel, E. K., Wyse, R. F. G., et al. 2006, AJ, 131, 895 [NASA ADS] [CrossRef] [Google Scholar]
  23. Koch, A., Grebel, E. K., Gilmore, G. F., et al. 2008, AJ, 135, 1580 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lanfranchi, G. A., & Matteucci, F. 2003, MNRAS, 345, 71 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lanfranchi, G. A., & Matteucci, F. 2004, MNRAS, 351, 1338 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lanfranchi, G. A., Matteucci, F., & Cescutti, G. 2006, A&A, 453, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] [CrossRef] [Google Scholar]
  28. Letarte, B., Hill, V., Tolstoy, E., et al. 2010, A&A, 523, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Mac Low, M.-M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] [Google Scholar]
  30. Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
  31. Majewski, S. R., Frinchaboy, P. M., Kunkel, W. E., et al. 2005, AJ, 130, 2677 [NASA ADS] [CrossRef] [Google Scholar]
  32. Martin, C. L., Kobulnicky, H. A., & Heckman, T. M. 2002, ApJ, 574, 663 [NASA ADS] [CrossRef] [Google Scholar]
  33. Mateo, M. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mateo, M., Hurley-Keller, D., & Nemec, J. 1998, AJ, 115, 1856 [NASA ADS] [CrossRef] [Google Scholar]
  35. Matteucci, F. 2003, Ap&SS, 284, 539 [Google Scholar]
  36. Matteucci, F., & Brocato, E. 1990, ApJ, 365, 539 [NASA ADS] [CrossRef] [Google Scholar]
  37. McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mighell, K. J. 1997, AJ, 114, 1458 [NASA ADS] [CrossRef] [Google Scholar]
  39. Monelli, M., Pulone, L., Corsi, C. E., et al. 2003, AJ, 115, 1856 [Google Scholar]
  40. Pasetto, S., Grebel, E. K., Berczik, P., Chiosi, C., & Spurzem, R. 2011, A&A, 525, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
  42. Piatek, S., Pryor, C., Olszewski, E. W., et al. 2003, AJ, 126, 2346 [Google Scholar]
  43. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
  44. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
  45. Pietrzyński, G., Górski, M., Gieren, W., et al. 2009, AJ, 138, 459 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pompéia, L., Hill, V., Spite, M., et al. 2008, A&A, 480, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Ramìrez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
  48. Revaz, Y., Jablonka, P., Sawala, T., et al. 2009, A&A, 501, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Rizzi, L., Held, E. V., Bertelli, G., & Saviane, I. 2003, ApJ, 589, 85 [Google Scholar]
  50. Saha, A., Monet, D. G., & Seitzer, P. 1986, AJ, 92, 302 [NASA ADS] [CrossRef] [Google Scholar]
  51. Salvadori, S., Ferrara, A., & Schneider, R. 2008, MNRAS, 386, 348 [NASA ADS] [CrossRef] [Google Scholar]
  52. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  53. Shetrone, M. D., Côt, P., & Sargent, W. L. W. 2001, ApJ, 548, 592 [NASA ADS] [CrossRef] [Google Scholar]
  54. Shetrone, M. D., Venn, K. A., Tolstoy, E., et al. 2003, AJ, 125, 684 [NASA ADS] [CrossRef] [Google Scholar]
  55. Shetrone, M. D., Siegel, M. H., Cook, D. O., & Bosler, T. 2009, AJ, 137, 62 [NASA ADS] [CrossRef] [Google Scholar]
  56. Smecker-Hane, T. A., Stetson, P. B., Hesser, J. E., & VandenBerg, D. A. 1996, ASPC 98, The Impact of Stellar Physics on Galaxy Evolution, ed. C. Leitherer, U. Fritzevon Alvensleben, & J. Huchra, 328 [Google Scholar]
  57. Smecker-Hane, T. A., Mandushev, G. I., Hesser, J. E., et al. 1999, ASPC 192, Spectrophotometric Dating of Stars and Galaxies, ed. I. Hubeny, S. Heap, & R. Cornett, 159 [Google Scholar]
  58. Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Spite, M. 1967, AnAp, 30, 211 [Google Scholar]
  60. Starkenburg, E., Hill, V., Tolstoy, E., et al. 2010, A&A, 513, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
  62. Stetson, P. B., Monelli, M., Fabrizio, M., et al. 2011, Msngr, 144, 32 [NASA ADS] [Google Scholar]
  63. Stinson, G. S., Dalcanton, J. J., Quinn, T., Kaufmann, T., & Wadsley, J. 2007, ApJ, 667, 170 [NASA ADS] [CrossRef] [Google Scholar]
  64. Tinsley, B. M. 1979, ApJ, 229, 1046 [NASA ADS] [CrossRef] [Google Scholar]
  65. Tolstoy, E. 2011, Science, 333, 179 [NASA ADS] [CrossRef] [Google Scholar]
  66. Tolstoy, E., Venn, K. A., Shetrone, M., et al. 2003, AJ, 125, 707 [NASA ADS] [CrossRef] [Google Scholar]
  67. Tolstoy, E., Hill, V., Irwin, M., et al. 2006, Msngr, 123, 33 [Google Scholar]
  68. Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
  69. Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 [NASA ADS] [CrossRef] [Google Scholar]
  70. Unavane, M., Wyse, R. F. G., & Gilmore, G. 1996, MNRAS, 278, 727 [NASA ADS] [CrossRef] [Google Scholar]
  71. Vader, J. P. 1986, ApJ, 305, 669 [NASA ADS] [CrossRef] [Google Scholar]
  72. Valcke, S., de Rijcke, S., & Dejonghe, H. 2008, MNRAS, 389, 1111 [NASA ADS] [CrossRef] [Google Scholar]
  73. Venn, K. A., Irwin, M., Shetrone, M. D., et al. 2004, AJ, 128, 1177 [NASA ADS] [CrossRef] [Google Scholar]
  74. Venn, K., et al. 2011, ApJ, submitted [Google Scholar]
  75. Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2007, ApJ, 667, L53 [NASA ADS] [CrossRef] [Google Scholar]
  76. Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2009, ApJ, 704, 1274 [NASA ADS] [CrossRef] [Google Scholar]
  77. Zinn, R., & Searle, L. 1976, ApJ, 209, 734 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Observing log.

In the text
Table 2

FLAMES-GIRAFFE gratings used.

In the text
Table 5

The atmospheric parameters (derived from photometry) for stars in our sample.

In the text
Table 6

Errors on abundances due to sensitivity on the stellar parameters, computed for MKV0770 and MKV0900.

In the text
Table 10

Ages and abundance ratios for all the stars in the Carina dSph with detailed abundance measurements.

In the text
Table 11

The median and median absolute deviation (mad) computed for 2 age groups (intermediate-age stars and old stars), either for the whole sample or for a more restricted sample in which all the stars whose age is betwen 6 and 10 Gyr have been removed.

In the text

All Figures

thumbnail Fig. 1

Representative spectra of two stars of our sample, centered on the Mg line at 552.841 nm. (Top) MKV0900: S/N = 44, Vmag = 17.79; (bottom) MKV0614: S/N = 22, Vmag = 18.72. A ScII line (λ = 552.679 nm) is located on the left of the Mg line.
In the text
thumbnail Fig. 2

a) The distribution of heliocentric radial velocities for our whole FLAMES/GIRAFFE sample, including a Gaussian fit which gives Vc = 224.4 km s-1 ± 5.95 km s-1. b) Comparison between radial velocities derived from our data (HR) compared to CaT (Helmi et al. 2006).
In the text
thumbnail Fig. 3

I vs. (V − I) CMD: our FLAMES/GIRAFFE sample is shown in red dots and other Carina members (from CaT) are shown in grey dots.
In the text
thumbnail Fig. 4

The distribution of errors on the stellar atmospheric diagnostics for the stars in our sample: a) the error on the mean [FeI/H] and b) [FeII/H] which are measured from the dispersion around the mean divided by the square root of the number of lines measured; c) the slope of [FeI/H] versus the excitation potential χex; d) the propagated error on the measurement of the slope of [FeI/H] versus the line strength.
In the text
thumbnail Fig. 5

The [Fe/H] distribution of our sample (in red) and the full HR sample showing the stronger effect of low S/N on more metal poor stars (in green). The larger set of CaT measurements (Starkenburg et al. 2010) is in gray for comparison.
In the text
thumbnail Fig. 6

For our sample of RGB stars in the Carina dSph, we show the comparison between [Fe/H] measured from our high resolution spectroscopy and from the CaT (Starkenburg et al. 2010). The solid line indicates where [Fe/H]CaT = [Fe/H]HR while the dashed lines indicate an uncertainty of  ± 0.2 dex.
In the text
thumbnail Fig. 7

The distribution of [Mg/Fe] for our sample of RGB stars in the Carina dSph as pink filled circles. Also included in the plot are the 5 RGB stars in the Carina dSph from Shetrone et al. (2003): pink open triangles; the 9 RGB stars from Venn et al. (2011): pink open squares and 6 of the RGB stars from Koch et al. (2008): pink open diamonds. Stars in Sculptor are in green crosses ((Shetrone et al. 2003; Geisler et al. 2005); Hill et al., in prep.). Milky Way halo stars are in small grey dots (from Venn et al. 2004, and references therein). Individual error bars are given for some peculiar stars and a representative error bar for the rest is given in bottom right hand corner.
In the text
thumbnail Fig. 8

The distribution of [Ca/Fe] for our sample of RGB stars in the Carina dSph. Additional data, definition of symbols and references are as in Fig. 7.
In the text
thumbnail Fig. 9

Age probability distributions built up from isochrone fitting and their Gaussian fits. We show here two examples: a) MKV0976, age = 2.61 ± 0.76 Gyr; and b) MKV0614, age = 6.80 ± 1.84 Gyr.
In the text
thumbnail Fig. 10

The ages (in Gyr) as a function of [Fe/H] (dex) for the RGB stars with high resolution abundances in the Carina dSph (see also Table 10). The shaded areas represent the expected age ranges of star formation as indicated by photometric studies.
In the text
thumbnail Fig. 11

The [Mg/Fe] distribution for the RGB stars from the Carina dSph separated into two ages groups: stars  >10 Gyr old are represented by red filled circles, stars  <10 Gyr old are represented by blue filled circles. Stars in the age range 6–10 Gyr are represented either by red open circles (8< age <10 Gyr) or by blue open circles (6< age <8 Gyr). Milky Way halo stars are shown as small grey dots.
In the text
thumbnail Fig. 12

The [Ca/Fe] distribution with the RGB stars from the Carina dSph separated into two ages groups as described in Fig. 11.
In the text
thumbnail Fig. 13

The [Ba/Fe] distribution for the RGB stars from the Carina dSph separated into two ages groups: stars  >10 Gyr old are represented by red filled circles, stars  <10 Gyr old are represented by blue filled circles. Stars in the age range 6–10 Gyr are represented either by red open circles (8< age <10 Gyr) or by blue open circles (6< age <8 Gyr). Sculptor stars (Shetrone et al. 2003; Geisler et al. 2005; Hill et al., in prep.) are shown as small green dots and Milky Way halo stars as small grey dots.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.