| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 5 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201118129 | |
| Published online | 14 February 2012 | |
High-resolution terahertz spectroscopy of the 15NH radical (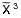 Σ−)
Σ−)
1 Laboratoire de Physique des Lasers, Atomes et Molécules, UMR 8523 CNRS, Université Lille 1, 59655 Villeneuve d’Ascq Cedex, France
e-mail: stephane.bailleux@univ-lille1.fr
2 Ligne AILES Synchrotron SOLEIL, l’Orme des Merisiers, Saint-Aubin, 91192 Gif-sur-Yvette Cedex, France
e-mail: olivier.pirali@synchrotron-soleil.fr
3 Institut des Sciences Moléculaires d’Orsay, ISMO, UMR 8214 CNRS, Université Paris-Sud, 91405 Orsay Cedex, France
e-mail: marie-aline.martin@synchrotron-soleil.fr
4 Laboratoire de l’Univers et de ses Théories, Observatoire de Paris-Meudon, 92195 Meudon, France
e-mail: evelyne.roueff@obspm.fr
5 LERMA, UMR 8112 CNRS, 24 rue Lhomond, 75231 Paris Cedex 05, France
e-mail: maryvonne.gerin@lra.ens.fr
6 Université Joseph-Fourier-Grenoble 1 / CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
e-mail: alexandre.faure@obs.ujf-grenoble.fr
Received: 20 September 2011
Accepted: 30 November 2011
Context. High-resolution rotational spectroscopy of the imidogen radical has been limited to the 14NH and 14ND isotopologues. Imidogen is an important intermediate in the astronomical synthesis of ammonia. Recently, the 14N/15N isotopic ratio in ammonia has been obtained in cold, dense molecular clouds.
Aims. We conducted a laboratory search for rotational transitions of 15NH to investigate in more detail the 14N/15N ratio in the interstellar medium.
Methods.15NH was generated in a positive column discharge in a flowing 15NH3 – He (SOLEIL synchrotron) or 15NH3 – Ar (PhLAM) mixture. High-resolution spectroscopic study of the 15NH isotopologue of imidogen in its ground electronic and vibrational state (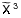 Σ−) was carried out in the THz range (up to 225 cm-1) with the AILES beamline of the SOLEIL synchrotron and subsequently with the PhLAM spectrometer (around 942 GHz). The observed fine and hyperfine structures were analysed, yielding an accurate set of rotational, fine, and hyperfine parameters.
Σ−) was carried out in the THz range (up to 225 cm-1) with the AILES beamline of the SOLEIL synchrotron and subsequently with the PhLAM spectrometer (around 942 GHz). The observed fine and hyperfine structures were analysed, yielding an accurate set of rotational, fine, and hyperfine parameters.
Results. The reported frequencies and molecular constants are suitable for radioastronomical searches of this key species and for 14N/15N isotopic ratio astronomical determination.
Key words: line: identification / molecular data / ISM: molecules / submillimeter: ISM
© ESO, 2012
1. Introduction
Extensive studies have long been carried out on the imidogen radical, NH, a fundamental hydride that plays a key role in a wide variety of environments. For example, this radical has been frequently observed in nitrogen combustion chemistry, and it has been detected in Earth’s atmosphere (Brewer et al. 1972). This radical also has important applications in astrophysics, where it is formed from the dissociative electron recombination reactions of NH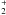 and NH
and NH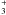 . These ionic species are generated in the ion-molecule reaction scheme for the production of NH3 from N+ (Herbst et al. 1987; Galloway & Herbst 1989). Other potential precursors include the protonated species N2H+ and NH
. These ionic species are generated in the ion-molecule reaction scheme for the production of NH3 from N+ (Herbst et al. 1987; Galloway & Herbst 1989). Other potential precursors include the protonated species N2H+ and NH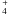 . Thus, imidogen is thought to be an intermediate species in the production of ammonia, a molecule commonly observed in space.
. Thus, imidogen is thought to be an intermediate species in the production of ammonia, a molecule commonly observed in space.
The main isotopologue of imidogen, 14NH, has been observed in many astronomical objects, such as in stellar atmospheres in the infrared via excited pure rotational transitions in v = 0 and v = 1 (including the Sun, Grevesse et al. 1990; Geller et al. 1991), towards comets (e.g. Feldmann et al. 1993) and in diffuse molecular clouds (Meyer & Roth 1991) via its UV absorption electronic transitions. The new observational capabilities available from the Herschel HIFI submillimetre spectroscopic instrument have allowed the ground rotational transition of NH to be detected for the first time towards diffuse clouds in front of high-mass star-forming regions (Persson et al. 2010) and in the envelope of a solar mass prestellar core (Hily-Blant et al. 2010). The deuterated isotopologue ND has been detected as well in the same envelope (Bacmann et al. 2010).
 |
Fig. 1 a) Fourier-transform, far infrared spectrum recorded at the SOLEIL synchrotron: 120 scans accumulated (~7 h) at the highest resolution (0.001 cm-1). b) Calculated spectra (at 300 K) of 15NH (red) and 15NH2 (green) radicals. Inset shows the fine-structure components of the N = 4 ← 3 transition of 15NH and the doublet structure of the NKaKc = 330 ← 221b-type rotational transition of 15NH2. |
The measurement of isotopic ratios from terrestrial and solar system objects (e.g. comets) and interstellar environments is a powerful tool for understanding the evolution and alteration of the cosmic material through its lifetime. The 14N/15N ratio has been measured with high accuracy in the solar wind by Marty et al. (2011) via the Genesis mission and has been found to be 441 ± 6, higher than in any solar system object. Because isotopic composition of nitrogen shows large variations mostly of unclear origin (see e.g. Marty et al. 2011), determining the 14N/15N ratio in imidogen is a useful complementary information on the already measured 14N/15N molecular ratios in ammonia and hydrogen cyanide in interstellar environments (Wannier et al. 1981; Lis et al. 2010; Gerin et al. 2009) and should help to better constrain the formation scenario of these molecules. Indeed, both gas-phase chemistry and grain-surface reactions fail to account for the observed abundance of light nitrogen hydrides like NH and NH3 (Persson et al. 2010). Nitrogen fractionation in the gas phase may occur via ion-molecule exchange reactions (Gerin et al. 2009, and references therein). However, the astronomical searches related to the detection of 15NH are currently not possible owing to the lack of the spectroscopic knowledge. The present work is aimed at addressing this question for the first time.
Probing the 14N/15N abundance ratio in imidogen radical can be achieved through the radioastronomical detection of pure rotational transitions of 15NH. The Herschel’s Heterodyne Instrument for the Far-Infrared (HIFI) provides complete coverage of the terahertz bands from 0.48 to 1.9 THz and is thus an ideal instrument for making the related observations. Although 14NH has received considerable attention both theoretically and experimentally (see e.g. Ram & Bernath 2010, for a recent bibliography of experimental studies), the spectroscopic investigation of 15NH has been limited to the laser magnetic resonance (LMR) work of Wayne & Radford (1976). They observed some hyperfine-structure components of the N,J = 1,1 ← 0,1 transition, but they did not provide field-free line positions. Thus they derived values for the hyperfine coupling parameters for both nuclei of this isotopologue (see the discussion section).
In this paper, we report on the first high-resolution spectroscopic research of 15NH in the ground electronic and vibrational state in the zero magnetic field condition. Our measurements involve both low- and high- N rotational quantum numbers, which will allow probing cold and warm astronomical environments, respectively.
2. Experiment
The rotational spectrum of 15NH has been investigated at the AILES beamline of SOLEIL synchrotron (Brubach et al. 2010) below 225 cm-1 (~7 THz) making use of the high-sensitivity, high-resolution (0.001 cm-1 or 30 MHz) and wide spectral range of the synchrotron radiation. The far infrared fine-structure components of 15NH were identified and assigned without difficulty, allowing accurate prediction of the three fine-structure components of the ground-state rotational transition, namely the J = 0 ← 1, 1 ← 1, and 2 ← 1 components. They were calculated to lie at 942.13, 970.17, and 995.65 GHz, respectively, aiming at measuring their hyperfine structures with microwave accuracy at the PhLAM laboratory. Given the submillimetre-wave radiation sources available, unfortunately only the J = 0 ← 1 fine-structure component of the ground-state transition could be observed. The PhLAM spectrometer (150–660 GHz) has been extensively described elsewhere (Ozeki et al. 2011). In this study, an all-solid-state frequency multiplier chain was used to carry out measurements below 950 GHz, the upper limit of our spectrometer. Briefly, an Agilent synthesizer (12.5–17.5 GHz) drives a Spacek active sextupler, thereby providing an output power of +15 dBm in the W-band range (75–110 GHz). This power is high enough to feed passive Schottky multipliers (Virginia Diodes, Inc.) at the next stage of the frequency multiplication chain. The total multiplication factor used in this experiment was 60.
Ammonia-15N served as precursor (~3.3 × 10-3 mBar), and 15NH radicals were generated in a positive column discharge using He (1.26 mBar) or Ar (1.8 × 10-2 mBar) as buffer gas at the SOLEIL and PhLAM laboratories, respectively. The discharge current sustained between water-cooled electrodes was adjusted to 100 mA and 65 mA, respectively.
The absorption cell employed at SOLEIL was 1 m long (with an effective optical path of 24 m using White-type optics) with a 13 cm inner diameter, and these dimensions at the PhLAM laboratory were 2 m and 5 cm. In both experiments the absorption cells were passively kept at room temperature. The Fourier-transform far-infrared spectrum was recorded using a 6 μm thick Mylar beamsplitter and a 4.2 K cooled Si-bolometer equipped with an 8 THz low-pass optical filter. The spectrum depicted in Fig. 1 contains absorption transitions not only of 15NH, but also those of 15NH2 (15N-amidogen radical). Transitions from residual 15NH3, 14NH3, 14NH2, 14NH, H2O, and OH are present in the spectrum, but their assignments are not indicated in Fig. 1. The 15NH lines were calibrated using residual H2O lines against accurate frequencies measured by Matsushima et al. (1995). The results concerning 15NH2 will be described elsewhere.
 |
Fig. 2 Fine-structure components of the N = 6 ← 5 rotational transition of 15NH recorded at SOLEIL. |
3. Results
The 15NH radical has a triplet (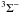 ) electronic ground state with the total electron spin angular momentum S = 1. Therefore, the rotational levels for N > 0 exhibit a fine structure of rotational J sublevels with J = N + 1, N, and N − 1. For N = 0, the only possible spin sublevel is J = 1. The electron spin-electron spin (λ) and the electron spin-rotation (γ) coupling constants contribute to the fine structure of the energy levels. In addition, the non-zero nuclear spins of 15N (
) electronic ground state with the total electron spin angular momentum S = 1. Therefore, the rotational levels for N > 0 exhibit a fine structure of rotational J sublevels with J = N + 1, N, and N − 1. For N = 0, the only possible spin sublevel is J = 1. The electron spin-electron spin (λ) and the electron spin-rotation (γ) coupling constants contribute to the fine structure of the energy levels. In addition, the non-zero nuclear spins of 15N (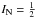 ) and H (
) and H (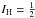 ) further split the fine-structure levels into hyperfine-structure levels. The splittings arise from the Fermi-contact (bF), magnetic dipole-dipole (t), and nuclear spin-rotation (C) interactions.
) further split the fine-structure levels into hyperfine-structure levels. The splittings arise from the Fermi-contact (bF), magnetic dipole-dipole (t), and nuclear spin-rotation (C) interactions.
The matrix elements needed to compute the energy levels were calculated according to the coupling scheme J = N + S, F1 = J + IH, and F = F1 + IN. As a result, for J ≠ 0, IH splits each J,N level into a doublet with 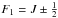 , and finally IN splits each J,N,F1 sublevel further into the next doublet with
, and finally IN splits each J,N,F1 sublevel further into the next doublet with 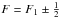 . For J = 0, the hyperfine-structure levels allowed are those with
. For J = 0, the hyperfine-structure levels allowed are those with 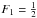 and F = 0 or 1.
and F = 0 or 1.
In the present work, we measured 17 fine-structure components (of which 16 were recorded at SOLEIL). The three fine-structure components of the N = 6 ← 5 transition recorded at SOLEIL near 193.8 cm-1 are shown in Fig. 2. The term diagram showing the fine splittings of the N = 1 ← 0 rotational transition is depicted in Fig. 3. The J = 0 ← 1 fine-structure component of this ground-state transition is the only one that could be observed at the PhLAM laboratory. It occurs near 942.130 GHz and is split into six hyperfine-structure components. They are displayed in Fig. 4.
Tables 1 and 2 list the frequencies observed at the SOLEIL and PhLAM laboratories, respectively. Transition frequencies that could not be observed are included for completeness and also to guide future radioastronomical searches. The observed transitions encompass 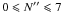 . They were subjected to a least-squares analysis using Pickett’s program SPFIT (Pickett 1991). The measured frequencies were weighted proportionally to the inverse square of their experimental uncertainties. For the fine-structure components measured at SOLEIL, the frequencies were calculated as the equally weighted average of the individual hyperfine components.
. They were subjected to a least-squares analysis using Pickett’s program SPFIT (Pickett 1991). The measured frequencies were weighted proportionally to the inverse square of their experimental uncertainties. For the fine-structure components measured at SOLEIL, the frequencies were calculated as the equally weighted average of the individual hyperfine components.
 |
Fig. 3 Schematic energy-level diagram showing the fine- (J) and hyperfine-structure (F1, F) splittings of the N = 1 ← 0 rotational transition of 15NH. Hyperfine level splittings shown are a hundred times the actual ones for clarity. The lower fine-structure component (J = 0 ← 1) occurring near 942.130 GHz recorded at PhLAM laboratory with partly resolved hyperfine-structure (see Fig. 4) is indicated by a solid line. |
 |
Fig. 4 Hyperfine structure observed in the N,J = 1,0 ← 0,1 transition recorded at PhLAM laboratory. F1 = J + IH and F = F1 + IN. |
The set of adjustable parameters comprises, in addition to the rotational and centrifugal distortion constants B, D, and H, the electron spin-spin (λ) and the electron spin-rotation (γ) fine-structure parameters and the Fermi-contact hyperfine coupling terms (bF) of both nuclei. The centrifugal distortion constants L and γD, the nuclear spin-rotation parameter of nitrogen, as well as the magnetic dipole-dipole hyperfine-structure t parameters for both nuclei were kept fixed at the value reported for the main isotopologue. The constants used in the least-squares procedure are provided in Table 3, together with their most recent values reported for the 14NH isotopologue for comparison (Lewen et al. 2004). We checked that no significant correlation occurred between the floated parameters.
Transition frequencies (in cm-1) of 15NH (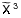 ) observed at SOLEIL.
) observed at SOLEIL.
Observed (J′ ← J′′ = 0 ← 1 at the PhLAM laboratory) and calculated (J′ ← J′′ = 2 ← 1 and 1 ← 1) frequencies (in MHz) of the N = 1 ← 0 ground-state rotational transition of 15NH (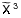 ), given together with the base-10 logarithm of the Einstein coefficient for spontaneous emission (in s-1).
), given together with the base-10 logarithm of the Einstein coefficient for spontaneous emission (in s-1).
4. Discussion
As expected, the B rotational constant of 15NH is slightly smaller than that of 14NH, and their ratio is explained very well by considering the change in the reduced mass between the two species having identical equilibrium bond length (re = 1.037186(2) Å, Ram et al. 1999). Furthermore, the values obtained for the D and H centrifugal distortion parameters of 15NH compare very well with those of 14NH. Considering the fine-structure parameters, it is readily seen from Table 3 that the electron spin-spin λ constants of the two isotopologues agree very well. It is well-known that in second-order perturbation theory, the electron spin-rotation γ constants are proportional to the rotational constant. Accordingly, it is more appropriate to compare the reduced γ/B constants of both species. Their values are nearly equal (within 0.04%) thus showing the consistency of our analysis. Finally, with the four hyperfine-structure components observed, which involve the coupling of the hydrogen and nitrogen nuclear spins, only two hyperfine-structure parameters could be determined, namely the Fermi-contact terms bF(H) and bF(N). The value obtained for the former one is identical to that of 14NH. The 15/14N isotopic ratio calculated for bF(N), − 1.4055(48), agrees well with the atomic nuclear g values of nitrogen ( − 1.4028, Harris et al. 2001). Consequently, the value of the t(N) magnetic dipole-dipole coupling constant of 15NH was fixed in the least-squares analysis to that of 14NH multiplied by −1.4028. The values (in MHz) reported by Wayne & Radford (1976) for the Fermi-contact and magnetic dipole-dipole coupling terms for hydrogen (bF(H) = −66.5(32); t(H) = 28.8(22)) and nitrogen (bF(N) = −28.3(34); t(N) = 31.3(22)) agree well with ours. Because their data did not provide sufficient constraints, they did not attempt to make a least-squares fit of the rotational or fine-structure constants so that a similar comparison cannot be made. The relatively high value of the nuclear spin-rotation constant, C(N), is mainly attributed to the large rotational B constant (Klaus et al. 1997). It was not possible to determine its value in the present analysis, but it was nevertheless included in the fit procedure for consistency. The nuclear spin-rotation constant of 15NH was scaled according to the ratio of the nuclear g values ( − 1.4028) and to that of the rotational constants.
Rotational, fine, and hyperfine coupling constants of 15NH and 14NH (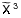 ), in MHz.
), in MHz.
The full width at half maximum (FWHM) of the lines recorded at SOLEIL synchrotron varies between 20 MHz in the lower frequency region and 30 MHz in the higher part of the spectrum. These values are significantly higher than the calculated frequency regions over which the hyperfine-structure components extend, except maybe for the J = N = 2 ← 1 transition. Therefore, it is believed that the unresolved hyperfine structures in the far infrared region contribute rather marginally to the broadening of the lines recorded at the SOLEIL synchrotron. Similarly, the impact on the estimated experimental errors for the derived line positions is considered negligible.
Generally speaking, the standard deviations of the molecular constants are one to two orders of magnitude greater than those of the main isotopologue. This is because a limited number of hyperfine-structure components could be observed in the present study and because most of the fine-structure components were not measured with microwave accuracy.
5. Conclusions
Rotational transitions of the 15NH radical in the ground electronic and vibrational state (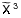 ) were observed below 225 cm-1 (~7 THz) for the first time in the zero magnetic field condition. These transitions can be used for radioastronomical
) were observed below 225 cm-1 (~7 THz) for the first time in the zero magnetic field condition. These transitions can be used for radioastronomical
searches of this species in various astronomical environments using HIFI on board the Herschel space observatory. In addition, the analysis of the fine- and hyperfine- structures yielded an accurate set of molecular constants, which compare very well with those of the main isotopologue, 14NH.
Acknowledgments
The National French Programme “Physique et Chimie du Milieu Interstellaire” (PCMI) is acknowledged for its financial support. The authors are grateful to SOLEIL for providing beamtime on the AILES beamline under the proposal 20110017.
References
- Bacmann, A., Caux, E., Hily-Blant, P., et al. 2010, A&A, 521, L42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brewer, A. W., Davis, P. A., & Kerr, J. B. 1972, Nature, 240, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Brubach, J.-B., Manceron, L., Rouzières, M., et al. 2010, AIP Conf. Proc., 1214, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, P. D., Fournier, K. B., Grinin, V. P., & Zvereva, A. M. 1993, ApJ, 404, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, E. T., & Herbst, E. 1989, A&A, 211, 413 [NASA ADS] [Google Scholar]
- Geller, M., Sauval, A. J., Grevesse, N., Farmer, C. B., & Norton, R. H. 1991, A&A, 249, 550 [NASA ADS] [Google Scholar]
- Gerin, M., Marcelino, N., Biver, N., et al. 2009, A&A, 498, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., Lambert, D. L., Sauval, A. J., et al. 1990, A&A, 232, 225 [NASA ADS] [Google Scholar]
- Harris, R. K., Becker, E. D., Cabral de Menezes, S. M., Goodfellow, R., & Granger, P. 2001, Pure Appl. Chem. 73, 1795; reprinted in: 2002, Magn. Reson. Chem., 40, 489 [Google Scholar]
- Herbst, E., DeFrees, D. J., & McLean, A. D. 1987, ApJ, 321, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Maret, S., Bacmann, A., et al. 2010, A&A, 521, L52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klaus, T., Takano, S., & Winnewisser, G. 1997, A&A, 322, L1 [NASA ADS] [Google Scholar]
- Lewen, F., Brünken, S., Winnewisser, G., Šimečková, M., & Urban, S. 2004, J. Mol. Spectrosc., 226, 113 [Google Scholar]
- Lis, D. C., Wootten, A., Roueff, E., & Gerin, M. 2010, ApJ, 710, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G., & Burnett, D. S. 2011, Science, 332, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Matsushima, F., Odashima, H., Iwasaki, T., Tsunekawa, S., & Takagi, K. 1995, J. Mol. Struct., 352/353, 371 [Google Scholar]
- Meyer, D. M., & Roth, K. C. 1991, ApJ, 376, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Ozeki, H., Bailleux, S., & Wlodarczak, G. 2011, A&A, 527, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., Black, J. H., Cernicharo, J., et al. 2010, A&A, 521, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectrosc., 148, 371 [Google Scholar]
- Ram, R. S., & Bernath, P. F. 2010, J. Mol. Spectrosc., 260, 115 [Google Scholar]
- Ram, R. S., Bernath, P. F., & Hinkle, K. H. 1999, J. Chem. Phys., 110, 5557 [NASA ADS] [CrossRef] [Google Scholar]
- Scarl, E. A., & Dalby, F. W. 1974, Can. J. Phys., 52, 1429 [NASA ADS] [Google Scholar]
- Wannier, P. G., Linke, R. A., & Penzias, A. A. 1981, ApJ, 247, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Wayne, F. D., & Radford, H. E. 1976, Mol. Phys., 32, 1407 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observed (J′ ← J′′ = 0 ← 1 at the PhLAM laboratory) and calculated (J′ ← J′′ = 2 ← 1 and 1 ← 1) frequencies (in MHz) of the N = 1 ← 0 ground-state rotational transition of 15NH (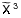 ), given together with the base-10 logarithm of the Einstein coefficient for spontaneous emission (in s-1).
), given together with the base-10 logarithm of the Einstein coefficient for spontaneous emission (in s-1).
All Figures
 |
Fig. 1 a) Fourier-transform, far infrared spectrum recorded at the SOLEIL synchrotron: 120 scans accumulated (~7 h) at the highest resolution (0.001 cm-1). b) Calculated spectra (at 300 K) of 15NH (red) and 15NH2 (green) radicals. Inset shows the fine-structure components of the N = 4 ← 3 transition of 15NH and the doublet structure of the NKaKc = 330 ← 221b-type rotational transition of 15NH2. |
| In the text | |
 |
Fig. 2 Fine-structure components of the N = 6 ← 5 rotational transition of 15NH recorded at SOLEIL. |
| In the text | |
 |
Fig. 3 Schematic energy-level diagram showing the fine- (J) and hyperfine-structure (F1, F) splittings of the N = 1 ← 0 rotational transition of 15NH. Hyperfine level splittings shown are a hundred times the actual ones for clarity. The lower fine-structure component (J = 0 ← 1) occurring near 942.130 GHz recorded at PhLAM laboratory with partly resolved hyperfine-structure (see Fig. 4) is indicated by a solid line. |
| In the text | |
 |
Fig. 4 Hyperfine structure observed in the N,J = 1,0 ← 0,1 transition recorded at PhLAM laboratory. F1 = J + IH and F = F1 + IN. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


