| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201118025 | |
| Published online | 31 January 2012 | |
CXOM31 J004253.1+411422: the first ultraluminous X-ray transient in M 31⋆
1
Department of Physics and AstronomyClemson University,
Clemson, SC
29634
USA
e-mail: akaur@clemson.edu
2
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse,
85748
Garching,
Germany
3
Department of Física i Enginyeria Nuclear, EUETIB
(UPC-IEEC), Comte d’Urgell
187, 08036
Barcelona,
Spain
4
Institut de Ciéncies de 1’Espai (CSIC-IEEC), Campus UAB, Facultat
Ciéncies, C5 parell
2 on, 08193
Bellaterra ( Barcelona), Spain
Received:
5
September
2011
Accepted:
30
October
2011
Context. We seek clarification of the nature of X-ray sources detected in M 31. Here we focus on CXOM31 J004253.1+411422, the brightness of which suggests that it belongs to the class of ultraluminous X-ray sources.
Aims. We determine the X-ray properties of sources detected in the XMM-Newton/Chandra monitoring program. We investigate spectral properties and search for periodic or quasi-periodic oscillations.
Methods. A multicomponent model was applied to the spectra obtained from XMM-Newton data to evaluate the relative contributions from thermal and nonthermal emission. The time dependence of this ratio was evaluated over a period of forty days. We simultaneously fit data from XMM-Newton EPIC-pn, MOS1, and MOS2 detectors with (nonthermal) powerlaw and (thermal) multicolored blackbody.
Results. The X-ray spectrum is best fit by the combination of a thermal component with kT ~ 1 keV and a powerlaw component with a photon index of approximately 2.6. From combined analysis of Chandra, Swift, and XMM-Newton data, the unabsorbed total luminosity of this source decreases from ~3.8 × 1039 erg s-1 in the first observation to ~0.5 × 1039 erg s-1 over a period of three months. The decay closely follows an exponential decline with a time constant of 32 days. The source spectrum evolves significantly, exhibiting a faster decline of the thermal component. We do not find evidence of any significant temporal features in the power density spectrum. The presence of a thermal component at kT ~ 1 keV in conjunction with a nonthermal high-energy tail, is also consistent with spectral properties of other ULXs in the “high state”.
Conclusions. Our analysis indicates that the underlying source of this first ULX in M 31 is a black hole of mass, M ≥ 13M⊙, accreting near the Eddington limit, that underwent a transient outburst followed by an exponential decay reminiscent of transients associated with galactic X-ray novae.
Key words: X-rays: binaries / X-rays: stars / galaxies: individual: M 31
© ESO, 2012
1. Introduction
Ultraluminous X-ray sources (ULXs) are very bright point sources with an X-ray luminosity of Lx > 1039 erg s-1, which exceeds the Eddington luminosity for compact objects with mass of approximately 10 M⊙. This source class was first identified by the Einstein Observatory in the eighties (Fabbiano 1989). These sources are not associated with the center of galaxies and thus do not belong to the class of super-massive black holes. On the other hand, they are too bright to be associated with stellar mass black holes with M < 10M⊙, which are accreting below the Eddington rate. An exciting possibility is that the underlying sources of ULXs are intermediate-mass black holes (IMBHs), in the mass range 102−104M⊙, accreting at sub-Eddington rates (Miller & Colbert 2004). For example, observations of a ULX in NGC 5408 suggested a mass of ~100 M⊙, indicating the possible existence of IMBHs (Fabian & Ward 1993). However, a recent study of this source’s variability indicates that the mass is likely below 100 M⊙ (Middleton et al. 2011). Although the identification of ULXs as IMBHs has not yet been firmly established, one should contemplate the theoretical progenitors, which could result in producing such objects.
Several theories have been suggested for the formation of IMBH. Madau & Rees (2001) studied the collapse of Population III stars, while others have considered the collapse of massive stars (in young super-massive star clusters) e.g. Portegies Zwart et al. (2004). Another possibility is of course that the masses are much less than 100 M⊙, but that the source accretes at a super-Eddington rate, as suggested by Begelman (2002). Yet another factor to be considered is deviations from the common assumption of isotropic emission as suggested by King et al. (2001). Along these lines for anisotropic emission, Reynolds et al. (1997) proposed a link between ULXs and extreme beaming, as observed in galactic microquasars. The nature of the ULX class remains unclear, which is in part because the sample size is still rather small.
To better understand the ULX phenomenon, an increase in sample size and careful consideration of spectral and sample properties is desirable. The ULX sources are mainly found in star-forming galaxies. Until recently, no ULX has been identified in M 31. Our ongoing monitoring program1 for resolving super-soft source states of optical novae in the central area of M 31 (Wolfgang Pietsch) with XMM-Newton and Chandra HRC-I has yielded a transient source, which, as discussed in this paper, represents the first recognized ULX in our companion galaxy.
We present the time development of the outburst and the spectral analysis of a ULX in M 31 using XMM-Newton, Chandra, and Swift data over a period of approximately three months (Sect. 2), followed by the summary of the results in Sect. 3. Conclusions are presented in Sect. 4.
Observations log.
 |
Fig. 1 XMM-Newton EPIC image of the central part of M 31 produced by combining pn, MOS1 and MOS2 data from all 5 observations. Red, green and blue show the (0.2–1.0) keV, (1.0–2.0) keV) and (2.0–12.0) keV energy bands, respectively. |
2. Observations and data analysis
CXOM31 J004253.1+411422 was discovered with Chandra HRC-I in a 19 ks observation on 2009 Dec 17.89 UT (Henze et al. 2009). The source position was determined to be RA (J2000) = 00:42:53.15, Dec (J2000) = +41:14:22.9, using the catalog of X-ray sources in M 31 assembled by Kaaret (2002) for relative astrometry. Figure 1 shows the position of the source with respect to other X-ray sources near the center of M 31 in an XMM-Newton color image. A transient optical counterpart with m(F435W) = 23.8 mag was identified in HST observations (Garcia et al. 2010). The X-ray source was first detected with Chandra HRC-I. Level 2 event files were analyzed using (Chandra Interactive Analysis of Observations; Fruscione et al. 2006)2 to obtain count rates as shown in Table 1. An adapted version of the XMMSAS tool emldetect was used to estimate background-corrected and exposure-corrected fluxes and count rates (see Henze et al. 2010). Continuous monitoring of this source was then carried out by Swift-XRT from December 22–27, 2009. The data were analyzed using the HEAsoft XIMAGE package (version 4.5.1) with the sosta command (source statistics) for estimations of count rates. We took into account the XRT PSF of the sources that we computed with the command psf, as well as exposure maps that were created with the XRT software task xrtexpomap within XIMAGE. The count rates obtained from Swift-XRT and Chandra HRC-I before and after the XMM-Newton observations were converted to unabsorbed fluxes using energy conversion factors (ecfs), which were computed using fakeit in XSPEC assuming the best fitting spectral model for the first and last XMM-Newton observations, respectively, and using publicly available instrument response files. We obtain ecfHRC−I−1 = 6.3 × 1010 cts erg-1 cm2 and ecfHRC−I−2 = 7.7 × 1010 cts erg-1 cm2, respectively. For the Swift-XRT data, the ecf has been computed to be 1.57 × 1010 cts erg-1 cm2.
The spectroscopic data were then obtained by XMM-Newton from December 28, 2009 until February 02, 2010 in five distinct observations using the European Photon Imaging Camera (EPIC). EPIC-pn (Strüder et al. 2001), MOS1 and MOS2 (Turner et al. 2001) CCD detectors are mounted on the three X-ray telescopes on XMM-Newton. The exposure times as well as the raw count rates obtained with these detectors are presented in Table 1. The XMMSAS version 10.0.0 was used to filter the standard pipeline event files, to generate images, light curves, spectra and the appropriate detector response functions. The event files for all three cameras, pn, MOS1 and MOS2 were analyzed with the following parameter settings: For spectrum generation, we set ‘‘FLAG = 0’’ to reject bad pixels, and PATTERN ≤ 4 for pn and ≤ 12 for MOS1 and MOS2 event files were allowed to reduce noise in the data. Light curves were derived to investigate the variability in the source. Barycenter correction was performed using the barycen task in XMMSAS. The light curves were then corrected from various effects such as bad pixels, GTIs, vignetting using epiclccorr. As an example Fig. 2 displays the observed count rate for XMM-Newton EPIC-pn for the first observation, binned in 100 s intervals. The power density spectra were generated using the task powspec in FTOOLS using the Fast Fourier transform algorithm (FFT). The normalization was chosen such that the white noise level expected from the data errors corresponds to a power of 2. For spectrum extraction, the XMMSAS tool epatplot was used to check for pile-up for appropriate source extraction region. The inner PSF part of these regions were excluded to avoid pile-up. Response files were generated by using SAS tools rmfgen and arfgen. The spectral binning was constructed to attain 20 counts per bin to assure uniform statistics across the energy range. Bad pixels were ignored and energy channels from 0.2–10.0 keV were considered for spectral fitting using XSPEC version 12.6.0.
3. Results
Our initial spectral fitting for XMM-Newton data used a broken powerlaw model (BKNPOWER in XSPEC), but the χ2/d.o.f. = 2953.96/1174 clearly indicated that this is not a satisfactory model. The luminosity derived from this simple fit indicated the fact that this source is a member of the ULX class. For these objects, an alternative, often better fitting model is a combination of a nonthermal (powerlaw) and thermal component (Gladstone et al. 2009). To explore this possibility we applied a model that combines a nonthermal powerlaw component (PO) with a multicolored blackbody component (DISKBB). The thermal component is associated with an accretion disk around a central black hole as developed by Mitsuda et al. (1984) and Makishima et al. (1986). This model gave a significantly improved fit, indicated by χ2/d.o.f. values in Table 2.
In addition to the intrinsic two component model, the source flux must be corrected for extinction by foreground gas in the Milky Way and the local gas along the line of sight through M 31. Extinction was modeled using the Tuebingen-Boulder ISM absorption model (TBABS) (Wilms et al. 2000). The hydrogen column density ascribed to the Milky Way was fixed to 5.32 × 1020 cm-2 (Dickey & Lockman 1990), whereas the column density for the host galaxy was included as a free parameter. However, the derived value of the column density in M 31 must thus be considered with caution because we do not have information about the actual metallicity along the line of sight through M 31 and simply assume the Milky Way template expressed in terms of a standard cross-section per hydrogen atom.
To illustrate this fitting procedure, Fig. 3 shows the XMM-Newton EPIC data for first of our five observational epochs. The decomposition of the X-ray spectrum into the model components in physical units is shown in Fig. 4.
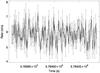 |
Fig. 2 Light curve from XMM-Newton EPIC-pn for observation 0600220201 with time binning of 100 s in 0.2–10 keV energy band. |
To convert fluxes to luminosities, we assume a source distance of 780 kpc (Holland 1998; Stanek & Garnavich 1998) and isotropic emission. The resulting luminosities during the XMM-Newton observations are about 1039 erg s-1, which places this source in the mid range of known ULXs (Gladstone et al. 2009). Table 2 summarizes the derived luminosities (from XMM-Newton only) as well as the effective inner disk radius. As a function of time, both the nonthermal (LPO) and thermal (LBB) component decrease, but the latter decreases more rapidly (see Fig. 5). Table 1 lists the calculated luminosities derived from count rates associated with observations of Chandra and Swift-XRT. The total unabsorbed luminosity declined from about 3.7 × 1039 to 0.5 × 1039 erg s-1 during the period of observation. We note that this source was initially more luminous than the total X-ray luminosity of M 31 in the (0.1–2.4) keV band sampled by ROSAT (Supper et al. 1997). Futhermore, this source was atleast one order of magnitude brighter than any of the 45 X-ray transients detected in M 31 by Chandra and XMM-Newton from October 1999 to August 2002 (Williams et al. 2006).
The spectral parameters obtained from the model fitting from XMM-Newton.
 |
Fig. 3 Combined powerlaw and multicolored blackbody fit to the joint set of data from EPIC-pn (black), MOS1 (green), MOS2 (red) with χ2/d.o.f. = 1318.87/1165 for the observation 0600660201 with XMM-Newton. The model parameters obtained from this spectral fit are presented in Table 2. |
 |
Fig. 4 The theoretical model underlying the data fit (solid line) in Fig. 3 is shown in decomposition between the thermal (dash-dotted line)and the nonthermal (dotted line) component. |
 |
Fig. 5 Temporal variation of the total unabsorbed luminosity (Lunabs) as per observations of XMM-Newton. The decomposition into the powerlaw (Lpo) and blackbody component (Lbb) reveals a distinct evolutionary behavior of these two components. The time zero corresponds to Chandra HRC-I observation ID 10886 (see Table 1). |
From the X-ray spectrum fits of the first XMM-Newton observation (when the source was nearly brightest and we had the best quality data), we extract an estimate of the mass of the black hole following the formalism given by Makishima et al. (2000). Under the assumption of a geometrically flat and optically thick accretion disk, these authors derived the following relation:
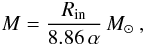 where
Rin is the inner radius of the accretion disk, measured in km
and α is a dimensionless parameter that relates the inner radius to the
Schwarzschild radius via
Rin = 3αRS.
where
Rin is the inner radius of the accretion disk, measured in km
and α is a dimensionless parameter that relates the inner radius to the
Schwarzschild radius via
Rin = 3αRS.
For the bolometric luminosity emitted by the accretion disk, Makishima et al. (2000) find (their Eq. (9)):
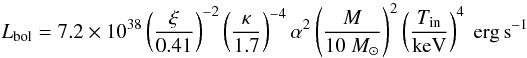 where
Tin is the temperature characterizing the inner accretion
disk. The remaining parameters specific to their model are here chosen to take their
standard values as indicated by the normalization. The spectral fit yields the products of
Rin and the square root of the cosine of the inclination angle
of the disk, as well as temperature, Tin, and the bolometric
luminosity (which we assume to be unabsorbed Lbb component (=
1.6 × 1039 erg s-1) integrated from 0.2–10.0 keV). From the two
equations above, we can therefore determine the mass and inclination angle, although
significant uncertainties in both quantities are associated with the model parameters,
α, ξ and κ fixed to the values 1, 0.41
and 1.7, respectively (see Makishima et al. 2000).
The α parameter has been defined above and ξ is a
correction factor, reflecting the fact that Tin occurs at a
radius somewhat larger than Rin. The specific value adopted here
was motivated by Kubota et al. (1998). The final
paramter, κ represents the ratio of color temperature to effective
temperature and the value adopted here has been taken from Shimura & Takahara (1995). With these caveats in mind, we find a mass of
13 M⊙ with a statistical uncertainity of about 4%. This
implies an inner radius of Rin = 124 km. From the fitting
parameter Rin
where
Tin is the temperature characterizing the inner accretion
disk. The remaining parameters specific to their model are here chosen to take their
standard values as indicated by the normalization. The spectral fit yields the products of
Rin and the square root of the cosine of the inclination angle
of the disk, as well as temperature, Tin, and the bolometric
luminosity (which we assume to be unabsorbed Lbb component (=
1.6 × 1039 erg s-1) integrated from 0.2–10.0 keV). From the two
equations above, we can therefore determine the mass and inclination angle, although
significant uncertainties in both quantities are associated with the model parameters,
α, ξ and κ fixed to the values 1, 0.41
and 1.7, respectively (see Makishima et al. 2000).
The α parameter has been defined above and ξ is a
correction factor, reflecting the fact that Tin occurs at a
radius somewhat larger than Rin. The specific value adopted here
was motivated by Kubota et al. (1998). The final
paramter, κ represents the ratio of color temperature to effective
temperature and the value adopted here has been taken from Shimura & Takahara (1995). With these caveats in mind, we find a mass of
13 M⊙ with a statistical uncertainity of about 4%. This
implies an inner radius of Rin = 124 km. From the fitting
parameter Rin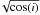 (see Table 2), one then infers an inclination angle
of i ~ 80°. The assumption of a non-rotating Schwarzschild black
hole (α = 1) can lead to a significantly underestimated black hole mass as
the extreme case of a maximally rotating Kerr black hole (α = 1/6) allows
for a more massive central object approaching the realm of IMBH. This increase with black
hole spin relies on the assumption that the inner edge of the accretion disk can be
identified with the location of the innermost stable circular orbit (ISCO). However,
determining the inner edge of a black hole accretion disk is a far more complex issue, e.g.
Abramowicz et al. (2010).
(see Table 2), one then infers an inclination angle
of i ~ 80°. The assumption of a non-rotating Schwarzschild black
hole (α = 1) can lead to a significantly underestimated black hole mass as
the extreme case of a maximally rotating Kerr black hole (α = 1/6) allows
for a more massive central object approaching the realm of IMBH. This increase with black
hole spin relies on the assumption that the inner edge of the accretion disk can be
identified with the location of the innermost stable circular orbit (ISCO). However,
determining the inner edge of a black hole accretion disk is a far more complex issue, e.g.
Abramowicz et al. (2010).
As described in Sect. 2, we searched for an underlying periodicity in each of the observing runs over a range of frequencies limited by the temporal extent of the observation and the binning time of 100 s. The observed count rates (e.g. Fig. 2) display fluctuations within the range expected from counting statistics. None of the power density spectra reveal a significant feature.
 |
Fig. 6 Temperature vs. Luminosity for 19 selected ULXs from Winter et al. (2006) along with the candidate ULX (red) in M 31. The M 31 source is a member of the “high temperature” subgroup. |
4. Discussion and conclusions
The intrinsic luminosity of the source is consistent with those found for other ULXs in nearby galaxies. The presence of a thermal component at kT ~ 1 keV in conjunction with a nonthermal high energy tail, is also consistent with spectral properties of other ULXs. The temperature and photon index of M 31 source fall in the center of observed distributions for ULXs (Winter et al. 2006), lending additional support to a ULX nature.
We compared various properties of this ULX with a selected sample from the XMM-Newton archival study of ULXs by Winter et al. (2006) in 32 nearby galaxies with distance <8 Mpc and unabsorbed luminosities, Lx > 1038 erg s-1 in the 0.3–10 keV energy range. Motivated by the observed properties of black hole binaries in the Milky Way, these authors classified their sample into two subsets, “low state” and “high state”, based on their respective spectral properties. Low state sources were characterized by a single powerlaw X-ray spectrum, while high state sources required an additional multicolored blackbody with powerlaw. Since the spectra described in Sect. 3 clearly exhibit the best fit when a powerlaw is combined with multicolored blackbody, this source should be classified as “high state” ULX. Therefore we limit our comparison to 19 of high state ULXs in their sample. This sample is slightly reduced because we selected the brightest epoch out of multiple XMM-Newton observations, and those were not always available in Winter et al. (2006).
Figure 6 displays the resulting set of “high state” ULXs in the L-T plane. As Winter et al. (2006) pointed out, the temperature distribution is possibly bimodal. The ULX in M 31 belongs to the high-T group, which is commonly believed to represent the class of stellar mass black holes. The low-T group is characterized by a larger range of X-ray luminosities and has been tentatively attributed to the hypothetical class of IMBHs (Winter et al. 2006). Although the sample size is still very small, it appears that a physical gap between these two groups exists. If that is the case, an explanation may be related to different formation scenarios for these groups. As Winter et al. (2006) suggested, one possibility is associated with the unique features of pair instability supernovae (PISNe) in the early universe (Population III origin, Heger et al. 2003). The mass of ~13 M⊙ derived in Sect. 3 suggests that we are dealing with a normal stellar remnant, one that could have been formed later in the universe, provided α is not significantly less than unity due to rotation.
 |
Fig. 7 For the same sample shown in Fig. 6, a comparison of photon index vs. temperature reveals that the M 31 ULX cools significantly, but remains within the range covered by the “high temperature” group. The labels 1 through 5 correspond to the chronological entry of XMM-Newton observations as listed in Table 1. |
 |
Fig. 8 Variation of the total unabsorbed luminosity (Lunabs) of ULX in M 31 as observed by Swift-XRT, Chandra HRC-I and XMM-Newton resembling an exponential decay with a time scale of 32 days. The time zero corresponds to ChandraHRC − I observation ID 10886 (see Table 1). |
Figure 7 shows the “high state” ULXs distribution in the T-Γ plane. The low-T group shows a large range in photon index, resembling the large range in luminosity, however we note that the uncertainties in this parameter are very large. In contrast to the previous figure, here we show the temporal evolution of the M 31 ULX, while for other ULXs, no evolution has been shown. Over a time span of forty days of observations with XMM-Newton, the spectral evolution clearly exhibits cooling, but almost no change in the shape of the powerlaw component. Referring back to Fig. 5, the drop in the temperature is also accompanied by a significant change in the luminosity of this component. The powerlaw component, on the other hand, exhibits a declining luminosity as well, but not as rapid as the thermal one. The overall evolution of this transient is thus a combination of a strongly varying thermal component and a significantly less varying nonthermal part.
Combining all data obtained with Chandra, Swift, and XMM-Newton indicates that the X-ray luminosity of this source follows closely an exponential decline (see Fig. 8) with a time constant of 32 days. A continuation of this trend is evident from data taken 150 days after the outburst when the source was detected at ~1038 erg s-1 (Barnard et al. 2011). This observed exponential decline of the luminosity is consistent with those determined for the class of galactic X-ray novae (Chen et al. 1997), which show FRED (Fast Rise Exponential Decay) like light curves, though the FR part in our case was missed. However, the light curves of this source class often exhibit more complex behavior than a simple exponential decay.
In summary, the Chandra discovery of CXOM31 J004253.1+411422 has established it as the first member of the class of ULXs in M 31. Follow up observations with Swift and XMM-Newton revealed an exponential decline, reminiscent of the late time evolution of Galactic X-ray novae. Spectral analysis of the XMM-Newton data suggests that this source was in a “high state” at the time of observation, and that the underlying source is likely a stellar mass black hole accreting near the Eddington limit.
Acknowledgments
The XMM project is supported by the Bundesministerium für Bildung und Forschung/Deutsches Zentrum für Luft- und Raumfahrt (BMBF/DLR) and the Max-Planck Society. We thank the Swift team for their help with scheduling the TOO observations. M. Henze acknowledges support from the BMWI/DLR, FKZ 50 OR 1010.
References
- Abramowicz, M. A., Jaroszyński, M., Kato, S., et al. 2010, A&A, 521, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnard, R., Garcia, M., Li, Z., Primini, F., & Murray, S. S. 2011, ApJ, 734, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C. 2002, ApJ, 568, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W., Shrader, C. R., & Livio, M. 1997, ApJ, 491, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fabbiano, G. 1989, ARA&A, 27, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Ward, M. J. 1993, MNRAS, 263, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, in SPIE, 6270 [Google Scholar]
- Garcia, M., Murray, S., Primini, F., Callanan, P., & Nooraee, N. 2010, The Astronomer’s Telegram, 2474, 1 [NASA ADS] [Google Scholar]
- Gladstone, J. C., Roberts, T. P., & Done, C. 2009, MNRAS, 397, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., & Greiner, J. 2009, The Astronomer’s Telegram, 2356, 1 [Google Scholar]
- Henze, M., Pietsch, W., Haberl, F., et al. 2010, A&A, 523, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holland, S. 1998, AJ, 115, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P. 2002, ApJ, 578, 114 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Davies, M. B., Ward, M. J., Fabbiano, G., & Elvis, M. 2001, ApJ, 552, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., Tanaka, Y., Makishima, K., et al. 1998, PASJ, 50, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Rees, M. J. 2001, ApJ, 551, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Maejima, Y., Mitsuda, K., et al. 1986, ApJ, 308, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Kubota, A., Mizuno, T., et al. 2000, ApJ, 535, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M. J., Roberts, T. P., Done, C., & Jackson, F. E. 2011, Astron. Nachr., 332, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. C., & Colbert, E. J. M. 2004, Inter. J. Mod. Phys. D, 13, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- PortegiesZwart, S. F., Dewi, J., & Maccarone, T. 2004, MNRAS, 355, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., Loan, A. J., Fabian, A. C., et al. 1997, MNRAS, 286, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Shimura, T., & Takahara, F. 1995, ApJ, 445, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., & Garnavich, P. M. 1998, ApJ, 503, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Supper, R., Hasinger, G., Pietsch, W., et al. 1997, A&A, 317, 328 [NASA ADS] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, B. F., Naik, S., Garcia, M. R., & Callanan, P. J. 2006, ApJ, 643, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, L. M., Mushotzky, R. F., & Reynolds, C. S. 2006, ApJ, 649, 730 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 XMM-Newton EPIC image of the central part of M 31 produced by combining pn, MOS1 and MOS2 data from all 5 observations. Red, green and blue show the (0.2–1.0) keV, (1.0–2.0) keV) and (2.0–12.0) keV energy bands, respectively. |
| In the text | |
 |
Fig. 2 Light curve from XMM-Newton EPIC-pn for observation 0600220201 with time binning of 100 s in 0.2–10 keV energy band. |
| In the text | |
 |
Fig. 3 Combined powerlaw and multicolored blackbody fit to the joint set of data from EPIC-pn (black), MOS1 (green), MOS2 (red) with χ2/d.o.f. = 1318.87/1165 for the observation 0600660201 with XMM-Newton. The model parameters obtained from this spectral fit are presented in Table 2. |
| In the text | |
 |
Fig. 4 The theoretical model underlying the data fit (solid line) in Fig. 3 is shown in decomposition between the thermal (dash-dotted line)and the nonthermal (dotted line) component. |
| In the text | |
 |
Fig. 5 Temporal variation of the total unabsorbed luminosity (Lunabs) as per observations of XMM-Newton. The decomposition into the powerlaw (Lpo) and blackbody component (Lbb) reveals a distinct evolutionary behavior of these two components. The time zero corresponds to Chandra HRC-I observation ID 10886 (see Table 1). |
| In the text | |
 |
Fig. 6 Temperature vs. Luminosity for 19 selected ULXs from Winter et al. (2006) along with the candidate ULX (red) in M 31. The M 31 source is a member of the “high temperature” subgroup. |
| In the text | |
 |
Fig. 7 For the same sample shown in Fig. 6, a comparison of photon index vs. temperature reveals that the M 31 ULX cools significantly, but remains within the range covered by the “high temperature” group. The labels 1 through 5 correspond to the chronological entry of XMM-Newton observations as listed in Table 1. |
| In the text | |
 |
Fig. 8 Variation of the total unabsorbed luminosity (Lunabs) of ULX in M 31 as observed by Swift-XRT, Chandra HRC-I and XMM-Newton resembling an exponential decay with a time scale of 32 days. The time zero corresponds to ChandraHRC − I observation ID 10886 (see Table 1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


