| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 11 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201118008 | |
| Published online | 03 February 2012 | |
Numerical solution of the radiative transfer equation: X-ray spectral formation from cylindrical accretion onto a magnetized neutron star
1
INAF, Istituto di Astrofisica Spaziale e Fisica Cosmica, via U. La Malfa
153,
90146
Palermo,
Italy
e-mail: farinelli@ifc.inaf.it
2
Dipartimento di Fisica, Università di Ferrara,
via Saragat 1, 44100
Ferrara,
Italy
3
NASA, Goddard Space Flight Center, Greenbelt, MD
20771,
USA
Received:
2
September
2011
Accepted:
6
November
2011
Context. Predicting the emerging X-ray spectra in several astrophysical objects is of great importance, in particular when the observational data are compared with theoretical models. This requires developing numerical routines for the solution of the radiative equation according to the expected physical conditions of the systems under study.
Aims. We have developed an algorithm solving the radiative transfer equation in the Fokker-Planck approximation when both thermal and bulk Comptonization take place. The algorithm is essentially a relaxation method, where stable solutions are obtained when the system has reached its steady-state equilibrium.
Methods. We obtained the solution of the radiative transfer equation in the two-dimensional domain defined by the photon energy E and optical depth of the system τ using finite-differences for the partial derivatives, and imposing specific boundary conditions for the solutions. We treated the case of cylindrical accretion onto a magnetized neutron star.
Results. We considered a blackbody seed spectrum of photons with exponential distribution across the accretion column and for an accretion where the velocity reaches its maximum at the stellar surface and at the top of the accretion column, respectively. In both cases higher values of the electron temperature and of the optical depth τ produce flatter and harder spectra. Other parameters contributing to the spectral formation are the steepness of the vertical velocity profile, the albedo at the star surface, and the radius of the accretion column. The latter parameter modifies the emerging spectra in a specular way for the two assumed accretion profiles.
Conclusions. The algorithm has been implemented in the xspec package for X-ray spectral fitting and is specifically dedicated to the physical framework of accretion at the polar cap of a neutron star with a high magnetic field (≳ 1012 G). This latter case is expected to be typical of accreting systems such as X-ray pulsars and supergiant fast X-ray transients.
Key words: methods: numerical / X-rays: binaries / radiative transfer / magnetic fields
© ESO, 2012
1. Introduction
The solution of the radiative transfer equation (RTE) that describes the modification of a seed photon spectrum due to Comptonization in a plasma is a much debated mathematical problem. The equation in its full form is indeed integro-differential (Pomraning 1973) and allows for analytical solutions under some particular assumptions, such as electron temperature Te = 0 (Titarchuk & Zannias 1998) or in the energy domain when the emerging spectrum is a powerlaw (Titarchuk & Lyubarskij 1995). If the photon energy exchange for scattering is low (Δν/ν ≪ 1), it is possible to perform a Taylor expansion of the Comptonization operator around the photon initial energy, which transforms the RTE from integro-differential to purely differential (Rybicki & Lightman 1979); this is known as the Fokker-Planck (FP) approximation. The necessary conditions to allow this mathematical approach are that the Compton-scattering process occurs below the Klein-Nishina regime, namely when the electron temperature kTe is subrelativistic (≲ 100 keV), and that the optical depth of the Comptonization region is τ ≳ 1. The regime of low temperature and high optical depth of the plasma indeed ensures that the spectrum is almost isotropized, so that it is possible to use the Eddington approximation for the specific intensity I(ν) = J(ν) + 3∇·F(ν), where J and F are the zero and first moment of the intensity field, respectively.
Moreover, if the plasma is not static but subject to dynamical (bulk) motion with velocity
v(τ), then another condition for using
the FP approximation is that v(τ) must be subrelativistic.
When all the above restrictions are considered, one obtains by computing the first two
moments of the RTE a main equation that describes the shape of the angle-averaged emerging
intensity J(ν) of the Comptonization spectrum. The general
form of the RTE for the photon occupation number
n(ν) = J(ν)/ν3
with subrelativistic electron temperature in the presence of bulk motion was first derived
by Blandford & Payne (1981, hereafter BP81).
Later, Titarchuk et al. (1997, hereafter TMK97)
showed that analytical solutions can be found if the velocity profile (assuming spherical
symmetry) of the matter follows the free-fall law,
vR ∝ R−1/2.
In this case, the equation can be written as
Lxn(x,τ) + Lτn(x,τ) = −s(x,τ)
and the solution can be obtained using the variable-separation method in the form
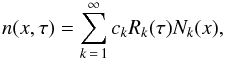 (1)where
ck and
Rk(τ) are the expansion
coefficients and eigenfunctions of the space operator
Lτ, respectively, while
Nk(x) is the solution of
the differential equation
(1)where
ck and
Rk(τ) are the expansion
coefficients and eigenfunctions of the space operator
Lτ, respectively, while
Nk(x) is the solution of
the differential equation 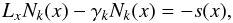 (2)where
(2)where
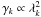 and
and
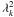 is the
kth-eigenvalue of the space operator.
is the
kth-eigenvalue of the space operator.
The Comptonization spectrum is mostly dominated by the first eigenvalue (see Fig. 3 in TMK97), while the terms Nk(x) with k ≥ 2 represent the fraction of photons that leave the medium without appreciable energy-exchange. Starting from the results of TMK97, Farinelli et al. (2008, hereafter F08) developed a model (comptb) for the X-ray spectral fitting package xspec, which computes the emerging spectrum by means of a numerical convolution of the Green’s function of the energy operator with a blackbody (BB)-like seed spectrum. The model has been successfully applied to a sample of low-mass X-ray binaries hosting a neutron star (NS). The method of the variable separation has also been adopted by Becker & Wolff (2007, hereafter BW07), to find analytical solutions of the RTE in the case of cylindrical accretion onto the polar cap of a magnetized NS. The starting equation in BW07 is formally the same as in BP81: the most significant difference is that the Thomson cross-section is replaced by an angle-averaged cross-section that takes into account the presence of the magnetic field (B ~ 1012 G). Following the results of Lyubarskii & Sunyaev (1982), BW07 assumed a velocity profile v(τ) ∝ − τ, which allowed the RTE to be separable in energy and space. Note that the assumed velocity profile implies that the matter flow stagnates at the stellar surface, which is at odds with the solution of TMK97, where the matter velocity is increasing towards the central object, which can be either a NS or a black hole (BH). When the velocity profile is not free fall-like (TMK97, F08), or ∝ τ (BW07), the variable separation method can no longer be applied and the solution of the RTE can be obtained only with numerical methods.
We report a numerical algorithm that allows the solution of the RTE in the FP regime using finite-differences for any desired velocity profile and seed photon spatial and energy distribution. We apply in particular it to cylindrical accretion towards the polar caps of a magnetized NS, following the approach of BW07. The algorithm essentially uses a relaxation method, therefore it finds the asymptotic (stationary) solution of the RTE for a given initial value (at time t = 0) condition. Our work is structured as follows: in Sect. 2 we describe the kernel of the algorithm for generic two-variable elliptic partial differential equations; in Sect. 3 we formulate the problem for the general RTE and appropriate boundary conditions; in Sect. 4 we consider the more specific case of a system configuration with azimuthal symmetry, typical of cylindrical accretion; in Sect. 5 we show the emerging spectra obtained for different sets of the theoretical parameter space; finally, in Sect. 6 we briefly discuss possible astrophysical consequences and implementations (e.g., for xspec) derived from the application of the algorithm.
2. The general elliptic partial differential equations
The algorithm we report is essentially based on the relaxation methods, which allow one to
find the solution of a boundary elliptical problem. The differential equation has to be
written by finite differences. Once the sparse matrix is defined, it can be split into
layers over which an iteration process is applied until a solution is found (Press et al. 1992). The general form of a linear
second-order elliptic partial differential equation with vanishing mixed derivatives and a
source term can be written as 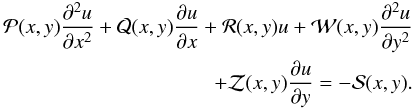 (3)The
solution is numerically obtained by including in the right hand side of Eq. (3) a derivative over a fictitious time
∂u/∂t. Iterating for a sufficient
number of steps over t, the initial guess function at
t = 0 converges for t → ∞ to the time-independent solution
of Eq. (3).
(3)The
solution is numerically obtained by including in the right hand side of Eq. (3) a derivative over a fictitious time
∂u/∂t. Iterating for a sufficient
number of steps over t, the initial guess function at
t = 0 converges for t → ∞ to the time-independent solution
of Eq. (3).
We define a three-dimensional grid of discrete points for the variables
x,y and t;
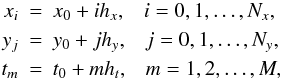 (4)where
hx,hy,ht
are the grid spacing. The function u(x,y,t) is evaluated
at any point of the grid, so we write it as
(4)where
hx,hy,ht
are the grid spacing. The function u(x,y,t) is evaluated
at any point of the grid, so we write it as 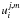 . We write the
first and second derivatives over the variables using finite differences:
. We write the
first and second derivatives over the variables using finite differences:
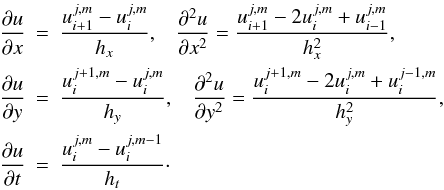 (5)Substituting
the above definitions into Eq. (3) and
collecting terms, we obtain
(5)Substituting
the above definitions into Eq. (3) and
collecting terms, we obtain 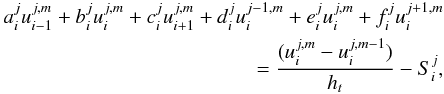 (6)where
(6)where
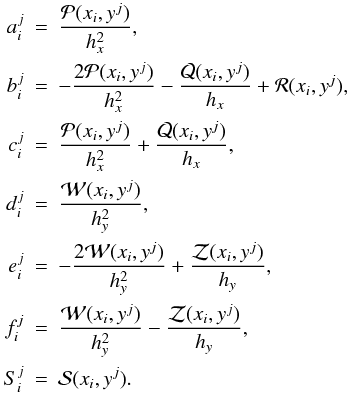 (7)The
operators over the x and y variables are then defined as
(7)The
operators over the x and y variables are then defined as
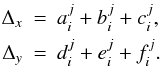 (8)The
solution procedure consists of dividing Eq. (6) into two equations. The first gives us the solution for an intermediate
m−1/2 layer, while the second provides the solution
for the m-layer. As starting point we need to establish an initial guess
for the function at m = 1. The system of equations to be solved is thus
(8)The
solution procedure consists of dividing Eq. (6) into two equations. The first gives us the solution for an intermediate
m−1/2 layer, while the second provides the solution
for the m-layer. As starting point we need to establish an initial guess
for the function at m = 1. The system of equations to be solved is thus
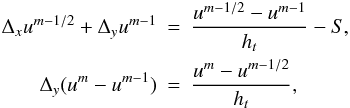 (9)in
which we have temporarily dropped the indices i,j. From the system we
notice that the intermediate layer m − 1/2 is needed
only to build up the solution at the subsequent layer in m. The numerical
accuracy of the solution can be estimated by combining both equations in the system (9), which gives
(9)in
which we have temporarily dropped the indices i,j. From the system we
notice that the intermediate layer m − 1/2 is needed
only to build up the solution at the subsequent layer in m. The numerical
accuracy of the solution can be estimated by combining both equations in the system (9), which gives 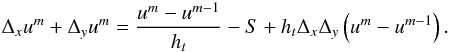 (10)The
third term on the right-hand side of Eq. (10) represents the residual error in the numerical solution. As a first step, we
collect the terms with the same index in both Eqs. (9) and obtain
(10)The
third term on the right-hand side of Eq. (10) represents the residual error in the numerical solution. As a first step, we
collect the terms with the same index in both Eqs. (9) and obtain 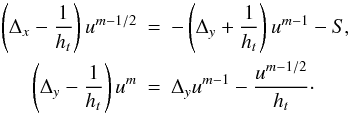 (11)Both
equations are defined inside a 2D (x,y)-domain, with boundary conditions
defined according to the specific problem under consideration. First, for any
m and j values, we must impose the boundary condition on
the left-hand side of the x-domain (i = 0) for the
function
(11)Both
equations are defined inside a 2D (x,y)-domain, with boundary conditions
defined according to the specific problem under consideration. First, for any
m and j values, we must impose the boundary condition on
the left-hand side of the x-domain (i = 0) for the
function 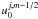
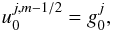 (12)while
the source term
(12)while
the source term 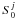 is defined at
the beginning. Thus, for i = 0, Eq. (6) can be written as
is defined at
the beginning. Thus, for i = 0, Eq. (6) can be written as 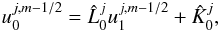 (13)where
(13)where
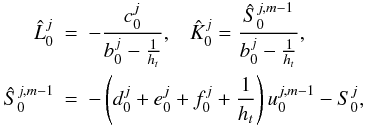 (14)with
the coefficients determined in Eq. (7). For
i = 1, using Eq. (13) we
obtain
(14)with
the coefficients determined in Eq. (7). For
i = 1, using Eq. (13) we
obtain 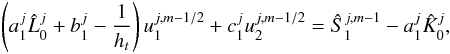 (15)which
can be written as
(15)which
can be written as 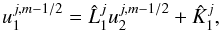 (16)where
(16)where
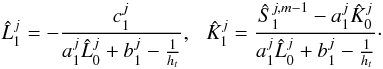 (17)Iterating the process, we
obtain the general form
(17)Iterating the process, we
obtain the general form 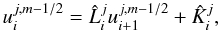 (18)where
(18)where 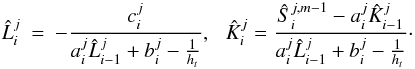 (19)At
the right boundary of the x-domain
(i = Nx), we impose the
second boundary condition
(19)At
the right boundary of the x-domain
(i = Nx), we impose the
second boundary condition 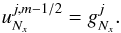 (20)Now, using Eq. (18) we can thus build up the solution over the
x-variable iteratively as
(20)Now, using Eq. (18) we can thus build up the solution over the
x-variable iteratively as
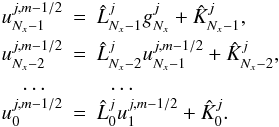 (21)Therefore,
the construction of the solution is obtained in two steps: a bottom-up process which allows
one to build the coefficients
(21)Therefore,
the construction of the solution is obtained in two steps: a bottom-up process which allows
one to build the coefficients 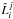 and
and 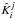 (Eq. (19)) starting from the left boundary condition on
(Eq. (19)) starting from the left boundary condition on
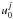 (Eq. (12)), followed by a top-down procedure
determined by the right boundary condition
(Eq. (12)), followed by a top-down procedure
determined by the right boundary condition 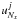 (Eq. (20)).
(Eq. (20)).
Once the solution over the x-variable for the
m − 1/2 layer is obtained for any j
(the index of the y variable), we then seek the solution of the second
equation in the system (9) by following the
same procedure described above with initial boundary condition at j = 0
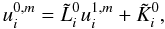 (22)and, similarly to
Eq. (19)
(22)and, similarly to
Eq. (19)
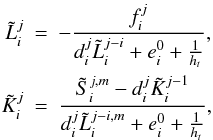 (23)where
(23)where
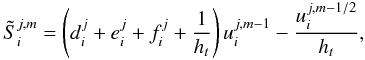 (24)depends on the
solutions
(24)depends on the
solutions 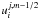 and
and 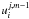 obtained in the layers m − 1/2 and
m − 1.
obtained in the layers m − 1/2 and
m − 1.
As required for the procedure over the x-variable, the coefficients
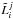 and
and
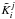 , built
from
, built
from 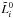 and
and 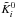 ,
are determined by the left boundary condition (j = 0) for the function
,
are determined by the left boundary condition (j = 0) for the function
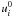 , and the
solution for any j is determined by the right boundary condition
, and the
solution for any j is determined by the right boundary condition
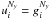 :
:
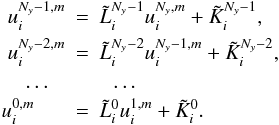 (25)After
constructing the solution over the x and y variable, the
solution of the top layer m becomes the initial function of the bottom
layer related to iteration m + 1 according to the scheme
(25)After
constructing the solution over the x and y variable, the
solution of the top layer m becomes the initial function of the bottom
layer related to iteration m + 1 according to the scheme 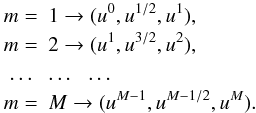 (26)It
is also worth mentioning that at the first iteration m = 1 an initial guess
function
(26)It
is also worth mentioning that at the first iteration m = 1 an initial guess
function 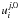 must
be assumed, which is needed to find the solutions
must
be assumed, which is needed to find the solutions 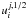 and
and
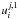 in the
system (9). The loop over
m stops when the same convergence criterion is satisfied, which
physically means that the solution has “relaxed” to its stationary value. One possible
criterion could be
1 − ε < |u|m−1 |/| u|m − 1/2 < 1 + ε
and
1 − ε < |u|m−1/2 |/| u|m < 1 + ε,
where ε is a user-defined numerical tolerance. In the next section we will
show instead another convergence criterion we have chosen for stopping the iteration
procedure, for the particular case of the RTE.
in the
system (9). The loop over
m stops when the same convergence criterion is satisfied, which
physically means that the solution has “relaxed” to its stationary value. One possible
criterion could be
1 − ε < |u|m−1 |/| u|m − 1/2 < 1 + ε
and
1 − ε < |u|m−1/2 |/| u|m < 1 + ε,
where ε is a user-defined numerical tolerance. In the next section we will
show instead another convergence criterion we have chosen for stopping the iteration
procedure, for the particular case of the RTE.
3. Application to the radiative transfer equation and boundary conditions
The general form of the RTE in the presence of subrelativistic bulk motion for a plasma
with constant temperature Te is given by (see Eq. (18) in BP81)
![\begin{eqnarray} \label{bpeqn} \frac{\partial n}{\partial t}+{\vec V}\cdot\nabla n & =&\nabla\cdot\left(\frac{1}{3 \ne\sigma(\nu)}\nabla n\right)+\frac{1}{3}\left(\nabla\cdot {\vec V}\right)\nu\frac{\partial n}{\partial \nu}\nonumber\\ \label{bp81_eq}&& + \frac{1}{\nu^2}\frac{\partial}{\partial \nu}\left[\frac{\ne \sigma(\nu)}{\me}\nu^4\left(n+T_e\frac{\partial n}{\partial \nu}\right)\right]+j(\nu, {\vec r}), \end{eqnarray}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq98.png) (27)where
n(ν,r) is the zero-moment
occupation number of the radiation field intensity, V is the
plasma bulk velocity vector, σ(ν) is the electron
scattering cross-section, ne(r) is
the electron density and
j(ν,r) is the source term.
Because the spectral formation is determined by the optical depth τ of the
system, we use the latter quantity as the actual space variable. The solution of Eq. (27) is fulfilled by imposing the boundary
condition at the surface defined by τ = 0, (which represents the starting
point of the integration domain) for the spectral flux, which is given by
(27)where
n(ν,r) is the zero-moment
occupation number of the radiation field intensity, V is the
plasma bulk velocity vector, σ(ν) is the electron
scattering cross-section, ne(r) is
the electron density and
j(ν,r) is the source term.
Because the spectral formation is determined by the optical depth τ of the
system, we use the latter quantity as the actual space variable. The solution of Eq. (27) is fulfilled by imposing the boundary
condition at the surface defined by τ = 0, (which represents the starting
point of the integration domain) for the spectral flux, which is given by ![\begin{equation} {\vec F}(\nu,r)= -\nu^3\left[\left(\frac{1}{3 \ne \sigma(\nu)}\nabla n\right)+\frac{1}{3}{\vec V}\nu\frac{\partial n}{\partial \nu}\right]\cdot \label{flux_nu} \end{equation}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq105.png) (28)Under particular symmetries
of the system configuration (e.g., cylindrical or spherical), the problem becomes
one-dimensional. For constant electron temperature Te it is also
more convenient to use the adimensional variable
x ≡ hν/kTe;
moreover, when performing numerical integration using finite-difference methods, we use a
logarithmic binning of the energy through the additional change of variable
x → eq. Under these assumptions, Eq. (28) becomes
(28)Under particular symmetries
of the system configuration (e.g., cylindrical or spherical), the problem becomes
one-dimensional. For constant electron temperature Te it is also
more convenient to use the adimensional variable
x ≡ hν/kTe;
moreover, when performing numerical integration using finite-difference methods, we use a
logarithmic binning of the energy through the additional change of variable
x → eq. Under these assumptions, Eq. (28) becomes ![\begin{equation} F(q,\tau)= -\left[\frac{1}{3}\frac{\partial J}{\partial \tau}+\frac{1}{3} V \left(\frac{\partial J}{\partial q}-J\right)\right], \label{flux_q} \end{equation}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq108.png) (29)where
J ≡ n x3 is the specific
intensity.
(29)where
J ≡ n x3 is the specific
intensity.
At the inner boundary we impose the condition 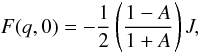 (30)where A
is the albedo at the surface. A fully absorptive surface (A = 0) is
appropriate for a BH, while 0 < A ≤ 1 accounts,
e.g., for a NS atmosphere. However, the inner boundary condition (30) depends on energy as well as space (see
Eqs. (28) and (29)). For mixed boundary value problems, no
analytical solutions are possible (see Appendix E in TMK97) and numerical methods prove to
be unstable. However, in the energy range where the spectrum is a powerlaw
J(x,τ) = R(τ)x−α,
Eq. (30) becomes
(30)where A
is the albedo at the surface. A fully absorptive surface (A = 0) is
appropriate for a BH, while 0 < A ≤ 1 accounts,
e.g., for a NS atmosphere. However, the inner boundary condition (30) depends on energy as well as space (see
Eqs. (28) and (29)). For mixed boundary value problems, no
analytical solutions are possible (see Appendix E in TMK97) and numerical methods prove to
be unstable. However, in the energy range where the spectrum is a powerlaw
J(x,τ) = R(τ)x−α,
Eq. (30) becomes 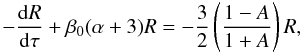 (31)where
β0 is the bulk velocity at the inner radius
(τ = 0), and here the problem is reduced to a standard boundary condition
over the space variable τ. Writing the derivative in terms of
finite-difference, Eq. (31) then becomes
(31)where
β0 is the bulk velocity at the inner radius
(τ = 0), and here the problem is reduced to a standard boundary condition
over the space variable τ. Writing the derivative in terms of
finite-difference, Eq. (31) then becomes
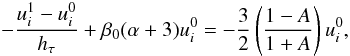 (32)which can be
written after collecting terms as
(32)which can be
written after collecting terms as ![\begin{equation} u^0_i=\frac{1}{1+\htau [\beta_{\rm 0} (\alpha+3)+ G(A)]}u^1_i, \label{leftbc_tau} \end{equation}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq118.png) (33)where
G(A) = 3/2(1 − A)/(1 + A).
We then set our problem as follows: first, because the solution
(33)where
G(A) = 3/2(1 − A)/(1 + A).
We then set our problem as follows: first, because the solution
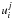 of the RTE
physically represents a specific intensity, it must by definition be equal to zero in the
limits E → 0 and E → ∞, therefore we set
of the RTE
physically represents a specific intensity, it must by definition be equal to zero in the
limits E → 0 and E → ∞, therefore we set
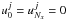 (see Eqs. (12) and (20)). For the behavior of the function
(see Eqs. (12) and (20)). For the behavior of the function
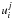 for
τ = 0 (j = 0), Eq. (33) immediately allows us to define (see Eq. (22))
for
τ = 0 (j = 0), Eq. (33) immediately allows us to define (see Eq. (22)) ![\begin{equation} \tcoeff{L}{i}{0}= \frac{1}{1+\htau [\beta_{\rm 0} (\alpha+3)+ G(A)]}, ~~~~~ \tcoeff{K}{i}{0}=0. \label{ltilde_ktilde_j0} \end{equation}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq124.png) (34)As outer boundary
condition over τ, we impose that
(34)As outer boundary
condition over τ, we impose that 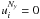 , which
means that the specific intensity goes to zero for
τ → τmax.
, which
means that the specific intensity goes to zero for
τ → τmax.
We emphasize that the condition 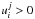 for any
(i,j)-value implies a specific restriction in the choice of the step size
hτ, which ensures that
for any
(i,j)-value implies a specific restriction in the choice of the step size
hτ, which ensures that
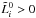 (as
β0 ≤ 0). More specifically, we imposed the condition on
hτ such that the number of steps
over τ be
Nτ = τmax/hτ ≥ 10.
(as
β0 ≤ 0). More specifically, we imposed the condition on
hτ such that the number of steps
over τ be
Nτ = τmax/hτ ≥ 10.
3.1. The iteration procedure
As already mentioned in Sect. 2, it is necessary to choose a convergence criterion for
stopping the iteration over the m variable. We proceeded in the following
way: at each iteration m, we computed the spectral index
αm of the solution
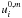 (corresponding to τ = 0) in a given energy range
Emin − Emax. To minimize bias or
wrong estimate of αm, the definition of the
energy interval for the computation of the spectral slope must be chosen carefully. If the
seed photon spectrum is a BB with
temperature kTbb, a reasonable choice can
be the assumption
Emin ≈ 7kTbb
and
Emax ≈ 20kTbb,
respectively, given that this interval is above the major contribution of the BB component
and below the expected high-energy cut-off value.
(corresponding to τ = 0) in a given energy range
Emin − Emax. To minimize bias or
wrong estimate of αm, the definition of the
energy interval for the computation of the spectral slope must be chosen carefully. If the
seed photon spectrum is a BB with
temperature kTbb, a reasonable choice can
be the assumption
Emin ≈ 7kTbb
and
Emax ≈ 20kTbb,
respectively, given that this interval is above the major contribution of the BB component
and below the expected high-energy cut-off value.
Once αm is estimated, it is inserted into
Eq. (34), which accordingly represents
the boundary condition at τ = 0 for the iteration m + 1
(see Eq. (22)). We then computed the new
index αm + 1 for
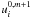 ,
and again inserted it into Eq. (34) at
iteration m + 2, and so on. The routine is stopped when
αm and
αm + 1 differ less than 10-5
provided that the condition holds for a sufficiently high number of iterations
(>100). Note that the same criterion is adopted also if
β0 = 0, even if then of course
,
and again inserted it into Eq. (34) at
iteration m + 2, and so on. The routine is stopped when
αm and
αm + 1 differ less than 10-5
provided that the condition holds for a sufficiently high number of iterations
(>100). Note that the same criterion is adopted also if
β0 = 0, even if then of course
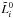 remains constant across the iteration. We have also verified that this criterion
automatically also satisfies the convergence of the norms
|u|m − 1,
|u|m − 1/2, and
|u|m.
remains constant across the iteration. We have also verified that this criterion
automatically also satisfies the convergence of the norms
|u|m − 1,
|u|m − 1/2, and
|u|m.
4. Cylindrical accretion onto a magnetized neutron star
We applied our algorithm to solve the RTE for accretion towards the polar cap of a magnetized NS, whose mathematical formalism was developed by BW07 in the framework of the spectral formation of accretion-powered X-ray pulsars. The relatively strong magnetic field (B ≳ 1012 G) of the NS is expected to channel the accretion flow towards the polar caps, and for low values of the altitude above the star surface, the problem can be treated in a axis-symmetric approximation where the space variable is defined by the vertical coordinate Z. The magnetic field moreover forces the medium to become birefringent as the effect of vacuum polarization, and birefringence entails the formation of two linearly polarized modes (ordinary and extraordinary) of the photons, each having a characteristic scattering cross-section. For ordinary mode photons with energy below the first cyclotron harmonic at Ec ≈ 11.57 B12 keV (where B12 ≡ B/1012 G), BW07 defined angle-averaged cross-sections parallel and perpendicular to the lines of the magnetic field as σ∥ = 10-3σT and σ⊥ = σT, respectively, where σT is the Thomson scattering cross-section. This is indeed the only approximation that allows to treat the problem analytically or numerically. We note that Ferrigno et al. (2009), starting from the analytical solutions reported in BW07, developed a model that was later almost successfully tested on the accreting pulsar 4U 0115+63. Their model is based essentially on the convolution of the column-integrated Green’s function of the thermal plus bulk scattering operator with a given seed photon distribution. The basic assumption of this derivation is that the velocity profile of the accreting matter is assumed to be v(τ) ∝ − τ, which allows one to find analytical solutions through the variable separation method (Eqs. (36) and (37) in BW07). The numerical algorithm we developed directly solves the RTE, without the need of this prescription for the dynamical configuration of the accreting matter field, and we included some modifications with respect to the approach of BW07 and Ferrigno et al. (2009).
 |
Fig. 1 Emerging spectra obtained from the solution of Eq. (37) for different values of the electron temperature kTe and velocity profile defined in Eq. (45). In both cases the fixed parameters are kTbb = 1 keV, τ = 0.2, η = 0.5, r0 = 0.25, A = 1. Left panel: β0 = 0.1. Right panel: β0 = 0.64. |
 |
Fig. 2 Same as Fig. 1 but for different values of the optical depth τ. Fixed parameters are kTbb = 1 keV, η = 0.5, β0 = 0.64, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
First, following TMK97, we include in Eq. (27) a second term in the thermal Comptonization operator that accounts for the
contribution of the bulk motion velocity of electrons in addition to their thermal
(Maxwellian) component. With this prescription in mind, Eq. (27) becomes ![\begin{eqnarray} \label{BW07eqn} \hspace{-0.2truecm} \frac{1}{c}\frac{\partial n}{\partial t} &-& \mathcal S(\epsilon,Z) = -\frac{v}{c}\frac{\partial n}{\partial Z} +\frac{{\rm d}v}{{\rm d}Z}\frac{\epsilon}{3c}\frac{\partial n}{\partial \epsilon}+\frac{\partial}{\partial Z} \left(\frac{1}{3 \ne \sigma_\parallel}\frac{\partial n}{\partial Z}\right)\nonumber\\ &-& \frac{n}{t_{\rm{esc}}}+ \hspace{-0.2truecm} \frac{\ne \overline\sigma}{\me c^2}\frac{1} {\epsilon^2}\frac{\partial}{\partial \epsilon}\left[\epsilon^4\left(n+(\kte + \me v^2/3) \frac{\partial n}{\partial\epsilon}\right)\right], \end{eqnarray}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq166.png) (35)where
ϵ ≡ hν,
(35)where
ϵ ≡ hν, 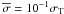 , while
tesc is the photon mean escape timescale (see Eq. (17) in
BW07)
, while
tesc is the photon mean escape timescale (see Eq. (17) in
BW07) 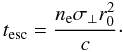 (36)Now, using the relation
dτ = neσ∥dZ
and the logarithmic binning of the adimensional energy
x ≡ hν/kTe,
Eq. (35) becomes
(36)Now, using the relation
dτ = neσ∥dZ
and the logarithmic binning of the adimensional energy
x ≡ hν/kTe,
Eq. (35) becomes ![\begin{eqnarray} \label{bweqn_aftersubs} \frac{1}{\ne \sigma_\parallel c H}\frac{\partial J}{\partial t}-\frac{\mathcal S(q,\tau)}{H} &=& \left[1+\frac{\me v(\tau)^2}{3\kte}\right]\frac{\partial^2 J}{\partial q^2}\nonumber\\ &&+\left[\frac{3\kte({\rm e}^q-3+\hat{\delta})-{\me v(\tau)^2}}{3\kte}\right]\frac{\partial J}{\partial q}\nonumber\\ &&\hspace*{-2cm}+ \left[{\rm e}^q-3\hat{\delta}-\frac{\xi^2v(\tau)^2}{Hc^2}\right]J+\frac{1}{3H} \frac{\partial ^2J}{\partial \tau^2}-\frac{v(\tau)}{Hc}\frac{\partial J}{\partial \tau}, \end{eqnarray}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq172.png) (37)where
we have defined the quantities
(37)where
we have defined the quantities 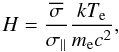 (38)and
(38)and
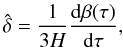 (39)where
β(τ) = v(τ)/c,
while the dimensionless parameter ξ is given by (see Eq. (26) in BW07)
(39)where
β(τ) = v(τ)/c,
while the dimensionless parameter ξ is given by (see Eq. (26) in BW07)
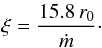 (40)Equation (37) is given in the general form (3) and for this particular case, we have
(40)Equation (37) is given in the general form (3) and for this particular case, we have
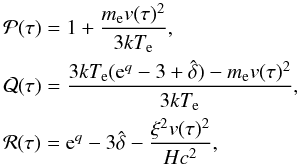
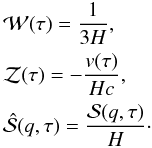 (41)To
solve Eq. (37), it is necessary to define
the behavior of the velocity profile β(τ). We considered
two possibilities: in the first one, we assumed a general form
(41)To
solve Eq. (37), it is necessary to define
the behavior of the velocity profile β(τ). We considered
two possibilities: in the first one, we assumed a general form 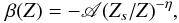 (42)where
the normalization constant is defined
A = β0(Z0/Zs)η,
and β0 is the terminal velocity at the altitude
Z0.
(42)where
the normalization constant is defined
A = β0(Z0/Zs)η,
and β0 is the terminal velocity at the altitude
Z0.
The continuity equation for the system here considered gives the electron number density
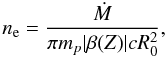 (43)where
ṁ ≡ Ṁ/ṀE
is the mass accretion rate in Eddington units and R0 is the
radius of the accretion column.
(43)where
ṁ ≡ Ṁ/ṀE
is the mass accretion rate in Eddington units and R0 is the
radius of the accretion column.
We then define the adimensional quantities z and
r0 through the change of variables
Z → RS ⊙ mz and
R0 → RS ⊙ mr0,
where
m ≡ M/M⊙,
while MS ⊙ and RS ⊙ are the Sun
mass and Schwarzschild radius, respectively. The effective vertical optical depth of the
accretion column is then given by 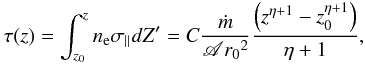 (44)where
C = 2.2 × 10-3, and z0 is the
vertical coordinate at the NS surface.
(44)where
C = 2.2 × 10-3, and z0 is the
vertical coordinate at the NS surface.
Inverting relation (44), we also define the
velocity profile of the accreting matter as a function of the optical depth
τ instead of the space variable z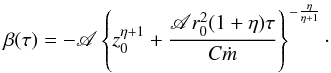 (45)As
a second possibility, following BW07, we considered the velocity profile
(45)As
a second possibility, following BW07, we considered the velocity profile 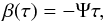 (46)where
Ψ = 0.67ξ/z0 (see Eq. (32)
in BW07).
(46)where
Ψ = 0.67ξ/z0 (see Eq. (32)
in BW07).
Given that in our model the optical depth τ represents one of the free parameters, once it is provided in input together with adimensional accretion column radius r0, the accretion rate ṁ must be first computed either from Eq. (44), if β(τ) is defined as in Eq. (45), or from Eq. (28) in BW07 if β(τ) belongs to Eq. (46). This step is necessary to determine the ξ parameter (Eq. (40)), and requires fixing the maximum altitude of the accretion column zmax. We assumed zmax = 2z0, and all emerging spectra (see next section) were computed with this choice.
5. Results
In this section we report some examples of the theoretical spectra obtained by the numerical solution of Eq. (37) for different sets of the physical quantities that define the system. We consider a BB seed photon spectrum at given temperature kTbb with exponential spatial distribution across the vertical direction, according to
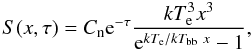 (47)with the
normalization constant defined as
(47)with the
normalization constant defined as 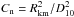 , where
Rkm and D10 are the BB emitting
area in kilometers and the source distance in units of 10 kpc, respectively. The spectra
were computed using the velocity profiles defined in Eqs. (45) and (46),
respectively. The common parameters for both cases are consequently the BB temperature
kTbb, the electron temperature
kTe, the optical depth τ,
the albedo at the inner surface A and the radius of the accreting column
r0. On the other hand, for
β(τ) belonging to Eq. (45), additional parameters are the index η and the
terminal velocity at the star surface β0. We first present the
results for this second physical case.
, where
Rkm and D10 are the BB emitting
area in kilometers and the source distance in units of 10 kpc, respectively. The spectra
were computed using the velocity profiles defined in Eqs. (45) and (46),
respectively. The common parameters for both cases are consequently the BB temperature
kTbb, the electron temperature
kTe, the optical depth τ,
the albedo at the inner surface A and the radius of the accreting column
r0. On the other hand, for
β(τ) belonging to Eq. (45), additional parameters are the index η and the
terminal velocity at the star surface β0. We first present the
results for this second physical case.
 |
Fig. 3 Same as Fig. 1 but for different values of the index of the velocity profile. Fixed parameters are kTbb = 1 keV, τ = 0.2, β0 = 0.64, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
 |
Fig. 4 Same as Fig. 1 but for different values of the inner velocity β0. Fixed parameters are kTbb = 1 keV, τ = 0.2, η = 0.5, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
In Fig. 1 we show the emerging spectra for different values of the electron temperature kTe and two terminal velocities β0 = 0.1 and β0 = 0.64. As expected, both times higher values of kTe produce flatter spectra and push the cut-off energy Ec to higher energies; on the other hand, the bulk contribution as a second channel of Comptonization depends on the value of kTe. The two extreme temperature values reported here, kTe = 5 keV and kTe = 50 keV, are particularly instructive: for low electron temperatures the spectrum changes from BB-like when β0 = 0.1 to a cut-off power law with Ec ≳ 30 keV when β0 = 0.64, while the spectral change is much less enhanced for a hot plasma. These can be considered as typical examples of bulk-dominated and thermal-dominated Comptonization spectra, respectively.
Together with the electron temperature, the optical depth τ is an important parameter that plays a key role in determining the spectral slope and cut-off energy, as clearly shown in Fig. 2. We note that in Figs. 1 and 2 the index of the velocity profile was chosen to be η = 0.5, typical of accretion onto a compact object where gravity and radiation pressure are the only force terms that determine the dynamical configuration. Here, the terminal value of the matter velocity β0 depends on the ratio of the radiative and gravitational forces, provided the condition |Fr |/| Fg| ≲ 1 is satisfied. This relatively simple approach is valid for low values of optical depth τ, while when τ > 1 radiative transfer becomes important and the problem requires in principle a more accurate radiation-hydrodynamics treatment.
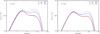 |
Fig. 5 Same as Fig. 1 but for different values of the albedo A, with the velocity profile of Eq. (45). Fixed parameters are kTbb = 1 keV, τ = 0.4, η = 0.5, β0 = 0.64, r0 = 0.25. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
 |
Fig. 6 Same as Fig. 1 but for different values of the accretion column radius r0, with the velocity profile of Eq. (45). Fixed parameters are kTbb = 1 keV, τ = 0.2, η = 0.5, β0 = 0.64, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
It is outside the scope of this paper to compute the exact velocity profile for accreting matter under the presence of a strong radiation field in a high optical depth environment. We merely introduced a simple parametrization for modifying the velocity field by changing the index η, with the results shown in Fig. 3, for two different values of the electron temperature kTe. As Fig. 3 shows, the lower the value of η, the harder the spectrum: this behavior can be explained in a quantitative and a qualitative way. Indeed, as η increases, the velocity profile β(z) becomes sharper, and for a fixed terminal velocity β0, electron temperature kTe, and optical depth τ, while photons diffuse through the bounded medium, on average the energy of the electrons (caused by their Maxwellian plus bulk motion) will be lower, and consequently the net energy gain of the photons due to inverse Compton will be less. From the mathematical point of view, it is worth mentioning that Mastichiadis & Kylafis (1992, hereafter MK92) reported the analytical solution of the RTE in the Fokker-Planck approximation with the variable separation method for spherical accretion without magnetic field in the limit Te = 0. Assuming a general velocity profile βr ∝ r−η, the authors showed that the spectral index of the kth-Comptonization order emerging spectrum yields αk = 3 + 3λk/(2 − η) (see Eq. (1)), where λk is the kth-eigenvalue of the space operator. Using Eq. (B12) of MK92, it follows immediately that as η increases, the spectral index αk increases as well. This mathematical result in terms of spectral formation can be considered as general in the framework of the FP treatment, and is accordingly qualitatively meaningful for our research.
We also emphasize that analytical solutions for η ≠ 0.5 have been possible for MK92 only because of the condition Te = 0, which drops the thermal Comptonization operator in the RTE, while when Te > 0 this is possible only for η = 0.5 (TMK97, F08).
In Fig. 4 we show results for different terminal bulk velocities β0 for two electron temperature values. The figure can be considered an extension and completion of Fig. 1 because more values of β0 are shown to better appreciate the induced changes in the emerging spectra.
The spectral modifications as a result of different values of the albedo A at the inner surface are instead shown in Fig. 5, where we explored full absorption (A = 0) and full reflection (A = 1), together with other intermediate values. In the framework of a physical link to astrophysical objects it would be natural to associate a BH to the condition A = 0 and a NS to the condition A = 1, respectively (Titarchuk & Fiorito 2004; Farinelli & Titarchuk 2011), even though this latter assumption may be considered an oversimplification of the problem. A most realistic approach would consist indeed in an energy-dependent treatment of the albedo, a problem that could be faced only with Montecarlo simulations, with the additional complications arising from a detailed treatment of the star photosphere (surface) properties.
 |
Fig. 7 Emerging spectra obtained from the solution of Eq. (37) for different values of the electron temperature kTe, with the velocity profile of Eq. (46). In both cases the fixed parameters are kTbb = 1 keV, r0 = 0.25, A = 1. Left panel: τ = 0.2. Right panel: τ = 0.4. |
 |
Fig. 8 Same as Fig. 1 but for different values of the optical depth τ, with the velocity profile of Eq. (46). Fixed parameters are kTbb = 1 keV, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
 |
Fig. 9 Same as Fig. 1 but for different values of the albedo A, with the velocity profile of Eq. (46). Fixed parameters are kTbb = 1 keV, τ = 0.4, r0 = 0.25. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
For our unavoidably simplified assumptions, the net effect of increasing values of A is a progressive flattening of the emerging spectra. This is physically explained because when A > 0, a fraction of photons (which becomes 100% when A = 1) suffers on average more scattering with respect to A = 0. Qualitatively, the spectral modification leads in the same direction as an enhanced optical depth of the system.
The last parameter that strongly influences the spectral formation is the radius of the
accretion column r0, whose effects are shown in Fig. 6. Indeed, following the BW07 prescription, the mean escape
time for photons using the diffusion approximation 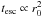 (see Eq. (36)). On the other hand, both the bulk and
thermal Comptonization parameters (ybulk and
yth, respectively) are related to the mean number of
scatterings that photons experience in the medium via
(see Eq. (36)). On the other hand, both the bulk and
thermal Comptonization parameters (ybulk and
yth, respectively) are related to the mean number of
scatterings that photons experience in the medium via 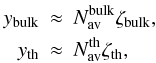 (48)where
(48)where
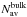 ,
ζbulk,
,
ζbulk, 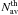 and
ζth are the averaged number of scatterings and the fraction
energy gain per scattering for bulk and thermal Comptonization, respectively. Both
and
ζth are the averaged number of scatterings and the fraction
energy gain per scattering for bulk and thermal Comptonization, respectively. Both
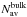 and
and
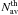 are of course also
proportional to tesc (see Eqs. (94)–(97) in BW07).
are of course also
proportional to tesc (see Eqs. (94)–(97) in BW07).
Evidently therefore, for fixed velocity profile parameters A and η (see
Eq. (42)), once the optical depth
τ is defined (see Eq. (44)), to keep its value constant for increasing r0 (as
reported in Fig. 6), the accretion rate
ṁ must also increase in a way to keep the ratio
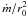 constant.
Combining Eq. (36) and (43) yields
tesc ∝ ṁ, which in turn leads to an
enhancement of the Comptonization parameters ybulk and
yth in Eq. (48) with a hardening of the spectral shape.
constant.
Combining Eq. (36) and (43) yields
tesc ∝ ṁ, which in turn leads to an
enhancement of the Comptonization parameters ybulk and
yth in Eq. (48) with a hardening of the spectral shape.
 |
Fig. 10 Same as Fig. 1 but for different values of the accretion column radius r0, with the velocity profile of Eq. (46). Fixed parameters are kTbb = 1 keV, τ = 0.2, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
Considering now the velocity profile defined in Eq. (46), we see that the results are qualitatively the same as in Eq. (45) as far as the spectral modifications induced
by variations of kTe are concerned (Fig. 7), τ (Fig. 8) and A (Fig. 9),
respectively. But there are opposite effects that are induced in the emerging spectra by
different values of the accretion column radius r0 for the
velocity profile here considered. Indeed, using Eq. (40) and the definition of τ in Eq. (28) of BW07, which
allows us to express the accreting matter velocity in terms of the
z-coordinate, in spite of the optical depth τ, it is
straightforward to see that 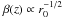 . In
particular, if z0 = 2.42 and
zmax = 2z0 we have
βmax = 0.60 for r0 = 0.1,
βmax = 0.38 for r0 = 0.25,
βmax = 0.27 for r0 = 0.5 and
βmax = 0.2 for r0 = 1,
respectively. Note that because Eq. (46)
describes matter that stagnates at the star surface, here βmax
represents the velocity at the accretion column altitude zmax.
In other words, while using Eq. (45), the
choice of r0 does not modify the velocity field of the accreting
matter, which is only determined by the choice of β0 and
η, for (46) as
r0 increases the bulk contribution to the spectral formation
becomes less important, and this drop is not compensated for by the increase of the photon
mean escape time tesc, which, as explained above, would instead
contribute to spectral hardening.
. In
particular, if z0 = 2.42 and
zmax = 2z0 we have
βmax = 0.60 for r0 = 0.1,
βmax = 0.38 for r0 = 0.25,
βmax = 0.27 for r0 = 0.5 and
βmax = 0.2 for r0 = 1,
respectively. Note that because Eq. (46)
describes matter that stagnates at the star surface, here βmax
represents the velocity at the accretion column altitude zmax.
In other words, while using Eq. (45), the
choice of r0 does not modify the velocity field of the accreting
matter, which is only determined by the choice of β0 and
η, for (46) as
r0 increases the bulk contribution to the spectral formation
becomes less important, and this drop is not compensated for by the increase of the photon
mean escape time tesc, which, as explained above, would instead
contribute to spectral hardening.
6. Implementation in the XSPEC package
Parameter description of the xspec model compmag.
Our model will be publically available and distributed as a contributed model to the official xspec1 web page.
In Table 1 we report a summary of the free
parameters of the model with their physical meaning. The code is written using C-language,
and can be easily installed following the standard procedure reported in the official
xspec manual and in the brief cookbook, which will be delivered together with the
source code. As a general concern for users, we point out that usually the emerging spectrum
obtained from the Comptonization of a seed photon population with any given energy
distribution S(E) can be presented as the sum of the seed
spectrum and its convolution with the scattering Green’s function
G(E,E0) of the electron
plasma, each with their relative weight, according to the general formalism ![\begin{equation} F(E)= \frac{C_{\rm n}}{A+1} [S(E)+ A \times S(E) \ast G(E,E_0)], \label{bmc} \end{equation}](/articles/aa/full_html/2012/02/aa18008-11/aa18008-11-eq256.png) (49)where
Cn is a normalization constant. The ratio
A/(A + 1) is the Comptonization
fraction, and its value qualitatively determines the contribution to the total spectrum of
the Comptonized photons. The value of A, here not to be confused with the
albedo, may depend on several geometrical and physical factors, such as the spatial seed
photon distribution inside the system configuration (see Fig. 4 in TMK97). The lower the
value of A, the more enhanced the direct seed photon spectrum
S(E). Examples of xspec models that use the
definition in Eq. (49) are bmc
(TMK97) and comptb (F08). Either model, however, does not solve the full RTE
including the photon spatial diffusion and distribution, the latter of which is an unknown
quantity that is phenomenologically described through the continuum parameter
log(A). On the other hand, it is not possible to change the value of
log(A) arbitrarily in our present model, i.e., according to the observed
spectra. Its value is implicitly determined once the seed photon spatial distribution is
fixed.
(49)where
Cn is a normalization constant. The ratio
A/(A + 1) is the Comptonization
fraction, and its value qualitatively determines the contribution to the total spectrum of
the Comptonized photons. The value of A, here not to be confused with the
albedo, may depend on several geometrical and physical factors, such as the spatial seed
photon distribution inside the system configuration (see Fig. 4 in TMK97). The lower the
value of A, the more enhanced the direct seed photon spectrum
S(E). Examples of xspec models that use the
definition in Eq. (49) are bmc
(TMK97) and comptb (F08). Either model, however, does not solve the full RTE
including the photon spatial diffusion and distribution, the latter of which is an unknown
quantity that is phenomenologically described through the continuum parameter
log(A). On the other hand, it is not possible to change the value of
log(A) arbitrarily in our present model, i.e., according to the observed
spectra. Its value is implicitly determined once the seed photon spatial distribution is
fixed.
We presented the results of simulated spectra assuming an exponential distribution over τ for S(E), which was assumed to be a BB; then, the transition from the low-energy part of the spectrum (the Rayleigh regime for E ≲ 3kTbb) to the high-energy (Comptonized) powerlaw shape is almost smooth, which corresponds approximately to A ≫ 1 in Eq. (49). Other seed photons spatial distributions can produce a different onset between the BB peak and the powerlaw-like regime. In general, for observed spectra where a direct and enhanced BB-like component is required by the fit, our claim is to model the source continuum with modelization of the type bb + compmag by preferably keeping equal to each other the temperatures of the direct and Comptonized BB component.
7. Conclusions
We have developed a numerical code for solving elliptic partial differential equations based on a relaxation method with finite differences. In particular, we reported a specific application of the algorithm to the radiative transfer equation in the Fokker-Planck approximation, which is of particular interest for high-energy astrophysical applications. We considered cylindrical accretion onto the polar cap of a magnetized neutron star, using the mathematical formulation of the problem reported in Becker & Wolff (2007) with some modifications. Specifically, we included the second-order bulk Comptonization term in the scattering operator and we considered different velocity profiles for the accreting matter.
The code for the computation of the emerging spectra in this configuration has been written with the aim to implement it in the xspec package and will be delivered to the scientific community. Because angle-averaged cross-sections caused by the magnetic field were included, the model is suitable to be applied to the observed spectra of sources where most of spectral formation is claimed to form close to a NS with high magnetic field (B ≳ 1012 G), such as accreting X-ray pulsars and supergiant fast X-ray transients. Of course there are some unavoidable simplifications in the model, such as the assumption of constant electron temperature of the accretion column. We note, however, that the isothermal condition is typical of any Comptonization model implemented in XSPEC because it is fundamental for users to reach a compromise between the accuracy of the physical treatment and the computational speed. More accurate theoretical investigations of the accretion processes can be performed only with MHD simulations performed through PC cluster-computing resources, which are beyond the scope of the present work.
As in many theoretical models, the number of available free parameters is higher than the number of the observable ones.
Therefore a correct working approach is to keep some parameters fixed during the X-ray spectral fitting procedure to avoid degeneracy.
If this model is used in any publication, we kindly ask the authors to cite this paper in the reference list.
Acknowledgments
We acknowledge financial contribution from the agreement ASI-INAF I/009/10/0.
References
- Becker, P. A., & Wolff, M. T. 2007, ApJ, 654, 435 (BW07) [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1981, MNRAS, 194, 1041 (BP81) [NASA ADS] [Google Scholar]
- Farinelli, R., & Titarchuk, L. 2011, A&A, 525, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinelli, R., Titarchuk, L., Paizis, A., & Frontera, F. 2008, ApJ, 680, 602 (F08) [NASA ADS] [CrossRef] [Google Scholar]
- Ferrigno, C., Becker, P. A., Segreto, A., Mineo, T., & Santangelo, A. 2009, A&A, 498, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyubarskii, Y. E., & Sunyaev, R. A. 1982, Soviet Astron. Lett., 8, 330 [Google Scholar]
- Mastichiadis, A., & Kylafis, N. D. 1992, ApJ, 384, 136 (MK92) [NASA ADS] [CrossRef] [Google Scholar]
- Pomraning, G. C. 1973, The equations of radiation hydrodynamics, ed. G. C. Pomraning [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in C, The art of scientific computing (Cambridge: University Press) [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Rad. processes Astrophys., ed. G. B. Rybicki, & A. P. Lightman [Google Scholar]
- Titarchuk, L., & Fiorito, R. 2004, ApJ, 612, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Lyubarskij, Y. 1995, ApJ, 450, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Zannias, T. 1998, ApJ, 493, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1997, ApJ, 487, 834 (TMK97) [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Emerging spectra obtained from the solution of Eq. (37) for different values of the electron temperature kTe and velocity profile defined in Eq. (45). In both cases the fixed parameters are kTbb = 1 keV, τ = 0.2, η = 0.5, r0 = 0.25, A = 1. Left panel: β0 = 0.1. Right panel: β0 = 0.64. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but for different values of the optical depth τ. Fixed parameters are kTbb = 1 keV, η = 0.5, β0 = 0.64, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
 |
Fig. 3 Same as Fig. 1 but for different values of the index of the velocity profile. Fixed parameters are kTbb = 1 keV, τ = 0.2, β0 = 0.64, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
 |
Fig. 4 Same as Fig. 1 but for different values of the inner velocity β0. Fixed parameters are kTbb = 1 keV, τ = 0.2, η = 0.5, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
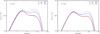 |
Fig. 5 Same as Fig. 1 but for different values of the albedo A, with the velocity profile of Eq. (45). Fixed parameters are kTbb = 1 keV, τ = 0.4, η = 0.5, β0 = 0.64, r0 = 0.25. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
 |
Fig. 6 Same as Fig. 1 but for different values of the accretion column radius r0, with the velocity profile of Eq. (45). Fixed parameters are kTbb = 1 keV, τ = 0.2, η = 0.5, β0 = 0.64, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
 |
Fig. 7 Emerging spectra obtained from the solution of Eq. (37) for different values of the electron temperature kTe, with the velocity profile of Eq. (46). In both cases the fixed parameters are kTbb = 1 keV, r0 = 0.25, A = 1. Left panel: τ = 0.2. Right panel: τ = 0.4. |
| In the text | |
 |
Fig. 8 Same as Fig. 1 but for different values of the optical depth τ, with the velocity profile of Eq. (46). Fixed parameters are kTbb = 1 keV, r0 = 0.25, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
 |
Fig. 9 Same as Fig. 1 but for different values of the albedo A, with the velocity profile of Eq. (46). Fixed parameters are kTbb = 1 keV, τ = 0.4, r0 = 0.25. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
 |
Fig. 10 Same as Fig. 1 but for different values of the accretion column radius r0, with the velocity profile of Eq. (46). Fixed parameters are kTbb = 1 keV, τ = 0.2, A = 1. Left panel: kTe = 5 keV. Right panel: kTe = 15 keV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


