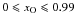| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117938 | |
| Published online | 13 February 2012 | |
Thermonuclear fusion in dense stars
Electron screening, conductive cooling, and magnetic field effects
1 CRAL (UMR CNRS No. 5574), École Normale Supérieure de Lyon, 69364 Lyon Cedex 07, France
e-mail: chabrier@ens-lyon.fr
2 Ioffe Physical-Technical Institute, Politekhnicheskaya 26, 194021 St. Petersburg, Russia
e-mail: palex@astro.ioffe.ru
3 Isaac Newton Institute of Chile, St. Petersburg Branch, Russia
4 School of Physics, University of Exeter, Exeter EX4 4QL, UK
Received: 23 August 2011
Accepted: 3 December 2011
We study the plasma correlation effects on nonresonant thermonuclear reactions of carbon and oxygen in the interiors of white dwarfs and liquid envelopes of neutron stars. We examine the effects of electron screening on thermodynamic enhancement of thermonuclear reactions in dense plasmas beyond the linear mixing rule. Using these improved enhancement factors, we calculate carbon and oxygen ignition curves in white dwarfs and neutron stars. The energy balance and ignition conditions in neutron star envelopes are evaluated, taking their detailed thermal structure into account. The result is compared to the simplified “one-zone model”, which is routinely used in the literature. We also consider the effect of strong magnetic fields on the ignition curves in the ocean of magnetars.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: neutron / white dwarfs / stars: interiors / dense matter
© ESO, 2012
1. Introduction
Thermonuclear reactions play a crucial role in stellar evolution scenarios. In particular, they are important in white dwarfs and neutron stars. Ignition of degenerate carbon and oxygen in the interiors of white dwarfs gives rise to Type Ia supernovae (Hoyle & Fowler 1960; Hillebrandt & Niemeyer 2000). Nuclear reactions in degenerate envelopes of accreting neutron stars are responsible for X-ray bursts and for the overall chemical and thermal structure of the envelopes (Fushiki & Lamb 1987; Brown & Bildsten 1998). Nuclear fusion rates in the interiors of degenerate stars can be significantly enhanced over the binary Gamow (1928) rates because of the many-body screening effect in the dense plasma (Schatzman 1948; for reviews, see Yakovlev & Shalybkov 1989; and Ichimaru 1993).
The screening in degenerate matter is usually treated under the assumption that the electron gas can be considered as a uniform “rigid” background. The influence of the electron polarization on the enhancement of nuclear reaction rates has been studied in some detail in several papers (Salpeter 1954; Itoh et al. 1977; Yakovlev & Shalybkov 1989; Sahrling & Chabrier 1998; Kitamura 2000), which confirms that the electron screening effect is rather weak in degenerate matter. At the time of these studies, uncertainties in the reaction rates due to other factors, viz. quantum effects and deviations from the linear mixing rule (LMR) in strongly coupled plasmas, as well as theoretical uncertainties in the nuclear effective potentials at short distances, were more important than the polarizable electron-screening effects.
The mentioned uncertainties have been substantially reduced in recent years. There has been significant progress in treating cross sections of binary nuclear fusion reactions (Beard et al. 2010, and references therein). Yakovlev et al. (2010) constructed an analytic model for calculating these cross sections, which accurately describes the data and parametrized it for a number of C, O, Mg, and Ne isotopes. Pollock & Militzer (2004) and Militzer & Pollock (2005) used the path-integral Monte Carlo (PIMC) method to determine contact probabilities of reacting nuclei for one-component plasma (OCP) with emphasis on many-body quantum effects (these calculations supersede the previous PIMC study by Ogata 1997). Chugunov et al. (2007) compared these PIMC results to semiclassical calculations and find good agreement between the two approaches at temperatures higher than about one fifth of the ion plasma temperature. These authors also obtained a simple parametrization of the reaction rates with allowance for the ion quantum effects. Chugunov & DeWitt (2009a) extended these results to reactions between different nuclei and suggested an analytic expression for reaction rates in multicomponent ion mixtures, based on the LMR. Chugunov & DeWitt (2009b) used extensive Monte Carlo simulations and discuss corrections to the LMR for the plasma-screening function in strongly coupled binary ionic mixtures. They also propose an analytic formula for the screening function in ion mixtures.
Chugunov & DeWitt (2009a,b) have employed the model of rigid electron background. In this paper we demonstrate that the electron screening effects are not negligible compared to the other improvements considered in recent publications. We derive a simple analytic formula for a quick evaluation of these effects. We also calculate the ignition curves for carbon, oxygen, and their mixtures. We consider plasma cooling by heat conduction and different neutrino emission mechanisms, which evacuate the heat released in nuclear burning, thereby determining the ignition curve. The account of the heat diffusion is taken by detailed calculation of the thermal structure of neutron star envelopes and corresponding heat fluxes. The result is compared to the simplified “one-zone approximation” (Brown & Bildsten 1998; Cumming & Bildsten 2001; Gasques et al. 2007). Finally, we consider the effects of strong magnetic fields on the ignition curves in neutron star envelopes.
In Sect. 2 we compare different approximations for the enhancement factors and study the effect of electron screening. In Sect. 3 we calculate carbon and oxygen ignition curves in degenerate stars, using the state-of-the-art treatment of carbon and oxygen fusion reactions, neutrino emission mechanisms, and heat conduction with allowance for strong magnetic fields. Results are summarized in Sect. 4.
2. Enhancement factors
2.1. Classical theory and modern approximations
It is customary to write the cross section of binary nuclear fusion reactions in the form (e.g., Yakovlev et al. 2010) 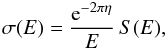 (1)where E is the center-of-mass kinetic energy of the reacting nuclei “1” and “2”,
(1)where E is the center-of-mass kinetic energy of the reacting nuclei “1” and “2”, 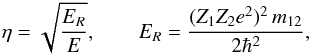 (2)Zje is the charge of nucleus “j”, e is the elementary charge, m12 = m1m2/(m1 + m2) is the reduced mass, and S(E) is a function called “astrophysical factor”. For the Boltzmann distribution of nuclei, the reaction rate (the number of fusion events per unit time in unit volume) in the absence of screening is given by
(2)Zje is the charge of nucleus “j”, e is the elementary charge, m12 = m1m2/(m1 + m2) is the reduced mass, and S(E) is a function called “astrophysical factor”. For the Boltzmann distribution of nuclei, the reaction rate (the number of fusion events per unit time in unit volume) in the absence of screening is given by 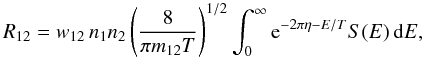 (3)where nj is the number density of the ions of type “j”, T is temperature in energy units, and the factor w12 accounts for statistics:
(3)where nj is the number density of the ions of type “j”, T is temperature in energy units, and the factor w12 accounts for statistics: 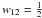 , if nuclei “1” and “2” are identical; otherwise w12 = 1. If T is small, then the integrand in Eq. (3) is strongly peaked at the energy Epk = (π2ERT2)1/3, and the integral can be evaluated as (Salpeter & Van Horn 1969)
, if nuclei “1” and “2” are identical; otherwise w12 = 1. If T is small, then the integrand in Eq. (3) is strongly peaked at the energy Epk = (π2ERT2)1/3, and the integral can be evaluated as (Salpeter & Van Horn 1969) 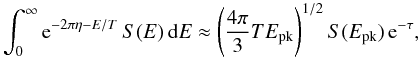 (4)where
(4)where 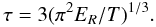 (5)Approximation (4) is valid, if τ ≫ 1.
(5)Approximation (4) is valid, if τ ≫ 1.
In order to take the plasma screening effects into account, it is convenient to write the radial pair-distribution function for ions in the form 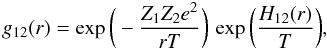 (6)where the first factor is the Boltzmann formula for an ideal gas, while the second one shows how the probability of separation of two chosen ions is affected by the surrounding plasma particles. The function H12(r) is often called screening potential of the plasma (e.g., DeWitt et al. 1973).
(6)where the first factor is the Boltzmann formula for an ideal gas, while the second one shows how the probability of separation of two chosen ions is affected by the surrounding plasma particles. The function H12(r) is often called screening potential of the plasma (e.g., DeWitt et al. 1973).
Along with the customary ion sphere radii aj = (3Zj/4πne)1/3, where ne is the electron number density, and Coulomb coupling parameters Γj = (Zje)2/ajT, it is convenient to introduce parameters 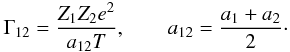 (7)Provided that H12(r) varies slowly on the scale of the classical turning point distance, which requires that 3Γ12/τ ≪ 1 (Ichimaru 1993), the screened reaction rate is approximately given by R12eh, where the enhancement exponent is (Salpeter 1954)
(7)Provided that H12(r) varies slowly on the scale of the classical turning point distance, which requires that 3Γ12/τ ≪ 1 (Ichimaru 1993), the screened reaction rate is approximately given by R12eh, where the enhancement exponent is (Salpeter 1954) 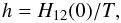 (8)and R12 is given by Eq. (3) with replacement of S(E) by S(E + H12(0)) (Chugunov & DeWitt 2009a). As discussed by Mitler (1977) and Itoh et al. (1977), approximation (8) needs to be corrected at higher densities, where 3Γ12/τ is not small; in the latter case, the quantum effects on ion motion become significant (Jancovici 1977; Alastuey & Jancovici 1978).
(8)and R12 is given by Eq. (3) with replacement of S(E) by S(E + H12(0)) (Chugunov & DeWitt 2009a). As discussed by Mitler (1977) and Itoh et al. (1977), approximation (8) needs to be corrected at higher densities, where 3Γ12/τ is not small; in the latter case, the quantum effects on ion motion become significant (Jancovici 1977; Alastuey & Jancovici 1978).
The Helmholtz free energy F(V,T; { Nj } ;Ne) depends on the numbers Nj = njV of ions of all kinds, the number of electrons Ne = neV, volume V and temperature T. We write it in the form F = Fid + Fex, where Fid is the free energy of the ensemble of noninteracting ions and electrons, and Fex is the excess free energy that accounts for the interactions. In this paper we consider only neutral plasmas, so that ne = ∑ jnjZj. One can rigorously prove (DeWitt et al. 1973; Jancovici 1977) that H12(0) equals the difference between the excess free energies before and after an individual act of fusion. In the thermodynamic limit this gives the relation (cf. Ichimaru & Kitamura 1996) ![\begin{equation} h = \bigg( \frac{\partial}{\partial n_1} + \frac{\partial}{\partial n_2} - \frac{\partial}{\partial n_3} \bigg) \,\left[ \nion f_\mathrm{ex}(\{ n_j \}, n_{\rm e},T) \right], \label{h0gen} \end{equation}](/articles/aa/full_html/2012/02/aa17938-11/aa17938-11-eq40.png) (9)where nion = ∑ jnj is the total number density of ions, including number density n3 of composite nuclei, which have charge number Z3 = Z1 + Z2 and mass m3 ≈ m1 + m2, and fex ≡ Fex/nionVT is the normalized excess energy.
(9)where nion = ∑ jnj is the total number density of ions, including number density n3 of composite nuclei, which have charge number Z3 = Z1 + Z2 and mass m3 ≈ m1 + m2, and fex ≡ Fex/nionVT is the normalized excess energy.
In strongly coupled Coulomb plasma mixtures of classical ions and degenerate electrons, the LMR is fulfilled (Hansen & Vieillefosse 1976; Chabrier & Ashcroft 1990), so that fex ≈ flm, where 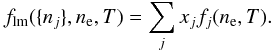 (10)Here, xj ≡ nj/nion denotes the number fractions and fj(ne,T) is the normalized excess free energy fex for a plasma containing only the jth type of ions. Accurate analytic expressions for fj in the Coulomb liquid have been derived in our previous work (Potekhin & Chabrier 2000), and we use these expressions hereafter. It follows from Eqs. (9) and (10) that the enhancement exponent in the LMR approximation is
(10)Here, xj ≡ nj/nion denotes the number fractions and fj(ne,T) is the normalized excess free energy fex for a plasma containing only the jth type of ions. Accurate analytic expressions for fj in the Coulomb liquid have been derived in our previous work (Potekhin & Chabrier 2000), and we use these expressions hereafter. It follows from Eqs. (9) and (10) that the enhancement exponent in the LMR approximation is 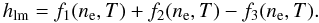 (11)In the approximation of rigid electron background, this reduces to
(11)In the approximation of rigid electron background, this reduces to 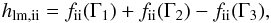 (12)where fii(Γ) is the normalized excess free energy of the OCP. In the ion sphere approximation, fii(Γ) = −0.9 Γ, hence hlm,ii becomes (Salpeter 1954)
(12)where fii(Γ) is the normalized excess free energy of the OCP. In the ion sphere approximation, fii(Γ) = −0.9 Γ, hence hlm,ii becomes (Salpeter 1954) 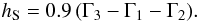 (13)We note, in passing, that Eq. (169) of Yakovlev & Shalybkov (1989) recovers this equation with a factor 1.055 instead of 0.9. We will see, however, that the factor 0.9 provides a much better approximation to the accurate screening function.
(13)We note, in passing, that Eq. (169) of Yakovlev & Shalybkov (1989) recovers this equation with a factor 1.055 instead of 0.9. We will see, however, that the factor 0.9 provides a much better approximation to the accurate screening function.
The LMR is not exact, and it becomes progressively inaccurate with decreasing Γj. When Γj ≪ 1 for all j, the excess free energy Fex is described by the Debye & Hückel (1923) approximation, FDH = −VT/12πD3, where D is the screening length. For nondegenerate electrons and ions, 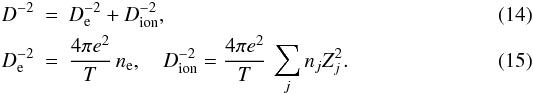 In the approximation of rigid electron background, D = Dion. In the Debye-Hückel approximation, Eq. (9) yields for the enhancement exponent (Salpeter 1954)
In the approximation of rigid electron background, D = Dion. In the Debye-Hückel approximation, Eq. (9) yields for the enhancement exponent (Salpeter 1954) 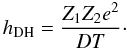 (16)For an arbitrary degree of degeneracy (but at not too strong Coulomb coupling; see Chabrier 1990), the screened interaction between ions is approximately described by a Yukawa potential, Z1Z2e2e − r/D/r, with
(16)For an arbitrary degree of degeneracy (but at not too strong Coulomb coupling; see Chabrier 1990), the screened interaction between ions is approximately described by a Yukawa potential, Z1Z2e2e − r/D/r, with 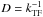 for electron screening or
for electron screening or 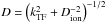 for electron and ion screening. Here,
for electron and ion screening. Here, 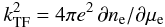 (17)is the Thomas-Fermi wave number, and μe is the chemical potential of Fermi gas of electrons. Using Eq. (24) of Chabrier & Potekhin (1998), one can write kTF(ne,T) in analytic form. We note, however, that the Yukawa model corresponds to the Thomas-Fermi limit, ϵ(k) ~ 1 + (kTF/k)2, for the static dielectric function ϵ(k), which may only be justified at k ≪ kTF (see, e.g., Galam & Hansen 1976). Therefore, this model is inappropriate at short distances (i.e., large wavenumbers k). In particular, it is not applicable for the evaluation of the screening potential at zero separation, H12(0).
(17)is the Thomas-Fermi wave number, and μe is the chemical potential of Fermi gas of electrons. Using Eq. (24) of Chabrier & Potekhin (1998), one can write kTF(ne,T) in analytic form. We note, however, that the Yukawa model corresponds to the Thomas-Fermi limit, ϵ(k) ~ 1 + (kTF/k)2, for the static dielectric function ϵ(k), which may only be justified at k ≪ kTF (see, e.g., Galam & Hansen 1976). Therefore, this model is inappropriate at short distances (i.e., large wavenumbers k). In particular, it is not applicable for the evaluation of the screening potential at zero separation, H12(0).
For the general case, Salpeter & Van Horn (1969) proposed the following interpolation between the Debye-Hückel and strong-coupling limits: 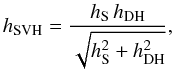 (18)where hS and hDH are given by Eqs. (13) − (16).
(18)where hS and hDH are given by Eqs. (13) − (16).
Another analytic approximation for the enhancement factor beyond the LMR was constructed by Chugunov & DeWitt (2009b), based on Monte Carlo simulation results for the rigid background model.
These analytic approximations can be compared to the result given exactly by Eq. (9). We write the normalized excess free energy in the form fex = flm + fmix, where flm is given by Eq. (10), and fmix( { xj } , { Zj } ;ne,T) is the correction to the LMR, which was recently obtained in analytic form (Potekhin et al. 2009). Then, from Eq. (9), we obtain the enhancement exponent 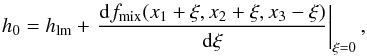 (19)where hlm is given by Eq. (11). Figure 1 shows enhancement factors for 12C fusion in different approximations, normalized to the Salpeter & Van Horn (1969) enhancement factor approximation (18). Here, we intentionally neglect ion quantum effects and postpone their discussion to Sect. 2.3. We compare the analytic expressions for the OCP (thus rigid background: the fit of Chugunov & DeWitt 2009b), and the result of using Eq. (19) for a rigid background, i.e. with hlm replaced by hlm,ii and fmix given by the fit of Potekhin et al. (2009) for the rigid background case. Hereafter, this approximation will be denoted hii. Comparison of the two dot-dashed curves shows that these approximations agree with each other within typically 2%.
(19)where hlm is given by Eq. (11). Figure 1 shows enhancement factors for 12C fusion in different approximations, normalized to the Salpeter & Van Horn (1969) enhancement factor approximation (18). Here, we intentionally neglect ion quantum effects and postpone their discussion to Sect. 2.3. We compare the analytic expressions for the OCP (thus rigid background: the fit of Chugunov & DeWitt 2009b), and the result of using Eq. (19) for a rigid background, i.e. with hlm replaced by hlm,ii and fmix given by the fit of Potekhin et al. (2009) for the rigid background case. Hereafter, this approximation will be denoted hii. Comparison of the two dot-dashed curves shows that these approximations agree with each other within typically 2%.
2.2. Electron screening
 |
Fig. 1 Plasma enhancement exponents for carbon fusion reactions in different approximations, neglecting the ion quantum effects, normalized to the enhancement exponent given by Eq. (18), as functions of mass density for 2 isotherms (top panel: T = 108 K; bottom panel: T = 109 K). Dot-dashed lines correspond to the electron rigid background model. Namely, dot-short-dashed lines show hii given by Eq. (19) for a rigid background, while dot-long-dashed lines show the approximation of Chugunov & DeWitt (2009b). The other lines correspond to the polarizable electron background case: dotted line: LMR [Eq. (11)]; solid line: h0 [Eq. (19)]; dashed line: happr [Eq. (21)]. |
In Fig. 1 we compare the enhancement factors obtained using Eq. (19), where fmix is given by the fit of Potekhin et al. (2009), for the case of a polarizable electron background, and for the OCP. This comparison illustrates the contribution of electron gas polarization to the screening exponent under the present conditions. Additionally we show hlm, given by Eq. (11), with the electron polarization taken into account in fj(ne,T). We see that the correct enhancement factor differs appreciably from the LMR result in the low-density regime, and the difference increases with temperature.
The electron screening contribution can be quickly estimated as follows. We define the effective ion screening length for the reacting nuclei as 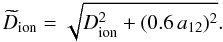 (20)At low densities, where the Debye-Hückel theory is appropriate,
(20)At low densities, where the Debye-Hückel theory is appropriate, 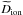 approaches Dion while at high densities it is proportional to a12. The numerical factor 0.6 is the only fitting parameter. Then the approximation for h0 reads as
approaches Dion while at high densities it is proportional to a12. The numerical factor 0.6 is the only fitting parameter. Then the approximation for h0 reads as 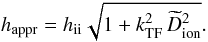 (21)The result is also illustrated in Fig. 1.
(21)The result is also illustrated in Fig. 1.
2.3. Quantum effects
Jancovici (1977) and Alastuey & Jancovici (1978) examined the short-range behavior of the internuclear correlation functions and showed that the quantum effects for the ions decrease the enhancement factor, which we write as ehq. They developed a perturbation expansion of the enhancement exponent hq in powers of the parameter (3Γ/τ). This theory is applicable at Γ ≫ 1 and 3Γ/τ ≲ 1. Pollock & Militzer (2004) and Militzer & Pollock (2005) performed PIMC calculations of the contact probabilities in the quantum regime. They confirm the conclusions of Jancovici (1977) and Alastuey & Jancovici (1978) and extended numerical results beyond the applicability range of the perturbation theory. Chugunov et al. (2007) find that the results of Militzer & Pollock (2005) agree with semiclassical calculations and suggest an analytic parametrization of the reaction rates that accounts for the quantum effects in an OCP. A similar parametrization for multicomponent mixtures has recently been derived by Chugunov & DeWitt (2009a), in the LMR approximation. They find that the quantum effects can be described by the use of Eq. (12) with the substitution1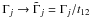 , where
, where ![\begin{eqnarray} t_{12}&=&\left[1+c_1\, (3\Gamma_{12}/\tau) + c_2\, (3\Gamma_{12}/\tau)^2 + c_3\, (3\Gamma_{12}/\tau)^3 \right]^{1/3}, \\ c_1 &=& 0.013\,\gamma^2, \, c_2 = 0.406\,\gamma^{0.14}, \, c_3 = 0.062\,\gamma^{0.19}+1.8/\Gamma_{12}, \nonumber \end{eqnarray}](/articles/aa/full_html/2012/02/aa17938-11/aa17938-11-eq103.png) (22)τ and Γ12 are defined by Eqs. (5) and (7), and γ = 4Z1Z2/(Z1 + Z2)2 (see Fig. 2).
(22)τ and Γ12 are defined by Eqs. (5) and (7), and γ = 4Z1Z2/(Z1 + Z2)2 (see Fig. 2).
 |
Fig. 2 Same enhancement exponents as in Fig. 1, but with other approximations. Solid, dotted, and dot-dashed lines correspond to results while neglecting ionic quantum effects on the enhancement factor: the dotted line corresponds to the LMR for OCP (Eq. (12)), the dot-dashed line demonstrates LMR for the polarizable electron background (Eq. (11)), and the solid line shows h0 beyond the LMR approximation (Eq. (19)). The dashed lines illustrate the impact of ionic quantum effects: the long-dashed line presents the fit of Chugunov & DeWitt (2009a), while the short-dashed line is the approximation qh0, which includes both the ionic and electronic screening contributions and takes both the quantum effects and the deviations from the LMR into account (see text). |
Expansions of the fitting functions of Chugunov et al. (2007) and Chugunov & DeWitt (2009a) in Taylor series do not recover the perturbation series of Alastuey & Jancovici (1978). This mismatch, however, is probably unimportant (unless one is interested in the second and higher derivatives of h), because the numerical agreement with the Alastuey-Jancovici results in their validity domain (3Γ/τ < 1) is quite good.
To include the quantum effects in the general case, we multiply the classical expression (e.g., Eqs. (19) or (Eq. (21))) by the quantum decreasing factor 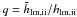 , where hlm,ii is given by Eq. (12), and
, where hlm,ii is given by Eq. (12), and 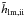 results from the replacement of Γj by
results from the replacement of Γj by 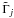 in Eq. (12). The function h0·q is also plotted in Fig. 2.
in Eq. (12). The function h0·q is also plotted in Fig. 2.
2.4. Discussion
Figures 1 and 2 demonstrate that electron screening always increases the value of the enhancement factor. This result is intuitively expected, because allowance for additional screening particles augments the overall effect. It qualitatively agrees also with the findings of Salpeter & Van Horn (1969), DeWitt et al. (1973), Yakovlev & Shalybkov (1989), Sahrling & Chabrier (1998), and Kitamura (2000). The opposite result was claimed by Pollock & Militzer (2004), who found that electron screening “reduces the enhancement effect”. This confusion arises from their use of a Yukawa potential to describe the electron screening. We pointed out in Sect. 2.1 that the Yukawa model becomes incorrect at short distances; in particular, it is incapable of determining the contact probabilities between fusing nuclei. Ichimaru (1993) mentioned two opposite effects of electron screening: first, the binary repulsive potentials between reacting nuclei are reduced by electrons (“short-range effect”), which increases H12(0); second, the reduction of particle interactions by the screening affects the many-body correlation function in such a way that it decreases H12(0) (“long-range effect”). In real electron-ion plasmas (without the Yukawa approximation) the first effect overpowers the second one. The Yukawa model grasps the second effect, but misses the first, dominant one.
In the high-density domain (ρ ≳ 108 g cm-3), where the fusion ignition in dense stars occurs, both corrections to h due to electron screening and due to the deviations from the LMR (see Fig. 1) become quite small, of a few percent or less. Moreover, since these two corrections have opposite signs, they can balance each other out. This is illustrated in Fig. 2, where the accurate result is the same as in Fig. 1, and we show also the result of application of the LMR for the cases of polarizable electron background according to Eq. (11) and the rigid background with LMR approximation according to Eq. (12).
At lower density, the corrections to the enhancement exponent h due to electron polarization and deviation from the LMR become relatively large, but h itself becomes rather small, so that its effect on the reaction rate is not very significant. This domain concerns partially degenerate objects, such as low-mass stars or brown dwarfs, and may affect the nuclear production of light elements, such as deuterium, lithium, beryllium, etc., which provide tracers for the mass and/or age determination of these objects (Chabrier & Baraffe 2000). These situations will be examined in a forthcoming paper.
One can note that the simple approximation of Salpeter & Van Horn (1969), which we have chosen for normalization, performs surprisingly well: in the presently explored ρ – T domain of astrophysical interest, it provides an accuracy of the enhancement factor better than 10%, i.e., better than 0.04 for log 10σ(E). Some later approximations (Yakovlev & Shalybkov 1989; Itoh et al. 1990) are not as good. (They would fall outside the frames of Fig. 2.)
Since the uncertainties in the nuclear part of the reaction rates are still larger (see, e.g., Aguilera et al. 2006), in practice it appears sufficient to use the approximation of Salpeter & Van Horn (1969) with the quantum correction: 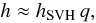 (23)where hSVH and q are given in Sects. 2.1 and 2.3, respectively. Including further improvements to h is currently just a question of completeness. However, as we have seen in Sect. 2.2, the electron-polarization corrections are generally comparable to or even larger than other corrections discussed in literature. Therefore, the electron screening should be taken into account in every treatment of the thermodynamic enhancement factor that goes beyond approximation (23).
(23)where hSVH and q are given in Sects. 2.1 and 2.3, respectively. Including further improvements to h is currently just a question of completeness. However, as we have seen in Sect. 2.2, the electron-polarization corrections are generally comparable to or even larger than other corrections discussed in literature. Therefore, the electron screening should be taken into account in every treatment of the thermodynamic enhancement factor that goes beyond approximation (23).
3. Ignition curves
3.1. Nuclear heating and neutrino cooling
The ignition curve is the line in the ρ – T plane that determines the highest densities and temperatures at which exothermic nuclear reactions in the plasma can be stable against thermal runaway. It is determined by the balance between nuclear energy generation rate and local heat losses. In this subsection we focus on the case where the heat losses are mainly caused by neutrino emission, which is appropriate in white dwarfs, e.g., for modeling supernova Ia events (Hillebrandt & Niemeyer 2000).
The thermonuclear fusion rate is given by Eq. (3), where for S(E) we substitute the parametrization of Yakovlev et al. (2010). The energy release power per unit volume equals R12Q12, where Q12 is the energy release in a single fusion event. We use the values of Q12 given by Fowler et al. (1975): 13.931 MeV for 12C + 12C, 16.754 MeV for 12C + 16O, and 16.541 MeV for 16O + 16O reactions.
At very high densities, pycnonuclear fusion due to zero-point ion vibrations (Cameron 1959) becomes more important than the thermonuclear one. We calculate it using Eq. (33) and Table II (the first line) of Yakovlev et al. (2006) and add it to the thermonuclear rate. The ignition curves portrayed in the figures, however, never enter the domain of pycnonuclear burning.
The dominant mechanism of energy loss due to neutrino emission differs, depending on the physical conditions. For the present conditions of interest, the main mechanisms are neutrino bremsstrahlung by electron scattering off nuclei, plasmon decay, and electron-positron annihilation. The energy loss rates are given, respectively, by Eqs. (76), (38), and (22) of Yakovlev et al. (2001).
 |
Fig. 3 Ignition curves for carbon (lower/left group of lines) and oxygen (upper/right group of lines) in different approximations. Solid lines are obtained using Eq. (19) and the quantum correction according to Sect. 2.3; long-dashed lines: Eq. (12) and the quantum correction; dot-dashed lines: Eq. (18) without any correction. The lines are plotted heavy if the characteristic nuclear fuel burning time tburn is shorter than 1 Myr; the lines are plotted thin if 1 Myr < tburn < 14 Gyr. In the domain where tburn > 14 Gyr the lines are dotted. For the carbon case we also plot the fit (Potekhin et al. 2003) to the results of Sahrling & Chabrier (1998) (the short-dashed line). |
Figure 3 illustrates the ignition curves for 12C+12C and 16O+16O reactions in different approximations. Here, the ignition curves are obtained with the enhancement factors given by Eq. (19) with the quantum correction included according to Sect. 2.3, and are copmpared with the approximations of Chugunov & DeWitt (2009a) and Salpeter & Van Horn (1969). In the low-temperature region, where the characteristic burning time tburn that is required to consume 63% of the nuclear fuel exceeds the Universe age, the ignition curves lose any astrophysical sense, because the burning becomes unrealistically slow, and also because the poorly known quantum effects become too strong (see the discussion in Gasques et al. 2005; Yakovlev et al. 2006).
We see that the electron screening slightly shifts the ignition curves to lower densities, a consequence of the increased enhancement factor, as mentioned previously. This result agrees with the previous findings by Sahrling & Chabrier (1998) and Kitamura (2000)2. In the figure we have also plotted the carbon ignition curve of Sahrling & Chabrier (1998) as fitted by Potekhin et al. (2003), which is close to our current result. The difference is mainly caused by modern improvements in the astrophysical factor (Yakovlev et al. 2010) and neutrino reaction rates (Yakovlev et al. 2001), included in the present treatment. In Appendix A we present a fit to the current carbon and oxygen ignition curves in a wide density range.
3.2. Conductive cooling
Nuclear burning in neutron stars occurs in relatively thin envelopes, whose geometric depth is not more than a few percent of the stellar radius (e.g., Brown & Bildsten 1998, and references therein). Thermal conductivity in these envelopes is high and thermal relaxation time is short, so that cooling by heat diffusion can stabilize nuclear burning beyond the ignition limits considered in Sect. 3.1.
Hansen & Van Horn (1975) estimated stability of H and He burning in envelopes of neutron stars by comparison of the characteristic time scale of thermonuclear heating with characteristic time scales for removal of energy from the shell by radiative and conductive thermal diffusion. Fushiki & Lamb (1987) introduced a differential criterion for such estimates. They defined the boundary of thermal stability of the nuclear burning from the condition 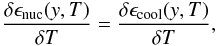 (24)where y is the column depth of the burning material (carbon or oxygen in our case), δT is a variation in temperature, δϵnuc is the respective variation in the nuclear energy release rate per unit mass (ϵnuc = R12 Q12/ρ), and δϵcool is the variation of the cooling rate ϵcool = −dFr(y)/dy, where Fr is the outward radial heat flux through unit surface. The cooling rate ϵcool depends on the first and second derivatives of the temperature, therefore the condition (24) is not local, but depends on the overall temperature and density structure of the envelope.
(24)where y is the column depth of the burning material (carbon or oxygen in our case), δT is a variation in temperature, δϵnuc is the respective variation in the nuclear energy release rate per unit mass (ϵnuc = R12 Q12/ρ), and δϵcool is the variation of the cooling rate ϵcool = −dFr(y)/dy, where Fr is the outward radial heat flux through unit surface. The cooling rate ϵcool depends on the first and second derivatives of the temperature, therefore the condition (24) is not local, but depends on the overall temperature and density structure of the envelope.
Thermal relaxation of the neutron star crust occurs on the scale of a few tens of years, while the relaxation time of the outer envelopes is still shorter (Lattimer et al. 1994; Gnedin et al. 2001; Fortin et al. 2010). Therefore, the outer envelopes are considered quasistationary for most of the astrophysical problems, and their thermal structure is calculated at stationary equilibrium (Gudmundsson et al. 1983). In particular, Fushiki & Lamb (1987) applied this approximation to the stability analysis of H and He shells of accreting neutron stars, and Brown & Bildsten (1998) and Cumming & Bildsten (2001) applied it to the stability analysis of carbon shells. The problem is that Eq. (24) depends not only on the equilibrium quasistationary temperature profile T(y), but also on the profile of its variation δT(y). In equilibrium dFr(y)/dy = ϵν − ϵnuc + T∂s/∂t, where ϵν is the neutrino emission power per unit mass, s is the entropy per unit mass, and t is time. (Here for simplicity we neglect the General Relativity corrections; for the complete set of accurate equations see, e.g., Richardson et al. 1979.) In the quasistationary approximation, one neglects ∂s/∂t. As a result, were the variations δT(y) in equilibrium, one would have ϵcool = ϵnuc − ϵν, which exhausts Eq. (24). Meanwhile, different nonequilibrium forms of δT(y) lead to different values of δϵcool. Fushiki & Lamb (1987) assumed the global temperature variation, dδT/dy = 0. For example, an assumption of the overall variation in the internal energy would result in dδT/dy = −(δT/cP) dcP/dy, where cP(y) is the heat capacity per unit mass at constant pressure, taken at equilibrium.
In modern literature (Brown & Bildsten 1998; Cumming & Bildsten 2001; Gasques et al. 2007), a simplified “one-zone approximation” is used for the cooling rate in Eq. (24): 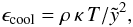 (25)where κ is thermal conductivity,
(25)where κ is thermal conductivity, 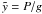 is the column depth in the plane-parallel nonrelativistic approximation, P is pressure, and g is the surface gravity. Definition (25) is local and, therefore, free of uncertainties. Because it is local, the variational derivatives δϵ/δT in Eq. (24) can be replaced by the partial derivatives ∂ϵ/∂T. However, it misses the information about the real dependence of conductivity on column depth, which is fraught with risk being inaccurate.
is the column depth in the plane-parallel nonrelativistic approximation, P is pressure, and g is the surface gravity. Definition (25) is local and, therefore, free of uncertainties. Because it is local, the variational derivatives δϵ/δT in Eq. (24) can be replaced by the partial derivatives ∂ϵ/∂T. However, it misses the information about the real dependence of conductivity on column depth, which is fraught with risk being inaccurate.
We define the ignition curve in the outer envelope of neutron stars in the quasistationary approximation, taking into account the detailed thermal and mechanical structure of the envelope and assuming equilibrium variations of the temperature profile δT(y). For definiteness, let us suppose that δT > 0. For a surface element dS of a shell confined between y1 = y and y2 = y + dy, an increase in temperature δT leads to an increase in the nuclear energy release power δϵnuc dydS, an increase in neutrino energy emission power δϵν dydS, and changes of the heat flux through the outer and inner boundaries of the shell, δF1,2 dS = δFr(y1,2) dS. If 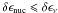 , the increase in the nuclear heat release is compensated for by the increase in the energy emission, and the nuclear burning is stable.
, the increase in the nuclear heat release is compensated for by the increase in the energy emission, and the nuclear burning is stable.
We now consider the case where δϵnuc > δϵν. If the stationary equilibrium requires an increase in the heat income rate F2 dS through the inner boundary, i.e., δF2 > 0, it means that the increase in the net heat release in the considered volume, δϵtot = δϵnuc − δϵν, is overcompensated for by the increase in the outward flux to the stellar surface. In this case, the nuclear burning is stable. In the opposite case, where δF2 < 0, δϵtot is not compensated by the conductive energy escape to the surface, so that thermal runaway occurs. Therefore, the largest column depth y, at which the burning can be stable, corresponds to the condition 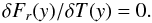 (26)At the column depth where the condition (26) is satisfied, the net energy release δϵtot is balanced exactly by the increase in surface luminosity. Beyond this stationary point, thermal runaway starts.
(26)At the column depth where the condition (26) is satisfied, the net energy release δϵtot is balanced exactly by the increase in surface luminosity. Beyond this stationary point, thermal runaway starts.
 |
Fig. 4 Carbon ignition curves in the ocean of a neutron star with mass M = 1.4 M⊙ and radius 12 km, according to different models: solid line corresponds to Eq. (26), long-dashed line to Eq. (25), short-dashed and dotted lines, respectively, to the original and modified approximations of Fushiki & Lamb (1987), Eq. (24). For comparison, the ignition curve without account of conductive cooling is plotted by the dot-dashed line. |
Figure 4 illustrates different approximations for the carbon ignition curve in the ocean of a typical neutron star with mass M = 1.4 M⊙ and radius 12 km. The carbon ignition curve without conductive cooling is calculated according to Eq. (A.1). The other lines have been obtained by calculating series of temperature profiles for carbon envelopes of the star, assuming different surface luminosities and applying different ignition conditions. The thermal structure has been calculated using the same code as in Kaminker et al. (2009), but the artificial heating model of Kaminker et al. has been replaced by the nuclear heating. The line corresponding to the Fushiki & Lamb (1987) model shows a jump at a certain temperature, which corresponds to a switch from conductive to neutrino cooling. The switch signifies that at higher temperatures the constant variation δT cannot provide a powerful enough off-equilibrium cooling rate δϵcool to compete with the neutrino cooling. Another functional choice of δT(y), corresponding to a constant variation of internal energy per mass, is shown by the dotted line. It displays a similar switch at a higher temperature, therefore the conductive cooling provided by this variation appears more efficient. The underestimation of the ignition densities and temperatures by the two artificial forms of δT(y) above the jump temperatures indicates that these functional variations are unstable on the characteristic cooling timescale.
The line corresponding to the one-zone approximation (25) is compared to the positions of the stationary points (26). The latter two models qualitatively agree with each other, with the quantitative difference caused by the local approximation embedded in the one-zone model.
A similar comparison of the models for the oxygen ignition curve gives similar results. For typical accreting neutron stars with low magnetic fields and effective temperatures from one to several MK, the ignition curves obtained in our calculations using the “stationary point” condition (26) can be reproduced by a modified one-zone approximation, where the right-hand side of Eq. (25) is multiplied by a constant factor α (or equivalently, an effective thermal conductivity κeff = ακ is substituted). As the surface gravity varies from g ≈ 0.7 × 1014 cm s-2 (e.g., for stellar mass M = M⊙ and radius about 15 km) to g ≈ 4 × 1014 cm s-2 (e.g., for M = 2 M⊙ and radius of 10 km), the correction factor α varies from 0.18 to 0.16 in the case of carbon shell and from 0.33 to 0.28 in the case of oxygen shell burning.
3.3. The effect of strong magnetic field
A strong magnetic field can affect conductivities and make the heat transport anisotropic, if the Hall parameter (the product of electron gyrofrequency and effective relaxation time) is larger than one (e.g., Urpin & Yakovlev 1980, and references therein). Therefore, it can affect the conductive cooling rate and shift the ignition curves in neutron star envelopes. We have evaluated the magnitude of this effect by calculating the temperature profiles for different magnetic field strengths B and inclinations θB at the neutron star surface.
 |
Fig. 5 Carbon (lower/left group of lines) and oxygen (upper/right group of lines) ignition curves in the ocean of a magnetar with mass M = 1.4 M⊙, radius 12 km, and magnetic field B = 1014 G for different angles between the field lines and the normal to the surface: θB = 0°, 60°, 75°, and 85° (respectively, 4 solid lines from top to bottom in each of the two groups). For comparison, the ignition curves given by Eq. (A.1) are plotted by the dot-dashed lines, and the ignition curves without accounting for the magnetic field effects are shown by dashed lines. |
In strongly magnetized neutron star envelopes, synchrotron neutrino emission becomes an important energy sink. We calculate it according to Eq. (56) of Yakovlev et al. (2001). Figure 5 illustrates a few examples. Here, a neutron star with M = 1.4 M⊙ and radius 12 km is supposed to possess a magnetic field B = 1014 G, typical of magnetars (Mereghetti 2008). The lower lines are drawn for the carbon envelope, and the upper lines for the case of oxygen. In each of these groups of lines, the four solid curves (from top to bottom) are plotted for angles θB between the field lines and the normal to the surface equal respectively to 0°, 60°, 75°, and 85°. We do not show the case of a strictly tangential field, because, for any reasonable distribution of the magnetic field over the stellar surface, the heat transport becomes essentially two-dimensional around the surface spots where θB is close to 90°, which invalidates the employed approximation of radial (one-dimensional) transport. For comparison, we show the nonmagnetic ignition curves and the fusion-vs-neutrino balance curves discussed in Sect. 3.1 (presumably appropriate for white dwarfs).
When the field lines are nearly tangential to the surface, the strong magnetic field increases the conductive opacity, because the heat transport perpendicular to the field is strongly suppressed. Such a field lowers the ignition curves and thus reduces the stability region.
In the opposite case of field lines perpendicular to the surface, the strong magnetic field somewhat raises the ignition curves and expands the stability region. The latter result could not be obtained in the one-zone approximation (25), which relies on the local values of thermal conductivity, κ, and thermodynamic quantities ρ, T, and P. Indeed, in the ρ – T domain shown in Fig. 5, thermal conductivity along the magnetic field is the same as without the field, because the field is nonquantizing at ρ ≫ ρB, where, for carbon-oxygen compositions, ρB = 1.41 × 107 (B/1014 G)3/2 g cm-3 (e.g., Potekhin 1999). The equation of state also does not depend on B, if ρ ≫ ρB. Finally, the synchrotron neutrino emission cannot produce the observed effect, because the neutrino synchrotron power is less than 5% of thermonuclear power along the full ignition lines for the conditions appropriate to Fig. 5. The effect is caused by the opacity decrease in the heat-blanketing envelope at densities ρ ≲ ρB, where the field is strongly quantizing. The opacity reduction in this outer region makes the entire envelope more transparent and facilitates the heat escape to the surface. Thus, the effect is intrinsically nonlocal.
4. Conclusions
We have studied the effects of electron screening on thermonuclear reactions in dense plasmas and compared different approximations to determine plasma enhancement factors for the nuclear fusion rates. The electron screening always increases the enhancement effect. The opposite conclusion, sometimes encountered in the literature, comes from using the Yukawa potential model, which is inappropriate to calculating the contact probability for fusing nuclei. The electron screening correction, which we calculate using accurate analytic expressions for the free energy, can be satisfactorily described by a simple approximation (21). This correction, although small for the case of dense stars, has the same order of magnitude as other recently suggested corrections to the enhancement factor, so it needs to be properly calculated.
Using our analytic formulae for the enhancement factors and state-of-the-art astrophysical factors for thermonuclear cross sections, we calculated carbon and oxygen ignition curves in degenerate stars. The ignition conditions in neutron star envelopes were evaluated, taking their detailed thermal structure into account. Comparison of the results to customary simplified models demonstrates the restricted applicability of these latter.
We also studied the effects of strong magnetic fields on the ignition curves in neutron star envelopes. These results show that the ignition surface shifts to lower densities in the stellar regions where the magnetic field is strongly inclined and to slightly higher densities in the regions of nearly radial magnetic field. The latter effect could not be obtained in the simplified one-zone model. For a magnetar, the shift in the ignition curve can be similar to the difference between the accurate and one-zone calculations and larger than the correction due to the electron screening in the plasma.
Here a typo in Chugunov & DeWitt (2009a) is corrected.
The carbon ignition curve of Kitamura (2000) substantially differs from our results, because it was calculated under the assumption of a fixed neutrino emission power.
Acknowledgments
A.Y.P. acknowledges useful discussions with Dima Yakovlev and partial support from the RFBR Grant 11-02-00253-a and the Russian Leading Scientific Schools program (Grant NSh-3769.2010.2).
References
- Aguilera, E. F., Rosales, P., Martinez-Quiroz, E., et al. 2006, Phys. Rev. C, 73, 064601 [NASA ADS] [CrossRef] [Google Scholar]
- Alastuey, A., & Jancovici, B. 1978, ApJ, 226, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Beard, M., Afanasjev, A. V., Chamon, L. C., et al. 2010, At. Data Nucl. Data Tables, 96, 541 [Google Scholar]
- Brown, E. F., & Bildsten, L. 1998, ApJ, 496, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. G. W. 1959, ApJ, 130, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 1990, J. Phys. (Paris), 51, 1607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., & Ashcroft, N. W. 1990, Phys. Rev. A, 42, 2284 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Potekhin, A. Y. 1998, Phys. Rev. E, 58, 4941 [NASA ADS] [CrossRef] [Google Scholar]
- Chugunov, A. I., & DeWitt, H. E. 2009a, Phys. Rev. C, 80, 014611 [NASA ADS] [CrossRef] [Google Scholar]
- Chugunov, A. I., & DeWitt, H. E. 2009b, Contrib. Plasma Phys., 49, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Chugunov, A. I., DeWitt, H. E., & Yakovlev, D. G. 2007, Phys. Rev. D, 76, 025028 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., & Bildsten, L. 2001, ApJ, 559, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Debye, P., & Hückel, E. 1923, Physikalische Z., 24, 185 [Google Scholar]
- DeWitt, H. E., Graboske, H. C., & Cooper, M. S. 1973, ApJ, 181, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Fortin, M., Grill, F., Margueron, J., Page, D., & Sandulescu, N. 2010, Phys. Rev. C, 82, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, W. A., Caughlan, G. R., & Zimmerman, B. 1975, ARA&A, 13, 69 [Google Scholar]
- Fushiki, I., & Lamb, D. Q. 1987, ApJ, 323, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Galam, S., & Hansen, J. P. 1976, Phys. Rev. A, 14, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Gamow, G. 1928, Z. Phys., 51, 204 [Google Scholar]
- Gasques, L. R., Afanasjev, A. V., Aguilera, E. F., et al. 2005, Phys. Rev. C, 72, 025806 [Google Scholar]
- Gasques, L. R., Brown, E. F., Chieffi, A., et al. 2007, Phys. Rev. C, 76, 035802 [CrossRef] [Google Scholar]
- Gnedin, O. Y., Yakovlev, D. G., & Potekhin, A. Y. 2001, MNRAS, 324, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Gudmundsson, E. H., Pethick, C. J., & Epstein, R. I. 1983, ApJ, 272, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., & Van Horn, H. M. 1975, ApJ, 195, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. P., & Vieillefosse, P. 1976, Phys. Rev. Lett., 37, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ichimaru, S. 1993, Rev. Mod. Phys., 65, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Ichimaru, S., & Kitamura, H. 1996, PASJ, 48, 613 [NASA ADS] [Google Scholar]
- Itoh, N., Totsui, H., & Ichimaru, S. 1977, ApJ, 218, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Kuwashima, F., & Munakata, H. 1990, ApJ, 362, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Jancovici, B. 1977, J. Stat. Phys., 17, 357 [Google Scholar]
- Kaminker, A. D., Potekhin, A. Y., Yakovlev, D. G., & Chabrier, G. 2009, MNRAS, 395, 2257 [NASA ADS] [CrossRef] [Google Scholar]
- Kitamura, H. 2000, ApJ, 539, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., Van Riper, K. A., Prakash, M., & Prakash, M. 1994, ApJ, 425, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S. 2008, A&ARv, 15, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Militzer, B., & Pollock, E. L. 2005, Phys. Rev. B, 71, 134303 [NASA ADS] [CrossRef] [Google Scholar]
- Mitler, H. E. 1977, ApJ, 212, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Ogata, S. 1997, ApJ, 481, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Pollock, E. L., & Militzer, B. 2004, Phys. Rev. Lett., 92, 021101 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2000, Phys. Rev. E, 62, 8554 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Yakovlev, D. G., Chabrier, G., & Gnedin, O. Y. 2003, ApJ, 594, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., Chugunov, A. I., DeWitt, H. E., & Rogers, F. J. 2009, Phys. Rev. E, 80, 047401 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, M. B., Van Horn, H. M., & Savedoff, M. P. 1979, ApJS, 39, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Sahrling, M., & Chabrier, G. 1998, ApJ, 493, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1954, Austr. J. Phys., 7, 373 [Google Scholar]
- Salpeter, E. E., & Van Horn, H. M. 1969, ApJ, 155, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Schatzman, E. 1948, J. Phys. Rad., 9, 46 [CrossRef] [EDP Sciences] [Google Scholar]
- Urpin, V. A., & Yakovlev, D. G. 1980, SvA, 24, 425 [Google Scholar]
- Yakovlev, D. G., & Shalybkov, D. A. 1989, Sov. Sci. Rev., Ser. E: Astrophys. Space Phys., 7, 311 [Google Scholar]
- Yakovlev, D. G., Kaminker, A. D., Gnedin, O. Y., & Haensel, P. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Gasques, L. R., Afanasjev, A. V., Beard, M., & Wiescher, M. 2006, Phys. Rev. C, 74, 035803 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Beard, M., Gasques, L. R., & Wiescher, M. 2010, Phys. Rev. C, 82, 044609 [Google Scholar]
Appendix A: Fit for C and O ignition curves
White dwarfs contain a mixture of carbon and oxygen nuclei. Therefore, it is of practical interest to determine ignition curves for such mixtures with different number fractions of carbon (xC) and oxygen (xO = 1 − xC). We have derived a fitting formula for ignition temperature as a function of mass density, which is relevant for densities ρ > 100 g cm-3, temperatures T > 108 K, and oxygen number fractions 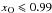 :
: ![\appendix \setcounter{section}{1} \begin{equation} T_\mathrm{fit}(\rho<\rho_\mathrm{lim}) = \frac{ T_1 \,[1+(\rho_1/\rho)^{\alpha_1}]^{\alpha_2} }{ \{1+[\alpha_0/\ln(\rho_\mathrm{lim}/\rho)]^{2.7}\}^{0.2} \, [1+(\rho_2/\rho)^2]^{\alpha_3} }, \label{ignfit} \end{equation}](/articles/aa/full_html/2012/02/aa17938-11/aa17938-11-eq199.png) (A.1)where ρlim, ρ1, ρ2, T1, and α0 – α3 are fitting parameters, given in Table A.1.
(A.1)where ρlim, ρ1, ρ2, T1, and α0 – α3 are fitting parameters, given in Table A.1.
At high ρ, the ignition curves determine the critical density of the ignition, rather than the critical temperature, as at smaller ρ. Therefore, there is no sense to measure the fit error by differences between the model (Tfit) and data (Tdat) values of temperature at a fixed ρ. Instead, we measure the fit error by the geometric distance in the log ρ – log (T4) plane between numerical points (ρdat, 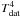 ) and the line
) and the line 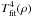 (the fourth power of T is relevant because it is proportional to the luminosity). The fractional error is defined as
(the fourth power of T is relevant because it is proportional to the luminosity). The fractional error is defined as ![\appendix \setcounter{section}{1} \begin{equation} \varepsilon(\rho_\mathrm{dat}) = \min_{\rho} \left[ \left( \frac{T_\mathrm{fit}^4(\rho)-T_\mathrm{dat}^4}{T_\mathrm{dat}^4} \right)^2 + \left( \frac{\rho-\rho_\mathrm{dat}}{\rho_\mathrm{dat}} \right)^2 \right]^{1/2}\cdot \end{equation}](/articles/aa/full_html/2012/02/aa17938-11/aa17938-11-eq236.png) (A.2)The maximum error maxρdatε(ρdat) varies from 0.06 for xO = 0.5 to 0.09 for xO = 0 and xO = 0.99. For oxygen, maxρdatε(ρdat) = 0.05 under the condition that T > 1.7 × 108 K (at lower temperatures the ignition curve is unreliable anyway). This is a good accuracy, given that the considered ρ and T4 values span several orders of magnitude.
(A.2)The maximum error maxρdatε(ρdat) varies from 0.06 for xO = 0.5 to 0.09 for xO = 0 and xO = 0.99. For oxygen, maxρdatε(ρdat) = 0.05 under the condition that T > 1.7 × 108 K (at lower temperatures the ignition curve is unreliable anyway). This is a good accuracy, given that the considered ρ and T4 values span several orders of magnitude.
All Tables
All Figures
 |
Fig. 1 Plasma enhancement exponents for carbon fusion reactions in different approximations, neglecting the ion quantum effects, normalized to the enhancement exponent given by Eq. (18), as functions of mass density for 2 isotherms (top panel: T = 108 K; bottom panel: T = 109 K). Dot-dashed lines correspond to the electron rigid background model. Namely, dot-short-dashed lines show hii given by Eq. (19) for a rigid background, while dot-long-dashed lines show the approximation of Chugunov & DeWitt (2009b). The other lines correspond to the polarizable electron background case: dotted line: LMR [Eq. (11)]; solid line: h0 [Eq. (19)]; dashed line: happr [Eq. (21)]. |
| In the text | |
 |
Fig. 2 Same enhancement exponents as in Fig. 1, but with other approximations. Solid, dotted, and dot-dashed lines correspond to results while neglecting ionic quantum effects on the enhancement factor: the dotted line corresponds to the LMR for OCP (Eq. (12)), the dot-dashed line demonstrates LMR for the polarizable electron background (Eq. (11)), and the solid line shows h0 beyond the LMR approximation (Eq. (19)). The dashed lines illustrate the impact of ionic quantum effects: the long-dashed line presents the fit of Chugunov & DeWitt (2009a), while the short-dashed line is the approximation qh0, which includes both the ionic and electronic screening contributions and takes both the quantum effects and the deviations from the LMR into account (see text). |
| In the text | |
 |
Fig. 3 Ignition curves for carbon (lower/left group of lines) and oxygen (upper/right group of lines) in different approximations. Solid lines are obtained using Eq. (19) and the quantum correction according to Sect. 2.3; long-dashed lines: Eq. (12) and the quantum correction; dot-dashed lines: Eq. (18) without any correction. The lines are plotted heavy if the characteristic nuclear fuel burning time tburn is shorter than 1 Myr; the lines are plotted thin if 1 Myr < tburn < 14 Gyr. In the domain where tburn > 14 Gyr the lines are dotted. For the carbon case we also plot the fit (Potekhin et al. 2003) to the results of Sahrling & Chabrier (1998) (the short-dashed line). |
| In the text | |
 |
Fig. 4 Carbon ignition curves in the ocean of a neutron star with mass M = 1.4 M⊙ and radius 12 km, according to different models: solid line corresponds to Eq. (26), long-dashed line to Eq. (25), short-dashed and dotted lines, respectively, to the original and modified approximations of Fushiki & Lamb (1987), Eq. (24). For comparison, the ignition curve without account of conductive cooling is plotted by the dot-dashed line. |
| In the text | |
 |
Fig. 5 Carbon (lower/left group of lines) and oxygen (upper/right group of lines) ignition curves in the ocean of a magnetar with mass M = 1.4 M⊙, radius 12 km, and magnetic field B = 1014 G for different angles between the field lines and the normal to the surface: θB = 0°, 60°, 75°, and 85° (respectively, 4 solid lines from top to bottom in each of the two groups). For comparison, the ignition curves given by Eq. (A.1) are plotted by the dot-dashed lines, and the ignition curves without accounting for the magnetic field effects are shown by dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.