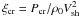| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117855 | |
| Published online | 08 February 2012 | |
Strong evidence for hadron acceleration in Tycho’s supernova remnant
INAF/Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 5, 50125 Firenze Italy
e-mail: morlino@arcetri.astro.it; caprioli@arcetri.astro.it
Received: 8 August 2011
Accepted: 3 October 2011
Context. Very recent gamma-ray observations of G120.1+1.4 (Tycho’s) supernova remnant (SNR) by Fermi-LAT and VERITAS have provided new fundamental pieces of information for understanding particle acceleration and nonthermal emission in SNRs.
Aims. We want to outline a coherent description of Tycho’s properties in terms of SNR evolution, shock hydrodynamics, and multiwavelength emission by accounting for particle acceleration at the forward shock via first-order Fermi mechanism.
Methods. We adopt here a quick and reliable semi-analytical approach to nonlinear diffusive shock acceleration. It includes magnetic field amplification due to resonant streaming instability and the dynamical backreaction on the shock of both cosmic rays (CRs) and self-generated magnetic turbulence.
Results. We find that Tycho’s forward shock accelerates protons up to at least 500 TeV, channelling into CRs about 10% of its kinetic energy. Moreover, the CR-induced streaming instability is consistent with all the observational evidence of very efficient magnetic field amplification (up to ~300 μG). In such a strong magnetic field, the velocity of the Alfvén waves scattering CRs in the upstream is expected to be enhanced and to make accelerated particles feel an effective compression factor lower than 4, in turn leading to an energy spectrum steeper than the standard prediction ∝ E-2. This effect is crucial for explaining GeV-to-TeV gamma-ray spectrum as the result of neutral pions decay produced in nuclear collisions between accelerated nuclei and the background gas.
Conclusions. The self-consistency of such hadronic scenario, along with the inability of the concurrent leptonic mechanism (inverse Compton scattering of relativistic electrons on several photon backgrounds) to reproduce both the shape and the normalization of the detected gamma-ray emission, represents the first clear and direct radiative evidence that hadron acceleration occurs efficiently in young Galactic SNRs.
Key words: shock waves / ISM: supernova remnants / radiation mechanisms: non-thermal / cosmic rays
© ESO, 2012
1. Introduction
Detection of high-energy gamma-rays from supernova remnants (SNRs) has long been considered as the most promising tool (see e.g. Drury et al. 1994) for probing the so-called supernova paradigm for the origin of Galactic cosmic rays (CRs). It states that SNRs are responsible for accelerating nuclei up to energies as high as a few times 106 GeV (see e.g. Hillas 2005, for a review).
In the past few years several SNRs have been detected in gamma rays, both in the GeV and in the TeV band (see Caprioli 2011a, for a recent summary), but in spite of this larger and larger amount of data, clear-cut evidence is still lacking that such an emission is due to the decay of neutral pions produced in nuclear interactions between accelerated nuclei and the background plasma. The very reason behind the probe of such a hadronic scenario for the origin of the detected gamma rays is so controversial is that processes involving relativistic electrons (leptonic scenario) may also provide a similar gamma-ray signature (see e.g. Ellison et al. 2007, for a general discussion on this topic).
The best example of this issue is indeed SNR RX J1713.7-3946, which for many years was regarded as the best candidate for a hadron accelerator because of its brightness in the TeV band (see e.g. Morlino et al. 2009; Zirakashvili & Aharonian 2010). Nevertheless, very recent high-resolution observations in the GeV band performed by the Fermi Large Area Telescope (Fermi-LAT, Abdo et al. 2011) have shown that the emission from the SNR shell is more likely due to inverse-Compton scattering (ICS) of relativistic electrons rather than to pion decay. Its spectrum in the GeV band is in fact very flat (∝ E-1.5), as predicted by a “leptonic” model, which is also supported by the lack of detection of thermal X-ray emission (Ellison et al. 2010).
Another leptonic mechanism that may be relevant for the gamma-ray emission from SNRs is the relativistic bremsstrahlung of accelerated electrons, which, always coupled with ICS, has been proposed as a viable alternative to the hadronic scenario to explain for instance the spectrum of Cas A (Abdo et al. 2010). There are several other examples of SNRs whose emission could be, and has been, accounted for either in hadronic or in leptonic scenario (see Caprioli 2011a, and references therein) but, at the moment the leptonic scenario has not been ruled out beyond a reasonable doubt for any gamma-ray-bright source.
In several cases the extended TeV emission has been suggested as developing from the interaction between particles accelerated in SNR and nearby molecular clouds (MCs), which naturally provide a large number of target nucleons. This scenario may be primarily associated with remnants produced by core-collapse SNe, whose progenitors evolve very quickly in those star formation regions still populated with parent MCs. In these environments, however, it is not very clear whether to expect high CR acceleration efficiencies, because of the small ionized fraction and, likely, because of ion-neutral damping (Drury et al. 1996).
As pointed out for instance by Caprioli (2011a), the best sources where to look for hadron acceleration signatures are the gamma-ray-bright SNRs not associated with MCs and showing rather steep spectral indexes both in the GeV and in the TeV bands. We identify Tycho’s SNR, freshly detected by Fermi-LAT and VERITAS, as the best candidate for investigating the effects that particle acceleration produces at all observable wavelengths, simultaneously using multiple sets of data to constraint our model. To discuss things consistently, we nevertheless need to adopt a very refined model that is able to account, at the same time, for the SNR evolution, the acceleration of particles at the shock and, as will be clearer soon, the magnetic field amplification produced by the streaming of the same relativistic particles.
In this work we therefore apply the nonlinear diffusive shock acceleration (NLDSA) theory to the Tycho’s SNR following the semi-analytical approach put forward by Amato & Blasi (2005, 2006); Caprioli et al. (2010b,a) and references therein. Thanks to the large amount of data available at various wave bands, this remnant can be considered one of the most promising objects for testing the shock acceleration theory, hence the CR–SNR connection. Tycho is among the youngest Galactic SNRs, being only 439 years old: recent observations have in fact confirmed that it is the remnant of a Type Ia SN exploded in 1572 by detecting its optical spectrum near maximum brightness from the scattered-light echo (Krause et al. 2008).
Tycho shows a radio spectral index of 0.6–0.65 and a flux density as high as 40.5 Jy at 1.4 GHz (Kothes et al. 2006). Very interestingly, such a spectral index requires electrons in the GeV energy range to have a spectral slope ~2.2−2.3, i.e. steeper than the standard prediction of linear acceleration theory. The radio morphology is clearly shell-like, with enhanced emission along the northeastern edge (see Fig. 1). A hint of curvature in the radio spectrum, consistent with nonlinear theories’ expectations, has also been reported by Reynolds & Ellison (1992), who also inferred a magnetic field strength ≳100 μG.
In gamma rays, instead, Tycho has been observed several times with no credible detection reported until only very recently the VERITAS Cherenkov telescope succeeded in measuring its TeV emission up to 10 TeV (Acciari et al. 2011), providing an integral flux over 1 TeV of only ~0.9% of the steady Crab Nebula emission above the same energy. Such low emission makes Tycho one of the weakest TeV sources ever detected. The TeV emission is compatible with a point like source since the telescope’s point spread function (PSF) of ~15 arcmin is larger than the angular size of the remnant (8 arcmin). Even more recently, the Fermi-LAT has reported a detection of Tycho as well, assessing an integral flux above 400 MeV of ~(3.5 ± 1.1stat ± 0.7sys) × 10-9 ph cm-2 s-1 and a spectral slope 2.3 ± 0.2stat ± 0.1sys (Giordano et al. 2012).
The question has been raised whether the gamma-ray emission were correlated with the interaction of the remnant with a nearby MC. The peak of the TeV emission might in fact be slightly displaced northeast of the remnant’s center, where a CO cloud has also been detected, but the statistical significance of this displacement seems rather low (Acciari et al. 2011). A possible interaction between the northeastern part of Tycho and dense molecular gas has indeed been suggested by many authors (Reynoso et al. 1999; Lee et al. 2004; Cai et al. 2009; Xu et al. 2011), but in a more recent study Tian & Leahy (2011) analyzed the 21 cm continuum, the HI, and 12CO-line data, concluding that there is no evidence of a direct interaction between the shock and an MC.
Interestingly enough, Tycho is also clearly visible in the infrared (IR) band (Ishihara et al. 2001). In particular, mid-IR images show a shell-like structure with brightness peaks at the northeast and northwest boundaries, probably due to dust collisionally heated up by the hot shocked plasma in the SNR downstream. The far IR band, instead, is dominated by cold dust emission, which spatially correlates with the CO MC mentioned above, so it is probably not related to the remnant. IR emission due to heated dust is particularly important because it provides the principal photon background for the ICS of accelerated electrons, as we show in Sect. 4.4.
High-resolution X-ray maps reveal strong nonthermal emission concentrated in thin filaments (Hwang et al. 2002; Bamba et al. 2005; Warren et al. 2005; Katsuda et al. 2010; Eriksen et al. 2011). The thickness of these filaments is usually interpreted as severe synchrotron losses of high-energy electrons radiating in a strong magnetic field (e.g. Ballet 2006). This interpretation allows us to estimate the magnetic field strength, which has to be as muchas ~250 μG inside the rim (Völk et al. 2005; Parizot et al. 2006). There is, however, also the possibility that the observed X-ray morphology may result from a rapid damping of the magnetic field in the downstream (Pohl et al. 2010). Marcowith & Casse (2010) investigated this scenario by considering different magnetic relaxation processes and different kinds of magnetic turbulence and show that, to have a relaxation length comparable to the X-ray rim thickness, the downstream magnetic field has invariably to be between 200 and 300 μG. Smaller fields would in fact require much longer distances to be damped. Regardless of the presence of any damping mechanisms, the small thickness of X-ray filaments can therefore be regarded as proof that the magnetic field is amplified from the typical interstellar value up to hundreds of μG. In Sect. 2.4 we show that the presence of a damping mechanism for the magnetic field can also be investigated by analyzing the radial profile of the radio emission.
It is interesting to recall that detailed X-ray morphology studies have already provided evidence of efficient hadron acceleration in Tycho. In fact, Warren et al. (2005) estimate the location of the contact discontinuity (CD) and the forward shock (FS) by comparing thermal and nonthermal X-ray emissions, concluding that they are too close to be described by purely gaseous hydrodynamical models. They therefore argue that the compression factor at the FS had to be greater than 4, as predicted in the case of efficient CR acceleration.
Finally we note that hints for the presence of accelerated ions also come from the detection of Hα lines. Analyzing some Balmer-dominated filaments in the eastern limb of the remnant, Lee et al. (2010) find a significant amount of the Hα emission to come from the region upstream of the shock, which has been interpreted as a CR-induced precursor.
All these things considered, several observations have already provided strong hints that efficient CR acceleration is occurring at Tycho’s FS. Our goal is therefore to provide a self-consistent picture able to account for all of these observational evidence and to couple this with brand new gamma-ray data. The NLDSA theory has already been adopted to predict the multiwavelength spectrum of Tycho (e.g. Völk et al. 2005, 2008); nevertheless, here we improve on previous attempts in some important aspects: 1) the magnetic field upstream of the shock is calculated from resonant streaming instability; 2) the dynamical reaction of the magnetic field onto the shock dynamics is accounted for; 3) the upstream scattering center velocity is properly calculated in the amplified magnetic field; 4) the nonlinear Landau damping of the magnetic field in the downstream is introduced; 5) the ICS of accelerated electrons is calculated considering not only the cosmic microwave background (CMB) radiation as target photons, but also the Galactic background and, more importantly, the IR photons produced by the local warm dust.
The inclusion of the dynamical reaction of the field reduces the compressibility of the plasma and affects the prediction for the shock compression factor (Caprioli et al. 2009a). A crucial ingredient is the velocity of the scattering centers, which is generally neglected with respect to the shock speed, but could be significantly enhanced when the magnetic field is amplified (Vladimirov et al. 2006; Caprioli et al. 2009a; Zirakasvhili & Ptuskin 2008). When this occurs, the total compression factor felt by accelerated particles may be reduced appreciably and, in turn, the spectra of accelerated particles may be considerably softer.
It is worth remembering that some observational features, especially the radio emission, are strongly affected by the past history of the remnant, hence any reliable calculation also has to take the SNR evolution into account. In this paper we use a stationary version of NLDSA theory, but we couple this theory to the hydrodynamical evolution of the remnant provided by Truelove & Mc Kee (1999). We divide the SNR evolution in several time steps and assume that the stationary theory can be applied for each time step, as in Caprioli et al. (2010a). However, as show by Caprioli et al. (2010c), stationary models and time-dependent approaches return very similar CR spectra for nonrelativistic shocks.
We compare the results of our kinetic model with the multiwavelength integrated spectrum of Tycho from the radio to the TeV range and also with the radial profile of X-ray and radio emissions. Our conclusion is that existing data of Tycho’s SNR are consistent with a moderately efficient acceleration of CR nuclei: at the present age we infer that a fraction around 12% of the total kinetic energy has been converted in CRs. Such efficiency also implies an amplified magnetic field of ~300 μG, which is perfectly consistent with the measured X-ray rim thickness. In addition, such a strong magnetic field enhances the velocity of the scattering centers, finally reducing the effective compression factor felt by accelerated particles, whose spectrum turns out to be as steep as ~E-2.2. The most important consequence of this is that this spectrum allows us to fit the observed gamma-ray emission from the GeV to the TeV band as neutral pion decay. Moreover, in this framework it is not possible to explain the TeV emission as the result of ICS without violating many other observational constraints.
The paper is organized as follows. In Sect. 2 we summarize the details of our model for nonlinear particle acceleration and our treatment of the SNR evolution. In Sect. 3 we outline the macroscopic properties of Tycho’s SNR, in order to fix the free parameters of our model, while in Sect. 4 we widely discuss the comparison between data and our findings for the multiwavelength spectrum, also by analyzing each different energy band separately. We conclude in Sect. 5.
 |
Fig. 1 Radio image of the Tycho’s remnant at 1.5 GHz in linear color scale. Image credit: NRAO/VLA Archive Survey, c) 2005−2007 AUI/NRAO. |
2. Description of the model
2.1. Remnant evolution
We model the evolution of Tycho by following the analytic prescriptions given by Truelove & Mc Kee (1999). More precisely, we consider an SN explosion energy ESN = 1051 erg and one solar mass in the ejecta, whose structure function is taken as ∝ (v/vej)-7 (see Sects. 3.2 and 9 in Truelove & Mc Kee 1999). Such a set of parameters has been showed to be suitable for describing the evolution of the FS position and velocity for a type Ia SNR: the parametrization given in Table 7 of Truelove & Mc Kee (1999) in fact differs from the exact numerical solution of about 3% typically, and of 7% at most. Such a solution, which does not explicitly include the possible role of the CR pressure in the SNR evolution, is still expected to hold for moderately low acceleration efficiencies (below about 10%). We checked a posteriori that the efficiency needed to fit observations does not require amore complex treatment of the shock evolution during the ejecta-dominated stage.
 |
Fig. 2 Time evolution of shock radius Rsh, shock velocity Vsh, magnetic field immediately behind the shock B2 and CR acceleration efficiency |
The circumstellar medium is taken as homogeneous with proton number density n0 = 0.3 cm-3 and temperature T0 = 104 K. Following the conclusion of Tian & Leahy (2011), we assume that the remnant expands into the uniform interstellar medium (ISM) without interacting with any MC. With these parameters, the reference value for the beginning of the Sedov-Taylor stage is TST = 463 yr, therefore Tycho is experiencing the transition between the ejecta-dominated and the adiabatic stages. The FS radius and velocity can then be written simply as (Truelove & Mc Kee 1999):  The time evolution of some relevant physical quantities is depicted in Fig. 2. The last point corresponds to an age of 439 yr, hence to our estimate for the present shock velocity, Vsh ≃ 4990 km s-1, and shock radius, Rsh = 3.94 pc.
The time evolution of some relevant physical quantities is depicted in Fig. 2. The last point corresponds to an age of 439 yr, hence to our estimate for the present shock velocity, Vsh ≃ 4990 km s-1, and shock radius, Rsh = 3.94 pc.
The radial structure of density and temperature profiles is then calculated by assuming that the downstream (from the CD to the FS), being subsonic, is roughly in pressure equilibrium. In our case, this recipe leads to a discrepancy of less than 10% with respect to the exact profile calculated by including the contribution of the CR pressure in the SNR evolution (see e.g. Chevalier 1983).
More precisely, since 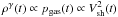 , the adiabatic decompression of a fluid element with density ρ0 shocked at time t0 can be calculated as
, the adiabatic decompression of a fluid element with density ρ0 shocked at time t0 can be calculated as ![\begin{equation} \label{eq:L} \frac{\rho(t)}{\rho_{0}}=L(t_{0},t)^{3}= \left[ \frac{V_{\rm sh}(t)}{V_{\rm sh}(t_{0})} \right]^{\frac{2}{\gamma}}, \end{equation}](/articles/aa/full_html/2012/02/aa17855-11/aa17855-11-eq34.png) (3)where γ is the effective adiabatic index of the CR+plasma fluid. In general we have 4/3 ≤ γ ≤ 5/3, but in our case γ = 5/3 is a very reasonable choice, justified by the fact that the CR acceleration efficiency we find is never much higher than ~10%. The quantity L(t0,t) ≤ 1 introduced above represents the adiabatic energy loss that CRs and magnetic fields undergone in the period t − t0, and it is consistently taken into account in modeling the emission from fluid elements shocked at earlier times.
(3)where γ is the effective adiabatic index of the CR+plasma fluid. In general we have 4/3 ≤ γ ≤ 5/3, but in our case γ = 5/3 is a very reasonable choice, justified by the fact that the CR acceleration efficiency we find is never much higher than ~10%. The quantity L(t0,t) ≤ 1 introduced above represents the adiabatic energy loss that CRs and magnetic fields undergone in the period t − t0, and it is consistently taken into account in modeling the emission from fluid elements shocked at earlier times.
In a similar way, this simple recipe allows us to also track the downstream temperature profile and therefore to work out the bremsstrahlung emission due to thermal electrons, which in general have a temperature Te different from the protons’, Tp. We assume Te = Tp me/mp immediately after the shock and calculate the heating of electrons downstream as due to Coulomb collisions against hotter protons. In Fig. 3 we plot the value of electron and proton temperatures between the CD and the FS at the present epoch, normalized to the proton temperature immediately behind the shock, Tp,sh = 5 × 108 K. The figure shows that Coulomb collisions rapidly enhance the electron temperature up to a few percent of Tp,sh, and also that the maximum value is reached close to the CD, where we have Te ≃ 2 × 107 K. We would like to stress that Coulomb collisions provide the minimum heating rate for electrons but other plasma processes could in principle balances protons and electrons even more rapidly. On the other hand, as we see in Sect. 4.2, the thermal electron bremsstrahlung predicted by assuming only Coulomb heating is compatible with not detecting X-ray thermal emission (Cassam-Chenaï et al. 2007).
 |
Fig. 3 Density (solid line) and temperature (dashed line) of the shocked ISM in the region between the CD (vertical solid line) and the FS, computed at the present age of the remnant, t = 439 yr, and normalized to the values immediately behind the shock. The dot-dashed line shows the electron temperature computed including the heating due to Coulomb collisions. |
2.2. Particle acceleration
Along with this SNR evolution, the spectrum of accelerated particles is calculated according to the semi-analytic kinetic formalism put forward in Caprioli et al. (2010b) and references therein (especially Amato & Blasi 2005, 2006), which self-consistently solves the equations for conservation of mass, momentum, and energy, along with the diffusion-convection equation describing the transport of non-thermal particles for quasi-parallel, non-relativistic shocks. In particular, we require the CR distribution function to vanish at a distance ~χescRsh upstream of the shock, mimicking the presence of a free-escape boundary beyond which highest energy particles cannot diffuse back at the shock and get lost in the ISM (Caprioli et al. 2010b). This constraint actually determines the instantaneous maximum momentum that can be achieved by CRs by imposing the diffusion length of particles with momentum pmax(t) to be comparable to the distance between the shock and the free escape boundary, namely, 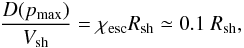 (4)where D(p) is the diffusion coefficient, here taken as Bohm-like; i.e.
(4)where D(p) is the diffusion coefficient, here taken as Bohm-like; i.e. 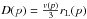 , with v(p) and rL(p) the particle velocity and the Larmor radius, respectively.
, with v(p) and rL(p) the particle velocity and the Larmor radius, respectively.
We also checked a posteriori that by posing χesc = 0.1 such a size-limited pmax is also consistent with requiring both the acceleration time up to pmax to be less than the age of the system (Blasi et al. 2007) and the diffusion length downstream to be smaller than the distance between FS and CD.
Particles are injected into the acceleration mechanism from the suprathermal tail of the Maxwellian distribution (thermal leakage) following the prescription by Blasi et al. (2005). We assume that all the particles with a momentum greater than ξinj times the downstream thermal momentum have a Larmor radius large enough to cross the shock from downstream to upstream, and in turn to be injected in the acceleration process. We fix ξinj = 3.7, corresponding to let a fraction ~10-4 of the particles crossing the shock to be accelerated as CRs.
 |
Fig. 4 Total spectrum of protons and electrons (divided by Kep) at the present age of the remnant, as a function of the particle momentum. For comparison, the dot-dashed line shows a power-law ∝ p-4.2 which emphasizes a small flattening of the proton spectrum at the highest momenta. |
It is worth stressing that the solution of the NLDSA problem obtained with the semi-analytical approximate solution worked out in Caprioli et al. (2010b) is in excellent agreement with the exact solution of the stationary diffusion-convection equation for CR transport coupled with conservation equations, but it is also very consistent with state-of-the-art numerical approaches to the time-dependent problem and also with Monte Carlo approaches able to retain all the information about the anisotropy of the whole (thermal particles + CRs) distribution function (Caprioli et al. 2010c).
2.3. Magnetic field amplification
The super-Alfvénic streaming of relativistic particles is expected to excite a plasma instability (streaming instability) that strongly enhances Alfvén waves resonant with the Larmor radii of relativistic particles (Skilling 1975; Bell 1978). Such a magnetic turbulence may grow well beyond the quasilinear limit, eventually producing a perturbation δB ≫ B0, where B0 is the component of the ordered background magnetic field parallel to the CR gradient, hence to the shock normal. This process, usually referred to as magnetic field amplification, has rather solid observational counterparts in the X-ray observations of many young SNRs: the downstream narrow X-ray rims due to severe synchrotron losses by relativistic electrons (see e.g. Völk et al. 2005; Parizot et al. 2006), the rapid variability of the X-ray-bright spots in RX J1713.7-3946 (Uchiyama et al. 2007) and also the limited extension of the upstream emission in SN 1006 (Morlino et al. 2010).
Tycho is no exception, showing evidence of narrow nonthermal X-ray rims pointing to magnetic fields as large as a few hundred μG (Hwang et al. 2002; Bamba et al. 2005; Warren et al. 2005; Katsuda et al. 2010; Eriksen et al. 2011). We model magnetic field amplification due to resonant streaming instability as in Caprioli et al. (2009a), i.e., by assuming that saturation is achieved when Pw ≃ Pcr/2MA, where Pw and Pcr are the pressure in Alfvén waves and in CRs, normalized to the ram pressure 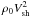 , and MA is the Alfvénic Mach number
, and MA is the Alfvénic Mach number 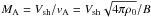 . In the limit
. In the limit 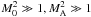 the solution for the wave transport equation reads (see Eq. (43) in Caprioli et al. 2009a) as
the solution for the wave transport equation reads (see Eq. (43) in Caprioli et al. 2009a) as 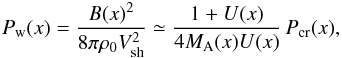 (5)where U(x) is the fluid velocity (normalized to Vsh) in the upstream precursor.
(5)where U(x) is the fluid velocity (normalized to Vsh) in the upstream precursor.
When magnetic field amplification occurs a strong nonlinear regime, as it is expected in our case, it is not clear whether the magnetic field entering the Alfvén velocity has to be the background one, B0, as predicted by an extrapolation of the quasilinear theory, or the amplified one, δB ≫ B0. Strictly speaking, the quasilinear prediction is related to the resonant transverse Alfvén waves (δB ⊥ B0) of arbitrary strength being exact solutions of the problem; however it is very likely that some mechanism may tend to make the field rather turbulent when δB ≫ B0, therefore we choose to calculate the Alfvén velocity in the amplified magnetic field. The implications of this choice are discussed more widely in Caprioli (2011a).
Here and in the following we label quantities measured immediately ahead (behind) the shock with the subscript 1 (2), while the subscript 0 is reserved for undisturbed quantities at upstream infinity. The maximum value of the upstream magnetic field is thus reached immediately ahead of the shock and it is given by 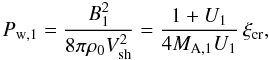 (6)where we posed ξcr = Pcr,1 ≃ 1 − U1. The relevant Alfvénic Mach number thus reads
(6)where we posed ξcr = Pcr,1 ≃ 1 − U1. The relevant Alfvénic Mach number thus reads 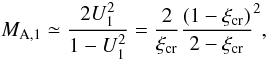 (7)and therefore we have upstream of the subshock:
(7)and therefore we have upstream of the subshock: 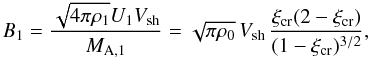 (8)where we also used the mass conservation ρ1U1 = ρ0.
(8)where we also used the mass conservation ρ1U1 = ρ0.
We then assume the downstream magnetic field to have a strength 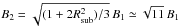 , where Rsub ≃ 4 is the subshock compression ratio, since only the components perpendicular to the shock normal are compressed. For the shock parameters considered above (ρ0 = 0.3 mp cm-3, Vsh ≃ 5000 km s-1) a CR acceleration efficiency of about 5–10% is therefore enough to provide a downstream magnetic field of a few hundred μG (see Eq. (8)), in agreement with the values inferred by X-ray observations of young remnants.
, where Rsub ≃ 4 is the subshock compression ratio, since only the components perpendicular to the shock normal are compressed. For the shock parameters considered above (ρ0 = 0.3 mp cm-3, Vsh ≃ 5000 km s-1) a CR acceleration efficiency of about 5–10% is therefore enough to provide a downstream magnetic field of a few hundred μG (see Eq. (8)), in agreement with the values inferred by X-ray observations of young remnants.
As outlined in the introduction, such large magnetic fields have additional consequences on both the shock hydrodynamics and on the spectrum of accelerated particles. More precisely, when the upstream pressure in magnetic fields becomes comparable to, or even higher than, the thermal plasma pressure, the global dynamics of the system is regulated by the interplay between the CR pressure and the pressure in magnetic turbulence (Caprioli et al. 2008, 2009a). To be more quantitative, at the shock 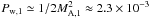 for ξcr = 0.06, hence MA,1 ≃ 15, which is much larger than
for ξcr = 0.06, hence MA,1 ≃ 15, which is much larger than 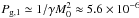 , since the sonic Mach number is M0 ≃ 443. The additional pressure and energy density in magnetic field thus help to balance the compression of the upstream fluid induced by CR pressure and is consistently included both in the conservation equations and in the calculation of the jump conditions at the subshock, as described by Caprioli et al. (2008, 2009a). Moreover, such a magnetic feedback helps in keeping the compression ratios rather close to 4, which in turn legitimates the adoption of Eqs. (1) and (2).
, since the sonic Mach number is M0 ≃ 443. The additional pressure and energy density in magnetic field thus help to balance the compression of the upstream fluid induced by CR pressure and is consistently included both in the conservation equations and in the calculation of the jump conditions at the subshock, as described by Caprioli et al. (2008, 2009a). Moreover, such a magnetic feedback helps in keeping the compression ratios rather close to 4, which in turn legitimates the adoption of Eqs. (1) and (2).
The second, and probably most important, effect of the efficient magnetic field amplification is that the phase velocity of the Alfvén waves CRs scatter against may become a non-negligible fraction of the fluid velocity. In particular, Alfvén waves produced by the CR gradient via streaming instability travel in opposite direction with respect to the fluid, so that upstream CRs actually feel a net velocity 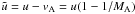 , while downstream it is likely for helicity mixing to lead to vA,2 ≈ 0. Since for DSA the spectral slope is determined only by the compression ratio
, while downstream it is likely for helicity mixing to lead to vA,2 ≈ 0. Since for DSA the spectral slope is determined only by the compression ratio 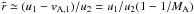 felt by diffusing particles, the non-negligible velocity of the scattering centers (often also called Alfvénic drift) naturally leads to particle spectra steeper than predicted without including this effect.
felt by diffusing particles, the non-negligible velocity of the scattering centers (often also called Alfvénic drift) naturally leads to particle spectra steeper than predicted without including this effect.
The potential role of Alfvénic drift in the DSA theory has already been pointed out by Bell (1978), but it is important to stress that steep particle spectra can be produced at SNR shocks only if the magnetic field is amplified via some instability to levels corresponding to MA ≃ 20 or lower (see also Caprioli 2011a). In our case, taking the saturation of the streaming instability in the amplified field makes this phenomenon even more nonlinear, with the final result that the larger the number of particles injected, the stronger the amplified magnetic field, and eventually the steeper the CR spectra achieved in a consistent NLDSA calculation (Caprioli 2011b).
Finally, another fundamental aspect of magnetic field amplification is that diffusion in the enhanced magnetic turbulence allows particles to return to the shock more quickly, in turn achieving a much larger momentum both in the age-limited and in the space-limited scenario (see Sect. 2.2). In our calculations we therefore take the Bohm-like diffusion coefficient in the amplified magnetic field B1 rather than in B0, finding pmax as high as ~500 TeV for the accelerated protons.
Nevertheless, the excitation of modes resonant with CR gyroradii is not the only phenomenon that may be responsible for magnetic field amplification. As shown by Bell (2004) and then by Riquelme & Spitkovsky (2010), also nonresonant modes with short wavelengths may effectively grow because of CR escaping the system. The relative importance of resonant and nonresonant modes has been investigated within a kinetic approach by Amato & Blasi (2009), who found that for young, strong shocks also nonresonant modes may play a non-negligible role. A comprehensive treatment of the interplay between CRs and magnetic fields from a kinetic point of view is, however, beyond the goal of this paper, therefore we simply assume a uniform magnetic field in the upstream given by Eq. (8). Such a recipe is very reasonable in the shock proximity and becomes more and more heuristic in the far upstream, where amplification should be prevalently due to the excitation of Bell’s modes. However, if the magnetic field far upstream were much lower than we assumed, we would have two effects: on one hand, the CR spectrum would be slightly flatter (∝ E-1.95) at the highest energies, where particles would feel a total compression ratio of about Rtot ≃ 4.2; and on the other hand, the maximum energy would be consistently reduced. These two effects would have a radiative signature in the TeV band but the quite large measurement errors and the lack of detection of a high-energy cut-off do not allow us to realistically investigate possible flattening at the highest energies, yet.
In addition, long-wavelength modes may also play a role in the problem that enhances the diffusion of the highest energy particles (see, e.g., Bykov et al. 2011, and references therein) up to PeV fractions. Our simple very common choice of adopting a constant magnetic field upstream is an oversimplification of the problem; but within the limits of our incomplete understanding of the mechanisms responsible for scattering the highest energy particles, it allows us to heuristically account for a crucial observational evidence. If the GeV-to-TeV emission is hadronic, as we demonstrate in the following, protons have to be accelerated up to at least a few hundred TeV (see also Eriksen et al. 2011).
2.4. Magnetic field damping
As will be clearer in the following discussion, in order to reproduce both the intensity and the radial profile of the synchrotron emission, it is necessary to account for some magnetic field damping in the downstream as well. Several damping mechanisms have been proposed as effective in SNRs (see e.g. Ptuskin & Zirakasvhili 2003, and references therein), but here we focus only on nonlinear Landau damping, which is expected to be fairly efficient in hot (low Mach number) plasmas, as outlined by Völk & McKenzie (1981) and McKenzie & Völk (1982).
We therefore assume that the magnetic field in the downstream is damped with a rate, averaged on the different scales, given by (see Eqs. (10)–(12) in Ptuskin & Zirakasvhili 2003): 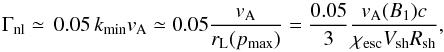 (9)where we took the maximum turbulence scale (i.e. the minimum wave number kmin) to be given by the Larmor radius of particles with momentum close to pmax. In the last equality we simply made use of Eq. (4).
(9)where we took the maximum turbulence scale (i.e. the minimum wave number kmin) to be given by the Larmor radius of particles with momentum close to pmax. In the last equality we simply made use of Eq. (4).
Since B1U1 ≃ B2U2, the typical length scale for the nonlinear Landau damping is thus given by 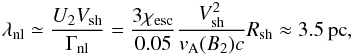 (10)and therefore we obtain the following recipe for the downstream magnetic field:
(10)and therefore we obtain the following recipe for the downstream magnetic field: 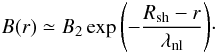 (11)The actual radial profile of B(r) is finally shown in Fig. 5 and compared with the undamped magnetic field and with the magnetic field subjected only to adiabatic expansion.
(11)The actual radial profile of B(r) is finally shown in Fig. 5 and compared with the undamped magnetic field and with the magnetic field subjected only to adiabatic expansion.
 |
Fig. 5 Radial profile of the magnetic field in the downstream at the present age of the remnant. The dashed curve shows B2(r/Rsh) as resulting from the amplification and compression at the shock. The dotted curve includes also adiabatic losses, while the solid curve is computed including both adiabatic losses and Landau damping. |
2.5. Electron spectrum
Once the proton spectrum has been calculated self-consistently with the shock dynamics, it is also possible to work out the spectrum of accelerated electrons, which is parallel to the protons one since DSA is independent of charge, but truncated at a lower maximum energy determined by synchrotron losses in the amplified magnetic field.
The instantaneous electron spectrum at the shock, fe,0(p), is computed as in Morlino et al. (2009), using the expression worked out by Zirakashvili & Aharonian (2007) for a ∝ p-4 proton spectrum: ![\begin{equation} \label{eq:f_e(p)} f_{\rm e,0}(p)= K_{\rm ep}\,f_{\rm p,0}(p) {\left[1+0.523 \left(p/p_{\rm e,\rm max}\right)^{\frac{9}{4}}\right]}^2 {\rm e}^{-p^2/p_{\rm e,\max}^2}, \end{equation}](/articles/aa/full_html/2012/02/aa17855-11/aa17855-11-eq106.png) (12)where pe,max is determined by equating the acceleration time with the energy loss timescale due to synchrotron emission, which, as a consequence of the efficient magnetic field amplification, turns out to be much smaller than Tycho’s age for large momenta (see Eqs. (3) and (4) in Morlino et al. 2009). Such a spectrum is expected to be a reasonable approximation of the true one (see e.g. Blasi 2010), since our proton spectrum is almost a power law slightly steeper than p-4, as shown in Fig. 4.
(12)where pe,max is determined by equating the acceleration time with the energy loss timescale due to synchrotron emission, which, as a consequence of the efficient magnetic field amplification, turns out to be much smaller than Tycho’s age for large momenta (see Eqs. (3) and (4) in Morlino et al. 2009). Such a spectrum is expected to be a reasonable approximation of the true one (see e.g. Blasi 2010), since our proton spectrum is almost a power law slightly steeper than p-4, as shown in Fig. 4.
A very important property of Eq. (12) is also to retain the correct shape of the cut-off, which is not a simple exponential, as assumed by several authors, but instead is exp [−(p/pe,max)2] (Blasi 2010). This trend is in fact crucial when studying the X-ray emission in the keV band.
Finally, the constant Kep accounts for the different normalization between electron and proton spectra, and are very likely related to the different mechanisms responsible for lepton and hadron injection. However, since electron injection in SNRs is still far from being understood from first principles (though see e.g. Amano & Hoshino 2010; Riquelme & Spitkovsky 2011) we do not fix Kep a priori but we leave it as a free parameter which has to be tuned in order to fit the observations, and in particular the synchrotron emission.
Another important piece of information needed to describe the nonthermal emission due to relativistic electrons is their downstream evolution. After being accelerated at the shock, electrons are in fact advected downstream, losing energy because of the remnant adiabatic expansion and of radiative losses (mostly synchrotron, but also ICS). The standard equation describing the energy evolution from t0 to t in this case reads as 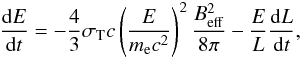 (13)where L = L(t0,t) accounts for adiabatic losses, as in Eq. (3), and
(13)where L = L(t0,t) accounts for adiabatic losses, as in Eq. (3), and 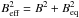 , with Beq ≃ 12 μG is the equivalent magnetic field which considers the IC losses due to CMB radiation, Galactic background light and IR emission due to local dust (see Sect. 4.4).
, with Beq ≃ 12 μG is the equivalent magnetic field which considers the IC losses due to CMB radiation, Galactic background light and IR emission due to local dust (see Sect. 4.4).
Electrons produced at time t0 with energy E0 will thus have an energy E(t) at a later time t given by (Reynolds 1998): 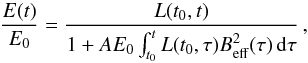 (14)where A = 1.57 × 10-3 in cgs units.
(14)where A = 1.57 × 10-3 in cgs units.
The electron spectrum at time t can therefore be computed by using number conservation, namely: fe(E)dE = fe,0(E0)dE0. The spectra of accelerated protons and electrons integrated over the downstream volume, at the present age of the remnant, are finally showed in Fig. 4 and in particular the electron spectrum can be described as follows.
For p ≲ proll ≃ 200 GeV/c, where proll is the roll-over momentum, i.e. the momentum for which the radiative loss time becomes comparable with the SNR age, synchrotron losses are negligible and so electron and proton spectra are parallel and ∝ p-4.2. Between proll and pcut ≃ 20 TeV/c, i.e. the momentum for which the loss rate exceeds the acceleration one, the electron spectrum is instead dominated by radiative losses, and therefore goes as ~p-5.2.
It is interesting to notice that the steepening due to synchrotron losses spans more than one order of magnitude in momentum below pcut, therefore it is expected to have peculiar observational counterparts both in the synchrotron and in the ICS emissions. We will discuss this topic in details in Sects. 4.3 and 4.4, respectively.
2.6. Radiative processes
In order to fit the emission observed from Tycho, we consider the following processes: 1) synchrotron emission of relativistic electrons; 2) thermal and nonthermal electron bremsstrahlung; 3) ICS of electrons on different microwave, IR and optical photons; 4) photons due to the decay of neutral pions produced in hadronic collisions. The synchrotron emission produced by accelerated electrons in the local amplified magnetic field (Eq. (11)) is carried out by using the exact synchrotron kernel (Rybicki & Lightman 1985).
The bremsstrahlung emission consists of a component due to thermal electrons, whose temperature is calculated as in Sect. 2.5, plus a nonthermal component produced by the accelerated ones. The total spectrum is the sum of both electron-nucleus and electron-electron bremsstrahlung: the latter process is however important at the highest energies and negligible at lower ones. For the e − e and the e − n bremsstrahlung, we adopt the differential cross sections provided by Haug (1998) and by Haug (1997), respectively.
Electrons contribute to the gamma-ray emission through ICS on local photons. We consider here the CMB radiation, the IR dust emission and the Galactic IR + optical background as a function of the distance from the Galactic center (Porter & Strong 2005). The flux and spectrum of ICS photons is calculated by using the exact kernel for ICS, with also the full Klein-Nishina regime accounted for.
Finally, flux and spectrum of the gamma rays produced by π0 decay are calculated following the analytical approximations by Kelner et al. (2006).
3. Modeling Tycho
In this section and in the next we apply the whole apparatus outlined above to explain Tycho’s properties, along with its multiwavelength spectrum and morphology.
Our model actually has very few free parameters other than the well-constrained ones related to a type Ia SN explosion: the number density of the upstream medium, n0 = ρ0/mp, the injection efficiency ξinj and the electron to proton normalization, Kep. The values of n0 and ξinj are simultaneously chosen to fit the gamma-ray emission detected by Fermi-LAT and VERITAS, in such a way that n0 also allows us to reproduce the inferred position and velocity of the SNR forward shock. Eventually, we may also regard the choice of χesc = 0.1 and the assumption of a constant magnetic field equal to B1 upstream as a heuristic way to account for the maximum hadron energy and, in turn, for the highest energy photons detected by VERITAS (see the discussion at the end of Sect. 2.3).
The best fitting is obtained by adopting n0 = 0.3 cm-3 and ξinj = 3.7. The chosen value for the upstream density is compatible with the upper limits existing in the literature: Cassam-Chenaï et al. (2007) derived n0 < 0.6 cm-3 from the absence of thermal emission from the shocked ejecta in the Chandra X-ray data, while a similar result, n0 < 0.4 cm-3, was obtained by Völk et al. (2008) using the upper limits on the gamma-ray emission measured by HEGRA and Whipple.
The value of n0 can also be checked indirectly by comparing the current estimates of the remnant’s distance and of the shock velocity with the same quantities as computed according to the evolution model explained in Sect. 2. Because Tycho is the remnant produced by a type Ia SN, we can safely fix the explosion energy in ESN = 1051 erg and the ejecta mass in about one solar mass. Therefore, once the density of the interstellar medium has also been fixed, all other quantities related to the SNR evolution are unequivocally determined.
Our estimate for the distance can be worked out by comparing the final radius of the FS with the observed size of the remnant: using n0 = 0.3 cm-3 we get d = 3.3 kpc. In the literature different techniques have been adopted to provide an estimate of such a distance, always returning a value ranging between 2 and 5 kpc (see Hayato et al. 2010, for a review). Kinematic methods give a distance of 2.5−3 kpc (Tian & Leahy 2011). It is worth noticing that kinematic estimates are affected by the fact that Tycho is located in the Perseus arm of the outer Galaxy, which is influenced by the spiral shock that causes a velocity reversal. Other method tends to prefer higher distances. In particular using the detection of echo light, Krause et al. (2008) determine a distance of 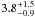 kpc. Combining the observed ejecta velocities with the ejecta proper-motion measurements by Chandra, Hayato et al. (2010) have derived a distance of 4 ± 1 kpc. Finally Völk et al. (2008) suggested a lower limit of 3.3 kpc by modeling the existing gamma-ray measurements. In summary our result of 3.3 kpc seems to be consistent with all the existing estimates.
kpc. Combining the observed ejecta velocities with the ejecta proper-motion measurements by Chandra, Hayato et al. (2010) have derived a distance of 4 ± 1 kpc. Finally Völk et al. (2008) suggested a lower limit of 3.3 kpc by modeling the existing gamma-ray measurements. In summary our result of 3.3 kpc seems to be consistent with all the existing estimates.
The shock speed that we found at the current age of the remnant is Vsh = 4990 km s-1. Measuring the proper motion of X-ray rim observed with the ROSAT satellite, Hughes (2010) derived Vsh = 4600 ± 400(d/2.3 kpc) km s-1, in perfect agreement with our findings. Similar results have been obtained by measuring the proper motion in the radio frequencies (Reynoso et al. 1997). Another independent technique sometimes used to infer the shock speed is to measure of the optical Hα emission. In fact, the line width of the so-called broad Hα emission is related to the temperature of the shocked plasma, which is in turn related to the shock speed (Chevalier et al. 1980). By adopting this technique Smith et al. (1991) derived shock velocities in the range 1500–2800 km s-1, about a factor 2–3 lower than our estimate. Nevertheless, we have to notice that the shock speed inferred from the Hα line width is systematically lower than the ones provided by other methods in basically all the SNRs considered. This discrepancy probably come from the downstream temperature being calculated using a regular hydrodynamical shock, without accounting for the possible presence of accelerated particles (see e.g. Helder at al. 2009) and/or the dynamical role of the neutral component.
Finally, we fix the electron-to-proton ratio from the fit of the synchrotron emission. Very interestingly, a unique value Kep = 1.6 × 10-3 allows us to fit both the X-ray data from Suzaku and the radio emission from several experiments (Reynolds & Ellison 1992). Our value of Kep is only a factor a few lower than the ratio measured at Earth in the diffuse spectrum of Galactic CRs, and such a discrepancy might be accounted for by remembering that the latter value is the result of all the SNR evolution (in principle Kep is a function of time) and it is also averaged over the contributions of different kinds of sources (e.g. type I/II SNRs and maybe pulsars as well). At the present time there are some hints about how electron injection into DSA may occur (Amano & Hoshino 2010; Riquelme & Spitkovsky 2011; Morlino 2009), but a complete theory coupled to NLDSA and therefore to a self-consistent calculation of the nonthermal emission from an SNR during its lifetime is still lacking. This is actually why two of our free parameters are somewhat related to the need to model the injection of particles into the acceleration mechanism.
With both model and environmental parameters fixed, we find that the Tycho’s FS is converting about 6% of its bulk pressure into CRs (Fig. 2), which in turn implies a downstream magnetic field B2 ≃ 300 μG. Our shock dynamics is only mildly modified by the presence of accelerated particles: apart from magnetic field amplification, all of the signature typical of NLDSA, like the formation of an upstream precursor where the incoming fluid is slowed down (and in turn the concavity in the spectrum because CRs with different momenta probe different regions of the precursor) are not very marked. For instance, the total and the subshock compression ratios turn out to be Rtot = 1/U2 ≃ 4.2 and Rsub = U1/U2 ≃ 3.9, respectively. This result also justifies a posteriori the treatment of the SNR evolution as governed by the gas pressure only (Sect. 2.1) rather than by the whole gas + CRs fluid.
We now compare the theoretical prediction for the ratio between the positions of CD and FS with the value inferred from the X-ray observations by Warren et al. (2005), which returned RCD/Rsh = 0.93 ± 2%. In our model we find RCD/Rsh = 0.87. This value has, however, to be taken with a grain of salt, sinceit may be enhanced by Rayleigh-Taylor instabilities at the CD. For instance, purely gaseous 1D hydrodynamical simulations predict a significantly lower value for this ratio, and namely RCD/Rsh = 0.77 (Wang & Chevalier 2001). In the same work the authors also performed a 2D simulation and showed that the Rayleigh-Taylor instability at the CD allows fingers of ejecta to protrude well beyond the average CD radius, also inferring the maximum extent of these fingers in about the 87% of the FS radius. Following this line of thought, we can estimate in about a 5% the boost in the CD/FS position ratio due to instabilities operating at the CD. When we multiply our prediction by 1.05, we get a CD/FS ratio of about 0.91, consistently with the value estimated by Warren et al. (2005).
Some authors (e.g. Ellison et al. 2005) have proposed that young SNRs can accelerate CRs efficiently also at the reverse shock (RS). This idea is supported by the fact that the RS moves with respect to the unshocked ejecta with a velocity comparable to that of the FS. The RS speed can in fact be estimated from the usual analytical model by Truelove & Mc Kee (1999), and for Tycho it turns out to be ~0.86 Vsh. On the other hand, an efficient DSA requires also a sizable magnetic field, say of a few μG, to efficiently scatter particles. The simple dilution by flux-freezing of the typical magnetic field on the surface of the progenitor would imply ~nG or lower magnetic field, therefore a very efficient magnetic field amplification at the RS would be required to make DSA work. On the other hand, Warren et al. (2005) show that the inferred distance between the CD and RS is compatible with hydrodynamical model excluding efficient CR acceleration at the RS.
Anyway, in case of non-negligible acceleration at the RS, we would expect an enhancement of the synchrotron emission only from the position of the RS towards the inside of the remnant. According to the measurement of Warren et al. (2005) the RS is located at 0.7 Rsh. From Fig. 7 we do not notice any clear excess in this region with respect to our prediction. We discuss in Sect. 4.1 how also our analysis is able to account for the observed radio profile without requiring acceleration of electrons at the RS.
4. Multiwavelength spectrum
In Fig. 6 we show our best fitting of the photon spectrum produced by the superposition of all the radiative processes outlined above, comparing it with the existing data. The overall agreement is quite good, therefore we want to analyze now in greater detail the emission in each single band.
 |
Fig. 6 Spatially integrated spectral energy distribution of Tycho. The curves show synchrotron emission, thermal electron bremsstrahlung and pion decay as calculated within our model (see text for details). The experimental data are, respectively: radio from Reynolds & Ellison (1992); X-rays from Suzaku (courtesy of Toru Tamagawa), GeV gamma-rays from Fermi-LAT (Giordano et al. 2012) and TeV gamma-rays from VERITAS (Acciari et al. 2011). Both Fermi-LAT and VERITAS data include only statistical error at 1σ. |
4.1. Radio emission
As depicted in Fig. 6, the total radio emission is nicely accounted for by our model, which returns a photon spectral index of 0.606 in the considered energy range (10 to 1500 MHz). Nevertheless, as already noticed by Reynolds & Ellison (1992), Tycho’s radio emission shows evidence for a curvature in the spectrum, which turns out to be slightly steeper (flatter) than E-0.6 below (above) 100 MHz. In fact, Kothes et al. (2006) find a spectral index α = 0.65 for the radio spectrum fitted to all flux densities and α = 0.61 in the range 408 to 1420 MHz. Reynolds & Ellison (1992) ascribed this effect to the curvature of the electron spectrum due to nonlinear effects induced by the CR precursor and stressed that, in the energy range involved in the radio emission, electron and proton energy spectra are not exactly parallel because protons are non relativistic and DSA is momentum dependent.
In our model we did not find any steepening in the lowest energy region of the electron spectrum, and the reason is the following. The emission in the 1–100 MHz band, where the curvature is observed, is produced by electrons with energy close to the injection energy. The typical synchrotron frequency is in fact 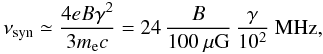 (15)from which, taking the typical injection Lorentz factor γe,inj ~ 10−100 and a downstream magnetic field strength of ~100−300 μG, we obtain νsyn ~ 1−100 MHz. The shape of the electron spectrum in this energy range is therefore quite uncertain, and our simple parametrization of particle injection via thermal leakage may indeed be too simplistic. A comparison between the thermal leakage model and more refined Monte Carlo approaches to particle injection, which is able to retain the smooth transition in the suprathermal energy range, seems however to confirm that a proper account for particle injection should quite naturally predict a spectral steepening in the 10–100 MeV energy range (see Fig. 1 of Caprioli et al. 2010c).
(15)from which, taking the typical injection Lorentz factor γe,inj ~ 10−100 and a downstream magnetic field strength of ~100−300 μG, we obtain νsyn ~ 1−100 MHz. The shape of the electron spectrum in this energy range is therefore quite uncertain, and our simple parametrization of particle injection via thermal leakage may indeed be too simplistic. A comparison between the thermal leakage model and more refined Monte Carlo approaches to particle injection, which is able to retain the smooth transition in the suprathermal energy range, seems however to confirm that a proper account for particle injection should quite naturally predict a spectral steepening in the 10–100 MeV energy range (see Fig. 1 of Caprioli et al. 2010c).
Therefore, the detection of a curvature in the low-energy radio emission from young SNRs (Reynolds & Ellison 1992) may not be necessary related to the presence of a CR precursor in the upstream, but rather be a crucial tool for probing electron injection. It is also worth stressing that this possibility is given by magnetic field being strongly amplified: for a standard interstellar field, the same radio emission would come from higher energy electrons, and more precisely in the GeV range.
Besides the volume-integrated emission, another precious information can be inferred from the remnant morphology: the radial profile of both radio and X-ray emissions provides strong evidence that the magnetic field inside the SNR is considerably amplified. In order to compare the observed radial profiles, we need to compute the emission projected along the line of sight. As already noticed, Tycho is clearly shell-like both in radio and X-ray bands: even if the northeastern region shows an enhancement of the emission, especially in the radio band, the spherical symmetry can be indeed considered a reasonable approximation. Under this assumption the local emissivity is a function of the radius alone, and the projected emission is thus simply due to the integration along the line of sight l: ![\begin{equation} \label{eq:proj} j_{\rm p} (\nu, \rho)= 2 \int_{\max\left[0,\sqrt{r_{\rm CD}^2-\rho^2}\right]}^{\sqrt{r_{\rm sh} ^2-\rho^2}} j\left(\nu, r=\sqrt{\rho^2+l^2} \right) {\rm d}l. \end{equation}](/articles/aa/full_html/2012/02/aa17855-11/aa17855-11-eq161.png) (16)The integration limits take into account that the emission is expected to come only from the shocked ISM located between the CD and the FS.
(16)The integration limits take into account that the emission is expected to come only from the shocked ISM located between the CD and the FS.
To be compared with the actual data, the projected emission has to be convolved with the instrumental point spread function, which we assume to be Gaussian. We use the radio map in Fig. 1, which was obtained with the VLA on January 2007 at the frequency of 1.5 GHz, (data from the NRAO/VLA Archive), and in Fig. 7 we compare our results with these data. The step line shows the measured surface brightness obtained by integrating the emission along the azimuthal angle, between 0 and 2π. Fig. 7 shows indeed a good overall agreement between the data and our prediction, after the convolution with the instrumental point spread function, which is equal to 15 arcsec. Nevertheless some little discrepancies can be noticed. The most evident one is that in the innermost region (r/Rsh ≲ 0.3), the theoretical prediction overestimates the observed brightness by about 20%. A plausible explanation of this difference may reside in a slight deviation from the spherical symmetry, which is somehow expected just because the northeastern region is brighter than the rest of the remnant.
Another subtle but interesting difference is that the emission peaks slightly more inwards than in our model; as a consequence, the emission detected in the region 0.6 ≲ r/Rsh ≲ 0.8 is also found to be a bit larger than the theoretical prediction. This difference might have different explanations. The most obvious, and already mentioned, is the possible deviation from the spherical symmetry. Another possibility is given by placing the CD in a different position: if one assumed the CD to be located closer to the center (i.e. if one took the CD/FS ratio to be a few percent lower), the theoretical prediction would nicely fit the data. However, we cannot forget that this explanation would be at odds with the findings of Warren et al. (2005), who estimated the position of the CD to be more towards the forward shock, namely around 0.93 Rsh.
A final comment on the radio profile concerns the effects of the nonlinear Landau damping in the determination of the magnetic field relevant for the synchrotron emission. If we neglected the damping, the magnetic field strength in the downstream (see Fig. 5) would lead to a total radio flux larger by a factor 50% or more with respect to the data, even if the radial radio profile would retain a rather similar shape.
4.2. X-ray emission
 |
Fig. 7 Surface brightness of the radio emission at 1.5 GHz as a function of the radius (data as in Fig. 1). The thin solid line represents the projected radial profile computed from our model using Eq. (16), while the thick solid line corresponds to the same profile convoluted with a Gaussian with a PSF of 15 arcsec. |
 |
Fig. 8 X-ray emission due to synchrotron (dashed line) and to synchrotron plus thermal bremsstrahlung (solid line). Data from the Suzaku telescope (courtesy of Toru Tamagawa). |
As it is clear from Fig. 6, the synchrotron emission spans from the radio to the X-ray band, where it sums up with the emission due to thermal bremsstrahlung. The best fit to the X-ray continuum observed by Suzaku data is illustrated in greater detail in Fig. 8, where both synchrotron emission and thermal bremsstrahlung are considered.
The electron temperature in the downstream, calculated only taking the heating due to Coulomb collisions with protons into account (Fig. 3), results in a bremsstrahlung emission peaked around 1.2 keV, which, at its maximum, contributes only about 6% of the total X-ray continuum emission only, in agreement with the findings of Cassam-Chenaï et al. (2007). In the same energy range, there is however a non-negligible contribution from several emission lines, which increases their intensity moving inwards from the FS, where the X-ray emission is mainly nonthermal (Warren et al. 2005). A detailed model of the line forest is, however, beyond the main goal of this paper.
 |
Fig. 9 Projected X-ray emission at 1 keV. The Chandra data points are from (Cassam-Chenaï et al. 2007, see their Fig. 15). The solid line shows the projected radial profile of synchrotron emission convolved with the Chandra point spread function (assumed to be 0.5 arcsec). |
The projected X-ray emission profile, computed at 1 keV, is shown in Fig. 9, where it is compared with the Chandra data in the region that Cassam-Chenaï et al. (2007) call region W. The resulting radial profile, already convoluted with the Chandra PSF of about 0.5 arcsec, shows a remarkable agreement with the data. As widely stated above, the sharp decrease in the emission behind the FS is due to the rapid synchrotron losses of the electrons in a magnetic field as large as ~300 μG. In Fig. 9 we also plot the radial radio profile computed without magnetic damping; since the typical damping length-scale is ~3 pc, it is clear that the nonlinear Landau damping cannot contribute to the determination of the filament thickness.
It is worth stressing that the actual amplitude of the magnetic field we adopt is not determined to fit the X-ray rim profile, but it is rather a secondary output, due to our modeling of the streaming instability, of our tuning the injection efficiency and the ISM density in order to fit the observed gamma-ray emission (see the discussion in Sect. 3). We in fact checked a posteriori whether the corresponding profile of the synchrotron emission (which, in shape, is also independent on Kep), were able to account for the thickness of the X-ray rims and for the radio profile as well.
4.3. Radio to X-ray fitting as a hint of magnetic field amplification
Another very interesting property of the synchrotron emission is that a simultaneous fit of both radio and X-ray data may provide a downstream magnetic field estimate independent of the one deduced by the rims’ thickness. In fact, assuming Bohm diffusion, the position of the cut-off frequency observed in the X-ray band turns out to be independent of the magnetic field strength, and actually depends on the shock velocity alone.
On the other hand, if the magnetic field is strong enough to make synchrotron losses dominate on ICS and adiabatic ones, the total X-ray flux in the cut-off region only depends on the electron density, in turn fixing the value of Kep independently of the magnetic field strength. Moreover, radio data suggest the slope of the electron spectrum to be equal to 2.2 at low energies, namely below Eroll ≃ 200 GeV. Above this energy the spectral slope in fact has to be 3.2 up to the cut-off determined by setting the acceleration time equal to the loss time, as discussed in Sect. 2.5.
 |
Fig. 10 Synchrotron emission calculated by assuming constant downstream magnetic field equal to 100 (dotted line), 200 (dashed line), and 300 μG (solid line). The normalization of the electron spectrum is taken to be Kep = 1.6 × 10-3 for all the curves. |
In Fig. 10 we plot the synchrotron emission from the downstream, assuming a given magnetic field at the shock and neglecting all the effects induced by damping and adiabatic expansion. The three curves correspond to different values of B2 = 100,200 and 300 μG, while the normalization factor Kep is chosen by fitting the X-ray cut-off, and it is therefore the same for all curves. As it is clear from the figure, in order to fit the radio data the magnetic field at the shock has to be ≳ 200 μG, even in the most optimistic hypothesis of absence of any damping mechanism acting in the downstream.
As a matter of fact, synchrotron emission alone can provide evidence of ongoing magnetic field amplification, independently of any other evidence related to X-ray rims’ thickness or emission variability. Such an analysis is in principle viable for any SNR detected in the nonthermal X-rays for which it is also possible to infer the spectral slope of the electron spectrum from the radio data, only requiring radio and X-ray emissions to come from the same volume and therefore from the same population of electrons.
4.4. Gamma-ray emission
The most intriguing aspect of Tycho’s broadband spectrum is its gamma-ray emission, which has been detected before in the TeV band by VERITAS (Acciari et al. 2011) and then in the GeV band by Fermi-LAT, too (Giordano et al. 2012). Gamma-ray emission from SNRs has been considered for long time a possible evidence of hadron acceleration in this class of objects (Drury et al. 1994), even if there are two distinct physical mechanisms that may be responsible for such an emission; in the so-called hadronic scenario, the gamma-rays are produced by the decay of neutral pions produced in nuclear collisions between CRs and the background gas, while in the so-called leptonic scenario the emission is due to ICS or relativistic bremsstrahlung of relativistic electrons.
 |
Fig. 11 Gamma-ray emission observed by Fermi-LAT and by VERITAS compared with spectral energy distribution produced by pion decay (dot-dashed line), relativistic bremsstrahlung (dot-dot-dashed) and ICS computed for three different photon fields: CMB (dashed), Galactic background (dotted) and IR photons produced by local warm dust (solid). The thick solid line is the sum of all the contributions. Both Fermi-LAT and VERITAS data points include only statistical errors at 1σ. For VERITAS data the systematic error is found to be ~30% (Acciari et al. 2011), while for Fermi-LAT the systematic uncertainties are comparable to or even larger than the statistical error especially for the lowest energy bins due to difficulties in evaluating the galactic background (see Fig. 3 in Giordano et al. 2012, and the related discussion). |
We show here, with unprecedented clarity for an SNR, that the gamma-ray emission detected from Tycho cannot have a leptonic origin, but has to come from accelerated hadrons, instead. This fact, along with the VERITAS detection of ~10 TeV photons and the lack of evidence of a cut-off in the spectrum, implies that hadrons have to be accelerated up to energies as high as a few hundred TeV.
In particular, the proton spectrum we obtain shows a cut-off around pmax = 470 TeV/c (see Fig. 4). In this respect, Tycho could be considered as a half-PeVatron at least, because there is no evidence of a cut-off in VERITAS data. The age-old problem of detecting SNRs emitting photons with energies over a few hundred TeV (i.e., responsible for the acceleration of particles up to the knee observed in the spectrum of diffuse Galactic CRs) may therefore be only a matter of time. Of course it may also be that not all the SNRs are actually PeVatrons, or even that it is quite unlikely to observe an SNR in the brief stage of its life when it may be acting like a PeVatron (Caprioli et al. 2009b, 2010a).
This very important result relies on the spectral slope in the sub-GeV to multi-TeV range being consistent, within measurement errors, with a single power law ∝ E-2.1 − E-2.2. Such a power law is steeper than the test-particle prediction of DSA, and more importantly, it is significantly different from what is expected in the framework of standard NLDSA theories, which predict concave spectra flatter than E-2 at the highest energies (see e.g. Drury 1983; Blandford & Eichler 1987; Jones & Ellison 1991; Malkov & Drury 2001, for some reviews).
A key role in our calculations is in fact played by having included in the NLDSA also magnetic field amplification and, in particular, by having assumed the relevant Alfvén velocity as the one calculated in the amplified magnetic field. That a small Alfvénic Mach number may imply quite steep spectra had already been put forward by Bell (1978), but only by coupling this with a very efficient streaming instability allows NLDSA theories to predict a proton spectrum steeper than E-2 over the full energy range (Zirakasvhili & Ptuskin 2008; Caprioli et al. 2009a), with the possibility of changing the spectral slope by tuning the injection efficiency (Caprioli 2011b).
In this respect, fixing a value for ξinj regulates both the slope and the normalization of the proton spectrum and, in turn, of the gamma-ray emission. In calculating the photon spectrum produced by π0 decay (Fig. 11) we also accounted for the presence of He nuclei in the target medium and for the likely presence of accelerated particles heavier than protons, which are expected to boost the total emission by a factor ~1.4 and ~1.5, respectively (Mori 2009; Caprioli et al. 2011).
There are two main reasons why the observed gamma rays cannot be of leptonic origin: 1) the intensities of both ICS and relativistic bremsstrahlung emission are too low; and 2) the expected shape of the leptonic emission is radically different from the one observed.
The former point is illustrated in Fig. 11, where we compare gamma emissions due to bremsstrahlung, ICS and pion decay. The contribution relativistic bremsstrahlung, however, is negligible at all the wavelengths of interest. The ICS was computed for three different target photon families: CMB radiation, Galactic background radiation and IR due to local dust emission. The ICS on the CMB radiation provides a contribution a factor 20–30 smaller than the one by pion decay, while the ICS on the IR + optical Galactic background at Tycho’s position is even smaller. For the Galactic background we used the estimate provided by Porter & Strong (2005) for a distance from the Galactic center of 12 kpc and inside the Galactic plane, which is a good approximation for Tycho’s position (~10 kpc away from the Galactic center).
For the ICS we have also included, for the first time as far as we know, a third contribution due to local dust emission. In fact IR radiation from Tycho’s direction has been detected by different satellites in the wavelength band ranging from 10 μm to 160 μm (Ishihara et al. 2001). This emission seems to be due to two distinct populations of dust, one which we refer to as warm, with a temperature T ~ 100 K and one we refer to as cold, with T ~ 20 K. According to Ishihara et al. (2001), the warmer component should originate in ISM dust collisionally heated by the hotter plasma downstream of the shock. In fact, the emission in the mid-IR band shows a shell-like structure that recalls both synchrotron and Hα emissions. On the other hand, the far-IR emission (140–160 μm) is dominated by a rather cold dust emission correlating with the position of the CO cloud, which has been showed not to be in physical contact with the SNR itself. We therefore consider only the photon background due to the warm dust. To compute the local energy density, we assume that IR photons are emitted uniformly from the shocked ISM between the CD and the FS. Following Ishihara et al. (2001), we fix the temperature of warm dust to be 100 K by fitting the observed IR data, and we get a local energy density of εwarm = 3.1 eV/cm3. It is important to notice that the ICS on this mid-IR radiation dominates all other photon backgrounds. Furthermore we notice that if one also assumes the far-IR emission (due to cold dust) to originate in a region close to the remnant, the ICS on these latter photons is negligible with respect to the ICS associated with warm dust photons. Summing up all the possible photon backgrounds, the resulting total ICS emission contributes not more than ~20% of the total gamma emission around 0.1 TeV, but it is negligible for lower and higher energies, as clearly shown in Fig. 11.
Explaining the gamma emission using only the ICS on the CMB photons and a higher value of Kep is inconsistent with the very efficient magnetic field amplification inferred. A Kep lower by a factor 20–30 would in fact require a downstream magnetic field a factor 5–6 lower in order to keep the synchrotron emission fixed, in turn raising issues not only with the radial profile of the synchrotron emission (see also Sect. 4.2), but also with the relevant effects induced by the high Alfvén velocity discussed in Sect. 2.3.
The second solid argument against a leptonic origin for the detected gamma-ray emission is given by the actual slope of the photon spectrum. After excludig the underdominant relativistic bremsstrahlung and ICS on the CMB radiation and Galactic background, we are left with ICS on the IR background due to local dust as the only viable candidate. However, as predicted by standard ICS theory and as shown in Fig. 11, the expected photon spectrum below the cut-off is typically flatter than parent electrons’ one and, more precisely, is ∝ ν-1.6 for an electron spectrum ∝ E-2.2, clearly at odds with Fermi-LAT data in the GeV range.
Another point worth noticing is that the ICS on the CMB radiation is sensitive to the steepening of the total electron spectrum above ~100 GeV (Fig. 4) due to the synchrotron losses particles undergo while being advected downstream, while for the ICS on the IR+optical background the onset of the Klein-Nishina regime (above Ee ≈ 7 TeV for photons of 1 eV) does not allow us to probe significantly the steep region of the electron spectrum.
In other words, the ICS on the CMB radiation is too low and cannot be boosted by invoking a higher electron density, while ICS on IR and/or optical background, which might as well be locally enhanced with respect to the mean Galactic value, cannot provide a spectral slope that agreee with both Fermi-LAT and VERITAS data.
We are therefore forced to conclude that the present multiwavelength analysis of Tycho’s emission represents the best evidence that SNRs accelerate protons, at least up to energies of about 500 TeV. The proton’s acceleration efficiency is found to be 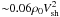 , corresponding to converting in CRs a fraction of about 12% of the kinetic energy density
, corresponding to converting in CRs a fraction of about 12% of the kinetic energy density 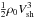 . As estimated for instance in Sect. 3 of the review by Hillas (2005), such a value is consistent with the hypothesis that SNRs are the sources of Galactic CRs, provided that the residence time in the Milky Way scales with ~E−1/3.
. As estimated for instance in Sect. 3 of the review by Hillas (2005), such a value is consistent with the hypothesis that SNRs are the sources of Galactic CRs, provided that the residence time in the Milky Way scales with ~E−1/3.
It is important to remember that the actual CRs produced by a single SNR is given by the convolution over time of different contributions with nontrivial spectra, namely the flux of particle escaping the remnant from upstream during the Sedov-Taylor stages and the bulk of particles released in the ISM at the SNR’s death (Caprioli et al. 2009b, 2010a). In this respect, the instantaneous spectrum of accelerated particles in Tycho, which is inferred to be as steep as ∝ E-2.2, provides a hint of that SNRs can indeed produce rather steep CR spectra as required to account for the ∝ E-2.7 diffuse spectrum of Galactic CRs (Caprioli 2011b).
5. Discussion and conclusions
Thanks to the large amount of data available at different wavelengths, Tycho’s SNR is one of the best object for studying the connection between CRs and SNRs. Using the observed nonthermal spectrum, and in particular the recent detection of GeV emission by Fermi-LAT, together with the TeV spectrum detected by VERITAS, we can infer that protons are accelerated up to energies as high as ~500 TeV at Tycho’s FS, and that the total energy converted into CRs can be estimated to be about 12% of the FS bulk kinetic energy.
To reach this conclusion we investigated particle acceleration at the forward shock using a state-of-the-art, semi-analytical NLDSA model including the dynamical reaction of the accelerated particles, the generation of magnetic fields as due to streaming instability excited by CRs, the dynamical reaction of these self-generated fields on the plasma, and also the modification of the speed of the scattering centers (Alfvénic drift) induced by the magnetic field amplification (Caprioli et al. 2009a, 2010a). The last effect is crucial because it produces a softening of the particle spectrum with respect to the standard prediction ∝ E-2, which allows us to fit both the radio and the gamma photon spectra. The stationary version of NLDSA we used is coupled to the dynamical evolution of the remnant according to the analytical prescription by Truelove & Mc Kee (1999). This allows us to account for information sensitive to the time evolution, such as the radio to X-ray connection, as illustrated in Sect. 4.3.
We would like to stress that our fit to the observed nonthermal spectrum and to the SNR morphology only depends on a few parameters. As for modeling particle acceleration, we are forced to introduce some parameters describing the not-yet-understood processes related to the microphysics of the magnetic fields involved, such as the injection of hadrons and electrons (two parameters, ξinj and Kep) and the scattering of highest energy particles (χesc, plus a heuristic choice of a constant magnetic field upstream, B1).
Because Tycho is the remnant of a type Ia SN explosion, the only free parameter related to the SNR environment is actually the density of the circumstellar medium where the remnant expands (see Sect. 3). We adopt a number density of n0 = 0.3 cm-3, which is consistent with all of the observational constraints coming from thermal and nonthermal emission and which also provides the position and velocity of the FS in decent agreement with the estimates provided by several authors who adopt different techniques.
Our findings show that the decay of neutral pions produced in hadronic collision between accelerated ions and gas nuclei is the dominant process in the gamma-ray band. In particular, we predict a slope for accelerated protons ∝ E-2.2, which accounts for Fermi-LAT and VERITAS detections well within the experimental errors. The ICS of relativistic electrons cannot explain the observed gamma-ray emission, as can be seen from Fig. 11 and as explained in Sect. 4.4.
The reasons supporting this conclusion are the following. First, the strong magnetic field produced by the CR-induced streaming instability forces the number density of relativistic electrons to be too low (the electron to proton ratio is Kep = 1.6 × 10-3) to explain the gamma-ray emission as due to ICS on the ambient photons. A high Kep would in fact lead to overestimating the synchrotron emission, both in the radio and in the X-ray bands.
Second, even if we arbitrarily reduced the magnetic field strength, enhancing at the same time the electron number density in order to fit the TeV gamma-rays with ICS emission, we could not account for the GeV gamma-rays because both the spectral slope and the flux would be incompatible with the recent Fermi-LAT observations.
Also the other competing leptonic process that may show the correct spectral slope throughout the whole gamma-ray spectrum, namely the nonthermal bremsstrahlung, has to be ruled out, in that it provides a flux that is two orders of magnitudes lower than the Fermi-LAT detection, and cannot be arbitrarily enhanced without overpredicting both the TeV and the X-ray emission.
In this work we also showed, for the first time as far as we know, that the main contribution to the ICS is due to the IR photons produced by circumstellar dust heated up through collisions with the shocked plasma, which dominates the CMB and Galactic photon background. This contribution, which is generally neglected in multiwavelength studies, may also be relevant for other SNRs, especially those produced by type Ia SNe that expand in the cold ISM.
As outlined above, the impossibility of fitting the gamma-ray spectrum with leptonic processes is tightly connected with the fact that much observational evidence points toward a very efficient magnetic field amplification, as we discuss in the following.
In our model CR-induced streaming instability amplifies the magnetic field upstream of the shock from the unperturbed Galactic value of ~5 μG up to ~90 μG, which becomes ~300 μG immediately downstream because of compression at the shock. Observationally speaking, such a large magnetic field has two main consequences: 1) it produces narrow X-ray filaments because electrons undergo severe synchrotron losses; and 2) it determines the roll-over frequency of the synchrotron spectrum to be ~4 eV/ħ (see Sect. 4.3). The former effect has been extensively investigated in the literature and it is indeed recovered in our study of the X-ray emission profile (see Fig. 9).
Also the latter effect represents independent evidence that the magnetic field has to be amplified up to a few hundred μG. As we show in Sect. 4.3, when the radio data are good enough to infer the electron spectral index, the value of νroll, i.e. the frequency emitted by electrons whose loss time equals the age of the remnant, is uniquely determined by a simultaneous fit of both radio and X-ray data as due to synchrotron emission. In fact, when synchrotron losses are dominant, νroll is a function of the average magnetic field downstream ⟨ B ⟩ only, and from Fig. 10 we can see that we have νroll ~ 4 eV/ħ for Tycho, which in turn implies ⟨ B ⟩ ≃ 200 μG.
The narrowness of X-ray filaments might also be produced by rapid damping of magnetic field downstream of the shock rather than by synchrotron losses (see e.g. Pohl et al. 2010). In the case of Tycho we can exclude this possibility simply by looking at the synchrotron emission: if the field were damped below 200 μG on a length-scale comparable to the X-ray rim width, we would in fact fail to fit the combination of radio plus X-ray emission, and the radio emission profile as well. This conclusion of course does not imply that any damping is not to be at work in the downstream, but only suggests that no damping mechanisms can determine the structure of the observed X-ray filaments.
Similar structures in Tycho’s interior have recently been detected also in the shape of radial stripes by Eriksen et al. (2011). These stripes show a surprisingly ordered pattern and have been interpreted by the authors as evidence of magnetic fields of a few hundred μG, compatible with acceleration of particles up to the knee. Nevertheless, we would like to stress that a large magnetic field is necessary but not sufficient to claim protons are actually accelerated up to consistently large energies. We showed that NLDSA at the FS is able to account for protons of about 500 TeV, i.e. with an energy only a factor a few lower than the knee’s in the CR spectrum. Higher energies might in principle be achieved at earlier or later times in Tycho, or even in peculiar regions of the FS with a favorable magnetic field topology. In any case, we cannot exclude either the possibility that type Ia SNRs, like Tycho, might not be responsible for the knee observed in the diffuse spectrum of Galactic CRs, or the possibility that we are somehow underestimating Emax, since VERITAS data do not provide evidence of a high-energy cut-off.
Some authors have proposed that CR acceleration may also occur at the RS of young SNRs (see e.g. Ellison et al. 2005; Zirakashvili & Aharonian 2010; Zirakasvhili & Ptuskin 2012), even if it is unlikely to have a very large magnetic field in the ejecta RS propagate into. In the present work we therefore investigated the radial profile of the radio emission, concluding that there is no evidence of acceleration at the RS. In Sect. 4.1 we showed that it is possible to account for the observed radio profile including only electrons accelerated at the FS.
In this work we tried to use all of the available observations, interpreting them in light of a semi-analytical approach to NLDSA to build up a consistent model of particle acceleration at Tycho’s FS. However, we are aware that we neglected the information coming from the detection of Balmer lines, which also point towards efficient particle acceleration (Lee et al. 2010). The reason is that, at the moment, a reliable NLDSA theory which take into accoinunt the presence of neutrals is still lacking. When shocks propagate into a partially ionized circumstellar medium, as might be the case for Tycho, the neutral fraction cannot be neglected because it is coupled to the ions via charge-exchange and ionization processes. As a consequence, shock dynamics and, in turn, particle acceleration are likely sensitive to this aspect of the problem. The study of these phenomena might indeed provide new insight into how particle acceleration works; nevertheless, it is unlikely for these effects to invalidate the most important findings of the present work, namely that Tycho provides us with the first clear-cut example of hadron acceleration in SNRs, up to ~500 GeV at least. This result, made possible by the present generation of gamma-ray instruments such as Fermi-LAT and VERITAS, is of prime importance in corroborating the SNR paradigm for the origin of Galactic CRs.
Acknowledgments
We would like to thank Gamil Cassam-Chenaï for useful discussions during a preliminary phase of this work and for providing us with the Chandra X-ray data for Tycho’s filaments. In a similar way, we are glad to thank Toru Tamagawa and Aya Bamba for providing us with the Suzaku X-ray spectrum. We also want to acknowledge Maite Beltran for helping us in handling the radio data. Last, but not the least, we express our gratitude to Pasquale Blasi and Elena Amato for being a constant source of support and scientific inspiration. The authors are supported through the contract ASI-INAF I/088/06/0 (grant TH-037).
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi-LAT Collaboration) 2010, ApJ, 710, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi-LAT Collaboration) 2011, ApJ, 734, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. (for the VERITAS collaboration) 2011, ApJ, 730, L20 [Google Scholar]
- Amano, T., & Hoshino, M. 2010, PhRvL, 104, 181102 [NASA ADS] [CrossRef] [Google Scholar]
- Amato, E., & Blasi, P. 2005, MNRAS, 364, L76 [NASA ADS] [Google Scholar]
- Amato, E., & Blasi, P. 2006, MNRAS, 371, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Amato, E., & Blasi, P. 2009, MNRAS, 392, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Bamba, A., Yamazaki, R., Yoshida, T., Terasawa, T., & Koyama, K. 2005, ApJ, 621, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Ballet, J. 2006, Adv. Sp. Res., 37, 1902 [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2004, MNRAS 353, 550 [Google Scholar]
- Blandford, R. D., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Blasi, P. 2010, MNRAS, 402, 2807 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Gabici, S., & Vannoni, G. 2005, MNRAS, 361, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Amato, E., & Caprioli, D. 2007, MNRAS, 375, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., Ellison, D. C., Osipov, S. M., Pavlov, G. G., & Uvarov, Y. A. 2011, ApJ, 735, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, Z. Y., Yang, J., & Lu, D. R. 2009, Chin. Astron. Astrophys., 33, 393 [Google Scholar]
- Caprioli, D. 2011a, JCAP, 5, 26 [Google Scholar]
- Caprioli, D. 2011b, PoS Proc. 25th Texas Symposium on Relativistic Astrophysics, December 6–10, Heidelberg, Germany [arXiv:1103.4798] [Google Scholar]
- Caprioli, D., Blasi, P., Amato, E., & Vietri, M. 2008, ApJ, 679, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., Blasi, P., Amato, E., & Vietri, M. 2009a, MNRAS, 395, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., Blasi, P., & Amato, E. 2009b, MNRAS, 396, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., Amato, E., & Blasi, P. 2010a, APh, 33, 160 [Google Scholar]
- Caprioli, D., Amato, E., & Blasi, P. 2010b, APh, 33, 307 [NASA ADS] [Google Scholar]
- Caprioli, D., Kang, H., Vladimirov, A. E., & Jones, T. W. 2010c, MNRAS, 407, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., Blasi, P., & Amato, E. 2011, APh, 34, 447 [Google Scholar]
- Cassam-Chenaï, G., Hughes, J. P., Ballet, J., & Decourchelle, A. 2007, ApJ, 665, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1983, ApJ, 272, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Kirshner, R. P., & Raymond, J. C. 1980, ApJ, 235, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O’C. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O’C., Aharonian, F., & Völk, H. J. 1994, A&A, 287, 959 [NASA ADS] [Google Scholar]
- Drury, L. O’C., Duffy, P., & Kirk, J. G. 1996, A&A, 309, 1002 [NASA ADS] [Google Scholar]
- Ellison, D. C., Decourchelle, A., & Ballet, J. 2005, A&A, 429, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, D. C., Patnaude, D. J., Slane, P., Blasi, P., & Gabici, S. 2007, ApJ, 661, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Patnaude, D. J., Slane, P., & Raymond, J. 2010, ApJ, 712, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, K. A., Hughes, J. P., Badenes, C., et al. 2011, ApJ, 728, 28 [Google Scholar]
- Giordano, F., Naumann-Godo, Ballet, J., et al. 2012, ApJ, 744, L2 [Google Scholar]
- Haug, E. 1997, A&A, 326, 417 [NASA ADS] [Google Scholar]
- Haug, E. 1998, SoPh, 178, 341 [Google Scholar]
- Hayato, A., Yamaguchi, H., Tamagawa, T., et al. 2010, ApJ, 725, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Helder, E. A., Vink, J., Bassa, C. G., et al. 2009, Science, 325, 5941, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Hillas, A. M. 2005, J. Phys. G, 31, 95 [Google Scholar]
- Hughes, J. P. 2000, ApJ, 545, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., Petre, R., Szymkowiak, A. E., & Holt, S. S. 2002, J. Astrophys. Astron., 23, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ishihara, D., Kaneda, H., Furuzawa, A., et al. 2010, A&A, 521, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, F. C., & Ellison, D. C. 1991, Space Sci. Rev. 58, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Petre, R., Hughes, J. P., et al. 2010, ApJ, 709, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Kothes, R., Fedotov, K., Foster, T. J., & Uyanıker, B. 2006, A&A, 457, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krause, O., Tanaka, M., Usuda, T., et al. 2008, Nature, 456, 617 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lee, J. J., Koo, B. C., & Tatematu, K. 2004, ApJ, 605, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-J., Raymond, J. C., Park, S., et al. 2010, ApJ, 715, L146 [Google Scholar]
- McKenzie, J. F., & Völk, H. J. 1982, A&A, 116, 191 [NASA ADS] [Google Scholar]
- Malkov, M. A., & Drury, L.O’C 2001, Rep. Progr. Phys., 64, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Marcowith, A., & Casse, F. 2010, A&A, 515, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mori, M. 2009, APh, 31, 341 [Google Scholar]
- Morlino, G. 2009, PRL, 103, 1102 [Google Scholar]
- Morlino, G., Amato, E., & Blasi, P. 2009, MNRAS, 392, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Morlino, G., Amato, E., Blasi, P., & Caprioli, D. 2010, MNRAS, 405, L21 [NASA ADS] [Google Scholar]
- Parizot, E., Marcowith, A., Ballet, J., & Gallant, Y. A. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohl, M., Yan, H., & Lazarian, A. 2005, ApJ, 626, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, T. A., & Strong, A. W. 2005, proc. 29th ICRC 4, 77 [Google Scholar]
- Ptuskin, V. S., & Zirakashvili, V. N. 2003, A&A, 403, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, S. P. 1998, ApJ, 493, L375 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P., & Ellison, D. C. 1992, ApJ, 339, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, E. M., Moffett, D. A., Goss, W. M., et al. 1997, ApJ, 491, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, E. M., Velázquez, P. F., Dubner, G. M., & Goss, W. M. 1999, AJ, 117, 1827 [NASA ADS] [CrossRef] [Google Scholar]
- Riquelme, M., & Spitkovsky, A. 2010, ApJ, 717, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Riquelme, M., & Spitkovsky, A. 2011, ApJ, 733, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1985, Radiative Processes In Astrophysics, 1st edn. (Weinheim: Wiley-Interscience) [Google Scholar]
- Skilling, J. 1975, MNRAS, 172, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. C., Kirshner, R. P., Blair, W. P., & Winkler, P. F. 1991, ApJ, 375, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, W. W., & Leahy, D. A. 2011, ApJ, 729, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Truelove, J. K., & Mc Kee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Aharonian, F. A., Tanaka, T., Takahashi, T., & Maeda, Y. 2007, Nature, 449, 576 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vladimirov, A., Ellison, D. C., & Bykov, A. 2006, ApJ, 652, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., & McKenzie, J. F. 1981, ICRC, 9, 246 [NASA ADS] [Google Scholar]
- Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2005, A&A, 433, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2008, A&A, 483, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, C.-Y., & Chevalier, R. A. 2001, ApJ, 549, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, J. S., Hughes, J. P., Badenes, C., et al. 2005, ApJ, 634, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, J. J., Wang, J. J., & Miller, M. 2011, Res. Astron. Astrophys., 11, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. 2007, A&A, 465, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2008, AIP Conf. Proc., 1085, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2012, Astropart. Phys., accepted [arXiv:1109.4482] [Google Scholar]
All Figures
 |
Fig. 1 Radio image of the Tycho’s remnant at 1.5 GHz in linear color scale. Image credit: NRAO/VLA Archive Survey, c) 2005−2007 AUI/NRAO. |
| In the text | |
 |
Fig. 2 Time evolution of shock radius Rsh, shock velocity Vsh, magnetic field immediately behind the shock B2 and CR acceleration efficiency |
| In the text | |
 |
Fig. 3 Density (solid line) and temperature (dashed line) of the shocked ISM in the region between the CD (vertical solid line) and the FS, computed at the present age of the remnant, t = 439 yr, and normalized to the values immediately behind the shock. The dot-dashed line shows the electron temperature computed including the heating due to Coulomb collisions. |
| In the text | |
 |
Fig. 4 Total spectrum of protons and electrons (divided by Kep) at the present age of the remnant, as a function of the particle momentum. For comparison, the dot-dashed line shows a power-law ∝ p-4.2 which emphasizes a small flattening of the proton spectrum at the highest momenta. |
| In the text | |
 |
Fig. 5 Radial profile of the magnetic field in the downstream at the present age of the remnant. The dashed curve shows B2(r/Rsh) as resulting from the amplification and compression at the shock. The dotted curve includes also adiabatic losses, while the solid curve is computed including both adiabatic losses and Landau damping. |
| In the text | |
 |
Fig. 6 Spatially integrated spectral energy distribution of Tycho. The curves show synchrotron emission, thermal electron bremsstrahlung and pion decay as calculated within our model (see text for details). The experimental data are, respectively: radio from Reynolds & Ellison (1992); X-rays from Suzaku (courtesy of Toru Tamagawa), GeV gamma-rays from Fermi-LAT (Giordano et al. 2012) and TeV gamma-rays from VERITAS (Acciari et al. 2011). Both Fermi-LAT and VERITAS data include only statistical error at 1σ. |
| In the text | |
 |
Fig. 7 Surface brightness of the radio emission at 1.5 GHz as a function of the radius (data as in Fig. 1). The thin solid line represents the projected radial profile computed from our model using Eq. (16), while the thick solid line corresponds to the same profile convoluted with a Gaussian with a PSF of 15 arcsec. |
| In the text | |
 |
Fig. 8 X-ray emission due to synchrotron (dashed line) and to synchrotron plus thermal bremsstrahlung (solid line). Data from the Suzaku telescope (courtesy of Toru Tamagawa). |
| In the text | |
 |
Fig. 9 Projected X-ray emission at 1 keV. The Chandra data points are from (Cassam-Chenaï et al. 2007, see their Fig. 15). The solid line shows the projected radial profile of synchrotron emission convolved with the Chandra point spread function (assumed to be 0.5 arcsec). |
| In the text | |
 |
Fig. 10 Synchrotron emission calculated by assuming constant downstream magnetic field equal to 100 (dotted line), 200 (dashed line), and 300 μG (solid line). The normalization of the electron spectrum is taken to be Kep = 1.6 × 10-3 for all the curves. |
| In the text | |
 |
Fig. 11 Gamma-ray emission observed by Fermi-LAT and by VERITAS compared with spectral energy distribution produced by pion decay (dot-dashed line), relativistic bremsstrahlung (dot-dot-dashed) and ICS computed for three different photon fields: CMB (dashed), Galactic background (dotted) and IR photons produced by local warm dust (solid). The thick solid line is the sum of all the contributions. Both Fermi-LAT and VERITAS data points include only statistical errors at 1σ. For VERITAS data the systematic error is found to be ~30% (Acciari et al. 2011), while for Fermi-LAT the systematic uncertainties are comparable to or even larger than the statistical error especially for the lowest energy bins due to difficulties in evaluating the galactic background (see Fig. 3 in Giordano et al. 2012, and the related discussion). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.