| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117478 | |
| Published online | 17 February 2012 | |
Stability of radiation-pressure dominated disks
I. The dispersion relation for a delayed heating α-viscosity prescription
1
Astronomical Observatory of the Jagiellonian University,
ul. Orla 171, 30-244
Kraków, Poland
e-mail: adam.ciesielski@uj.edu.pl
2
M. Smoluchowski Institute of Physics, Jagiellonian
University, ul. Reymonta
4, 30-059
Kraków,
Poland
3
Institute of Micromechanics and Photonics, Warsaw University of
Technology, ul. Św. Andrzeja Boboli
8, 02-525
Warszawa,
Poland
e-mail: maciek.wielgus@gmail.com
4
Nicolaus Copernicus Astronomical Center, Polish Academy of
Sciences, ul. Bartycka
18, 00-716
Warszawa,
Poland
e-mail: wlodek@camk.edu.pl; asadowski@cfa.harvard.edu
5
Department of Physics, Göteborg University,
412-96
Göteborg,
Sweden
e-mail: marek.abramowicz@physics.gu.se
6
Institut d’Astrophysique de Paris, UMR 7095 CNRS, UPMC Univ Paris
06, 98bis Boulevard
Arago, 75014
Paris,
France
e-mail: lasota@iap.fr
7
Kavli Institute for Astrophysics and Space Research,
MIT, Cambridge,
MA
02139,
USA
e-mail: pao@space.mit.edu
Received:
15
June
2011
Accepted:
20
December
2011
We derive and investigate the dispersion relation for accretion disks with retarded or advanced heating. We follow the α-prescription but allow for a time offset τ between heating and pressure perturbations, as well as for a diminished response of heating to pressure variations. We study in detail solutions of the dispersion relation for disks with radiation-pressure fraction, 1 − β, and ξ, the ratio of viscous stress response to pressure perturbations. For τ < 0 (advanced heating) the number and sign of real solutions for the growth rate depend on the values of τ, and ξ: if the magnitude of τ is larger than a critical value (e.g., more than twice the thermal time, −τ > 2 τth, for β = 0 and ξ = 1) two real solutions exist, which are both negative. These results imply that radiation-pressure dominated accretion disks may be stabilized when there is a time delay between stress fluctuations and fluctuations in heating.
Key words: accretion, accretion disks / hydrodynamics / instabilities
© ESO, 2012
1. Introduction
The Shakura & Sunyaev (1973)α -viscosity accretion disk model has been extremely successful in describing various astronomical objects and systems. The only exception is its application to systems accreting at high rates. At rates where pressure is dominated by that of radiation, and opacity by electron scattering, the α disk is thermally and viscously (secularly) unstable (Lightman & Eardley 1974; Shakura & Sunyaev 1976; Shibazaki & Hōshi 1975). In the case of accretion onto black holes this regime corresponds to luminosities in excess of ≳0.01 LEdd, where LEdd = GMmp c/σT, mp is the proton mass and σT the Thompson cross-section. However, black-hole X-ray sources cross this limit upwards to maximum luminosity and downwards to minimum luminosity showing no dramatic symptoms at all (but they enter the so-called hard/low state, see e.g., McClintock & Remillard 2006), and certainly not the behavior anticipated by models (e.g., Lasota & Pelat 1991; Taam & Lin 1984). Observations suggest that disks in black-hole transient systems are stable up to at least ~0.5 LEdd (Done et al. 2004).
Models of radiation-pressure dominated disks are unstable only when the viscous stress is proportional to the total pressure (α being the proportionality constant). Models with ad hoc viscosity prescriptions have been studied but their relation to reality remains unknown. Simulations of the magneto-rotational instability in radiation-pressure dominated disks (see e.g., Turner 2004) showed that stress was approximately proportional to the total pressure, but they exhibited no sign of instability.
Recently, Hirose et al. (2009) showed that although the linear correlation of vertically integrated stress and pressure is roughly satisfied in shearing-box MHD simulations of radiation-pressure dominated disks, these quantities are shifted in time – pressure responds to stress variations after ~10−20 dynamical times. We interpret these results to represent a delay in heating with respect to magnetic stress fluctuations. Using these simulation results as a guideline, we perform an analytical, perturbative study of stability of disks that allows for such a time lag between stress and pressure. In the purely hydrodynamic calculations performed in this paper, we can only model magnetic stress as pressure, and heating as the square of the off-diagonal components of the stress tensor. Thus, delayed heating is modeled as a delayed response to fluctuations in pressure of the r-φ component of the stress tensor.
The theory of delayed oscillators has already been extensively developed (e.g., Minorsky 1944; Cooke & Grossman 1982; Bellman & Cooke 1963). It predicts that an oscillator may be easily stabilized (or destabilized) if only the system parameters are chosen properly. We show that this is the case also for accretion disks. Similar conclusions were recently obtained in another analytic study parallel to this work by Lin et al. (2011) – the results of that study and ours agree in their common domain (see Sect. 4.2, below).
This work is devoted to the mathematical part of this project. In Sect. 2.1 we discuss our choice of the modified viscosity prescription. In Sect. 2.2 we derive the dispersion relation. In Sect. 3 we present a detailed discussion of the long wavelength limit. In Sect. 4 we discuss solutions of the dispersion relation. Finally, in Sect. 5 we summarize our results. Detailed discussion of their physical implications will be given in a separate paper.
2. Perturbative analysis of disk stability
We base our study on a linear perturbative analysis following the approach pioneered by
Piran (1978). The unperturbed disk is assumed to be
steady, so that time dependence can only be found in the perturbations. In the following, it
is understood that the characteristic lengthscales of radial variation of unperturbed
variables are ~r. We consider small axisymmetric perturbations with
radial wavenumber k, assuming that their wavelength
λ = 2π/k satisfies the relation
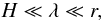 (1) where H is the half-thickness
of the disk. (The assumption of geometrical thinness ceases to be valid for disks with
L ≳ few × 0.01 LEdd, so that strictly
speaking our results apply only to the low luminosity region of the regime where the
thermal-viscous instability would appear according to the standard model.) Since the radial
flow is slow in comparison to the azimuthal motion, we make the usual assumption (Kato et al. 2008) in calculations of instability that
vr0 = 0, where the index 0 will denote
unperturbed quantities. We define the following dimensionless variables corresponding to the
Eulerian perturbations of vertically integrated pressure (P1),
radial velocity (vr1), surface density
(Σ1), disk thickness (H1), and vertically
integrated viscous stress (T1),
(1) where H is the half-thickness
of the disk. (The assumption of geometrical thinness ceases to be valid for disks with
L ≳ few × 0.01 LEdd, so that strictly
speaking our results apply only to the low luminosity region of the regime where the
thermal-viscous instability would appear according to the standard model.) Since the radial
flow is slow in comparison to the azimuthal motion, we make the usual assumption (Kato et al. 2008) in calculations of instability that
vr0 = 0, where the index 0 will denote
unperturbed quantities. We define the following dimensionless variables corresponding to the
Eulerian perturbations of vertically integrated pressure (P1),
radial velocity (vr1), surface density
(Σ1), disk thickness (H1), and vertically
integrated viscous stress (T1),
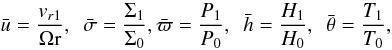 (2) where
(2) where 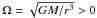 is the Keplerian rotational frequency. We
assume that all of these quantitites represent complex waveforms
enΩt−ikr, e.g.,
is the Keplerian rotational frequency. We
assume that all of these quantitites represent complex waveforms
enΩt−ikr, e.g.,
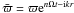 and
and 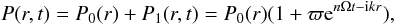 (3) where n stands for the
dimensionless frequency, and ϖ is a constant and uniform dimensionless
amplitude. Negative values of the real part of the dimensionless frequency,
ℜ(n), correspond to damped (stable) perturbations while positive values
to exponentially growing (unstable) ones. The imaginary part of n
determines the frequency of the corresponding oscillations.
(3) where n stands for the
dimensionless frequency, and ϖ is a constant and uniform dimensionless
amplitude. Negative values of the real part of the dimensionless frequency,
ℜ(n), correspond to damped (stable) perturbations while positive values
to exponentially growing (unstable) ones. The imaginary part of n
determines the frequency of the corresponding oscillations.
2.1. Viscosity prescription
In the standard approach, based on the α-prescription (Shakura & Sunyaev 1973), one assumes that the
rϕ component of the stress tensor,
Trϕ, is proportional to pressure:
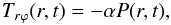 (4) where
Trϕ and P are given in
terms of the unperturbed and perturbed quantities as
(4) where
Trϕ and P are given in
terms of the unperturbed and perturbed quantities as  Although resultssimilar to those presented
below can be obtained with a constant value of alpha, in this work we find it convenient
to assume a modified prescription for viscosity. With the following prescription, a time
offset will appear in the heating term alone, and not in the angular momentum equation
(through linear order). Instead of assuming that α is constant both in
time and radius we write
Although resultssimilar to those presented
below can be obtained with a constant value of alpha, in this work we find it convenient
to assume a modified prescription for viscosity. With the following prescription, a time
offset will appear in the heating term alone, and not in the angular momentum equation
(through linear order). Instead of assuming that α is constant both in
time and radius we write ![\begin{equation} \alpha(r,t)=\alpha_0(1+\bar\alpha)=\alpha_0\left[1+(\theta {\rm e}^{-n\Omega\tau} -\varpi){\rm e}^{n\Omega t-{\rm i}kr}\right], \label{e.alpha} \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq43.png) (7) with
(7) with 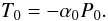 (8) We introduce the viscous stress to pressure
response factor, defined as the ratio of the dimensionless amplitudes of stress and
pressure perturbations,
(8) We introduce the viscous stress to pressure
response factor, defined as the ratio of the dimensionless amplitudes of stress and
pressure perturbations, 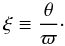 (9) We assume ξ to be realand
positive. A value of ξ < 1 signifies that short-term fluctuations in
pressure correspond to fluctuations in viscous stress and heating that are diminished in
comparison with long-term averages. The perturbation of α, defined in
Eq. (7), may be expressed in terms of
(9) We assume ξ to be realand
positive. A value of ξ < 1 signifies that short-term fluctuations in
pressure correspond to fluctuations in viscous stress and heating that are diminished in
comparison with long-term averages. The perturbation of α, defined in
Eq. (7), may be expressed in terms of
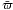 ,
and ξ of Eq. (9) :
,
and ξ of Eq. (9) :
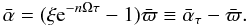 (10) As we will see in Eq. (49), the heating perturbation contains a term
proportional to the perturbation in α, and thus includes the term
(10) As we will see in Eq. (49), the heating perturbation contains a term
proportional to the perturbation in α, and thus includes the term
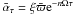 ,
which is delayed by τ with respect to pressure fluctuations:
,
which is delayed by τ with respect to pressure fluctuations:
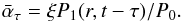 (11) In this sense τ can be
called a heating delay1.
(11) In this sense τ can be
called a heating delay1.
2.2. Derivation of the dispersion relation
In the following four subsections we derive perturbed forms of hydrostatic balance, mass conservation, angular momentum balance and energy equation for geometrically thin, axisymmetric accretion disks.
2.2.1. Hydrostatic balance
The balance of vertical forces, after integrating along the vertical coordinate, takes
the following form, 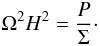 (12) Writing this form of the vertical force
balance we assume the disk to be in hydrostatic equilibrium, since the thermal and
secular timescales are much longer than the dynamical timescale.
(12) Writing this form of the vertical force
balance we assume the disk to be in hydrostatic equilibrium, since the thermal and
secular timescales are much longer than the dynamical timescale.
Perturbing Eq. (12) with small-amplitude
axisymmetric perturbations, and assuming that the azimuthal component of velocity
undergoes no change, we get 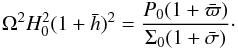 (13) Using the unperturbed Eq. (12), we get
(13) Using the unperturbed Eq. (12), we get 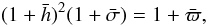 i.e., through linear order
i.e., through linear order 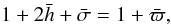 and finally
and finally 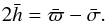 (14)
(14)
2.2.2. Mass conservation
The vertically integrated form of the continuity equation can be written as
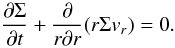 (15) Its perturbed form is
(15) Its perturbed form is ![\begin{equation} \label{Mass2}\pder{ }{t} \Sigma_0 (1+\bar{\sigma}) + \kpder{ }{r}{r}[r \Sigma_0 (1+\bar{\sigma}) r \Omega \bar{u}] = 0. \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq57.png) (16) Neglecting terms of the second order
(
(16) Neglecting terms of the second order
(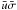 )
and using Eq. (15) in its unperturbed
form, ∂Σ0/∂t = 0, we obtain
)
and using Eq. (15) in its unperturbed
form, ∂Σ0/∂t = 0, we obtain ![\begin{equation} \label{Mass4} \Sigma_0 \Omega n\bar{\sigma} + \Sigma_0\Omega \bar{u}\left[\pderln{(r^2 \Sigma_0\Omega)}{r} -{\rm i}kr \right] = 0. \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq60.png) (17) The logarithmic derivative term may be
neglected on the strength of the assumption stated in Eq. (1). Thus, we obtain the final relation
(17) The logarithmic derivative term may be
neglected on the strength of the assumption stated in Eq. (1). Thus, we obtain the final relation 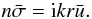 (18)
(18)
2.2.3. Angular momentum conservation
The angular momentum conservation law is 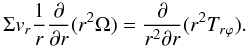 (19) For the first order perturbations we obtain
(19) For the first order perturbations we obtain
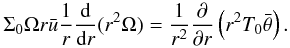 (20) According to Eq. (1) the derivative on the right hand side is
dominated by the
(20) According to Eq. (1) the derivative on the right hand side is
dominated by the 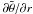 term. Using Eq. (8), and introducing the
speed of sound squared
term. Using Eq. (8), and introducing the
speed of sound squared 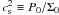 , and the vertical epicyclic frequency
, and the vertical epicyclic frequency
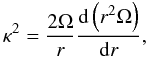 (21) we obtain
(21) we obtain 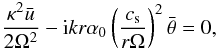 (22) and finally,
(22) and finally, 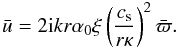 (23) Incidentally, in our study
κ = Ω and Eq. (12) reads
cs/(rΩ) = H0/r,
so
cs/(rκ) = H0/r.
(23) Incidentally, in our study
κ = Ω and Eq. (12) reads
cs/(rΩ) = H0/r,
so
cs/(rκ) = H0/r.
2.2.4. Energy equation
We start from the second law of thermodynamics in the form (e.g., Kato et al. 2008)
![\begin{eqnarray} \pder{E}{t} + P \pder{\ln H}{ t} + \kpder{}{r}{r}[r v_r(E+P)] -&& v_r\pder{P}{r} \notag\\ + v_r P \pder{\ln H}{r} &=& Q_{\rm vis}^{+} - Q_{\rm rad}^{-}, \end{eqnarray}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq72.png) (24) or simply,
(24) or simply, ![\begin{equation} \label{Ene1} \pder{E}{t} + \kpder{}{r}{r}(r v_rE) + \frac{P}{H} \left[\pder{H}{ t} + \kpder{}{r}{r}(r v_rH)\right] = Q_{\rm vis}^{+} - Q_{\rm rad}^{-}, \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq73.png) (25) where E is the vertically
integrated specific energy,
(25) where E is the vertically
integrated specific energy, ![\begin{equation} \label{Ene2} E = \left[3(1-\beta)+\frac{\beta}{\gamma-1}\right] P \equiv A P, \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq75.png) (26) β is the gas to total
pressure ratio, γ is the ratio of specific heats,
(26) β is the gas to total
pressure ratio, γ is the ratio of specific heats,
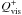 and
and
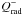 are the (per unit area) viscous heating
and radiative cooling rates, respectively.
are the (per unit area) viscous heating
and radiative cooling rates, respectively.
Let us differentiate both sides of Eq. (25) with respect to time. Assuming that 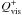 is a function of P and
α (following the α-prescription) while
is a function of P and
α (following the α-prescription) while
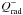 is a function of P and
Σ (as is the case for radiative cooling in the optically thick regime), we obtain
is a function of P and
Σ (as is the case for radiative cooling in the optically thick regime), we obtain
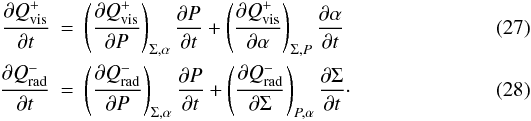 Introducing the perturbations and
differentiating we get,
Introducing the perturbations and
differentiating we get, 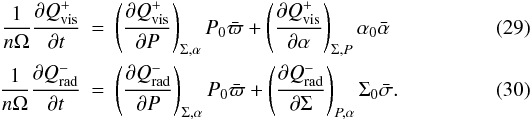 Finally, we have,
Finally, we have, 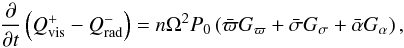 (31) where
(31) where 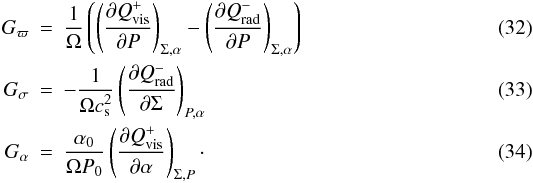 Following the
α-prescription, these quantities simplify to (Kato et al. 2008),
Following the
α-prescription, these quantities simplify to (Kato et al. 2008),  The perturbation of β is
given by the following expression (Chandrasekhar
1958),
The perturbation of β is
given by the following expression (Chandrasekhar
1958), 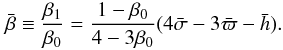 (38) Hence, like all the other time derivatives,
the time derivative of A is first order in the perturbation:
(38) Hence, like all the other time derivatives,
the time derivative of A is first order in the perturbation:
![\begin{equation} \pder{A}{t}=\pder{}{t}\left[3(1-\beta)+\frac{\beta}{\gamma-1}\right]= \beta_0\frac{4-3\gamma}{\gamma-1}\pder{\bar\beta}{t}\cdot \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq90.png) (39) The time derivative of the first term on
the left hand side of Eq. (25) is given
by,
(39) The time derivative of the first term on
the left hand side of Eq. (25) is given
by, 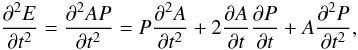 (40) where Eq. (26) has been taken into account. The derivatives of
A and P are both first order, so the middle term is
second order and may be neglected. The other terms are
(40) where Eq. (26) has been taken into account. The derivatives of
A and P are both first order, so the middle term is
second order and may be neglected. The other terms are 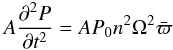 (41) and
(41) and 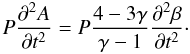 (42) The second time derivative of
(42) The second time derivative of
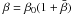 equals,
equals, 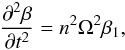 (43) so finally,
(43) so finally, 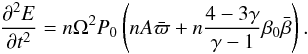 (44) Perturbing the second term on the left hand
side of Eq. (25), keeping in mind the
assumption of Eq. (1), we get through
first order
(44) Perturbing the second term on the left hand
side of Eq. (25), keeping in mind the
assumption of Eq. (1), we get through
first order 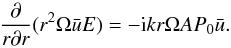 (45) The time derivative of this expression is
(45) The time derivative of this expression is
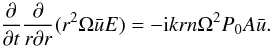 (46) The time derivatives of the terms involving
H in Eq. (25) are
straightforward to compute. The first order terms are
(46) The time derivatives of the terms involving
H in Eq. (25) are
straightforward to compute. The first order terms are
![\begin{eqnarray} \frac{P}{H} \left[\pder{H}{ t} + \kpder{}{r}{r}(r v_rH)\right] &&= P_0n\Omega\bar{h} + \frac{P_0}{H_0}\kpder{}{r}{r}(r^2\Omega\bar{u}H_0)\notag\\ &&=P_0n\Omega\bar{h} -{\rm i}kP_0r\Omega\bar{u} \end{eqnarray}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq99.png) (47) and their time derivative is
(47) and their time derivative is ![\begin{equation} \label{Ene7} \pder{}{t} \left[\frac{P}{H}\pder{H}{ t} + \frac{P}{H}\kpder{}{r}{r}(r v_rH)\right] =n\Omega^2P_0(n\bar{h} -{\rm i}kr\bar{u}). \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq100.png) (48) Collecting Eqs. (31), (44), (46) and (48), we obtain the final form of the
perturbed energy equation,
(48) Collecting Eqs. (31), (44), (46) and (48), we obtain the final form of the
perturbed energy equation, 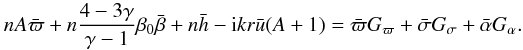 (49)
(49)
2.2.5. System of perturbed equations and the dispersion relation
Equations (14), (18), (23) and (49) form a system of four algebraic equations.
Taking Eq. (10) into account we obtain
four coupled homogeneous algebraic equations in the following form, 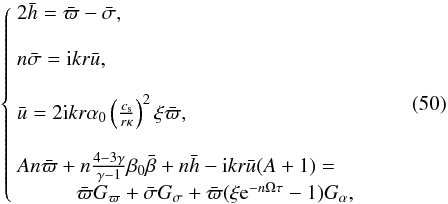 where
where
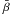 is given by Eq. (38). This system has
nontrivial solutions for the four variables
is given by Eq. (38). This system has
nontrivial solutions for the four variables 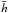 ,
,
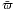 ,
,
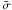 ,
and
,
and 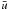 ,
iff
,
iff ![\begin{equation} \label{disperse} n^2 C_1 + n \left[ \xi FC_2 +G_{\alpha}( 1-\xi {\rm e}^{-n\Omega\tau}) - G_{\varpi}\right] + \xi F G_{\sigma}= 0, \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq108.png) (51) where
(51) where 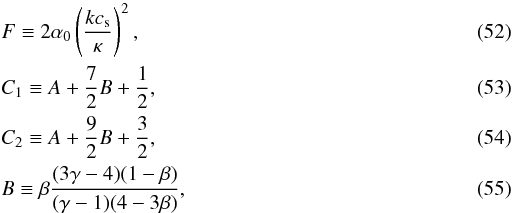 and A is given in
Eq. (26). For β = 0
the coefficients of Eq. (51) do not
depend on γ. For ξ = 1 and Ωτ = 0 the
condition given in Eq. (51) simplifies to
the standard dispersion relation for perturbed accretion disks (e.g., Kato et al. 2008). Note that
0 ≤ β ≤ 1, and that for γ ≥ 4/3, A
and B satisfy A > 0, and B ≥ 0.
Thus, both C1 and C2 are
positive for any value of β. In the following, we will take
γ = 5/3 whenever a specific value is required for numerical results.
We also specialize to
F = 2α0(kH0)2,
in accordance with the comment following Eq. (23).
and A is given in
Eq. (26). For β = 0
the coefficients of Eq. (51) do not
depend on γ. For ξ = 1 and Ωτ = 0 the
condition given in Eq. (51) simplifies to
the standard dispersion relation for perturbed accretion disks (e.g., Kato et al. 2008). Note that
0 ≤ β ≤ 1, and that for γ ≥ 4/3, A
and B satisfy A > 0, and B ≥ 0.
Thus, both C1 and C2 are
positive for any value of β. In the following, we will take
γ = 5/3 whenever a specific value is required for numerical results.
We also specialize to
F = 2α0(kH0)2,
in accordance with the comment following Eq. (23).
3. Long-wave limit
Let us first consider the solutions of the dispersion relation Eq. (51) in the long wavelength limit, i.e.,
kH → 0, which is very useful in classifying solutions of arbitrary
wavelength. In the limit kH → 0 we neglect terms proportional to
F and obtain ![\begin{equation} \label{lw1} n\left[n C_1 + (1-\xi {\rm e}^{-n\Omega\tau})G_{\alpha}-G_{\varpi}\right] = 0, \end{equation}](/articles/aa/full_html/2012/02/aa17478-11/aa17478-11-eq122.png) (56) with a trivial solution n = 0.
Dividing by n ≠ 0 and using Eqs. (35) –(37) we get for the remaining
solutions
(56) with a trivial solution n = 0.
Dividing by n ≠ 0 and using Eqs. (35) –(37) we get for the remaining
solutions 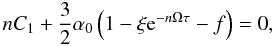 (57) where
(57) where
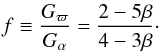 (58)
(58)
3.1. The case of no delay, Ωτ = 0
Solving Eq. (57) is easy for
Ωτ = 0. In this case n is real and is given by,
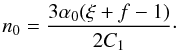 (59) As C1 is positive
for all values of β, the sign of n is determined by the
sign of ξ + f − 1. For ξ = 1,
n0 = Gϖ/C1
and it is positive for β < 2/5 and negative for
β > 2/5. The latter inequality is the standard condition for disk
stability.
(59) As C1 is positive
for all values of β, the sign of n is determined by the
sign of ξ + f − 1. For ξ = 1,
n0 = Gϖ/C1
and it is positive for β < 2/5 and negative for
β > 2/5. The latter inequality is the standard condition for disk
stability.
In general, we get the following criterion for the negative sign of n,
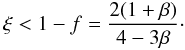 (60) The shaded area in Fig. 1 presents the region in the (β,ξ) plane for which
n is negative. Note that it suffices to decrease the amplitude of
stress variations by a factor of two (ξ = 0.5) to stabilize the disk for
all β. Despite the fact that the condition (60) has been derived assuming Ωτ = 0, it remains
satisfied for the negative roots of Eq. (57) for all Ωτ ≥ 0, as will be shown in Sect. 3.3.
(60) The shaded area in Fig. 1 presents the region in the (β,ξ) plane for which
n is negative. Note that it suffices to decrease the amplitude of
stress variations by a factor of two (ξ = 0.5) to stabilize the disk for
all β. Despite the fact that the condition (60) has been derived assuming Ωτ = 0, it remains
satisfied for the negative roots of Eq. (57) for all Ωτ ≥ 0, as will be shown in Sect. 3.3.
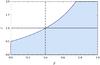 |
Fig. 1 The shaded area denotes the region in the (β, ξ) plane for which the real root of Eq. (57) is negative for all Ωτ ≥ 0. |
3.2. Arbitrary Ωτ
Let us now consider the general case of Ωτ ≠ 0. Equation (57) is no longer trivial as it involves an exponential function of n. An infinite number of complex solutions is expected as the exponential function e−nΩτ involves periodic trigonometric functions whenever the imaginary part of n is nonzero, ℑ(n) ≠ 0. All imaginary solutions are conjugate. As will be shown in the following section, no more than two real solutions may exist. To find the roots of a nonlinear complex equation such as Eq. (57) one has to use numerical methods. We used the MINPACK routines (More et al. 1984). First, the locations of minima of the absolute value of the left hand side of Eq. (57) were roughly estimated. The values so obtained served as starting points for the nonlinear solver.
In Fig. 2 we plot color-coded absolute values of the left hand side of Eq. (57) for β = 0, ξ = 1, α = 0.1 and three values of Ωτ = −50 (left), Ωτ = 0 (middle), Ωτ = 50 (right panel). Only ℑ(n) ≥ 0 regions are shown. The darker the color, the smaller the value. Red crosses denote real solutions while red squares show locations of solutions with non-zero imaginary part. For each of the values Ωτ = 0 and Ωτ = 50 a single real solution exists, and it satisfies ℜ(n) > 0. For Ωτ ≠ 0 there is an infinite number of complex solutions. The sign of their real part (with the exception of the first imaginary root when Ωτ < 0) is in general opposite to the sign of Ωτ.
 |
Fig. 2 Maps presenting absolute values of the left hand side of Eq. (57) (dispersion relation in the limit of long waves) on the complex plane for β = 0, ξ = 1, α = 0.1 and three values of Ωτ = −50 (left), 0 (middle) and 50 (right panel). Crosses and rectangles denote locations of the real and complex solutions, respectively. |
Figure 3 presents the real part of solutions of Eq. (57) in the (Ωτ,ℜ(n)) plane for the chosen values of α, β and ξ. Solid lines present real solutions (crosses in Fig. 2). Dotted lines correspond to ordinary complex roots (squares in Fig. 2) – only the first 20 are plotted. The dashed line connecting two real branches is a special class of complex solutions.
Taking Ωτ = 0 we recover the real solution given by Eq. (59). For small but negative Ωτ there are two real solutions, one of which satisfies limΩτ → 0−ℜ(n) = +∞. These two real solutions converge to each other and merge into complex conjugate solutions (empty star in Fig. 3) at a critical value of Ωτ1 ≈ −11. These roots split into two real solutions, but this time negative, at Ωτ2 ≈ −125 (solid star). The upper branch of these two approaches ℜ(n) = 0− for Ωτ → −∞. For Ωτ > 0 there is only one real solution, which is positive and approaches ℜ(n) = 0+ for Ωτ → +∞.
In addition to these solutions, an infinite number of periodic complex solutions exists (dotted lines). For most of the range of Ωτ presented in Fig. 3 they appear in the second and fourth quadrant of (Ωτ,ℜ(n)) plane for negative and positive Ωτ, respectively. For |Ωτ| ≳ 150, however, the first complex root, and subsequently the others too (but at much larger absolute values of Ωτ), crosses the ℜ(n) = 0 axis.
3.3. Real roots
Let us examine the real branches in detail. Equation (57) may be rewritten in the following form, 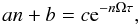 (61) where
(61) where  Convexity of the exponential function on the
right hand side of Eq. (61) implies that
there are no more than two real numbers n satisfying this equation. For
Ωτ ≥ 0 the exponential function is decreasing with n
and therefore has exactly one intersection with an+b,
and only for n > 0 (or n = 0, or
n < 0) as long as b/c < 1 (or
b/c = 1, or
b/c > 1, respectively). This yields the same
criterion for stability as in the Ωτ = 0 case, inequality (60). In this sense, retarded heating does not
qualitatively alter the viscous and thermal stability properties of the disk.
Convexity of the exponential function on the
right hand side of Eq. (61) implies that
there are no more than two real numbers n satisfying this equation. For
Ωτ ≥ 0 the exponential function is decreasing with n
and therefore has exactly one intersection with an+b,
and only for n > 0 (or n = 0, or
n < 0) as long as b/c < 1 (or
b/c = 1, or
b/c > 1, respectively). This yields the same
criterion for stability as in the Ωτ = 0 case, inequality (60). In this sense, retarded heating does not
qualitatively alter the viscous and thermal stability properties of the disk.
For Ωτ < 0 the exponential function is, on the contrary, increasing and may not intersect the linear one at all, may have a single intersection point or may cross it twice. All three cases occur and are clearly visible in Fig. 3, the single solutions are marked by stars and the complex branch connecting these real solutions corresponds to the no intersection case.
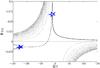 |
Fig. 3 Real part of solutions of Eq. (57) for β = 0, ξ = 1 and α = 0.1 as a function of τ. The solid lines denote real solutions, the dashed line shows complex solutions linking the real branches, while the dotted lines present periodic complex solutions (only first 20 solutions are drawn). Stars denote points where the real branches merge into the complex one (and its conjugate). |
The condition for a single real solution of Eq. (57) for Ωτ < 0 may be obtained by matching the gradient of
the linear function with the derivative of the right hand side of Eq. (61), 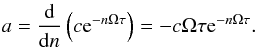 (65) Equations (61) and (65) form a set
of two equations corresponding to the linear function being tangent to the exponential one
at a given n and providing the condition, on Ωτ for
instance, under which Eq. (57) has only one
real solution. After some algebra we get,
(65) Equations (61) and (65) form a set
of two equations corresponding to the linear function being tangent to the exponential one
at a given n and providing the condition, on Ωτ for
instance, under which Eq. (57) has only one
real solution. After some algebra we get, 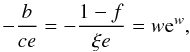 (66) where
(66) where
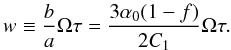 (67) Solutions of Eq. (66) are given by the multivalued Lambert W
function (Wright 1959) of its left hand side. Real
solutions exist only for values of the left hand side of the equation greater or equal
than −1/e. This condition corresponds to,
(67) Solutions of Eq. (66) are given by the multivalued Lambert W
function (Wright 1959) of its left hand side. Real
solutions exist only for values of the left hand side of the equation greater or equal
than −1/e. This condition corresponds to, 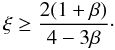 (68) As
wew has a single minimum, of value
−1/e at w = −1, Eq. (66) has two solutions for all −1 < w < 0, i.e.,
when the inequality in (68) is sharp. As
long as condition (68) is satisfied, the
values of Ωτ for which Eq. (57) has only one real solution are therefore given by
(68) As
wew has a single minimum, of value
−1/e at w = −1, Eq. (66) has two solutions for all −1 < w < 0, i.e.,
when the inequality in (68) is sharp. As
long as condition (68) is satisfied, the
values of Ωτ for which Eq. (57) has only one real solution are therefore given by 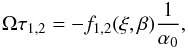 (69) where
f1,2(ξ,β) is double-valued, and these
critical delays, τ1,2, scale with the thermal time
τth = 2π/(Ωα). We take
f1 ≤ f2, i.e.,
Ωτ2 ≤ Ωτ1 < 0. In Fig. 4 we plot values of
f1,2(ξ, β) as a function of
β for various values of ξ. For the standard case of
ξ = 1 and radiation pressure dominated disks (β = 0)
we have f1(1,0) ≈ 1.08 and
f2(1,0) ≈ 12.50, i.e.,
τ1 = −0.172τth, and
τ2 = −1.99τth. Thus, for, e.g.,
α = 0.1, Eq. (57) has
only one real solution for Ωτ1 ≈ −10.8 and
Ωτ2 ≈ −125.0 (corresponding to the stars in Fig. 3). A moment’s reflection leads to the conclusion that
there are two positive roots of Eq. (57) for Ωτ1 < Ωτ < 0, two
negative ones for Ωτ < Ω2τ, and no real
roots for
Ω2τ < Ωτ < Ωτ1.
When condition (60) is satisfied, instead
of (68), there are two solutions for
n, one positive and one negative.
(69) where
f1,2(ξ,β) is double-valued, and these
critical delays, τ1,2, scale with the thermal time
τth = 2π/(Ωα). We take
f1 ≤ f2, i.e.,
Ωτ2 ≤ Ωτ1 < 0. In Fig. 4 we plot values of
f1,2(ξ, β) as a function of
β for various values of ξ. For the standard case of
ξ = 1 and radiation pressure dominated disks (β = 0)
we have f1(1,0) ≈ 1.08 and
f2(1,0) ≈ 12.50, i.e.,
τ1 = −0.172τth, and
τ2 = −1.99τth. Thus, for, e.g.,
α = 0.1, Eq. (57) has
only one real solution for Ωτ1 ≈ −10.8 and
Ωτ2 ≈ −125.0 (corresponding to the stars in Fig. 3). A moment’s reflection leads to the conclusion that
there are two positive roots of Eq. (57) for Ωτ1 < Ωτ < 0, two
negative ones for Ωτ < Ω2τ, and no real
roots for
Ω2τ < Ωτ < Ωτ1.
When condition (60) is satisfied, instead
of (68), there are two solutions for
n, one positive and one negative.
3.4. Limits of infinite time offset (Ωτ → ± ∞)
Let us now investigate the limits of real solutions of Eq. (57). Assuming that n is finite, Eq. (61) simplifies in the limit of
nΩτ → +∞ to, 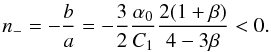 (70) Therefore, this value is valid only for
Ωτ → −∞. For the standard choice of α = 0.1,
β = 0 and ξ = 1 one gets,
(70) Therefore, this value is valid only for
Ωτ → −∞. For the standard choice of α = 0.1,
β = 0 and ξ = 1 one gets,
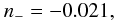 (71) which corresponds to the limit of the lower
real branch in the third quadrant of Fig. 3.
(71) which corresponds to the limit of the lower
real branch in the third quadrant of Fig. 3.
To find limits of the other two branches let us assume that
nΩτ remains finite for |Ωτ| → ∞. This
assumption implies n → 0 and Eq. (61) takes in this limit the following form,
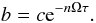 (72) Therefore, n has to fulfill
the relation,
(72) Therefore, n has to fulfill
the relation, 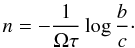 (73) The sign of the logarithm depends on
ξ and β:
(73) The sign of the logarithm depends on
ξ and β: 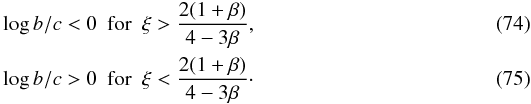 Thus, for ξ and
β satisfying (74) n approaches 0+ for Ωτ → +∞ and
0− for Ωτ → −∞. If condition (75) is satisfied we have
limΩτ → +∞n = 0− and
limΩτ → −∞n = 0+.
Thus, for ξ and
β satisfying (74) n approaches 0+ for Ωτ → +∞ and
0− for Ωτ → −∞. If condition (75) is satisfied we have
limΩτ → +∞n = 0− and
limΩτ → −∞n = 0+.
3.5. Parameter study
In Fig. 5 we show the roots of Eq. (57) for β = 0, ξ = 1 and three values of α0 = 0.02 (green), α0 = 0.1 (blue) and α0 = 0.2 (red line). The second case corresponds to Fig. 3. For clarity, from among the infinite number of complex periodic solutions (dotted lines), only the first one (in the sense of the smallest modulus value) is plotted. All the curves have qualitatively similar shapes – the sign of solutions in a given region does not depend on α0 (Table 1). However, the values of Ωτ1 and Ωτ2, which limit the regions with double real solutions for Ωτ < 0, are sensitive to the value of α0. Equation (69) predicts that their values are inversely proportional to α0 and therefore, e.g., the region with two negative roots of Eq. (57) extends to larger values of Ωτ (closer to Ωτ = 0) for high values of α. The limit for the lower real branch (n−) also depends on α0 according to Eq. (70) – the higher the value of α0, the lower the value of n−.
 |
Fig. 5 Real part of solutions of Eq. (57) for β = 0 and ξ = 1 as a function of τ. Solutions for three values of α are presented with different colors (increasing values of α0 from left to right). Solid lines are for real solutions while dotted and dashed lines show the real part of complex solutions. Only the first periodic exponential root is plotted. |
The impact of β on solutions of the dispersion relation for α = 0.1 and ξ = 1 is presented in Fig. 6. For ξ = 1 the crucial inequality (60) corresponds to β > 2/5. For values of β smaller than this critical value solutions exhibit qualitatively the same behavior as discussed previously. The values of Ωτ1,2 and n− depend on β according to Eqs. (69) and (70), respectively. Once β exceeds 2/5 the character of the solution changes. For Ωτ ≥ 0 the root is negative and approaches 0− with Ωτ → +∞. For any negative value of Ωτ there are two real solutions with opposite signs – the complex conjugate branch connecting the real solutions does not appear and Ωτ1,2 are not defined.
 |
Fig. 6 Real part of solutions of Eq. (57) for α = 0.1 and ξ = 1 versus τ. Solutions for different values of β are presented (for the solid lines in the Ωτ > 0 region, β increases from top to bottom). Solid lines are for real solutions while dotted and dashed lines show the real part of complex solutions. Only the first periodic exponential root is plotted. In this figure, we take γ = 5/3. |
Very similar behavior is shown in Fig. 7 which presents the impact of ξ for α = 0.1 and β = 0. For this case inequality (60) is not satisfied for ξ > 1/2. The solutions change their nature once ξ becomes larger than 1/2, similarly to solutions with β > 2/5 discussed in the previous paragraph. In accordance with Eq. (70), n−, the limit of the lower real branch at Ωτ → −∞, does not depend on ξ.
 |
Fig. 7 Same as Fig. 6 but for α = 0.1, β = 0 and varying ξ. For the solid lines in the Ωτ > 0 region, ξ decreases from top to bottom. |
In Table 1 we summarize general features of the real solutions of Eq. (57) which have been derived in this section.
4. Solutions of the dispersion relation
4.1. Short-wave limit
Let us now consider the short-wave limit (kH → ∞) of Eq. (51). Strictly speaking, this limit violates
the first of the assumptions of Eq. (1). If
we assume that n is finite then the terms with F
dominate, 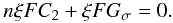 (76) Despite the fact that n in
general is complex, in this case it must be real to satisfy this real equation. We obtain,
(76) Despite the fact that n in
general is complex, in this case it must be real to satisfy this real equation. We obtain,
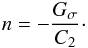 (77) Both
Gσ = (3α0/2)(2 + 3β)/(4−3β)
and C2 are positive. Thus, this value of n is
negative and satisfies the dispersion relation in the short-wave limit for all values of
parameters ξ and Ωτ.
(77) Both
Gσ = (3α0/2)(2 + 3β)/(4−3β)
and C2 are positive. Thus, this value of n is
negative and satisfies the dispersion relation in the short-wave limit for all values of
parameters ξ and Ωτ.
Let us now assume that the absolute value of n is large
(| n| ≫ 1 and
|n| ≫ Gσ/C2).
In this (and kH ≫ 1) limit Eq. (51) reduces to 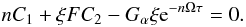 (78) Assuming in addition that
nΩτ ≥ 0 we get
(78) Assuming in addition that
nΩτ ≥ 0 we get
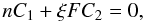 (79) which is satisfied for
(79) which is satisfied for 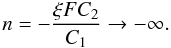 (80) Hence, this limit is valid for
Ωτ ≤ 0.
(80) Hence, this limit is valid for
Ωτ ≤ 0.
 |
Fig. 8 Real part of solutions of Eq. (51) as a function of the wave length 1/(kH) for α0 = 0.1, ξ = 1, Ωτ = 0 and various values of β. The line convention is the same as in previous figures. In this figure, we take γ = 5/3. |
If, on the contrary, we assume nΩτ < 0 then
Eq. (78) reduces to,
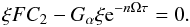 (81) The solution of which is,
(81) The solution of which is,
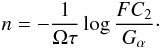 (82) Thus, we have two additional limits,
(82) Thus, we have two additional limits,
 Summing up, there is a common limit
n = −Gσ/C2
for all values of Ωτ. In addition, solutions with Ωτ ≥ 0
have another branch approaching −∞ while for negative Ωτ two branches are
expected approaching both +∞ and −∞.
Summing up, there is a common limit
n = −Gσ/C2
for all values of Ωτ. In addition, solutions with Ωτ ≥ 0
have another branch approaching −∞ while for negative Ωτ two branches are
expected approaching both +∞ and −∞.
4.2. Arbitrary wavelength
In this section we consider solutions of the dispersion relation for an arbitrary value of the wavelength λ = 2π/k.
We start with discussing the standard case with no time lag (Ωτ = 0) and ξ = 1. Figure 8 presents the real part of solutions of Eq. (51) obtained assuming α = 0.1 and various values of β. The limit of 1/(kH) → ∞ corresponds to the long-wave limit discussed in Sect. 3.
For β < 2/5 there are two positive real solutions: one of them approaches zero for long wavelengths (the trivial solution of Eq. (56) ) while the other corresponds to n0 given in Eq. (59). According to the classical theory of disk instabilities they are related to the secular and thermal instabilities, respectively. The branches corresponding to the secular and thermal modes approach each other with decreasing wavelength and merge into complex conjugate solutions (dashed lines). Two real and negative branches appear again for short wavelengths. The 1/(kH) → 0 limit of the upper one corresponds to Eq. (77). The lower branch approaches −∞ according to Eq. (80). The same picture holds for β > 2/5, except that now all real solutions are negative, at large wavelengths one of the roots corresponds to the trivial one and approaches 0− in the limit of 1/(kH) → ∞, while the other one approaches n0 < 0.
For β = 2/5 there are two negative real roots at short wavelengths, F > 4GσC1/C2. In the limit 1/(kH) → 0 one root corresponds to Eq. (77), −Gσ/C2 = −0.038 for γ = 5/3, while the other tends to −∞. At F = 4GσC1/C2 these merge into complex conjugate solutions tending to the origin of the complex plane (n = 0) in the long-wave limit (F → 0), while never becoming real for F < 4GσC1/C2 – the real part of these conjugate solutions is negative.
The critical inequality (60) relates β and ξ. Thus, for fixed β similar effects to the ones discussed above may be obtained by varying ξ. In Fig. 9 we plot roots of the dispersion relation, Eq. (51), for α0 = 0.1, β = 0, Ωτ = 0 and a few values of ξ. For radiation pressure dominated disks (β = 0) the critical value is ξ = 1/2. For ξ higher than this value, the solutions exhibit similar behavior to those discussed above for β < 2/5 – two positive roots for long waves (one approaching 0+), a common complex conjugate branch and two negative real solutions for short waves. The latter approach −∞ and the limit defined in Eq. (77), which does not depend on ξ. For ξ < 1/2 both solutions are negative for all wavelengths and approach the same limits for the shortest waves as before. The complex conjugate branch does not appear at all for the lowest presented value of ξ = 0.01.
 |
Fig. 9 Real part of solutions of Eq. (51) as a function of the wave length 1/(kH) for α0 = 0.1, β = 0, Ωτ = 0 and various values of ξ. The line convention is the same as in previous figures. |
Figure 10 presents similar plots for α0 = 0.1, β = 0, ξ = 1 and a few values of the time delay Ωτ. The long-wave limit corresponds to the solutions presented in Fig. 3. The bottom plot zooms in the shaded region in the top panel. For Ωτ = 0 (black curves) we recover one of the standard cases presented in the previous plots. Positive values of Ωτ (e.g., magenta curves) result in two positive roots (one approaching 0+) for long waves. This is the case considered by Lin et al. (2011) – with the identification tps = τ, the thick line (Ω tps = 20) in their Fig. 1 corresponds approximately to our magenta curve (Ωτ = 10). The two positive roots merge into the complex conjugate branch with decreasing wavelength and again split into two negative real solutions, similarly to some of the cases discussed above.
 |
Fig. 10 Real part of solutions of Eq. (51) as a function of the wave length 1/(kH) for α0 = 0.1, β = 0, ξ = 1 and various values of the time delay τ. The bottom panel zooms in the shaded area on the top panel. The line convention is the same as in previous figures. In this figure, we take γ = 5/3. |
The behavior of solutions obtained with negative time delays (Ωτ < 0) is more complicated. The number of solutions in the long-wave limit depends on the relation of the time delay to the quantities Ωτ1 and Ωτ2 (for the case presented in Fig. 10 these are −11 and −125, respectively, Eq. (69) ). For negative Ωτ > Ωτ1 we expect in total three real roots: two positive, and one equal to zero in the long wavelength limit (the trivial one). The red curve in Fig. 10 (Ωτ = −10) corresponds to this case – there are three positive roots, two tending to n ≈ 0.04 and ≈ 0.12, and one approaching zero.
When Ωτ < Ωτ2 (e.g., Ωτ = −150, green lines in Fig. 10) there are two negative real roots of Eq. (57) (compare Fig. 3) clearly visible in the bottom panel of Fig. 10. The dotted green line approaching ℜ(n) ≈ 0.002 in the long-wave limit corresponds to the first complex periodic solution (dotted lines in the second quadrant of Fig. 3). The third, positive, solution becomes the trivial one, ℜ(n) → 0 for kH → 0.
The branches corresponding to the trivial solution of the long-wave limit leave the ℜ(n) = 0 axis and reach positive values with decreasing wavelength. For Ωτ > Ωτ1 they merge with another positive real branch corresponding to the smaller of the real roots and transform into complex conjugate branches (red dashed line). The larger real and positive root diverges with decreasing wavelength, approaching +∞ according to Eq. (84).
Once Ωτ2 < Ωτ < Ωτ1 no real solution of Eq. (57) exists. The dashed blue line (corresponding to Ωτ = −12) reflects the complex conjugate solution. At large (but finite) wavelengths, the single positive solution of Eq. (51) corresponds to the trivial solution n = 0 of the long wavelength limit, Eq. (56). However, two additional real and positive solutions appear in a range of moderate wavelengths. These new branches behave similarly to the case previously discussed: one of them merges with the trivial branch, the other diverges at zero wavelenth.
For Ωτ < Ωτ2 (e.g., green line) the trivial branch diverges on its own, there is only one positive root for all wavelengths and the complex conjugate branch does not appear. For the shortest wavelengths and for all negative Ωτ there are three real solutions: two negative solutions, one with the limit given by Eq. (77) and the other approaching −∞ (Eq. (80) ), and one positive solution approaching +∞ according to Eq. (84).
5. Summary
We have derived the dispersion relation, Eq. (51), for perturbations of an accretion disk with heating that is offset in time relative to pressure perturbations. The standard α-prescription was generalized to account for a time shift τ between the viscous stress response and perturbation of pressure, as well as for an arbitrary ratio αξ of the corresponding perturbations (Sect. 2.1). No restrictions were placed on the allowed gas pressure to total pressure ratio, 0 ≤ β ≤ 1.
In the limit of long waves the number of real solutions for the perturbation growth rate,
Ωn, and their signs depend both on the relation between
ξ and β, and on the value of the time shift
τ. For all cases there is one trivial solution n = 0.
For the standard case with no time shift (τ = 0) there is an additional
real solution. It is negative if (Eq. (60) ),
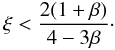 (85) The same condition applies when
τ > 0, i.e., retarded heating does not affect the appearance of the
viscous and thermal instabilities in radiation pressure dominated disks. However, advanced
heating may stabilize (or destabilize) the disk. For τ < 0, if
inequality (85) is satisfied then two real
roots with opposite signs exist (in addition to the trivial one). If the inequality is not
satisfied two negative roots appear, but only if heating is advanced by a sufficiently large
time interval, larger than a critical value,
τ < τ2 < 0. The specific value of this
critical delay, τ2, is proportional to the thermal time and
depends on β and ξ according to Eq. (69). For smaller values of |τ|,
the non-trivial real solutions are positive or do not exist. Properties of real solutions of
the dispersion relation in the limit of long wavelengths are summarized in Table 1.
(85) The same condition applies when
τ > 0, i.e., retarded heating does not affect the appearance of the
viscous and thermal instabilities in radiation pressure dominated disks. However, advanced
heating may stabilize (or destabilize) the disk. For τ < 0, if
inequality (85) is satisfied then two real
roots with opposite signs exist (in addition to the trivial one). If the inequality is not
satisfied two negative roots appear, but only if heating is advanced by a sufficiently large
time interval, larger than a critical value,
τ < τ2 < 0. The specific value of this
critical delay, τ2, is proportional to the thermal time and
depends on β and ξ according to Eq. (69). For smaller values of |τ|,
the non-trivial real solutions are positive or do not exist. Properties of real solutions of
the dispersion relation in the limit of long wavelengths are summarized in Table 1.
In addition to the real roots of the dispersion equation discussed above there exist (for τ ≠ 0) an infinite number of complex periodic solutions. Their real part, i.e., the growth rate, is opposite in sign to τ (for moderate values of Ωτ).
For very short waves there are two negative real solutions (one of the damping rates is finite, the other approaches inifnity) independently of the system parameters. For τ < 0 there is an additional positive root diverging to +∞.
Based on these properties we may conclude that the thermal and secular branches are stable for τ ≥ 0 if criterion (85) is satisfied. For τ < 0 the thermal branch is stable only for time shifts that are sufficiently large in magnitude, but the growth rates of the secular branch are always positive. However, for negative τ complex solutions with a positive real part exist (Fig. 3) and therefore the issue of disk stability in this regime is more complicated.
In a forthcoming paper we shall present a detailed physical discussion of the stability of disks with retarded heating, applying our conclusions to recent results of MHD numerical simulations of radiation-pressure dominated disks.
Acknowledgments
This work was supported in part by Polish Ministry of Science grants NN203 381436, N203 0093/1466 and N203 380336. J.P.L. was supported by the French Space Agency CNES. We are very grateful to Omer Blaes for fruitful discussions. We also thank Mateusz Janiak for helpful comments. We thank the anonymous referee for the very helpful and insightful comments.
References
- Bellman, R., & Cooke, K. L. 1963, New York, Academic [Google Scholar]
- Chandrasekhar, S. 1958, An Introduction to the Study of Stellar Structure (New York: Dover) [Google Scholar]
- Cooke, K. L., & Grossman, Z. 1982, J. Math. Anal. Appl., 86, 592 [CrossRef] [MathSciNet] [Google Scholar]
- Done, C., Wardziński, G., & Gierliński, M. 2004, MNRAS, 349, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Hirose, S., Krolik, J. H., & Blaes, O. 2009, ApJ, 691, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, S., Fukue, J., & Mineshige, S. 2008, Black-Hole Accretion Disks, Towards a New Paradigm (Kyoto, Japan: Kyoto University Press) [Google Scholar]
- Lasota, J. P., & Pelat, D. 1991, A&A, 249, 574 [NASA ADS] [Google Scholar]
- Lightman, A. P., & Eardley, D. M. 1974, ApJ, 187, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D.-B., Gu, W.-M., & Lu, J.-F. 2011, MNRAS, 415, 2319 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2006, Compact stellar X-ray sources, 157 [Google Scholar]
- Minorsky, N. 1944, Proc. N.A.S., 308 [Google Scholar]
- More, J. J., Sorensen, D. C., Hillstrom, K. E., & Garbow, B. S. 1984, The MINPACK Project, in Sources and Development of Mathematical Software (Prentice-Hall), 88 [Google Scholar]
- Piran, T. 1978, ApJ, 221, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1976, MNRAS, 177, 65 [NASA ADS] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1976, MNRAS, 175, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Shibazaki, N., & Hōshi, R. 1975, Progress Theoret. Phys., 54, 706 [CrossRef] [Google Scholar]
- Taam, R. E., & Lin, D. N. C. 1984, ApJ, 287, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J. 2004, ApJ, 605, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. M. 1959, Bull. Amer. Math. Soc., 65, 89 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The shaded area denotes the region in the (β, ξ) plane for which the real root of Eq. (57) is negative for all Ωτ ≥ 0. |
| In the text | |
 |
Fig. 2 Maps presenting absolute values of the left hand side of Eq. (57) (dispersion relation in the limit of long waves) on the complex plane for β = 0, ξ = 1, α = 0.1 and three values of Ωτ = −50 (left), 0 (middle) and 50 (right panel). Crosses and rectangles denote locations of the real and complex solutions, respectively. |
| In the text | |
 |
Fig. 3 Real part of solutions of Eq. (57) for β = 0, ξ = 1 and α = 0.1 as a function of τ. The solid lines denote real solutions, the dashed line shows complex solutions linking the real branches, while the dotted lines present periodic complex solutions (only first 20 solutions are drawn). Stars denote points where the real branches merge into the complex one (and its conjugate). |
| In the text | |
 |
Fig. 4 f1,2(ξ,β) (Eq. (69) ) dependence on β for various ξ. In this figure, we take γ = 5/3. |
| In the text | |
 |
Fig. 5 Real part of solutions of Eq. (57) for β = 0 and ξ = 1 as a function of τ. Solutions for three values of α are presented with different colors (increasing values of α0 from left to right). Solid lines are for real solutions while dotted and dashed lines show the real part of complex solutions. Only the first periodic exponential root is plotted. |
| In the text | |
 |
Fig. 6 Real part of solutions of Eq. (57) for α = 0.1 and ξ = 1 versus τ. Solutions for different values of β are presented (for the solid lines in the Ωτ > 0 region, β increases from top to bottom). Solid lines are for real solutions while dotted and dashed lines show the real part of complex solutions. Only the first periodic exponential root is plotted. In this figure, we take γ = 5/3. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 but for α = 0.1, β = 0 and varying ξ. For the solid lines in the Ωτ > 0 region, ξ decreases from top to bottom. |
| In the text | |
 |
Fig. 8 Real part of solutions of Eq. (51) as a function of the wave length 1/(kH) for α0 = 0.1, ξ = 1, Ωτ = 0 and various values of β. The line convention is the same as in previous figures. In this figure, we take γ = 5/3. |
| In the text | |
 |
Fig. 9 Real part of solutions of Eq. (51) as a function of the wave length 1/(kH) for α0 = 0.1, β = 0, Ωτ = 0 and various values of ξ. The line convention is the same as in previous figures. |
| In the text | |
 |
Fig. 10 Real part of solutions of Eq. (51) as a function of the wave length 1/(kH) for α0 = 0.1, β = 0, ξ = 1 and various values of the time delay τ. The bottom panel zooms in the shaded area on the top panel. The line convention is the same as in previous figures. In this figure, we take γ = 5/3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


