| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117419 | |
| Published online | 26 January 2012 | |
On the deviations of the classical von Zeipel’s theorem at the upper layers of rotating stars
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
e-mail: claret@iaa.es
Received: 6 June 2011
Accepted: 2 December 2011
Aims. In this paper we investigate the deviations from von Zeipel’s theorem at the upper layers of a distorted star. In addition, we derive an analytic expression for the gravity-darkening exponent β1.
Methods. We introduce two different methods to derive the theoretical gravity-darkening exponents. In the first one we use a perturbation theory to derive an analytical expression for the gravity-darkening exponent for slow rotating stars as a function of the rotation law, colatitude, and opacity derivatives. In the second procedure we explore the validity of the mentioned theorem in the upper layers of a distorted star by adapting grey and non-grey atmosphere models to our numerical method, designed originally for stellar envelopes.
Results. We have found significant deviations from von Zeipel’s theorem when we compute gravity-darkening exponents at the upper layers of a distorted star using our modified numerical method. This is a consequence of using a transfer equation that is more elaborated than the diffusion approach, therefore such a theorem is not strictly valid at lower optical depths. The shifts depend on the optical depth, on the effective temperature, and on the adopted atmosphere models. For large depths, we restore the classical value of β1, say, 1.0 for hotter stars. Taking such deviations into account, it may be possible to explain the scattering around the theoretical predictions for double-lined eclipsing binaries, as well as the low value of β1 (0.75), recently inferred for the very fast rotating star α Leo for which the classical von Zeipel’s theorem predicts β1 = 1.0.
Key words: stars: evolution / binaries: eclipsing / stars: rotation
© ESO, 2012
1. Introduction
In close binary stars, both components are distorted by rotation and by tides, with the tides tending to elongate the star, while rotation tends to flatten it at the poles. In a pioneer work, von Zeipel (1924) showed that the flux is not constant on the surface of a distorted star: 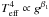 , where g is the local gravity, Teff the effective temperature, and β1 the gravity-darkening exponent (equal to 1.0 for configurations in radiative equilibrium). Later, Lucy (1967) found a mean value 0.32 for β1 for convective envelopes. Still discussing theoretical investigations, Claret (1998) introduced a numerical method to compute β1, which embraces both mechanisms of transport of energy and β1 were presented as continuous functions of the stellar masses, age, chemical composition, and mixing-length parameter.
, where g is the local gravity, Teff the effective temperature, and β1 the gravity-darkening exponent (equal to 1.0 for configurations in radiative equilibrium). Later, Lucy (1967) found a mean value 0.32 for β1 for convective envelopes. Still discussing theoretical investigations, Claret (1998) introduced a numerical method to compute β1, which embraces both mechanisms of transport of energy and β1 were presented as continuous functions of the stellar masses, age, chemical composition, and mixing-length parameter.
On the other hand, many researchers working on double-lined eclipsing binaries were able to infer β1 semi-empirically for several systems (Rafert & Twigg 1980; Pantazis & Niarchos 1998; Niarchos 2000; Djurasevic et al. 2003) to be compared with the theoretical predictions. By using interferometric techniques, some very rapid isolated rotating stars were also investigated, opening a new window on the stellar rotation (van Belle et al. 2001, 2006; Domiciano de Souza et al. 2003; Aufdenberg et al. 2006; Peterson et al. 2006; Monnier et al. 2007; Zhao et al. 2009). In Che et al. (2011) the predicted theoretical transition zone between radiative/convective envelopes (Claret 1998) was confirmed by using rapid rotators, some of them near the break-up velocities.
This amount of data on gravity-darkening permitted a robust comparison with the theoretical values of β1. A general good inter-agreement between theory and observations was found (see for example, Fig. 3 in Claret 2003). However, some discrepancies are present too, as such Che et al. (2011), who studied the hot star α Leo and found β1 = 0.75, significantly lower than the value predicted by von Zeipel’s theorem (β1 = 1.0). On the other hand, the detected scattering of the semi-empirical values of β1 around the theoretical values of double-lined eclipsing binaries also demand a theoretical explanation. To try to advance in this direction, we introduce in this paper two different methods to derive the theoretical gravity-darkening exponents. In the first one, we use a generalization of von Zeipel’s theorem to obtain an approximated expression for β1 for slow rotating stars. In the second procedure, we explore the validity of the mentioned theorem in the upper layers of a distorted star by adapting grey and non-grey atmosphere models to our numerical method. We have found deviations in the von Zeipel theorem that could explain the low value of β1 for α Leo, as well as the mentioned scattering in double-lined eclipsing binaries.
2. An analytical approach to the gravity-darkening exponent
We are interested in calculating the gravity-darkening exponent of a distorted star by using the perturbation theory. To do this, we derive a generalization of von Zeipel’s theorem, first obtained by Kippenhahn (1977). In addition to the generalization, we use it to derive the gravity-darkening exponent. By choosing the integrating factor Λ (to be determined) in such a way that Λg can be derived from a potential, it can be shown, with the equation of hydrostatic equilibrium, that the pressure is constant on equipotential surfaces. For constant mean molecular weight (ideal gas), the temperature will depend on Λ-1 while the density varies as Λ.
Here we follow Kippenhahn’s (1977) method of deriving the integrating factor Λ. Adopting a general law for the stellar rotation of the form 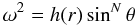 (1)where θ is the angle characterizing the colatitude, ω is the angular velocity and h(r) a generic function. If we assume that the effect of the centrifugal force on the stellar structure is small, including that the gravitational potential at the stellar surface is the Roche potential, the integrating factor for the potential equation is
(1)where θ is the angle characterizing the colatitude, ω is the angular velocity and h(r) a generic function. If we assume that the effect of the centrifugal force on the stellar structure is small, including that the gravitational potential at the stellar surface is the Roche potential, the integrating factor for the potential equation is 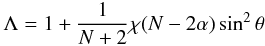 (2)where
(2)where 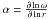 , χ = r3ω2 / (GM) and M is the stellar mass.
, χ = r3ω2 / (GM) and M is the stellar mass.
On the other hand, the equation that governs the radiative transfer in stellar interior is 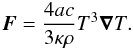 (3)If we assume that the density and temperature are functions of the potential, that is, ρ = d(Ψ)Λ and T = t(Ψ) / Λ, then Eq. (3) can be written as
(3)If we assume that the density and temperature are functions of the potential, that is, ρ = d(Ψ)Λ and T = t(Ψ) / Λ, then Eq. (3) can be written as 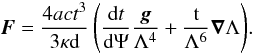 (4)The above equation is a generalization of von Zeipel’s theorem (Kippenhahn 1977). In fact, if Λ is constant (a conservative centrifugal force), we recover the classical version of the mentioned theorem; i.e., the flux will be proportional to the gravity. With Eqs. (2) and (4) we can evaluate the gravity-darkening exponent β1. To advance in the derivation of β1, we calculate the gravities and the fluxes at the pole and at the equator for an equipotential. The potential is given by
(4)The above equation is a generalization of von Zeipel’s theorem (Kippenhahn 1977). In fact, if Λ is constant (a conservative centrifugal force), we recover the classical version of the mentioned theorem; i.e., the flux will be proportional to the gravity. With Eqs. (2) and (4) we can evaluate the gravity-darkening exponent β1. To advance in the derivation of β1, we calculate the gravities and the fluxes at the pole and at the equator for an equipotential. The potential is given by 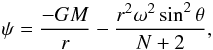 (5)and the radius of the respective equipotential r can be written as
(5)and the radius of the respective equipotential r can be written as 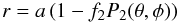 (6)where
(6)where 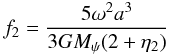 (7)and P2(θ,φ) is the second surface harmonic, a the mean radius of the level surface, η2 is the logarithmic derivative of the spherical harmonic defined through Radau’s equation (η2 = 3 at the surface for the Roche model), and Mψ the mass enclosed by an equipotential. By using Eqs. (5) and (6) we can calculate the gravity at the pole and at the equator:
(7)and P2(θ,φ) is the second surface harmonic, a the mean radius of the level surface, η2 is the logarithmic derivative of the spherical harmonic defined through Radau’s equation (η2 = 3 at the surface for the Roche model), and Mψ the mass enclosed by an equipotential. By using Eqs. (5) and (6) we can calculate the gravity at the pole and at the equator: 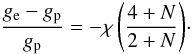 (8)Similarly, we can derive the fluxes at the pole and at the equator. At the pole the expression for the flux has a simple form. However, at the equator the calculation of the flux is a little bit more complex. By using Eq. (4) and expanding the value of Λ, we have (in units of
(8)Similarly, we can derive the fluxes at the pole and at the equator. At the pole the expression for the flux has a simple form. However, at the equator the calculation of the flux is a little bit more complex. By using Eq. (4) and expanding the value of Λ, we have (in units of 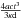 ):
): 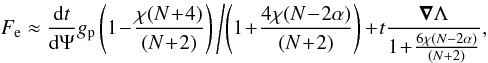 (9)and therefore
(9)and therefore ![\begin{eqnarray} {{F_{\mathrm{e}}-F_{\mathrm{p}}}\over{F_{\mathrm{p}}}}&=& {\chi\over{(N+2)}}\left[\hspace*{-4.7cm}\phantom{\frac{{{t} (N+2)}\left( {(N-2\alpha){\partial{ln \chi}\over{\partial{r}}} - 2\alpha{\partial{ln \alpha}\over{\partial{r}}}}\right)}{{{\rm d}t\over{{\rm d}\Psi}}g_{\mathrm{p}}{[2+N+6(N-2\alpha)\chi]}}} -(5N + 4 - 8\alpha) \right. \notag\\ &&\left. + \frac{{{t} (N+2)}\left( {(N-2\alpha){\partial{{\rm ln} \chi}\over{\partial{r}}} - 2\alpha{\partial{{\rm ln} \alpha}\over{\partial{r}}}}\right)}{{{\rm d}t\over{{\rm d}\Psi}}g_{\mathrm{p}}{[2+N+6(N-2\alpha)\chi]}}\right] \end{eqnarray}](/articles/aa/full_html/2012/02/aa17419-11/aa17419-11-eq36.png) (10)Equation (10) is different from the similar one obtained by Kippenhahn (1977), probably due to misprints or to the adopted level of approximation. At the surface, the term
(10)Equation (10) is different from the similar one obtained by Kippenhahn (1977), probably due to misprints or to the adopted level of approximation. At the surface, the term 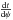 is much larger than the variation of ω and α with r. Therefore, the term containing
is much larger than the variation of ω and α with r. Therefore, the term containing 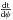 in Eq. (10) can be neglected. We finally obtain the value of β1 by approximating the logarithmic derivatives of the flux and effective gravity through Eqs. (10) and (8), respectively. By incorporating the effects of the variable opacity we get
in Eq. (10) can be neglected. We finally obtain the value of β1 by approximating the logarithmic derivatives of the flux and effective gravity through Eqs. (10) and (8), respectively. By incorporating the effects of the variable opacity we get ![\begin{equation} { {\beta_1}= {1} + {\left[(4 + \kappa_{\rho}-\kappa_{\mathrm{T}})(N-2\alpha)\over{4 + N}\right]}} \end{equation}](/articles/aa/full_html/2012/02/aa17419-11/aa17419-11-eq39.png) (11)with
(11)with 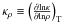 and
and 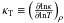 .
.
 |
Fig. 1 Gravity-darkening exponent for a 4 M⊙ model. Continuous thick line refers to grey calculation (τg = 80), continuous thin (the same but for τg = 5), dashed (the same but for τg = 1). The dashed-dotted line indicates computations by using the ATLAS atmosphere model at τA = 35 and the dotted line, the same but for τA = 1.0. The error bars denote the location of α Leo. |
We recover von Zeipel’s value for β1 (1.0) for uniform rotation and no angle dependence or if κρ = κT − 4 and/or N = 2α, in the general case. If we use the semi-empirical value of the gravity-darkening exponent for α Leo by Che et al. (2011) as a constraint, we can estimate the effects of the geometry and differential rotation in that star. The logarithmic derivatives κT and κρ can be evaluated from appropriated tables of opacities, such as those by Ferguson et al. (2005). For a typical chemical composition (X = 0.70, Z = 0.02) and for log T = 4.0, log ρ = −6.0 → κT = 9.20 and κρ = 0.28. Considering no dependence on the angle θ we obtain α = −0.1. Of course, such value will depend on the depth of the stellar envelope we are dealing with. We should only take such an estimation as an approximation. Equation (11) was derived by using a perturbation theory (slow rotation), but since α Leo is rotating near the break-up velocity, it is not sufficient to analyse such stars. However, this equation can be applied in those distorted binary systems or slow isolated rotators for which the rotation rates are far from the critical ones. A more adequate approach to β1 for rapid rotators is analysed in the next section.
3. Deviations from von Zeipel’s theorem at the upper layers; final remarks
Our numerical method which was introduced to derive β1 is based on the triangle strategy used in stellar evolution calculations (Claret 1998). This method does not depend on the details of the rotation laws. It is based fundamentally on the star’s distortions simulated by different temperature distribution corresponding to different log g’s and log Teff’s. We now comment on the main characteristics of this method. As is usual in stellar evolution calculations, the outer-layer integration should be carried out after each time step. If the external boundary conditions of the interior are unchanged at the fitting point, the envelope integrations would be the same as before. Such calculations can be avoided thus saving computational time. In practice, three envelope computations are performed corresponding to three points in the HR Diagram. If the next point on the evolutionary track is still within this triangle, the same envelope integrations can be used without loss of accuracy (provided that the triangle is sufficiently small). Of course, new integrations are necessary if this condition is not fulfilled.
To simulate a distorted stellar configuration we increased the number of points in the triangle strategy. Given a point on an evolutionary track (characterized by log Teff and log g), a series of envelopes with log g′ = log g + Δlog g and trial values of effective temperatures are computed. Often, these new envelopes do not present the same physical conditions – pressure x temperature relationship – at the bottom as the original envelope. By interpolation in these envelopes, another envelope is found that presents the same physical conditions as the reference point (such an envelope has an effective temperature 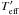 , which is different from the original). By repeating the process n times (by varying the values of Δlog g), a family of n interpolated envelopes (characterized by log g′ (n) and log
, which is different from the original). By repeating the process n times (by varying the values of Δlog g), a family of n interpolated envelopes (characterized by log g′ (n) and log 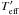 (n) is found with the same physical conditions at the bottom. Finally, by numerically differentiating this family of envelopes, we obtain β1 for each point on a given evolutionary track (
(n) is found with the same physical conditions at the bottom. Finally, by numerically differentiating this family of envelopes, we obtain β1 for each point on a given evolutionary track (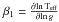 ). However, in calculating the corresponding envelopes, the equation of diffusion was used throughout. On the other hand, von Zeipel’s theorem was also derived by using this approximation. Intuitively, diffusion is only an appropriate approach for the deeper layers. In fact, the moment of the transfer equation can be written as
). However, in calculating the corresponding envelopes, the equation of diffusion was used throughout. On the other hand, von Zeipel’s theorem was also derived by using this approximation. Intuitively, diffusion is only an appropriate approach for the deeper layers. In fact, the moment of the transfer equation can be written as 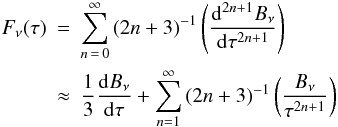 (12)where Fν(τ) is flux, Bν the Planck’s function and τ the optical depth scale. At great depth (there are too many photon mean free paths from the surface), the second term on the right-hand side of Eq. (12) vanishes and the transfer equation reduces to a simple form, i.e., the diffusion approximation. As a consequence, Eq. (12) reduces to Eq. (3), which is the basis of the derivation of the classical von Zeipel’s theorem (β1 = 1.0). This result is used as a control of our method at large optical depths as well as the solution for τ = 0.
(12)where Fν(τ) is flux, Bν the Planck’s function and τ the optical depth scale. At great depth (there are too many photon mean free paths from the surface), the second term on the right-hand side of Eq. (12) vanishes and the transfer equation reduces to a simple form, i.e., the diffusion approximation. As a consequence, Eq. (12) reduces to Eq. (3), which is the basis of the derivation of the classical von Zeipel’s theorem (β1 = 1.0). This result is used as a control of our method at large optical depths as well as the solution for τ = 0.
It is interesting to explore the behaviour of β1 at the atmosphere of a distorted star where the diffusion equation is no longer valid. Fortunately, our numerical method can be extended to the surface layers, and we are able to evaluate the influence of the optical depth on β1. For each stellar model generated with our evolution stellar code (Claret 2004), characterized by a given mass, log Teff, log g, and metallicity, a grey atmosphere is computed. By transferring our numerical method to these upper layers we can derive the behaviour of β1 as a function of the effective temperature and on the optical depth. We restrict our calculations here to hotter models because we are interested in exploring the range of validity of von Zeipel’s theorem. The maximum value of Δlog g adopted was 0.25 (corresponding to the difference between the log g at the pole and at the equator of α Leonis). Figure 1 shows the results of these calculations for three optical depths using an evolutionary model with 4 M⊙. As expected, at great optical depth, we restore the classical value of β1 (1.0). However, when we consider more external layers, the corresponding values of β1 decrease and there are also shifts in the transition zone (radiative/convective). This indicates that von Zeipel’s theorem is not strictly valid at the upper layers. The values of β1 shown in Fig. 1 for colder models (based on grey atmospheres) are not fully reliable.
To check the reliability of the results described in the last paragraph by adopting more elaborated atmosphere models, we also use our numerical method but with a flag to use the structure of the ATLAS stellar atmosphere models, instead of the grey models. The ATLAS 9 (Kurucz, priv. comm.) models make use of a much more complex transfer equation, and the resulting calculations are more reliable than those by adopting the grey approximation. As in the grey case, the values of β1 are systematically lower than 1.0, except at great depth, where the von Zeipel value is restored for hotter models. There are some differences if we compare β1(ATLAS) with the β1s derived by adopting grey models, but they are not as large for a given optical depth. We also note the numerical noise for ATLAS that is caused by the interpolation process in the atmosphere structure. (The neighbouring grid points in log g and effective temperatures differ 0.5 and up to 2500 K, respectively.)
As mentioned in the Introduction, the semi-empirical values of β1 obtained from double-lined eclipsing binaries and rapid rotating stars compare well with the theoretical predictions based on our original method (see for example, Pantazis & Niarchos 1998; Niarchos 2000; Djurasevic et al. 2003; Che et al. 2011). There is some scattering around the theoretical predictions based on our numerical method using stellar envelopes, based on the diffusion equation. Within this context, we may interpret the detected deviations from von Zeipel’s theorem at lower optical depths as theoretical error bars, i.e., as lower limits for β1. The recent derivation of the semi-empirical β1 for the hot rapidly rotating star α Leo (Che et al. 2011), which is between 0.64 and 0.80, could be explained if we consider the deviations found here (see Fig. 1). One question arising from this discussion is where we should put such a lower limit, say, what is the optical depth we should select to compute the deviations of β1? A measure of the drift of the radiation field can be evaluated by taking the ratio between the anisotropic/isotropic terms, which is given approximately by [Teff / T(τ)] 4. The deviations from the diffusion equation become important for τc of the order of 1. We expect that the mentioned critical optical depth depends on spectral type. We adopt τc = 1 provisionally, although it may also depend on the adopted stellar atmosphere models and perhaps on more accurate observational constraints. The mentioned scattering for close binaries could be explained with the help of Eq. (11), including presence of disks, or a combination of that equation and the effects described in this section.
The progress in deriving semi-empirical values of β1 is notorious for isolated rapid rotating stars, including those near
the break-up velocities. On the other hand, the researchers in eclipsing binaries are continually bringing new data to be compared with theoretical predictions. That conjunction surely will contribute to refine a little more the theoretical calculation of the gravity-darkening exponents. Among the improvements that can be implemented, we plan to introduce a dependence of β1 on the details of the rotation laws, including the degree of the distortions.
Acknowledgments
This paper is dedicated to the memory of Jens Viggo Clausen. I would like to thank V. Costa and an anonymous referee for useful suggestions. The Spanish MEC (AYA2006-06375, AYA2009-14000-C03-01) is gratefully acknowledged for its support during the development of this work. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Abstract Service.
References
- Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006, ApJ, 645, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 1998, A&AS, 131, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2003, A&A, 406, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Djurasevic, G., Rovithis-Livaniou, H., Rovithis, P., Georgiades, N., & Erkapic, S. 2003, A&A, 402, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Jankov, S., et al. 2003, A&A, 407, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1967, Z. Astrophys., 65, 89 [Google Scholar]
- Kippenhahn, R. 1977, A&A, 58, 267 [NASA ADS] [Google Scholar]
- Kopal, Z. 1959, Close Binary Systems (Chapman & Hall) [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Niarchos, P. G. 2000, in Variable Stars as Essential Astrophysical Tools, ed. C. Ibanoglu (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Pantazis, G., & Niarchos, P. G. 1998, A&A, 335, 199 [NASA ADS] [Google Scholar]
- Peterson, D. M., Hummel, C. A., Pauls, T. A., et al. 2006, Nature, 440, 896 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rafert, J. B., & Twigg, L. W. 1980, MNRAS, 193, 79 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Ciardi, D. R., Thompson, R. R., Akeson, R. L., & Lada, E. A. 2001, ApJ, 559, 1155 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van Belle, G. T., Ciardi, D. R., ten Brummelaar, T., et al. 2006, ApJ, 637, 494 [NASA ADS] [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, M., Monnier, J. D., Pedretti, E., et al. 2009, ApJ, 701, 209 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Gravity-darkening exponent for a 4 M⊙ model. Continuous thick line refers to grey calculation (τg = 80), continuous thin (the same but for τg = 5), dashed (the same but for τg = 1). The dashed-dotted line indicates computations by using the ATLAS atmosphere model at τA = 35 and the dotted line, the same but for τA = 1.0. The error bars denote the location of α Leo. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


