| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117271 | |
| Published online | 14 February 2012 | |
Research Note
Near-infrared light curves of type Ia supernovae
1
Hamburger Sternwarte, Gojenbergsweg 112, 21029
Hamburg, Germany
e-mail: djack@hs.uni-hamburg.de; yeti@hs.uni-hamburg.de
2
Homer L. Dodge Department of Physics and Astronomy, University of
Oklahoma, 440 W Brooks, Rm
100, Norman,
OK
73019-2061,
USA
Received:
17
May
2011
Accepted:
3
January
2012
Aims. With our time-dependent model atmosphere code PHOENIX, our goal is to simulate light curves and spectra of hydrodynamical models of all types of supernovae. In this work, we simulate near-infrared light curves of SNe Ia and confirm the cause of the secondary maximum.
Methods. We apply a simple energy solver to compute the evolution of an SN Ia envelope during the free expansion phase. Included in the solver are energy changes due to expansion, the energy deposition of γ-rays and interaction of radiation with the material.
Results. We computed theoretical light curves of several SN Ia hydrodynamical models in the I, J, H, and K bands and compared them to the observed SN Ia light curves of SN 1999ee and SN 2002bo. By changing a line scattering parameter in time, we obtained quite reasonable fits to the observed near-infrared light curves. This is a strong hint that detailed NLTE effects in IR lines have to be modeled, which will be a future focus of our work.
Conclusions. We found that IR line scattering is very important for the near-infrared SN Ia light curve modeling. In addition, the recombination of Fe III to Fe II and of Co III to Co II is responsible for the secondary maximum in the near-infrared bands. For future work the consideration of NLTE for all lines (including the IR subordinate lines) will be crucial.
Key words: radiative transfer / methods: numerical / stars: atmospheres / supernovae: general
© ESO, 2012
1. Introduction
We focus on the near-infrared light curves of type Ia supernovae (SNe Ia). The light curves in the near-infrared are of particular interest, because they have been claimed to be near standard candles at the time of B-band maximum in the IR (Krisciunas et al. 2004a). In addition, many, but not all SNe Ia exhibit a secondary maximum in the IR bands. The secondary maximum was first noted by Elias et al. (1981). Höflich et al. (1995) explained the secondary maximum as due to the expansion of the IR pseudo-photosphere, whereas Suntzeff (1996) suggested that it was due to a global shift of radiation from blue to red. Pinto & Eastman (2000) suggested that the transition from Fe III to Fe II as the dominant ionization stage was important although they implied that the secondary maximum occurs when the photosphere has receded into the non-radioactive center. Kasen (2006) performed a detailed study of SN Ia light curves in the near-infrared and obtained reasonable fits to observations. He also finds that the secondary maximum is an effect of the ionization evolution of iron group elements in the expanding envelope. We apply our time-dependent model atmosphere code PHOENIX and investigate SNe Ia by comparing model light curves in the near-infrared to observed light curves. We will also focus on the origin of the secondary maximum.
We present model light curves of SNe Ia in the near-infrared. In Sect. 2 we present the methods we used in some detail. In Sect. 3 we present light curves of SNe Ia for different hydrodynamical models in the I, J, H, and K bands. We consider a parametrized IR line scattering in the solution of the radiative transfer to improve our fits to observed light curves. An investigation of the secondary maximum that has been observed in near-infrared light curves is discussed in a final section.
2. Methods
We use our time dependent model atmosphere code PHOENIX, version 16, to compute model light curves of type Ia supernovae. We use the time dependent extension and the method as described in Jack et al. (2009, 2011). We calculate SN Ia model light curves for different hydrodynamic (explosion) models. In our previous work, we presented model light curves in the optical bands with reasonable fits to observations. In this work, we focus on the near-infrared wavelength region and model the light curves in the I, J, H, and K bands.
To compute SN Ia light curves, our approach is a simple energy solver that solves for an energy change of the material during a time step of the envelope evolution. The energy can change due to the free adiabatic expansion, the deposition of energy from γ-rays from the radioactive decay of 56Ni and 56Co, and the interaction of radiation with the material. In our calculations, we assume homologous expansion. The γ-ray deposition is solved with the assumption of a gray atmosphere. Changes of ionization state are also included in our solver.
To determine the energy change of the material due to the interaction with the radiation, we have to solve the radiative transfer. For each time step, we solve the non-gray spherical symmetric radiative transfer equation for expanding atmospheres including special relativistic effects. We typically use about 2000 wavelength points to keep the computation time reasonable.
Given the problems with the simple LTE treatment of line scattering as shown in Jack et al. (2011), we investigate the effects of IR line scattering on SN Ia light curves in the near-infrared. In our previous paper (Jack et al. 2011), we indicated how important UV/optical line scattering is during the later phases of the light curve evolution. Here, we study this effect in more detail.
The source function of the radiative transfer equation including scattering for an equivalent two level atom can be written as 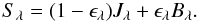 (1)The source function is represented by Sλ, the Planck function by Bλ and the mean intensity by Jλ. All these quantities depend on the wavelength λ. Here, we used ϵλ as the line thermal coupling parameter. For ϵλ = 1 there is only true absorption and no line scattering takes place. The source function is then given by Sλ = Bλ (pure LTE). In reality, the thermal coupling parameter ϵλ will vary over the whole wavelength range. For the calculation with PHOENIX, it is possible to set a wavelength independent factor ϵ = ϵλ = const. to approximate LTE line scattering over the whole wavelength range.
(1)The source function is represented by Sλ, the Planck function by Bλ and the mean intensity by Jλ. All these quantities depend on the wavelength λ. Here, we used ϵλ as the line thermal coupling parameter. For ϵλ = 1 there is only true absorption and no line scattering takes place. The source function is then given by Sλ = Bλ (pure LTE). In reality, the thermal coupling parameter ϵλ will vary over the whole wavelength range. For the calculation with PHOENIX, it is possible to set a wavelength independent factor ϵ = ϵλ = const. to approximate LTE line scattering over the whole wavelength range.
 |
Fig. 1 Synthetic spectrum of a SN Ia at day 20 plotted with the filter functions of the I, J, H, and K band. |
For our approach to model light curves of SNe Ia, we use the results of hydrodynamical explosion simulations, as our initial atmosphere structures which we then evolve in time. In this work, we use the explosion model results of the deflagration model W7 (Nomoto 1984). We also used one delayed detonation model, the model DD25 calculated by Höflich et al. (2002). Model DD16 (Höflich et al. 2002) which we studied in previous work is not considered here, because its low yield of 56Ni makes it too dim to account for normal SNe Ia. We used our hydrodynamic solver to obtain detailed spectra at certain days in the light curve evolution, (see Jack et al. 2011, for details). Light curves are calculated by convolving the appropriate filter functions with the theoretical spectra. We compare our synthetic light curves to observed light curves of two SN Ia events: SN 1999ee and SN 2002bo. The filter functions we used here are shown in Fig. 1. The photometric observations of SN 1999ee in the J and H band are presented in Krisciunas et al. (2004b). For SN 2002bo photometric observations in the J, H, and K band have been obtained by Krisciunas et al. (2004c).
3. Near-infrared light curves of SNe Ia
 |
Fig. 2 Model and observed light curves in the I band. Two different explosion models were used to compute the model light curves. |
We first present the results of an approach of a constant line scattering factor ϵ = 0.8 to the light curve modeling, where we compare the results of two different hydrodynamical models. Figure 2 shows the calculated model light curves of two hydrodynamical models in the I band. They are compared to two observed light curves of SN 1999ee and SN 2002bo. Both model light curves produce the steep rise during the first days after the explosion reasonably well. However, the model light curve rises further, although the observed light curves show a decline after maximum at around 13 days after explosion. During the later phase around 30 days after the explosion, the model light curves are much too bright compared to the observed light curves. There is also no indication of a secondary maximum in the model light curves.
 |
Fig. 3 Light curves in the J band. Two different explosion models were used to compute the model light curves and to compare them to observations. |
In Fig. 3, the model light curves in the J band are shown together with the observed light curves. Again, the first phase is well represented by the model light curves. The model light curves rise after a first maximum to a secondary maximum, which is much brighter and earlier than the secondary maximum in the observed light curves. Furthermore, the secondary maximum of the DD25 model is earlier than the one of hydrodynamical model W7. However, the difference of 2.5 mag around day 35 between models and observations is enormous.
 |
Fig. 4 Light curves in the H band. Two different explosion models were used to compute the model light curves. |
 |
Fig. 5 Light curves in the K band. The model light curves of W7 and DD25 are significantly brighter than the observations during the later phase. |
A similar picture is seen in the H and K band as shown in Figs. 4 and 5.
So far, we used for the calculations of our LTE model light curves a constant time independent factor of ϵ = 0.8. We now use this LTE line scattering factor to approximate the effect of line scattering on the shape of the light curves in the near-infrared. We calculated several model light curves each with a different LTE line scattering factor, ϵ. At each point of the light curve, we let the atmosphere structure adapt to the new conditions with its ϵ until a radiative equilibrium state is reached. This led to different resulting atmosphere structures or more precisely temperature structures at each day and thus to differences in the shapes of the model light curves.
 |
Fig. 6 Light curves in the I band computed with different values of the line scattering factor ϵ. |
 |
Fig. 7 Temperature structure of the envelope at day 30. A smaller line scattering factor ϵ leads to a hotter atmosphere. |
Figure 6 shows the I band light curves obtained with different values of ϵ. With a smaller ϵ, the light curve becomes fainter. A look at the temperature structure in Fig. 7 reveals that decreased ϵ leads to a hotter atmosphere. In the hotter atmosphere, the iron and cobalt are mostly doubly ionized. As the atmosphere cools down, the iron and cobalt recombine to Fe II and Co II, and the flux increases due to numerous lines of these species in the near-infrared. This recombination effect in the near-infrared light curve has also been found by Kasen (2006) and Höflich et al. (1995). The intersection of the model light curves with the observed light curves shows that the best value of ϵ changes during the evolution of the light curve. ϵ decreases with time (i.e., line scattering becomes more and more important) in order to fit the observed light curves. This is reasonable, because the ongoing expansion leads to lower densities at later times, and line scattering becomes more important because of the thinner atmosphere. However, during the early phase near maximum light, ϵ has to be closer to pure LTE (Baron et al. 1996).
We now seek to fit the entire light curve with a single function for ϵ, that is we choose ϵ = ϵ0f(t) where f(t) is a function of time. Our model light curves now reproduce the observed light curves much more faithfully. Even the secondary maximum is well reproduced for each band. For instance, we show in Fig. 12 the new best fitting light curve in the I band. The solid line shows the W7 model light curve, which has an ϵ that decreases with time. We chose the light curve of SN 1999ee to obtain the best fit. It is clear that different values of f(t) can be used to obtain a better fit to the light curve of SN 2002bo.
4. Secondary maximum in the near-infrared SN Ia light curves
In all bands in the near-infrared, the observed light curves show a secondary maximum around 30 to 40 days after explosion. Since with a time-dependent ϵ our model light curves reproduce the observed light curves pretty well, we will focus on the specific cause of the secondary maximum in each IR band. We investigate the cause of the secondary maximum in each of the near-infrared bands by looking at the spectral evolution of the model light curves in the respective band. Basically, we confirm the results of Kasen (2006). However, we can additionally assign features of certain elements to the individual bands and show detailed spectra.
The I band is known to be dominated by the Ca IR triplet.
 |
Fig. 8 Spectral evolution in the I band from day 20 to day 50 after the explosion. The solid line displays the filter function. |
In Fig. 8 the spectral evolution in the I band is shown. The broad feature at 8500 Å is the Ca triplet. This feature stays present as the flux outside of the feature declines while the SN Ia envelope evolves. This leads to the decline in the light curve after the first maximum. Starting at day 40 a new “W-shaped” feature emerges at around 7500 Å. These are lines of Fe II, and the feature is even more significant in the spectrum at day 50. From day 30 to day 50 the temperature in the expanding envelope is decreasing. The temperature eventually reaches the temperature/pressure regime where Fe III recombines to Fe II. This increases the brightness in the I band due to emission lines of Fe II present in this wavelength region. Thus, emission lines of Fe II are responsible for the rise to a secondary maximum in the I band.
 |
Fig. 9 Spectral evolution in the J band from day 20 to day 45 after the explosion. The solid line shows the filter function. |
We now examine the secondary maximum in the J band. The spectral evolution in that wavelength range is shown in Fig. 9. With the SN Ia evolving, the flux is decreasing in the J band because the temperature of the envelope decreases. At day 30, new features arise, which increase the brightness in the J band. These features are caused by lines of Fe II and Co II. Therefore, the recombination of Fe III to Fe II is responsible for the rise in the J band. Additionally, Co III recombines to Co II at about the same temperature and therefore time in the light curve evolution. Thus, Co II lines emerge in the J band due to this recombination. The secondary maximum in the J band is caused by both emerging Fe II and Co II lines.
 |
Fig. 10 Spectral evolution in the H band from day 16 to day 45 after the explosion. The solid line shows the filter function. |
The spectral evolution in the H band is shown in Fig. 10. In the spectrum at day 26, two broad features emerge in this wavelength range. In the spectrum of days 35 and 45, these two features are clearly visible. They cause the rise in the brightness of the H band to a secondary maximum. We found that these features are caused by lines of Co II. Thus, the recombination of Co III to Co II causes the rise to a secondary maximum in the light curve of the H band.
 |
Fig. 11 Spectral evolution in the K band from day 16 to day 45 after the explosion. The solid line shows the filter function. |
In the K band, the spectral evolution of our SN Ia model is shown in Fig. 11. The flux is decreasing as the envelope expands and cools down. However, at days 40 and 45 features emerge and cause a rise in the brightness of the K band. These features are again lines of Co II. The recombination of Co III to Co II causes the secondary maximum in the K band.
4.1. Non-radioactive core
 |
Fig. 12 Light curve in the I band with and without the non-radioactive iron core. |
The W7 model has a non-radioactive iron core. Pinto & Eastman (2000) showed that the consequent negative temperature gradient leads to a further reduction in the mean opacity. This may have an influence on the duration or magnitude of the IR secondary maximum. Therefore, it is worthwhile checking wether the non-radioactive center affects the shape of the secondary maximum in the near-infrared. We replaced the iron core of the W7 model with radioactive 56Ni and computed the light curve. This increases the total mass of 56Ni from 0.56 to 0.66 solar masses. As shown in Fig. 12, there are only small difference between the light curves with and without the non-radioactive iron core. This simple variation does not capture the full effect of the presence or absence of a non-radioactive core, since a shift in the nickel distribution can have important effects on the light curve (Baron et al., in prep.). Additionally, late time spectra show that that a non-radioactive core seems to be required in most SNe Ia (Höflich et al. 2004; Motohara et al. 2006; Fesen et al. 2007; Gerardy et al. 2007; Maeda et al. 2010).
5. Conclusion
We applied our time-dependent model atmosphere code PHOENIX to model light curves of type Ia supernovae in the near-infrared wavelength range. In a first approach with a constant LTE line scattering parameter ϵ in the radiative transfer, we reproduced the observed light curves during the first phase quite well. However, the model light curves during the later phase were too bright, and we could not reproduce the secondary maximum.
We show that a more detailed treatment of IR line scattering is very important for the modeling of the later phase of the
near-infrared light curves of SNe Ia. We used as an approximation an LTE line scattering parameter that decreases in time. This is a good approach, because the atmosphere becomes thinner as expansion goes on and scattering becomes more important. We use this approximation to obtain fits to the observed light curves of SN 1999ee and SN 2002bo, improving our model light curves significantly. The next step is to treat the atmosphere in full non-LTE, where the temperature needs to adapt to the non-LTE condition, which requires substantial time on parallel supercomputers. Kasen (2006) also found that his models overshot the observed secondary maximum in H and K, while he mainly attributed this to incomplete line lists in the IR, he also suggested that his treatment of LTE might be a possible cause.
The secondary maximum in each band of the near-infrared was quite accurately reproduced by our model light curves with time-dependent ϵ. We investigated the spectral evolution and found that the I band secondary maximum arises due to recombination of Fe III to Fe II. An Fe II feature emerges in this band and increases the brightness. For the secondary maximum in the J band, a mix of Fe II and Co II lines emerges and causes the rise to a secondary maximum in the model light curve. The bands H and K also show a secondary maximum. This is caused by the recombination of Co III to Co II. We confirmed that ionization stage changes in iron group elements are responsible for the secondary maximum as previously found (Kasen 2006). In fact, since we use neither expansion opacities, nor the Sobolev approximation, our results robustly indicate the need for a full NLTE treatment. Furthermore, we can explicitly assign lines of different elements to different bands. These results also show how important the treatment of Fe and Co in non-LTE is and should be used in future work, when faster computers are available.
Acknowledgments
This work was supported in part by the Deutsche Forschungsgemeinschaft (DFG) via the SFB 676, NSF grant AST-0707704, US DOE Grant DE-FG02-07ER41517, and by program number HST-GO-12298.05-A which is supported by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. This research used resources of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231, and the Höchstleistungs Rechenzentrum Nord (HLRN). We thank all these institutions for generous allocations of computation time.
References
- Baron, E., Hauschildt, P. H., Nugent, P., & Branch, D. 1996, MNRAS, 283, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Elias, J. H., Frogel, J. A., Hackwell, J. A., & Persson, S. E. 1981, ApJ, 251, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Höflich, P. A., Hamilton, A. J. S., et al. 2007, ApJ, 658, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Gerardy, C. L., Meikle, W. P. S., Kotak, R., et al. 2007, ApJ, 661, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Khokhlov, A., & Wheeler, J. C. 1995, ApJ, 444, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Gerardy, C., Fesen, R., & Sakai, S. 2002, ApJ, 568, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Gerardy, C. L., Nomoto, K., et al. 2004, ApJ, 617, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Jack, D., Hauschildt, P. H., & Baron, E. 2009, A&A, 502, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jack, D., Hauschildt, P. H., & Baron, E. 2011, A&A, 528, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasen, D. 2006, ApJ, 649, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Phillips, M. M., & Suntzeff, N. B. 2004a, ApJ, 602, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Phillips, M. M., Suntzeff, N. B., et al. 2004b, AJ, 127, 1664 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Suntzeff, N. B., Phillips, M. M., et al. 2004c, AJ, 128, 3034 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Benetti, S., Stritzinger, M., et al. 2010, Nature, 466, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Motohara, K., Maeda, K., Gerardy, C. L., et al. 2006, ApJ, 652, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, P. A., & Eastman, R. G. 2000, ApJ, 530, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B. 1996, in Supernovae and Supernova Remnants, ed. T. S. Kuhn (Cambridge, UK: Cambridge University Press), IAU Colloq., 145, 41 [Google Scholar]
All Figures
 |
Fig. 1 Synthetic spectrum of a SN Ia at day 20 plotted with the filter functions of the I, J, H, and K band. |
| In the text | |
 |
Fig. 2 Model and observed light curves in the I band. Two different explosion models were used to compute the model light curves. |
| In the text | |
 |
Fig. 3 Light curves in the J band. Two different explosion models were used to compute the model light curves and to compare them to observations. |
| In the text | |
 |
Fig. 4 Light curves in the H band. Two different explosion models were used to compute the model light curves. |
| In the text | |
 |
Fig. 5 Light curves in the K band. The model light curves of W7 and DD25 are significantly brighter than the observations during the later phase. |
| In the text | |
 |
Fig. 6 Light curves in the I band computed with different values of the line scattering factor ϵ. |
| In the text | |
 |
Fig. 7 Temperature structure of the envelope at day 30. A smaller line scattering factor ϵ leads to a hotter atmosphere. |
| In the text | |
 |
Fig. 8 Spectral evolution in the I band from day 20 to day 50 after the explosion. The solid line displays the filter function. |
| In the text | |
 |
Fig. 9 Spectral evolution in the J band from day 20 to day 45 after the explosion. The solid line shows the filter function. |
| In the text | |
 |
Fig. 10 Spectral evolution in the H band from day 16 to day 45 after the explosion. The solid line shows the filter function. |
| In the text | |
 |
Fig. 11 Spectral evolution in the K band from day 16 to day 45 after the explosion. The solid line shows the filter function. |
| In the text | |
 |
Fig. 12 Light curve in the I band with and without the non-radioactive iron core. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


