| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 14 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201016422 | |
| Published online | 07 February 2012 | |
Automatic spectral classification of stellar spectra with low signal-to-noise ratio using artificial neural networks ⋆
1 Instituto de Astronomía y Meteorología (IAM), University of Guadalajara Av. Vallarta 2602, Guadalajara, Jal., C.P. 44130, México
e-mail: silvana@astro.iam.udg.mx
2 Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
e-mail: rcorradi@iac.es; amr@iac.es
3 Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
Received: 31 December 2010
Accepted: 20 October 2011
Context. As part of a project aimed at deriving extinction-distances for thirty-five planetary nebulae, spectra of a few thousand stars were analyzed to determine their spectral type and luminosity class.
Aims. We present here the automatic spectral classification process used to classify stellar spectra. This system can be used to classify any other stellar spectra with similar or higher signal-to-noise ratios.
Methods. Spectral classification was performed using a system of artificial neural networks that were trained with a set of line-strength indices selected among the spectral lines most sensitive to temperature and the best luminosity tracers. The training and validation processes of the neural networks are discussed and the results of additional validation probes, designed to ensure the accuracy of the spectral classification, are presented.
Results. Our system permits the classification of stellar spectra of signal-to-noise ratio (S/N) significantly lower than it is generally considered to be needed. For S/N ≥ 20, a precision generally better than two spectral subtypes is obtained. At S/N < 20, classification is still possible but has a lower precision. Its potential to identify peculiar sources, such as emission-line stars, is also recognized.
Key words: methods: data analysis / planetary nebulae: general / astronomical databases: miscellaneous
© ESO, 2012
1. Introduction
The use of artificial neural networks (ANNs) as a classification tool in astronomy has been widely developed in recent decades. For instance, ANNs have been used to recognize stars and galaxies in images from large digital surveys (Bertin 1994; Odewahn 1995), in the morphological classification of galaxies (Adams 1994; Naim et al. 1995; Bazel 2001), and in the spectral classification of both galaxies (Folkes 1996; Lahav & Maddox 1996; Ball et al. 2004) and stars. Many papers have been devoted to this last subject: von Hippel et al. (1994), Bailer-Jones (1996), Bailer-Jones et al. (1998), in the visible region; Vieira & Ponz (1995) in the UV region; and Weaver & Torres-Dodgen (1997) in the red and near infrared. In all of these studies the results are highly satisfactory, resulting in a classification accuracy better than two spectral subtypes
The rapid evolution of astronomical instrumentation and the advent of more sensitive and sophisticated detectors has permitted the acquisition of huge quantities of astronomical data. High performance multi-object spectrographs in operation at many observatories allow the acquisition of several hundred spectra in one night. Spectrographs such as the one used in the Sloan Digital Sky Survey (SDSS) can produce 460 spectra at a time (York et al. 2000), or some 104 spectra in one observing run. In the near future projects such as the Global Astrometric Interferometer for Astrophysics (GAIA) will produce medium resolution spectra for 108 stars (Perryman et al. 2001).
The reduction and management of this vast amount of information, and the related extraction of physical quantities, require the use of advanced analysis techniques. With this in mind, many authors have developed automatic spectral classification processes. von Hippel et al. (1994) present a review of the efforts made in this direction in previous years.
The non-linearity of the classification process ensures that it is an ideal candidate for the application of one of the most robust and, at the same time, most versatile mathematical tools: the artificial neural networks. Bailer-Jones et al. (1998) reported a σrms in the spectral classification of 1.1 subtypes, using a database of 5000 spectra in the visible region (3800 to 5200 Å) with a resolution of 3 Å. Singh et al. (1998) reached a precision of 2.2 spectral subtypes using a training catalog with only 55 spectra at a resolution of 11 Å. In the red and near infrared region, Weaver & Torres-Dodgen (1997), using a spectral catalog of 250 stellar spectra (from O to M stars) with a resolution of 15 Å in the 5800 to 8900 Å region, achieved an accuracy of 0.5 spectral subtypes and 0.3 luminosity classes (similar to obtained by a human expert). In addition, Weaver (2000) used ANNs to classify unresolved binary stars.
Rodríguez et al. (2004) compared the results obtained using expert systems, fuzzy logic, and ANNs with the human expert results. They found that only ANNs could equal the human expert precision. Manteiga et al. (2009) used ANNs and fuzzy reasoning to classify stellar spectra. The precision they reach in spectral classification is similar to that of human experts in more than 80% of the sample.
Another possible means of automatic classification is the direct determination of the atmospheric parameters (Teff, log g, and [M/H]) without the mediation of the spectral type. This approach has several advantages, such as the determination of stellar parameters in a continuum domain (not discretized like the spectral type), but it depends on the selected stellar model. Bailer-Jones et al. (1997) used a database of synthetic spectra generated with SPECTRUM (Gray & Corbally 1994; Gray & Arlt 1996) and based on the fully blanketed stellar Kurucz models (Kurucz 1979, 1992). With this database, they trained ANNs to obtain the stellar physical parameters (Teff and log g) and concluded that it is possible to obtain also the [M/H] parameter using the ad-hoc trained ANNs (see also Bailer-Jones 2000). Munari et al. (2005a) and Zwitter et al. (2005) used X2 minimization to obtain the best-fit spectra from a synthetic database (Munari et al. 2005b). They determined the template that provides the closest match to the observed spectrum, hence derived values of the parameters Teff, log g, and [M/H].
Recio-Blanco et al. (2006) determined these three parameters, as well as individual chemical abundances using their algorithm MATISSE (MATrix Inversion for Spectral SyntEsis). The physical parameters (θ) associated with an observed spectra were determined by projecting the spectra over the corresponding basis vector Bθ(λ), which was obtained from an optimal linear combination of theoretical spectra Si(λ) whose coefficients were determined via a maximum correlation and least squares linear regression process.
In all these works, the training and validation catalogs were built with spectra of similar characteristics as required by human experts, i.e. with a signal-to-noise ratio (S/N) of about 100 or greater. The same condition is required for the spectra to be classified. However, typical spectra obtained in many observational campaigns do not reach this quality. In our case, 75% of our spectra has a S/N < 40, and fewer than 5% of the sample has S/N > 100. Snider et al. (2001) carried out a three-dimensional classification (Teff, log g, and [Fe/H]) for F and G stars, and explored the impact of the S/N on the classification with ANNs. They found that it is possible to accurately estimate the physical parameters if they use ANNs trained on spectra of commensurate S/N, for a ratio as low as 13. They reach an accuracy from 135 K to 150 K in Teff and from 0.25 to 0.30 dex in log g.
Recio-Blanco et al. 2006, included artificial noise to simulate observed spectra from a synthetic one. They considered five values of S/N from 20 to 200 and found that the error in the parameters determination increases considerably for S/N lower than ~ 25, especially for metal-poor hot sub-giants.
In this paper, we present a new and robust classification scheme based on artificial neural networks that allows us to classify spectra of S/N as low as 20 with an accuracy better than two spectral subtypes. For S/N ~ 10, it is still possible to determine the spectral class, but the typical accuracy is around three subtypes. Our database includes all spectral types from O5 to M7, and all luminosity classes, although the spectral classes II and IV are underrepresented.
2. Observations and reduction process: spectra to be classified
More than 2000 stars distributed in the field of view of 35 planetary nebulae, and 31 stars from the spectral catalog of Jacoby et al. (1984) were observed with the LDSS2 (Low Dispersion Survey Spectrograph) at the William Herschel Telescope (WHT) on La Palma, Spain. The spectral resolution of the data was around 5 Å, (2.5 A/pix scale). The spectral region covers ~2600 Å within the range 3800–8000 Å, the exact blue and red limits depending on the spatial position of the corresponding slit in the mask. These observations, made in July 1997 and August 1998, were part of a project devoted to the determination of distances to planetary nebulae using the extinction-distance method (Corradi et al. 1998; Navarro et al., in prep.). The method requires an accurate spectral classification, more precise than two spectral subtypes, to obtain reliable distances. Given that 75% of our spectra have S/N < 40, our first goal was to achieve as high precision as possible in the spectral classification of spectra with these characteristics.
The reduction of the observations was made using standard packages (ccdproc and onedspec packages) in IRAF. Bias and flat-field corrections were applied, both bad pixels and cosmic rays were removed, and the spectra were then wavelength calibrated. The extraction of the stellar spectra was not made automatically because of the extreme proximity of many spectra within adjacent slits. The length of each slit was fixed at a minimum (of 6 arcsec) in order to allocate the maximum number of slits in each mask. In addition, before the extraction of the spectra, the curvature close to the CCD border was corrected. To perform sky substraction, we generally used sky spectra extracted from the same slit for each object, although owing to the small size of the slits the sky extraction had to be done very carefully and, in some cases it was necessary to use sky spectra extracted from adjacent slits.
The spectral lines were found to contain enough information to enable us to perform an accurate classification. For this reason, the stellar continuum was not considered, and spectra were normalized by fitting a cubic spline to the continuum with no need for flux calibration. The normalization for each spectra was visually checked to prevent an incorrect fit to the continuum near the main spectral lines, which could cause an underestimate of their equivalent width.
Some spectra could not be used because they were contaminated by lines from fiducial stars spectra (four or five fiducials were used to center the plate on the field) In a few cases, we obtained two spectra in one slit, and in these cases we could not use these spectra owing to the uncertainty in the identification.
Our final sample consists of almost 1500 normalized spectra of field stars uniformly sampled at 1.4 Å step. The S/N per resolution element was measured at the spectral region around 5630 Å, where no strong lines were located. Their S/N distribution is shown in Fig. 1.
The relevant spectral lines were selected and analyzed previously by Navarro (2005) and will be presented in Navarro et al. (in prep.). They were measured in each spectra, obtaining the pseudo-equivalent width of each line in the same way as the indices defined by Worthey et al. (1994) using three spectral intervals: two intervals for the determination of local continuum at each side of the line and the central one representing the integration interval for each line (Table 2).
3. The artificial neural network system
An ANN is a mathematical tool inspired by the brain structure. As the brain, it is composed of several layers of neurons (or nodes). Each neuron in a layer is connected to all neurons in the next layer and sends them its output signal. In some ANNs (suited to the simulation of competitive processes), the neurons
Radial velocity and S/N of the stars in the JHC catalog.
of the same layer are also interconnected. Each neuron performs the function of an integrator, summing all inputs and generating an output according to a transmission function. The transmission function between one node and another is a nonlinear function, as in the biological neurons; this gives the ANN its versatility. In our case, the initial inputs of the ANN are the spectral data, and the final output is the stellar classification.
 |
Fig. 1 Signal-to-noise ratio distribution of the observed spectra. |
Each connection between the nodes of the network has a weight wij associated with it; the function of the ANN is to determine the weights that lead to the most accurate classification. The ANN finds this weights via a specialized training. The training may be supervised or not supervised, and is carried out by means of a training catalog. A validation catalog is also needed to test the classification ability and the precision of each ANN.
A supervised training requires that the output (in our case, the spectral class) is known for each input vector (spectra) in the training catalog. For the unsupervised training, this is not necessary but the resulting spectral groups may not coincide with the standard MKK spectral types.
For spectral classification purposes, the supervised training is the most advisable one because a well-established classification system (the MKK system) is available, and there are a sufficient number of stellar spectra classified to high accuracy to enable us to compile an adequate training catalog.
3.1. ANN requirements
The principal requirements for a correct application of ANNs to a set of spectral data are:
-
The training and the validation catalogs. These catalogs are essential to obtain an accurate classification. They must include stellar spectra from all the spectral types to be classified. The capacity of the ANNs to interpolate is well-established but their performance extrapolating out of the range defined by the training catalog is highly uncertain.
-
Input vectors. The ANN input vectors must be defined according to the characteristics of the data. For spectral classification, it is possible to use all of the information contained in the spectra (i.e. each wavelength resolution element) as input, but this means, in our case, that the input vectors would have 2000 elements. This demands a huge training catalog. The other possibility is to use only some spectral elements as input vectors; these can be determined using a principal component analysis (PCA, cf. Bailer-Jones 1996; Bailer-Jones et al. 1997), or determined based on well-known classification criteria. In both cases, the number of input elements is drastically reduced and, with it, the time required for the training.
-
Architecture of the ANN. It is necessary to determine the kind of architecture (number of layers and nodes in each layer) that would provide the highest precision in the spectral classification.
3.1.1. Training and validation catalogs
Our training catalog was compiled using the spectral library of Jacoby et al. (1984; JHC in the following), because its resolution and spectral coverage (4.5 Å and 3530–7430 Å, respectively) nearly coincide with our spectra characteristics (5.5 Å and 3900–6600 Å). Only a small amount of Gaussian smoothing was therefore required to degrade the JHC spectra to the resolution of our spectra.
The JHC catalog contains 161 stellar spectra with spectral types from O5 to M7 and luminosity classes mainly covering the I, III, and V types (only a few spectra are available with classes II and IV). In Table 1, we list the identification of each star, the JHC spectral classification (Clasif JHC), the numerical code for the adopted spectral type (Code AdSpT), and the luminosity class (LC). The spectral type is coded in numerical form, where 2000 corresponds to B0 type stars, 3000 to A0 stars, etc., and one spectral subtype corresponds to a hundred step. In this way, an F5 type corresponds to 4500, while 7600 indicates a M6 star. This notation is also be used in the next sections for the graphical representation of results. All spectral types of the JHC catalog were revised by Navarro (2005): those that differ from the original JHC classification are indicated as comments in Table 1.
In Table 1, the radial velocity correction (RV cor, in km s-1) and the S/N measured on each spectra are also listed. Radial velocity corrections were applied to each spectra to shift all spectral lines to their laboratory rest wavelengths. Different spectral lines were used for different classes: He and H lines for early O, B, and A stars; Ca, Fe, and H lines for F and G stars, and some Fe, Ca, and Mg lines for K and M stars.
Among the whole sample of 161 objects, we selected 40 spectra with spectral types from O5 to M7 and used them to assemble the validation catalog. Seven of these stars have emission lines (Jacoby’s ID number 106 and 156 to 161 in Table 1), which we include only in the validation catalog of some ANNs to investigate their ability to help us to identify emission-line objects. The remaining 121 spectra were used for the networks training.
To achieve the ambitious goal of performing an accurate classification of spectra with low S/N (see Fig. 1), a large number of spectra with a wide range of S/N were generated and added to the training catalog. This was done by adding different levels of Poissonian noise to each spectrum of the original JHC catalog. We finally created 4650 spectra: 3630 were used for the training and 1020 for the validation catalogs. The S/N ratio distribution of these spectra is similar to that of the program spectra.
Indices used for the automatic spectral classification.
In some JHC spectra we found that the wavelength calibration was inaccurate in the region near Hβ. For these stars, we add a comment in Table 1 (“calib problems”). We did not include any of these “problematic” spectra in the training catalog, and they were included only in some validation catalogs, to analyze the effect of these errors on the classification. The overall result was that the error did not significantly modify the classification because it affects only one or two spectral indices.
3.1.2. Input vectors
We trained the ANNs with a set of spectral indices, and not with the whole spectra, in order to limit the computing time to a practical amount. In addition, we used indices related to spectral lines instead of principal components, because we preferred to use parameters with a direct physical meaning. The shorter training time allowed us to test more architectures and a wider combination of spectral indices.
The complete set of indices (presented in Table 2) was defined and calibrated by Navarro (2005) and will be discussed in Navarro et al. (in prep.). They were defined in the same way as the Lick indices (Worthey et al. 1994), and we indeed used some of the Lick indices in the training, and in particular those that are more sensitive to either spectral type and/or luminosity class. Some of them were modified in their continuum definition in order to eliminate contamination by neighboring spectral lines. The index measurement is based on the pseudo-equivalent width of the spectral lines. Each index is defined by three intervals, the central one defining the line or band to be measured and the other two intervals defining the local continuum, one interval either side of the line.
Architectures used in the first stage of spectral classification.
Indices were measured using the INDEX program1, which allows us to perform a visual confirmation of each index measurement and check the fitted continuum to prevent the inclusion of spectral lines affecting the fit. Figure 2 shows an example of an A5V star spectrum where three of the indices and the corresponding continuum intervals are marked. As it can be seen in this figure and in Table 2, some neighbouring lines were measured using the same continuum intervals, especially where the line ratio is important to the classification.
 |
Fig. 2 Intervals used to measure the indices 4300GS, 4340, and 4861w. Here they are measured on the spectra of an A5 V star. The intervals that define the continuum are shown above the spectra and the integration intervals are marked below it. |
Another advantage of the INDEX program is the possibility to correct the spectra for radial velocity before performing the line-strength index measurements. This guarantees the correct wavelength position of the lines before the measurement of each index.
The indices most sensitive to either temperature (i.e. spectral type) or luminosity class in each spectral group were subsequently used as input parameters to the ANNs.
3.1.3. Architecture
We tested several architectures for the ANNs: including either one or two hidden layers, from a few to up to either 40 or 50 nodes in each layer and with either one or two output parameters. The main selection criterion for the ANN architecture was the minimization of the classification error. In Table 3, we list the selected architectures to be used for the first layer of ANNs (as described below), and the errors obtained in the classification of the validation catalog.
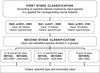 |
Fig. 3 Artificial neural networks (ANNs) system designed for spectral classification. It consists in two stages of neural networks. At each stage, we trained two or three ANNs with different input parameters covering different spectral intervals. Each input spectra is classified with the most appropriate ANN. |
3.2. The artificial neural network system
We used statnet2, a neural network code written by Bailer-Jones (1996). It is a supervised ANN trained by retro-propagation. It uses the tanh as the transfer function and has two possible types of input and output scalings (mean and variance) and optimisations of the training process. We used the variance scaling and “macopt” the conjugate gradient optimiser. The code enables us to adjust different weights to the input and output parameters and calculates the training and validation errors at each step, but its principal advantage is its capacity to train a group of ANNs (a “committeè”), with the same architecture and input parameters but different initial weights. This allows us to evaluate the average internal error in the network committeè (Int_err), which is related to the intrinsic network classification error, a parameter that can be difficult or impossible to evaluate, especially when the ANN is applied to unclassified stellar spectra.
In Fig. 3, we present a block diagram of our ANN system designed for spectral classification. As we can see, a two-stage classification is proposed. At each stage, we trained two or three neural networks each differing in terms of the indices used as input parameters.
The coincidence in wavelength of some spectral lines and the degeneration observed in some indices, related mainly to Balmer lines (see Navarro et al., in prep.), advised us to set up the two-step classification system shown in the figure. The ANNs in the first step carry out a pre-classification of the spectra using the most prominent lines (marked with a ∗ in Table 2). With this pre-classification, we were able to separate the spectra into three broad groups: 1) early-type stars (O5 to A2); 2) intermediate stars (type A, F, G, and early K, until K3); and 3) late-type stars (K and M). In the second stage, the ANNs classify the spectra inside each group and also determine the most likely luminosity class.
Since our spectra were acquired with a multi-slit spectrograph, the spectral region covered by each spectrum varies. Some spectra range from 3800 Å to near 7000 Å, others only begin redward of 4200 Å, and other ones end blueward of 6200 Å. When a classification is made using an ANN trained with all the indices (from 3900 Å to 7000 Å), the classification error caused by the lack of some spectral indices is notably larger than the error obtained if we use an ANN trained only with the indices included in the spectral range effectively covered by each spectrum. This was expected and it was the reason for defining two or even three different ANNs at each stage (Fig. 3 and Table 3): each one is optimized to a particular wavelength range.
Errors resulting from the application of the neural networks Net0, Net1 and Net2 to validation catalogs formed by spectra with three different levels of S/N.
3.2.1. First stage neural networks
As mentioned above, for the training of the first stage we need to use the complete training and validation catalogs, which include all spectral types. The indices used as input parameters in this stage were those associated with the most relevant spectral lines (marked with a ∗ in Table 2). In this way a more reliable classification of all the spectra, even those with the lowest S/N, is ensured.
After many tests with different architectures, we determine the ANNs that provide the most accurate spectral classification. In Table 3, we present the characteristics of these three ANNs. In this table (and subsequent) we list: the number of iterations in the retro-propagation process (N_Iter); the errors obtained in the classification of the validation catalog, i.e. the rms error (RMS_err), the average error (AVG_err), and the internal committeè error (Int_err); the architecture of each ANN; and the spectral range covered by the indices used in each network. The first two errors (rms and AVG) are the root mean square and the average of the differences between the network classification and the classification in the validation catalog. The Int_error is calculated as the average of the differences between the classification of the five ANNs forming each committeè.
Errors are expressed in units of spectral subtypes (an interval of one hundred represent one spectral subtype). The number of iterations were selected according to the classification errors in the validation process: we choose the number of iterations that minimize the rms error.
From the many architectures tested, we observed that a higher precision in the classification was obtained when we used ANNs with two hidden layers, with more than 20 nodes in each layer, and when we requested only one output parameter (the spectral type) instead of two (the spectral type and luminosity class). Moreover, the convergence of the iterative process occurs earlier in the case of only one output.
We labeled the selected nets Net0, Net1 and Net2. We used Net0 for the classification of spectra that include the whole 3930–6563 spectral range. Net1 was trained with the 15 indices included in the 4227–6200 spectral region and used to classify the spectra whose signal in the blue region is very noisy or exceedingly faint. Finally, Net2 was trained with the 18 indices included in the 3933–6162 spectral range and used to classify spectra that lack the end of the red region.
Taking advantage of the different S/N of the spectra used to train and validate the ANNs, we were able to analyze the behavior of the classification errors as a function of the S/N. We separated the spectra into three groups of different S/N. In Table 4, we present the errors obtained in this tests; in the last column, the mean S/N (S/N avg) of the spectra included in each group and the range of S/N are listed. As we can see, the errors increase significantly only when the S/N decreases below 20.
As a second validation of the automatic classification, we apply the same neural networks to those spectra of JHC stars (marked with ∗ in Table 1) observed by us with the same instrumentation as the program stars. In Table 5, we present the errors obtained in the automatic classification using the ANNs of the first stage. The errors here are larger than obtained in the first validation process. This happens because in this case we classify the spectra regardless of their spectral range. When this is taken into account, the error becomes smaller than two spectral subtypes (RMS_err = 196.1).
As a final remark, we note that the accuracy of the spectral type obtained with this first stage of ANNs is remarkable. With the subsequent application of the second stage of neural networks we improve this classification and determine the luminosity class.
Uncertainties in the spectral classification obtained with the first stage ANNs, when they were applied to the stars from the JHC catalog observed in our program.
 |
Fig. 4 Traditional classification compared with the results of the first stage of our ANN automatic classification, for stars near the line of sight to the planetary nebulaAbell 63. Symbols indicate the quality of the spectra: open circles for S/N > 30, filled triangles for spectra with S/N between 20 and 30, and filled squares for spectra with S/N ratio lower than 20. The size of the symbols is related to the internal error in the ANN classification. |
 |
Fig. 5 Traditional classification compared with the second stage ANN classification for stars near the line of sight to Abell 63. Symbols are the same as in Fig. 4. |
 |
Fig. 6 Traditional vs. first stage ANN classification for stars near the line of sight to the planetary nebula NGC 7027. Symbols have the same significance as in Fig. 4. |
 |
Fig. 7 Traditional vs. second stage ANN classification for stars along the line of sight to NGC 7027. In panel “c”, two early A type stars that were classified with NET2ARL (not with NET2KRL) are added. |
Accuracy in spectral classification of the validation catalogs constructed with stars belonging to the three spectral groups defined in the text.
3.2.2. Second stage neural networks
The second stage of the classification was performed with three sets of ANNs, one for each of the spectral groups mentioned in Sect. 3.2. The corresponding ANNs have now two output parameters: the spectral type (SpT) and the luminosity class (LC). The input parameters are the indices that were selected to be the most sensitive to both of them (SpT and LC):
For the first group (early stars: type O,B, and early A), we used the indices with key “1” in the last column of Table 2. Depending on the spectral range, only a subset of these indices were employed. In particular, only 16 indices were used to train the ANNs selected to classify spectra whose red region is noisy or missing (NET2AL, NET3AL, etc.), and only the 11 indices redder than 4300 Å were considered to train the ANNs (NET2AR, NET2ARL, etc.) devoted to classify the spectra whose blue region was not observed.
For the second group (late A, F, G, and early K stars) the indices indicated by “2” in the last column of Table 2 were used. For NET2GL, we used 23 indices from 3933 Å until 6162 Å, and for NET2GRL, the 19 indices between 4227 Å and 6563 Å.
Finally, for the third group (late type: K and M stars), as the number of sources in the JHC catalog is limited, spectra of 33 Galactic giant and supergiant K and M stars from Malyuto et al. (1997) were obtained and added to the training catalog. These spectra have a resolution (10 Å) that are lower than ours, a S/N > 80, and range from 4800 Å to 7700 Å. For this reason, only indices redder than 4861 Å and marked with a label “3” in Table 2 were used for the training of the ANNs that classify the group of late-type stars.
Different training and validation catalogs are used for each spectral group. To produce them, we considered only JHC spectra with the same spectral types included in each group.
As in the first stage, the type of ANN to be used was selected among more than 50 test architectures to determine the one that provides the most reliable classification. In Table 6, we present the NNs selected to classify the spectra. All networks were trained in committees of 5 ANNs, and the internal average error (Int_err) of each committeé was determined. In Table 6 we also list the number of iterations for which the validation rms error was found to be a minimum (N_iter), the rms error (RMS_err), and the average error (AV_err) obtained by comparing the original classification and the network classification. The parameters Nval and Ntrain indicate the number of elements used in the validation and training catalogs. In the last column, the wavelength intervals for the indices considered in each network is listed.
In this table, we list two different results for each ANN, each one with a different number of iterations, for one of which the minimum RMS_err in the SpT determination occurs and for the other the minimum error in the LC determination is obtained. Comparing errors in both cases we found that the relative difference in the RMS_err for the LC determination is smaller than the difference in the RMS_err of the SpT classification, thus we generally used the ANN with N_iter corresponding to the minimum error in SpT.
As we can see from the uncertainties obtained in the validation process of these ANNs (Table 6), the improvement in the precision of the resulting spectral type is significant. In all cases, the SpT classification is determined more accurately than in the first stage. Only for the ANN used to classify early-type stars in the red region (NET2ARL) we obtained an average error larger than two spectral subtypes, although this was expected because the most suitable lines for classifying early-type stars are in the blue region.
However, the typical precision of the LC determinations is no smaller than one luminosity class. This means that we cannot distinguish between a LC II and III or V and IV. This limitation is a consequence of the small number of stars with LC II and IV in the training catalog. In the future, the catalog should be completed with more stars belonging to these luminosity classes.
The analysis of the classification errors for the different levels of S/N in this second stage provides very similar results as for the first stage, confirming that errors are considerably larger only for S/N < 19.
4. Application of the ANN system: results and analysis
We performed a third validation of our ANNs by applying it to a selected sample of field stars located along the line of sight toward the planetary nebulae Abell 63 (Abell, 1966), NGC 6781, and NGC 7027. The spectral types determined by our ANN were compared with visual classification performed in the traditional way (Navarro, 2005). Figures 4 and 5 show the results for Abell 63 after the first and second stages of the ANN, respectively, and Figs. 6 and 7 present in a similar way the results for NGC 7027. In all these figures, the different sizes and symbols indicate the classification error and the quality (q) of the spectra, respectively. Open circles represent spectra with S/N > 40 (q = 1) and spectra with 30 < S/N < 40 (q = 2), filled triangles indicate spectra with S/N between 20 and 30 (q = 3), and squares spectra with S/N < 20 (q = 4). In these figures the effect of noise on the accuracy of the ANNs classification is observed, especially in Figs. 6 and 7 where triangles and squares clearly show a larger dispersion.
Figures 4 to 7 also show the rms value for the differences between the traditional and the corresponding ANN classifications. In Figs. 6d and 7d appears, additionally, the rms value corresponding to the lower 90% of the errors because in this case a small number of stars (3–4) have a large difference that considerably increases the rms value.
The different panels of Figs. 4 and 6 correspond to the different networks described in Sect. 3.2.1, with panels “d” showing the adopted classification at the end of the first stage. Figures 5 and 7 show the classification obtained with the second-stage ANNs. In the plots 5a, 5b, 7a, and 7b, we present the results for spectra classified with the first stage as type A5 to K3 and in Figs. 5c and 7c the classification of stars previously classified as either late-type, K,or M.
As we can see, in the case of Abell 63, the classification obtained with the first stage ANNs is already very accurate (Fig. 4d), and close to the classification obtained in the second stage (Fig. 5d). Similar results were obtained for stars in the line of sight of NGC 6781 (not shown here). We note that one K6 star (SpTCode = 6600) around Abell 63 was better classified with the ANNs of the first stage than with those of the second stage. This was because only the blue spectral region (λ ≤ 5400 Å) was available for this star. It is therefore understandable why the first stage ANN classification, which considers blue line-strength indices (from 3933 Å to 5400 Å) was more accurate than the second stage classification, which used the few indices redder than 4800 Å available for this star.
However, for stars around NGC 7027 the improvement between the first and second stage ANNs is significant (Figs. 6 and 7). These spectra are displaced mainly to the red side, and lines bluer than 4300 Å are not observed. The impact of this on the classification carried out by the networks of the first stage is significant. With nets Net0 and Net2, the dispersion in the plot is notably higher than that obtained with Net1, which was trained specifically for the classification of the spectra with these characteristics. In Fig. 7, we present the classification made with the ANNs of the second stage. As in the case of Abell 63, the spectra previously classified between A0 and K2 were “re-classified” with the networks NET2GL and NET2GRL, and those pre-classified as either K or M with NET2KRL. In this case, we have two early-type stars that were classified using NET2ARL, and added to the plot in Fig. 7c. As in the case of Abell 63, and for the same reasons, one late-type star (SpTCode = 7100) was better classified in the first rather than in the second stage.
5. Conclusions and discussion
-
We have constructed an ANN system able to classify stellar spectra with considerably lower S/N than generally considered to be needed. The ANNs were trained and tested with observed spectra of different S/N levels. The system was designed to determine spectral types and luminosity classes for thousands of field stars in an ongoing project to determine the extinction-distances of planetary nebulae.
-
The precision achieved is higher than two spectral subtypes for spectra of S/N as low as 20. For lower S/N, (of around ten) the accuracy is reduced to near three spectral subtypes. This confirms the insensitivity of ANNs to noise.
-
Algorithms used previously by other authors (Munari et al. 2005a; Recio-Blanco et al. 2006) are based on minimisation distance methods, and employ different types of metric. However, an important problem with this type of algorithm is that it is very sensitive to noise, which cannot be easily distinguished from real differences between spectra. In our case, the ANNs have proven to be highly robust even when there are high levels of noise in spectra.
-
We have found that the convergence on the training process is faster, and the rms error in the classification of the validation catalog is smaller, when we use only one output parameter, i.e. when we determine only the spectral type instead of both spectral type and luminosity class.
-
The classification error of the ANNs was found to be smaller when we used two hidden layers and more than 20 nodes in each one. Although the size of the training catalog limits the number of nodes we can use in each layer, the number of weights to be determined in the training process is proportional to the product of the number of nodes in one layer (N) and the number of nodes (M) in the next one. As our training catalog contains a large number of items (several thousands), we can use hidden layers with a considerable number of nodes. This cannot be done when the training catalog is small, owing to the large number of weights to be determined.
-
The possibility of comparing the classification made by several networks of similar characteristics and all trained with the same data allows us to assess the intrinsic accuracy of the classification. In this way, the uncertainty in the classification of previously unclassified spectra can be determined without assuming that it is the same as for the validation catalog.
-
We have found that peculiar spectra (e.g. of emission-line stars) have associated extremely large classification errors. This opens the way to detecting unusual spectra in future classifications and demonstrates that it is possible to train the networks to identify these peculiar objects.
-
All our target stars are located very close to the line of sight towards bright planetary nebulae that were selected for their proximity to the Galactic plane, so we do not expect large variations in metallicity among the stars. However, it is possible to extend the scope of the ANN classification by adding information about metallicity to the training and validation catalogs, when this information is available for the catalogued stars.
To improve the precision of the luminosity class determination, we should enhance the training catalog with more spectra of stars with luminosity class II and IV.
Part of the REDUCEME reduction package (Cardiel et al. 1998).
Acknowledgments
We acknowledge the support of Consejo Superior de Investigación Científica for the execution of this work, the invaluable informatics support of Centro de Atención a Usuarios (CAU) staff at Instituto de Astrofísica de Canarias (IAC), and the guidance of M. Serra and R. Gullati at the beginning of this work. We acknowledge N. Cardiel and J. Gorgas for facilitate and help with the use of REDUCEME software. SGN acknowledge the support of Consejo Nacional de Ciencia y Tecnología for her stay at IAC, and the PROMEP program support for a recent brief stay: PROMEP/103.5/09/5285. The work of RLMC and AMR is supported by the Spanish Ministry of Science and Innovation (MICINN) under the grant AYA2007-66804.
This work has made use of the statnet neural network code written by Coryn A.L. Bailer-Jones.
References
- Abell, G. O. 1966, ApJ, 144, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, A., & Wooley, A. 1994, Vistas Astron., 38, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. 1996, Ph.D. Thesis. Cambridge University [Google Scholar]
- Bailer-Jones, C. A. L. 2000, A&A, 357, 197 [NASA ADS] [Google Scholar]
- Bailer-Jones, C. A. L., Irwin, M., Gilmore, G., & von Hippel, T. 1997, MNRAS, 292, 157 [NASA ADS] [Google Scholar]
- Bailer-Jones, C. A. L., Irwin, M., & von Hippel, T. 1998, MNRAS, 298, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, N. M., Loveday, J., Fukugita, M., et al. 2004, MNRAS, 348, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Bazell, D., & Aha, D. W. 2001, ApJ 548, 219 [Google Scholar]
- Bertin, E. 1994, Ap&SS, 217, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D., Faber, S. M., & González, J. J. 1986, AJ, 91, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Cardiel, N., Gorgas, J., Cenarro, J., & González, J. J. 1998, A&ASS, 127, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corradi, R. L. M., Mampaso, A., & Navarro, S. G. 1998, In Proc. IX Latin American Regional IAU Meeting, Rev. Mex. Astron. Astrofis. Ser. Conf., in press [Google Scholar]
- Folkes, S. R., Lahav, O., & Maddox, S. J. 1996, MNRAS, 283, 651 [NASA ADS] [Google Scholar]
- Gray, R. O., & Arlt, J. S. 1996, BAAS, 188, 58.01 [NASA ADS] [Google Scholar]
- Gray, R. O., & Cobally, C. J. 1994, AJ, 107, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Hunter, D. A., & Christian, C. A. 1984, ApJS, 56, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1992, Proc. IAU Symp. 149, ed. B. Barbuy, & A. Renzini (Dordrecht: Kluwer), 225 [Google Scholar]
- Malyuto, V., & Schmidt-Kaler, Th. 1997, A&A, 325, 693 [NASA ADS] [Google Scholar]
- Malyuto, V., Oestreicher, M. O., & Schmidt-Kaler, Th. 1997, MNRAS, 286, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Manteiga, M., Carricajo, I., Rodríguez, A., Dafonte, C., & Arcay, B. 2009, AJ, 137, 3245 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Zwitter, T., & Siebert, A. 2005a, ESASP, 576, 529 [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005b, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naim, A., Lahav, O., Sodre, L. Jr., & Storrie-Lombardi, M. C. 1995, MNRAS, 275, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, S. G. 2005, Ph.D. Thesis. Universidad de La Laguna [Google Scholar]
- Odewahn, S. C. 1995, PASP, 107, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, A., Arcay, B., Dafonte, C., Manteiga, M., & Carricajo, I. 2004, Expert Syst. Appl., 27, 237 [CrossRef] [Google Scholar]
- Singh, H. P., Gulati, R. K., & Gupta, R. 1998, MNRAS, 295, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Snider, S., Allende-Prieto, C., von Hippel, T., et al. 2001, ApJ, 562, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Vieira, E. F., & Ponz, J. D. 1995, A&AS, 111, 393 [NASA ADS] [Google Scholar]
- von Hippel, T., Storrie-Lombardi, L. J., Storrie-Lombardi, M. C., & Irwin, M. J. 1994, MNRAS, 269, 97 [NASA ADS] [Google Scholar]
- Weaver, W. B. 2000, ApJ, 541, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, W. B., & Torres-Dodgen, A. V. 1997, ApJ, 487, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., González, J. J., & Burstein, D. 1994, ApJSS, 94, 687 [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zwiter, T., Munari, U., & Siebert, A. 2005, ESA SP, 576, 623 [NASA ADS] [Google Scholar]
All Tables
Errors resulting from the application of the neural networks Net0, Net1 and Net2 to validation catalogs formed by spectra with three different levels of S/N.
Uncertainties in the spectral classification obtained with the first stage ANNs, when they were applied to the stars from the JHC catalog observed in our program.
Accuracy in spectral classification of the validation catalogs constructed with stars belonging to the three spectral groups defined in the text.
All Figures
 |
Fig. 1 Signal-to-noise ratio distribution of the observed spectra. |
| In the text | |
 |
Fig. 2 Intervals used to measure the indices 4300GS, 4340, and 4861w. Here they are measured on the spectra of an A5 V star. The intervals that define the continuum are shown above the spectra and the integration intervals are marked below it. |
| In the text | |
 |
Fig. 3 Artificial neural networks (ANNs) system designed for spectral classification. It consists in two stages of neural networks. At each stage, we trained two or three ANNs with different input parameters covering different spectral intervals. Each input spectra is classified with the most appropriate ANN. |
| In the text | |
 |
Fig. 4 Traditional classification compared with the results of the first stage of our ANN automatic classification, for stars near the line of sight to the planetary nebulaAbell 63. Symbols indicate the quality of the spectra: open circles for S/N > 30, filled triangles for spectra with S/N between 20 and 30, and filled squares for spectra with S/N ratio lower than 20. The size of the symbols is related to the internal error in the ANN classification. |
| In the text | |
 |
Fig. 5 Traditional classification compared with the second stage ANN classification for stars near the line of sight to Abell 63. Symbols are the same as in Fig. 4. |
| In the text | |
 |
Fig. 6 Traditional vs. first stage ANN classification for stars near the line of sight to the planetary nebula NGC 7027. Symbols have the same significance as in Fig. 4. |
| In the text | |
 |
Fig. 7 Traditional vs. second stage ANN classification for stars along the line of sight to NGC 7027. In panel “c”, two early A type stars that were classified with NET2ARL (not with NET2KRL) are added. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


