| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201118333 | |
| Published online | 20 January 2012 | |
Siphon flow in a cool magnetic loop
1 Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
2 High Altitude Observatory, National Center for Atmospheric Research, PO Box 3000, Boulder, CO 80307, USA ⋆
e-mail: bethge@ucar.edu
3 Instituto de Astrofísica de Canarias (CSIC), via Lactea, 38205 La Laguna, Tenerife, Spain
4 Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
5 Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
Received: 25 October 2011
Accepted: 22 November 2011
Context. Siphon flows that are driven by a gas pressure difference between two photospheric footpoints of different magnetic field strength connected by magnetic field lines are a well-studied phenomenon in theory, but observational evidence is scarce.
Aims. We investigate the properties of a structure in the solar chromosphere in an active region to find out whether the feature is consistent with a siphon flow in a magnetic loop filled with chromospheric material.
Methods. We derived the line-of-sight (LOS) velocity of several photospheric spectral lines and two chromospheric spectral lines, Ca ii H 3968.5 Åand He i 10 830 Å, in spectropolarimetric observations of NOAA 10978 done with the Tenerife Infrared Polarimeter (TIP-II) and the POlarimetric LIttrow Spectrograph (POLIS). The structure can be clearly traced in the LOS velocity maps and the absorption depth of He i. The magnetic field configuration in the photosphere is inferred directly from the observed Stokes parameters and from inversions with the HELIX+ code. Data from the full-disk Chromospheric Telescope (ChroTel) in He i in intensity and LOS velocity are used for tracking the temporal evolution of the flow, along with TRACE Fe ix/x 171 Ådata for additional information about coronal regions related to the structure under investigation.
Results. The inner end of the structure is located in the penumbra of a sunspot. It shows downflows whose strength decreases with decreasing height in the atmosphere. The flow velocity in He i falls abruptly from above 40 km s-1 to about zero further into the penumbra. A slight increase of emission is seen in the Ca ii H spectra at the endpoint. At the outer end of the structure, the photospheric lines that form higher up in the atmosphere show upflows that accelerate with height. The polarization signal near the outer end shows a polarity opposite to that of the sunspot, the magnetic field strength of 580 G is roughly half as large as at the inner end. The structure exists for about 90 min. Its appearance is preceeded by a brightening in its middle in the coronal TRACE data.
Conclusions. The observed flows match theoretical predictions of chromospheric and coronal siphon flows, with accelerating upflowing plasma at one footpoint with low field strength and decelerating downflowing plasma at the other end. A tube shock at the inner end is probable, but the evidence is not conclusive. The TRACE data suggest that the structure forms because of a reorganization of field lines after a reconnection event.
Key words: Sun: chromosphere / Sun: magnetic topology
© ESO, 2012
1. Introduction
Siphon flows in magnetic flux tubes were suggested first by Meyer & Schmidt (1968). Since then they have been addressed theoretically for the most part, both in the upper solar atmosphere (e.g., Cargill & Priest 1980; Noci 1981) and in the photosphere (e.g., Thomas 1988; Degenhardt 1989; Thomas & Montesinos 1991). These flows are driven by a difference in gas pressure between the footpoints of the flux tube caused by a difference of the magnetic field strength. If one assumes for simplicity a static field-free atmosphere outside of the flux tube footpoints, the pressure balance can be described as 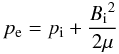 (1)at the location of the footpoints, with pi being the internal gas pressure, Bi2/2μ the magnetic pressure inside the flux tube, and pe the external gas pressure. An increased magnetic field strength in one of the footpoints (Binner > Bouter) therefore leads to an imbalance in gas pressure, which can then drive a plasma flow along the flux tube.
(1)at the location of the footpoints, with pi being the internal gas pressure, Bi2/2μ the magnetic pressure inside the flux tube, and pe the external gas pressure. An increased magnetic field strength in one of the footpoints (Binner > Bouter) therefore leads to an imbalance in gas pressure, which can then drive a plasma flow along the flux tube.
Observational evidence of such siphon flows is, however, scarce: Rüedi et al. (1992) report a siphon flow signature in Fe i 15 648 Åand Fe i 15 653 Åacross the polarity-inversion line of an active region. For the same observation, Degenhardt et al. (1993) presented evidence for both the siphon flow and a standing tube shock in the flow based on a comparison of the observed line profiles with synthetic line profiles from computed siphon flows. Uitenbroek et al. (2006) identified a siphon flow in Ca ii 8542 Ånear a pore with downflow velocities up to 27 km s-1. A similar siphon flow in Ca ii 8542 Åwithout a clear outer footpoint was reported by Beck et al. (2010).
All of these observations employed scans with a slit spectrograph, i.e., the information is co-temporal only along the slit and not throughout the whole scanned region. Because the scans were not done repeatedly, there is no temporal information about the flow, and it can be hard to distinguish an actual persistent flow from a plasma motion co-moving with the slit.
Doyle et al. (2006) detected a short-lived siphon flow in N v 1238 Åin a time sequence of slit spectra. The authors used additional imaging data in C iv 1550 Å and Fe ix/x 171 Å to estimate both the temperature of the plasma and the duration of the event; the latter was done by tracking brightenings moving from one footpoint to the other. At the time the brightening arrived at the slit placed over the “destination” footpoint, redshifts of about 20 km s-1 were seen. Nevertheless, because no information about line-shifts was available in the C iv 1550 Åand Fe ix/x 171 Å data, one cannot necessarily assume that the brightenings are indeed indicative of moving plasma.
Siphon flows are frequently found in loops reaching high up into the corona. When seen close to the limb in the extreme ultraviolet (EUV), these sometimes show velocities along the loop exceeding the sound speed (e.g., Peres 1997; Brekke et al. 1997). In the past, these siphon flows were used as one possible explanation to understand why cool loops can be seen far higher than expected from the pressure scale height (e.g., Peres 1997; Aschwanden et al. 2001). Similar to the loop we investigate in this study, these were associated with active regions, but in contrast to the (most probably low-lying) loop we study here, the EUV loops host plasma well above 105 K and easily reach heights of 50 Mm and more. The flows in the coronal EUV loops are (most probably) driven by a difference in the coronal pressure due to asymmetric heating (the heating in one leg is stronger than in the other). This scenario is quite different from the siphon flows in low-lying photospheric and chromospheric loops as originally suggested by Meyer & Schmidt (1968), which are driven by a photospheric pressure imbalance caused by the difference of the magnetic field strength.
In the present study, high-resolution spectropolarimetric data in the He i 10 830 Åmultiplet, i.e., in the upper chromosphere, are complemented with spectroscopic data in Ca ii H in the lower chromosphere and imaging data from a full-disk filtergraph instrument observing the spectral range of He i. Thanks to a tunable filter, the latter also allows one to infer the line-of-sight (LOS) velocity of the plasma motions. The high cadence of the full-disk observations of 30 s is essential to track the temporal evolution of the flow. The magnetic field configuration of the structure in which the siphon flow takes place is deduced from line parameters and inversions of the spectropolarimetric data. TRACE Fe ix/x 171 Åcoronal data are used to investigate the relation to the upper atmosphere.
In the following, the observations and data analysis are described first (Sect. 2), followed by a description of the morphology of the structure and the dynamics within at high spatial resolution in Sect. 3. The same section also addresses the temporal evolution of the flow. Section 4 deals with the magnetic field configuration of the structure. The results are discussed in Sect. 5. Based on what is seen in the TRACE data in the beginning and at the end of the flow, we speculate on the causes of the initiation and termination of the flow in Sect. 6 before concluding remarks are being made in Sect. 7.
2. Observations and data analysis
Observations in He i 10 830 Å were made in parallel with the Tenerife Infrared Polarimeter (TIP-II, Collados et al. 2007) and the full-disk Chromospheric Telescope (ChroTel, Kentischer et al. 2008; Bethge et al. 2011) at the German Vacuum Tower Telescope (VTT), Izaña, Spain. The same observations were used before to calibrate the derivation of velocities from ChroTel intensity filtergrams by a comparison to simultaneous high-resolution spectra (see Bethge et al. 2011 for a description of the approach). Simultaneous with the He spectra from TIP-II (just termed “TIP” in the following), we used the POlarimetric LIttrow Spectrograph (POLIS, Beck et al. 2005) to obtain co-spatial intensity spectra of Ca ii H.
 |
Fig. 1 Overview maps of the observed FOV. Clockwise from upper left: continuum intensity in the infrared, total circular polarization of Si i, line-core intensity of Ca ii H, absorption depth of He i. The contour outlines the structure hosting the siphon flow under investigation. All maps are shown on a linear scale, the total circular polarization is scaled over a range of [− 3%, 6%] of the continuum intensity. The red line in the continuum map denotes the central spine of the structure. |
Line parameters.
2.1. Spectropolarimetric and spectroscopic data
The spatial scan with the two slit-spectrographs TIP and POLIS covered a part of the active region NOAA 10978 on 8 December 2007 at 68° E and 14.5° S, i.e., at cos` = 0.63. The scanning procedure took 15 min from 11:05–11:20 UT. The total size of the map was 100′′ × 82′′ for TIP and 100′′ × 70′′ for POLIS, consisting of 200 steps of 0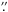 5 step width. The spatial sampling along the slit was 0
5 step width. The spatial sampling along the slit was 0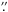 3 for Ca and 0
3 for Ca and 0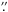 18 for TIP, which was binned by two to 0
18 for TIP, which was binned by two to 0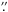 36 afterwards. The slit width was 0
36 afterwards. The slit width was 0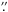 36 for TIP and 0
36 for TIP and 0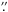 5 for POLIS, respectively. The spectral resolution of the TIP (POLIS) data was 10.91 (19.2) mÅ/pixel, the spatial resolution is estimated to be about 1′′. We used an integration time of 3 s per scan step. The mean noise level of the TIP spectra in Stokes I and Stokes V is 1.5 × 10-3 and 3.9 × 10-3 times the continuum intensity, respectively. The TIP data cover a spectral range of 10 823.25–10 834.25 Å, so both the photospheric Si i 10 827 Åline and the chromospheric He i 10 830 Åtriplet are contained in the spectra (shortened “Si i” and “He i” in the following). The Ca ii H (“Ca ii” in the following) spectra from POLIS cover the core and the blue wing of the line that contains several photospheric blends. Table 1 lists the observed spectral lines, together with estimates of their formation height in the quiet Sun (QS) and in the umbra of sunspots.
5 for POLIS, respectively. The spectral resolution of the TIP (POLIS) data was 10.91 (19.2) mÅ/pixel, the spatial resolution is estimated to be about 1′′. We used an integration time of 3 s per scan step. The mean noise level of the TIP spectra in Stokes I and Stokes V is 1.5 × 10-3 and 3.9 × 10-3 times the continuum intensity, respectively. The TIP data cover a spectral range of 10 823.25–10 834.25 Å, so both the photospheric Si i 10 827 Åline and the chromospheric He i 10 830 Åtriplet are contained in the spectra (shortened “Si i” and “He i” in the following). The Ca ii H (“Ca ii” in the following) spectra from POLIS cover the core and the blue wing of the line that contains several photospheric blends. Table 1 lists the observed spectral lines, together with estimates of their formation height in the quiet Sun (QS) and in the umbra of sunspots.
The total linear and total circular polarization (Ltot and Vtot) were calculated separately for Si i and He i according to the definition given in Lites et al. (1999) as a first estimate of the magnetic field configuration in the photosphere and chromosphere.
The LOS velocity in Si i was determined in every pixel by looking for the position of the minimum intensity of the (smoothed) spectrum in the wavelength range between 10 826.6 and 10 827.4 Å. For the velocities in He i, the chosen wavelength range was between 10 828.5 and 10 831.9 Å, i.e., between the outer wing of the Si i line and the water vapor line on the red side of the He i line. The minimum intensity and absorption depth refer to the stronger red component of the He i triplet. The determination of the line shifts was done with pixel precision in the spectra, corresponding to an uncertainty in velocity of about 300 m s-1. For the Ca ii spectra from POLIS, we determined the LOS velocities of three of the photospheric line blends and of the very line core. For locations with a single emission peak in Ca ii instead of an absorption core such as found in the umbra, we calculated the center-of-gravity (COG) of the emission pattern. This quantity yields a similar spatial distribution of velocities across the FOV, but with a reduced dynamic range, because the absorption core is only one component of the central emission. We thus scaled the COG velocities up by a factor of about 10, which was motivated through a scatterplot between COG velocities and line-core velocities. We then substituted the unreliable line-core velocity values on the locations of single emission peaks (cf. Rezaei et al. 2008; Beck et al. 2009) with the corresponding values of the COG.
An overview of the observed region on the Sun is shown in Fig. 1. To mark the relevant structure for the present investigation, we manually drew a contour line around the feature in the He i Doppler map (top right panel of Fig. 2). The latter is overlayed on all other maps, it also coincides with the boundary of the structure in the He absorption depth and the Ca ii core intensity (see Fig. 1).
2.2. Chromospheric Doppler shift imaging: ChroTel
ChroTel full-disk filtergrams in He i 10 830 Åwere acquired before, during, and after the spectrograph scan with a cadence of 30 s. Data are available from 9:07 to 12:19 UT with some gaps caused by the flatfielding procedure. The same region that was scanned with TIP and POLIS was cut out from the ChroTel filtergrams and carefully aligned with the spectrograph data.
 |
Fig. 2 Line-of-sight velocities. Left column, bottom to top: Fe i at 396.55 nm, Fe i at 396.61 nm, Si i at 1082.71 nm. Right column, bottom to top: Fe i at 396.93 nm, Ca ii H core at 396.85 nm, He i at 1083.03 nm. |
With a tunable Lyot-type filter, ChroTel takes seven filtergrams (FWHM = 1.3 Å) in and around the He i triplet within less than 8 s. As shown in Bethge et al. (2011), it is possible to derive line shifts and therefore LOS velocities from these filtergrams. He i absorption depth maps and LOS velocity maps were created for the region of interest about two hours before, fifteen minutes before, during, and one hour after the TIP scan. To derive these maps, the data were averaged over 7 min to increase the S/N ratio. Bethge et al. (2011) showed that high velocities (>~5 km s-1) are underestimated by a factor of about 3 in the ChroTel maps. The color bars for the Doppler velocities in Fig. 6 are scaled accordingly for an easier comparison with the LOS velocities shown in Fig. 2.
2.3. Coronal context data: TRACE
Raw Fe ix/x 171 Å data from the Transition Region And Coronal Explorer (TRACE, Handy et al. 1999), co-temporal with the ChroTel data, are employed for coronal context. The emission in this band samples plasma at a temperature of about 106 K.
The TRACE maps were rotated, rescaled, and aligned. The alignment was done by eye, both with the ChroTel He i maps and among the TRACE maps themselves. Since Fe ix/x 171 Åand He i 10 830 Åsample completely different layers, of course not all features in the TRACE data are commensurate to features seen with ChroTel. Nevertheless, the observed region exhibits quite characteristic structures and we estimate the alignment to be no worse than 2′′ to 3′′.
3. Hydrodynamics of the flow
3.1. Morphology and dynamics at high spatial resolution
The structure outlined in Fig. 1 has a (projected) size of about 30′′ × 6′′, i.e., about 21 Mm × 4 Mm on the Sun. The contour was selected by eye roughly along the strongest velocity gradients seen in He i outside of the apparently coherent region of the dark loop-like feature seen in He i (cf. lower left panel of Fig. 1 and top right panel of Fig. 2). The He i absorption pattern coincides well with the outlined structure based on the velocities. The same holds for the line-core intensity of Ca ii that, however, also shows more substructure with a brightening in the middle towards the right end of the structure. The He i absorption is strongest in the middle of the contour where the LOS velocities are close to zero.
The structure terminates at its left end (“inner footpoint” in the following) in the penumbra of a sunspot with positive polarity in the map of the signed total circular polarization (Vtot) of the photospheric Si i line (Fig. 1, top right). At the right end (“outer footpoint”), black patches are seen in the same map just outside of the contour, indicating the opposite direction of the magnetic field than in the penumbra. The LOS velocities of both chromospheric lines (He i and Ca ii H, Fig. 2) show a smooth change from upflows at the outer footpoint in the QS to downflows of up to 40 km s-1 in the penumbra. The surroundings of the feature show no strong upflows outside the contour in the two chromospheric lines, especially none to the right of the outer footpoint. The same holds for the downflows at the inner footpoint: they extend as far as the contour line into the penumbra, but disappear abruptly there.
The various photospheric lines (left column and lower right column of Fig. 2) have been roughly sorted by their corresponding formation height, from bottom up in each column. They show a clear pattern: in the lowermost forming lines (left column), the inner footpoint with downflows is not clearly seen because the lines are dominated by the line shift from the Evershed effect, yielding upflows on the center-side penumbra and downflows on the limb-side penumbra. The signature of the Evershed flow diminishes with increasing formation height, and reveals a patch of downflows near the inner end of the contour in the higher atmosphere. These downflows are most pronounced and cover the largest area in the Fe i line at 396.93 nm (lowermost panel in the right column), but can also be seen for Si i (topmost panel in the left column) and rudimentarily in the Fe i line at 396.61 nm (middle panel in the left column). In the latter two lines, the downflows are just at the edge of the contour. For the outer footpoint, the case is clearer. All photospheric lines show upflows at the very end and outside of the contour, whose amplitude increases with formation height from 0.5 km s-1 to 1 km s-1 in, e.g., Si i. The upflows are more localized than the downflows and only slightly increase in area in the upper atmosphere.
 |
Fig. 3 Line-of-sight velocities along the central axis of the loop structure under investigation. Top panel: chromospheric lines of He i and Ca ii H. Bottom panel: photospheric lines. The dashed vertical lines denote the inner and outer end of the structure. The dotted lines indicate the locations of upflows and downflows. |
Within the structure, the He i velocities are in the range from − 6to − 12 km s-1 in the upflow region and up to +43 km s-1 at the far end of the downflow region. In between, the velocities gradually change from blueshifts to redshifts, with a slight tilt of the isovelocity levels relative to the spine of the structure. The velocity structure is visualized in the LOS velocities along the central axis of the structure, which are shown in Fig. 3. The photospheric lines (lower panel) show upflows at the outer footpoint of about 1 − 2′′ extent, and more spatially extended downflow patches near the inner footpoint. There the velocity reduces with formation height, with the maximum downflows located closer to the end of the structure the lower the spectral line forms. The two chromospheric lines show the gradual change from up- to downflows, but the trend is interrupted partly at d ~ 28″ near the outer footpoint. At the inner footpoint, the velocity in, e.g., He i drops from above 40 km s-1 to zero over less than 2″.
 |
Fig. 4 Spectra along the central axis of the structure. Top to bottom: intensity spectra of Ca ii H, Stokes IQUV of He i. The two horizontal dashed lines in each panel denote the inner (lower line) and outer end (upper line) of the structure. The vertical solid lines denote the rest wavelength of the respective line. |
The variation of the velocity trend near the outer footpoint is caused by the presence of multiple atmospheric components that are seen in the spectra along the central axis of the structure (see Fig. 4). Whereas the structure and its corresponding velocities can clearly be seen in the He i and Ca ii spectra as the curved trace of the absorption core, additional spectral components appear around d ~ 28′′ with about zero velocity or small downflows. These additional components can best be seen in the individual Ca ii profiles of Fig. 5. For instance, the second Ca ii profile from the bottom shows two different absorption cores over a broad emission, where the structure corresponds to the one with the large blue shift. In the He i profiles, the components overlap more strongly because of the intrinsic width of the absorption components, they only can be clearly seen at the inner footpoint (uppermost profile): the downflows related to the structure produce an absorption near the telluric water vapor line near 10 831.5 Å, whereas a second unshifted component is seen at the rest wavelength of He i.
 |
Fig. 5 Individual profiles along the central axis of the structure. Top/bottom panel: He i/Ca ii H. The inner footpoint corresponds to the uppermost profile, the outer to the lowermost one. The solid vertical lines denote the rest wavelength of the respective line. The dashed vertical lines in the lower panel mark the used photospheric iron lines. The spatial separation between two subsequent profiles was 5′′. The profiles were offset in intensity from each other arbitrarily for better visibility. |
3.2. Temporal evolution: ChroTel and TRACE
In the ChroTel data, upflowing material is seen already two hours before the spectrograph scan. Strong upflows with velocities of around −15 km s-1 set in at around 9:12–9:13 UT and persist until the first data gap at 9:23 UT. At 9:38 UT, after the data gap, the upflows have slowed down to about −5 to −10 km s-1. The top row of Fig. 6 shows data that was averaged over the period from 9:46–9:53 UT. Velocities around −6 to −12 km s-1 are seen in the upflowing branch, whereas still no enhanced downflows are discernible yet from the general downdraft region in the surroundings. The absorption depth in He i shows no visible enhancement with respect to the background.
After another data gap of 35 min, the observations continued from 10:27–11:33 UT without interruption. During this period of roughly one hour, a continuous, but not necessarily steady flow is seen in the structure. The second row of Fig. 6 shows averaged data from 10:53–11:00 UT, i.e., around 15 min before the spectrograph scan. The structure exhibits a symmetric flow with very strong up- and downflow velocities of at least 30 km s-1. The He i absorption is strongly enhanced at that time, predominantly in the middle of the structure. This is also the case in the next snapshot during the spectrograph scan at 11:08–11:15 UT. The velocity map confirms what was already seen in the previous velocity maps (Fig. 2). After the last data gap of 30 min, the flow has completely disappeared in He i at 12:03–12:10 UT.
In the TRACE snapshots, a dark feature is seen when also the absorption in He i is strong (two middle rows in Fig. 6). The dark feature in the TRACE Fe ix/x data is found exactly within the contour derived from the He i velocities in the TIP data. At 9:52 UT, when only weak upflows were present and no enhanced absorption in He i is discernible yet, one gets the impression that the so-called moss emission from below is partially absorbed by overlying, optically thin material in the middle of the contour. After the flow has disappeared in He i at 12:25 UT, the moss emission is clearly visible again in the middle of the contour.
 |
Fig. 6 Temporal evolution of the flow. Left and middle column: He i absorption depth and line-of-sight velocity from averaged ChroTel data. The time range denotes the averaging period for the data. Note that the color bars for the velocities were scaled by a factor of 3 to take into account the underestimation of high velocities in the velocity determination with the ChroTel filtergrams (see Bethge et al. 2011). Right column: intensity in the Fe ix/x 171 Åchannel of co-temporal raw TRACE data (linear scale; only the right half of the map is shown). |
4. Magnetic structure of the loop
4.1. Total polarization signals
Figure 7 shows the total linear and total circular polarization signals in Si i and He i. The additional spectropolarimetric data of the two Fe i lines at 630 nm from the second channel of POLIS have not been included in the current investigation, because they are similar to the Si i line. The polarization signals in Si i show no exceptional match with the contour, which is expected because only the footpoint signatures should be visible in the photosphere. As the map of the signed total circular polarization in Si i showed, patches with a polarity opposite to that at the downflow footpoint are seen at the very border of the contour in the upflow region, i.e., the upflow footpoint is likely to be located in these regions of opposite polarity.
The polarization signals in He i correspond well to the contour. The total linear polarization signal is strongest at the location where the velocities are close to zero. This means that we are looking at predominantly horizontal magnetic fields and flows within, which is likely to be the loop apex. However, both linear and circular polarization signals are present at the same time almost everywhere in the outlined structure, i.e., the magnetic field configuration is in reality more complicated than the simple picture of a flux tube arching from one footpoint to the other. The presence of multiple spectral components (Figs. 4 and 5) also already indicated that the structure is not the only feature present in the area marked by the contour.
4.2. Inversions of Si I
As a first estimate of the photospheric magnetic field properties, we inverted the spectra of the Si i line with the HELIX+ Code (Lagg et al. 2004, 2009). HELIX+ uses the Milne-Eddington approximation and provides the average values of magnetic field properties throughout the formation height of the line. The inversion of this and the other lines observed (He i, Fe i at 630.15 nm and 630.25 nm) will be discussed in more detail in a subsequent publication. Here, we only show the map of the photospheric magnetic field strength as derived from the Si i spectra (see Fig. 8). In addition, we point out that the magnetic field inclination in the photosphere in the local reference frame (z perpendicular to the solar surface) from the inversions confirmed that the field orientation in the upflow point was opposite to that in the downflow point in the penumbra.
For a comparison of the magnetic field strength in the upflow and downflow footpoint, two regions were defined: an upflow region where the plasma is flowing faster than −300 m s-1 in Si i, and a downflow region where the plasma is flowing faster than +35 km s-1 in He i. The upflow region is located partly outside of the contour of the structure because the upflows in all photospheric lines extend slightly beyond the contour (Fig. 2). In both regions, the mean magnetic field strength in the photosphere was computed from the inversion results. The mean magnetic field strength in the upflow region is 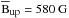 , while we find
, while we find 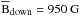 in the downflow region. The inversions in Si i therefore show that the magnetic field at the inner footpoint in the sunspot penumbra is stronger than at the outer footpoint in the plage region.
in the downflow region. The inversions in Si i therefore show that the magnetic field at the inner footpoint in the sunspot penumbra is stronger than at the outer footpoint in the plage region.
5. Discussion
5.1. Magnitude of the siphon flow
Driving a siphon flow through a flux tube requires a difference in gas pressure between the two footpoints. The observations show that the main requirement of Eq. (1) is fulfilled: the downflow footpoint is located in the penumbra of a sunspot with a higher magnetic field strength than in the upflow footpoint situated in a plage region. The photospheric magnetic field in the upflow region is on average about 1/3 weaker than in the downflow region. The total pressure, however, is not directly provided by the data, and could be different in both locations because of their fairly different surroundings. But exactly these surroundings provide also another argument in favor of a gas pressure difference: the continuum intensity, and hence, the temperature and the corresponding internal gas pressure, is significantly lower at the inner footpoint. Thus, one can reasonably assume a lower gas pressure at the inner footpoint that suffices to drive a siphon flow between the two points, flowing from weaker to stronger magnetic fields and likewise from a hotter to a colder region.
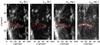 |
Fig. 7 Total linear (Ltot) and total circular (Vtot) polarization in Si i and He i, in percent of the continuum intensity. Only the right half of the map is shown. From left to right: Vtot in Si i (0–4 %), Ltot in Si i (0–1.5%), Vtot in He i (0–1%), Ltot in He i (0.05–0.2%). |
One can roughly estimate the magnitude of the flow based on the difference in magnetic field. Assuming that the total external pressure at both footpoints is the same, the difference in gas pressure inside the flux tube equals the difference in magnetic pressure. The difference in magnetic field strength of ΔB = 370 G at the footpoints as mentioned in Sect. 4.2 translates into a magnetic pressure difference of 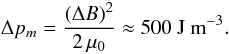 (2)If we approximate the pressure gradient
(2)If we approximate the pressure gradient 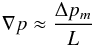 (3)through the pressure difference Δpm and the length of the loop of approximately L ≈ 20 Mm, we can estimate the acceleration a caused by this pressure difference to be
(3)through the pressure difference Δpm and the length of the loop of approximately L ≈ 20 Mm, we can estimate the acceleration a caused by this pressure difference to be 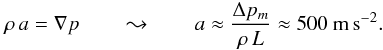 (4)As we estimate the effect on the chromospheric plasma seen in He i, we used ρ ≈ 5 × 10-8 kg m-3 as an estimate for the density (at a height of about 1000 km, e.g. Vernazza et al. 1981). The resulting acceleration of some 500 m s-2 is about twice the solar surface gravitational acceleration of g⊙ ≈ 274 m s-2, and thus the material can be lifted up against gravity to flow along the loop.
(4)As we estimate the effect on the chromospheric plasma seen in He i, we used ρ ≈ 5 × 10-8 kg m-3 as an estimate for the density (at a height of about 1000 km, e.g. Vernazza et al. 1981). The resulting acceleration of some 500 m s-2 is about twice the solar surface gravitational acceleration of g⊙ ≈ 274 m s-2, and thus the material can be lifted up against gravity to flow along the loop.
The speed v of the siphon flow can be roughly estimated if we assume that the pressure difference Δpm from Eq. (2), which essentially is a (magnetic) energy density, is turned into kinetic energy: 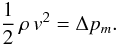 (5)Here, we also assume that the two footpoints are at the same height, i.e., that they have the same potential energy. This yields a velocity of about v ≈ 140 km s-1.
(5)Here, we also assume that the two footpoints are at the same height, i.e., that they have the same potential energy. This yields a velocity of about v ≈ 140 km s-1.
 |
Fig. 8 Magnetic field strength in the photosphere as derived from an inversion of the Si i spectra. |
The observations show speeds along the line-of-sight of more than 40 km s-1 (see Fig. 3). Depending on the loop geometry, this is a lower limit for the true velocity along the loop. From this we can conclude that the speed of about 140 km s-1 that we have roughly estimated for the siphon flow is consistent with the observed flows.
5.2. Comparison to siphon flow models
During the whole observation, the moving plasma stays confined within the outlined structure, as it becomes apparent from the ChroTel data and the absorption features seen in the TRACE images (see Sect. 3.2). The total polarization signals in He i coincide extremely well with the structure outlined from the velocities (Sect. 4.1), supporting the view that the plasma is moving within a magnetic loop in the chromosphere.
The ChroTel data show a continuous flow for at least one hour; the direction of the flow is always maintained. Cargill & Priest (1980) found that pressure perturbations in already existing flows can lead to reverse flows from the footpoint with lower gas pressure to the one with higher gas pressure. In this observation, this seems not to be the case. Nevertheless, the unidirectional flow observed here goes through different stages, from an asymmetrical velocity distribution with little He i absorption and subsonic flow speeds to a very symmetrical flow with strong He i absorption and velocities that clearly exceed the sound speed of about 10 km s-1 at typical formation temperatures of the He i triplet. At first sight, the latter stage seems to resemble the “purely supercritical flow” steady-state solutions for siphon flows described in Cargill & Priest (1980) or in Thomas (1988, his Fig. 3d). In these solutions, the velocity increases monotonically and the gas pressure decreases monotonically all along the descending part of the tube. In reality however, the downflow must become subcritical at some point to fulfill the pressure balance condition at (or beneath) the photospheric downstream footpoint. Because the He i observations are limited to chromospheric heights, they should therefore rather represent something similar to the upper parts of the flux tube in the “critical solution” of Thomas (1988, his Fig. 3c). In this solution, the flow speeds are only supercritical near the loop apex and become subcritical further down in the atmosphere.
The velocity distribution during the spectrograph scan is completely compatible with the “critical solutions” in both Cargill & Priest (1980) and Thomas (1988, his Fig. 3 c), with subsonic upflow velocities and supersonic downflow velocities (Figs. 2 and 3). For this case, a tube shock in the downflow branch is predicted, where the velocities undergo a sharp transition from super- to subsonic. In He i, there are indeed two velocity components present in the spectra in most pixels at the edge of the downflowing branch: a fast component at about 40 km s-1 and a slow component at about 5 km s-1. However, the latter might also represent plasma from the general downdraft region in the background that is consistently present during the observations.
In the solution of Thomas (1988), the sharp velocity transition is accompanied by an increase in tube diameter and a decrease in magnetic field strength. Whereas for the latter we find no direct indications, the former is supported by the highest-forming photospheric spectral line Fe i at 396.93 nm. Even if it already shows only subsonic velocities, the size of the downflow patch is clearly larger than the very localized upflow patch (Fig. 3). The fact that only small redshifts are seen near the inner footpoint in all photospheric lines means that the deceleration of the plasma must have taken place between the formation heights of He i or Ca ii H and the upper photosphere (about 600 km height, cf. Table 1). The tube shock – if present – has therefore occurred in an intermediate layer, where the plasma is already too cool to be visible in He i, but still too hot to appear in the photospheric lines. The emission near the Ca ii line core presents the only evidence in favor of a possible tube shock. At the inner end of the structure, the core emission is slightly enhanced (at the lower dashed horizontal line in the upper panel of Fig. 4). If the tube shock has thus occurred in an intermediate layer, it is of course not surprising that no observational signature is present in He i or photospheric lines. Also, the theoretical calculations referred to a high-β plasma, i.e., for conditions found primarily in the photosphere. Since the sharp velocity transition occurs in a layer above the formation height of Fe i at 396.93 nm, the condition of a high-β plasma might not apply. This is supported by the fact that the flows seen in He i are confined within the outlined structure at all times, suggesting that within the structure the magnetic field dominates the plasma motions at any height.
5.3. Relation to TRACE 171 Å observations
That the dark structures in the TRACE 171 Å images represent the same material that is seen in He i 10 830 Åis suggested not only by the remarkable correlation with the contour, but also from a study from Anzer & Heinzel (2005). They showed that the Fe ix/x radiation around 171 Åoriginating from a 106 K hot plasma can be effectively absorbed by the Lyman continuum of neutral hydrogen (λ < 912 Å), by neutral helium (λ < 504 Å), and by singly ionized helium (λ < 228 Å). The cool material can therefore absorb the moss emission originating from below the structure.
It is an assumption that the emission under the loop is present during the whole observation, but there are three arguments in favor: (1) The moss emission is visible through a somewhat “semi-transparent” layer when the siphon flow sets in. (2) It can be seen on either side of the middle of the contour at all times. (3) It is present in the contour after the siphon flow has disappeared. The latter is the strongest indication for constant presence of the moss emission below the structure. This would mean that the magnetic loop in which the siphon flow takes place is embedded in the corona in its uppermost parts. According to 3D MHD coronal models (e.g., Bingert & Peter 2011) the magnetic transition into the corona occurs at some 5 Mm height. Thus one could assume that the apex of the loop is located well above 5 Mm (while the footpoints are separated by about 20 Mm).
This would also explain the high absorption depth in He i that is seen in the middle of the structure, which is probably not only caused by the higher plasma density inside the loop, but also by the enhanced EUV radiation from the corona in the surroundings that populates the triplet states of the He i 10 830 Å transition (Centeno et al. 2008). While the coronal illumination reaches the lower-lying parts of the loop only from above and is additionally partially absorbed on its way to the chromosphere, the coronal part of the loop gets illuminated “in situ” and from all directions, leading to a higher population of the triplet states and therefore to a stronger absorption in He i.
In a future study we will investigate the magnetic topology of the siphon flow in the photosphere and in the chromosphere from inversions of all observed lines, and determine the mass flux balance through the structure from one end to the other.
6. Initiation and termination of the flow
In the following we will give some speculations on what might have triggered the onset and termination of the flow. Figure 9 shows TRACE images at three times: at 9:13 UT when the strong upflow velocities started in He i, at 9:10 UT just before that for comparison, and at 11:38 UT, which is the last point in time before the flow disappeared and for which TRACE data was still available.
At 9:13 UT, at about the same time when the strong upflows start in He i, a brightening appears inside the contour. It becomes clear when the TRACE images are watched as a movie that this is not moss emission from below, but a short-lived (~3 min) brightening inside the (already existing) structure. This brightening could be caused by heating as a result of reconnection near the apex while the loop-like structure is presumably rising into the upper atmosphere. Then the magnetic field lines eventually reconnected to a different location in the (subsequent) downflow region, a location with a magnetic field strength large enough to initiate the siphon flow because of the difference in gas pressure between the new inner and the old outer footpoint.
Small brightenings are also seen in the contour in the last available TRACE image at 11:38 UT, 25 min before the flow itself disappears. The idea is the same as before: a reconnection event causing the brightening, this time leading to a disintegration of the structure and the flow within. This is even more speculative than for the initiation of the flow because there is no ChroTel data available at that time, and therefore we have no information about a possible co-temporal termination of the flow.
 |
Fig. 9 The siphon flow region in TRACE Fe ix/x 171 Ådata when the strong upflows in He i set in (9:13 UT), just before that for comparison (9:10 UT), and within the data gap in the ChroTel data in which the flow disappeared (11:38 UT). Notice the brightenings within the contour in the two rightmost images. |
7. Conclusions
We presented observational evidence for a long-lasting siphon flow of chromospheric material in a magnetic loop structure, driven by a difference in magnetic pressure (and therefore in gas pressure) in the footpoints of the loop. The presented data is consistent with the picture of cold material flowing in an arch-like structure that reaches from the photosphere up into the corona. The flow could be initiated and terminated by reconnecting magnetic fields, as it is indicated from the coronal context data.
The observed difference of the magnetic field strength in the two footpoints of the structure is sufficient to drive a siphon flow, and the estimated speed of the siphon flow is consistent with the observed Doppler shifts. Direct evidence of a tube shock in the downflowing branch of the loop as predicted from theoretical work on siphon flows is not prominent in the data. However, the weak photospheric counterpart of the strong downflows in the chromosphere indicates that a tube shock might have occurred at a height between about 600 km and the formation height of He i ( > 1000 km).
For the interpretation one has to follow the temporal evolution not only in intensity images, but also in Doppler shift maps, as done here using full-disk data from ChroTel. The line-of-sight velocities determined from filtergram intensities in He i are crucial in this study to track the temporal evolution of the flow, which emphasizes that siphon flows are dynamic phenomena going through different phases to which existing theoretical steady-state solutions fit only temporarily.
Acknowledgments
The ChroTel project was funded in part by the Deutsche Forschungsgemeinschaft (DFG). C. Bethge would like to thank R. Hammer, R. Rezaei, and R. Schlichenmaier for valuable discussions. C. Beck acknowledges support by the Spanish Ministry of Science and Innovation through project AYA2010–18029 and JCI-2009-04504.
References
- Anzer, U., & Heinzel, P. 2005, ApJ, 622, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Schrijver, C. J., & Alexander, D. 2001, ApJ, 550, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Bard, S., & Carlsson, M. 2008, ApJ, 682, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C., Schmidt, W., Kentischer, T., & Elmore, D. 2005, A&A, 437, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Khomenko, E., Rezaei, R., & Collados, M. 2009, A&A, 507, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Tritschler, A., & Wöger, F. 2010, Astron. Nachr., 331, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Bethge, C., Peter, H., Kentischer, T. J., et al. 2011, A&A, 534, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bingert, S., & Peter, H. 2011, A&A, 530, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brekke, P., Kjeldseth-Moe, O., & Harrison, R. A. 1997, Sol. Phys., 175, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., & Priest, E. R. 1980, Sol. Phys., 65, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Trujillo Bueno, J., Uitenbroek, H., & Collados, M. 2008, ApJ, 677, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Collados, M., Lagg, A., Díaz García, J. J., et al. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 611 [Google Scholar]
- Degenhardt, D. 1989, A&A, 222, 297 [NASA ADS] [Google Scholar]
- Degenhardt, D., Solanki, S. K., Montesinos, B., & Thomas, J. H. 1993, A&A, 279, L29 [NASA ADS] [Google Scholar]
- Doyle, J. G., Taroyan, Y., Ishak, B., Madjarska, M. S., & Bradshaw, S. J. 2006, A&A, 452, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Felipe, T., Khomenko, E., Collados, M., & Beck, C. 2010, ApJ, 722, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Kentischer, T. J., Bethge, C., Elmore, D. F., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 701413 [CrossRef] [Google Scholar]
- Lagg, A., Woch, J., Krupp, N., & Solanki, S. K. 2004, A&A, 414, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Ishikawa, R., Merenda, L., et al. 2009, in The Second Hinode Science Meeting, ed. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 327 [Google Scholar]
- Lites, B. W., Rutten, R. J., & Berger, T. E. 1999, ApJ, 517, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F., & Schmidt, H. U. 1968, Z. Angew. Math. Mech., 48, 218 [CrossRef] [Google Scholar]
- Noci, G. 1981, Sol. Phys., 69, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Peres, G. 1997, in The corona and solar wind near minimum activity, ed. A. Wilson, Proceedings of Fifth SOHO Workshop (ESA SP–404), 55 [Google Scholar]
- Rezaei, R., Bruls, J. H. M. J., Schmidt, W., et al. 2008, A&A, 484, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüedi, I., Solanki, S. K., & Rabin, D. 1992, A&A, 261, L21 [NASA ADS] [Google Scholar]
- Thomas, J. H. 1988, ApJ, 333, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J. H., & Montesinos, B. 1991, ApJ, 375, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H., Balasubramaniam, K. S., & Tritschler, A. 2006, ApJ, 645, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Overview maps of the observed FOV. Clockwise from upper left: continuum intensity in the infrared, total circular polarization of Si i, line-core intensity of Ca ii H, absorption depth of He i. The contour outlines the structure hosting the siphon flow under investigation. All maps are shown on a linear scale, the total circular polarization is scaled over a range of [− 3%, 6%] of the continuum intensity. The red line in the continuum map denotes the central spine of the structure. |
| In the text | |
 |
Fig. 2 Line-of-sight velocities. Left column, bottom to top: Fe i at 396.55 nm, Fe i at 396.61 nm, Si i at 1082.71 nm. Right column, bottom to top: Fe i at 396.93 nm, Ca ii H core at 396.85 nm, He i at 1083.03 nm. |
| In the text | |
 |
Fig. 3 Line-of-sight velocities along the central axis of the loop structure under investigation. Top panel: chromospheric lines of He i and Ca ii H. Bottom panel: photospheric lines. The dashed vertical lines denote the inner and outer end of the structure. The dotted lines indicate the locations of upflows and downflows. |
| In the text | |
 |
Fig. 4 Spectra along the central axis of the structure. Top to bottom: intensity spectra of Ca ii H, Stokes IQUV of He i. The two horizontal dashed lines in each panel denote the inner (lower line) and outer end (upper line) of the structure. The vertical solid lines denote the rest wavelength of the respective line. |
| In the text | |
 |
Fig. 5 Individual profiles along the central axis of the structure. Top/bottom panel: He i/Ca ii H. The inner footpoint corresponds to the uppermost profile, the outer to the lowermost one. The solid vertical lines denote the rest wavelength of the respective line. The dashed vertical lines in the lower panel mark the used photospheric iron lines. The spatial separation between two subsequent profiles was 5′′. The profiles were offset in intensity from each other arbitrarily for better visibility. |
| In the text | |
 |
Fig. 6 Temporal evolution of the flow. Left and middle column: He i absorption depth and line-of-sight velocity from averaged ChroTel data. The time range denotes the averaging period for the data. Note that the color bars for the velocities were scaled by a factor of 3 to take into account the underestimation of high velocities in the velocity determination with the ChroTel filtergrams (see Bethge et al. 2011). Right column: intensity in the Fe ix/x 171 Åchannel of co-temporal raw TRACE data (linear scale; only the right half of the map is shown). |
| In the text | |
 |
Fig. 7 Total linear (Ltot) and total circular (Vtot) polarization in Si i and He i, in percent of the continuum intensity. Only the right half of the map is shown. From left to right: Vtot in Si i (0–4 %), Ltot in Si i (0–1.5%), Vtot in He i (0–1%), Ltot in He i (0.05–0.2%). |
| In the text | |
 |
Fig. 8 Magnetic field strength in the photosphere as derived from an inversion of the Si i spectra. |
| In the text | |
 |
Fig. 9 The siphon flow region in TRACE Fe ix/x 171 Ådata when the strong upflows in He i set in (9:13 UT), just before that for comparison (9:10 UT), and within the data gap in the ChroTel data in which the flow disappeared (11:38 UT). Notice the brightenings within the contour in the two rightmost images. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


