| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117572 | |
| Published online | 12 December 2011 | |
The XMM-Newton view of the eclipse and dips of the dwarf nova Z Chamaleontis
1
Department of PhysicsUniversity of Salento, via per Arnesano, CP 193, 73100, Lecce, Italy
e-mail: nucita@le.infn.it
2
INFN, Sez. di Lecce, via Per Arnesano, CP 193, 73100 Lecce, Italy
3 European Space Astronomy Centre, SRE-O, PO Box 78, 28691 Villanueva de la Cañada (Madrid), Spain
Received: 27 June 2011
Accepted: 25 September 2011
Context. A cataclysmic variable contains a white dwarf that accretes material from a secondary star via the Roche lobe mechanism. Systems with high line-of-sight inclination angles offer the possibility to pinpoint the location of the X-ray emitting region by characterizing the observed eclipse by the secondary star.
Aims. We present an XMM-Newton observation of the dwarf nova Z Chamaleontis that we analyzed to determine the properties of the X-ray and optical light curves, as well as the high-energy spectrum.
Methods. We performed a spectral analysis of the data taken by the EPIC camera, and a timing analysis of the observed X-ray and optical OM light curves.
Results. We find that a multi-temperature plasma component absorbed by ionized material is required to describe the data. In particular, we estimate that the total absorbed flux in the 0.2–9.0 keV band is FAbs0.2-9.0 = (4.1±0.1) × 10-12 erg s-1 cm-2, which, when accounted for absorption and bolometric correction, corresponds to a bolometric luminosity of LBolX = (6.9±0.1) × 1030 erg s-1 at a distance of 97 pc. The mass accretion rate onto the white dwarf turns out to be about 1.1 × 10-11M⊙ yr-1. Our analysis of the optical and X-ray eclipse light curves and the mid-eclipse times of Z-Chamaleontis, in addition to the eclipse (during which the observed EPIC count rate is 0.033 ± 0.003 count s-1), implies that the X-ray light curve contains dips (at the orbital phases 0.30 ± 0.02 and 0.73 ± 0.02) that can be naturally explained as absorption effects by intervening stable gas clouds close to the accretor.
Key words: X-rays: binaries / white dwarfs / novae, cataclysmic variables
© ESO, 2011
1. Introduction
A cataclysmic variable (hereafter CV) is a binary system constituted by a white dwarf (the primary) accreting material from a late main-sequence star by means of the formation of a Roche lobe (for a review, we refer to Warner 1995). In non-magnetic CVs (with magnetic field ≲ 0.1 MG), the accretion occurs via a Keplerian disk so that as much as half of the total potential gravitational energy is dissipated by the viscosity, while the other half is radiated away by the boundary layer (BL), i.e., the region between the inner disk and the white dwarf surface. In this picture, the radiation emitted by the disk peaks in the optical and ultraviolet bands, while the BL mainly radiates in the extreme ultraviolet and X-rays, typically with luminosities in the range 1030–1032 erg s-1 (Lamb 1982; Baskill et al. 2005; for a review on X-rays from CVs we refer to Kuulkers et al. 2006).
Systems in which the secondary star eclipses the white dwarf, i.e. those characterized by high line-of-sight inclination angles, offer the possibility to test whether the X-ray photons originate in the BL and constrain its size. However, these observations are complicated by eclipsing CVs having very low X-ray flux during an eclipse phenomenon because the X-ray photons are in part absorbed by the accretion disk. The XMM-Newton satellite (Jansen et al. 2001) is particularly helpful because of the large effective area and the possibility to observe the source simultaneously in the optical band via the optical monitor (OM) instrument.
X-ray eclipses have been observed by the XMM-Newton satellite in various CVs, including OY Car (Ramsay et al. 2001; but see also Wheatley & West 2003, for a detailed study) and HT Cas (Nucita et al. 2009). In both cases, it was possible to find that the X-ray emitting region (possibly a BL) has a size comparable with that of the central white dwarf, confirming the mass accretion scenario for a dwarf nova system.
Another binary system that is particularly suitable for these kind of studies is Z Chamaleontis, i.e. a dwarf nova of the SU Ursae Majoris subclass (Hefner et al. 1979), which is often defined by outbursts and superoutbursts. The binary systems are highly inclined (81.6°−81.9°, see, e.g., Wood et al. 1986) to the line-of-sight, thus deep eclipses must affect the observed optical light curve. This provides the opportunity to study in detail the source and extract the binary system parameters: Z Chamaleontis contains a secondary star orbiting the central white dwarf1 at the orbital period, Porb ≃ 1.78 h. As first observed by Baptista et al. (2002), Z Chamaleontis also shows evidence of a cyclical period change of about 30 yr. This variation could be due to a tertiary component (possibly a brown dwarf, see Dai et al. 2009) orbiting the binary system.
In this article, we present the result of a ~99 ks XMM-Newton observation of the Z Chamaleontis. The paper is structured as follows: in Sect. 2, we briefly review the results from previous X-ray observations; in Sect. 3, we present our observation and the analysis (Sects. 4.3 and 4.2) that we conducted; and finally, in Sect. 5, we present our conclusions.
2. Previous ROSAT observation of the X-ray eclipses in Z Chamaleontis
The existence of X-ray eclipses in the Z Chamaleontis binary system was demonstrated by van Teeseling (1997) when analyzing the ROSAT data acquired with the PSPC and HRI instruments. Here, for completeness, we briefly review the results of this work to which we refer for more details.
The X-ray spectral properties of Z Chamaleontis were derived using the PSPC data and it was found that a thermal bremsstrahlung model (with temperature 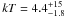 keV and column density nH = (1.9 ± 0.6) × 1020 cm-2) is an acceptable description of the data. The unabsorbed flux in the 0.1–2.4 keV band was
keV and column density nH = (1.9 ± 0.6) × 1020 cm-2) is an acceptable description of the data. The unabsorbed flux in the 0.1–2.4 keV band was 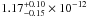 erg cm-2 s-1 such that, for an estimated distance to the source of 97 pc (Wood et al. 1986), the X-ray accreting luminosity is ≃ 1.3 × 1030 erg s-1. Correcting for a bolometric factor, van Teeseling (1997) found a bolometric luminosity of ≃ 2.5 × 1030 erg s-1, corresponding to an accretion rate ≃ 10-12 M⊙ yr-1.
erg cm-2 s-1 such that, for an estimated distance to the source of 97 pc (Wood et al. 1986), the X-ray accreting luminosity is ≃ 1.3 × 1030 erg s-1. Correcting for a bolometric factor, van Teeseling (1997) found a bolometric luminosity of ≃ 2.5 × 1030 erg s-1, corresponding to an accretion rate ≃ 10-12 M⊙ yr-1.
The HRI data unequivocally showed the existence of X-ray eclipses which when folding the light curve with the ephemeris given by Robinson et al. (1995). According to the analysis of van Teeseling (1997), the X-ray eclipse occurs simultaneously with the white dwarf occultation, even if a phase shift of about 90 s (possibly due to the used ephemeris) was observed. The HRI count rates in and out of the eclipses were found to be 0.0221 ± 0.0008 and 0.0011 ± 0.0013 count s-1, respectively. Interestingly, van Teeseling (1997) also detected a dip close to the phases 0.7–0.8, possibly caused by the absorption of X-ray photons by intervening material along the line-of-sight.
3. XMM-Newton observation of Z Chamaleontis: data reduction
The XMM-Newton satellite (Jansen et al. 2001) has a much larger effective area than ROSAT and permits the source to be observed simultaneously in the optical band with the optical monitor (OM).
Z Chamaleontis was observed by XMM-Newton on two occasions in 2003 and 2005 (Observation IDs 0205770101 and 0306560301) for ≃99 ks and ≃87 ks, respectively. In this paper, we focus on characterizing the X-ray eclipse of Z Chamaleontis and, consequently, use only the first observation corresponding to the quiescent state of the CV whose light curve clearly show eclipses. The observation started on 2003 December 19 (20:45:52.0 UT) and ended on 2003 December 21 (00:56:0.9 UT).
The target was observed by the three X-ray instruments (RGS, EPIC-MOS, and EPIC-PN), and by the Optical Monitor (OM) onboard XMM-Newton. Here, we concentrate on the EPIC and OM data only. The RGS data will be presented elsewhere. The PN was operated in full frame mode, while the two MOS were operated in large window mode, and started ≃ 1300 s before the PN. In addition, the fast mode of OM allowed us to obtain the optical light curve (in the B filter, 400 − 500 nm) of the source.
The observation data files (ODFs) were processed using the XMM-Science Analysis System (SAS version 11.0.0) and with the latest available calibration constituent files. The event lists for the EPIC cameras were obtained by running the standard emchain and epchain tools, while the task omfchain was executed to get the optical background-subtracted light curve of Z Chamaleontis.
In the B filter (400 − 500 nm), the average out-of-eclipse magnitude2 is 16.06 ± 0.25. Using Vega magnitude to flux conversion3, the observed quiescent magnitude corresponds to a flux of 2.48 × 10-15 erg cm-2 s-1 Å-1. The observed OM flux and magnitude are consistent with previous quiescent observations.
 |
Fig. 1 Upper panel: the 0.2–10 keV EPIC background-corrected light curve of Z Chamaleontis with a time resolution of 40 s. Bottom panel: the OM light curve with a bin size of 40 s. The photons were barycentrically corrected (see text for details). |
We produced light curves in the energy range 10–12 keV for both the MOS and PN cameras to discard portions of the observation affected by high levels of background. To achieve this, we followed the recipe described in the XRPS User’s manual (2008)4. The MOS cameras were practically unaffected by high-energy flares, while the resulting exposure time for the PN camera turned out to be ≃ 83 ks. Events within good time intervals were used in the spectral analysis.
In contrast, the timing analysis was performed without applying good time intervals in order to avoid gaps, which could introduce spurious effects in the power spectral analysis. The X-ray emission from the source was extracted from a circular region centered on the nominal position of Z Chamaleontis (α = 08h07m27.75s, δ = −76°32′00.7′′). The background signal was extracted from circular regions on the same chip and, where possible, at the same vertical location of the source extraction regions. The radii of the source and background extraction regions were chosen to be ≃ 80′′ and ≃ 40′′, respectively.
Finally, the source and background spectra, as well as the light curves, are extracted and used in the following analysis.
 |
Fig. 2 The X-ray eclipses in the 0.2−10 keV (upper part of each panel) band and the corresponding view of the OM instrument (bottom part). The vertical dashed line represents the position of the optical mid eclipse (using the ephemeris of Baptista et al. 2002). The number of the cycle corresponding to the plotted eclipse is also given. |
4. Analysis and results
4.1. Optical temporal analysis results
As previously described, the standard pipeline for the reduction of the OM data was applied. In doing this, we decided to produce light curves in the B filter with bin sizes of 40 s, for graphical purposes only, and 5 s, which we found to correspond to a good compromise between a sufficiently high sampling rate light curve and an adequately high quality statistic per bin. The whole 40 s binned light curve is shown in Fig. 1 (bottom panel). We note that the solar system barycentric correction was also applied to both light curves.
For clarity, we show all the observed optical eclipses in separate panels (see the bottom part of each panel in Fig. 2) and indicate with a vertical dashed line the position of the optical mid eclipse expected by using the sinusoidal ephemeris of Baptista et al. (2002). In this respect, the first eclipse appearing in the OM light curve occurs at the time JD = 52 992.907 81 ± 0.000 03 days corresponding to the orbital cycle 170 857.
We note that the OM light curve is characterized by small gaps (at cycles 170 862, 170 865, and 170 868) corresponding to ground station handovers during which the instrument was not operating (see XRPS User’s manual 20084), while the large gap at cycle 170 860 was caused by a telemetry problem (during the exposure #007), implying that there are incorrect time stamps in the light curve.
The 5 s binned light curve was used to characterize the white dwarf eclipse in the optical band via the digital technique described by Wood et al. (1985). Thus, we evaluated the mid-eclipse (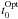 ) time of each of the identified eclipses measuring the mid-ingress (
) time of each of the identified eclipses measuring the mid-ingress (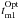 ) and mid-egress (
) and mid-egress (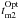 ) times.
) times.
When the method was applied to the mean (folded) light curve, the optical eclipse was passed through a median filter characterized by a width no larger than one quarter the extention of the ingress/egress. In Z Chamaleontis, the optical ingress/egress of the white dwarf eclipse lasts for ≃ 55 s (see e.g. Wood et al. 1986), corresponding to a median filter of width ≃ 13.8 s (i.e. ≃ 3 bins for the 5 s binned light curve). However, when dealing with the original (not folded) light curve, more smoothing is required (Wood et al. 1986). In our case, we used a median filter width of ≃ 20 s (4 bins).
The light curve derivative was then numerically calculated, the ingress and egress intervals being characterized by values of the derivative significantly different from 0. These regions were identified by applying a matched detection filter (a box car of width equal to the expected duration of the ingress and egress) to the derivative light curve. The two resulting negative and positive peaks indicate the location of the mid-ingress and mid-egress times.
Finally, the mid-eclipse time was calculated as the average of ingress and egress mid-points, i.e. 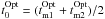 .
.
The algorithm was then repeated for all the cycles observed by the OM, apart from those containing time gaps. The times of mid-eclipse of the resulting 11 eclipses are listed in Table 1. We associated an error of half bin (≃3 s) to the ingress/egress mid-point times. In the same table, we also give the (O–C) values computed using the sinusoidal ephemeris of Baptista et al. (2002) and the (O–C) values with respect to the linear ephemeris of Dai et al. (2009). The average (O–C) values (and the associated errors evaluated as the standard deviation in the mean) in the two cases was found to be − (2.6 ± 0.3) × 10-4 days and (0.05 ± 0.20) × 10-4 days, respectively.
Timings of the optical mid-eclipses observed with OM.
4.2. X-ray temporal analysis results
As mentioned above, we used the original event list files to avoid introducing gaps in the light curves and artifacts in the timing analysis.
We then applied the Solar System barycentric correction, after which the event times were in barycentric dynamical time instead of spacecraft time.
Using the extraction regions previously described, the source and background synchronized light curves were extracted from the barycenter-corrected event files. The time series produced were used as input to the SAS task epiclccorr to account for absolute and relative corrections, as well as the background subtraction. In addition, the background-corrected light curves of the three instruments were combined to increase the signal-to-noise ratio. We produced light curves with a bin size of 40 s (for graphical purposes) and 10 s (for the subsequent timing analysis), respectively.
The resulting EPIC 0.2–10 keV light curve has an average count rate of 0.71 ± 0.10 count s-1 and is shown in Fig. 1 (upper panel). In Fig. 2, we also show each X-ray eclipse on separate panels and compare directly with the OM time series.
 |
Fig. 3 The Lomb-Scargle periodogram of the EPIC light curve in the energy range 0.2–10 keV band. The dashed vertical lines correspond to the orbital period of Z Chamaleontis and to two major harmonic features (see text for details). |
We performed a blind search for periodicities in the X-ray light curve. We applied the well-known Lomb-Scargle technique (Scargle 1982) and the result of this analysis is shown in Fig. 3. The detected period of 1.788 h is fully consistent with that corresponding to the sinusoidal ephemeris of Baptista et al. (2002). In the same figure, other peaks corresponding to harmonics of the orbital period are evident. For clarity, only those corresponding to Porb/2 and Porb/3 are indicated by the dashed vertical lines. We also note that the same method gives consistent results when applied to the optical light curve. We did not detect any other significant periodicity for timescales longer than 2.8 h (or equivalently for frequencies less than 10-4 Hz). We did not detect significant peaks5 either for timescales shorter than 500 s (2 × 10-3 Hz).
This is also consistent with the scenario according to which X-ray modulations (other than the orbital period) are not expected in non-magnetized CVs. We note that a sample of 30 non-magnetized CVs was studied by Baskill et al. (2005), who identified extra periodicities in a few of them. However, as the same authors recognized, a careful analysis is required to verify whether the identified peaks represent true periodicities or red noise features. In this context, Z Chamaleontis appears to be a typical member of the non-magnetized CV class.
 |
Fig. 4 Upper panels: two orbital periods of the OM (left) and EPIC 0.2–10 keV (right) light curves. Bottom panels: a zoom around both the optical and X-ray eclipse. |
Hence, we folded the EPIC and OM light curves to the orbital period of Z Chamaleontis assuming the epoch of the first eclipse noted in the OM light curve (at cycle 170 857) as the epoch of phase 0. In Fig. 4, using 643 phase bins per cycle (corresponding to a folded light curve with ≃ 10 s bins), we show two orbital periods of the folded OM (upper left) and EPIC 0.2–10 keV (upper right) light curves. A zoom around the optical6 (left) and X-ray (right) eclipse is shown in the bottom part of the same figure.
We then fit the X-ray folded light curve (restricted to the phase range − 0.1 − − 0.1 cycles) using a phenomenological piecewise model consisting of two flat portions (inside and outside the eclipse) and two linear ingress and egress functions (see e.g. Wheatley & West 2003, for a similar approach). Our model has six parameters, i.e. the ingress and egress starting phases, the ingress and egress durations, and the eclipse and out of eclipse count rates. The best-fit curve (red solid line, 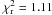 for 123 d.o.f.) is given in Fig. 5. Here, the dashed green vertical lines indicate the contact points, i.e. the phases corresponding to which the emitting region disappears and reappears, while the dashed black lines represent the mid ingress and egress phases, respectively. The count rate during the X-ray eclipse is 0.033 ± 0.003 count s-1. In particular, we find that that the X-ray ingress and egress last for ≃ 40 ± 3 s and ≃ 54 ± 3 s, respectively, and the eclipse duration (measured between mid-ingress and mid-egress7) is 324 ± 5 s, i.e. shorter than that measured in van Teeseling (1997) using ROSAT data. We note that residuals appear during the ingress and egress phases when a simpler model, consisting of equal ingress and egress durations, is used. All the quoted errors are at the 1σ confidence level and were derived from the square root of the covariance matrix diagonal elements. The measure of the ingress and egress allowed us to estimate the size of the X-ray emitting region. In doing this, we adopted a geometry similar to that describing the X-ray eclipse observed for the CV HT Cassiopea (see Nucita et al. 2009) and, by using the orbital parameters given in Wood et al. (1986), we find that the size of the X-ray source is ≃ 0.0119 R⊙, which is comparable to the white dwarf radius (0.0125 R⊙).
for 123 d.o.f.) is given in Fig. 5. Here, the dashed green vertical lines indicate the contact points, i.e. the phases corresponding to which the emitting region disappears and reappears, while the dashed black lines represent the mid ingress and egress phases, respectively. The count rate during the X-ray eclipse is 0.033 ± 0.003 count s-1. In particular, we find that that the X-ray ingress and egress last for ≃ 40 ± 3 s and ≃ 54 ± 3 s, respectively, and the eclipse duration (measured between mid-ingress and mid-egress7) is 324 ± 5 s, i.e. shorter than that measured in van Teeseling (1997) using ROSAT data. We note that residuals appear during the ingress and egress phases when a simpler model, consisting of equal ingress and egress durations, is used. All the quoted errors are at the 1σ confidence level and were derived from the square root of the covariance matrix diagonal elements. The measure of the ingress and egress allowed us to estimate the size of the X-ray emitting region. In doing this, we adopted a geometry similar to that describing the X-ray eclipse observed for the CV HT Cassiopea (see Nucita et al. 2009) and, by using the orbital parameters given in Wood et al. (1986), we find that the size of the X-ray source is ≃ 0.0119 R⊙, which is comparable to the white dwarf radius (0.0125 R⊙).
4.2.1. Absorption dips
Apart from the clear eclipses, we detect broad dips close to the orbital phases 0.3 and 0.7. These dips can also be identified in the individual light curves presented in Fig. 2. As noted earlier, van Teeseling (1997) also found the existence of a dip at the orbital phase 0.7–0.8 in the ROSAT HRI data.
In Fig. 6, we show a zoomed image around each of the identified dip (in the 0.2–10 keV light curve).
In both cases, the dip could be closely fitted by a phenomenological quadratic polynomial model. This resulted in a best-fit with 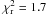 (222 d.o.f.) for the first dip and
(222 d.o.f.) for the first dip and 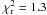 (286 d.o.f.) for the second one (see in the same figure the superimposed red best-fit lines). In particular, the central phase of each dip (i.e. the locus of the minimum of each best-fit curve) was evaluated to be φDip1 = 0.30 ± 0.02 and φDip2 = 0.73 ± 0.02. We also note that the two dips last for ΔT1 ≃ 2250 s and ΔT2 ≃ 2890 s, respectively.
(286 d.o.f.) for the second one (see in the same figure the superimposed red best-fit lines). In particular, the central phase of each dip (i.e. the locus of the minimum of each best-fit curve) was evaluated to be φDip1 = 0.30 ± 0.02 and φDip2 = 0.73 ± 0.02. We also note that the two dips last for ΔT1 ≃ 2250 s and ΔT2 ≃ 2890 s, respectively.
 |
Fig. 5 Upper panel: the best-fit to the X-ray data with a piecewise function (solid line). Bottom panel: the residuals between data and best-fit model. |
To clarify the nature of the dip features, we produced background-corrected light curves in the energy ranges 0.1 − 2.0 keV and 2.0 − 10.0 keV, namely the soft and hard bands. The resulting epoch-folded light curves have an average count rate of 0.47 ± 0.10 count s-1 (soft band) and 0.23 ± 0.05 count s-1 (hard band), respectively. From Fig. 7, we can see that the modulation observed in the soft band (upper panel) almost completely disappears in the hard band (middle panel). We can consequently define the hardness ratio as the counts in the hard energy range divided by the counts in the soft energy range. The hardness ratio is given as a function of the phase in the bottom part of Fig. 7. Inspection of this figure shows that the hardness ratio increases during the dipping phenomenon, particularly at phase ≃ 0.7. This indicates that the photon counts in the soft energy range decreased more than those in the hard band with time, suggesting that the absorption by intervening material – as gas clouds – along the line-of-sight is the main cause of the observed modulation.
 |
Fig. 6 The two dip features detected in the X-ray light curve and the individual best-fit quadratic models superimposed (see text for details). |
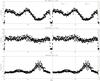 |
Fig. 7 Upper and middle panels: the epoch-folded light curves (643 phase bins per cycle) in the soft and hard bands. Bottom panel: the hardness ratio. |
At the dip minima, the count rates are I1 ≃ 0.72 count s-1 and I2 ≃ 0.39 count s-1 at orbital phases ~0.3 and ~0.7, respectively. Outside the eclipse and dips regions, the average count rate is I0 ≃ 0.95 count s-1.
The existence of absorption dips in the observed light curve indicates that the apparent spectrum changes over the orbital cycle. As explained in the next section, the spectral analysis was also performed on spectra extracted on different time ranges. In Fig. 7, the dashed vertical lines and the corresponding labels represent the two phase intervals (each including an absorption dip) into which the X-ray data were divided to study the spectral variations.
4.3. X-ray spectral analysis results
The EPIC source (background-corrected) spectra were accumulated and rebinned to ensure that there were at least 25 counts per energy bin. Then, the data were imported into the XSPEC package (version 12.4.0) for the spectral analysis and fitting procedure.
We were unable to achieve an acceptable fit using a single thermal plasma component absorbed by neutral gas (Mekal and Wabs in XSPEC). Fixing the hydrogen column density to the average value found in the direction of the target (nH = 0.091 × 1020 cm-2, Dickey & Lockman 1990) and the metallicity abundance to the solar value resulted in a best-fit solution with 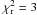 for 635 d.o.f. Relaxing the assumption of solar abundance did not improve our fit (
for 635 d.o.f. Relaxing the assumption of solar abundance did not improve our fit (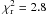 for 634 d.o.f.).
for 634 d.o.f.).
We were also unable to fit the spectrum with a simple single temperature model. Furthermore, we observed the existence of residuals at low energies (around the iron L-shell complex at 1 keV) and around the iron lines at ≃ 6.4 keV.
These residuals may be the consequence of two effects respectively: the improper modelling of photoelectric absorption in the spectrum and the fluorescence from cold material and/or a multi-temperature structure of the spectrum.
Since we also expect that in a CV the emission originates from a plasma with a range of temperature, we were tempted to use a complex model similar to that described by Baskill et al. (2005), i.e. a multi-temperature plasma emission model (Cemekl) with absorption by a partially ionized gas (Absori).
The Absori model was used with two free parameters: the column density n of the absorbing material and the ionization parameter ξ = L/nR2, where L is the integrated source luminosity between 5 eV and 300 keV and R is the distance of the material from the central source. The temperature of the absorber material was fixed to 5 × 104 K.
The multi-temperature plasma emission model is characterized by an emission measure following a power-law temperature profile of the form (T/Tmax)α, where Tmax and α are free fit parameters. In addition, the metallicity abundance was allowed to vary.
Finally, the interstellar absorption by the neutral gas was accounted for by the Wabs model in XSPEC and the column density of neutral hydrogen was considered as a free fit parameter.
After minimizing χ2 with the above model, we still found residuals close to 1 keV, thus we included a narrow emission line around this energy.
 |
Fig. 8 Upper panel: the MOS (green and red crosses) and PN (black crosses) mean overall spectra together with the best-fit model (solid lines). Bottom panel: the residuals between data and best-fit model. |
Hence, the best-fit model (with 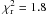 for 628 d.o.f.) corresponds to nH = (5.8 ± 0.4) × 1020 cm-2 for the neutral hydrogen column density, nH = (1.7 ± 0.1) × 1021 cm-2 for the ionized hydrogen column density, ξ = 0.3 ± 0.1 for the ionization parameter, α = 1.6 ± 0.1 for the power-law index, Tmax = 11.4 ± 0.2 keV for the maximum temperature in the plasma, Z = 0.75 ± 0.03 for the metallicity abundance, and E = 1.11 ± 0.01 keV for the Gaussian line centroid, respectively. We, note that all the errors are quoted at the 90% confidence level.
for 628 d.o.f.) corresponds to nH = (5.8 ± 0.4) × 1020 cm-2 for the neutral hydrogen column density, nH = (1.7 ± 0.1) × 1021 cm-2 for the ionized hydrogen column density, ξ = 0.3 ± 0.1 for the ionization parameter, α = 1.6 ± 0.1 for the power-law index, Tmax = 11.4 ± 0.2 keV for the maximum temperature in the plasma, Z = 0.75 ± 0.03 for the metallicity abundance, and E = 1.11 ± 0.01 keV for the Gaussian line centroid, respectively. We, note that all the errors are quoted at the 90% confidence level.
In Fig. 8, we show the MOS 1, MOS 2, and PN spectral data in the energy band 0.2–9.0 keV together with the best-fit model (solid lines).
The total absorbed flux in the 0.2–9.0 keV band is 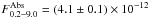 erg s-1 cm-2. Correcting for the absorption, we obtained
erg s-1 cm-2. Correcting for the absorption, we obtained 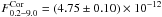 erg s-1 cm-2, which, after applying a bolometric correction of a factor ≃ 30% (as estimated using XSPEC), corresponds to a unabsorbed bolometric flux
erg s-1 cm-2, which, after applying a bolometric correction of a factor ≃ 30% (as estimated using XSPEC), corresponds to a unabsorbed bolometric flux 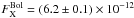 erg s-1 cm-2. Thus, for an estimated distance of 97 pc (see, e.g., Wood et al. 1986), the luminosity of Z Chamaleontis turns out to be
erg s-1 cm-2. Thus, for an estimated distance of 97 pc (see, e.g., Wood et al. 1986), the luminosity of Z Chamaleontis turns out to be 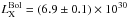 erg s-1, i.e. a factor ≃ 2.8 higher than that found by van Teeseling (1997) as expected for a multi-temperature component model.
erg s-1, i.e. a factor ≃ 2.8 higher than that found by van Teeseling (1997) as expected for a multi-temperature component model.
The total accretion luminosity in a CV can be estimated by Lacc = GṀMWD/RWD, where Ṁ is the mass accretion rate onto a white dwarf of mass MWD and radius RWD. Assuming that the observed X-ray luminosity mainly comes from a BL, one has8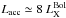 . In the case of Z Chamaleontis, where we assume MWD = 0.54 M⊙ and RWD = 8.84 × 108 cm (van Teeseling 1997), we estimated the mass accretion rate onto the white dwarf to be 1.1 × 10-11 M⊙ yr-1, which is consistent with the typical value expected for quiescent CVs. Furthermore, it is important to know the mass accretion rate if one wishes to understand the accretion scenario in Z Chamaleontis (see Sect. 5 for a detailed discussion on this point).
. In the case of Z Chamaleontis, where we assume MWD = 0.54 M⊙ and RWD = 8.84 × 108 cm (van Teeseling 1997), we estimated the mass accretion rate onto the white dwarf to be 1.1 × 10-11 M⊙ yr-1, which is consistent with the typical value expected for quiescent CVs. Furthermore, it is important to know the mass accretion rate if one wishes to understand the accretion scenario in Z Chamaleontis (see Sect. 5 for a detailed discussion on this point).
As discussed in the previous section, the timing analysis on the X-ray light curve showed the existence of dips at the phases ≃ 0.3 and ≃ 0.7. The analysis of the hardness ratio light curve suggests that the nature of these features is the absorption by intervening material. Thus, the apparent spectrum depends on the orbital cycle and explains why the fit to the mean overall spectra (of both MOS and PN cameras) is characterized by a poor 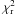 .
.
We extracted the spectra over two different phase intervals (see the dashed and vertical lines and the corresponding labels in Fig. 7). Referring for clarity to the same figure, the first interval (labeled dip 1) was chosen to be between the phase of the eclipse egress and the phase 0.5, while the second interval (labeled dip 2) was between the phase 0.5 and the eclipse ingress phase.
The spectra corresponding to the dip 1 interval were fitted with the same model described above and with the same free parameters. In this case, we noted that a narrow Gaussian line is necessary to avoid residuals close to 1.1 keV. The best-fit model (with 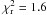 for 626 d.o.f.) corresponds to
for 626 d.o.f.) corresponds to 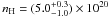 cm-2 for the neutral hydrogen column density, nH = (1.7 ± 0.1) × 1021 cm-2 for the ionized hydrogen column density,
cm-2 for the neutral hydrogen column density, nH = (1.7 ± 0.1) × 1021 cm-2 for the ionized hydrogen column density, 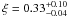 for the ionization parameter,
for the ionization parameter, 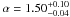 for the power-law index, Tmax = 11.1 ± 0.2 keV for the maximum temperature in the plasma, Z = 0.66 ± 0.04 for the metallicity abundance, and E = 1.11 ± 0.01 keV for the Gaussian line centroid, respectively.
for the power-law index, Tmax = 11.1 ± 0.2 keV for the maximum temperature in the plasma, Z = 0.66 ± 0.04 for the metallicity abundance, and E = 1.11 ± 0.01 keV for the Gaussian line centroid, respectively.
To constrain the parameters, the spectra corresponding to the dip 2 interval were fitted by fixing the neutral hydrogen column density, the power-law index, the plasma temperature, and the abundance parameters to the values obtained fitting the dip 1 interval data.
In this case, the best-fit model (with 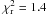 for 578 d.o.f.) corresponds to nH = (2.9 ± 0.1) × 1021 cm-2 for the ionized hydrogen column density, ξ = 0.25 ± 0.10 for the ionization parameter, and E = 1.12 ± 0.02 keV for the Gaussian line centroid, respectively.
for 578 d.o.f.) corresponds to nH = (2.9 ± 0.1) × 1021 cm-2 for the ionized hydrogen column density, ξ = 0.25 ± 0.10 for the ionization parameter, and E = 1.12 ± 0.02 keV for the Gaussian line centroid, respectively.
As expected, the ionized hydrogen column density evaluated in the dip 2 region is larger than that found in the dip 1 region and this is finally responsible of the features observed in the hardness ratio light curve (see Fig. 7).
5. Result and discussion
We have analyzed an XMM-Newton observation of the eclipsing dwarf nova Z Chamaleontis. The binary system was observed in both X-ray and optical bands for ≃ 99 ks during its quiescent state, hence it has been possible to extract both a high quality spectrum and light curve.
A single thermal plasma component absorbed by neutral gas did not provide a good fit, so that we had to use a more complicated multi-temperature model (see e.g. Baskill et al. 2005).
The adopted model is consisted of a multi-temperature plasma emission component (as in Cemekl) absorbed by a partially ionized absorber (modelled using Absori) and by neutral gas (Wabs). In particular, the emission measure follows a power-law in temperature with the maximum temperature Tmax = 11.4 ± 0.2 keV and a power-law index of α = 1.6 ± 0.1. The derived best-fit parameters are comparable to those found by Baskill et al. (2005) when studying other similar CVs.
We have found a total absorbed flux in the 0.2–9.0 keV band of 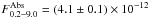 erg s-1 cm-2, which, when corrected for both the absorption and the bolometric factor, corresponds to a bolometric flux of
erg s-1 cm-2, which, when corrected for both the absorption and the bolometric factor, corresponds to a bolometric flux of 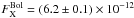 erg s-1 cm-2. Assuming a distance of ≃ 97 pc, the luminosity of Z Chamaleontis turns out to be
erg s-1 cm-2. Assuming a distance of ≃ 97 pc, the luminosity of Z Chamaleontis turns out to be 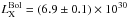 erg s-1. With these numbers, and assuming a common scenario in which the observed X-ray luminosity originates in the BL as a consequence of the mass accretion, the matter accretion rate onto the white dwarf was estimated to be Ṁ = 1.1 × 10-11 M⊙ yr-1, i.e. fully consistent with the common picture of the accretion mechanism in CVs (see e.g. Warner 1995).
erg s-1. With these numbers, and assuming a common scenario in which the observed X-ray luminosity originates in the BL as a consequence of the mass accretion, the matter accretion rate onto the white dwarf was estimated to be Ṁ = 1.1 × 10-11 M⊙ yr-1, i.e. fully consistent with the common picture of the accretion mechanism in CVs (see e.g. Warner 1995).
The combined EPIC light curve shows a periodicity consistent with the orbital period of the binary system, i.e. Porb ≃ 1.788 h. The most prominent feature in the light curve is the existence of an eclipse characterized by a X-ray count rate of 0.033 ± 0.003 count s-1. We estimated the durations of the X-ray ingress, egress, and eclipse phenomena to be ≃ 40 s, ≃ 54 s and ≃ 324 s, respectively. This allows us to measure the size of the X-ray emitting region. In particular, adopting a geometry similar to that described in Nucita et al. (2009) and using the orbital parameters given in Wood et al. (1986), we estimated an X-ray source size of ≃ 0.0119 R⊙, which is comparable to the white dwarf radius (0.0125 R⊙).
The XMM-Newton light curve of Z Chamaleontis clearly shows the existence of dips at the orbital phases 0.3 and 0.7. This confirms the finding of van Teeseling (1997) of a dip in the orbital phase range 0.7–0.8 in the ROSAT 0.1–2.4 keV light curve. The two dips last for ΔT1 ≃ 2250 s and ΔT2 ≃ 2890 s, respectively. Our study of the hardness ratio light curve has demonstrated that the dips can be naturally explained by material (such as gas clouds) absorbing the X-ray photons emitted by the central source.
We have evaluated the optical depth of the absorbing materials at each dip to be τ1 ≃ 0.27 and τ2 ≃ 0.87, respectively. An estimate of the matter column density for the intervening clouds is found to be n1L1 ≃ 4 × 1023 cm-2 and n2L2 ≃ 1 × 1024 cm-2, respectively.
Our detections of these kind of features in X-ray light curves of CVs is not the first. Szkody et al. (2001) found in U Geminorum periodic orbital dips during both outburst and quiescence states and Hoard et al. (2010), studying simultaneous X-ray and ultraviolet data from the nova-like system DW Ursae Majoris, observed the existence of absorption structures in the high-energy light curve at the phase 0.2 − 0.3. Baskill et al. (2005), by studying 30 non-magnetic CVs observed by the ASCA satellite, found that in a few cases the high-energy light curves show an orbital modulation that is anti-correlated with the hardness ratio, implying that their signal originate in photoelectric absorption. In addition, magnetic systems seem to be characterized by similar features (see e.g. the XMM-Newton observations of the polar CV V1432 Aql in Singh & Rana 2003, and of the new eclipsing AM Her binary discovered by Ramsay et al. 2009).
One possible explanation of dense absorbing clouds around compact objects with an accretion disk can be found in the framework of the theoretical model9 proposed (initially for the low mass X-ray binaries) by Frank et al. (1987). The model accounts for the “dipping” phenomenon that has been observed in Z Chamaleontis. According to this theory, the accreting material that flows through the inner Lagrangian point (L1), after hitting the accretion disk, follows a ballistic stream and finally settles to a more internal circular ring of radius 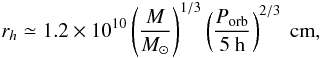 (1)where M is the mass of the accreting object in solar masses and P the orbital period in 5 h units. In correspondence with the ring radius, the velocity of the stream is of the order of the local free-fall velocity
(1)where M is the mass of the accreting object in solar masses and P the orbital period in 5 h units. In correspondence with the ring radius, the velocity of the stream is of the order of the local free-fall velocity 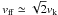 , where
, where 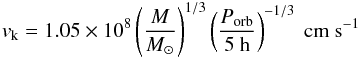 (2)is the circular Keplerian velocity.
(2)is the circular Keplerian velocity.
The matter accumulating at the ring radius forms gas clouds of size 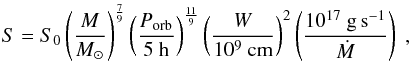 (3)where S0 = 4 × 107 cm, W is the half width of the gas stream, and Ṁ is the mass accretion rate. This is the main cause of the dipping phenomenon because the dense gas clouds occult the central X-ray source. Interestingly enough, the model predicts that dips form at the phases 0.3 and 0.8.
(3)where S0 = 4 × 107 cm, W is the half width of the gas stream, and Ṁ is the mass accretion rate. This is the main cause of the dipping phenomenon because the dense gas clouds occult the central X-ray source. Interestingly enough, the model predicts that dips form at the phases 0.3 and 0.8.
In the case of Z Chamaleontis, assuming W = 109 cm, M ≃ 0.54 M⊙, Porb ≃ 1.78 h, and Ṁ ≃ 1.1 × 10-11 M⊙ yr-1 in the previous equations, one gets rh ≃ 4.9 × 109 cm, vk ≃ 1.2 × 108 cm s-1 and S ≃ 109 cm. Finally, the gas cloud number density can be evaluated by recalling that the estimated column density of the gas clouds is nH ≃ 1021 cm-2, which in turns implies a typical particle number density of n ≃ 1012 cm-3.
From the optical eclipses, Wood et al. (1986) estimated the mass of the white dwarf and its companion to be MWD ≃ 0.54 M⊙ and Mc ≃ 0.081 M⊙, respectively. However, Wade & Horne (1988) found slightly different values (MWD ≃ 0.84 M⊙ and Mc ≃ 0.125 M⊙) by analyzing the radial velocity curve of the system. In the following, we assume that the white dwarf mass is 0.54 M⊙.
Details of the conversion between OM count rates to magnitude and/or fluxes can be found at http://xmm.esac.esa.int/sas/11.0.0/watchout.
The significance of a feature identified in the Lomb-Scargle periodogram was evaluated by comparing the peak height with the power threshold corresponding to a given false alarm probability in white noise simulations (Scargle 1982). In Fig. 3, the three horizontal lines correspond to false alarm propability thresholds of 68% (solid line), 90% (dotted line), and 99% (dashed line), respectively.
For comparison, we refer to Wood et al. (1986) where the optical eclipse light curve of Z Chamaleontis is shown.
As in the case of the optical data, the mid-eclipse phase was calculated as the average of the ingress and egress mid-points. The difference between the obtained values and the expected ones is fully consistent with that (the average O–C value quoted in Table 1) derived using the OM data, depending of course on the adopted ephemeris.
The origin of the adopted factor 8, instead of the more usual factor 2, between the BL and disk energy output comes from considerations about the energy transferred to spin up the white dwarf (see e.g. Popham & Narayan 1995).
This scenario was also supported by the numerical simulations of Hirose et al. (1991) and Armitage & Livio (1998).
Acknowledgments
This paper is based on observations from XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. B. M. T. Maiolo is grateful to ESAC (ESA) for their hospitality. We thank our referee for useful comments on the first version of this paper and M. Guainazzi, F. Strafella, and V. Testa for interesting discussions.
References
- Armitage, P. J., & Livio, M. 1998, ApJ, 470, 1024 [Google Scholar]
- Baptista, R., Jablonski, F., Oliveira, E., et al. 2002, MNRAS, 335, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Baskill, D. S., Wheatley, P. J., & Osborne, J. P. 2005, MNRAS, 357, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z., Qian, S., & Lajus, E.-F., 2009, ApJ, 703, L13 [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Frank, J., King, A. R., & Lasota, J.-P. 1987, A&A, 178, 137 [NASA ADS] [Google Scholar]
- Haefner, R., Schoembs, R., & Vogt, N. 1979, A&A, 77, 7 [NASA ADS] [Google Scholar]
- Hirose, M., Osaki, Y., & Mineshige, S. 1991, PASP, 43, 809 [Google Scholar]
- Hoard, D. W., Lu, Tuing-Ni, Knigge, C., Homer, L., et al. 2010, AJ, 140, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Kuulkers, E., Norton, A., Schwope, A., & Warner, B. 2006, in Compact Stellar X-ray Sources, ed. W. H. G. Lewin, & M. van der Klis, Cambridge Astrophysics Ser., 39, 421 [Google Scholar]
- Lamb, D. Q. 1982, Cataclysmic Variables and Related Objects: proceeding of the 72nd colloquium of the international astronomical union, ed. M. Livio, & G. Shaviv [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nucita, A. A., Maiolo, B. M. T., Carpano, S., et al. 2009, A&A, 504, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popham, R., & Narayan, R. 1985, ApJ, 442, 337 [Google Scholar]
- Ramsay, G., Poole, T., Mason, K., et al. 2001, A&A, 365, L288 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramsay, G., Rosen, S., Hakala, P., Crdova, F., & Barclay, T. 2009, MNRAS, 395, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, E. L., Wood, J. H., Bless, R. C., et al. 1995, ApJ, 443, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, K. P., & Rana, V. R. 2003, A&A, 410, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szkody, P., Nishikida, K., Long, K. S., & Fried, R. 2001, ApJ, 121, 2761 [Google Scholar]
- van Teeseling, A. 1997, A&A, 319, L25 [NASA ADS] [Google Scholar]
- Wade, R. A., & Horne, K. 1988, ApJ, 324, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B., 1995, in Cataclysmic Variable Stars, Cambridge Astrophysics Ser., 28 (CUP) [Google Scholar]
- Wheatley, P. J., & West, R. G. 2003, MNRAS, 354, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, J. H., Irwin, M. J., & Pringle, J. E. 1985, MNRAS, 214, 475 [NASA ADS] [Google Scholar]
- Wood, J. H., Horne, K., Berriman, G., et al. 1986, MNRAS, 219, 629 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper panel: the 0.2–10 keV EPIC background-corrected light curve of Z Chamaleontis with a time resolution of 40 s. Bottom panel: the OM light curve with a bin size of 40 s. The photons were barycentrically corrected (see text for details). |
| In the text | |
 |
Fig. 2 The X-ray eclipses in the 0.2−10 keV (upper part of each panel) band and the corresponding view of the OM instrument (bottom part). The vertical dashed line represents the position of the optical mid eclipse (using the ephemeris of Baptista et al. 2002). The number of the cycle corresponding to the plotted eclipse is also given. |
| In the text | |
 |
Fig. 3 The Lomb-Scargle periodogram of the EPIC light curve in the energy range 0.2–10 keV band. The dashed vertical lines correspond to the orbital period of Z Chamaleontis and to two major harmonic features (see text for details). |
| In the text | |
 |
Fig. 4 Upper panels: two orbital periods of the OM (left) and EPIC 0.2–10 keV (right) light curves. Bottom panels: a zoom around both the optical and X-ray eclipse. |
| In the text | |
 |
Fig. 5 Upper panel: the best-fit to the X-ray data with a piecewise function (solid line). Bottom panel: the residuals between data and best-fit model. |
| In the text | |
 |
Fig. 6 The two dip features detected in the X-ray light curve and the individual best-fit quadratic models superimposed (see text for details). |
| In the text | |
 |
Fig. 7 Upper and middle panels: the epoch-folded light curves (643 phase bins per cycle) in the soft and hard bands. Bottom panel: the hardness ratio. |
| In the text | |
 |
Fig. 8 Upper panel: the MOS (green and red crosses) and PN (black crosses) mean overall spectra together with the best-fit model (solid lines). Bottom panel: the residuals between data and best-fit model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


