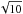| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117468 | |
| Published online | 13 December 2011 | |
Implications of the measured parameters of PSR J1903+0327 for its progenitor neutron star
1
N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
e-mail: bejger@camk.edu.pl; fortin@camk.edu.pl; haensel@camk.edu.pl; jlz@camk.edu.pl
2
LUTh, UMR 8102 du CNRS, Observatoire de Paris, 92195 Meudon Cedex, France
Received: 13 June 2011
Accepted: 19 October 2011
Context. The millisecond pulsar PSR J1903+0327 rotating at 465 Hz has the second highest precisely measured mass (1.67 M⊙) and a weak surface magnetic field (≃2 × 108 G). It is located in the Galactic plane, bound in a highly eccentric (e = 0.44) orbit in a binary system with a solar-mass main-sequence star. These observational findings pose a challenge for the theory of stellar evolution.
Aims. Using the intrinsic parameters of PSR J1903+0327 evaluated from radio observations (mass M, rotation period P, and magnetic field B deduced from P and Ṗ) and a model of spin evolution during the “recycling” phase (spin-up by accretion from a low-mass companion lost afterwards) that takes into account the accretion-induced magnetic field decay, we aim to calculate the mass of its neutron star progenitor, Mi, at the onset of accretion. In addition, we derive constraints on the average accretion rate Ṁ and the pre-accretion magnetic field Bi. We also seek for the imprint of the poorly known equation of state of dense matter at supra-nuclear densities on the spin-up tracks and the progenitor neutron star.
Methods. Spin-up is modeled by accretion from a thin magnetized disk, using the magnetic-torque disk-pulsar coupling model proposed by Kluźniak and Rappaport. We adopt an observationally motivated model of the surface magnetic field dissipation caused by accretion. We consider three equations of state of dense matter, which are consistent with the existence of 2.0 M⊙ neutron star. Orbital parameters in the accretion disk are obtained using the space-time generated by a rotating neutron star within the framework of general relativity.
Results. Constraints on the progenitor neutron star parameters and the accretion itself are obtained. The minimum average accretion rate should be higher than 2−8 × 10-10 M⊙ yr-1, the highest lower bound corresponding to the stiffest equation of state. Allowed Bi-dependent values of Mi are within 1.0 − 1.4 M⊙, much lower than the oversimplified but widely used B ≡ 0 result, where one gets Mi > 1.55 M⊙.
Conclusions. The influence of magnetic field in the “recycling” process is crucial – it leads to a significant decrease in the spin-up rate and higher accreted masses, in comparison to the B = 0 model. The estimated initial neutron-star mass depends on the assumed dense-matter equation of state. We also show that the otherwise necessary relativistic corrections to the Newtonian model of Kluźniak and Rappaport, related to the existence of the marginally-stable circular orbit, can be neglected in the case of PSR J1903+0327.
Key words: stars: neutron / equation of state / accretion, accretion disks / dense matter
© ESO, 2011
1. Introduction
The discovery of PSR J1903+0327, which was the first millisecond radio pulsar found in a binary system with a 1.03 M⊙ main-sequence (MS) companion in an eccentric (e = 0.44) 95-day orbit, poses a challenge to formation theories of millisecond pulsars (Champion et al. 2008). On the one hand, its timing parameters – spin frequency f = 465 Hz and spin period derivative Ṗ = 1.88 × 10-20 s s-1 – are nothing unusual for millisecond pulsars. On the other hand however, the high eccentricity of the orbit and the nature of the companion (main-sequence star), as well as its location in the vicinity of the Galactic plane make it unique. Pulsar-clock stability and the high eccentricity of the orbit enabled the pulsar mass measurement to be determined (by means of the Shapiro delay) with formidable precision. An analysis of the timing data obtained from 2006 December through to 2010 January using the 305-m Arecibo radio telescope and the 105-m Green Bank Telescope, found that the pulsar mass is 1.67 ± 0.021 M⊙ (at the 99.7% confidence limit) and showed strong evidence that effects other than space-time curvature, e.g., stellar winds or tidal forces acting on MS companion, are negligible (Freire et al. 2011).
According to the current theory of neutron-star (NS) evolution, millisecond radio pulsars (P < 10 ms) originate from “radio-dead” pulsars via the accretion-caused spin-up in low-mass X-ray binaries (LMXB, see Alpar et al. 1982; Radhakrishnan & Srinivasan 1982). This so-called “recycling” process is believed to facilitate the spin-up from the initial ~0.1 Hz frequency to ~500 Hz in ~109 yrs and is associated with accretion of ~0.1 M⊙. This idea was corroborated by the detection of millisecond X-ray pulsations in LMXBs, which were interpreted as the manifestation of rotating and accreting NSs (Wijnands & van der Klis 1998). These millisecond X-ray pulsars are thought to become radio millisecond pulsars after the accretion process expires. Radio millisecond pulsars are extremely stable rotators, with Ṗ ~ 10-20 − 10-19 s s-1. The surface magnetic fields estimated from the timing properties are three – four orders of magnitude weaker than those in normal radio pulsars, for which B ≃ 1012 G. This is explained either by the “burying” of the original magnetic field under a layer of accreted ~0.1 M⊙ material (Bisnovatyi-Kogan & Komberg 1974; Taam & van den Heuvel 1986; Cumming et al. 2001) or/and by the Ohmic dissipation of electric currents in the accretion-heated crust (Romani 1990; Geppert & Urpin 1994). The “recycling” in LMXBs is a particularly efficient mechanism in dense stellar systems such as globular clusters and is in accordance with specific statistics of radio millisecond pulsars (Lorimer 2008). Out of a total of 213 millisecond pulsars, some 100 (i.e., nearly half) are indeed located within binaries, while among the 1850 radio pulsars, only 141 (i.e., 8%) are in binaries. Moreover, out of all radio millisecond pulsars, more than half (130) are found in 26 Galactic globular clusters! Finally, as much as 40% of the 130 globular-cluster radio millisecond pulsars are in binaries.
Efficient spin-up to the kHz frequencies is possible because the low-mass companion remains for ~108 − 109 yrs in the post-MS phase, overflowing its Roche lobe and feeding the accretion disk around a NS. Consequently, tidal friction within the extended companion has ample time to circularize the orbit. Only an additional dynamic perturbation involving a third star, an occurrence that is not so rare within a globular cluster, can make the orbit highly eccentric or even tear the system apart. This may be the origin of eccentric binaries as well as some isolated millisecond pulsars, both in globular clusters and the Galactic disk.
However, PSR J1903+0327 does not fit the above picture because neither its orbit is circular, nor its companion a post-MS star. It is thus a first specimen of a new group; constructing a viable scenario of its formation turns out to be a difficult challenge. We briefly and critically review the principal scenarios that have been proposed since the discovery of the PSR J1903+0327 binary in Sect. 2. All but one are excluded although the surviving triple system scenario is not free of its own problems either (Freire et al. 2011; Portegies Zwart et al. 2011). Nevertheless, it is clear that PSR J1903+0327 was not “recycled” by its current MS companion. In the following, we focus on the LMXB stage of the pulsar evolution that certainly preceded the formation of the presently observed binary. We consider the millisecond-pulsar formation model in order to (hopefully) deduce the parameters of the pre-accretion progenitor NS and to place constraints on the poorly known equation of state (EOS) of dense matter.
We provide a brief introduction to accretion spin-up scenario and the dissipation of pulsar magnetic field due to accretion in Sects. 3 and 4. In Sect. 5, we describe the main elements of the Kluźniak & Rappaport (2007) magnetic-torque model (hereafter referred to as KR) acting on a NS accreting from a thin accretion disk. We report on efforts to extend the Newtonian KR model to include the effects of the space-time curvature, especially to take into account the existence of the marginally-stable circular orbit predicted by General Relativity. In our “recycling” simulations, we use three EOS of dense matter consistent with the existence of a 2.0 M⊙ NS (Demorest et al. 2010) – these equations are briefly described in Sect. 6, while the results of our simulations are presented in Sect. 7. As a final result, we place constraints on the average accretion rate during the spin-up stage, the initial magnetic field, and the mass of the progenitor NS. In Sect. 8, we summarize our main results. An Appendix contains a terse overview of the influence of the space-time curvature effects, something that was neglected in the original KR model, on the spin-up tracks of PSR J1903+0327.
2. Proposed scenarios for the formation of the PSR J1903+0327 binary
Three formation scenarios, denoted below as I − III, were previously proposed in the discovery paper (Champion et al. 2008), and the first scenario was developed further by Liu & Li (2009). These three scenarios were ruled out by new observational data combined with theoretical modeling and a fourth scenario was advanced by Freire et al. (2011) and Portegies Zwart et al. (2011). These scenarios, together with their critique, are briefly discussed below:
I. Rapid rotation at birth
The pulsar was born spinning rapidly in a core-collapse supernova, in a binary system in the Galactic disk, with a MS companion, the supernova kick making the orbit strongly eccentric (Liu & Li 2009). A spin frequency of 465 Hz was reached as a consequence of accretion from the fallback disk, which requires less than 103 − 104 yrs before the accretion (or rather hyperaccretion – the mean rate is ~10-4 M⊙ yr-1) stops and the pulsar becomes an active radio emitter. This scenario was considered unlikely by Champion et al. (2008), because of the very low surface magnetic field (B ~ 108 G) implied by the measured value of Ṗ. Liu & Li (2009) proposed that the low magnetic field value was caused by its dissipation associated with accretion. However, they used a model of a magnetic field dissipation developed originally for slow accretion in an LMXB, which is not valid for a hyperaccreting newly born NS. Additional arguments, in particular observational ones, against this scenario can be found in Freire et al. (2011) and Portegies Zwart et al. (2011), which is therefore unacceptable.
II. Hierarchical triple system
The pulsar was recycled in a LMXB and is currently a member of a hierarchical triple system containing a white dwarf (inner binary with the pulsar) and a MS star (outer binary). The high eccentricity of the pulsar orbit is generated by the Kozai resonance (Kozai 1962) between the inner and outer binaries. The scenario is ruled out by the precise measurement of the optical spectra of the MS companion of the pulsar permitting the calculation of the companion radial velocity, which turned out to be consistent with predictions based on the orbital parameters determined from the pulsar timing. The optical data lead to an independent estimate of the mass ratio in the binary (Freire et al. 2011). Finally, there was no time dependence of the eccentricity e in the TEMPO2 timing analysis, while e growth is expected owing to the Kozai resonance in the triple hierarchical system (Gopakumar et al. 2009). The scenario should therefore be ruled out as inconsistent with observations (see also Freire et al. 2011; Portegies Zwart et al. 2011)
III. Pulsar spun up in a LMXB and then ejected into the Galactic disk together with a newly captured MS companion
The pulsar was spun up in an LMXB within a globular cluster and then exchanged the evolved companion in a process of interaction with a MS star in the cluster core, its binary orbit becoming very eccentric. The kick-off in the three-body interaction was sufficient to eject the final NS-MS binary out of the globular cluster and into the Galactic disk. However, measurements of the proper three-dimensional velocity of the binary allowed to track its position back in time (Freire et al. 2011). The binary was found to always be within 270 pc from the Galactic disk and farther than 3 kpc from the Galactic center. Therefore, an exchange interaction (where an evolved companion in a LMXB is exchanged for a MS star), which is probable in a dense stellar environment such as a globular cluster or the Galactic center, is so unlikely that it leads to the rejection of the scenario (Freire et al. 2011).
IV. Pulsar in a triple (tertiary) system with two MS stars of different masses, the pulsar being spun-up by accretion from the evolved, more massive companion that was afterwards expelled from the tertiary to make it a binary
This scenario was proposed by Freire et al. (2011) and Portegies Zwart et al. (2011). A starting point is a tertiary composed of a massive star and two MS stars of different masses. The massive star collapses, giving birth to a pulsar, the tertiary still being bound. The initially more massive MS star (MS1) evolves forming a LMXB with the pulsar and spinning it up by accretion. After a substantial mass loss, MS1 is removed from the system owing to the ablation/accretion induced by the interaction with the millisecond pulsar or ejected from the system by means of the three-body interactions (Freire et al. 2011). This leaves a system as the observed one, with a 1.03 M⊙ companion still at the MS stage, in an eccentric orbit. The ablation/accretion removal of the companion was previously proposed as a mechanism producing isolated recycled pulsars in the Galactic disk. Ablation by the NS radiation indeed operates in the PSR B1957+20 binary (Black Widow), whose companion mass was reduced to 0.025 M⊙ (Fruchter et al. 1988; Kluźniak et al. 1988). However, details of the ablation process are rather uncertain and the timescale needed to completely vaporize the companion can be longer than the Hubble time (Levinson & Eichler 1991). Alternatively, the expulsion of the lower-mass companion owing to the chaotic character of a three-body interaction in the triple system is proposed. We note, however that references quoted in Freire et al. (2011) do not seem to provide an accurate explanation of PSR J1903+0327: Hut (1984) assumes equal masses for the three bodies, and Phillips (1993) studies the reflection of the pulsar radio beam from the swarm of asteroids orbiting the pulsar and derives an upper bound of ~10-4 M⊙ to the mass of the asteroid-like material orbiting the Vela pulsar within 1 AU. In our opinion, the scenario presented by Freire et al. (2011) is not yet properly supported by reliable quantitative estimates. In Portegies Zwart et al. (2011), both the evolution and the dynamics of the NS+MS1+MS2 system are studied in detail. Several competing channels of evolution for the tertiary are compared using advanced numerical simulations. The available parameter space leading to the observed PSR J1903+0327+MS2 binary is estimated and the birth-rate of these binaries in the Galactic disk is found to be acceptable. Portegies Zwart et al. (2011) highlighted the need to (observationally) find a “missing link” in the scenario: a wide LMXB orbited by a tertiary low-mass MS star. It is clear that the discovery of such a system would strongly fortify the triple-star scenario.
Four scenarios, reviewed critically above, have been proposed until now. Only one of them cannot be immediately ruled out by observations, but even this one lacks a solid quantitative basis. However, it is clear that PSR J1903+0327 has been “recycled” in order to explain its present spin period, low surface magnetic field, and mass, which is much higher than the average 1.4 M⊙. From now on, we focus exclusively on the spin-up phase of the pulsar evolution, to deduce its pre-accretion parameters.
3. Spin-up by accretion in LMXBs
We consider a binary consisting of a young radio pulsar (of a “canonical” surface magnetic field Bi ≃ 1012 G, and a spin period of a fraction of a second) and a low-mass MS companion. In a few million years, it spins down by means of magnetic dipole braking down to the period of a few seconds, without suffering any significant magnetic field decay. Consequently, it crosses the radio pulsar death line and disappears as a pulsar. On a much longer timescale of a billion years, the low-mass companion enters the red giant phase and fills its Roche lobe. This entails the mass transfer onto the NS via an accretion disk. The binary system becomes a LMXB, remaining in this stage for 108 − 109 yrs. Accretion of the plasma onto a NS increases its mass, while accelerating its rotation, as well as inducing the decay (dissipation) of its surface magnetic field.
The accretion rate is expressed in terms of the baryon mass Mb, since it is the parameter that can be uniquely determined for the binary system; indeed Mb is related to the star’s total baryon number Nb by Mb = Nbm0, where m0 is the mass per nucleon of the 56Fe atom. The increase in Mb is straightforward and proportional to the accretion rate – at time t (measured by a distant observer) it is denoted as Ṁb(t). Assuming that accretion starts at ti, the integrated (total) baryon mass increase is 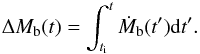 (1)Since the detailed history of accretion is unknown, we treat Ṁb as a constant, such that ΔMb(t) ≈ Ṁb(t − ti). While Mb is a very important global stellar parameter, the quantity that is actually measured is the gravitational mass M. We define its increase as
(1)Since the detailed history of accretion is unknown, we treat Ṁb as a constant, such that ΔMb(t) ≈ Ṁb(t − ti). While Mb is a very important global stellar parameter, the quantity that is actually measured is the gravitational mass M. We define its increase as 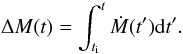 (2)It is found that ΔM depends on ΔMb according to the relation between dM, dMb, and the total angular momentum J (see e.g., Friedman et al. 1988)
(2)It is found that ΔM depends on ΔMb according to the relation between dM, dMb, and the total angular momentum J (see e.g., Friedman et al. 1988) 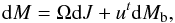 (3)where ut, the time component of fluid 4-velocity as seen by a distant observer, has the meaning of chemical potential (divided by m0c2). For ΔM(t), one then obtains
(3)where ut, the time component of fluid 4-velocity as seen by a distant observer, has the meaning of chemical potential (divided by m0c2). For ΔM(t), one then obtains 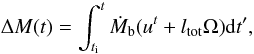 (4)using the total angular momentum J evolution equation
(4)using the total angular momentum J evolution equation 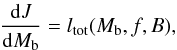 (5)where ltot includes the angular momentum transferred to the star by the infalling matter and the influence of the magnetic torque (for details, see Sect. 5). The values of the gravitational mass M and spin frequency f = 1/P for a given Mb and J are calculated for stationary rigidly rotating two-dimensional NS models (Bonazzola et al. 1993), with the rotstar code implementation from the numerical relativity library LORENE1.
(5)where ltot includes the angular momentum transferred to the star by the infalling matter and the influence of the magnetic torque (for details, see Sect. 5). The values of the gravitational mass M and spin frequency f = 1/P for a given Mb and J are calculated for stationary rigidly rotating two-dimensional NS models (Bonazzola et al. 1993), with the rotstar code implementation from the numerical relativity library LORENE1.
4. Decay of neutron-star magnetic field in LMXBs
Millisecond pulsars have typically a low surface polar magnetic field of strength Bp ~ 108 − 109 G (see e.g., Lorimer 2008), but observations do not provide any evidence of the Bp decay during the radio-pulsar phase. However, a substantial Bp decay (of some four orders of magnitude) is thought to occur during the accretion “recycling” in a LMXB, leading to the formation of a millisecond pulsar (Taam & van den Heuvel 1986; for a review see Colpi et al. 2001). We relate Bp to measured values of P and Ṗ by a standard formula, Bp = 3.2 × 1019(PṖ 1/s)1/2 (Manchester & Taylor 1977). This assumes a stellar moment of inertia I = 1045 g cm2 and radius R = 10 km, and enables one to replace the measured value of Ṗ by Bp.
4.1. Decay of magnetic field – theory
Theoretical modeling of accretion-induced decay of Bp turns out to be a challenging task. The original idea that Bp decays in close binaries because it is “buried” (“screened”) by the accreted matter was proposed by Bisnovatyi-Kogan & Komberg (1974). Romani (1990) suggested that a combination of crustal heating due to accretion, accelerating Ohmic dissipation, and advection of magnetic field lines from the poles towards the equator could explain the Bp decay. Some other authors focused on the realistic modeling of the acceleration of the Ohmic dissipation of the crustal B caused by the heating induced by accretion (Geppert & Urpin 1994; Urpin & Geppert 1995). The decay of Bp due to the diamagnetic screening by the accreted layer was studied in Zhang et al. (1994) and Zhang (1998). Dependence of the screening of crustal magnetic field on the accretion rate was studied in more detail later by Cumming et al. (2001). These authors considered in detail the interplay between the advection of magnetic field and its Ohmic diffusion, and used realistic microscopic models of the outer “ocean” (molten crust) and the crust. Magneto-hydrodynamical simulation of accretion-burial of Bp have also been performed by several authors (e.g. Payne & Melatos 2004, 2007; see also the study of Wette et al. 2010, and references therein). This very brief and incomplete (especially as far as the references are concerned) review illustrates the theoretical effort to explain the decay of Bp during the accretion-driven recycling of the millisecond pulsars. Unfortunately, no reliable and robust scenario based on realistic microphysics combined with complete magneto-hydrodynamical treatment, and consistent with astronomical observations, is available today. Therefore, in what follows we limit our description of the Bp decay to simple phenomenological models, based to some extent on observations of three populations: old radio pulsars, accreting binary neutron stars, and millisecond pulsars. Our basic assumption (which is widely accepted) is that these populations are linked by the recycling process, which in turn is driven by accretion onto a magnetized neutron star in a close binary.
4.2. Decay of magnetic field – phenomenology (with some observational basis)
Taam & van den Heuvel (1986) analyzed a set of LMXBs of different ages and therefore different amounts of accreted mass. They suggested that there is a possible inverse correlation between Bp and the (estimated) total amount of accreted material. Their conclusion was confirmed in a later study by van den Heuvel & Bitzaraki (1995). Shibazaki et al. (1989) presented more detailed arguments based on a subset of LMXBs that enabled this inverse correlation to be quantified as 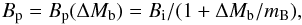 (6)where Bi is the initial (pre-accretion) magnetic field, Bp(ΔMb) is the magnetic field after
(6)where Bi is the initial (pre-accretion) magnetic field, Bp(ΔMb) is the magnetic field after 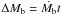 is accreted by the neutron star, and mB is a constant setting the scale of dissipation of Bp with increasing ΔMb. We note that Shibazaki et al. (1989) do not advocate any physical model leading to Eq. (6). They report astrophysically interesting bounds on mB, resulting from the application of Eq. (6) to some LMXBs, X-ray pulsars, and millisecond pulsars. In particular, for mB ≳ 10-3 M⊙, the evolution at an X-ray pulsar stage proceeds along the equilibrium spin-up line, with accretion (advection) torque balanced by the magnetic torque (Ghosh & Lamb 1979; Fig. 1 of Shibazaki et al. 1989) – rapid millisecond rotation cannot be obtained in this way. If, however, mB ≲ 10-4 M⊙, then the evolutionary tracks in the log Bp − log P plane are consistent with measured pairs of Bp and P for binary and isolated millisecond radio pulsars. Finally, taking mB ~ 10-4 M⊙ allows a reasonable representation of the inverse correlation between Bp and ΔMb noted by Taam & van den Heuvel (1986).
is accreted by the neutron star, and mB is a constant setting the scale of dissipation of Bp with increasing ΔMb. We note that Shibazaki et al. (1989) do not advocate any physical model leading to Eq. (6). They report astrophysically interesting bounds on mB, resulting from the application of Eq. (6) to some LMXBs, X-ray pulsars, and millisecond pulsars. In particular, for mB ≳ 10-3 M⊙, the evolution at an X-ray pulsar stage proceeds along the equilibrium spin-up line, with accretion (advection) torque balanced by the magnetic torque (Ghosh & Lamb 1979; Fig. 1 of Shibazaki et al. 1989) – rapid millisecond rotation cannot be obtained in this way. If, however, mB ≲ 10-4 M⊙, then the evolutionary tracks in the log Bp − log P plane are consistent with measured pairs of Bp and P for binary and isolated millisecond radio pulsars. Finally, taking mB ~ 10-4 M⊙ allows a reasonable representation of the inverse correlation between Bp and ΔMb noted by Taam & van den Heuvel (1986).
One has to be aware that Eq. (6) is based on a limited and uncertain set of data referring to LMXBs. It is clear that Eq. (6) is too simplistic to describe magnetic field decay for all kinds of accreting neutron stars. It is natural to expect that the decay of Bp depends not only on ΔMb, but also on Ṁ, which is decisive in the heating of the neutron-star interior (Wijers 1997; Urpin & Geppert 1996; Urpin et al. 1998; Cumming et al. 2001). Specifically, Wijers (1997) demonstrated that the decay law Bp ∝ 1/ΔMb is inconsistent with a broader set of available data for accreting neutron stars in both X-ray binaries and recycled millisecond pulsars.
In spite of the limitations and uncertainties discussed above, we adopt Eq. (6) as our baseline description of the Bp decay in LMXBs and compare it with other proposed phenomenological formulae for the accretion-induced Bp decay to assess the model-independent features of our basic results.
For example, Wijers (1997) discussed the square dependence on ΔMb/mB in the denominator of Eq. (6) as well: 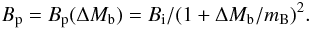 (7)In this case, one has to use a lower value of mB ≃ 10-3 ÷ 10-2 M⊙, which allows to form a millisecond pulsar before the field decays to very low values.
(7)In this case, one has to use a lower value of mB ≃ 10-3 ÷ 10-2 M⊙, which allows to form a millisecond pulsar before the field decays to very low values.
An exponential decay of Bp was employed by Kiel et al. (2008) and Osłowski et al. (2011) to be 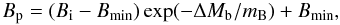 (8)where Bmin = 108 G is the assumed minimal residual magnetic field, to reproduce the observed P − Ṗ distribution by means of the population synthesis studies (Osłowski et al. 2011). We discuss briefly how the final results depend on the assumed magnetic field decay model in Sect. 7.3.
(8)where Bmin = 108 G is the assumed minimal residual magnetic field, to reproduce the observed P − Ṗ distribution by means of the population synthesis studies (Osłowski et al. 2011). We discuss briefly how the final results depend on the assumed magnetic field decay model in Sect. 7.3.
5. Spin-up by disk accretion onto a magnetized neutron star
We assume that the evolution of an accreting NS can be represented as a sequence of stationary rotating configurations of increasing baryon mass. We use the KR formalism to determine the circular orbit r0, from where the accretion effectively takes place – the radial inner boundary of the Keplerian accretion disk in which the viscous torque is non-vanishing. Following KR, we define the corotation radius 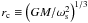 (i.e., the radial distance at which the Keplerian orbital angular frequency ΩK is equal to the rotation frequency of a central star, ωs = 2πf), the magnetospheric radius
(i.e., the radial distance at which the Keplerian orbital angular frequency ΩK is equal to the rotation frequency of a central star, ωs = 2πf), the magnetospheric radius 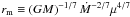 (where μ = BpR3 approximates the stellar magnetic dipole moment), the magnetic-to-corotating radius ratio ξ ≡ rm/rc, and the so-called “fastness” parameter
(where μ = BpR3 approximates the stellar magnetic dipole moment), the magnetic-to-corotating radius ratio ξ ≡ rm/rc, and the so-called “fastness” parameter 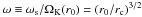 . In addition, we include relativistic effects – inevitable in the space-time generated by a rotating NS – especially the existence of the marginally stable orbit rms and denote the Schwarzschild gravitational radius as rs ≡ 2GM/c2, and the corotation radius in rs units, β ≡ rc/rs.
. In addition, we include relativistic effects – inevitable in the space-time generated by a rotating NS – especially the existence of the marginally stable orbit rms and denote the Schwarzschild gravitational radius as rs ≡ 2GM/c2, and the corotation radius in rs units, β ≡ rc/rs.
We then solve the equation that corresponds to the vanishing of the viscous torque to determine the disk inner boundary, namely 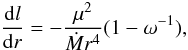 (9)where l is the specific angular momentum of a particle calculated in a relativistic way. To avoid the arduous calculations of the NS space-time that would be needed to obtain the specific angular momentum l at a given disk radius r in every time-step of the evolution, we exploit the result of Bejger et al. (2010), who provide an approximation of the value of l(r), defined as
(9)where l is the specific angular momentum of a particle calculated in a relativistic way. To avoid the arduous calculations of the NS space-time that would be needed to obtain the specific angular momentum l at a given disk radius r in every time-step of the evolution, we exploit the result of Bejger et al. (2010), who provide an approximation of the value of l(r), defined as 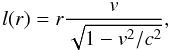 (10)with an approximate value of the particle orbital velocity v
(10)with an approximate value of the particle orbital velocity v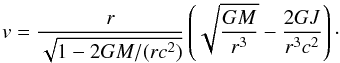 (11)This approximate value of l(r) deviates by less than one per cent from the true value for spin frequencies and masses similar to PSR J1903+0327 measurements (for details see Bejger et al. 2010). Equations (9) − (11) yield an algebraic equation for r0 of
(11)This approximate value of l(r) deviates by less than one per cent from the true value for spin frequencies and masses similar to PSR J1903+0327 measurements (for details see Bejger et al. 2010). Equations (9) − (11) yield an algebraic equation for r0 of 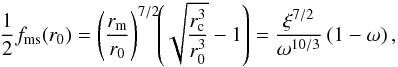 (12)with a dimensionless function fms defined as
(12)with a dimensionless function fms defined as 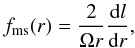 (13)which for l(r) given by Eqs. (10) and (11) equals
(13)which for l(r) given by Eqs. (10) and (11) equals 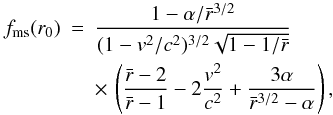 (14)where
(14)where 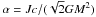 and
and 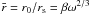 .
.
In general, Eqs. (12) and (14) allow us to calculate r0 in the “recycling” process of even very rapidly rotating and massive millisecond pulsars, when the existence of a relativistic marginally-stable orbit cannot be neglected i.e., when the KR condition of r0 ≪ rms is no longer valid. The value of rms corresponds to the solution of 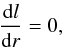 (15)which is determined by assuming that fms(rms) = 0. The validity of employing this general, refined approach in the case of PSR J1903+0327 is studied in the Appendix.
(15)which is determined by assuming that fms(rms) = 0. The validity of employing this general, refined approach in the case of PSR J1903+0327 is studied in the Appendix.
To calculate the increase in the total stellar angular momentum J, we take into account the transfer of specific angular momentum l0 ≡ l(r0) and the KR prescription for the magnetic torque 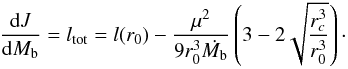 (16)
(16)
6. Equations of state
The EOS of dense cores of NSs remains poorly constrained. This is due to, on the one hand, a lack of knowledge of strong interactions in dense matter, and on the other hand, deficiencies in the available many-body theories of dense matter. This uncertainty has been reflected as a rather broad scatter in the theoretically derived and EOS dependent maximum allowable masses for NSs, Mmax(EOS) (see, e.g. Haensel et al. 2007). Fortunately, the measurement of the mass of PSR J1614-2230, of 1.97 ± 0.04 M⊙ (Demorest et al. 2010), introduces a rather strong constraint of Mmax ≥ 2.0 M⊙. This means that the true EOS is rather stiff. To illustrate a remaining uncertainty in the stiffness, we considered three different models of the EOS. In all cases, the simplest composition of matter was assumed – neutrons, protons, electrons, and muons in β-equilibrium (npeμ):
-
DH
This model of Douchin & Haensel (2001) isnon-relativistic and its energy density functional is based on theSLy4 effective nuclear interaction. The model describes in aunified way both the dense liquid core of NS and its crust, yieldingMmax = 2.05 M⊙ and a circumferential radius at the maximum mass of RMmax = 10.0 km.
-
APR
= A18 + δv + UIX ∗ from Akmal et al. (1998) is a non-relativistic model with some relativistic corrections. It consists of a two-nucleon Argonne potential A18 with relativistic boost corrections δv and an adjusted three-nucleon Urbana UIX* potential. A variational solution of the many-body problem yields Mmax = 2.21 M⊙ and a circumferential radius at the maximum mass of RMmax = 10.0 km.
-
BM
= TM16S0 (with some minor changes) was drawn from a set of relativistic models of Bednarek & Mańka (2009). It consists of a Lorentz-covariant effective nonlinear Lagrangian including up to quartic terms in meson fields, based on chiral-symmetry breaking expansions. The EOS was calculated in the mean field approximation, yielding Mmax = 2.11 M⊙ and a circumferential radius at the maximum mass of RMmax = 11.95 km.
7. Results
To illustrate the laws and relations governing the “recycling” process, we begin by constraining the final spin frequency, f = 465 Hz. We then calculate sets of the evolutionary tracks labeled with the NS initial parameters – Mi, Pi, and Bi – covering a broad range of possible values. If not stated otherwise, the figures relate to results obtained using the DH EOS. In what follows, we denote Bp by B and Ṁb by Ṁ.
7.1. Constraining the parameter space: final frequency f = 465 Hz
 |
Fig. 1 Mass-radius relation for accreting stars with different initial magnetic field Bi and accretion rate Ṁ. Solid black curve denotes static configurations. Evolutionary tracks (arrows mark the direction of evolution) correspond to the following initial parameters (Bi [G], Ṁ [M⊙/yr] ) – a): (1012, 3 × 10-11), b): (1012, 10-10), c): (1012, 10-9), d): (1011, 10-11), and e): (1011, 10-9). Tracks c) and d) coincide, as explained in Sect. 7.1 (color online). |
Figure 1 presents the mass-radius relation for accreting NSs for different values of accretion rate Ṁ and initial magnetic field Bi. The initial mass is fixed at 1.4 M⊙. The upper ends of each curve correspond to the final frequency, 465 Hz. For Bi = 1012 G, the lowest accretion rate considered is 3 × 10-11 M⊙/yr because for lower rates the configurations enter the axisymmetric-perturbation instability region already for frequencies lower than 465 Hz. The same configurations are shown in Fig. 2, where the rotational frequency as a function of mass is presented for different accretion rates. For some evolutionary tracks in Fig. 2, the initial frequency is set to fi = 50 Hz, the value corresponding to a typical frequency expected for newly-born pulsars (Table 7 of Faucher-Giguere & Kaspi 2006). These curves are indistinguishable from those corresponding to initially non-rotating configurations, as the braking timescale is by many orders of magnitude shorter than the spin-up time. The difference is visible on a logarithmic scale in Fig. 3, where we present the frequency evolution of an accreting star for two initial configurations: non-rotating NS and a configuration rotating initially with frequency 50 Hz. The accretion rate here is fixed to Ṁ = 10-9 M⊙/yr. For Bi ~ 1012 G, the spin-down predominates for ~103 yrs, and afterwards the accretion spins-up the star. The amount of accreted material depends very sensitively on the strength of the initial magnetic field; correspondingly, for Bi = 1011 G the spin-down timescale is two orders of magnitude longer (105 yrs) than for Bi = 1012 G. This is a direct consequence of the quadratic dependence of the magnetic torque on the magnetic field B, Eq. (16). The minimum value of rotation frequency corresponds to the exact balancing of angular momentum l0(r0) at the accretion disk edge, r0, by the magnetic torque. In Figs. 4 and 5, we show the magnetic field vs. mass dependence in such a case (the error bar corresponds to the 3-σ measurement of the mass, M = 1.667 ± 0.021 M⊙).
 |
Fig. 2 Spin frequency evolution during accretion, for initial frequencies zero and 50 Hz, as a function of stellar mass. Three different cases of accretion rates (in M⊙/yr) for initial magnetic field Bi = 1012 G (solid line), 1011 G (dashed line) are shown (color online). |
 |
Fig. 3 Spin frequency evolution for initial spin frequencies of zero and 50 Hz and for an initial magnetic field of Bi = 1012 G and 1011 G as a function of the accreted mass (upper axis) or time (lower axis) calculated for a constant accretion rate Ṁ = 10-9 M⊙/yr, on a logarithmic scale (color online). |
 |
Fig. 4 Final magnetic field Bf versus gravitational mass M for configurations rotating at f = 465 Hz. Colors correspond to different accretion rates. For a given accretion rate (in M⊙/yr), different curves are defined by a given initial configuration (i.e., central density or initial mass). Along each curve, the initial magnetic field increases upwards. The error bar corresponds to the uncertainty (3σ) in the mass measurement (color online). |
We note that the problem under consideration is degenerate with respect to the constant 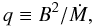 (17)(see Fig. 4), as a consequence of Eqs. (12) and (16) depending on the quantity q, and not B and Ṁ separately.
(17)(see Fig. 4), as a consequence of Eqs. (12) and (16) depending on the quantity q, and not B and Ṁ separately.
To obtain the results for some Ṁ2, the magnetic field B corresponding to Ṁ1 should be multiplied by the factor 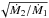 . This relation allows us to determine the lower bound to the accretion rate for given observed values of B and M or, assuming an accretion rate, to determine the maximum value of the final magnetic field e.g., if Ṁ = Ṁ10 = 10-10 M⊙/yr (red curve in Fig. 4), Bmax = 1.16 × 108 G for M = 1.67 M⊙. From the observations, we infer that Bf ≃ 2 × 108 G; since the condition Bmax > Bf should be fulfilled, we use the scaling law
. This relation allows us to determine the lower bound to the accretion rate for given observed values of B and M or, assuming an accretion rate, to determine the maximum value of the final magnetic field e.g., if Ṁ = Ṁ10 = 10-10 M⊙/yr (red curve in Fig. 4), Bmax = 1.16 × 108 G for M = 1.67 M⊙. From the observations, we infer that Bf ≃ 2 × 108 G; since the condition Bmax > Bf should be fulfilled, we use the scaling law 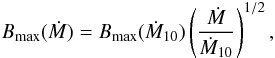 (18)to obtain a lower limit to the accretion rate
(18)to obtain a lower limit to the accretion rate 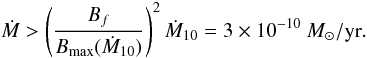 (19)
(19)
 |
Fig. 5 Final magnetic field Bf vs. the gravitational mass for a star rotating at f = 465 Hz. Different colors correspond to different EOSs (solid red – DH, dashed blue – APR, dotted green – BM). The accretion rate is Ṁ = 3 × 10-10 M⊙/yr. The error bar reflects the uncertainty (3σ) in the mass measurement (color online). |
In Fig. 5, we present the relation between the magnetic field and the gravitational stellar mass for the configuration spun up to 465 Hz, for three different EOSs described in Sect. 6. The lower limit to Ṁ assessed above is marginally consistent with the DH EOS for the measured values of M = 1.67 M⊙ and B = 2 × 108 G.
7.2. Constraining the parameter space even further: f = 465 Hz and M = 1.67 M⊙
Lines presented in Fig. 6 correspond to different initial parameters (magnetic field Bi and mass Mi) that lead to configurations of M = 1.67 M⊙ at the spin frequency f = 465 Hz. We employ two fixed accretion rates of Ṁ = 10-10 M⊙/yr and Ṁ = 10-9 M⊙/yr. The scaling relation 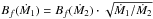 holds and allows us to set limits on Ṁ for a given value of the magnetic field.
holds and allows us to set limits on Ṁ for a given value of the magnetic field.
 |
Fig. 6 Final magnetic field, Bf, versus initial gravitational mass, for a star with final parameters M = 1.67 M⊙ and the frequency f = 465 Hz, for APR, DH, and BM EOSs. The accretion rate is Ṁ = 10-10 M⊙/yr (solid curves) and Ṁ = 10-9 M⊙/yr (dashed curves). Scaling relation |
The differences between the DH and APR EOSs are small in comparison to the difference of them both with a much stiffer BM EOS. The value of the stellar moment of inertia is responsible for such a discrepancy: I(M) for the BM EOS is about 25% higher than the corresponding values for the DH and APR EOS (for the same M). Consequently, to obtain the same final frequency one needs a larger J and a larger amount of accreted mass, which leads to the lower value of Bf.
7.3. From a progenitor NS to PSR J1903+0327: M = 1.67 M⊙, f = 465 Hz, and B = 2 × 108 G
One can obtain a stringent limit on the parameters of the progenitor NS by fixing the final value of the magnetic field. Some tracks considered in this subsection are shown in Fig. 7, labeled by the initial value of the magnetic field Bi and the accretion rate Ṁ. The final magnetic field is fixed to B = 2 × 108 G. For comparison, we present the case in which we neglect the effect of the magnetic field entirely: the accretion takes place from the marginally-stable orbit calculated exactly in accordance with General Relativity (see, e.g., Zdunik et al. 2002).
 |
Fig. 7 Spin-up tracks of the accreting NSs leading to the final configuration rotating at f = 465 Hz and with gravitational mass M = 1.67 M⊙ and magnetic field B = 2 × 108 G. Curves are labeled by the average accretion rate (in M⊙/yr and initial value of the magnetic field (in G). For comparison the spin-up for B = 0 (dashed line), via accretion from marginally stable orbit, is shown (color online). |
The spin-up in the B = 0 case is very efficient, one needs ≃ 0.1 M⊙ only to reach the observed frequency of 465 Hz. Neglecting a magnetic field therefore leads to a rather high progenitor-NS mass, 1.58 M⊙, whereas reasonable values of the progenitor B and Ṁ enable Mf to be reached starting from a moderate value of Mi ~ 1.3 M⊙. The amount of accreted matter in the B = 0 case can be larger if we allow for the reduction in the angular momentum transport efficiency (parameter xl ≪ 1 in Zdunik et al. 2002), here however we assume a 100% efficiency (xl ≡ 1), in accordance with recent numerical calculations (Beckwith et al. 2008; Shafee et al. 2008).
The accretion rate as a function of Mi (assuming final Bf = 2 × 108 G) is presented in Fig. 8. The lower limit to the accretion rate depends on the EOS and ranges from 2.5 × 10-10 M⊙/yr (DH, APR) to 8.5 × 10-10 M⊙/yr (BM). For a given EOS, the required Ṁ depends weakly on the accreted mass needed to spin up the star to 465 Hz, provided that ΔM > 0.2 M⊙. For ΔM < 0.1 M⊙, the required accretion rate increases dramatically with decreasing ΔM. Using 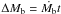 , we obtain the time needed to spin up the star to its presently observed frequency. The result is presented in Fig. 9.
, we obtain the time needed to spin up the star to its presently observed frequency. The result is presented in Fig. 9.
 |
Fig. 8 Average accretion rate vs. initial mass needed to evolve a NS by disk accretion to the frequency f = 465 Hz, mass M = 1.67 M⊙, and magnetic field B = 2 × 108 G for the three EOSs under consideration (color online). |
 |
Fig. 9 Accretion rate versus time of accretion needed to reach observable configuration (color online). |
We also performed calculations for other B(ΔM) dependences (Eqs. (7) and (8) in Sect. 4). The results are qualitatively similar in the case of an inverse quadratic dependence (Eq. (7)); the value of Ṁ at the “plateau” region in Figs. 8 and 9 is slightly higher, 3.6 × 10-10 M⊙/yr, than 3 × 10-10 M⊙/yr, while the Eq. (6) is adopted. For the exponential field decay (Eq. (8)) however, the resulting Ṁ is 8 × 10-10 M⊙/yr (for the mass decay scale mB = 0.05 M⊙, which according to Osłowski et al., gives the closest agreement between their population synthesis model predictions and the observed P − Ṗ data for Galactic pulsars). This discrepancy is due to the different behavior of Bp(ΔM) close to the final Bp value, where Eq. (8) gives significantly larger values of Bp than Eq. (6). For an efficient spin-up, the “magnetic term” proportional to 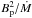 in ltot should be small (Eq. (16)), hence the relatively large value of Bp has to be compensated for by a higher value of Ṁ – for example, assuming Bi = 1012 G, Eq. (6) yields ΔM = 0.5 M⊙ in 1.7 × 109 yrs, while the exponential decay of Osłowski et al. (2011) gives 0.46 M⊙ in 6 × 108 yrs, that is, the accretion of almost the same amount of matter but somewhat more rapidly. One should however treat this kind of empirical formulae with caution, since in the case of parameters obtained by population synthesis methods they may be uncontrollably affected by other assumptions.
in ltot should be small (Eq. (16)), hence the relatively large value of Bp has to be compensated for by a higher value of Ṁ – for example, assuming Bi = 1012 G, Eq. (6) yields ΔM = 0.5 M⊙ in 1.7 × 109 yrs, while the exponential decay of Osłowski et al. (2011) gives 0.46 M⊙ in 6 × 108 yrs, that is, the accretion of almost the same amount of matter but somewhat more rapidly. One should however treat this kind of empirical formulae with caution, since in the case of parameters obtained by population synthesis methods they may be uncontrollably affected by other assumptions.
8. Conclusions
Our simulations have allowed to estimate the intrinsic parameters of the progenitor NS required to reach, in the process of recycling, the measured parameters of PSR J1903+0327. To some extent, as we have shown, the progenitor NS parameters depend on the EOS of dense matter. This was studied using three EOSs consistent with the measurement of 2 M⊙ NS (Demorest et al. 2010).
We have found that the mean accretion rate Ṁ during recycling should be larger than (2.5 ÷ 8.5) × 10-10 M⊙/yr, the highest lower bound being obtained for the stiffest EOS.
For each EOS, the required mean accretion rate is approximately constant for a broad range of initial masses, 1 M⊙ ÷ 1.4 M⊙. Therefore, depending on the initial magnetic field Bi we can reproduce parameters of PSR J1903+0327, or more generally, observed millisecond pulsars, for a specific range of initial masses. In other words, the present parameters of a recycled millisecond pulsar do not allow us to determine its initial mass, in contrast to the case of recycling by accretion with B = 0. Simulations that neglect the magnetic field (following the seminal paper of Cook et al. 1994) give a rather high value of the lower bound to the progenitor NS mass of Mi > 1.55 M⊙ (1.58 M⊙ for DH and APR EOS, and 1.55 M⊙ for the BM EOS). This is a direct consequence of the finding that the magnetic field significantly decreases the spin-up rate (effectively decreasing the efficiency of angular momentum transfer onto the star, as in to the B = 0 and xl ≪ 1 case). Accounting for the magnetic field effect (magnetic torque) is therefore crucial for the understanding of the observable pulsar population properties, especially in view of the proposal that gravitational wave emission is a major dissipative agent that prevents efficient spin-up (Arras et al. 2003; Watts et al. 2008; Watts & Krishnan 2009). In other words, for evolutionary reasons there may not be sufficient time and/or a sufficient amount of matter to accrete, to form a rapidly-spinning pulsar with a magnetic field sufficiently strong to produce a detectable radio beam.
The framework presented here is suitable for testing the global properties of the Galactic pulsar population, as well as for studying other millisecond pulsars with precisely measured masses, e.g., massive millisecond pulsars recycled in intermediate-mass X-ray binaries, where the recycling process is much shorter than the one studied here (Tauris et al. 2011). Our analysis can also be easily extended to take into account time-varying accretion rates and more detailed multi-parameter magnetic field decay prescriptions – this paper is the first of a series devoted to these studies.
 |
Fig. 10 Upper panel: spin-up tracks of accreting NSs leading to presently observed PSR J1903+0327 parameters on radius-spin frequency plane. The relevant characteristic radii are: stellar radius (solid curves), the radius of a marginally stable orbit (dotted curves), and the radius of the inner boundary of accretion disk (dashed curves). Colors correspond to the specific values of accretion rate and the initial value of the magnetic field. Lower panel: effective radial potential V(r,l(r)) in the energy (mc2) units for an exact, approximate, and Schwarzschild solution; the dot marks the final r0. See the text for more details (color online). |
Appendix: The importance of relativistic effects in the “recycling” process of PSR J1903+0327
The original framework of Kluźniak & Rappaport (2007) is restricted to the non-relativistic limit, i.e., it does not include the effects of the existence of a marginally stable orbit of radius rms. As mentioned by these authors, their model should be used only where r0 ≫ rms. To establish a more general model that can be applied to compact and massive configurations near the mass-shedding limit, we have amended this shortcoming here by introducing Eq. (12). We demonstrate in this Appendix however, that in the case of moderately fast-spinning PSR J1903+0327 this refined approach is not essential.
The upper panel of Fig. 10 shows three characteristic radii of the problem, r0, stellar radius R, and rms, calculated along a spin-up evolutionary track. For the final configuration, f = 465 Hz, M = 1.67 M⊙, and B = 2 × 108 G, where r0 reaches its minimum value, r0/rms ≃ 2. We compare two results, one where the effect of General Relativity is mitigated by Eq. (12), and the original model of KR, fms = 1 in Eq. (12). The difference in r0 values is ~200 m, i.e., 0.7%. Lower panel shows the effective radial potential V(r,l(r)) (l(r) is the particle specific angular momentum on the circular orbit of the radius r; see, e.g., Eq. (2) of Bejger et al. 2010); the final r0 is sufficiently far from the rms, hence we conclude that in the particular case of PSR J1903+0327 the relativistic correction necessary to account for rms can be omitted.
Acknowledgments
We are grateful to W. Kluźniak for his helpful comments referring to the Kluźniak-Rappaport model of magnetically-torqued accretion disks. We also acknowledge the helpful remarks of participants of the CompStar 2011 Workshop (Catania, Italy, 9 − 12 May, 2011), after the talk by one of the authors (JLZ). This work was partially supported by the Polish MNiSW grant No. N N203 512 838, by the LEA Astrophysics Poland-France (Astro-PF) program, and the ESF Research Networking Programme CompStar. M.B. acknowledges Marie Curie Fellowship within the 7th European Community Framework Programme (ERG-2007-224793).
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Arras, P., Flanagan, E. E., Morsink, S. M., et al. 2003, ApJ, 591, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Backer, D. C., Kulkarni, S. R., Heiles, C., et al. 1982, Nature, 300, 61 [Google Scholar]
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2008, MNRAS, 390, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, I., & Manka, R. 2009, J. Phys. G: Nucl. Phys., 36, 095201 [Google Scholar]
- Bejger, M., Zdunik, J. L., & Haensel, P. 2010, A&A, 520, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Komberg, B. V. 1974, SvA, 18, 217 [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marc, J. A. 1993, A&A, 278, 421 [NASA ADS] [Google Scholar]
- Champion, D. J., Ransom, S. M., Lazarus, P., et al. 2008, Science, 320, 1309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Colpi, M., Possenti, A., Popov, S., & Pizzolato, F. 2001, in Physics of neutron star interiors, ed. D. Blaschke, A. Sedrakian, & N. K. Glendenning (Springer), LNP, 578, 440 [Google Scholar]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1994, ApJ, 423, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Zweibel, E., & Bildsten, L. 2001, ApJ, 557, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., et al. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faucher-Giguére, C., & Kaspi, V. 2006, ApJ, 643, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, J. L., Ipser, J. R., & Sorkin, R. D. 1988, ApJ, 325, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C., Bassa, C. G., Wex, N., et al. 2011, MNRAS, 412, 2763 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., Stinebring, D. R., & Taylor, J. H. 1988, Nature, 333, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, U., & Urpin, V. 1994, MNRAS, 271, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Gopakumar, A., Bagchi, M., & Ray, A. 2009, MNRAS, 399, L123 [NASA ADS] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1. Equation of State and Structure (New York: Springer) [Google Scholar]
- van den Heuvel, E. P. J., & Bitzaraki, O. 1995, A&A, 297, L41 [NASA ADS] [Google Scholar]
- Hut, P. 1984, ApJS, 55, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Kiel, P. D., Hurley, J. R., Bailes, M., & Murray, J. R. 2008, MNRAS, 388, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźniak, W., & Rappaport, S. 2007, ApJ, 671, 1990 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźniak, W., Ruderman, M., Shaham, J., & Tavani, M. 1988, Nature, 334, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Konar, S., & Bhattacharya, D. 1997, MNRAS, 284, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Levinson, A., & Eichler, D. 1991, ApJ, 379, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X.-W., & Li, X.-D. 2009, ApJ, 692, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R. 2008, Binary and Millisecond Pulsars, Liv. Rev. Relativity, 11, 8, URL (cited on 19 August 2009): http://www.livingreviews.org/lrr-2008-8 [Google Scholar]
- Manchester, R. N., & Taylor, J. H. 1977, Pulsars (San Francisco: Freeman) [Google Scholar]
- Osłowski, S., Bulik, T., Gondek-Rosińska, D., & Belczyński, K. 2011, MNRAS, 413, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Payne, D. J. B., & Melatos, A. 2004, MNRAS, 351, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Payne, D. J. B., & Melatos, A. 2007, MNRAS, 376, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. A. 1993, in Planets around Pulsars, ed. J. A. Phillips, S. E. Thorsett, & S. R. Kulkarni, ASP Conf. Ser., 36, 321 [Google Scholar]
- Portegies Zwart, S., van den Heuvel, E. P. J., van Leeuwen, J., & Nelemans, G. 2011, ApJ, 734, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Radhakrishnan, V., & Srinivasan, G. 1982, Curr. Sci., 51, 1096 [NASA ADS] [Google Scholar]
- Romani, R. W. 1990, Nature, 347, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Shafee, R., McKinney, J. C., Narayan, R., et al. 2008, ApJ, 687, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Shibazaki, N., Muarakami, T., Shaham, J., & Nomoto, K. 1989, Nature, 342, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., & van den Heuvel, E. P. J. 1986, ApJ, 305, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2011, MNRAS, 416, 2130 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V. A., & Geppert, U. 1995, MNRAS, 275, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V. A., & Geppert, U. 1996, MNRAS, 278, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V. A., Geppert, U., & Konenkov, D. 1998, A&A, 331, 244 [NASA ADS] [Google Scholar]
- Watts, A. L., & Krishnan, B. 2009, Adv. Space Res., 43, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Watts, A. L., Krishnan, B., Bildsten, L., & Schutz, B. F. 2008, MNRAS, 389, 839 [Google Scholar]
- Wette, K., Vigelius, M., & Melatos, A. 2010, MNRAS, 402, 1090 [Google Scholar]
- Wijnands, R., & van der Klis, M. 1998, Nature, 394, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Wijers, R. A. M. J. 1997, MNRAS, 287, 607 [NASA ADS] [Google Scholar]
- Zdunik, J. L., Haensel, P., Gondek, D., & Gourgoulhon, E. 2000, A&A, 356, 612 [NASA ADS] [Google Scholar]
- Zdunik, J. L., Haensel, P., & Gourgoulhon, E. 2002, A&A, 381, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, C.-M. 1998, A&A, 330, 195 [NASA ADS] [Google Scholar]
- Zhang, C.-M., Wu, X.-J., & Yang, G.-C. 1994, A&A, 283, 889 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Mass-radius relation for accreting stars with different initial magnetic field Bi and accretion rate Ṁ. Solid black curve denotes static configurations. Evolutionary tracks (arrows mark the direction of evolution) correspond to the following initial parameters (Bi [G], Ṁ [M⊙/yr] ) – a): (1012, 3 × 10-11), b): (1012, 10-10), c): (1012, 10-9), d): (1011, 10-11), and e): (1011, 10-9). Tracks c) and d) coincide, as explained in Sect. 7.1 (color online). |
| In the text | |
 |
Fig. 2 Spin frequency evolution during accretion, for initial frequencies zero and 50 Hz, as a function of stellar mass. Three different cases of accretion rates (in M⊙/yr) for initial magnetic field Bi = 1012 G (solid line), 1011 G (dashed line) are shown (color online). |
| In the text | |
 |
Fig. 3 Spin frequency evolution for initial spin frequencies of zero and 50 Hz and for an initial magnetic field of Bi = 1012 G and 1011 G as a function of the accreted mass (upper axis) or time (lower axis) calculated for a constant accretion rate Ṁ = 10-9 M⊙/yr, on a logarithmic scale (color online). |
| In the text | |
 |
Fig. 4 Final magnetic field Bf versus gravitational mass M for configurations rotating at f = 465 Hz. Colors correspond to different accretion rates. For a given accretion rate (in M⊙/yr), different curves are defined by a given initial configuration (i.e., central density or initial mass). Along each curve, the initial magnetic field increases upwards. The error bar corresponds to the uncertainty (3σ) in the mass measurement (color online). |
| In the text | |
 |
Fig. 5 Final magnetic field Bf vs. the gravitational mass for a star rotating at f = 465 Hz. Different colors correspond to different EOSs (solid red – DH, dashed blue – APR, dotted green – BM). The accretion rate is Ṁ = 3 × 10-10 M⊙/yr. The error bar reflects the uncertainty (3σ) in the mass measurement (color online). |
| In the text | |
 |
Fig. 6 Final magnetic field, Bf, versus initial gravitational mass, for a star with final parameters M = 1.67 M⊙ and the frequency f = 465 Hz, for APR, DH, and BM EOSs. The accretion rate is Ṁ = 10-10 M⊙/yr (solid curves) and Ṁ = 10-9 M⊙/yr (dashed curves). Scaling relation |
| In the text | |
 |
Fig. 7 Spin-up tracks of the accreting NSs leading to the final configuration rotating at f = 465 Hz and with gravitational mass M = 1.67 M⊙ and magnetic field B = 2 × 108 G. Curves are labeled by the average accretion rate (in M⊙/yr and initial value of the magnetic field (in G). For comparison the spin-up for B = 0 (dashed line), via accretion from marginally stable orbit, is shown (color online). |
| In the text | |
 |
Fig. 8 Average accretion rate vs. initial mass needed to evolve a NS by disk accretion to the frequency f = 465 Hz, mass M = 1.67 M⊙, and magnetic field B = 2 × 108 G for the three EOSs under consideration (color online). |
| In the text | |
 |
Fig. 9 Accretion rate versus time of accretion needed to reach observable configuration (color online). |
| In the text | |
 |
Fig. 10 Upper panel: spin-up tracks of accreting NSs leading to presently observed PSR J1903+0327 parameters on radius-spin frequency plane. The relevant characteristic radii are: stellar radius (solid curves), the radius of a marginally stable orbit (dotted curves), and the radius of the inner boundary of accretion disk (dashed curves). Colors correspond to the specific values of accretion rate and the initial value of the magnetic field. Lower panel: effective radial potential V(r,l(r)) in the energy (mc2) units for an exact, approximate, and Schwarzschild solution; the dot marks the final r0. See the text for more details (color online). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.