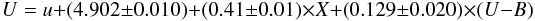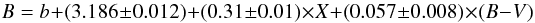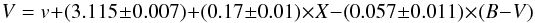| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201117238 | |
| Published online | 15 December 2011 | |
Photometric distances to young stars in the inner Galactic disk
I. The L = 314° direction⋆,⋆⋆
1 ESO, Alonso de Cordova 3107, 19001, Santiago de Chile Chile
e-mail: gcarraro@eso.org
2 Dipartimento di Astronomia, Universitá di Padova, Vicolo Osservatorio 3, 35122 Padova, Italy
e-mail: giovanni.carraro@unipd.it
Received: 11 May 2011
Accepted: 24 October 2011
Context. The spiral structure of the Milky Way is nowadays receiving renewed attention thanks to the combined efforts of observational campaigns in different wavelength regimes from the optical to the radio.
Aims. We start in the paper exploration of several key sectors (line of sights) in the inner Milky Way, where the spiral structure is still poorly known.
Methods. We searched for density enhancements of young stars that might plausibly be associated with spiral structure. To this aim we collected sufficiently wide-field UBVI photometry to allow us to probe in a statistical sense the distribution in reddening and distance of young stars in the field. Although heavily demanding in terms of observational efforts, the intensive usage of U-band photometry ensures robust determination of reddening, hence distance for stars with earlier than A0 spectral type, which are well-known spiral arm tracers, even though no spectroscopic information are available. The fields we use are large enough to include in most cases well-studied Galactic clusters, which we use as benchmarks to assess the quality and standardization of the data and to validate our method.
Results. We focus on the line of sight to the Galactic longitude l = 314°, where previous surveys have already detected Hα emitters at different standard-of-rest velocities, hence distances. The difficulty, however, to translate velocity into distance make predictions on the spiral structure quite vague. First of all, we made exhaustive tests to show that our dataset is in the standard system, and calibrated our method using the two open clusters NGC 5617 and Pismis 19, which happen to be in the field and for which we found estimates of the basic parameters in full agreement with the literature. We then applied the method to the general field stars and detected signatures of three different groups of stars, evenly distributed across the field of view, at 1.5+0.5-0.2, 2.5+0.3-0.5, and 5.1+1.5-1.1 kpc. These distances are compatible with the location of the nowadays commonly accepted description of the Carina-Sagittarius and Scutum-Crux arms, at heliocentric distance of ~2 an 5 kpc, respectively. As a consequence, we consider these groups to be good candidates for tracing the location of these two inner arms.
Conclusions. In line with previous studies, this investigation demonstrates once again how powerful is to use of U-band photometry to characterize ensembles of young stars, and make predictions on the spiral structure of the Milky Way.
Key words: open clusters and associations: general / stars: early-type / Galaxy: disk
Full Table 2 is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/536/A101
© ESO, 2011
1. Introduction
The study of the spiral structure of the Milky Way, long time dormant, is now an active field of astronomical research (Efremov 2010; Grosbol et al. 2011). New wide-area surveys in different wavelength domains have been conducted in recent years, which have allowed us to significantly improve our knowledge of the spiral structure of the Galaxy in several Galactic zones.
Among the various important contributions, we would like to recall here three recent fundamental investigations, that, interestingly enough, employed very different techniques and to demonstrate how lively this field of research is today. The first is the Green Bank Telescope HII Region Discovery Survey (Anderson et al. 2011), which detected a large number of new discovered HII regions in the first Galactic quadrant, delineating for the first time the distant outer (Norma Cygnus) arm in that quadrant.
The second is the detailed study of the third quadrant performed in optical and radio by Vázquez et al. (2008, and references therein), which traced for the first time the local (Orion, or Local arm) all the way to the outer disk and the outer (Norma-Cygnus) arm. This study, however, did not find clear indications of the Perseus arm, which on the other hand, is very well traced in the second quadrant. The third, finally, is the first-ever detection of a distant arm beyond the Outer Arm – the arm traced by Anderson et al. (2011) in the first quadrant – using 21 cm surveys (Dame & Thaddeus 2011).
 |
Fig. 1 Distribution of OB type stars in the plane of the Milky Way as taken from the Reed (2003) catalog. The lower panels show the distribution of B type stars alone (left panel) with Vallée (2005) spiral arms super-posed (right panel). The same is shown in the upper panel, but for O type stars. The position of the Galactic center (GC) is indicated, and the Sun is located at (0.0, 8.5). With the symbols I, II, and III in the bottom-right panel we indicate the Scutum-Crux, Carina-Sagittarius, and Perseus arm, respectively. |
Little effort has been made in recent years to probe the spiral structure in the fourth Galactic quadrant after the important discovery of a distant arm (most probably the outer, Norma-Cygnus arm) in HI by McClure-Griffiths et al. (2004). No indications have been found so far of the Perseus arm extension in this quadrant – between l = 270° and 290° – in spite of model predictions (Valleé 2005; Russeil et al. 2003). The region around l = 270° is a complicated one to study because of the presence of the Vela molecular ridge close to the Sun, which significantly limits optical and near infrared techniques (Carraro & Costa 2010). The line of sight to l = 290° coincides with the tangent to the Carina-Sagittarium arm in the fourth quadrant, again making it very difficult to detect features in optical or infrared beyond it (Shorlin et al. 2004; Carraro & Costa 2009; Baume et al. 2009).
In a series of papers, Russeil (2003, and references therein) carried out deep a Hα survey of the inner Milky Way and confirms the old picture that the inner disk is dominated by the Carina-Sagittarius arm between l = 290° and 360° (Georgelin & Georgelin 1976). However, the difficulty of translating local standard of rest (LST) velocities into distances makes it difficult to position with confidence features having velocities different from the expected one for the conspicuous Carina arm. Only in CO and HI, beyond Carina-Sagittarius, have clear traces of Scutum-Crux, the molecular ring, been found in this Galactic sector (Dame & Thaddeus 2011), which, again, are tricky to interpret in terms of helio-centric distances.
A more effective technique of measuring distances to possible spiral features is the one extensively used by Carraro et al. (2005), Moitinho et al. (2006), Vázquez et al. (2009) and Carraro et al. (2010), which employs deep U-band photometry to estimate the reddening of OB stars in the field or associated to star clusters, hence to constrain their distance.
This technique is an old one that was employed at the very beginning of spiral structure research by Morgan et al. (1952). Historically, this method was motivated by the failure of star count techniques to detect spiral features (Gingerich 1985) and by the evidence that blue stars and gas (typical population I objects) outline spiral armsin external spiral galaxies. Morgan et al. (1952) built up the first compilation of about 900 OB stars, whose distances were measured using UBV photometry and which delineated the Orion and Perseus arm for the very first time.
The sudden rise in HI observations to trace the spiral arm of the Milky Way overtook the optical campaigns for decades, until Georgelin and collaborators undertook a survey in the seventies of HII regions and mapped several portions of the Galactic disk. Their results are summarized in Russeil (2003 and references therein) and lead to the conclusion that our Galaxy is a four-arm spiral (Georgelin 1975).
Attempts to use OB stars in the field or in young clusters were also resumed in the seventies with the UBV star cluster campaign of the southern sky by Moffat & Vogt (1972 and references therein). This survey was, however, not deep enough and could not be used to trace spiral features beyond the Orion and Carina arm (say beyond about 2 kpc from the Sun).
To summarize the state of the art in the field, we plot in Fig. 1 the projected distribution of OB stars in the plane of the MW with and without alleged spiral arms (from Vallée et al. 2005). The data are taken from the homogeneous compilation performed by Reed (2003, and reference therein). This catalog1 contains about 16 000 OB stars for which spectrophotometric distances are known. In the lower panels we plot only B-type stars, while in the upper panel we restrict ourself to O-type stars. To highlight possible spiral features, we only consider stars beyond half an kpc from the Sun. The lefthand panels do show evidence of spiral arms but only when O-type stars are considered. The most striking evidence is a blob of stars around the Sun and the many strikes corresponding to best surveyed lines of sight. In the upper panel only the tilted Orion spurs (Local arm) is evident. When alleged spiral arms are superimposed, a somewhat better picture appears, and it is possible to tentatively assign stars to more distant spiral arms, like Perseus in the second Galactic quadrant and Carina in the first and fourth quadrants. No clear association of stars to the Scutum-Crux arm is visible.
In this paper, we apply this technique in a field (located at l = 314°) where Russeil et al. (1998) have found indications of features with higher velocities than the ones expected for the Carina-sagittarius arm, and look for spiral features extending beyond that arm, hopefully in the Scutum-Crux one. The technique is the same as the one we employed in Carraro & Costa (2009) and Baume et al. (2010). Up to now, the only optical detection of this arm is reported by Vázquez et al. (2005), where a group of early type field stars compatible with the expected position of the arm have been found in the background of the open cluster Stock 16 at 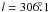 ,
, 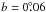 .
.
As mentioned also by Russeil et al. (1998), this line of sight (at l = 314°) contains, the young star cluster NGC 5617, and also happens to contain the old star cluster Pismis 19. These two clusters are well known and have been studied several times in the past. NGC 5617 (Ahumada 2005; Kjeldsen & Frandsen 1991) is a young cluster ~100 Myr old, while Pismis 19 (Phelps et al. 1994; Carraro & Munari 2004; Piatti et al. 1998) is much older, probably around 1 Gyr. The presence of these two clusters offers us the possibility to first check whether our photometry is in the standard system, and second to validate our method of estimating the parameters for the young diffuse population, using star clusters as benchmarks.
This is a pilot study to introduce the method and illustrate the results for a representative line of sight where a possible detection of the Scrutum-Crux arm is claimed for in the optical. A few other lines of sights have been considered in the first and fourth quadrants to specifically look for signatures of this arm in the first and fourth quadrants. They are under analysis and will be presented in forth-coming papers. These lines of sight have been chosen following two criteria. First, we considered directions where at least one well-known star cluster is present, to check the method and the results. Second, we used Scheghel et al. (1998) maps to control that the reddening along these line of sight is relatively low to permit seeing beyond the Carina-Sagittarius arm.
As a consequence, the present work is organized as follows. In Sect. 2 we describe how data were collected and pre-reduced, then discuss the photometric calibration, astrometry, and completeness, and compare our data with literature studies. The reddening law toward l = 314° is discussed in Sect. 3, while Sect. 4 introduces the basics of the method we used to isolate groups of stars at different distances. As an application of the method, we redetermine the fundamental parameters of NGC 5617 and put in the wider context of the spiral structure of the Milky Way in Sect. 9.
UBVI photometric observations of target field and standard star.
 |
Fig. 2 DSS (B band) image showing the field studied in this paper. North is up, and east to the left. The field is 14.8 arcmin wide in RA, and 22.8 arcmin wide in Dec. Notice the presence of the old compact cluster Pismis 19 in the southeast corner (green circle), and the young diffuse cluster NGC 5617 in the northwest region (red circle) |
2. Observations and data reduction
The field under analysis was observed at Las Campanas Observatory (LCO) on the nights of June 26 and 29, 2006, as illustrated in Table 1, which lists useful details of the observations, such as filter coverage, airmass range, and exposure time and sequences. We used the SITe#3 CCD detector onboard the Swope 1.0 m telescope2. With a pixel scale of 0.435 arcsec/pixel, this CCD allows to cover 14.8 × 22.8 arcmin on the sky. Both the nights were photometric with seeing ranging from 0.9 to 1.4 arcsec. The field we covered is shown in Fig. 2, where a bias- and flat-field- corrected image in the V band (30 s) is shown.
To determine the transformation from our instrumental system to the standard Johnson-Kron-Cousins system and to correct for extinction, we observed stars in Landolt’s areas PG 1047, PG 1323, SA 110, PG 1657, and MarkA (Landolt 1992) multiple times and with different air-masses ranging from ~1.05 to ~2.0, and covering quite a wide color range −0.3 ≤ (B − V) ≤ 1.7 mag. We secured night-dependent calibrations, which we then merged, after checking for stability.
2.1. Basic photometric reduction
Basic calibration of the CCD frames was done using IRAF3 package CCDRED. For this purpose, zero-exposure frames and twilight sky flats were taken every night. All the frames were pre-reduced by applying trimming, bias, and flat-field correction. Before flat-fielding, all frame were corrected for linearity, following the recipe discussed in Hamuy et al. (2006).
Photometry was then performed using the IRAF DAOPHOT/ALLSTAR and PHOTCAL packages. Instrumental magnitudes were extracted following the point-spread function (PSF) method (Stetson 1987). A quadratic, spatially variable, master PSF (PENNY function) was adopted because of the large field of view of the detector. Aperture corrections were then determined making aperture photometry of a suitable number (typically 15 to 20) of bright, isolated, stars in the field. These corrections were found to vary from 0.160 to 0.290 mag, depending on the filter. The PSF photometry was finally aperture corrected, filter by filter.
2.2. Photometric calibration
After removing problematic stars and stars having only a few observations in Landolt’s (1992) catalog, our photometric solution for the run was extracted by combining measures from both nights, after checking they were stable and similar. This yielded a grand total of 83 measurements per filter, and turned out to be
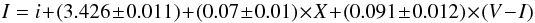 where X indicates the airmass. The final rms of the fitting in this case was 0.030, 0.020, 0.013, and 0.013 in U, B, V, and I, respectively.
where X indicates the airmass. The final rms of the fitting in this case was 0.030, 0.020, 0.013, and 0.013 in U, B, V, and I, respectively.
Global photometric errors were estimated using the scheme developed by Patat & Carraro (2001, Appendix A1), which considers the errors resulting from the PSF fitting procedure (i.e., from ALLSTAR), and the calibration errors (corresponding to the zero point, color terms, and extinction errors). In Fig. 3 we present our global photometric errors in V, (B − V), (U − B), and (V − I) plotted as a function of V magnitude. Quick inspection shows that stars brighter than V ≈ 20 mag have errors lower than ~0.05 mag in magnitude and lower than ~0.10 mag in (B − V) and (V − I). Higher errors, as expected, are seen in (U − B).
 |
Fig. 3 Trend in the global photometric errors in magnitude and colors as a function of V magnitude. See text for details. |
The final catalog contains 3003 UBVI and 13965 VI entries.
2.3. Completeness and astrometry
Excerpt of the optical photometric table exploited in this paper.
Completeness corrections were determined by running artificial star experiments on the data. Basically, we created several artificial images by adding artificial stars to the original frames. These stars were added at random positions, and had the same color and luminosity distribution of the true sample. To avoid generating overcrowding, in each experiment we added up to 20% of the original number of stars. Depending on the frame, between 1000 and 5000 stars were added. In this way we estimated that the completeness level of our photometry is better than 90% down to V = 20.5.
The optical catalog was then cross-correlated with 2MASS, which resulted in a final catalog including UBVI and JHKs magnitudes. As a byproduct, pixel (i.e., detector) coordinates were converted to RA and Dec for J2000.0 equinox, thus providing 2MASS-based astrometry, useful for e.g. spectroscopic follow-up. An excerpt of the optical photometric table used in this investigation is illustrated in Table 2.
2.4. Comparison with previous photometry
As mentioned in the introduction, the region under investigation contains two Galactic clusters, which have been studied several times in the past. This offers us the opportunity of assessing the quality of our dataset and verifying that it is in the same system. Among the various possibilities we chose Piatti et al. (1998) to compare our VI photometry with, since they overlap in the Pismis 19 area. As for UBV, the only study that we can compare with is Kjeldsen & Frandsen (1991), which overlaps with the present study in the area of the star cluster NGC 5617. Although both these studies cover significantly smaller areas than the present study, still the number of stars in common is statistically useful for such a comparison.
As for UBV, we found 129 stars in common with Kjeldsen & Frandsen (1991). The comparison is shown in Fig. 4, in the sense of this study minus Kjeldsen & Frandsen (1991). From this figure one can readily see that the two photometric datasets are in the same system. However, while V and (B − V) compare nicely, the (U − B) color, while in the same system, show quite a significant scatter. However, most of the scatter in the (U − B) comes from stars fainter than V ≈ 17 mag, close to the limiting magnitude of Kjeldsen & Frandsen (1991) photometry, where photometric errors are much larger than in the present study. As a confirmation, such an increase in the scatter is also visibile in the V and (B − V) comparisons at the same magnitude level, where the errors affecting our photometry are lower than 0.02 mag (see Fig. 2). If we restrict the comparison for U − B to stars brighter than V ≈ 17, σ drops to 0.05 mag. We therefore conclude that the two studies are fully compatible down to V ≈ 17. Below these values, the scatter increases because of the increasing errors in the faint end of Kjeldsen & Frandsen (1991) photometry.
 |
Fig. 4 Comparison of our UBV photometry with Kjeldsen & Frandsen (1991) in the region of the open cluster NGC 5617. |
 |
Fig. 5 Comparison of our VI photometry with Piatti et al. (1998) in the region of the open cluster Pismis 19. |
In the case of the VI photometry, we found 228 stars in common with Piatti et al. (1998), and the comparison is shown in Fig. 5, in the sense of this study minus Piatti et al. (1998). Again, the two studies compare nicely, which confirms that our wide-field photometry is in the standard system.
3. The reddening law toward l = 314
A basic requirement before analyzing our photometric material is to investigate the nature of reddening in this Galactic line of sight. The reddening law is described by the ratio of total-to-selective absorption 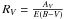 , and the typical value in the Galaxy is about 3.1, with exceptions in star-forming regions. Deviations from the standard value normally stand out in the (V − I) vs. (B − V) color-color diagram, which for the region under study is shown in Fig. 6. If the reddening law is normal, in this diagram stars follow – in other words, distribute with the same mean slope of – the reddening free relation, which for this color combination is
, and the typical value in the Galaxy is about 3.1, with exceptions in star-forming regions. Deviations from the standard value normally stand out in the (V − I) vs. (B − V) color-color diagram, which for the region under study is shown in Fig. 6. If the reddening law is normal, in this diagram stars follow – in other words, distribute with the same mean slope of – the reddening free relation, which for this color combination is  (Dean et al. 1978). As a reddening-free relation relation we adopt the zero age main sequence (ZAMS) from Schmidt-Kaler (1982), which is drawn for dwarf stars (luminosity class (LC) V), and for giant stars (LC III). The two long arrows in the plot indicate the reddening vectors for a normal reddening law (RV = 3.1), and for an anomalous one (RV = 4.0), to guide the eye. By inspecting Fig. 6 we conclude that the reddening law towards l = 314° does not show any evident deviation, and therefore in the following discussion we adopt
(Dean et al. 1978). As a reddening-free relation relation we adopt the zero age main sequence (ZAMS) from Schmidt-Kaler (1982), which is drawn for dwarf stars (luminosity class (LC) V), and for giant stars (LC III). The two long arrows in the plot indicate the reddening vectors for a normal reddening law (RV = 3.1), and for an anomalous one (RV = 4.0), to guide the eye. By inspecting Fig. 6 we conclude that the reddening law towards l = 314° does not show any evident deviation, and therefore in the following discussion we adopt 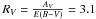 and, in turn,
and, in turn, 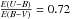 .
.
 |
Fig. 6 (V − I) vs. (B − V) color − color diagram for stars in our field with UBVI photometry. The reddening vectors for the normal extinction law (RV = 3.1 and an anomalous one (RV = 4.0) are plotted with arrows. The the red dashed line represents the reddening-free Schmidt-Kaler (1982) zero age main sequence (ZAMS) relations for dwarf (LC V), while the blue is for giant stars (LC III). |
4. The method
Having shown that our data is in the standard system and the reddening law looks normal, we are now ready to use UBV photometry to measure young stars’ reddening and distance. The foundations of the method we are going to use are described in full detail in Johnson (1965) and Straizys (1991). We remind the reader that this purely photometric method, as described in the introduction, has been succesfully used in the past to detect groups of field stars having common reddening and distance in the background of Galactic clusters (see, e.g., Carraro et al. 2005, 2010; Vázquez et al. 2005, 2008; Pandey et al. 2006, to cite a few examples), both in the third and in the fourth Galactic quadrant.
Briefly, the heart of the method is the simultaneous inspection of the various photometric diagrams to search for stars with common properties (reddening and distance). In the (B − V) vs. (U − B) color − color diagram (CCD), the position of a star only depends on it reddening. To determine reddening, spectral type, and photometric distance, we then proceed as follows. First we derive intrinsic colors using the two relationships (from Straizys 1991), which are valid if the reddening law is normal, as we have shown above: 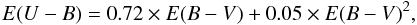 (1)and
(1)and  (2)The intrinsic color (B − V)0 is the positive root of the second-order equation one derives combines the above two expressions. Intrinsic colors ((U − B)0 and (B − V)0) are then directly correlated to spectral type, as compiled for instance in Schmidt-Kaler (1982). The solution of the equations above therefore allows us to encounter stars having spectral types earlier than A0.5. For these stars we then know the absolute magnitude MV (again from the Schmidt-Kaler 1982 compilation) and, from the apparent extinction-corrected magnitude V0, we finally infer the photometric distance.
(2)The intrinsic color (B − V)0 is the positive root of the second-order equation one derives combines the above two expressions. Intrinsic colors ((U − B)0 and (B − V)0) are then directly correlated to spectral type, as compiled for instance in Schmidt-Kaler (1982). The solution of the equations above therefore allows us to encounter stars having spectral types earlier than A0.5. For these stars we then know the absolute magnitude MV (again from the Schmidt-Kaler 1982 compilation) and, from the apparent extinction-corrected magnitude V0, we finally infer the photometric distance.
Errors in distances are then computed using a series of equations, as follows:![\begin{eqnarray} &&\Delta (Dist) = \ln (10) \times Dist \times \Delta [\log(Dist)];\\ &&\Delta [\log(Dist)] = \frac{1}{5} \times \Delta V + \Delta (M_V) + \Delta (A_V)];\\ &&\Delta (M_V) = 0;\\ &&\Delta (A_V) = 3.1 \times \Delta (B-V); \end{eqnarray}](/articles/aa/full_html/2011/12/aa17238-11/aa17238-11-eq62.png) \arraycolsep1.75ptwhere Δ (V) and Δ(B − V) directly come from photometry. Finally,
\arraycolsep1.75ptwhere Δ (V) and Δ(B − V) directly come from photometry. Finally, ![\begin{equation} \Delta (Dist) = \ln (10) \times Dist \times \frac{1}{5} \times [ \Delta V + 3.1\times \Delta (B-V) ]. \end{equation}](/articles/aa/full_html/2011/12/aa17238-11/aa17238-11-eq65.png) (7)As anticipated above, this method is only effective for stars having spectral-types as late as A0V (Straizys 1991), since a unique reddening solution cannot evidently be determined for spectral types beyond the A0V knee in the ZAMS. This is less than a problem for the purpose of this study, since stars with spectral types earlier than A are exactly what we are looking for as spiral features candidates.
(7)As anticipated above, this method is only effective for stars having spectral-types as late as A0V (Straizys 1991), since a unique reddening solution cannot evidently be determined for spectral types beyond the A0V knee in the ZAMS. This is less than a problem for the purpose of this study, since stars with spectral types earlier than A are exactly what we are looking for as spiral features candidates.
To caution the reader, we stress here that the distances we are obtaining are purely photometric and are subject in most cases to large uncertianties, which depend not only on photometric errors, but mostly on spectral type misclassification. This is especially the case here since we do not have spectroscopic confirmations for the spectral types of the stars we consider as early type stars solely according to their position in the CCD. To partially cope with these limitations we first check our method against well-known star clusters in the same field to see if we can recover their fundamental parameters with reasonably small uncertainties.
In general, photometric distances will be of lower precision than, e.g., trigonometric parallaxes (see Reid et al. 2009, and references therein), which, however, are unfortunately available only for a few lines of sight. When comparing different distance sources, Reid et al. (2009) emphasize that kinematic distances (derived mostly from CO and HI radio observations) can be longer than trigonometric parallaxes by factors greater than 2.0, especially in in the first and fourth quadrants, because of distance ambiguities and the existence of sizeable noncircular motions. However, for the few lines of sight they consider – mostly towards Perseus and Sagittarius – the position of star-forming regions derived with the trigonometric parallax method do not deviate significantly from the position inferred from spectrophotometric distances. Masers located in the Perseus arms in the Galactic latitude range 115° − 189° are in virtually the same heliocentric-distance range (2.1 − 2.6 kpc) as most young open clusters associated to Perseus, in the same Galactic sector. Consistency between trigonometric parallaxes and photometric distances has also been found by the same group in the case of W3(OH) (Hachisuka et al. 2006), in the second Galactic quadrant.
5. Checking the method: basic parameters of NGC 5617
The basic parameters of NGC 5617 have been measured in the past by Ahumada (2005) and Kjeldsen & Frandsen (1991), and the two studies basically agree. In fact, Ahumada (2005) estimate a reddening E(B − V) = 0.54 ± 0.09 and a distance modulus (m − M)o = 11.53 ± 0.40, while Kjeldsen & Frandsen (1991) obtained E(B − V) = 0.48 ± 0.02 and (m − M)o = 11.55 ± 0.20. The results from Kjeldsen & Frandsen (1991) are, however, to be considered more reliable, since they are based on UBV photometry, while Ahumada (2005) estimates the reddening by comparing the stars distribution in the color magnitude diagram with theoretical isochrones.
We are going to redetermine these parameters here as a cross-check of our method. To this aim we isolate spatially NGC 5617 most probable member as those stars which lie within 5 arcmin from the cluster center (Dias et al. 2002). The selection is shown in the map in Fig. 1, where NGC 5617 is indicated as a red circular concentration centered at 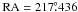 ,
, 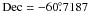 , J2000.0.
, J2000.0.
We constructed the (B − V) vs. (U − B) color − color diagram for these stars, which we show in Fig. 7. The reddening-free Schmidt-Kaler (1982) ZAMS relations for dwarf stars is drawn as a solid black line. The same relation, but shifted along the reddening vector to fit the distribution of blue stars in NGC 5617 is drawn in blue. The reddening vector is indicated in the plot with an arrow. To guide the eye, we indicate the location of some spectral type stars in the reddening-free ZAMS, and move them along the reddening vector to reach the reddened ZAMS that best fits NGC 5617 data.
 |
Fig. 7 (B − V) vs. (U − B) color − color diagram for NGC 5617 stars within 5.0 arcmin from the cluster center. The solid lines are empirical ZAMS for no reddening (black line) and for E(B − V) = 0.45 (blue line). The reddening vector is shown as an arrow in the topright corner. The positions of a few spectral types are indicated to guide the eye. |
From this exercise we can derive the following conclusions.
-
The reddening E(B − V) turns out to be 0.45 ± 0.05, where the uncertainty depends mostly on the width of NGC 5716 sequence. It is difficult to say whether this broadness is caused by differential reddening, since photometric errors (~0.04 in U − B) account almost completely for that.
-
The reddening we derive is therefore in perfect agreement with previous studies;
-
NGC 5617 harbors stars with spectral types as early as B5, which implies ages around 70 ± 10 million years (Marigo et al. 2008).
We are now in a good position to estimate NGC 5617 heliocentric distance, and to this aim we built up the reddening-corrected color magnitude diagram in (U − B)0 vs. V0 and (B − V)0 vs. V0. While the latter is the most widely used, the former has the strong advantage that the MS is tilted, allowing for a more reliable comparison with empirical ZAMS. This comparison is shown in Fig. 8 for (U − B) vs. V (left panel), and (B − V) vs. V (right panel). Quite a good fit is reached by shifting the ZAMS in a vertical direction by (m − M)o = 11.60 ± 0.15, in both diagrams. The uncertainty depends, once again, on the width of the MS.
 |
Fig. 8 Reddening-corrected color − magnitude diagrams for NGC 5617 stars within 5.0 arcmin from the cluster center. The blue lines are empirical ZAMS vertically shifted for the value of the distance modulus indicated in both panels. |
 |
Fig. 9 Color − magnitude diagrams for Pismis 19 stars within 5.0 arcmin of the cluster center. In the left panel the V vs. (V − I) CMD is shown, while in the right panel we show the V vs. B − V CMD. The blue lines are empirical ZAMS adjusted to fit the star distribution using the parameters indicated in the top of the figure. |
This yields heliocentric distance to the cluster of 2.08 ± 0.20 kpc, in close agreement with previous studies. We note that the turn-off point (TO) is located at Vo ~ 12.00 ± 0.10, hence at MV = 0.40 ± 0.10, which is consistent with an age around 70 ± 10 million years (Marigo et al. 2008). At such an age, we expect NGC 5617 to be still very close to its birth-place.
6. Checking the method: basic parameters of Pismis 19
The other cluster in the field, Pismis 19, has a radius of 3 arcmin (Dias et al. 2002). Its stars are enclosed in green circle centered at 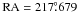 ,
, 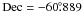 , J2000.0 (see Fig. 1). The cluster is known to be heavily reddened and have an intermediate-age, and therefore we cannot rely on U photometry to infer reddening and distance. We therefore make use of BVI photometry and fit an empirical ZAMSto the data. The exercise is illustrated in Fig. 9, where the V vs. (V − I) CMD is shown in the lefthand panel, and the V vs. B − V CMD is shown in the righthand panel. Only stars within the cluster radius are used. First of all, we notice that our photometry is almost two magnitudes deeper than previous studies, which allows more solid comparison with empirical sequences, since the magnitude baseline is larger. Besides, we would like to emphasize the vertical sequence of stars to the blue of Pismis 19, which is composed of field stars located between us and the clusters (interlopers), and not to NGC 5617 (Phelps et al. 1994), which is about 15 arcmin away.
, J2000.0 (see Fig. 1). The cluster is known to be heavily reddened and have an intermediate-age, and therefore we cannot rely on U photometry to infer reddening and distance. We therefore make use of BVI photometry and fit an empirical ZAMSto the data. The exercise is illustrated in Fig. 9, where the V vs. (V − I) CMD is shown in the lefthand panel, and the V vs. B − V CMD is shown in the righthand panel. Only stars within the cluster radius are used. First of all, we notice that our photometry is almost two magnitudes deeper than previous studies, which allows more solid comparison with empirical sequences, since the magnitude baseline is larger. Besides, we would like to emphasize the vertical sequence of stars to the blue of Pismis 19, which is composed of field stars located between us and the clusters (interlopers), and not to NGC 5617 (Phelps et al. 1994), which is about 15 arcmin away.
We made use of the reddening-free Schmidt-Kaler (1982) ZAMS relations for dwarf stars to fit the blue side of the MS, and the fit yields the values indicated in the top of the plot. The uncertainties on these parameters can be estimated by eye and amount to 0.2 for the reddening and to 0.3 at least for the distance modulus. These values very nicely agree with previous studies and confirm that Pismis 19 is indeed a highly obscured cluster. Its heliocentric distance is estimated to be 2.5 ± 0.5 kpc, somewhat farther than NGC 5617.
The presence of a clump of red giant stars at V ~ 17 and B − V ~ 2.4 suggests an intermediate age for Pismis 19, and makes this cluster useless for tracing spiral features. Therefore providing a solid estimate of the age goes beyond the scope of this investigation.
7. The young, diffuse stellar population in the field
 |
Fig. 10 (B − V) vs. (U − B) color − color diagram for field stars. The solid lines are empirical ZAMS for no reddening (black line) and for E(B − V) = 0.40 (blue line), 0.70 (green line), and 1.00 (red line). The reddening vector is shown as an arrow in the topright corner. The position of a few spectral types is indicated to guide the eye. Stars crowding along the various ZAMS are depicted with empty squares, colored in the same way as the corresponding ZAMS. See text for more details. |
By using of our UBVI photometry, which is in the standard system, and the CCD and CMDs we confirmed previous results in the case of NGC 5617 and Pismis 19. We can therefore extend the same technique to field stars, with the aim of searching for common reddening stars in the field, which can indicate spiral features at the same distance to NGC 5617 or even more distant, as found for instance in the field of Shorlin 1 by Carraro & Costa (2009), in the field of Danks 1 and 2 by Baume et al. (2010) and in the background of Stock 16 (Vázquez et al. 2005).
The color − color diagram of field stars is shown in Fig. 10. This has been constructed by masking the region of the young cluster NGC 5617 alone, since no young blue stars in the field of Pismis 19 actually belong to it. To help the reader follow our arguments, which are mainly based on visual inspection of the diagram, we overplot the zero-reddening ZAMS and three additional ZAMS, shifted according to the reddening E(B − V) indicated on top of them. They were drawn to highlight the location of common reddening sequences. These sequences are made of early type stars shifted by interstellar reddening and not falling in the crowded region of later than A0 type stars. One cannot expect these sequences to be very tight, since they are made up of field stars with different spatial locations (see Carraro & Costa 2009, for additional details).
The most prominent and obvious sequence is the one through which we overplot the E(B − V) = 0.40 ZAMS. This is made of stars as early as B4. Two less conspicuous sequences are at average reddening of E(B − V) = 0.70 and E(B − V) = 1.00, respectively. While there might be even more reddened sequence, we consider them not very reliable, since they are at the limit of U-band sensitivity.
We used the Q-method (Strayzis 1991) to extract stars having reddening around these three values, and counted 47, 41, and 29 stars close to the ZAMS reddened by about 0.40, 0.70, and 1.00 mag, respectively. For these sequences we estimated a mean reddening of E(B − V) = 0.37 ± 0.06, 0.76 ± 0.05, and 1.05 ± 0.09 mag, respectively.
The stars belonging to each common reddening group are indicated in the CCD with empty boxes, and with the same color as the ZAMS superimposed for their mean reddening value.
 |
Fig. 11 Variable extinction diagram for the groups of stars identified in the color − color diagram in Fig. 10. The color coding is the same as in Fig. 10. |
To appreciate the discreteness in distance of these three sequences, we make use of the variable extinction diagram in Fig. 11, whose use is fully described in, e.g., Johnson (1965). Briefly, it has been widely employed in the past to establish the reddening law in different regions of the Milky Way. This reddening law, represented by the parameter RV, is the slope in a diagram of apparent distance moduli (V − MV) versus reddening (E(B − V)), and it has been succesfully used when a wide range of reddening (namely variable extinction) was detected along the line of sight. The usage of this diagram to estimate RV is possible when stars’ spectral types are available from spectroscopy, which allow their absolute magnitude to be estimated independently of photometry. In this study, we make use of the variable extinction diagram to show the reddening distribution of the discrete groups we identified along the line of sight and visually appreciate their distance distribution and spread, since we already know from the (V − I) vs. (B − V) TCD that the reddening law is normal. The dispersion in the X-axis of Fig. 11 is the one derived with the Q-method above, while the dispersion in the Y-axis is graphically shown with histograms using the same color coding as in Fig. 10. The three distributions peaks at (V − MV) = 12.10 ± 0.40, 14.20 ± 0.30, and 16.80 ± 0.80.
Once corrected for extinction, these distance moduli imply distances of 1.5 , 2.5
, 2.5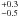 , and 5.1
, and 5.1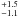 kpc, respectively.
kpc, respectively.
We notice that the first two groups bracket NGC 5617 in distance. According to Bronfman et al. (2000) the Carina-Sagittarius arm in this Galactic sector is centered on about 2 kpc and has a width of about 1 kpc, which would imply that the two groups encompass the arm in heliocentric distance, and NGC 5617 falls just inside the arm.
The third group is much more scattered, mostly because of the significant uncertainty and spread in reddening. In spite of that, it clearly traces a group of young stars located beyond Carina-Sagittarius.
 |
Fig. 12 Spatial distribution of the stars belonging to the three common reddening groups we detected in the field of view. Color coding is the same as in Fig. 10. |
8. Spatial distribution of B type stars in the field
In this section we study the spatial distrution of the three groups we identified in the CCD and described in previous section. The underlying motivation is to investigate whether the stars belonging to them are evenly distributed across the field or are grouped together. In the latter case, this would mean these bright stars are part of some cluster/association.
The situation is illustrated in Fig. 12. The stars in the region under study are plotted, and the size of symbols is proportional to their magnitude. The star clusters NGC 5617 and Pismis 19 are clearly visible. We then used the same colors as in Fig. 10 to overplot the young stars belonging to the three different groups we indentified in the field and which fall outside NGC 5617 area.
Interestingly enough, they are evenly distributed across the field, and do not show any significant clustering. We exclude therefore these B-type stars being part of an overlooked stellar cluster, but are most probably genuine field stars.
9. Discussion and conclusions
We have presented and discussed UBVI photometry in a field centered at l = 314, b = −0.6, with the aim of searching for young star candidates to be part of the inner Galaxy spiral arms. Two star clusters are presentIn the same field of view, NGC 5617 and Pismis 19, for which we estimated fundamental parameters, and found they are in close agreement with previous studies. This makes us confident that our photometry is in the standard system and the method of analysis correct.
By analyzing the TCD of field stars in the line of view, we detected three common reddening groups, for which we provide mean reddening and distance. The three groups have reddening E(B − V) = 0.37 ± 0.06, 0.76 ± 0.05, and 1.05 ± 0.09 mag, and are located at distances of 1.5 , 2.5
, 2.5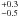 , and 5.1
, and 5.1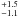 kpc from the Sun. We also showed that stars belonging to the three groups are evenly distributed across the field of view, which means they do not belong to any overlooked star cluster.
kpc from the Sun. We also showed that stars belonging to the three groups are evenly distributed across the field of view, which means they do not belong to any overlooked star cluster.
We now discuss the importance of theses groups as candidates spiral arm tracers.
In the context of the deep Hα survey of the Milky Way Russeil et al. (1998) studied the same line of sight at l = 314°. They found signatures of three different radial velocity structures, which imply the presence of emitters at three different distances. The lower velocity group, with LSR velocity Vlsr ~ 2−5 km s-1 corresponds to local, solar vicinity emission, with no traces of any condensation.
We find no hint for young stars so close to the Sun in our field, most probably because the field of view is not large enough to detect features that close in a statistically significant way.
 |
Fig. 13 Vallée (2005) realization of the Milky Way spiral structure. The position of the Sun is indicated with the usual symbol, while GC refers to the Galactic center. The Carina-Sagittarius and Scutum-Crux arms are labeled to make the figure easy to read. The three common reddening groups identified in Fig. 10 are drawn here with the same color-coding. |
A second component is associated with the HII regions RCW 83 (311.85, − 00.54) and RCW 85 (313.40, −00.36) and coincides with the Carina-Sagittarius arm at a distance of ~1.5−2.0 kpc, where NGC 5617 is located, together with Lynga 1 and 2, Hogg 17, Trumpler 22, and NGC 5606. This component possesses a velocity in the range −24 to −31 km s-1, very close to the ~−35.77 ± 0.82 km s-1 recently measured by Mermilliod et al. (2008) for NGC 5617. In fact, if we convert this radial velocity value into Vlsr by adopting Russeil (2003) values for the solar motion (U,V,W) = (−10.4,14.8,7.3) km s-1, we obtain − 32.3 km s-1. This similarity in velocity strengthens the spatial coincidence of this component, which is clearly associated with the main body of Carina-Sagittarius arm (Vallée 2005; Russeil 2003) at this longitude.
Our analysis in Sect. 10 fully agrees with this scenario, since we detected – together with NGC 5617 – young field stars at heliocentric distances between 1.5 and 3.0 kpc, which encompass the whole width of the Carina spiral arm (Bronfman et al. 2000).
Finally, a third group is detected behind CRW 83 and 85, with velocities ranging from −46 to −52 km s-1. Russeil et al. (1998) assign to this group a distance of 3.4 ± 0.9 kpc, which would place it beyond the Carina-Sagittarius arm. Unfortunately, there is only a marginal overlap with the most distant group we found in Sect. 10, which according to our study would lie farther away. This noncoincidence might also be due to the well known difficulties in deriving distances from radial velocities.
To clarify whether this group traces a population belonging to a more distant arm, we use the Vallée (2005) spiral arm description of the Milky Way, as depicted in Fig. 12. Vallée (2005) performed a statistical analysis of the data available in the literature on the properties of the spiral arms in the Milky Way, such as arm number, pitch angle, arms’ shape and distance. He then provided an analytical description to draw spiral arms using the most updated values of their parameters. We caution the reader that the description we are going to use here is by no means an absolute one, since parameter values change as long as new data are being accumulated.
We use the same color-coding as in Figs. 10 and 11 to position in the heliocentric distance direction the estimated location of the three groups we claim we have detected. The two closest groups, as anticipated in Sect. 10, very likely trace the Carina-Sagittarius arm, at least as predicted by the Vallée (2005) model.
The third group, although significantly more widespread in distance, overlaps with the fourth quadrant portion of the inner Galaxy Scutum-Crux arm at a heliocentric distance of about 5 kpc, and therefore we consider it to be a group of star candidates that belong to this more distant arm.
To lend further support to this scenario, we finally compare our distance determinations with the expected positions of the Carina-Sagittarius and Scutum-Crux arm from another source, say the Russeil (2003) Galactic spiral arm description. In that study, data from different spiral arm indicators (Hα, CO, radio continuum, absorption features, and H109α) was performed, and an analytical fitting done on the data to predict the number and mean positions of the various arms in the plane of the disk. Russeil (2003) concludes that the data are best fitted by a four-arm model where, in the direction we are considering here, the Carina-Sagittarius arm is about 2 kpc from the Sun, and the Scutum-Crux arm at about 5 kpc from the Sun, in agreement with Vallée (2005) statistical models. This seems to reinforce our results that the most distant group we detect represents a population candidate to be part of the Scutum-Crux arm.
To close, we stress that the results presented in this study have to be considered preliminary, and, in this respect, a spectroscopic follow-up of these stars would be very welcome to confirm or deny our findings.
Acknowledgments
This study is based on data acquired at Las Campanas Observatory. The author is very grateful for the technical support and the kind environment at the Observatory. The author also acknowlegdes very fruitful exchange of information with Cameron Reed, Ruben A. Vázquez, and Brian Skiff. The crucial help of an anonymous referee in improving the paper’s presentation is also deeply recognized. We finally made use of the WEBDA database, maintained at Vienna University by E. Paunzen, and the SIMBAD database.
References
- Ahumada, J. A. 2005, AN, 326, 3 [Google Scholar]
- Anderson, L. D., Bania, T. M., Balser, D. S., & Rood, R. T. 2011, ApJS, 194, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Baume, G., Carraro, G., & Momany, Y. 2009, MNRAS, 398, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Bronfman, L., Casassus, S., May, J., & Nyman, L.-Å. 2000, A&A, 358, 521 [NASA ADS] [Google Scholar]
- Carraro, G., & Costa, E. 2009, A&A, 493, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carraro, G., & Munari, U. 2004, MNRAS, 347, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., Vázquez, R. A., Moitinho, A., & Baume, G. 2005, ApJ, 630, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., Vázquez, R. A., Costa, E., Perren, G., & Moitinho, A. 2010, ApJ, 718, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 2011, ApJ, 734, 24 [Google Scholar]
- Dean, J. F., Warren, P. R., & Cousins, A. W. J. 1978, MNRAS, 183, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Alessi, B. B., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efremov, Yu. N. 2010, Ast. Rep., 55, 108 [Google Scholar]
- Georgelin, Y. M. 1975, CRASB, 280, 349 [NASA ADS] [Google Scholar]
- Gingerich, O. 1985, in The Milky Way Galaxy, Proceedings of the 106th Symposium, Groningen, Netherlands, 59 [Google Scholar]
- Grosbol, P., Carraro, G., & Beletski, Y. 2011, the Messenger, 143, 47 [Google Scholar]
- Hamuy, M., Folatelli, G., Morrell, N. I., et al. 2006, PASP, 118, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisuka, K., Brunthaler, A., Menten, K. M., et al. 2006, ApJ, 645, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L. 1965, ApJ, 141, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Frandsen, S. 1991, A&AS, 87, 119 [NASA ADS] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., & Green, A. J. 2004, ApJ, 611, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J.-C., Mayor, M., & Udry, S. 2008, A&A, 485, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moitinho, A., Vázquez, R. A., Carraro, G., et al. 2006, MNRAS, 368, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, W. W., Sharpley, S., & Osterbrock, D. 1952, AJ, 57, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, A. K., Sharma, S., & Ogura, K. 2006, MNRAS, 373, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., & Carraro, G. 2001, MNRAS, 325, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Phelps, R. L., Janes, K. A., & Montgomery, K. A. 1994, AJ, 107, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., Clariá, J. J., Bica, E., Geisler, D., & Minniti, D. 1998, AJ, 116, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, C. B. 2003, AJ, 125, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Georgelin, Y. M., Amram, P., Georgelin, Y. P., & Marcelin, M. 1998, A&AS, 130, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt-Kaler, Th. 1982, Landolt-Börnstein, Numerical data and Functional Relationships in Science and Technology, New Series, Group VI, ed. K. Schaifers, & H. H. Voigt (Berlin: Springer Verlag), 2, 14 [Google Scholar]
- Shorlin, S. L., Turner, D. G., & Pedreros, M. H. 2004, PASP, 116, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Straizys, V. 1991, A&AS, 15 [Google Scholar]
- Vázquez, R. A., May, J., Carraro, G., et al. 2008, ApJ, 672, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Vallée, J. 2005, AJ, 130, 569 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Distribution of OB type stars in the plane of the Milky Way as taken from the Reed (2003) catalog. The lower panels show the distribution of B type stars alone (left panel) with Vallée (2005) spiral arms super-posed (right panel). The same is shown in the upper panel, but for O type stars. The position of the Galactic center (GC) is indicated, and the Sun is located at (0.0, 8.5). With the symbols I, II, and III in the bottom-right panel we indicate the Scutum-Crux, Carina-Sagittarius, and Perseus arm, respectively. |
| In the text | |
 |
Fig. 2 DSS (B band) image showing the field studied in this paper. North is up, and east to the left. The field is 14.8 arcmin wide in RA, and 22.8 arcmin wide in Dec. Notice the presence of the old compact cluster Pismis 19 in the southeast corner (green circle), and the young diffuse cluster NGC 5617 in the northwest region (red circle) |
| In the text | |
 |
Fig. 3 Trend in the global photometric errors in magnitude and colors as a function of V magnitude. See text for details. |
| In the text | |
 |
Fig. 4 Comparison of our UBV photometry with Kjeldsen & Frandsen (1991) in the region of the open cluster NGC 5617. |
| In the text | |
 |
Fig. 5 Comparison of our VI photometry with Piatti et al. (1998) in the region of the open cluster Pismis 19. |
| In the text | |
 |
Fig. 6 (V − I) vs. (B − V) color − color diagram for stars in our field with UBVI photometry. The reddening vectors for the normal extinction law (RV = 3.1 and an anomalous one (RV = 4.0) are plotted with arrows. The the red dashed line represents the reddening-free Schmidt-Kaler (1982) zero age main sequence (ZAMS) relations for dwarf (LC V), while the blue is for giant stars (LC III). |
| In the text | |
 |
Fig. 7 (B − V) vs. (U − B) color − color diagram for NGC 5617 stars within 5.0 arcmin from the cluster center. The solid lines are empirical ZAMS for no reddening (black line) and for E(B − V) = 0.45 (blue line). The reddening vector is shown as an arrow in the topright corner. The positions of a few spectral types are indicated to guide the eye. |
| In the text | |
 |
Fig. 8 Reddening-corrected color − magnitude diagrams for NGC 5617 stars within 5.0 arcmin from the cluster center. The blue lines are empirical ZAMS vertically shifted for the value of the distance modulus indicated in both panels. |
| In the text | |
 |
Fig. 9 Color − magnitude diagrams for Pismis 19 stars within 5.0 arcmin of the cluster center. In the left panel the V vs. (V − I) CMD is shown, while in the right panel we show the V vs. B − V CMD. The blue lines are empirical ZAMS adjusted to fit the star distribution using the parameters indicated in the top of the figure. |
| In the text | |
 |
Fig. 10 (B − V) vs. (U − B) color − color diagram for field stars. The solid lines are empirical ZAMS for no reddening (black line) and for E(B − V) = 0.40 (blue line), 0.70 (green line), and 1.00 (red line). The reddening vector is shown as an arrow in the topright corner. The position of a few spectral types is indicated to guide the eye. Stars crowding along the various ZAMS are depicted with empty squares, colored in the same way as the corresponding ZAMS. See text for more details. |
| In the text | |
 |
Fig. 11 Variable extinction diagram for the groups of stars identified in the color − color diagram in Fig. 10. The color coding is the same as in Fig. 10. |
| In the text | |
 |
Fig. 12 Spatial distribution of the stars belonging to the three common reddening groups we detected in the field of view. Color coding is the same as in Fig. 10. |
| In the text | |
 |
Fig. 13 Vallée (2005) realization of the Milky Way spiral structure. The position of the Sun is indicated with the usual symbol, while GC refers to the Galactic center. The Carina-Sagittarius and Scutum-Crux arms are labeled to make the figure easy to read. The three common reddening groups identified in Fig. 10 are drawn here with the same color-coding. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.