Table 4
Summary of the main characteristics of HFI early maps.
| HFI Early maps – Main characteristics | ||||||||
|
|
||||||||
| a1 | ν | [GHz] | 100 | 143 | 217 | 353 | 545 | 857 |
| a2 | N Bolo | 8 | 11 | 12 | 12 | 3 | 3 | |
| a3 | cWN | [μK degree] | 1.6 | 0.9 | 1.4 | 5.0 | 70 | 1180 |
|
|
||||||||
| b1 | θS | [arcmin] | 9.53 | 7.08 | 4.71 | 4.50 | 4.72 | 4.42 |
| b2 | ΔθS | [arcmin] | 0.10 | 0.12 | 0.17 | 0.14 | 0.21 | 0.28 |
| b3 | e S | 1.20 | 1.03 | 1.13 | 1.10 | 1.17 | 1.35 | |
| b4 | ΔαS | [degree] | 0.80 | 2.08 | 0.28 | 0.28 | 0.13 | 0.07 |
|
|
||||||||
| c1 | 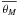 |
[arcmin] | 9.88 | 7.18 | 4.87 | 4.65 | 4.72 | 4.39 |
| c2 | σθM | [arcmin] | 0.04 | 0.02 | 0.03 | 0.04 | 0.06 | 0.05 |
| c3 |
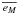
|
1.15 | 1.01 | 1.06 | 1.05 | 1.14 | 1.19 | |
| c4 | σ e M | 0.02 | 0.01 | 0.02 | 0.02 | 0.03 | 0.05 | |
|
|
||||||||
| d1 | CMB relative calibration accuracy | ≲1% | ≲1% | ≲1% | ≲2% | |||
| d2 | CMB absolute calibration accuracy | ≲2% | ≲2% | ≲2% | ≲2% | |||
| d3 | FIRAS gain calibration accuracy | ~7% | ~7% | |||||
| d4 | FIRAS zero point uncertainty | [MJy sr-1] | 0.8 | 1.4 | 2.2 | 1.7 | ||
|
|
||||||||
| e1 | FU | [MJy sr-1/mKCMB] | 2.42 × 10-1 | 3.69 10-1 | 4.81 × 10-1 | 2.88 10-1 | 5.83 10-2 | 2.24 × 10-3 |
| e2 | ΔFU | ≲1% | ≲1% | ≲1% | ≲1% | ≲1% | ~3% | |
| e3 | C(α),α = −2 | 1.011 | 1.025 | 0.999 | 0.997 | 0.998 | 1.011 | |
| C(α),α = 0 | 0.999 | 0.985 | 1.009 | 1.011 | 1.012 | 0.999 | ||
| C(α),α = 1 | 1.008 | 0.980 | 1.027 | 1.031 | 1.035 | 1.007 | ||
| C(α),α = 2 | 1.027 | 0.985 | 1.053 | 1.060 | 1.068 | 1.024 | ||
| e4 | FCO | [μKCMB/KRJ] | 14.2 ± 1.0 | 44.2 ± 1.0 | 171.0 ± 6.0 | |||
Notes. The first column refers to following notes pertaining to the content of the line, while the units are between brackets [] at the right of Col. 2.
This estimate of the small scale noise in the maps comes from the average level between ℓ = 100 and ℓ = 1000 of the power spectra of the Jackknife map (1st versus 2nd half of rings), with 40% of it masked, of Fig. 35.
Average FWHM of the scanning beam, θS,
determined on planets (Mars); it is obtained by unweighed averaging the individual
detectors FWHM. Each FWHM is that of the Gaussian beam which would have the same
solid angle (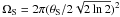 ) as that determined by using a full
Gauss-Hermite expansion on destriped data. FWHM from straight Gaussian Elliptical
fit would rather give 9.45, 7.01, 4.68, 4.45, 4.48 and 4.22 arcmin.
) as that determined by using a full
Gauss-Hermite expansion on destriped data. FWHM from straight Gaussian Elliptical
fit would rather give 9.45, 7.01, 4.68, 4.45, 4.48 and 4.22 arcmin.
Uncertainty in determining the scanning beam FWHM, θS. This conservative uncertainty is derived through the dispersion of results of several methods.
Ellipticity of the scanning beam. The formal uncertainty on these numbers is quite small, always smaller than 1%, but it is likely misleading. This formal uncertainty is defined as the square root of the second diagonal element of Es, the 3 × 3 covariance matrix for fitting (θS,eS,αS) to the data.
Typical uncertainty in determining the direction of the scanning beam elongation. (Square root of the third diagonal element of the covariance matrix ES defined in note b3.)
Average FWHM of the effective beam at map level, θM. This gives the typical width of the beam, as an average over 3000 locations in the map of the local effective beam resulting from combining many measurements per pixel. It tends to increase the beam FWHM by a few percent with respect to the scanning one.
Standard deviation of the variation of the FWHM of the effective beam at the map level (at the location of the Planck ERCSC sources), assuming the input scanning beam is exact. This line shows that the variation of the effective beam FWHM from one location to the other is smaller than the uncertainty on the scanning beam FWHM quoted above.
Relative calibration accuracy between frequency channels. Estimate based on cross-correlation between maps of the CMB component, see details in Sect. 7.5.
Estimate based on simulations of the calibration procedure on the solar system kinematic dipole. This assumes WMAP determination is exact, and perfect data (e.g., no LFER-induced systematics).
Estimate of the systematic error (which dominates the error budget) through the dispersion of estimates obtained in different regions of the sky.
Colour correction C(α), assuming a sky emission of the form Iν ∝ να. This factor C is the one by which the flux of the source need to be multiplied in order to compare with the HFI map or catalogue value. All colour corrections quoted are good at the 2% level or better.
CO correction obtained as described in Sect. 9.4. These factors corresponds to the CO lines J 1–0, J 2–1 and J 3–2 (respectively) at 100, 217 and 353 GHz.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


