| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201118319 | |
| Published online | 23 November 2011 | |
Letter to the Editor
Using observations of distant quasars to constrain quantum gravity
1
Department of Physics & Space SciencesFlorida Institute of Technology, 150 W. University Blvd., Melbourne, FL 32901, USA
e-mail: eperlman@fit.edu
2
Department of Physics and Astronomy, University of North Carolina, Chapel Hill, NC 27599, USA
e-mail: yjng@physics.unc.edu; wayne@physics.unc.edu
3
Monash Centre for Astrophysics, School of Physics, Monash University, PO Box 27, Clayton, Victoria 3800, Australia
e-mail: david.floyd@monash.edu
Received: 21 October 2011
Accepted: 13 November 2011
Aims. The small-scale nature of spacetime can be tested with observations of distant quasars. We comment on a recent paper by Tamburini et al. (2011, A&A, 533, A71) which claims that Hubble Space Telescope (HST) observations of the most distant quasars place severe constraints on models of foamy spacetime.
Methods. If space is foamy on the Planck scale, photons emitted from distant objects will accumulate uncertainties in distance and propagation directions thus affecting the expected angular size of a compact object as a function of redshift. We discuss the geometry of foamy spacetime, and the appropriate distance measure for calculating the expected angular broadening. We also address the mechanics of carrying out such a test. We draw upon our previously published work on this subject, which carried out similar tests as Tamburini et al. and also went considerably beyond their work in several respects.
Results. When calculating the path taken by photons as they travel from a distant source to Earth, one must use the comoving distance rather than the luminosity distance. This then also becomes the appropriate distance to use when calculating the angular broadening expected in a distant source. The use of the wrong distance measure causes Tamburini et al. to overstate the constraints that can be placed on models of spacetime foam. In addition, we consider the impact of different ways of parametrizing and measuring the effects of spacetime foam. Given the variation of the shape of the point-spread function on the chip, as well as observation-specific factors, it is important to select carefully – and document – the comparison stars used as well as the methods used to compute the Strehl ratio.
Key words: quasars: general / techniques: high angular resolution / cosmology: miscellaneous
© ESO, 2011
1. Introduction
Even at the minute scales of distance and duration examined with increasingly discriminating instruments, spacetime still appears to be smooth and structureless. However, a variety of models of quantum gravity posit that spacetime is, on Planck scales, subject to quantum fluctuations. Hence, if probed at a small enough scale, spacetime will appear complicated – something akin in complexity to a turbulent froth that Wheeler (1963) has dubbed “quantum foam,” also known as “spacetime foam.” The detection of spacetime foam is important for constraining models of quantum gravity. If a foamy structure is found, it would require at least a probabilistic rather than deterministic nature of spacetime itself, as the paths taken by different photons emitted by a distant source would not be identical to one another.
In this commentary paper, we discuss the use of astronomical observations of distant sources to test models of quantum gravity. We concentrate particularly on a recent paper by Tamburini et al. (2011), published in Astronomy & Astrophysics in September 2011. Some of the points discussed below were discussed in our own paper Christiansen et al. (2011), which was published nine months earlier. The present paper is organized as follows. In Sect. 2 we discuss the nature of quantum fluctuations and the proper distance measure to use. This has important implications for the predicted size of the seeing disk, and hence the constraints one can put on spacetime foam models given a non-detection, as we then discuss in Sect. 3. In Sect. 4 we discuss practicalities of carrying out these tests. These include the need to characterize the point-spread function (PSF) of a given telescope in terms that can be compared to the profile observed in a distant, unresolved source, such as a quasar or supernova. Finally, in Sect. 5 we close with a summary.
2. The nature of quantum fluctuations and the predicted seeing disk
To quantify the problem, let us recall that, if spacetime undergoes quantum fluctuations, the intrinsic distance to an object will vary, thus producing an intrinsic limitation to the accuracy with which one can measure a macroscopic distance. If we denote the fluctuation of a distance l by δl, we expect 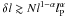 , (see Ng 2003), where N is a numerical factor ~1 and
, (see Ng 2003), where N is a numerical factor ~1 and 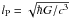 is the Planck length, the characteristic length scale in quantum gravity. The length in this expression, δl, must be defined with reference to the macroscopic distance, l (rather than locally). The parameter α ≲ 1 specifies the different spacetime foam models.
is the Planck length, the characteristic length scale in quantum gravity. The length in this expression, δl, must be defined with reference to the macroscopic distance, l (rather than locally). The parameter α ≲ 1 specifies the different spacetime foam models.
Distance fluctuations ± δl imply phase fluctuations ± Δφ = ± 2πδl/λ (see Lieu & Hillman 2003; Ragazzoni et al. 2003; Ng et al. 2003). One practical method of searching for these fluctuations is to look for “halos” in images of distant, unresolved sources, which can be produced by fluctuations in the direction of the local wave-vector, ± δψ ≡ ± Δφ/(2π) = ± δl/λ. The point is that due to quantum foam-induced fluctuations in the phase velocity of an incoming light wave from a distant point source, the wave front itself develops a small scale “cloud of uncertainty” equivalent to a “foamy” structure, because parts of the wave-front lag while other parts advance. This results in the wave vector, upon detection, acquiring a jitter in direction with an angular spread of the order of δψ. In effect, spacetime foam creates a “seeing disk” whose angular diameter is 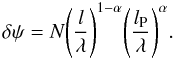 (1)We note that the magnitude of δψ as given in the above equation is consistent with our assumption of isotropic fluctuations which implies comparable sizes of the wave-vector fluctuations perpendicular to and along the line of sight (see Christiansen et al. 2006). For a telescope or interferometer with baseline length Dtel, this means that the dispersion (~δψ, normal to the wave front) will be recorded as a spread in the angular size of a distant point source, causing a reduction in the Strehl ratio, and/or the fringe visibility when δψ ~ λ/Dtel for a diffraction limited telescope.
(1)We note that the magnitude of δψ as given in the above equation is consistent with our assumption of isotropic fluctuations which implies comparable sizes of the wave-vector fluctuations perpendicular to and along the line of sight (see Christiansen et al. 2006). For a telescope or interferometer with baseline length Dtel, this means that the dispersion (~δψ, normal to the wave front) will be recorded as a spread in the angular size of a distant point source, causing a reduction in the Strehl ratio, and/or the fringe visibility when δψ ~ λ/Dtel for a diffraction limited telescope.
The fundamental uncertainties caused by spacetime foam are spatial, not angular, even though they result in a “seeing disk”. Strictly speaking, the models specify the uncertainty ± δl, in distance between a source and observer along the line of sight. This is because δl is defined by the uncertainty in the distance measured by light travel times. Of course, there is also a corresponding uncertainty in the transit time for light from source to observer, δt ~ δl/c. Furthermore, since the globally averaged wavefront is effectively spherical, globally averaged photon trajectories will deviate from the direct line of sight by an angle less than or equal to δl/l. As a direct consequence, the expected blurring of distant images is not the result of a random walk of small angle photon scatterings along the line of sight, since the uncertainties in the derived directions of the local wave vectors must result in the same spatial uncertainty, δl (no matter how many wave crests pass the observer’s location). For example, in the “thin screen approximation”, the accumulated transverse path of multiply scattered photons would be approximated as (δψ)l ≫ δl. This would lead to expected time lags, δψ(l/c) ≫ δl/c, in conflict with the basic premises for spacetime foam models.
The above background, given in greater detail in our recent paper (Christiansen et al. 2011), illustrates why, when measuring the length l for sources at cosmological distances, the appropriate distance measure to use is the line-of-sight comoving distance (see Hogg 2000) given by  (2)where
(2)where 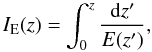 (3)and
(3)and 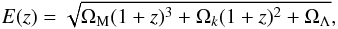 (4)with DH = c/H0 being the Hubble distance, ΩM,Ωk and ΩΛ being the (fractional) density parameter associated with matter, curvature and the cosmological constant respectively. Consistent with the latest WMAP + CMB data, we will use ΩM = 0.25,ΩΛ = 0.75 and Ωk = 0, and for the Hubble distance we will use DH = 1.3 × 1026 m.
(4)with DH = c/H0 being the Hubble distance, ΩM,Ωk and ΩΛ being the (fractional) density parameter associated with matter, curvature and the cosmological constant respectively. Consistent with the latest WMAP + CMB data, we will use ΩM = 0.25,ΩΛ = 0.75 and Ωk = 0, and for the Hubble distance we will use DH = 1.3 × 1026 m.
3. Predicting the halo size
In terms of the comoving distance, for the various models of spacetime foam (parametrized by α), the equivalent halo size is given by 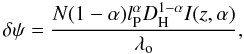 (5)with
(5)with 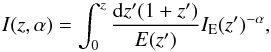 (6)where the factor (1 + z′) in the integral corrects the observed wavelength λo, back to the wavelength λ(z′) at redshift z′. That is, λ(z′) = λo/(1 + z′).
(6)where the factor (1 + z′) in the integral corrects the observed wavelength λo, back to the wavelength λ(z′) at redshift z′. That is, λ(z′) = λo/(1 + z′).
 |
Fig. 1 The detectability of various models of foamy spacetime for existing and planned telescopes. We show the diagonal tracks for halo size δψ for an unresolved, z = 6.3 source, using the comoving distance [Eq. (5), dashed lines], naive application of the luminosity distance [i.e., not redoing the integral I(z,α) as per Eq. (9), in dotted lines], and correct application of the luminosity distance (dash-dot lines). Tracks are shown for α = 0.6,2/3, and N = 1.8. See Sects. 2, 3 for discussion. It appears to us that Tamburini et al. (2011) used the phase uncertainty Δφ = 2πδψ as a measure of halo size, which would exaggerate the expected halo size by nearly an order of magnitude. This displacement would make it appear that quantum foam may be easily tested by HST imaging, which it is not. |
We have used these results to produce Fig. 1. The diagonal lines in Fig. 1 show predictions for the size of the seeing disk for different models of spacetime foam, for a source at redshift z = 6.3, which represents the highest redshift quasar examined by Tamburini et al. (2011). We note that δψ in Fig. 1 is a factor of 2π smaller than the phase, Δφ, which was used incorrectly by Tamburini et al. (2011) to calculate expected halo size. In the case of a non-detection of angular broadening, the region above the diagonal line for a given α may be excluded.
The discussion above illustrates the importance of a correct understanding of the seeing disk caused by spacetime foam as a spatial, rather than angular effect, thus requiring the use of the comoving distance. Figure 1 also shows how the prediction (for δψ not Δφ) changes if one were to incorrectly model the seeing disk as being the result of angular fluctuations, and hence use the luminosity distance, 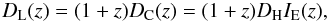 (7)rather than the comoving distance. This is the assumption made by Tamburini et al. (2011) as well as Steinbring (2007).
(7)rather than the comoving distance. This is the assumption made by Tamburini et al. (2011) as well as Steinbring (2007).
As an illustration of the cosmological effects we use Eq. (7) to calculate the equivalent halo size that one would predict if one incorrectly used the luminosity distance. To do this we make use of the last part of Eq. (7) as our l′, in which case 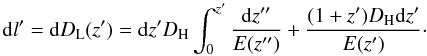 (8)The result is that in calculating δψ one cannot simply use the luminosity distance in Eq. (5), and multiply it by (1 + z). Instead one must replace I(z,α) in Eq. (6) with the following:
(8)The result is that in calculating δψ one cannot simply use the luminosity distance in Eq. (5), and multiply it by (1 + z). Instead one must replace I(z,α) in Eq. (6) with the following: ![\begin{equation} I_2(z,\alpha)=\int_0^z {\rm d}z'(1+z')\big[{{(1+z')}\over{E(z')}}+I_{\rm E}(z')\big]\big[(1+z')I_{\rm E}(z')\big]^{-\alpha}. \end{equation}](/articles/aa/full_html/2011/11/aa18319-11/aa18319-11-eq48.png) (9)Unfortunately, Tamburini et al. (2011) do precisely this (their Eqs. (2) and (3)). We can use the above formalism to estimate how this affects their quoted constraints. In Fig. 1 we have overplotted tracks for the application of luminosity distance, both in the case of redoing I(z,α) and not redoing the integral. As can be seen, in Fig. 1 the use of the incorrect distance measure causes a rather large miscalculation of the expected halo size that leads to an exaggeration in size by a factor of about 20 at a given wavelength. Furthermore, because the parallel set of diagonal lines in Fig. 1 represents trajectories for δψ versus λ that are specified by α, this reduction in halo size leads to a reduction in the limiting value of α that can be determined from observations. Tamburini et al. (2011) claim that current data exclude models with α < 0.68 (a0 ~ 1, including the holographic model which has α = 2/3) (the “red zone” in their Fig. 5). However, by using the correct co-moving distance, we find that their limit for excluding quantum foam models should be reduced by Δα = 0.021, much more consistent with the limit of α ~ 0.65 previously established by Christiansen et al. (2011).
(9)Unfortunately, Tamburini et al. (2011) do precisely this (their Eqs. (2) and (3)). We can use the above formalism to estimate how this affects their quoted constraints. In Fig. 1 we have overplotted tracks for the application of luminosity distance, both in the case of redoing I(z,α) and not redoing the integral. As can be seen, in Fig. 1 the use of the incorrect distance measure causes a rather large miscalculation of the expected halo size that leads to an exaggeration in size by a factor of about 20 at a given wavelength. Furthermore, because the parallel set of diagonal lines in Fig. 1 represents trajectories for δψ versus λ that are specified by α, this reduction in halo size leads to a reduction in the limiting value of α that can be determined from observations. Tamburini et al. (2011) claim that current data exclude models with α < 0.68 (a0 ~ 1, including the holographic model which has α = 2/3) (the “red zone” in their Fig. 5). However, by using the correct co-moving distance, we find that their limit for excluding quantum foam models should be reduced by Δα = 0.021, much more consistent with the limit of α ~ 0.65 previously established by Christiansen et al. (2011).
4. Observing practicalities: Strehl ratio and PSF
In conventional imaging the best way to characterize the halo is in terms of the observed Strehl ratio. This is defined as the ratio of the observed peak intensity from a point source as compared to the theoretical maximum peak intensity of a perfect telescope working at its diffraction limit. As can be seen by reference to Fig. 1, quasars are expected to be barely resolved in HST observations, and the Strehl ratio gives a concrete way to quantify how unresolved they are. This comparison must be done with reference to known stars in one’s image, because the PSF of the HST varies significantly with position on the focal plane (and hence each individual camera). The Strehl ratio is defined as the ratio of the observed image peak to the peak diffraction spike. In Christiansen et al. (2011) we approximated this ratio as
![\begin{equation} S_\mathrm{Obs} = S_{\rm M} \exp \left[-(\sigma_{\rm I}^2 + \sigma_{\psi}^2)\right] \label{eq5} \end{equation}](/articles/aa/full_html/2011/11/aa18319-11/aa18319-11-eq55.png) (10)where SM ≤ 1 represents a degradation of the observed Strehl ratio due to masking effects, σI represents uncorrelated wavefront errors induced by the instrumentation (i.e., telescope plus instruments) and σψ represents uncorrelated wavefront “errors” induced by spacetime foam. Both of these dispersions are expressed in units of the telescope’s diffraction limit, λ/Dtel. A similar treatment is taken in Tamburini et al. (2011), along with a superficially similar procedure, although it should be noted that they do not publish a list of the comparison stars used to compute σI (as we did explicitly in Christiansen et al. 2011). This last makes it difficult to reproduce their results.
(10)where SM ≤ 1 represents a degradation of the observed Strehl ratio due to masking effects, σI represents uncorrelated wavefront errors induced by the instrumentation (i.e., telescope plus instruments) and σψ represents uncorrelated wavefront “errors” induced by spacetime foam. Both of these dispersions are expressed in units of the telescope’s diffraction limit, λ/Dtel. A similar treatment is taken in Tamburini et al. (2011), along with a superficially similar procedure, although it should be noted that they do not publish a list of the comparison stars used to compute σI (as we did explicitly in Christiansen et al. 2011). This last makes it difficult to reproduce their results.
If we follow this prescription, we can then define the spacetime foam degraded Strehl Sψ as 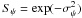 , where σψ is δψ divided by λ/Dtel. Provided the comoving distance is used, as argued in Sect. 2, we then obtain for σψ
, where σψ is δψ divided by λ/Dtel. Provided the comoving distance is used, as argued in Sect. 2, we then obtain for σψ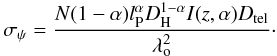 (11)This approximation, of course, breaks down when σψ ~ 1, i.e., when the wave front angular dispersion is comparable to the telescope’s angular resolution. A fully parametrized version of the resultant Strehl ratio then is
(11)This approximation, of course, breaks down when σψ ~ 1, i.e., when the wave front angular dispersion is comparable to the telescope’s angular resolution. A fully parametrized version of the resultant Strehl ratio then is 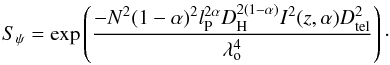 (12)
(12)
 |
Fig. 2 Expected Strehl ratio as a function of redshift (top) and wavelength (bottom). In both plots, we assume α = 2/3 and N = 1.8. In the top figure we examine the change in Strehl ratio expected for a point source with varying redshift, z, for an observed wavelength of 400 nm. In the bottom plot, we specifically show the case of a z = 6.3 quasar, as examined by Tamburini et al. (2011), for an observed wavelength of 400 nm. As in Fig. 1, the dashed line refers to the use of comoving distance, dotted line refers to the naive use of luminosity distance, and dash-dot line refers to the treatment in Eq. (9). |
However, just as with the expected halo size, the use of the luminosity distance drastically affects this expression. We cannot simply replace DC in Eq. (12) by DL, as was done in Tamburini et al. (2011). Instead, I(z,α) must also be replaced with I2(z,α) (Eq. (9)). This causes an overestimate in the magnitude of the exponential argument, thus causing a corresponding reduction in the Strehl ratio which is consistent with the discussion following Eq. (9).
In Fig. 2, we show the result of this error. As can be seen, even in the case of a source at z = 6.3 – the highest redshift source considered by Tamburini et al. (2011) – the effects of spacetime foam simply are not detectable in HST observations. From Fig. 2, as was pointed out in Christiansen et al. (2011), it is not surprising that effects of spacetime foam are likely not to be detectable in HST images cross-referenced with high redshift SDSS quasars, because the only Hubble images from the SDSS sample are in the near IR band. At a wavelength of 8000 Å, typical of the observations used in Tamburini et al. (2011), which used the ACS + F775W and F850LP filters, the expected Strehl ratio is Sψ > 0.98 for both the comoving distance as well as a naive application of the luminosity distance – i.e., just using Eq. (7) and not including the modified integral I2 (Eq. (9)). Even if both of these factors are included, we still expect Sψ > 0.95, at most just a 5% reduction in the measured Strehl with respect to that of the instrument. By comparison, in our paper (Christiansen et al. 2011, Table III), we used comparison stars for the HUDF quasars to measure the instrumental Strehl ratios, finding values between SI = 0.27 (F435W) and 0.64 (F850LP), with the low Strehl ratios in the blue being a result of the undersampling of the PSF by the ACS. While we are unable to comment exactly on the success of the method of Tamburini et al. (2011) because they did not specify which stars were used or provide adequate information on the mechanics of deriving the phase (in their formulation), we can say that we find highly unrealistic their claim to have achieved the maximum possible constraint on α for this wavelength, based on our extensive experience with HST data. Indeed, as our work showed (Christiansen et al. 2011, Table IV) even for the much deeper observations of the UDF quasars (which extended to shorter wavelengths, but were at typical redshifts z = 4, translating to a comoving distance about 15% lower than z = 6.3), the corrected Strehl ratio, SM/SI, that was achieved ranged from 1.04 down to 0.40, depending on the band, with two of the four being at Strehl ratios of ~0.90. The lower Strehl ratios were no doubt caused by a combination of factors, including not only the imperfections in the PSF of the HST and distortions across the chip and light path of individual images, but also factors intrinsic to the QSO such as the host galaxy. This is why in our paper, even though theoretically the observations of the HUDF quasar could probe to α ~ 0.66, in practice the constraint that could be set was only α = 0.65 (see Fig. 5 in Christiansen et al. 2011). On the basis of our experience, we believe it is likely that a similar statement can be made for the observations examined by Tamburini et al. (2011).
It is worth mentioning that with current telescopes a second method of measuring possible effects of spacetime foam is becoming available. This is through the use of interferometry, e.g., by using the VLTI. As can be seen in Fig. 1, the VLTI would have
a significant advantage in resolution over any optical-IR telescope, simply because its longest baseline is ~ factor 20 longer than the largest telescope currently in use or under construction. Moreover, it would not suffer from some of the problems we have noted in the HST observations, namely undersampling. As well, since interferometers are very effective spatial filters the effect of the quasar’s host galaxy would also be minimized. We therefore believe that the best way to probe the α ~ 0.7 regime is with interferometers.
We should point out that time lags from distant pulsed sources have also been posited as a possible test of quantum foam models. But, as explained in Christiansen et al. (2011), the new Fermi Gamma-ray Space Telescope results (Abdo et al. 2009) only exclude models with α < 0.3.
5. Summary
We have reviewed the theoretical basis for expecting halos due to spacetime foam, and also the correct distance measure. We have shown explicitly that, while we agree with the basic result of Tamburini et al. (2011) that current observations with HST show no evidence for quantum gravity, as shown in our previously published paper Christiansen et al. (2011), we cannot agree with the resulting constraint they placed on models of quantum gravity. Because their calculations overstated the size of quantum foam induced halos of distant quasars by a factor 20, their limit for α, is also overstated by a minimum of Δα = 0.021. Based on our experience with HST data, we also believe – but cannot verify (because of the lack of documentation in Tamburini et al. 2011) – that even this resulting level (α = 0.66) cannot be reached because of details specific to each observation, including the variation of the PSF of HST with position on the chip, the undersampling of the PSF by every instrument on HST, as well as the host galaxy of the quasar.
Acknowledgments
This work was supported in part by the US Department of Energy under contract DE-FG02-06ER41418.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Nature, 462, 331 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Christiansen, W., Ng, Y. J., & van Dam, H., 2006, Phys. Rev. Lett. 96, 051301 [Google Scholar]
- Christiansen, W., Ng, Y. J., Floyd, D. J. E., & Perlman, E. S. 2011, Phys. Rev. D, 83, 084003 [Google Scholar]
- Hogg, D. W. 2000, unpublished [arXiv:astro-ph/9905116] [Google Scholar]
- Lieu, R., & Hillman, L. W. 2003, ApJ, 585, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, Y. J. 2003, Mod. Phys. Lett. A, 18, 1073 [Google Scholar]
- Ng, Y. J., Christiansen, W., & van Dam, H. 2003, ApJ, 591, L87 [Google Scholar]
- Ragazzoni, R., Turatto, M., & Gaessler, W. 2003, ApJ, 587, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Steinbring, E. 2007, ApJ, 655, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Tamburini, F., Cuofano, C., Della Valle, M., & Gilmozzi, R. 2011, A&A, 533, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheeler, J. A. 1963, in Relativity, Groups and Topology, ed. B. S. DeWitt, & C. M. DeWitt (New York: Gordon and Breach), 315 [Google Scholar]
All Figures
 |
Fig. 1 The detectability of various models of foamy spacetime for existing and planned telescopes. We show the diagonal tracks for halo size δψ for an unresolved, z = 6.3 source, using the comoving distance [Eq. (5), dashed lines], naive application of the luminosity distance [i.e., not redoing the integral I(z,α) as per Eq. (9), in dotted lines], and correct application of the luminosity distance (dash-dot lines). Tracks are shown for α = 0.6,2/3, and N = 1.8. See Sects. 2, 3 for discussion. It appears to us that Tamburini et al. (2011) used the phase uncertainty Δφ = 2πδψ as a measure of halo size, which would exaggerate the expected halo size by nearly an order of magnitude. This displacement would make it appear that quantum foam may be easily tested by HST imaging, which it is not. |
| In the text | |
 |
Fig. 2 Expected Strehl ratio as a function of redshift (top) and wavelength (bottom). In both plots, we assume α = 2/3 and N = 1.8. In the top figure we examine the change in Strehl ratio expected for a point source with varying redshift, z, for an observed wavelength of 400 nm. In the bottom plot, we specifically show the case of a z = 6.3 quasar, as examined by Tamburini et al. (2011), for an observed wavelength of 400 nm. As in Fig. 1, the dashed line refers to the use of comoving distance, dotted line refers to the naive use of luminosity distance, and dash-dot line refers to the treatment in Eq. (9). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


