| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201117372 | |
| Published online | 21 November 2011 | |
Automatic stellar spectra parameterisation in the IR Ca ii triplet region
1
Université de Nice Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur,
Cassiopée UMR 6202,
BP 4229,
06304
Nice,
France
e-mail: georges.kordopatis@oca.eu
2
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
3
Johns Hopkins University, Baltimore, MD, USA
Received: 30 May 2011
Accepted: 19 September 2011
Context. Galactic archaeology aims to determine the evolution of the Galaxy from the chemical and kinematical properties of its individual stars. This requires the analysis of data from large spectroscopic surveys, with sample sizes in tens of thousands at present, with millions of stars being reached in the near future. Such large samples require automated analysis techniques and classification algorithms to obtain robust estimates of the stellar parameter values. Several on-going and planned spectroscopic surveys have selected their wavelength region to contain the IR Ca ii triplet (~λλ 8500 Å) and the work presented in this paper focuses on the automatic analysis of such spectra.
Aims. We aim to develop and test an automatic method by which one can obtain estimates of values of the stellar atmospheric parameters (effective temperature, surface gravity, overall metallicity) from a stellar spectrum. We also explore the degeneracies in parameter space, estimate the uncertainties in the derived parameter values and investigate the consequences of these limitations for achieving the goals of galactic archaeology.
Methods. We investigated two algorithms, both of which compare the observed spectrum to a grid of synthetic spectra, but each uses a different mathematical approach for finding the optimum match and hence the best values of the stellar parameters. Our investigation of these algorithms’ robustness can be widely applied because it amplifies the main problems that the other methods can encounter. The first algorithm, MATISSE, derives the values of each stellar parameter through a local fit to the spectrum such that each pixel in wavelength space is treated separately. The sensitivity of the flux at each wavelength to the value of a given stellar parameter is determined from the synthetic spectra. The observed spectrum is then projected using these sensitivity vectors to give an estimated value of the stellar parameters. This value depends on finding the true minimum in the fit and the algorithm must avoid being trapped in false local minima. The second algorithm, DEGAS, uses a pattern-recognition approach and consequently has a more global vision of the parameter space. The best-fit synthetic spectrum is derived through a series of comparisons between the observed and synthetic spectra, summed over wavelength pixels, with additional refinements in the set of synthetic spectra after each stage, i.e. a decision tree.
Results. We identified physical degeneracies in different regions of the H − R diagram: hot dwarf and giant stars share the same spectral signatures. Furthermore, it is very difficult to determine an accurate value for the surface gravity of cooler dwarfs. These effects are intensified when the lack of information increases, which happens for low-metallicity stars or spectra with low signal-to-noise ratios (SNRs). Our results demonstrate that the local projection method is preferred for spectra with high SNR, whereas the decision-tree method is preferred for spectra of lower SNR. We therefore propose a hybrid approach, combining these methods, and demonstrate that sufficiently accurate results for the purposes of galactic archaeology studies are retrieved down to SNR ~ 20 for typical parameter values of stars belonging to the local thin or thick disc, and for SNR down to ~50 for the more metal-poor giant stars of the halo.
Conclusions. If unappreciated, degeneracies in stellar parameters can introduce biases and systematic errors in derived quantities for target stars such as distances and full space motions. These can be minimised using the knowledge gained by thorough testing of the proposed stellar classification algorithm, which in turn lead to robust automated methods for the coming extensive spectroscopic surveys of stars in the Local Group.
Key words: stars: fundamental parameters / stars: abundances / techniques: spectroscopic / methods: data analysis
© ESO, 2011
1. Introduction
Understanding the formation and evolution of the Milky Way Galaxy from the properties of its long-lived constituent stars (also known as the field of galactic archaeology) requires the collection of photometric and/or spectroscopic data for statistically significant samples of stars throughout the Galaxy. Photometry has the advantage of faster completion of deep wide-field/all-sky surveys but spectroscopy provides more accurate, detailed information about the target stars. For example, depending on the spectral resolution, one can more easily determine overall metallicities ([M/H]), the enhancements of α-elements with respect to iron (with respect to the Sun, [α/Fe]), individual elemental abundances and the fundamental stellar parameters effective temperature (Teff) and surface gravity (log g). The combination of these parameters allows one to derive line-of-sight distances through a comparison of a given star’s position on the H − R diagram and an appropriate set of theoretical isochrones. Full 6D phase-space coordinates can be determined if proper motions are available, which additionally constrain models of Galaxy formation and evolution.
The wavelength range around the IR Ca ii triplet is more and more frequently used in studies of galactic archaeology. The IR Ca ii triplet (λλ8498.02, 8542.09, 8662.14 Å) lines are strong for most stellar spectral types and luminosity classes, as well as for very metal-poor stars (see, for example Zwitter et al. 2004; Wilkinson et al. 2005), providing ideal features for a robust determination of the star’s radial velocity. The usefulness of this wavelength range goes beyond line-of-sight kinematics, because there are numerous absorption lines from many species, including iron and several α-elements (Ca ii, Si i, Mg i) and these remain visible even at relatively low spectral resolution and low signal-to-noise ratio (SNR1). The pattern of the ratios of these α-elements to iron can be used to trace the star formation time-scale in the parent system owing to distinctive roles played by the supernovae of different type (and explosion timescale) in creating and ejecting the different elements. In addition, an estimate of overall metallicity can be derived from empirical calibrations between metallicity ([M/H]) and the equivalent widths of the Ca ii triplet (Battaglia et al. 2008; Starkenburg et al. 2010; Fulbright et al. 2010). Furthermore, Paschen lines (for example λλ8502.5, 8545.4, 8598.4, 8665.0, 8750.5 Å) are visible for stars hotter than spectral type G3. The Mg i (λλ8807 Å) line, which is a useful indicator of surface gravity (see Ruck & Smith 1993; Battaglia et al. 2011), is also visible, even in spectra of low SNR. Finally, lines from molecules such as TiO and CN can be seen in spectra of the cooler stars.
The collection of very large samples of spectroscopic data to undertake studies in galactic archaeology has become feasible in recent years. For example, multifiber instruments such as the GIRAFFE/FLAMES spectrograph, mounted on Kueyen, the second-unit telescope of the Very Large Telescope (VLT) of the European Southern Observatory (ESO) allows spectra of more than a hundred objects to be obtained at a time with adequate SNR (typically higher than ~20) after only a few hours of exposure time. The first galactic archaeology survey to use the IR Ca ii triplet region has been the RAdial Velocity Experiment survey (RAVE, λλ8410−8795 Å, see Steinmetz 2003). This targets bright (limit of I ~ 13) stars and uses the 6dF multi-object spectrograph on the UKSchmidt telescope with a resolution of R = λ/Δλ ~ 7500; the RAVE project has already collected more than four hundred thousand spectra. In addition, several studies of the stellar populations of the Milky Way and its satellite dwarf galaxies have been conducted with the FLAMES multifiber spectrograph of ESO, using instrumental setups centred on the IR Ca ii triplet (specifically, the LR8 and HR21 setups). The series of papers related to the ESO large programmes DART (Tolstoy et al. 2006; Battaglia et al. 2006, 2011) and that of Gilmore et al. 171.B-0520(A) (see Wyse et al. 2006; Koch et al. 2007, 2008, and references therein) are good examples of the use of the IR Ca ii triplet for galactic archaeology. Furthermore, in the near future the ESA Gaia mission will collect several tens of millions of spectra with its Radial Velocity Spectrometer (RVS, Wilkinson et al. 2005), at a spectral resolution R ~ 11500 and two different samplings – 0.02453 nm and 0.07359 nm (effective resolution of ~7000) – depending on the brightness of the targets.
Despite this extensive use of the IR Ca ii triplet region and its previously mentioned advantages, the determination of the values of stellar atmospheric parameters from low- to medium-resolution spectra in this wavelength domain is far from trivial. In particular, as we will see below, there exists a strong degeneracy between the effective temperature and the surface gravity, in that varying either produces similar changes in the normalised stellar flux of several spectral features. This degeneracy can lead to the misclassification of dwarf stars as giant stars, and vice versa, a problem that becomes more severe for low-metallicity stars. This misclassification obviously creates errors in the derived stellar distances based on the estimated values of the atmospheric parameters. The ability to mitigate this degeneracy must be built-in to the automated methods of stellar parameter determination and that is the only feasible way of dealing with the massive datasets produced by the coming galactic archaeology surveys.
The goal of this paper is to show which astrophysical information can be retrieved from spectra observed around the calcium triplet. We investigate the performances of two methods of automated estimation of the values of stellar parameters based on very different mathematical approaches, which allows us to describe the main problems encountered in this spectral region. As a specific example of the application of these two algorithms, we consider the case of spectra obtained with the LR8 setup of FLAMES (8206–9400 Å, R ~ 6500, sampling = 0.2 Å). The spectra obtained using the other instruments and/or setups mentioned above (RAVE – RVS – FLAMES/HR21) have either broader wavelength ranges or higher spectral resolutions, and each of these provides more information that can help to disentangle some of the degeneracies. Consideration of the degeneracies resulting from spectra obtained with the LR8 setup will therefore cover those likely to result from the other setups.
The structure of this paper is as follows: in Sect. 2 we introduce the two methods whose performances we test, and in Sect. 3 we explain how the synthetic spectra used as training and testing sets have been computed. In Sect. 4 we present the performances that are achieved by each of the two applied algorithms and present the final adopted strategy for the derivation of the values of the stellar atmospheric parameters. Section 5 is dedicated to the application of the method to real spectra, dealing with errors in the derived parameter values that are introduced by uncertainties in the radial velocity and in the continuum normalisation. Finally, in Sect. 7 we discuss the effects of the errors in the parameter determinations on the science goals of galactic archaeology.
2. Automatic parameter estimation methods
The parameter estimation problem consists in finding the stellar atmospheric parameters (mainly effective temperature, surface gravity, global metallicity and individual chemical abundances) that define a synthetic spectrum that is an optimal fit to an observed spectrum. This estimation cannot be made analytically, because of the complexity of the theoretical spectra, which involve the very complex physics included in stellar model atmosphere and spectral line formation theory. As a consequence, the stellar spectra parameterisation has to be performed by using synthetic spectra grids which span the parameter space that we are concerned with here.
We point out that we favour in our study parameter estimations from synthetic spectra grids rather than grids of real observed stars, mainly because a sufficiently accurate parameterisation of large samples of different types of stars does not exist. Therefore, the isolation of flux variations caused by variations of only one of the atmospheric parameters cannot be easily performed, which is different from synthetic spectra.
The main problems encountered by the different automated estimation methods are caused by the possible non-linearity of the model spectra and the non-convexity of the distance function, which quantifies the difference between a model and the data. On one hand, a change in the atmospheric parameters can induce non-linear variations of the spectral flux, which is more important for large-scale parameter variations: two sets of parameters, distant in parameter space, can result in very similar spectra. On the other hand, the flux changes caused by the variation of a given parameter, for instance, the effective temperature, can be very similar to those induced by another parameter, usually the surface gravity or the metallicity. Therefore, secondary minima and multiple solutions to the stellar spectra fitting problem may exist. Parameter degeneracy is usually more severe when the available information about the parameters decreases: e.g. with a more narrow spectral range, lower spectral resolution, lack of spectral signatures, and so on. In addition, secondary minima can also be artificially generated by noise disturbing the distance function.
As presented in Bijaoui et al. (2010), several methods exist in the literature for the automatic parameter estimation from stellar spectra. The methods can be separated into i) solving an optimisation problem (e.g. minimum distances, Nelder-Mead algorithm, Gauss-Newton algorithm); ii) optimising a projection on given vectors (e.g. principal component analysis, MATISSE algorithm, penalized χ2); or iii) as a classification problem (e.g. artificial neural networks, support vector machines, decision trees).
Optimisation and projection algorithms usually rely either on the convexity of a distance function or the linearity of the models. Nevertheless, a local parameter space treatment is sometimes considered to minimise the failure of these conditions. On the other hand, classification algorithms tackle the parameterisation problem from a completely different point of view: the pattern recognition one. This different approach can have many advantages in severe conditions of parameter degeneracy.
As the work of this paper shows, each method has its optimal application field, and a combination of algorithms can be necessary for achieving the best results. We will illustrate the difficulties that we encountered when performing the stellar parameterisation of IR Ca ii triplet region low-resolution spectra. To do this, we will apply two different parameterisation methods: a projection algorithm, MATISSE (Recio-Blanco et al. 2006) and a classification method, DEGAS (Bijaoui et al. 2010), based on an oblique k-d decision tree. Those two algorithms, which are representative of two very different mathematical approaches, exemplify the main problems that the other methods can encounter when dealing with this kind of spectra.
2.1. The MATISSE method
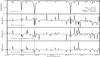 |
Fig. 1 Illustration of the MATISSE basis functions. For every set of parameters θi, corresponding to a spectrum in a grid of synthetic spectra, a set of Bθ(λ) was computed. Here, we can see the computed BTeff(λ) functions (and the corresponding synthetic spectrum) for a star with Teff = 5250 K, log g = 4.5, [M/H] = −0.75 dex, [α/Fe] = 0.3 dex. For clarity we represent only a part of the wavelength range in the plot. The strongest features in the spectrum (top panel), identified with dashed vertical lines, correspond to the Ca ii triplet. In the second row we show the BTeff(λ) computed with a direct inversion of the correlation matrix, whereas the last two panels show the BTeff(λ) functions computed with the Landweber iterative algorithm, imposing a coefficient of correlation between the input and the output parameters of 0.97 and 0.80, respectively. As described in Sect. 2.1, the smaller the coefficient, the less weight is given to the second-order variations of the spectral flux. The spectral analysis can therefore be optimised according to the quality of the spectrum, which is typically quantified in the signal-to-noise ratio. |
The MATISSE algorithm (MATrix Inversion for Spectral SynthEsis) is a local multi-linear regression method. We briefly recall now the basic equations of the method, but we encourage the reader to review Recio-Blanco et al. (2006) and Bijaoui et al. (2008) for a more comprehensive description.
MATISSE estimates a 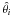 stellar atmospheric parameter (Teff, log g, [M/H]) by projecting the observed spectrum O(λ) on a particular vector Bθ(λ) associated to a theoretical θi parameter, as follows:
stellar atmospheric parameter (Teff, log g, [M/H]) by projecting the observed spectrum O(λ) on a particular vector Bθ(λ) associated to a theoretical θi parameter, as follows: 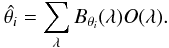 (1)These vectors, called Bθ(λ) functions hereafter, are computed during a learning phase from a library of synthetic spectra that cover the same wavelength range and have the same spectral resolution and wavelength sampling as the observed spectra. They relate in a quantitative way the pixel-pixel flux variations in a spectrum to a given variation of the θi parameter. If the Bθ(λ) are orthogonal, the effects from each parameter affect the spectrum in a different way, and therefore the atmospheric parameters are derived accurately. When this is not the case, possible degeneracies in parameter space can occur, which cause a correlation of the parameter errors. The Bθ(λ) functions are computed from an optimum multi-linear combination of theoretical, synthetic spectra S(λ), as follows:
(1)These vectors, called Bθ(λ) functions hereafter, are computed during a learning phase from a library of synthetic spectra that cover the same wavelength range and have the same spectral resolution and wavelength sampling as the observed spectra. They relate in a quantitative way the pixel-pixel flux variations in a spectrum to a given variation of the θi parameter. If the Bθ(λ) are orthogonal, the effects from each parameter affect the spectrum in a different way, and therefore the atmospheric parameters are derived accurately. When this is not the case, possible degeneracies in parameter space can occur, which cause a correlation of the parameter errors. The Bθ(λ) functions are computed from an optimum multi-linear combination of theoretical, synthetic spectra S(λ), as follows: 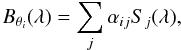 (2)where the αij factor is the weight associated with each synthetic spectrum Sj(λ) to retrieve the
(2)where the αij factor is the weight associated with each synthetic spectrum Sj(λ) to retrieve the 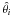 parameter. To compute these weights during the learning phase, Eq. (1) is applied to a subset of synthetic spectra. Accordingly, we obtain by combining Eqs. (1) and (2):
parameter. To compute these weights during the learning phase, Eq. (1) is applied to a subset of synthetic spectra. Accordingly, we obtain by combining Eqs. (1) and (2): 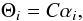 (3)where C = [cjj′] is the correlation matrix between Sj and Sj′, and Θi as well as αi the vectors of the parameters θi and the weights αij for all considered spectra. The weights αij are then computed by inverting the correlation matrix C.
(3)where C = [cjj′] is the correlation matrix between Sj and Sj′, and Θi as well as αi the vectors of the parameters θi and the weights αij for all considered spectra. The weights αij are then computed by inverting the correlation matrix C.
We have as many Bθ(λ) functions as there are spectra in the library of synthetic spectra. Each of them is computed using a small parameter range, for which we assumed the parameter variations to have a linear effect on the spectral flux variations. In practice, to converge to a parameter sub-space, one can use either generic 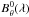 functions, or impose a priori the Bθ(λ), if a first estimation of the parameters is available2. When applying Eq. (1) to an observed spectrum, the method iterates for as long as the derived parameters are not included in the considered parameter sub-space for which the Bθ(λ) functions were computed. Usually, the final convergence is attained after a few iterations.
functions, or impose a priori the Bθ(λ), if a first estimation of the parameters is available2. When applying Eq. (1) to an observed spectrum, the method iterates for as long as the derived parameters are not included in the considered parameter sub-space for which the Bθ(λ) functions were computed. Usually, the final convergence is attained after a few iterations.
Here, the MATISSE method deals with normalised spectra and consequently all the necessary information for deriving the atmospheric parameters is provided by the spectral lines, i.e. their relative strengths. This strength changes according to the spectral type, the luminosity class and the metal content of the stars. In noiseless spectra and when the synthetic spectra perfectly match real stellar spectra, all astrophysical information (i.e. spectral lines) can be taken into account during the training phase of MATISSE. Nevertheless, for noisier spectra or if there is a mismatch between the observed and the synthetic stellar spectra, it is better to consider only the most relevant features, and give less weight to second-order variations.
The possibility of identifying a specific subset of the spectral signatures that are to be used for an atmospheric parameter derivation, which is a particular feature of MATISSE, allows us to adopt an optimised strategy according to the SNR and the type of the star, and therefore to optimise the analysis according to the quality of each spectrum. This optimisation is achieved when computing the Bθ(λ) functions, and more precisely while inverting the correlation matrix C of Eq. (3). A direct inversion would take into account all the n-order variations caused by the parameters. If one only considers the first order variations of the spectral flux though, one has to approximate the inverse of C. The degree of approximation can be controlled by using an iterative algorithm, such as that of Landweber (Landweber 1951). In that case, one can impose a correlation coefficient between the input and the output parameters to be equal to the desired degree of approximation. The higher the factor of correlation, the lower the degree of approximation. A correlation coefficient of one would be similar to a direct inversion.
In practice, the correlation matrix can sometimes be ill-conditioned, and can therefore imply many near-zero eigenvalues. The Landweber algorithm adapts the inversion to the matrix conditioning, in the sense that the first eigenvectors are inversed during the first iterations, and the inversion of the smallest ones need more iterations to be accomplished. The iteration number is linked with the correlation coefficient cited above.
We took the grid of the synthetic spectra described in Sect. 3.1, stopped the iterations for the different values of correlations of 0.75, 0.80, 0.90, 0.95 and 0.98, and computed the Bθ(λ) functions with the respective approximations of C-1. This is illustrated in Fig. 1, where we plot the same BTeff(λ) function computed with different correlation factors. As we notice in this figure, all minor features of the spectrum are given a very low weight for a correlation factor of 0.80 (bottom panel of Fig. 1). These approximated Bθ(λ) functions are fully justified as long as the spectra are of low quality, where these minor features are anyway lost in the noise.
Application of the various approximated Bθ(λ) functions on noisy synthetic spectra allowed us to select the most suitable combination, as a function of spectral type, metallicity, and SNR (see Sect. 4.1).
2.2. DEGAS: an oblique k-d decision-tree method
In the limit of the sampling precision, the parameter estimation is a recognition problem. The grid of synthetic spectra can be treated as a known set of patterns among which we aim to identify the observed spectra. In the learning phase, the recognition rules are established using the grid of theoretical spectra.
Decision trees are commonly used for data mining (Quinlan 1993). At each tree node, a decision is taken to split the data subset into two or more subsets. The leaf level corresponds to the identified classes. A k − d tree is a basic space-partitioning structure in a k-dimensional space (in our case, k = 3, Teff, log g and [M/H]). The decisions result from the projection of the observations on a node vector. Classical, or axis-parallel decision trees, check only one variable at each node. In the particular case of oblique decision trees, the node vectors (called Dn hereafter) are obtained from a linear combination of the structural features (i.e. the atmospheric parameters), resulting in a simpler and more accurate tree (White 2008).
The DEGAS (DEcision tree alGorithm for AStrophysics) algorithm is an oblique k-d decision tree, for which a preliminary version has already been presented in Bijaoui et al. (2010). The recognition rules at each node are built during the learning phase as follows:
-
1.
The mean vector M of the flux values per pixel is computed.
-
2.
For each spectrum Sj associated to the node, we calculate the scalar product cj = Sj·M. Let
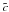 be the median value of cj.
be the median value of cj. -
3.
The data are bisected into two subsets, T1 and T2, according to the following criteria: Sj belongs to the subset T1 if
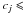
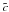 Sj belongs to the subset T2 if cj >
Sj belongs to the subset T2 if cj > 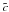 .
. -
4.
The mean vectors M1 and M2 of each subset are then computed, and the difference vector D = M1 − M2 is determined.
-
5.
According to the Huygens theorem, the best separation between T1 and T2 corresponds to the case for which the dispersions around M1 and M2 are minimal, which is when M and D are parallel. Indeed, we examined the variation V of the dispersions that resulted from spectra exchange between the two sets T1 and T2. Because the V expression introduced the vector D, we chose to get M and D parallel in order to maximise V. This dramatically improved the separation compared to the use of M. Hence, in practice, if the angle between M and D is too wide (correlation coefficient smaller than 0.999), we iterate until convergence, re-separating the data by the hyperplane defined by D (going back to step 2, replacing M by D).
Once this procedure has converged for a particular node n, we determine the final projection node vector Dn, which will display the features that allow one to separate the data at that node, and the final median value 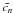 of cj = Sj·Dn.
of cj = Sj·Dn.
In this way, the recognition tree with log2(N) levels is built, where N is the number of spectra of the training grid. At the lowest level nodes of the tree, the leaves, only one training spectrum remains associated with each node. During the application phase, the target data Oi passes through all levels of the recognition tree, and a template is associated to it.
Nevertheless, noise can induce possible misclassifications. At each node one has to take into account that the projection coefficient ci = Oi·Dn is distributed according to a Gaussian law, defined for the entire real axis. So, theoretically both branches can be chosen, and the algorithm should fully explore the decision tree. This would lead to an inefficient method. To allow the assignation of a probability to each of the directions, we chose to replace the Gaussian distribution by an Epanechnikov kernel, which corresponds to a truncated parabola. Let us consider 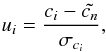 (4)where
(4)where 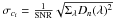 . If
. If 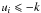 we decide that the correct direction is 1. If
we decide that the correct direction is 1. If 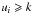 direction 2 is chosen. If −k < ui < k both directions are considered. Owing to the threshold, generally only one direction is chosen, and in the end only few leaves are selected.
direction 2 is chosen. If −k < ui < k both directions are considered. Owing to the threshold, generally only one direction is chosen, and in the end only few leaves are selected.
After scanning all nodes, a subset of synthetic templates is selected, and the distances of the templates from the observed spectrum are computed. Then, a weighted mean is evaluated on the parameters taking into account these distances, setting 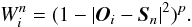 (5)The value p of the polynomial exponent is fairly arbitrary. If the noise is important, the distances between the selected templates and the observed spectrum are quite similar, and therefore a strong exponent is needed to put more weight to the most similar solution. We tested several values (p = 16, 32, 64, 128) on a set of noisy synthetic spectra and decided to use p = 64 throughout.
(5)The value p of the polynomial exponent is fairly arbitrary. If the noise is important, the distances between the selected templates and the observed spectrum are quite similar, and therefore a strong exponent is needed to put more weight to the most similar solution. We tested several values (p = 16, 32, 64, 128) on a set of noisy synthetic spectra and decided to use p = 64 throughout.
3. Creating the training and testing spectroscopic set
As noted earlier, most automatic spectral analysis methods, e.g. artificial neural networks or maximum likelihood algorithms, require a library of synthetic or observed spectra with well-known parameters for their learning phase. These reference spectra have to cover the whole parameter space Teff, log g, [M/H] where the selected targets are expected. No available observed libraries with those characteristics that covered our wavelength range with sufficiently accurate parameters were available in our case. We therefore chose to compute a synthetic library to fulfil our objectives.
3.1. Grid of synthetic spectra for the learning phase.
Atmospheric parameters of the synthetic spectra of the learning grid.
A library of synthetic spectra spanning the parameter space as detailed in Table 1 was computed using MARCS model atmospheres (Gustafsson et al. 2008) and the Turbospec code (Alvarez & Plez 1998, and further improvements by Plez). We assumed a coupling between the overall metallicity and the α-element abundances3 according to the commonly observed enhancements in metal-poor galactic stars. We considered
-
[α/Fe] = 0.0 dex for 0.0 ≤ [M/H] ≤ +1.0 dex
-
[α/Fe] = +0.1 dex for [M/H] = −0.25 dex
-
[α/Fe] = +0.2 dex for [M/H] = −0.50 dex
-
[α/Fe] = +0.3 dex for [M/H] = −0.75 dex
-
[α/Fe] = +0.4 dex for [M/H] ≤ −1.0 dex.
Each spectrum was computed assuming hydrostatic and local thermodynamic equilibrium (LTE), covering the wavelength range 8390–8860 Å with a wavelength step of 0.02 Å. For stars with 3.5 < log g < 5.0 (cgs units), plane-parallel models were used, with a microturbulence parameter ξ = 1 km s-1. For giant stars (log g < 3.0), spherical symmetry, with ξ = 2 km s-1 was preferred. These models, for which the sphericity effects may be considerable for low gravities (see Heiter & Eriksson 2006), have been calculated for a mass of 1 M⊙. The final library contains 2905 spectra of 23501 pixels. Let us note that a few models are missing in the synthetic library owing to the approach to the Eddington flux limit or poor convergence, as described in Gustafsson et al. (2008).
This paper deals with spectra that will be obtained with the LR8 setup of FLAMES (Pasquini et al. 2003). Therefore, this library had to be adapted to the observational setup. The spectra were restricted to the wavelengths 8400–8820 Å, which contain all the predominant lines, and we trimmed out spurious effects in the CCDs (border effects, presence of a glow in the red part) and possible sky residuals. For this reason, the range between 8775 Å and 8801 Å, which contains few iron lines and possibly has important sky residuals, was also removed. The spectral feature corresponding to Mg i around ~8807 Å was kept though.
The spectra were then convolved with a Gaussian kernel and re-binned to match the sampling and resolution of the LR8 spectra. In addition, eight re-sampled pixels4 corresponding to the cores of the strong Ca ii lines were also removed from the spectra (two pixels for the first line, and three for the other two lines, corresponding to 0.8 and 1.2 Å, respectively), because a disagreement is expected between the synthetic spectra and the true ones for these pixels. Indeed, the cores of strong lines have a significant contribution from the upper layers of the stellar atmospheres, where LTE, one of the assumptions of the model atmospheres which were used, is not applicable any more. Removing them will accordingly avoid possible biases to the final parameter extraction. We checked this with the tests presented in Sect. 4. The final spectrum contains in the end only 957 pixels with a sampling of 0.4 Å.
3.2. Line-list calibration
In order to compute realistic synthetic spectra, it is necessary to know the atomic and the molecular parameters of the existing lines as accurately as possible. Whereas central wavelengths and excitation potentials are fairly well established for most of the atomic lines, the probabilities of electronic transitions (illustrated by the oscillator strengths log gf) are more subject to uncertainties. The combination of a line-list, a set of model atmospheres and a spectral synthesis method has to be calibrated on standard stars of different spectral types to check the line-list quality and obtain reliable synthetic stellar spectra.
For that purpose, we used the set extracted from the VALD database5 in May 2009 (Kupka et al. 2000) as an initial atomic line-list and combined it with MARCS model atmospheres to reproduce the observed high resolution, high SNR spectra of the Sun (Brault & Neckel 1987) and Arcturus (Hinkle et al. 2003; Allende Prieto et al. 2004) as precisely as possible.
All radiative transfer computations were made assuming LTE and hydrostatic equilibrium, and therefore no effort was made to fit the cores of strong spectral features better (e.g. Ca ii triplet or Mg i line). Instead we removed the pixels corresponding to the cores of the Ca ii triplet as described in the previous section.
The VALD atomic line-list set was first modified, adopting the oscillator strength corrections by Gustafsson et al. (2008) for some lines. The molecular line-list includes ZrO, TiO, VO, CN, C2, CH, SiH, CaH, FeH and MgH lines with their corresponding isotopic variations (kindly provided by B. Plez). The adopted solar abundances were those of Grevesse (2008), except for CNO, in which case we used Asplund et al. (2005). In addition, we considered ξ = 1 km s-1 and Vsini = 2 km s-1. We then calibrated manually more than 250 lines to match the observed solar spectrum, checking that the overall χ2 between the synthetic template and the observed spectrum was decreasing with each adjustment.
In addition, roughly 50 lines were calibrated on Arcturus under the condition that this calibration did not increase the overall χ2 for the Sun. We also note that the calibration process did not consider a correction of the molecular bands, even though some incorrect minor features were noticed.
For Arcturus we used the parameters and the abundances of Smith et al. (2000): Teff = 4300 K, log g = 1.7, [M/H] = −0.6 dex, [α/Fe] = +0.3 dex, Vsini = 1.5 km s-1, macroturbulence parameter η = 5.2 km s-1 with a radial-tangential profile, and ξ = 1.7 km s-1. We note though that the observed spectrum of Hinkle et al. (2003) was already normalised, but had an imperfect normalisation around the second line of the Ca ii triplet, noticeable as clearly asymmetric wing strengths.
Finally, because of the fairly poor constraints on its atmospheric parameters, no line-list calibrations additional to those made from the Sun and Arcturus were made on Procyon A (spectral type F5-IV). Although we checked if the previously made calibrations were reproducing the Procyon observed spectrum correctly, which is available from the S4N library (Allende Prieto et al. 2004). As expected, we found that the overall fitting quality was improved compared to the computed spectrum using the non-calibrated line-list of VALD.
Relative errors of MATISSE at 70% of the error distribution.
3.3. Testing set
 |
Fig. 2 Input parameters for the testing set. The spectra were computed based on a catalogue of pseudo-stars requested from the website of the Besançon Galaxy model. |
In order to test the MATISSE and the DEGAS algorithms, we required a set of synthetic spectra that did not sit on the learning grid nodes. We used the specificities of the local Bθ(λ) functions of MATISSE associated with a synthetic spectrum S0(λ) with  parameters to compute a set of interpolated spectra. Indeed, the variations from a grid’s spectrum S0(λ) with
parameters to compute a set of interpolated spectra. Indeed, the variations from a grid’s spectrum S0(λ) with  parameters can be computed according to the following expression:
parameters can be computed according to the following expression: 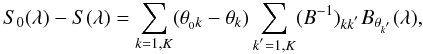 (6)where Bkk′ is the correlation matrix between the basis vectors, defined as
(6)where Bkk′ is the correlation matrix between the basis vectors, defined as 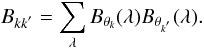 (7)We used Eq. (6) to compute a synthetic spectrum of the Sun, and compared it to the observed one. The spectra agreed well, validating in this way the interpolation routine.
(7)We used Eq. (6) to compute a synthetic spectrum of the Sun, and compared it to the observed one. The spectra agreed well, validating in this way the interpolation routine.
To test the methods efficiently, these interpolated spectra have to represent realistic cases, i.e. they have to follow a plausible H − R diagram. For that purpose, we made use of the Besançon model of the Milky Way (Robin et al. 2003), which returns atmospheric parameters of simulated stars towards a given line-of-sight. We queried from the website of the Besançon model6 simulated mock catalogues of stars towards the galactic bulge, the north galactic pole and towards intermediate latitudes (l = 245°,b = 45°) to model the range of stellar parameters encountered in different galactic stellar populations. 104 of these stars were selected randomly, to create our testing sample (see Fig. 2). For each of these pseudo-stars, two different metallicity values were considered to obtain a catalogue spanning the whole metallicity range: the one given by the model of Besançon, and another lowered by –0.75 dex. The 2 × 104 spectra of these pseudo-stars, were then interpolated from the learning grid using Eq. (6), at the sampling and resolution of the FLAMES LR8 spectra.
Finally, to test the robustness of the methods, four different values of white Gaussian noise (SNR ~ 10, 20, 50, 100 pixel-1) were used to degrade these spectra, raising the final number of testing spectra to 8 × 104.
4. Individual performances of the two methods
We considered that no photometric information is available for the stars whose spectra we analysed. We therefore aimed to explore the performances of each method without additional data. We recall that often this is not true. In particular, this will not be the case for the Gaia space mission, because the two spectrophotometers BP/RP together with astrometric information will provide a handful of information, constraining that way the allowed ranges for Teff and log g.
4.1. Performance of MATISSE
 |
Fig. 3 Dependence of the H − R diagram for spectra analysed with the MATISSE algorithm as a function of signal-to-noise ratio. The colour code, quantifying metallicity, is the same as in Fig. 2. As expected, stars with lower metallicities and hence less spectral information are those with the greatest scatter. |
 |
Fig. 4 Relative errors of the stellar parameters derived by MATISSE (left column), DEGAS (middle column), and the final adopted pipeline (right column), at 70% of the error distribution as a function of the signal-to-noise ratio. Intermediate temperature (5000 < Teff < 6000 K) thin disc (−0.25 < [M/H] < 0.5 dex) and thick disc (−1.5 < [M/H] < −0.25 dex) dwarf stars are represented as black diamonds and red triangles symbols, respectively. Halo giant stars (Teff < 6000 K, log g < 3.5, −2.5 < [M/H] < −1.25 dex) are blue squares. |
We ran MATISSE with the first solution found with the 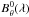 functions as input (i.e. without any a priori information) on the 8 × 104 synthetic spectra of the testing set described in Sect. 3.3. Figure 3 and Table 2 show, respectively, the evolution of the shape of the H − R diagram and the relative errors at 70 % of the error distribution, as a function of the SNR for different types of stars. In the left column of Fig. 4 we represent the evolution of the typical errors according to the SNR for thin disc (−0.25 < [M/H] < 0.5 dex) and thick disc (−1.5 < [M/H] < −0.25 dex) dwarf stars and halo giants (Teff < 6000 K, log g < 3.5, −2.5 < [M/H] < −1.25 dex). These values (also represented in the last lines of Table 2) were obtained for the above mentioned testing set and the best Bθ(λ) functions combination (see Sect. 2.1). Two main conclusions can be derived:
functions as input (i.e. without any a priori information) on the 8 × 104 synthetic spectra of the testing set described in Sect. 3.3. Figure 3 and Table 2 show, respectively, the evolution of the shape of the H − R diagram and the relative errors at 70 % of the error distribution, as a function of the SNR for different types of stars. In the left column of Fig. 4 we represent the evolution of the typical errors according to the SNR for thin disc (−0.25 < [M/H] < 0.5 dex) and thick disc (−1.5 < [M/H] < −0.25 dex) dwarf stars and halo giants (Teff < 6000 K, log g < 3.5, −2.5 < [M/H] < −1.25 dex). These values (also represented in the last lines of Table 2) were obtained for the above mentioned testing set and the best Bθ(λ) functions combination (see Sect. 2.1). Two main conclusions can be derived:
-
Good results are obtained down to SNR ~ 20 for spectra where a lot of spectral information is available, typically, metal-rich dwarfs. The errors increase with decreasing metallicity (see Table 2). For GV type stars (dwarfs, Teff > 5000−6000 K), with SNR ~ 50, the internal errors on Teff rise from 90 K for metal-rich ([M/H] > –0.5 dex) to 290 K for metal-poor stars (−1 < [M/H] < −2 dex). Errors on log g are increased from 0.15 dex to 0.50 dex, and for metallicity from 0.10 dex to 0.21 dex.
-
Two degeneracy regimes occur. The first, between the hot sub-dwarfs (Teff > 6000 K) and the giant branch, is caused by to the common spectral signatures shared by Teff and log g. The second concerns the cool dwarfs and originates in the poor constraints on log g available with this wavelength range and resolution.
These two degeneracies are mainly caused by the behaviour of the Ca ii lines (the strongest spectral signatures) for different spectral types. Indeed, considering that pressure dependence can be translated into approximate gravity dependences, the wings of the Ca ii lines grow proportionally to g1/3 for cool main sequence stars (see Gray 2008), but strongly depend on the Teff. For dwarfs with 3000 < Teff ≲ 5000 K, where no Paschen lines are developed, the only relevant spectral signatures concerning log g come from the weaker metallic lines which, depending on the SNR and the global metallicity of the star, can be lost in the noise.
On the other hand, parameter degeneracies (and also the secondary minima) that affect hot dwarfs involve very distant locations in parameter space. Indeed, if we compare the spectra of a star with Teff = 6500 K; log g = 4.5; [M/H] = −1.0 dex and another that is significantly cooler and more giant, with Teff = 5500 K; log g = 3.0; [M/H] = −1.5 dex (see Fig. 5), we can see that they are almost identical. Only the cores of the strong lines (calcium, magnesium) are different, and their wings differ weakly. In addition, the few Paschen lines that both spectra exhibit are almost identical (only Pa12, around 8750 Å, is significantly different). This additionally supports our removal of the cores of the Ca ii lines in our automated analysis. Indeed, our tests have revealed that avoiding the Ca ii line cores in the reference grid helped to decrease the number of secondary minima. The disagreement between the synthetic templates and the true spectra, in addition to the effect of noise on these line-core pixels, can induce important biases, because spectra with similar cores will have a lower overall χ2. The price to pay to avoid these biases is a bigger dispersion in the final parameter estimates. This effect becomes even more critical when the metallicity decreases, owing to the lack of spectral information.
The absence of distinct spectral signatures can also be seen from the angles between the Bθ(λ) functions at different regions of the H − R diagram. We recall that if the Bθ(λ) functions are perpendicular, the parameters can be perfectly derived, because they use different spectral signatures. For example, a star with Teff = 6500 K; log g = 4.5; [M/H] = −1.0 dex has an angle between Teff and log g of 33.4°, 66.5° between [M/H] and Teff, and finally 89.2° between log g and [M/H]. We can therefore expect a degeneracy between the Teff and log g determination, and a milder one between Teff and metallicity, as we noticed with our testing set.
On the other hand, for the cool dwarfs, inaccurate log g derivation is only caused by the lack of spectral sensitivity, and not because the spectral signatures are shared between the parameters. Indeed, for a star with Teff = 4500 K; log g = 4.5; [M/H] = −1.0 dex the angle between Teff and log g is 89.7°, between [M/H] and Teff is 82.9°, and finally between log g and [M/H] is 109.9°.
In terms of χ2 between the MATISSE parameter solution and the true reference values, the secondary minima for cool dwarfs lie close to the parameter space formed by Teff; log g; [M/H] and consequently MATISSE still derives accurate parameter estimates, even at low SNR. For hot dwarfs the low-SNR estimates are farther from the true parameter values, resulting in higher overall errors. Adding noise to the signal will accentuate this behaviour, increase the number of secondary minima, and hence decrease the accuracy of MATISSE.
 |
Fig. 5 Noise-free synthetic spectra showing the degeneracy in parameter space between a hot dwarf star (black, solid line) and a cool giant (red dotted line). The spectra differ significantly only at the cores of the strong lines and at Pa12 (~8750 Å), but their wings differ weakly. |
In addition, Fig. 3 shows that some stars are estimated to have log g > 5. This effect is more important for low-metallicity stars, but also affects metal-rich stars at low SNR. This effect, which is typical of the projection algorithms, appears because MATISSE may perform extrapolations in parameter space to obtain the atmospheric parameters. Indeed, the Bθ(λ) functions on which the spectra are projected, still attach too much weight to certain spectral signatures even when they are optimised to a spectral type and an SNR value, which enhances the sensitivity to noise. Of course, results lying outside the grid boundaries have to be considered as unreliable and need to be treated separately (see Sect. 4.4 for more details on how these values are finally treated).
The correlation of the parameter errors is non-negligible, as seen in Fig. 6, which illustrates again the effects of the non convexity and the degeneracies of the distance function. Indeed, we found the well-known Teff-[M/H] correlation as well as the correlation between log g − Teff. The correlation between log g and [M/H], however, is almost insignificant for metal-rich and intermediate-metallicity stars, down to SNR ~ 20.
 |
Fig. 6 Error correlations for MATISSE (left column) and DEGAS (right column) for spectra with SNR ~ 20. The colour code, which corresponds to the metallicity, is the same as in Fig. 2. The general shape of these figures shows the degeneracy between the atmospheric parameters. For higher SNRs the correlation slopes are similar, but less extended, because the errors are smaller. The specific properties of each analysis method lead to the somewhat different extension and dispersion of the correlations. |
Relative errors of DEGAS at 70% of the error distribution.
4.2. Performances of the DEGAS algorithm
Unlike MATISSE and its local Bθ(λ) functions, the DEGAS method allows a more global view of the parameter space, and therefore, it is less affected by local minima traps. Accordingly degradation of the parameter accuracies is slow with decreasing SNR (see Table 3 and the middle column of Fig. 4). The critical SNR value for which DEGAS gives better results than MATISSE is around SNR ~ 35. Above that value, DEGAS is incapable of inferring an appropriate interpolated parameter combination between the grid points (Fig. 7) because Eq. (5) assigns too much weight to the resulting leaves of the decision tree. However, the closest grid point (absolute minimum) is usually found. Of course this effect results in relatively higher errors compared to those of MATISSE. This feature cannot be improved without affecting the results at lower SNR.
 |
Fig. 7 Dependance of the H − R diagram structure recovered with the DEGAS algorithm as a function of the spectrum’s signal-to-noise ratio. The colour code is the same as in Fig. 2. |
 |
Fig. 8 Sensitivity to radial velocity errors for MATISSE (left) and DEGAS (right). The values at Vrad = 0 km s-1 correspond to the values found in Fig. 4. Additional errors caused by an incorrect Vrad correction are almost null as long as the Doppler shift remains lower than 7 km s-1. For lower SNR the robustness of the algorithms is higher, which has an almost negligible effect even for an extreme velocity error of Vrad = 15 km s-1. |
Nevertheless, even at higher SNR, the pattern recognition approach deals better with spectra having low metallities ([M/H] < −1 dex). For instance, at SNR ~ 50, a G-type giant with [M/H] < −2 dex is expected to have errors of 182 K, 0.43 dex, 0.22 dex for Teff, log g and [M/H], respectively. These accuracies are 35% better than those obtained with MATISSE. Furthermore, the same effect can be observed for KV metal-poor type stars, resulting in a (partial) resolution of the thickening of the cool part of the main sequence seen with MATISSE (Fig. 3).
DEGAS gives quite good results down to SNR ~ 20 for stars with [M/H] > −1 dex. Typical errors for giants are 121 K, 0.29 dex, 0.13 dex for Teff, log g and [M/H], respectively. These values are ~168 K, 0.30 dex, 0.14 dex for dwarfs, and hotter dwarfs have lower accuracies compared to cooler ones.
Let us stress though that an additional reason why this method gives smaller errors compared to MATISSE is that the derived parameter values cannot lie outside the grid boundaries. This is also illustrated when comparing the dispersion of the error correlation for the two algorithms in Fig. 6. However, the general shape of the correlations has not changed, as expected, because the physical degeneracies are impossible to separate for any of the methods.
4.3. Errors caused by the radial velocity estimation
The automated stellar parameterisation relies on a good radial velocity correction of the observed spectra to the rest frame where the synthetic templates are calculated. It is therefore necessary to test the robustness of each method in the case where the spectra are not perfectly at the rest frame.
To this purpose we used the random set of spectra presented in Sect. 3.3, with SNR ~ 100, 50, 20 and 10 pixel-1, and introduced four different values of Doppler shifts ( Vrad = 5, 7, 10 and 15 km s-1, corresponding to 1/3, 1/2, 2/3 and 1 pixel shift). We then ran the two algorithms with these spectra and checked the resulting error distribution for each parameter. In Fig. 8 we show the relative errors obtained for the different radial velocity shifts for an SNR = 50 and for both methods. The results show that the spectra need to be corrected to better than half a pixel (corresponding to a Vrad accuracy of less than ~7 km s-1) to obtain estimates that are still similar to those obtained for spectra at the rest frame. Most of the times, this condition is fulfilled, because the errors commonly obtained on Vrad for FGK stars at SNR ~ 20 in the LR8 setup are less than 5 km s-1 (see the companion paper Kordopatis et al. 2011b). However, the atmospheric parameter errors, induced by a non-perfect Vrad correction, tend to increase more rapidly when the metallicity decreases. This is because the few spectral signatures present in the signal have a relatively small equivalent width (the spectral lines are spread on only a few pixels), and even at high SNR their misplacement have a serious effect on the parameter estimations.
Furthermore, good estimates are obtained for both methods for shifts up to 2/3 of a pixel at any SNR for intermediate- to high-metallicity stars. We point out though that DEGAS is in general more stable than is MATISSE when dealing with spectra that are not in the rest frame, especially for metal-poor stars.
At lower SNR (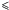 20) both algorithms are stable to Doppler shifts and show a similar behaviour. Indeed, for low-quality spectra the errors induced by noise dominate those arising from a poor radial velocity correction.
20) both algorithms are stable to Doppler shifts and show a similar behaviour. Indeed, for low-quality spectra the errors induced by noise dominate those arising from a poor radial velocity correction.
4.4. Summary: adopted strategy
We decided to set up a procedure that would combine the benefits of MATISSE (very good results in a local environment, easy interpretation) and DEGAS (global view and better tackling of the secondary minima problem). The MATISSE algorithm gives better results if there are no significant secondary minima in the distance function, because of the local application of its learning Bθ(λ) functions. In the particular case of low-resolution IR Ca ii spectra, this condition is achieved for data with an SNR value higher than ~35 and global metallicity [M/H] > −2.0 dex. Nevertheless, the use of 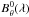 is not the optimal approach to obtain the best possible results. Indeed, the number of local minima tends to increase with noise and the lack of spectral signatures. Given the properties of the parameter space around the Ca ii region, the generic
is not the optimal approach to obtain the best possible results. Indeed, the number of local minima tends to increase with noise and the lack of spectral signatures. Given the properties of the parameter space around the Ca ii region, the generic 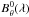 functions will not provide the absolute minimum and hence will accentuate the degeneracies. Therefore, to fully exploit the capabilities of MATISSE, we decided to use the results of DEGAS as an initial input. This operation reduces the effect caused by the secondary minima, and can therefore provide more accurate results (up to 50% accuracy improvement for Teff and log g).
functions will not provide the absolute minimum and hence will accentuate the degeneracies. Therefore, to fully exploit the capabilities of MATISSE, we decided to use the results of DEGAS as an initial input. This operation reduces the effect caused by the secondary minima, and can therefore provide more accurate results (up to 50% accuracy improvement for Teff and log g).
For lower SNR (less than 35) and very metal-poor stars, the non-convexity of the distance function is too severe to infer good results with a projection method such as MATISSE. The use of DEGAS is therefore preferred. Indeed, DEGAS can derive errors lower by 75% than those of MATISSE for a low-SNR metal-poor spectrum.
Finally, as seen in Figs. 3 and 7, because of the non-convexity of the distance function, both methods can return results in regions of the H − R diagram where no stars can exist. Removing these parameter combinations from the possible solution space will therefore reduce the degeneracies and increase the method accuracy. Based on the Y2 isochrones (Yi et al. 2001) of stars spanning ages from 0.25 Gyr to 15 Gyr and metallicities from −3 dex to +0.8 dex, we decided to exclude the Bθ(λ) functions and the grid points used for DEGAS, where no possible isochrones were nearby. In practice, to avoid too important astrophysical priors in the derived parameters, we removed only the templates with log g = 5 and Teff > 6250 K, those with Teff ≤ 4250 K and 4 ≤ log g ≤ 3 dex, as well as all stars with [M/H] ≤ −3 dex, Teff ≤ 4000 K and log g ≤ 4 dex. We checked in Sect. 5.2 that this selection did not introduce biases in the final results.
5. Final adopted pipeline
Based on the results and the discussion in the above sections, we adopted a final pipeline. This procedure took into account the following points:
-
The applied parameterisation method has to be chosen accordingto its optimal application conditions defined inSect. 4.4.
-
Spectra normalisation (when the data are not flux-calibrated) is coupled to the atmospheric parameter determination.
-
The parameterisation algorithms are optimised for a given SNR value, which implies a robust SNR measurement.
However, the SNR determination itself depends on the spectra normalisation and the atmospheric parameter estimation. The final adopted pipeline therefore iterates on the parameter estimation until convergence of the normalisation solution and the SNR measurement, as described in the following steps:
-
1.
A rough sigma-clipping, polynomial fit normalisation is performed and an initial value of the SNR is assumed that is constant for all the spectra (we adopted an intermediate value of SNR ~ 50). This will give us a first rough estimation of the parameters using DEGAS to compute a synthetic spectrum with the parameters of the first guess. Using this template, the SNR is estimated for the first time, as described in Sect. 5.1.
-
2.
DEGAS is re-applied with the newly found SNR values. The new atmospheric parameters are then used to compute a synthetic template and re-normalise the input spectrum. This step is repeated several times to obtain a normalisation as perfect as possible (see Sect. 5.2). Convergence is achieved when the continuum shape is unchanged compared to the previous iteration.
-
3.
The SNR is re-computed for the final normalised spectra. If its value is higher than 35 and the [M/H] value determined by DEGAS is higher then –2.0 dex, MATISSE is run with the set of Bθ(λ) functions corresponding to the spectral type and the SNR value. The results of DEGAS from the previous step are kept for low-SNR or very metal-poor stars.
-
4.
For other stars, the final atmospheric parameter estimations are obtained when the convergence of MATISSE is achieved. If the MATISSE results are beyond the parameter grid boundaries shown in Table 1, the results of DEGAS are taken. The final SNR is derived only at the end of this step, with a template corresponding to the adopted stellar atmospheric values.
Relative errors of the final adopted pipeline, at 70% of the error distribution.
5.1. Measurement of the signal-to-noise ratio
The SNR is estimated following the procedure described in Zwitter et al. (2008). First, the atmospheric parameter guesses obtained by a given method are used to obtain a synthetic spectrum with the same atmospheric parameters. The difference between the template and the observed spectrum is then computed, keeping only the pixels where the difference changes sign from the previous or the next adjacent pixel and has a relative flux close to 1. This selection criterion allows us to keep only the continuum pixels, where the difference is caused by pure noise, and avoids the selection of pixels that are affected by systematic effects (for example due to a bad template selection). This difference is then divided by the theoretical spectrum and the SNR estimate is obtained by taking the inverse of its standard deviation.
As we previously pointed out, the measurement of the SNR strongly depends on the normalisation and the synthetic template selection. In addition, the selection of the synthetic template depends on the accuracy of the results of the used method (selected Bθ(λ) functions for MATISSE or the considered leaves for DEGAS), which also depend on the SNR. The redundancy of the problem therefore requires several iterations before a convergence of the values can be achieved. For that reason, the SNR needs to be estimated several times during our procedure to obtain a good normalisation (see Sect. 5.2).
5.2. Normalisation effects
Because the parameter derivation is very sensitive to the relative depths of specific lines, a poorly-determined pseudo-continuum shape can have sizeable effects. Normalisation is therefore a matter of prime importance and special care must be taken. Comprehensive tests were made to minimise this effect as much as possible.
The final adopted procedure consisted of running DEGAS several times, renormalising the initially roughly normalised spectrum after each iteration. To accomplish this, we use a few consecutive iterations to fit the shape of the ratio between the interpolated spectrum and the observed spectrum with a fifth-order polynomial7 and with symmetric rejection criteria (clipping away points farther than 0.5σ). The continuum shape of the observed spectrum is then re-adjusted according to the shape of the fitted function.
 |
Fig. 9 Sensitivity of the recovered H − R diagram for simulated data to the spectrum signal-to-noise ratio using the final adopted pipeline. The colour code is the same as in Fig. 2. |
To test the robustness of our procedure, we performed various tests with the random spectra grid described in Sect. 3.3. We modified the spectral shape (and hence the continuum) up to 3% by multiplying the spectrum with either a slope, a third-degree polynomial, or a fifth-degree polynomial. The amplitude of 3% is considered to be a pessimistic case for roughly normalised spectra corrected for instrumental effects. The tests were also run on the perfectly normalised spectra, passing through the whole pipeline to verify that our procedure is not degrading the already perfectly normalised input spectra (see the left column of Fig. 4, Fig. 9 and Table 4). The results show that this strategy is quite rapidly converging to a stable solution which minimises the errors caused by normalisation independent of the deformation of the continuum. In addition, as we show in Fig. 10, a good re-normalisation is obtained even for the cool metal-rich stars. Indeed, in that case the large wings of the spectral lines and the huge amount of atomic and molecular lines can be a challenge to find the continuum. An unchanged continuum shape is achieved after a few iterations. The number of needed iterations depends on the SNR, the departure from the true continuum and the spectral type. Practically, this procedure is performed ten consecutive times and convergence is checked.
It can also be noticed that in some cases, this pipeline derives the parameters with even better accuracies than the better of the two individual methods (Tables 2–4). This is because the 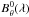 are not used any more, which better constrains the parameter sub-space, as already discussed in Sect. 4.4. Another factor that explains the better results is that the final adopted pipeline does not consider grid points in unphysical regions of the H − R diagram. Nevertheless, the extrapolation properties of MATISSE still derive stellar parameters with “unphysical” values in some cases, as seen in the two top plots of Fig. 9.
are not used any more, which better constrains the parameter sub-space, as already discussed in Sect. 4.4. Another factor that explains the better results is that the final adopted pipeline does not consider grid points in unphysical regions of the H − R diagram. Nevertheless, the extrapolation properties of MATISSE still derive stellar parameters with “unphysical” values in some cases, as seen in the two top plots of Fig. 9.
Finally, the method is robust to deformation of the continuum, with errors on Teff, log g and [M/H] obtained after the re-normalisation procedure almost identical (within 10%) with the errors obtained for perfectly normalised spectra.
 |
Fig. 10 Re-normalisation process for a cool metal-rich dwarf star. Plot A) shows in black the theoretical spectrum and in red the spectrum with a modified continuum (see Sect. 5.2), which is analysed with our method. The change applied on the input spectrum can be viewed in plot B) of this figure, where the ratio between the theoretical spectrum and the input is shown. A corrected continuum shape is obtained at the end of our pipeline, as can be seen in the two bottom plots (C) and D)). |
6. Application to observed spectra
 |
Fig. 11 Comparisons between the results of our pipeline and values found in the literature for the S4N (red crosses) and CFLIB (black dots) stellar spectral libraries. The error bars shown for the CFLIB spectra represent the dispersion of the parameter values found in the literature, when available. The red dashed diagonal lines, plotted for an easier interpretation of the results, represent errors of ± 250 K, 0.5 dex and 0.3 dex for Teff, log g and [M/H], respectively. Typical errors of our pipeline are represented in the upper left corner of each plot. |
The errors estimated in the previous sections and illustrated in Table 4 can be viewed as the expected relative errors of the method when one compares stars within a catalogue of observed stars. Nevertheless, differences between model spectra and real stellar spectra can potentially introduce systematic biases. Therefore we needed to test our pipeline with real data.
We attempted to recover the atmospheric parameters from spectra in observed stellar libraries. It was a challenge to find spectra that covered the same wavelength region with a sufficiently high resolution and good parameter estimates. Only two datasets were found: the S4N from Allende Prieto et al. (2004), and the CFLIB described in Valdes et al. (2004). We smoothed the spectra from both libraries with a Gaussian kernel to match our working resolving power and re-sampling, and applied the whole pipeline.
The S4N catalogue8 consists of a survey of 118 stars in the solar neighbourhood, therefore these stars are mostly metal-rich dwarfs. The covered spectral range is very broad (3620–9210 Å), observed in a single spectral setup at high-resolution (R ~ 50 000) and high SNR (>200). Nevertheless, only 68 spectra include our wavelength range without any inter-order gap. The effective temperatures for this catalogue were obtained using Strömgrem photometry and the (B − V) colour index with the Alonso et al. (1996, 1999) calibrations. Furthermore, these Teff were confirmed by fitting synthetic profiles of the Hα and Hβ lines, as described by Barklem et al. (2002) and are therefore considered reliable. In addition, the gravities published for these stars have been derived from the Hipparcos trigonometric parallaxes and are also very reliable. Nevertheless, one may expect differences between physical gravities and gravities obtained spectroscopically, especially for cool main-sequence stars, for which the isochrones give roughly the same value of log g (see Fig. 11). In addition, differences are expected for the determination of the metallicities. The narrow spectral range and the poor spectral signatures available around the IR Ca ii triplet cannot be compared to the plethora of lines present in the whole wavelength range of the S4N.
Biases and dispersions for the derived parameters of the S4N and CFLIB libraries.
Table 5 shows the biases and the dispersions between our derived parameters (plotted in Fig. 11 in red crosses) and the values found in Allende Prieto et al. (2004). We find that the biases for Teff, log g and [M/H] are reasonable but not negligible, of the order of ~−108 K, −0.21 dex and −0.08 dex, respectively. The dispersions are 145 K, 0.32 dex and 0.09 dex, respectively. Let us note though that the biases on [M/H] and log g disappear completely if we consider the published values derived only from the same wavelength range as we use here (strictly, the Gaia RVS wavelength range, with results kindly provided by C. Allende-Prieto, see Allende Prieto (2008) for a detailed description).
However, the S4N library alone is not sufficient to test our method fully. It does not cover the astrophysical parameter space well enough to fulfil our goals of testing our pipeline over the entire H − R diagram, and especially on intermediate and low-metallicity stars. The CFLIB library9 consists of ~900 high SNR spectra that cover the entire wavelength range of 3460–9464 Å with a spectral resolution of 1.2 Å. This catalogue was conceived to cover the whole H − R diagram down to metallicities of ~−2.5 dex, with the purpose to be a testing library for automatic synthesis methods. The parameters published for these stars, however, are a compilation of independent studies of several authors, obtained by various methods. Hence, some dispersion is expected, and the comparison between the method’s results with the published parameters of this library needs to be performed carefully.
Together with the 900 spectra of the CFLIB catalogue, we used the on-line database of PASTEL10 (Soubiran et al. 2010) instead of the published values in Valdes et al. (2004) to obtain updated values for the relevant stellar parameters. We chose then to keep only those spectra for which at least two measurements were available from different authors, and all stars with [M/H] < −1 dex11 (ignoring the previous selection criterion for metal poor stars). In Fig. 11 we can see the results obtained for the 162 CFLIB stars that fulfil our criteria, where the estimates from our pipeline are plotted against the mean values found in the literature (black dots). The error bars, if any, represent the dispersion in the published values. The scatter found is 171 K, 0.42 dex and 0.21 dex for Teff, log g and [M/H], respectively. Table 5 shows the error dispersions for the whole CFLIB library, and separately for the dwarfs (log g > 3) and the giants (log g ≤ 3). No significant biases are found, except for a small effect (~0.1 dex) in the metallicity of dwarf stars. It can be noticed that the stars for which our estimates are the most distant from the published values are the ones which had only one associated measurement. Therefore, it is difficult to know if the reason for these outliers is an error of this method or an error in the published values.
We also tested the pipeline on the spectra of the Sun and Arcturus. The spectra of Allende Prieto et al. (2004) and Hinkle et al. (2003) were degraded to SNR ~ 100 pixel-1, with 200 noise realisations. For each of the considered cases, 400 spectra were processed. For the Sun the results are very close to the standard solar parameter values, except for the metallicity, for which a difference of –0.1 dex is noticed. Similar parameters are derived for the Teff and the [M/H] of Arcturus, but log g is less well derived, perhaps because of the imperfect normalisation of the spectrum of Hinkle et al. (2003) (Sect. 3.2)
We comment briefly on the apparent bias found in metallicity for the dwarfs. As we can see from Table 5, a similar bias of ~−0.1 dex is found for the Sun, the S4N stars and the dwarfs of CFLIB. We decided to make no zero-point correction because the suspected bias is within the error bars found for the metallicity, while inadequate statistics make it impossible to quantify any bias as a function of stellar type. Application of the pipeline to Arcturus showed no particular bias on the [M/H] parameter. As a consequence, given our fairly arbitrary separation between metal-rich and metal-poor stars and between giants and dwarfs, we decided not to correct any systematic bias.
Finally, we tested the pipeline by introducing four different values of white Gaussian noise (SNR ~ 10, 20, 50, 100 pixel-1) to the S4N and CFLIB spectra. In addition, to increase the statistics of our tests, twenty noise realisations for each spectrum were performed for each value of the SNR. Table 6 shows the error at 70% of the total distribution for each of the libraries. Good estimates are found down to SNR ~ 20, as expected, validating in this way our method for the case of observed spectra.
Derived errors for the S4N and CFLIB libraries, at different signal-to-noise ratios.
7. Conclusions
In the era of large spectroscopic surveys, the automated parameterisation of stellar spectra in the infra-red ionised calcium triplet region is a fundamental problem that must be addressed and solved. We here presented such a method to derive automatically values of the effective temperatures, surface gravities and overall metallicities of observed stars. Although the application discussed in this paper was to spectra with wavelength coverage around ~8500 Å, the method we derived is easily adaptable to any other wavelength range and spectral resolution, provided there exists a grid of synthetic spectra with the same characteristics as the observed spectra. Furthermore, the dimensionality of the parameter space can be increased from that discussed here, if desired, by adding the [α/Fe] chemical ratio (Gazzano et al. 2010).
We studied two different approaches to the problem of automated classification, which led to a new hybrid method that combines the two approaches. At high SNR, a projection algorithm, the MATISSE method is preferred, because of its capability to interpolate between the spectra of a synthetic grid, its lower errors and the easy interpretation of its output. At low SNR, the problem of secondary minima in the solution for the best-fit synthetic spectrum is better treated with DEGAS, the algorithm based on pattern recognition. A quantification of the internal errors showed that results that are sufficiently accurate for galactic archaeology surveys which aim to study the full metallicity distribution (σ [M/H] < 0.1 dex), can be obtained down to SNR ~ 35 for all metal-rich and intermediate-metallicity stars ([M/H] < −1 dex). Furthermore, accurate results (σ [M/H] < 0.2 dex) that suffice to separate the different galactic components can be obtained down to SNR ~ 20. Indeed, we obtained σ [M/H] < 0.12 dex, 0.18 dex and 0.23 dex for typical old thin disc, thick disc and halo stars, respectively.
The application of this hybrid method was tested successfully on stellar libraries of observed targets, validating it for extended surveys such as Gaia. Our results show for the first time the expected accuracies that are possible from the spectra gathered by the RVS of Gaia at its low sampling. Furthermore, in addition to deriving accurate parameters, the method is well suited for big datasets, because it is not very time-consuming computationally – processing 2 × 104 spectra takes less than an hour on a current laptop. The method is already coded in Java and will be delivered to the Gaia Data Processing and Analysis Consortium (DPAC) as one of the possible nodes of the whole processing pipeline.
We identified those regions of the H − R diagram where special care must be taken to avoid systematic biases. To illustrate this point, consider a survey that mainly targets giant stars. In this case, the derived line-of-sight distances, obtained by the projection of the estimated stellar atmospheric parameters on a set of isochrones, can be seriously under-estimated because a giant star can be misclassified as a hot dwarf. Spurious effects can therefore be introduced when computing the galactocentric positions and space velocities of the sample and therefore compromise any conclusions. Nevertheless, to minimise the effect of this degeneracy, we can consider a synthetic grid composed only of the spectra of giant stars, and consequently avoid populating regions of the H − R diagram that should be left empty. Furthermore, if a variety of spectral types are observed, appropriate photometric ((B − V) for warm stars, (V − K) for cooler stars) measurements can also help to constrain the parameter space.
The conclusions presented in this paper will be used in a companion paper Kordopatis et al. (2011), where we will present the chemical and dynamical properties of roughly 700 stars, selected to probe the galactic thick disc, outside the solar neighbourhood.
Acknowledgments
The authors would like to thank the Mesocentre computer centre of the Observatoire de la Côte d’Azur for computing the grid of synthetic spectra and the B(λ) functions. We are grateful to B. Edvardsson for providing the grid of MARCS model atmospheres, B. Plez for his molecular line-lists and the improved Turbospec code, M. Irwin for his very fruitful comments and suggestions as a referee, A. Robin for her useful advices on the use of the Besançon model, C. C. Worley for the careful reading of this paper, and C. Allende-Prieto for letting us use his re-normalisation routine for IDL. RFGW acknowledges support from the US National Science Foundation, through grant AST-0908326, and from the Gordon & Betty Moore Foundation. Finally, G.K. would like to thank the Centre National d’Etudes Spatiales (CNES) and the Centre National de Recherche Scientifique (CNRS) for the financial support.
References
- Allende Prieto, C. 2008, in AIP Conf. Ser. 1082, ed. C. A. L. Bailer-Jones, 47 [Google Scholar]
- Allen de Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Barklem, P. S., Stempels, H. C., Allen de Prieto, C., et al. 2002, A&A, 385, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Tolstoy, E., Helmi, A., et al. 2006, A&A, 459, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008, MNRAS, 383, 183 [Google Scholar]
- Battaglia, G., Tolstoy, E., Helmi, A., et al. 2011, MNRAS, 411, 1013 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bijaoui, A., Recio-Blanco, A., & de Laverny, P. 2008, in AIP Conf. Ser. 1082, ed. C. A. L. Bailer-Jones, 54 [Google Scholar]
- Bijaoui, A., Recio-Blanco, A., de Laverny, P., & Ordenovic, C. 2010, in ADA 6 – Sixth Conference on Astronomical Data Analysis [Google Scholar]
- Brault, J., & Neckel, H. 1987, Spectral Atlas of Solar Absolute Disk-Averaged and Disk-Center Intensity from 3290 to 12 510 Å, available from ftp.hs.uni-hamburg.de/pub/outgoing/FTS-Atlas/ [Google Scholar]
- Fulbright, J. P., Wyse, R. F. G., Ruchti, G. R., et al. 2010, ApJ, 724, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Gazzano, J., de Laverny, P., Deleuil, M., et al. 2010, A&A, 523, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [Google Scholar]
- Grevesse, N. 2008, Commun. Asteroseismol., 157, 156 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., & Eriksson, K. 2006, A&A, 452, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkle, K., Wallace, L., Livingston, W., et al. 2003, in The Future of Cool-Star Astrophysics: 12th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (2001 July 30 – August 3), ed. A. Brown, G. M. Harper, & T. R. Ayres (University of Colorado), 12, 851 [Google Scholar]
- Koch, A., Kleyna, J. T., Wilkinson, M. I., et al. 2007, AJ, 134, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Grebel, E. K., Gilmore, G. F., et al. 2008, AJ, 135, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Kordopatis, G., Recio-Blanco, A., de Laverny, P., et al. 2011, A&A, 535, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Landweber, L. 1951, Am. J. Math., 73, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Alonso, J., Avila, G., et al. 2003, in SPIE Conf. Ser., ed. M. Iye & A. F. M. Moorwood, 4841, 1682 [Google Scholar]
- Quinlan, J. R. 1993, C 4.5: Programs for machine learning, ed. J. R. Quinlan [Google Scholar]
- Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruck, M. J., & Smith, G. 1993, A&A, 277, 165 [NASA ADS] [Google Scholar]
- Smith, V. V., Suntzeff, N. B., Cunha, K., et al. 2000, AJ, 119, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Le Campion, J., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starkenburg, E., Hill, V., Tolstoy, E., et al. 2010, A&A, 513, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinmetz, M. 2003, in GAIA Spectroscopy: Science and Technology, ed. U. Munari, ASP Conf. Ser., 298, 381 [Google Scholar]
- Tolstoy, E., Hill, V., Irwin, M., et al. 2006, The Messenger, 123, 33 [NASA ADS] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. L. 2008, in AIP Conf. Ser. 1082, ed. C. A. L. Bailer-Jones, 37 [Google Scholar]
- Wilkinson, M. I., Vallenari, A., Turon, C., et al. 2005, MNRAS, 359, 1306 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, R. F. G., Gilmore, G., Norris, J. E., et al. 2006, ApJ, 639, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y., Lee, Y., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Castelli, F., & Munari, U. 2004, A&A, 417, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwitter, T., Siebert, A., Munari, U., et al. 2008, AJ, 136, 421 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Biases and dispersions for the derived parameters of the S4N and CFLIB libraries.
Derived errors for the S4N and CFLIB libraries, at different signal-to-noise ratios.
All Figures
 |
Fig. 1 Illustration of the MATISSE basis functions. For every set of parameters θi, corresponding to a spectrum in a grid of synthetic spectra, a set of Bθ(λ) was computed. Here, we can see the computed BTeff(λ) functions (and the corresponding synthetic spectrum) for a star with Teff = 5250 K, log g = 4.5, [M/H] = −0.75 dex, [α/Fe] = 0.3 dex. For clarity we represent only a part of the wavelength range in the plot. The strongest features in the spectrum (top panel), identified with dashed vertical lines, correspond to the Ca ii triplet. In the second row we show the BTeff(λ) computed with a direct inversion of the correlation matrix, whereas the last two panels show the BTeff(λ) functions computed with the Landweber iterative algorithm, imposing a coefficient of correlation between the input and the output parameters of 0.97 and 0.80, respectively. As described in Sect. 2.1, the smaller the coefficient, the less weight is given to the second-order variations of the spectral flux. The spectral analysis can therefore be optimised according to the quality of the spectrum, which is typically quantified in the signal-to-noise ratio. |
| In the text | |
 |
Fig. 2 Input parameters for the testing set. The spectra were computed based on a catalogue of pseudo-stars requested from the website of the Besançon Galaxy model. |
| In the text | |
 |
Fig. 3 Dependence of the H − R diagram for spectra analysed with the MATISSE algorithm as a function of signal-to-noise ratio. The colour code, quantifying metallicity, is the same as in Fig. 2. As expected, stars with lower metallicities and hence less spectral information are those with the greatest scatter. |
| In the text | |
 |
Fig. 4 Relative errors of the stellar parameters derived by MATISSE (left column), DEGAS (middle column), and the final adopted pipeline (right column), at 70% of the error distribution as a function of the signal-to-noise ratio. Intermediate temperature (5000 < Teff < 6000 K) thin disc (−0.25 < [M/H] < 0.5 dex) and thick disc (−1.5 < [M/H] < −0.25 dex) dwarf stars are represented as black diamonds and red triangles symbols, respectively. Halo giant stars (Teff < 6000 K, log g < 3.5, −2.5 < [M/H] < −1.25 dex) are blue squares. |
| In the text | |
 |
Fig. 5 Noise-free synthetic spectra showing the degeneracy in parameter space between a hot dwarf star (black, solid line) and a cool giant (red dotted line). The spectra differ significantly only at the cores of the strong lines and at Pa12 (~8750 Å), but their wings differ weakly. |
| In the text | |
 |
Fig. 6 Error correlations for MATISSE (left column) and DEGAS (right column) for spectra with SNR ~ 20. The colour code, which corresponds to the metallicity, is the same as in Fig. 2. The general shape of these figures shows the degeneracy between the atmospheric parameters. For higher SNRs the correlation slopes are similar, but less extended, because the errors are smaller. The specific properties of each analysis method lead to the somewhat different extension and dispersion of the correlations. |
| In the text | |
 |
Fig. 7 Dependance of the H − R diagram structure recovered with the DEGAS algorithm as a function of the spectrum’s signal-to-noise ratio. The colour code is the same as in Fig. 2. |
| In the text | |
 |
Fig. 8 Sensitivity to radial velocity errors for MATISSE (left) and DEGAS (right). The values at Vrad = 0 km s-1 correspond to the values found in Fig. 4. Additional errors caused by an incorrect Vrad correction are almost null as long as the Doppler shift remains lower than 7 km s-1. For lower SNR the robustness of the algorithms is higher, which has an almost negligible effect even for an extreme velocity error of Vrad = 15 km s-1. |
| In the text | |
 |
Fig. 9 Sensitivity of the recovered H − R diagram for simulated data to the spectrum signal-to-noise ratio using the final adopted pipeline. The colour code is the same as in Fig. 2. |
| In the text | |
 |
Fig. 10 Re-normalisation process for a cool metal-rich dwarf star. Plot A) shows in black the theoretical spectrum and in red the spectrum with a modified continuum (see Sect. 5.2), which is analysed with our method. The change applied on the input spectrum can be viewed in plot B) of this figure, where the ratio between the theoretical spectrum and the input is shown. A corrected continuum shape is obtained at the end of our pipeline, as can be seen in the two bottom plots (C) and D)). |
| In the text | |
 |
Fig. 11 Comparisons between the results of our pipeline and values found in the literature for the S4N (red crosses) and CFLIB (black dots) stellar spectral libraries. The error bars shown for the CFLIB spectra represent the dispersion of the parameter values found in the literature, when available. The red dashed diagonal lines, plotted for an easier interpretation of the results, represent errors of ± 250 K, 0.5 dex and 0.3 dex for Teff, log g and [M/H], respectively. Typical errors of our pipeline are represented in the upper left corner of each plot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


