| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201117098 | |
| Published online | 16 November 2011 | |
POKER: estimating the power spectrum of diffuse emission with complex masks and at high angular resolution⋆
IAS, Institut d’Astrophysique Spatiale, CNRS Université Paris 11, Bâtiment 121, 91405 Orsay, France
e-mail: Nicolas.Ponthieu@ias.u-psud.fr
Received: 18 April 2011
Accepted: 9 June 2011
We describe the implementation of an angular power spectrum estimator in the flat sky approximation. POKER (P. Of k EstimatoR) is based on the MASTER algorithm developped by Hivon and collaborators in the context of CMB anisotropy. It works entirely in discrete space and can be applied to arbitrary high angular resolution maps. It is therefore particularly suitable for current and future infrared to sub-mm observations of diffuse emission, whether Galactic or cosmological.
Key words: methods: numerical / cosmic background radiation / methods: data analysis / infrared: diffuse background / ISM: structure / submillimeter: diffuse background
A copy of the code is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/535/A90
© ESO, 2011
1. Introduction
Whether it is due to Galactic dust or synchrotron, to cosmological backgrounds such as the cosmic microwave background (CMB) or to the cosmic infrared background (CIB), that traces the integrated radiation of unresolved galaxies, diffuse emission is omnipresent in infrared and millimetric observations. The angular power spectrum of this radiation is one of the main tools used to constrain the structure of the interstellar medium, the clustering of IR galaxies (CIB), or the cosmological parameters (CMB). In short, its estimation requires to Fourier transform the image and to average the modulus square of the Fourier amplitudes into frequency bins. However, the image has both boundaries and often masked regions (e.g. to remove bright point sources) that induce power aliasing and biases the estimation of the power spectrum if not accounted for properly. The effect becomes quite significant when the signal has a steep power spectrum such as k-3, similar to that measured for Galactic cirrus emission (Miville-Deschênes et al. 2007) or even steeper than k-4 as for CMB anisotropy on angular scales smaller than a few arcmin (e.g. Reichardt et al. 2009; Brown et al. 2009). To account for non-periodic boundaries, Das et al. (2009) proposed an original apodizing technique that helps us to deconvolve the estimated power spectrum from that of the observed patch boundaries. These authors also mitigate the impact of holes by applying a pre-whitening technique to data in real space.
In the context of CMB anisotropy, Hivon et al. (2002) developed the MASTER method that allows us to correct for mask effects on the output binned power spectrum. They analyze data accross the full sky and account for the sky curvature. Instead of classical Fourier analysis, they project the data onto spherical harmonics and go through the algebra of pseudo angular power spectra (see Sect. 2). This idea has been successfully used in several experiments (e.g. de Bernardis et al. 2000; Benoît et al. 2003) and is also the basis of more refined algorithms used in e.g. WMAP (Hinshaw et al. 2003) and Archeops (Tristram et al. 2005). However, direct use of MASTER in the context of infrared observations with a resolution of typically a few arcsec requires us to estimate Legendre polynomials up to orders ℓ of 10 000 or more for which current recurrences and integration methods are numerically unstable. Other techniques developed in the context of CMB anisotropy such as maximum likelihood estimation (Bond et al. 1998) could be transposed to high angular resolution maps, but the numerical cost 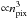 is prohibitive for common applications when the analysis pipeline requires Monte Carlo simulations.
is prohibitive for common applications when the analysis pipeline requires Monte Carlo simulations.
This paper aims to transpose the pseudo-spectrum approach pioneered by MASTER to high angular resolution observations and a classical Fourier analysis in the context of the flat sky approximation. Its originality compared to other approaches is that it works exclusively in discrete space and therefore avoids the complexity of resampling the data and integrating Bessel functions. Our algorithm was nicknamed POKER, for “P. Of k EstimatoR”. The paper is organized as follows. Section 2 provides the definitions and algebra involved in POKER and Sect. 3 shows its applications to simulations of various astrophysical components spectra and a complex mask. Detailed derivations of our results are presented in the appendices. Although this work focuses on temperature power spectrum estimation, we also show in Appendices B and C how the formalism can be generalized to the case of polarization.
2. Power spectrum estimation for an incomplete observation of the sky
We first briefly state the limits of the flat sky approximation, then recall the definitions of both the power spectrum and pseudo-power spectrum of data in the context of continuous Fourier transforms. Finally, we consider their counterpart in discrete space and the implementation of POKER.
2.1. Flat sky approximation
Projecting an observed fraction of the sky onto a plane rather than a sphere alters the image properties in a way that depends on the specific reprojection scheme (e.g. gnomonic, tangential, cylindrical etc.). The angular power spectrum of the data as measured on the projection plane therefore differs from that on the sphere. Two comments can be made at this stage. First, as long as the observation patch does not span more than a few degrees, as in most infrared experiments, the distortions are very small. For a gnomonic projection for instance, an observation point at an angular distance θ from the map center (the point tangent to the sphere) is projected at a distance tan(θ) rather than θ. The relative difference between the two is only 2.6 × 10-3 for a map of 10 degree diameter i.e. the projected map is stretched by 46 arcsec in each direction. As long as this remains small compared to the angular scales over which the angular power spectrum is estimated, the distortion can be neglected (e.g. Pryke et al. 2009). In this work, we stay well above this limit by considering square maps of only 5 × 5 deg2 and 2 arcmin resolution and therefore neglect distortion effects. Second, the impact of the projection on the estimation of the power spectrum is equivalent to a transfer function that can be estimated and corrected for when dealing with the convolution kernel (Eq. (21)), as detailed in Sect. 2.5. Both of these reasons allow us to estimate the angular power spectrum of a map built in the flat sky approximation limit.
2.2. Continuous Fourier analysis and masked data
On a flat two-dimensional (2D) surface, a scalar field Tr depending on the direction of observation r is represented in Fourier space by  For a random isotropic process, the 2D power spectrum
For a random isotropic process, the 2D power spectrum 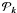 is defined as
is defined as 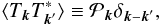 (3)where the brackets denote the statistical average. We denote by one-dimensional (1D) power spectrum its azimuthal average
(3)where the brackets denote the statistical average. We denote by one-dimensional (1D) power spectrum its azimuthal average 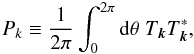 (4)where Pk is the physical quantity of interest which we want to reconstruct. It is the Fourier transform of the two-point correlation function. If the process is isotropic, the 2D and 1D-power spectra are related by
(4)where Pk is the physical quantity of interest which we want to reconstruct. It is the Fourier transform of the two-point correlation function. If the process is isotropic, the 2D and 1D-power spectra are related by 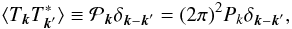 (5)in the following, we neglect the 1D or 2D qualifiers to improve readability and in both 1D and 2D cases use the term power spectrum unless the difference needs to be emphasized. In practice however, the integrals of Eqs. (1, 2) cannot run up to infinity simply because of the limited size of the observation patch. This is accounted for by a weight function Wr applied to the data. Its most simple form is unitary on the data, zero outside the observation range or where strong sources are masked out. More subtle choices such as inverse noise variance weighting or apodization (cf. Sect. 3) are usually used. Instead of the true Fourier amplitudes, we are then bound to measure the amplitudes of the masked data, a.k.a. the pseudo-amplitudes
(5)in the following, we neglect the 1D or 2D qualifiers to improve readability and in both 1D and 2D cases use the term power spectrum unless the difference needs to be emphasized. In practice however, the integrals of Eqs. (1, 2) cannot run up to infinity simply because of the limited size of the observation patch. This is accounted for by a weight function Wr applied to the data. Its most simple form is unitary on the data, zero outside the observation range or where strong sources are masked out. More subtle choices such as inverse noise variance weighting or apodization (cf. Sect. 3) are usually used. Instead of the true Fourier amplitudes, we are then bound to measure the amplitudes of the masked data, a.k.a. the pseudo-amplitudes 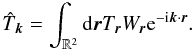 (6)Equation (4) applied to the pseudo-amplitudes gives the 1D-pseudo-power spectrum
(6)Equation (4) applied to the pseudo-amplitudes gives the 1D-pseudo-power spectrum 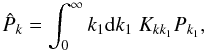 (7)where Kkk1 is the mixing matrix that depends on the weighting function Wr. To determine the signal power spectrum, we need to solve this equation for Pk1. A detailed derivation of the analytic solution can be found in Hivon et al. (2002). The impact of the instrumental beam, the pixel window function, the projection algorithm, the scanning, and the data processing can be accounted for in this formalism as transfer functions and incorporated in the definition of Kkk1 (Sect. 2.5). In the next two subsections, we focus on mask effects and the global picture of our algorithm.
(7)where Kkk1 is the mixing matrix that depends on the weighting function Wr. To determine the signal power spectrum, we need to solve this equation for Pk1. A detailed derivation of the analytic solution can be found in Hivon et al. (2002). The impact of the instrumental beam, the pixel window function, the projection algorithm, the scanning, and the data processing can be accounted for in this formalism as transfer functions and incorporated in the definition of Kkk1 (Sect. 2.5). In the next two subsections, we focus on mask effects and the global picture of our algorithm.
2.3. Discrete Fourier analysis and POKER
Any data set is by construction discretely sampled. Computing the quantities defined in the previous section requires mathematical interpolation and/or resampling of these data and appropriate integration tools, especially if the underlying data power spectrum is steep as for Galactic cirrus for which P(k) ∝ k-3 (Miville-Deschênes et al. 2007). Rather than dealing with these difficulties, we keep the native pixelized description of the data and work completely in discrete space. We use the discrete fourier transform (hereafter DFT) as provided by data analysis software. For a map of scalar quantity Dμν and size Nx × Ny pixels, it is defined as ![\begin{eqnarray} \label{eq:dft}D_{mn} & = & \frac{1}{N_xN_y}\sum_{\mu,\nu} D_{\mu\nu} {\rm e}^{-2{\rm i}\pi(\mu m/N_x+\nu n/N_y)}, \\[-1mm] D_{\mu\nu} & = & \sum_{m,n} D_{mn} {\rm e}^{+2{\rm i}\pi(\mu m/N_x+\nu n/N_y)}. \end{eqnarray}](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq27.png) Throughout this work, although we denote quantities in direct and Fourier space by the same name, Greek indices denote pixel indices in real space whereas roman indices refer to amplitudes in Fourier space. Unless stated otherwise, sums over μ and m (resp. ν and n) run from 0 to Nx − 1 (resp. Ny − 1), Δθ is the angular resolution of the map in radians. For a given wave-vector kmn, labeled by the m and n indices, its corresponding norm is denoted by
Throughout this work, although we denote quantities in direct and Fourier space by the same name, Greek indices denote pixel indices in real space whereas roman indices refer to amplitudes in Fourier space. Unless stated otherwise, sums over μ and m (resp. ν and n) run from 0 to Nx − 1 (resp. Ny − 1), Δθ is the angular resolution of the map in radians. For a given wave-vector kmn, labeled by the m and n indices, its corresponding norm is denoted by 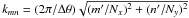 with m′ = m (resp. n′) if m ≤ Nx/2 and m′ = Nx − m if m > Nx/2. This convention ensures that on small angular scales k matches the multipole ℓ used in the description of CMB anisotropy. The Nyquist mode is π/Δθ.
with m′ = m (resp. n′) if m ≤ Nx/2 and m′ = Nx − m if m > Nx/2. This convention ensures that on small angular scales k matches the multipole ℓ used in the description of CMB anisotropy. The Nyquist mode is π/Δθ.
It is well known that the DFT slightly differs from the theoretical continuous Fourier transform, hence Dmn does not strictly equal Tkmn. In particular, the DFT deals with amplitudes for modes kmn larger than the Nyquist mode π/Δθ and in some directions for θmn only (see Fig. 1). It is therefore not possible to integrate Eq. (4) on the full range θ ∈ [0,2π] for such modes and so, the 1D power spectrum is undefined outside the Nyquist range. In the following, we therefore restrict ourselves to the Nyquist range for power spectrum estimation. We note, however, that mathematical sums implied in the following may still run over the full range of pixels or DFT amplitude indices.
The direct DFT of the masked data results from the convolution of the DFT amplitudes by a kernel 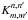 that depends only on the mask DFT amplitudes (Appendix A). If the data D consist of signal T and noise N, we have
that depends only on the mask DFT amplitudes (Appendix A). If the data D consist of signal T and noise N, we have 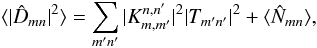 (10)which is the transcription in discrete space of Eq. (7).
(10)which is the transcription in discrete space of Eq. (7).
 |
Fig. 1 Map of the Fourier modes of the worked examples of Sect. 3. The inner circle delimits the Nyquist range. Modes that lie on the outer circle are examples of modes of larger modulus than kNyquist. For these modes, not all directions are sampled in the Fourier plane (dashes represent the missing modes). |
The rapid oscillations of the convolution kernel introduce strong correlations between spatial frequencies and make its inversion numerically intractable. (Pseudo-)Power spectra are therefore estimated on some frequency band-powers (labeled b hereafter). The binning operator reads 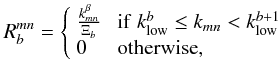 (11)where
(11)where 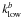 is the mode of lowest modulus that belongs to bin b and Ξb is the number of wave vectors kmn that fall into this bin. The reciprocal operator that relates the theoretical value of the 1D binned power spectrum Pb to its value at kmn is
is the mode of lowest modulus that belongs to bin b and Ξb is the number of wave vectors kmn that fall into this bin. The reciprocal operator that relates the theoretical value of the 1D binned power spectrum Pb to its value at kmn is 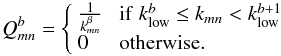 (12)Although not strictly required, results may be improved when the spectral index β is chosen so that kβPk is as flat as possible1. In the case of the cosmic infrared background anisotropy, β ≃ 1 (Planck Collaboration et al. 2011). The binned pseudo-power spectrum is therefore given by
(12)Although not strictly required, results may be improved when the spectral index β is chosen so that kβPk is as flat as possible1. In the case of the cosmic infrared background anisotropy, β ≃ 1 (Planck Collaboration et al. 2011). The binned pseudo-power spectrum is therefore given by 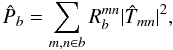 (13)and the data power spectrum is related to its binned value Pb via
(13)and the data power spectrum is related to its binned value Pb via 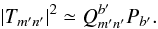 (14)With such binned quantities, Eq. (10) reads
(14)With such binned quantities, Eq. (10) reads 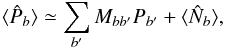 (15)where
(15)where 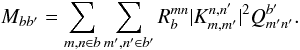 (16)An unbiased estimate of the binned angular power spectrum of the signal is thus given by
(16)An unbiased estimate of the binned angular power spectrum of the signal is thus given by 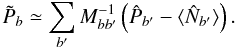 (17)It can indeed be easily verified that
(17)It can indeed be easily verified that 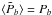 . Uncertainties in
. Uncertainties in 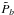 come from sampling and noise variance that are estimated via Monte Carlo simulations as described in the next section.
come from sampling and noise variance that are estimated via Monte Carlo simulations as described in the next section.
2.4. Statistical uncertainties
 |
Fig. 2 Top: mask applied to the simulated data. This mask is 1 where data are available and 0 outside the observation patch and where bright sources have been masked out. Bottom: same mask with apodized boundaries but still with the same number of masked pixels. |
Statistical uncertainties in Pb come from signal sampling variance and noise variance. They are estimated via Monte Carlo simulations. For each realization, a map of signal+noise is produced (see Sect. 2.6) and treated in the same way as described for the data in the previous section to give an estimate, 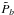 , with the same statistical properties as that of the true data. Altogether, these simulations provide the uncertainties in our estimate. The covariance matrix of
, with the same statistical properties as that of the true data. Altogether, these simulations provide the uncertainties in our estimate. The covariance matrix of 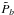 is
is 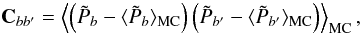 (18)where ⟨ · ⟩ MC denotes the Monte-Carlo averaging. The error bar in each
(18)where ⟨ · ⟩ MC denotes the Monte-Carlo averaging. The error bar in each 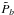 is
is 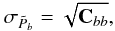 (19)and the bin-bin correlation matrix is given by its standard definition
(19)and the bin-bin correlation matrix is given by its standard definition 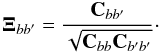 (20)
(20)
2.5. Beam, map making and transfer functions
The above sections describe the main features of the algorithm that provides an unbiased estimate of the power spectrum of data projected onto a map. This power spectrum may however differ from the signal power spectrum. The map making process may indeed alter the statistical properties of the signal, together with data filtering and the convolution by the instrumental beam. For instance, the pixelization caused by the map making is equivalent to a convolution in real space by a square kernel and therefore translates into a multiplication in Fourier space by a factor sinc. In the case of CMB anisotropy for which power spectrum estimation has been most extensively studied, to a good approximation, the transfer function Fk of the map making and the data processing together reduces to a function of k that multiplies the data power spectrum Pk. The determination of Fk is performed by a set of Monte Carlo simulations of data processing and map making. The beam smearing effect is also described by a multiplicative function Bk. In the present framework, it is possible to be even more precise and to account for the exact beam shape and orientation because the beam can be completely described by its Fourier coefficients Bmn rather than its approximated annular average Bk. This may be of particular relevance for small fields over which the scanning directions are approximately constant and increase the effect of beam asymmetry. The map making together with the filtering transfer function is also likely to be more accurately represented by a function of both Fourier indices Fmn, such that Eq. (10) is given by 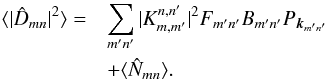 (21)These new contributions can be incorporated in the definition of the convolution kernel
(21)These new contributions can be incorporated in the definition of the convolution kernel 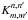 such that no additional modification of the algorithm is needed from Eq. (10) onward.
such that no additional modification of the algorithm is needed from Eq. (10) onward.
2.6. Algorithm
An outline of the algorithm is presented in Fig. 6. To perform the complete process of power spectrum and statistical uncertainty estimation, one needs:
-
(a)
a tool to simulate the sky that is observed by the instrumentgiven an input angular power spectrum;
-
(b)
a tool to simulate the instrument observations given the simulated sky;
-
(c)
the data processing pipeline that derives from these observations the map from which the user can then estimate the angular power spectrum. The pipeline includes optical beam smearing, time domain filtering, data flagging, map making etc. This tool is required to determine the transfer function of the map making and data processing (Eq. (21));
-
(d)
a tool to compute the power spectrum of a 2D map and to bin it into a set of predefined bins with a weight that may be a function of k;
-
(e)
a tool to compute Mbb′, which involves the computation of the convolution kernel
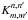 . This is actually the longest part of the process because it is a
. This is actually the longest part of the process because it is a 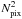 operation, but it only needs to be done once.
operation, but it only needs to be done once.
All these tools are provided in the POKER library23. The algorithm can be summarized as follows:
-
1.
Insert the observed sky patch of sizeNx × Ny pixels into a “large patch”
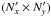 and padd it with zeros. This will allow for the correction of aliasing by scales larger than the observed sky. The size of the patch and the zero padding that should be used have both to be determined by the user. A factor from 1.2 to 2 is enough in most cases. A compromise must be chosen between the uncertainty on large scales that the user tries to estimate and the uncertainty associated with the unknown power in these large scales that needs to be assumed for the simulations. It is also possible to apodize the observation patch to limit large-scale aliasing (see Sect. 3 for more details) and improve the bin to bin decorrelation at high k.
and padd it with zeros. This will allow for the correction of aliasing by scales larger than the observed sky. The size of the patch and the zero padding that should be used have both to be determined by the user. A factor from 1.2 to 2 is enough in most cases. A compromise must be chosen between the uncertainty on large scales that the user tries to estimate and the uncertainty associated with the unknown power in these large scales that needs to be assumed for the simulations. It is also possible to apodize the observation patch to limit large-scale aliasing (see Sect. 3 for more details) and improve the bin to bin decorrelation at high k. -
2.
Define a binning for the estimated power spectrum on the large patch. Typically, modes sampled by the data set are the DC level and modes between kmin = 2π/Δθ/max(Nx,Ny) and the Nyquist mode kc = π/Δθ. The minimum bandwidth of the bins may be chosen as ~ 2kmin.
-
3.
Determine the noise pseudo-power spectrum –
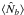 of Eq. (15). If it cannot be determined analytically, perform a set of Monte Carlo realizations of noise-only maps (with (a)) and compute the power spectrum with (b) of the masked maps inserted into the large patch. The average of these Monte Carlo realizations gives
of Eq. (15). If it cannot be determined analytically, perform a set of Monte Carlo realizations of noise-only maps (with (a)) and compute the power spectrum with (b) of the masked maps inserted into the large patch. The average of these Monte Carlo realizations gives 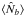 .
. -
4.
Run a set of noise-free simulations of the observed and reprojected sky to determine the transfer function Fmn of the data processing pipeline – Eq. (21).
-
5.
Compute Mbb′ with (c) – Eqs. (11, 12, 16). This operation scales as
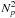 but it only needs to be done once. The implementation proposed in the POKER library can be run on a multiprocessor machine.
but it only needs to be done once. The implementation proposed in the POKER library can be run on a multiprocessor machine. -
6.
Compute the pseudo-power spectrum of the masked data on the large patch
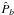 with (b) – Eq. (A.1).
with (b) – Eq. (A.1). -
7.
Apply Eq. (17) to obtain the binned power spectrum of the data Pb. The resolution of this equation can be done with any suitable method of linear algebra. Note that Mbb′ can be rather small and its inversion straightforward with standard numerical tools such that Eq. (17) can be computed as is. At this stage, it may be useful to discard the first bin of the matrix, which describes the coupling of the DC level of the map to the mask and is therefore irrelevant for a power spectrum analysis but tends to alter the conditioning of Mbb′.
-
8.
Determine the statistical error bars associated with this estimate. For that, perform a set of Monte Carlo realizations of signal+noise. The input spectrum required for these simulations can be a smooth interpolation of the binned power spectrum determined at the previous step. For each realization, compute the pseudo-power spectrum (using (b) on the masked data embedded in the large patch), subtract
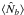 , and then solve Eq. (17). This provides a set of random realizations of
, and then solve Eq. (17). This provides a set of random realizations of 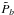 . The error bars and the bin-to-bin covariance matrix are then given by Eqs. (18, 19).
. The error bars and the bin-to-bin covariance matrix are then given by Eqs. (18, 19).
 |
Fig. 3 Typical maps of dust with a k-3 power spectrum (top) and CMB temperature (bottom). The square is the outline of the observed patch. It is extracted from a larger simulated map to ensure non-periodic boundary conditions. Masked data appear in white. |
3. Worked example
 |
Fig. 4 Dust (k-3). Comparison between the input theoretical power spectrum (black) and the average result of POKER (red) applied to 500 signal+noise simulations. The “naive” approach (blue, see text) is also shown for reference. Error bars in the top plots are those associated with the data (i.e. those of a single realization). The square line shows the binned theoretical power spectrum to which POKER’s average result should be compared. The bottom plots shows the ratio of the reconstructed binned power spectrum to the input theoretical binned power spectrum (the bias) and the displayed error bar is that of the average of the Monte Carlo realization (in other words: the error bar of the top plot divided by |
POKER was applied to real data to measure the cosmic infrared background anisotropy in the Planck-HFI data (Planck Collaboration et al. 2011). The whole data processing and how it is accounted for with POKER is described in detail in that paper. We do not replicate this analysis here but instead present complementary examples on simulated data with steeper power spectra and a more complex mask. It is in this context that mask aliasing effects are the strongest.
 |
Fig. 5 Left: same as Fig. 4 in the case of CMB. POKER’s estimation is unbiased but mask aliasing induces strong correlations between bins at high k where the power spectrum is very steep. Right: this time, the mask with apodized boundaries (bottom of Fig. 2) is used. High k bin-to-bin correlations are significantly reduced. Apodization however reduces the effective observed fraction of the sky and therefore slightly increases error bars at low k compared to the plots on the left. Note that although apodization also improves the “naive” estimate, it remains not compatible with the input spectrum for almost every bin and to more than the 1σ error of a single realization. |
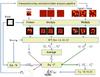 |
Fig. 6 Schematic flow chart of POKER. |
We assume that the observation patch is a square of 100 pixels of 2 arcmin side. These parameters are chosen so that they sample a range of angular modes over which the CMB temperature power spectrum exhibits peaks and a varying slope. Note however that the map resolution can be arbitrary high because fast Fourier transform algorithms work in dimensionless units. To force non-periodic boundary conditions, we extract the patch from a map that is 50% larger and the simulation is performed on the latter. Finally, we draw random holes across the observation patch to mimic point source masking. We consider two types of signal. In the first case, we assume that the data are represented by a pure power law spectrum k-3 typical of Galactic dust emission. In the second case, we assume that the data are CMB with a standard ΛCDM power spectrum. At these angular scales, the slope of the CMB power spectrum varies from ~k-2 to even steeper than k-6 and exhibits oscillations. Figure 3 shows an example of these simulated data. The result of POKER applied to each case is presented in Figs. 4 and 5. In the case of dust, we choose a binning index β = 3 as defined in Eq. (12), and in the case of CMB, we make no assumptions, i.e. we choose β = 0. We also show what the direct Fourier transform of the observed patch without any further correction would give to illustrate the magnitude of the effect corrected by POKER. Note that this reference estimate labeled “naive P(k)” is not the pseudo-power spectrum of the data in the sense of Sect. 2. Indeed, it is not computed on the whole map from which the observation patch is extracted and padded with zeros. The bottom plots of Figs. 4 and 5 show the bin-to-bin correlation matrix of each estimate. In the case of dust, the correlations are small (~15%). This is not the case for the simulated CMB, for which there is strong bin to bin correlation, although the power spectrum remains unbiased. This correlation is due to large-scale aliasing induced by the holes in the mask and show up so significantly because at high k, the CMB spectrum is very steep. A way to improve on this is to apodize the mask around the edges and the holes left by point-source masking (Fig. 2). In this work, we simply use a Gaussian kernel with a FWHM of twice the map resolution to smooth the edges. The same analysis as before is performed with this mask and results are presented in the right hand side of Fig. 5. On this occasion, the bin-to-bin correlation is significantly reduced, albeit the sampling variance is slighty increased at low k owing to the effective reduction in the observation area. A more efficient way of performing this apodization is described in Grain et al. (2009). Finally, on larger angular scales, there is a slight bias in the recovery of the CMB power spectrum. This does not however occur in the case of dust, because for a pure power-law spectrum, Eq. (14) is then an equality. This is no longer the case for a CMB spectrum whose average slope varies with k and exhibits peaks. No binning could faithfully represent such a spectrum. However, the remaining bias is negligible relative to the statistical error bar in the data. If we force the simulated CMB to have a constant power spectrum over frequency bins, the recovery is unbiased. There is no general prescription regarding the definition of the binning and the apodization. They must however be chosen with care because the bin-to-bin residual correlation may lead to residual ringing (mask aliasing) in the data power spectrum (considered as a single random realization), even if the estimator is, on average, unbiased.
4. Conclusion
We have developed a tool that provides an unbiased estimate of the angular power spectrum of diffuse emission in the flat sky approximation limit, for arbitrary high resolution and complex masks. POKER corrects for mask aliasing effects, even in the context of steep power spectra and provides a way to estimate statistical error bars and bin-to-bin correlations. It complements tools developed in the context of spherical sky and potentially full sky surveys (e.g. Hivon et al. 2002) but at the moment for lower angular resolutions. POKER also complements other methods in the flat sky approximation such as Das et al. (2009).
POKER can readily be generalized to polarization power-spectra estimation. To date, experiments that have measured polarized diffuse emission (Kovac et al. 2002; Kogut et al. 2003; Ponthieu et al. 2005; Ade et al. 2008; Chiang et al. 2010; Bierman et al. 2011) have been closely related to CMB experiments and studied observation patches of a few to a hundred percent of the sky and angular resolutions larger than a few arcmin. Optimal tools have been developed to measure the polarization power spectra in this context (Chon et al. 2004; Smith 2006; Smith & Zaldarriaga 2007; Grain et al. 2009, and references therein) and it is unlikely that POKER will bring something significantly new to the analysis of these observations. It is however expected that smaller, deeper, and higher-resolution polarized surveys will happen in the future, for which POKER might be an interesting approach. One of the main features that should then be addressed is the ability of POKER to correct for E − B leakage. Although we postpone the detailed studies of POKER’s properties regarding polarized power spectra estimation to future work, we provide the formalism in Appendices B and C for the sake of completeness. All the software used in this work is publicly available4.
http://www.ias.u-psud.fr/poker. This library makes use of some of the HEALPix programs (Gorski et al. 1999).
The sky simulator provided in the library works directly in flat space. Indeed, we cannot anticipate neither on the user’s favorite reprojection scheme from the sphere to the plane nor on his/her data processing pipeline and map making. Furthermore, simulating directly a flat sky of a known power spectrum is a convenient first stage to optimize the binning and apodization scheme before running the full fledge Monte Carlo simulations.
Acknowledgments
We thank E. Hivon, O. Doré, S. Prunet, K. Benabed and T. Rodet for fruitful discussions. J. Grain was supported by the “Groupement d’Intérêt Scientifique (GIS) Physique des 2 Infinis (P2I)”. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231.
References
- Ade, P., Bock, J., Bowden, M., et al. 2008, ApJ, 674, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Benoît, A., Ade, P., Amblard, A., et al. 2003, A&A, 399, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bierman, E. M., Matsumura, T., Dowell, C. D., et al. 2011 [arXiv:1103.0289] [Google Scholar]
- Bond, J. R., Jaffe, A. H., & Knox, L. 1998, Phys. Rev. D, 57, 2117 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. L., Ade, P., Bock, J., et al. 2009, ApJ, 705, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, H. C., Ade, P. A. R., Barkats, D., et al. 2010, ApJ, 711, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Chon, G., Challinor, A., Prunet, S., Hivon, E., & Szapudi, I. 2004, MNRAS, 350, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Das, S., Hajian, A., & Spergel, D. N. 2009, Phys. Rev. D, 79, 083008 [NASA ADS] [CrossRef] [Google Scholar]
- de Bernardis, P., Ade, P. A. R., Bock, J. J., et al. 2000, Nature, 404, 955 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gorski, K. M., Wandelt, B. D., Hansen, F. K., Hivon, E., & Banday, A. J. 1999 [arXiv:astro-ph/9905275] [Google Scholar]
- Grain, J., Tristram, M., & Stompor, R. 2009, Phys. Rev. D, 79, 123515 [Google Scholar]
- Hinshaw, G., Spergel, D. N., Verde, L., et al. 2003, ApJS, 148, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Hivon, E., Górski, K. M., Netterfield, C. B., et al. 2002, ApJ, 567, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Spergel, D. N., Barnes, C., et al. 2003, ApJS, 148, 161 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kovac, J. M., Leitch, E. M., Pryke, C., et al. 2002, Nature, 420, 772 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Miville-Deschênes, M.-A., Lagache, G., Boulanger, F., & Puget, J.-L. 2007, A&A, 469, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration, 2011, A&A, 536, A18, DOI: 10.1051/0004-6361/201116461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponthieu, N., Macías-Pérez, J. F., Tristram, M., et al. 2005, A&A, 444, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pryke, C., Ade, P., Bock, J., et al. 2009, ApJ, 692, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Reichardt, C. L., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 694, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. M. 2006, New A Rev., 50, 1025 [Google Scholar]
- Smith, K. M., & Zaldarriaga, M. 2007, Phys. Rev. D, 76, 043001 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, M., Patanchon, G., Macías-Pérez, J. F., et al. 2005, A&A, 436, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Mask convolution kernel for temperature
If not specified, sums run from 0 to Nx − 1 and 0 to Ny − 1. The pseudo-Fourier coefficients of the weighted data are given by ![\appendix \setcounter{section}{1} \begin{eqnarray} \hat{T}_{mn} & = & \frac{1}{N_xN_y}\sum_{\mu,\nu}T_{\mu\nu}W_{\mu\nu}{\rm e}^{-2{\rm i}\pi(\mu m/N_x+\nu n/N_y)}, \label{eq:raw_ft} \\ & = & \frac{1}{N_xN_y}\sum_{\mu,\nu}\sum_{m_1,n_1} T_{m_1n_1}{\rm e}^{2{\rm i}\pi(\mu m_1/N_x+\nu n_1/N_y)} \sum_{m_2,n_2}W_{m_2n_2}{\rm e}^{2{\rm i}\pi(\mu m_2/N_x+\nu n_2/N_y)}{\rm e}^{-2{\rm i}\pi(\mu m/N_x+\nu n/N_y)}, \nonumber \\ & = & \frac{1}{N_xN_y}\sum_{m_1,n_1,m_2,n_2}\sum_{\mu,\nu}T_{m_1n_1}W_{m_2n_2}{\rm e}^{2{\rm i}\pi[\mu(m_1N_x+m_2-m)/N_x+\nu(n_1+n_2-n)/N_y]}. \end{eqnarray}](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq102.png) m1 + m2 belongs to [0,2Nx − 2] , so
m1 + m2 belongs to [0,2Nx − 2] , so 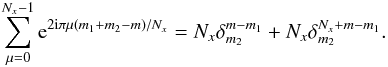 (A.3)Similar relations hold for indices n, hence
(A.3)Similar relations hold for indices n, hence 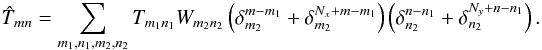 (A.4)Equation (8) specifies that Fourier coefficients are only defined for m,n ∈ [0,Nx − 1] × [0,Ny − 1] , hence
(A.4)Equation (8) specifies that Fourier coefficients are only defined for m,n ∈ [0,Nx − 1] × [0,Ny − 1] , hence 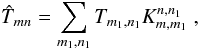 (A.5)where
(A.5)where 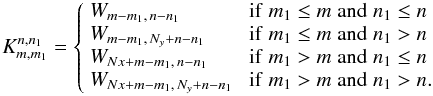 (A.6)
(A.6)
Appendix B: Mask convolution kernel for polarization only
Polarization maps are represented in direct space by Stokes parameters Q and U, in angular space by E and B. These parameters are related by
![\appendix \setcounter{section}{2} \begin{eqnarray} Q_{\mu\nu}&=&\displaystyle\sum_{m_1,n_1}\left[\cos(2\phi_{m_1n_1}^{\mu\nu})E_{m_1n_1}-\sin(2\phi_{m_1n_1}^{\mu\nu})B_{m_1n_1}\right]{\rm e}^{2{\rm i}\pi(\mu m_1/N_x+\nu n_1/N_y)}~~~~~~~~~~~~~~~~~~\\ U_{\mu\nu}&=&\displaystyle\sum_{m_1,n_1}\left[\sin(2\phi_{m_1n_1}^{\mu\nu})E_{m_1n_1}+\cos(2\phi_{m_1n_1}^{\mu\nu})B_{m_1n_1}\right]{\rm e}^{2{\rm i}\pi(\mu m_1/N_x+\nu n_1/N_y)}. \end{eqnarray}](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq115.png) The polarization pseudo-Fourier coefficients are given by
The polarization pseudo-Fourier coefficients are given by ![\appendix \setcounter{section}{2} \begin{eqnarray} \hat{E}_{mn}&=&\frac{1}{N_xN_y}\displaystyle\sum_{\mu,\nu}\left[\cos(2\phi_{mn}^{\mu\nu})Q_{\mu\nu}+\sin(2\phi_{mn}^{\mu\nu})U_{\mu\nu}\right]W_{\mu\nu}{\rm e}^{-2{\rm i}\pi(\mu m/N_x+\nu n/N_y)} , \\ &=&\frac{1}{N_xN_y}\displaystyle\sum_{m_1,n_1}\sum_{m_2,n_2}\sum_{\mu,\nu}W^{n_2}_{m_2}\left[\cos{(2\phi_{mn}^{\mu\nu}-2\phi_{m_1n_1}^{\mu\nu})}E_{m_1n_1}+\sin{(2\phi_{mn}^{\mu\nu}-2\phi_{m_1n_1}^{\mu\nu})}B_{m_1n_1}\right] \\ &&\times {\rm e}^{2{\rm i}\pi(\mu m_1/N_x+\nu n_1/N_y)}{\rm e}^{2{\rm i}\pi(\mu m_2/N_x+\nu n_2/N_y)}{\rm e}^{-2{\rm i}\pi(\mu m/N_x+\nu n/N_y)}, \nonumber \\ \hat{B}_{mn}&=&\frac{1}{N_xN_y}\displaystyle\sum_{\mu,\nu}\left[-\sin(2\phi_{mn}^{\mu\nu})Q_{\mu\nu}+\cos(2\phi_{mn}^{\mu\nu})U_{\mu\nu}\right]W_{\mu\nu}{\rm e}^{-2{\rm i}\pi(\mu m/N_x+\nu n/N_y)} ,\\ &=&\frac{1}{N_xN_y}\displaystyle\sum_{m_1,n_1}\sum_{m_2,n_2}\sum_{\mu,\nu}W^{n_2}_{m_2}\left[-\sin{(2\phi_{mn}^{\mu\nu}-2\phi_{m_1n_1}^{\mu\nu})}E_{m_1n_1}+\cos{(2\phi_{mn}^{\mu\nu}-2\phi_{m_1n_1}^{\mu\nu})}B_{m_1n_1}\right]~~~~~~~~~~~~~~~~~~~~~~ \\ &&\times {\rm e}^{2{\rm i}\pi(\mu m_1/N_x+\nu n_1/N_y)}{\rm e}^{2{\rm i}\pi(\mu m_2/N_x+\nu n_2/N_y)}{\rm e}^{-2{\rm i}\pi(\mu m/N_x+\nu n/N_y)}. \nonumber \end{eqnarray}](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq116.png) We now have to compute the two summations
We now have to compute the two summations 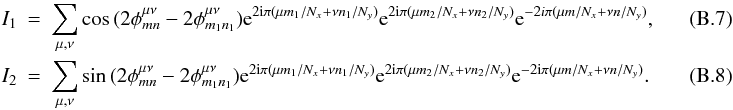 Because
Because 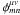 is the angle between kmn and rμν and
is the angle between kmn and rμν and 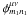 is the angle between km1n1 and rμν, we have
is the angle between km1n1 and rμν, we have 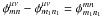 with
with
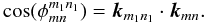 As a consequence, the sine and cosine do not depend on pixel indices, μ and ν, so we can use the orthogonality relation used for temperature, i.e. ∀ m1 + m2 belongs to [0,2N − 2] :
As a consequence, the sine and cosine do not depend on pixel indices, μ and ν, so we can use the orthogonality relation used for temperature, i.e. ∀ m1 + m2 belongs to [0,2N − 2] :
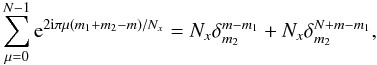 to finally get
to finally get ![\appendix \setcounter{section}{2} \begin{eqnarray} \hat{E}_{mn}&=&\displaystyle\sum_{m_1,n_1}K_{m,m_1}^{n,n_1}\left[\cos{(2\phi_{mn}^{m_1n_1})}E_{m_1n_1}+\sin{(2\phi_{mn}^{m_1n_1})}B_{m_1n_1}\right], \\ \hat{B}_{mn}&=&\displaystyle\sum_{m_1,n_1}K_{m,m_1}^{n,n_1}\left[-\sin{(2\phi_{mn}^{m_1n_1})}E_{m_1n_1}+\cos{(2\phi_{mn}^{m_1n_1})}B_{m_1n_1}\right].~~~~~~~~~~~~~~~~~ \end{eqnarray}](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq131.png) From these last set of results, we can compute the pseudo-power spectra, keeping in mind that
From these last set of results, we can compute the pseudo-power spectra, keeping in mind that
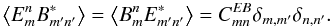 We define the estimated pseudo-spectra as
We define the estimated pseudo-spectra as
By using those definitions, we can easily show that
In a matrix formulation, this reads 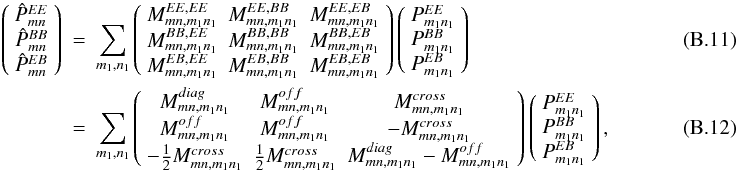
where
When the above mixing matrices are averaged over the two azimuthal (or polar for flat sky) angles, it can be shown that 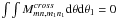 . However, before such an averaging, it is not a priori zero.
. However, before such an averaging, it is not a priori zero.
Appendix C: Mask convolution kernel for temperature polarization cross-correlation
For the cross-correlation of the temperature with CMB maps, we remind first that
The estimated cross-pseudo-spectrum are defined as
and
From this and from the above defined pseudo-Fourier coefficients, we show that 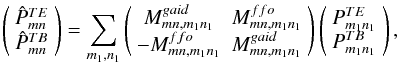 (C.1)with
(C.1)with 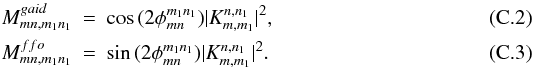 As for the cross blocks in the polarization case, the azimuthal average of
As for the cross blocks in the polarization case, the azimuthal average of 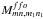 vanishes, i.e.
vanishes, i.e. 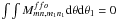 . However, before this averaging, it is not a priori zero.
. However, before this averaging, it is not a priori zero.
All Figures
 |
Fig. 1 Map of the Fourier modes of the worked examples of Sect. 3. The inner circle delimits the Nyquist range. Modes that lie on the outer circle are examples of modes of larger modulus than kNyquist. For these modes, not all directions are sampled in the Fourier plane (dashes represent the missing modes). |
| In the text | |
 |
Fig. 2 Top: mask applied to the simulated data. This mask is 1 where data are available and 0 outside the observation patch and where bright sources have been masked out. Bottom: same mask with apodized boundaries but still with the same number of masked pixels. |
| In the text | |
 |
Fig. 3 Typical maps of dust with a k-3 power spectrum (top) and CMB temperature (bottom). The square is the outline of the observed patch. It is extracted from a larger simulated map to ensure non-periodic boundary conditions. Masked data appear in white. |
| In the text | |
 |
Fig. 4 Dust (k-3). Comparison between the input theoretical power spectrum (black) and the average result of POKER (red) applied to 500 signal+noise simulations. The “naive” approach (blue, see text) is also shown for reference. Error bars in the top plots are those associated with the data (i.e. those of a single realization). The square line shows the binned theoretical power spectrum to which POKER’s average result should be compared. The bottom plots shows the ratio of the reconstructed binned power spectrum to the input theoretical binned power spectrum (the bias) and the displayed error bar is that of the average of the Monte Carlo realization (in other words: the error bar of the top plot divided by |
| In the text | |
 |
Fig. 5 Left: same as Fig. 4 in the case of CMB. POKER’s estimation is unbiased but mask aliasing induces strong correlations between bins at high k where the power spectrum is very steep. Right: this time, the mask with apodized boundaries (bottom of Fig. 2) is used. High k bin-to-bin correlations are significantly reduced. Apodization however reduces the effective observed fraction of the sky and therefore slightly increases error bars at low k compared to the plots on the left. Note that although apodization also improves the “naive” estimate, it remains not compatible with the input spectrum for almost every bin and to more than the 1σ error of a single realization. |
| In the text | |
 |
Fig. 6 Schematic flow chart of POKER. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



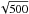
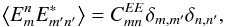
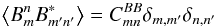
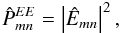
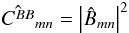
![\appendix \setcounter{section}{2} $$\hat{P}^{EB}_{mn}=\displaystyle\frac{1}{2}\left[\hat{E}_{mn}\hat{B}_{mn}^*+\hat{B}_{mn}\hat{E}_{mn}^*\right]=\mathrm{Re}\left[\hat{E}_{mn}\hat{B}_{mn}^*\right]=\mathrm{Re}\left[\hat{B}_{mn}\hat{E}_{mn}^*\right].$$](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq137.png)
![\appendix \setcounter{section}{2} \begin{eqnarray} \hat{P}^{EE}_{mn}&=&\displaystyle\sum_{m_1,n_1}|K_{m,m_1}^{n,n_1}|^2 \left[\cos^2{(2\phi_{mn}^{m_1n_1})}C^{EE}_{m_1n_1}+\sin^2{(2\phi_{mn}^{m_1n_1})}C^{BB}_{m_1n_1}+\sin{(4\phi_{mn}^{m_1n_1})}C^{EB}_{m_1n_1}\right], \nonumber \\ \hat{P}^{BB}_{mn}&=&\displaystyle\sum_{m_1,n_1}|K_{m,m_1}^{n,n_1}|^2 \left[\sin^2{(2\phi_{mn}^{m_1n_1})}C^{EE}_{m_1n_1}+\cos^2{(2\phi_{mn}^{m_1n_1})}C^{BB}_{m_1n_1}-\sin{(4\phi_{mn}^{m_1n_1})}C^{EB}_{m_1n_1}\right], \nonumber \\ \hat{P}^{EB}_{mn}&=&\displaystyle\sum_{m_1,n_1}|K_{m,m_1}^{n,n_1}|^2 \left[-\frac{1}{2}\sin{(4\phi_{mn}^{m_1n_1})}C^{EE}_{m_1n_1}+\frac{1}{2}\sin{(4\phi_{mn}^{m_1n_1})}C^{BB}_{m_1n_1}+\left(\cos^2{(2\phi_{mn}^{m_1n_1})}-\sin^2{(2\phi_{mn}^{m_1n_1})}\right)C^{EB}_{m_1n_1}\right]. \nonumber \end{eqnarray}](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq138.png)
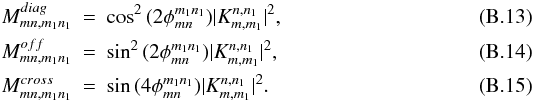
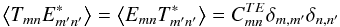
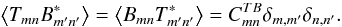
![\appendix \setcounter{section}{3} $$\hat{P}^{TE}_{mn}=\displaystyle\frac{1}{2}\left[\hat{T}_{mn}\hat{E}_{mn}^*+\hat{E}_{mn}\hat{T}_{mn}^*\right]=\mathrm{Re}\left[\hat{T}_{mn}\hat{E}_{mn}^*\right]=\mathrm{Re}\left[\hat{E}_{mn}\hat{T}_{mn}^*\right]$$](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq144.png)
![\appendix \setcounter{section}{3} $$\hat{P}^{TB}_{mn}=\displaystyle\frac{1}{2}\left[\hat{T}_{mn}\hat{B}_{mn}^*+\hat{B}_{mn}\hat{T}_{mn}^*\right]=\mathrm{Re}\left[\hat{T}_{mn}\hat{B}_{mn}^*\right]=\mathrm{Re}\left[\hat{B}_{mn}\hat{T}_{mn}^*\right].$$](/articles/aa/full_html/2011/11/aa17098-11/aa17098-11-eq145.png)