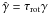EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 535 (November 2011) A&A, 535 (2011) L2 Full HTML
Free Access
Issue
A&A
Volume 535, November 2011
Article Number L2
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201116776
Published online 28 October 2011

© ESO, 2011

1. Introduction

The classical dynamo mechanism for generating cosmic magnetic fields is based on the inductive effects of rotating anisotropic turbulence. Because the same turbulence prevents uniform rotation from being a solution of the Reynolds equation, in the majority of dynamo models, the basic mechanism for producing toroidal fields from poloidal fields is differential rotation. However, it alone only produces toroidal fields that grow linearly in time, until the resulting Maxwell stresses suppress the differential rotation. To produce a self-excitation of magnetic fields as an instability that grows exponentially in time, another effect is needed to produce poloidal fields from toroidal ones.

There are many possibilities. The simplest one is a meridional flow. For certain combinations of differential rotation, meridional flows, and finite conductivity, the coupled system allows the self-excitation of (purely non-axisymmetric) fields (e.g. Dudley & James 1989). It is also possible to close the circuit by the α-effect, which represents the existence of an electromotive force parallel to the mean magnetic field. The result is a so-called αΩ-dynamo, which for a high magnetic Prandtl number can be modified by the action of meridional flow (Choudhuri et al. 1995; Küker et al. 2001). Driven turbulence subject to a shear flow in liquid metals is also able to work as a dynamo if the turbulence intensity is stratified in the direction orthogonal to the shear-flow plane (Rüdiger & Kitchatinov 2005).

The dynamo equations resulting from purely hydrodynamic flows are all linear, and the amplification can start from arbitrarily weak seed fields. This is not the case, however, for possible dynamo mechanisms where the coupling Btor → Bpol depends on magnetic instabilities. Such alternative mechanisms only work if the seed field is sufficiently strong. There are a variety of magnetic instabilities on which the dynamo mechanism can be based. Schmitt et al. (1996) started the construction of such models with their on-off dynamo model where the α-effect only exists if the magnetic field exceeds a certain threshold value determined by the magnetic buoyancy instability. Other possibilities have been suggested on the basis of both the magnetorotational instability (MRI) and the Tayler instability (Spruit 2002).

In this Letter it is demonstrated that in the presence of a shear flow, including the Hall term in Ohm’s law is enough to produce a “shear-Hall instability” (SHI). The Hall effect produces off-diagonal elements in the conductivity tensor that are of the first order in the magnetic field. The SHI is thus a magnetically nonlinear instability, but with the particularity that there is no threshold value. That is, if the shear is strong enough, the Hall effect, hence the initial seed field, can be arbitrarily weak.

The natural application of this shear-Hall instability is in newly born neutron stars. In the first few minutes of its life, the crust of the star can rotate differentially, as shown in a number of numerical computations of the supernova core (Mönchmeyer & Müller 1989; Janka & Moenchmeyer 1989; Dimmelmeier et al. 2002; Kotake et al. 2004; Ardeljan et al. 2005; Burrows et al. 2007). Differential rotation in the core of the collapsing progenitor will induce strong differential rotation in the newly formed neutron star (Ott et al. 2005).

Initially, the star cools down by neutrino emission. As a result of this cooling, the core becomes distinct from the outer layer, and the crust condenses at a temperature of a few 109   K (Dall’Osso et al. 2009, and references therein). Any differential rotation can thus only exist in a limited time-interval that depends on the type of reactions causing the cooling. In the case of the direct URCA process, the cooling is extremely fast, with estimates giving a characteristic time of a few minutes (Page et al. 2006).

However, the very rapid rotation rates, with periods of order 10-2   s, mean that even just a few minutes is long enough for the star to undergo several thousand revolutions. Furthermore, we show that the SHI grows on this very fast rotational timescale, so even though it only exists for a few minutes, this is sufficient for it to amplify a seed field by many orders of magnitude. Of course, the time evolution of the shear is excluded in this simplified model, so the exact amplitude of the field at the end of the SHI phase must still be deduced from full nonlinear simulations of the Hall-MHD system.

2. The shear-Hall instability

The Hall effect is important whenever a plasma is magnetized enough. The level of magnetization is determined by the Hall parameter, RB = σB0/nec, with B0 a characteristic magnitude of the field, σ the electric conductivity, n the electron number density, e the electron charge, and c the speed of light. If the Hall parameter RB is large, the Hall effect is important.

In a neutron star, both the electron number density and the conductivity vary with depth. The conductivity also varies with temperature. To focus on the basic physics of the instability process, we neglect all such variations and treat both n and σ as constants. However variations in n in particular can interact with the Hall effect in interesting and unexpected ways (Vainshtein et al. 2000; Hollerbach & Rüdiger 2004).

The magnetic Reynolds number is Rm = R2   Ω0/η, where R is the star’s radius, Ω0 the maximal angular velocity, and η its magnetic diffusivity. Scaling length by R, time by R2/η, u by RΩ0, and B by B0, the induction equation becomes 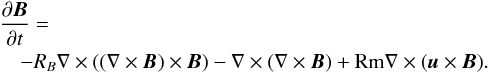∂B∂t=−RB∇×((∇×B)×B)−∇×(∇×B)+Rm∇×(u×B).\begin{eqnarray} \lefteqn{\frac{\partial\vec{B}}{\partial t} = }\nonumber\\ \label{eq:normind} & & -R_{B}\nabla\times((\nabla\times\vec{B})\times\vec{B}) -\nabla\times(\nabla\times\vec{B})+{\rm Rm}\nabla\times(\vec{u}\times\vec{B}). \end{eqnarray}(1)We linearize this equation about the uniform axial field B0 = ez,yielding 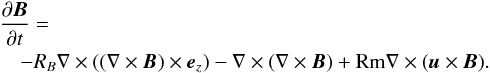∂B∂t=−RB∇×((∇×B)×ez)−∇×(∇×B)+Rm∇×(u×B).\begin{eqnarray} \lefteqn{\frac{\partial\vec{B}}{\partial t} =}\nonumber\\ \label{eq:linear} & & -R_{B}\nabla\times((\nabla\times\vec{B})\times\vec{e}_z) -\nabla\times(\nabla\times\vec{B})+{\rm Rm}\nabla\times(\vec{u}\times\vec{B}). \end{eqnarray}(2)The flow u is kinematically prescribed as 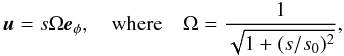u=sΩeφ, where Ω=11+(s/s0)2,\begin{equation} \vec{u}=s\Omega\vec{e}_{\phi},\quad{\rm where}\quad\Omega=\frac{1}{\sqrt{1+(s/s_{0})^{2}}},\label{Om} \end{equation}(3)where s is cylindrical radius, and s0 = 0.5. By itself such a flow generates no interaction with the imposed field B0 = ez, not even a linearly growing toroidal field. It is only with the addition of the Hall term that instabilities may develop in this otherwise stationary basic state.

Investigations of the full field/flow coupling have already been conducted by Wardle (1999) and Balbus & Terquem (2001) in the local approximation, as well as globally by Rüdiger & Kitchatinov (2005). These works show that the interaction between the Hall effect and the MRI may lead to both stabilization or destabilization of the system, depending on the values of the Lundquist number (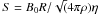S=B0R/(4πρ)η\hbox{$ S= B_{\rm 0}R/\sqrt(4\pi\rho)\eta $}, where ρ is the mass density) and RB. In the context of Rüdiger & Kitchatinov (2005), our case corresponds to the limit of small S. For example, Fig. 1 illustrates how the increase in S (the influence of the Lorentz force) has a stabilizing effect.

It is also useful to derive the energy equation associated with either Eq. (1) or (2). Taking the dot product of either equation with B and integrating over the volume, one obtains 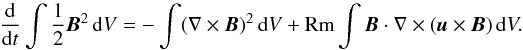ddt∫12B2 dV=−∫(∇×B)2 dV+Rm∫B·∇×(u×B) dV.\begin{equation} {\frac{{\rm d}}{{\rm d}t}}\int\frac{1}{2}\vec{B}^{2}\, {\rm d}V=-\int(\nabla\times\vec{B})^{2}\, {\rm d}V+{\rm Rm}\int\vec{B}\cdot\nabla\times(\vec{u}\times\vec{B})\, {\rm d}V.\label{energy} \end{equation}(4)The Hall term exactly conserves magnetic energy, in both the fully nonlinear and the linearized versions of the induction equation. The only source of energy is from the differential rotation. The Hall term is therefore essentially a catalyst, necessary for the instability to proceed, but energetically incapable of driving instabilities itself (Wareing & Hollerbach 2009). This situation is exactly analogous to the MRI, where the energy source is also purely from the differential rotation, but a magnetic field is nevertheless necessary. It is, perhaps, not surprising then that the shear-Hall instability, like the MRI, grows on the fast rotational timescale, as we demonstrate below.

thumbnail Fig. 1

Stability curves for the axisymmetric (S0 and A0) and non-axisymmetric (S1 and A1) modes. The single points belong to the system where the flow equation was treated in addition to the induction equation.

According to the local analysis of Urpin & Rüdiger (2005), for a general differential rotation depending on both s and z, a necessary condition for the existence of unstable modes is 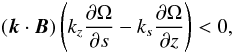(k·B)(kz∂Ω∂s−ks∂Ω∂z)<0,\begin{equation} (\vec{k}\cdot\vec{B})\left(k_{z}\frac{\partial\Omega}{\partial s}-k_{s}\frac{\partial\Omega}{\partial z}\right)<0,\label{veck} \end{equation}(5)where k is the wavenumber. For Ω = Ω(s), this reduces to 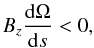BzdΩds<0,\begin{equation} B_{z}\frac{{\rm d}\Omega}{{\rm d}s}<0,\label{Bzet} \end{equation}(6)so that, for a given gradient of the angular velocity, instability only occurs for one sign of Bz (Wardle 1999; Balbus & Terquem 2001). For our particular profile (3) this condition is only fulfilled for positive Bz, hence RB. For negative RB there is no SHI instability.

Because Eq. (2) is linear with an axisymmetric basic state, the different azimuthal modes exp(imφ) decouple and can be studied separately. Each azimuthal mode further decouples into equatorially symmetric and anti-symmetric modes. We will present results for S0, A0, S1, and A1, where “S” or “A” refers to the radial component of the field being equatorially symmetric or anti-symmetric, and the “0” or “1” refers to the wavenumber m.

Equation (2) is solved in a spherical shell using the spherical harmonics code described by Hollerbach (2000). At both Rin = 0.7 and Rout = 1 boundaries, the solution smoothly matches a potential external field. At Rout this is indeed the correct condition, but at Rin it is clearly a considerable simplification of the true physics governing the coupling to an internal core field. Resolutions up to 30 Chebyshev polynomials in r and 70 Legendre functions in θ were used, which was sufficient to resolve the eigenmodes up to RB = 8. The Hall parameter close to unity is appropriate during the initial stages of a neutron star, and also turns out to be where the shear-Hall instability operates most efficiently.

3. Results

3.1. Stability maps

Figure 1 shows the instability curves for the four modes S0, A0, S1, and A1. Over most of the RB range the axisymmetric modes are slightly preferred over the non-axisymmetric ones, but the curves are otherwise all qualitatively similar. The minimum value of Rm occurs when RB ≃ 2−4. At this minimum the shear frequency ωsh is around 400 times the Hall frequency ωH, consistent with the result of Urpin & Rüdiger (2005) that the instability only exists for |ωsh| > |ωH|.

If RB is smaller than  ≃ 2–4 the system tends toward the (stable) pure differential rotation case, thus explaining the asymptote Rm → ∞ as RB → 0. At the other end, as RB becomes large the Hall effect increasingly dominates, but as noted above, it is energetically incapable of driving any instability itself, so Rm must again increase to compensate. For both RB ≪ 1 and RB ≫ 1, therefore, the differential rotation must become increasingly strong for the instability to operate.

An intriguing feature of the small RB ends of all four instability curves is that none of them shows any evidence of tilting back over to the right (down to our lowest investigated RB value of 0.4), that is, there is no indication of the instability switching off again for sufficiently large Rm. This is perhaps not so surprising for the axisymmetric modes; For example, the classical, axisymmetric MRI has the same feature. For nonaxisymmetric modes, though, it is often the case that a strong enough differential rotation suppresses them again (e.g. Rüdiger et al. 2007; Hollerbach et al. 2010). It is not entirely clear why this does not occur here – or perhaps it does, but only at much higher values of Rm than what we were able to compute here.

It is also interesting that there is no region where a single mode dominates: both A and S modes, and both axisymmetric and non-axisymmetric ones, are excited at comparable parameter values. This suggests that the fully nonlinear regime might consist of a mixture of several modes, which can also be considered as an “oblique rotator”. If different modes are indeed present simultaneously, the field configuration and amplitude in the two hemispheres would necessarily be different. If the heat transport is furthermore dominated by the magnetic suppression of the thermal conductivity tensor (Schaaf 1990; Heyl & Hernquist 2001), then the Hall effect would thereby lead to different temperatures, and hence X-ray emission (Becker & Pavlov 2002), in the two hemispheres.

3.2. Growth rates

To assess the possible astrophysical significance of the shear-Hall instability, we need to know not only for what parameter values it exists, but also what its associated growth rates are. Figure 2 shows the growth rate scaled on the rotational timescale. (That is, if γdiff is the growth rate on the chosen diffusive timescale R2/η, then 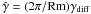\hbox{$\hat{\gamma}=(2\pi/\rm Rm)\gamma_{\rm diff}$} is the growth rate on the rotational timescale τrot = 2π/Ω0.) For both RB = 1 and RB = 5, for large enough Rm these growth rates 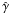\hbox{$\hat{\gamma}$} eventually saturate at O(1) values. As before, for the initial onset, all four modes behave comparably, although the axisymmetric modes do have higher growth rates. There is no preferred equatorial symmetry, because the S and A modes are very similar. Surprisingly, even though the stability map shows that a nonaxisymmetric mode S1 is less stable in the RB region from 4 onward, its growth is only stronger near the stability line. For higher Rm, the axisymmetric modes are more dominant.

Of the three timescales that are “obviously” present in the problem, namely the fast rotational timescale τrot, the much slower diffusive τdiff = R2/η = (Rm/2π)τrot, and Hall τHall = τdiff/RB timescales, the shear-Hall instability thus grows the fastest, and is independent of both τdiff and τHall. This is surprising, given that it does clearly depend on both the shear-effect and the Hall effect. On the other hand, as noted above, its energy source is entirely drawn from the differential rotation. In this regard it is quite different from a classical αω dynamo, for example, where the growth rate is the geometric mean of τrot and τα, but both the differential rotation and α also contribute to the energy balance.

thumbnail Fig. 2

\hbox{$\hat{\gamma}$} is a nondimensionalized growth rate (\hbox{$\hat{\gamma}=\tau_{\rm rot}\gamma$}, where γ is in physical units), of the S0 and S1 modes, for RB = 1 and 5. The profiles for A0 and A1 are very similar, and are not shown here.

3.3. Wave numbers

The spatial properties of the eigensolutions are given in Fig. 3. The color map represents the toroidal field structure, while the contours depict the field lines of the poloidal component. Comparing the two plots, at Rm = 2000 and 10   000, suggests a transition to smaller scales as Rm increases. The wavenumber also increases for (turbulent) mean-field dynamos at increasingly supercritical dynamo numbers. However, thanks to the high values of their eddy diffusivity, turbulent dynamos operate with moderate values of Rm. The SHI though may easily operate with very high Rm, and may play a dominant role in driving MHD turbulence if Rm ≫ 1.

The relative amplitudes of the toroidal field never exceed that of the poloidal field by more than one order of magnitude. Independent of the ratio of the Hall time and the rotation time, the coupling between the components via the Hall term enables their simultaneous, and comparable, amplification.

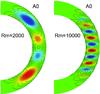thumbnail Fig. 3

The axisymmetric solution A0 for RB = 1, and Rm = 2000 on the left and Rm = 10   000 on the right. The other modes have the same pattern of exhibiting finer structure in z for larger Rm.

4. Discussion

It remains to be seen to what extent the SHI is important in the regime of newborn neutron stars. We first need to establish the reasonable values for the Hall parameter and the magnetic Reynolds number. It turns out that owing to a low diffusivity (η = 10 − (2..3)   cm2   s-1) (as treated in the code of Potekhin 2008), the microphysical Rm is orders of magnitude above the stability line in Fig. 1. If the effects of turbulence are important, according to Naso et al. (2008) diffusivity is much larger and the corresponding Rm is lower (~103), but still supercritical.

The onset of the shear-Hall instability requires a seed field of the magnitude determined by the actual Rm. This field can be provided by various other proposed mechanisms, from flux-conservation to dynamo processes (for an overview, see Spruit 2009). The turbulent Rm would require RB ≳ 1, which, for the temperatures of 109...10   K and densities of 1010...13   g   cm-3, corresponds to B ≳ 1012   G. If no turbulence is present, the seed field can be much smaller provided that the stability line remains univalued when RB tends to zero.

In the situation where the magnetic fields are strong, there is a coupling between the fields and the differentially rotating flow, which leads to a stable state of uniform rotation. The timescale for this process is 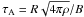τA=R4πρ/B\hbox{$\tau_{\rm A}=R\sqrt{4\pi\rho}/B$}, the Alfvén time

(Shapiro 2000), which is only  ~10   s for the neutron star conditions. Is the SHI quick enough to be of any significance? Taking the fast rotation of neutron stars into account , our results (Fig. 2) show that the field can easily amplify several orders of magnitude within the constraining time interval.

Because we are convinced that the instability conditions are fulfilled and the growth is quick enough, there is only the field geometry left to analyze in the context of the standard, inclined magnetic dipole model, which is used to explain the spin-down of pulsars. The SHI generates, as shown, small-scale fields for large Rm. The presence of turbulence is, it seems, a necessary requirement for producing a global field via this instability. On the other hand, X-ray spectra of pulsars sometimes indicate an additional, strong small-scale surface component (Pavlov et al. 2002; Sanwal et al. 2002). It is possible that the SHI is involved in generating the small-scale structure, while the large-scale component should be attributed to another process.

Rapid growth, as well as the easy excitation, indicates that the shear-Hall instability may play an important role in the evolution of the field of newborn neutron stars, prompting further, nonlinear analysis of the field/flow coupling and raising questions about its interaction with other field-generating mechanisms.

References

  1. Ardeljan, N. V., Bisnovatyi-Kogan, G. S., & Moiseenko, S. G. 2005, MNRAS, 359, 333 [NASA ADS] [CrossRef] [Google Scholar]
  2. Balbus, S. A., & Terquem, C. 2001, ApJ, 552, 235 [Google Scholar]
  3. Becker, W., & Pavlov, G. 2002, in The Century of Space Science, Vol. I, ed. J. A. Bleeker, J. Geiss, & M. C. E. Huber (Kluwer), 721 [Google Scholar]
  4. Burrows, A., Dessart, L., Livne, E., Ott, C. D., & Murphy, J. 2007, ApJ, 664, 416 [NASA ADS] [CrossRef] [Google Scholar]
  5. Choudhuri, A. R., Schüssler, M., & Dikpati, M. 1995, A&A, 303, L29 [NASA ADS] [Google Scholar]
  6. Dall’Osso, S., Shore, S. N., & Stella, L. 2009, MNRAS, 398, 1869 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dimmelmeier, H., Font, J. A., & Müller, E. 2002, A&A, 393, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Dudley, M. L., & James, R. W. 1989, Proc. R. Soc. London, Ser A., 425, 407 [Google Scholar]
  9. Heyl, J. S., & Hernquist, L. 2001, MNRAS, 324, 292 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hollerbach, R. 2000, Int. J. Numer. Meth. Fluids, 32, 773 [CrossRef] [Google Scholar]
  11. Hollerbach, R., & Rüdiger, G. 2004, MNRAS, 347, 1273 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hollerbach, R., Teeluck, V., & Rüdiger, G. 2010, Phys. Rev. Lett., 104, 044502 [NASA ADS] [CrossRef] [Google Scholar]
  13. Janka, H.-T., & Moenchmeyer, R. 1989, A&A, 226, 69 [NASA ADS] [Google Scholar]
  14. Kotake, K., Sawai, H., Yamada, S., & Sato, K. 2004, ApJ, 608, 391 [NASA ADS] [CrossRef] [Google Scholar]
  15. Küker, M., Rüdiger, G., & Schultz, M. 2001, A&A, 374, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Mönchmeyer, R., & Müller, E. 1989, in Timing Neutron Stars, ed. H. Ögelman, & E. P. J. van den Heuvel (Kluwer), 549 [Google Scholar]
  17. Naso, L., Rezzolla, L., Bonanno, A., & Paternò, L. 2008, A&A, 479, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Ott, C. D., Ou, S., Tohline, J. E., & Burrows, A. 2005, ApJ, 625, L119 [NASA ADS] [CrossRef] [Google Scholar]
  19. Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
  20. Pavlov, G. G., Zavlin, V. E., Sanwal, D., & Trümper, J. 2002, ApJ, 569, L95 [NASA ADS] [CrossRef] [Google Scholar]
  21. Potekhin, A. Y. 2008, Electron Conductivity of Stellar Plasmas, http://www.ioffe.ru/astro/conduct/index.html [Google Scholar]
  22. Rüdiger, G., & Kitchatinov, L. L. 2005, A&A, 434, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Rüdiger, G., Hollerbach, R., Gellert, M., & Schultz, M. 2007, AN, 328, 1158 [Google Scholar]
  24. Sanwal, D., Pavlov, G. G., Zavlin, V. E., & Teter, M. A. 2002, ApJ, 574, L61 [NASA ADS] [CrossRef] [Google Scholar]
  25. Schaaf, M. E. 1990, A&A, 227, 61 [NASA ADS] [Google Scholar]
  26. Schmitt, D., Schüssler, M., & Ferriz-Mas, A. 1996, A&A, 311, L1 [NASA ADS] [Google Scholar]
  27. Shapiro, S. L. 2000, ApJ, 544, 397 [NASA ADS] [CrossRef] [Google Scholar]
  28. Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Spruit, H. C. 2009, in IAU Symp. 259, ed. K. G. Strassmeier, A. G. Kosovichev, & J. E. Beckman, 61 [Google Scholar]
  30. Urpin, V., & Rüdiger, G. 2005, A&A, 437, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Vainshtein, S. I., Chitre, S. M., & Olinto, A. V. 2000, Phys. Rev. E, 61, 4422 [NASA ADS] [CrossRef] [Google Scholar]
  32. Wardle, M. 1999, MNRAS, 307, 849 [NASA ADS] [CrossRef] [Google Scholar]
  33. Wareing, C. J., & Hollerbach, R. 2009, A&A, 508, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1

Stability curves for the axisymmetric (S0 and A0) and non-axisymmetric (S1 and A1) modes. The single points belong to the system where the flow equation was treated in addition to the induction equation.
In the text
thumbnail Fig. 2

\hbox{$\hat{\gamma}$} is a nondimensionalized growth rate (\hbox{$\hat{\gamma}=\tau_{\rm rot}\gamma$}, where γ is in physical units), of the S0 and S1 modes, for RB = 1 and 5. The profiles for A0 and A1 are very similar, and are not shown here.
In the text
thumbnail Fig. 3

The axisymmetric solution A0 for RB = 1, and Rm = 2000 on the left and Rm = 10   000 on the right. The other modes have the same pattern of exhibiting finer structure in z for larger Rm.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.