| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 6 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117403 | |
| Published online | 12 August 2011 | |
The size of the Universe according to the Poincaré dodecahedral space hypothesis
Toruń Centre for Astronomy, Nicolaus Copernicus University, ul. Gagarina 11, 87-100 Toruń, Poland
e-mail: boud@astro.uni.torun.pl
Received: 3 June 2011
Accepted: 20 July 2011
Context. One of the Friedmann-Lemaître-Robertson-Walker (FLRW) models that best fits the Wilkinson microwave anisotropy probe (WMAP) sky maps of the cosmic microwave background is that whose comoving space is the Poincaré dodecahedral space. The optimal fit of this model to WMAP data was recently found using an optimal cross-correlation method. For geometrical reasons, there was concern that systematic error in the estimate of the matched-circle (observer-centred) angular radius α, or equivalently, the (comoving) size of the Universe 2rinj (twice the injectivity radius), might be much higher than the random error.
Aims. In order to increase the falsifiability of the model, especially by multiple imaging of collapsed objects, it would be useful to reduce the uncertainty in this estimate and to estimate the fraction of the sky where multiply imaged gravitationally bound objects should potentially be detectable.
Methods. A corollary of the matched circles principle – the existence of matched discs – is introduced in order to describe a useful subset of multiply imaged objects. The cross-correlation method at ≲ 1 h-1 Gpc is applied to WMAP 7-year data in order to improve the estimate of α.
Results. The improved matched-circle radius estimate is α = 23 ± 1.4°, where the uncertainty represents systematic error dependent on the choices of galactic mask and all-sky map. This is equivalent to 2rinj = 18.2 ± 0.5 h-1 Gpc for matter density parameter Ωm = 0.28 ± 0.02. The lowest redshift of multiply imaged objects is z = 106 ± 18. Multiply imaged high overdensity (rare) peaks visible during 200 > z > 106 should be present in matched discs of radius 14.8 ± 2.3°.
Conclusions. The accuracy in the matched circle radius estimate is considerably improved by using the higher resolution signal. The predicted matched discs (over 200 > z > 106) project to about 20% of the full sky. Since any object located exactly in the discs would be multiply imaged at equal redshifts, evolutionary effects would be small for objects that are nearly located in the discs.
Key words: cosmology: observations / cosmological parameters / cosmic background radiation / distance scale
© ESO, 2011
1. Introduction
The near lack of 10 h-1 Gpc scale structure in cosmic microwave background (CMB) temperature fluctuation maps was tentatively detected by the COsmic Background Explorer (COBE) and supported by the Wilkinson microwave anisotropy probe (WMAP) (Bennett et al. 2003). This has long been considered as a sign that the Universe, phenomenologically well-approximated as a Friedmann-Lemaître-Robertson-Walker (FLRW) model, is spatially small. Structures bigger than comoving space itself cannot exist physically, and their observational statistical description in the universal covering space (apparent space) should approximately reveal this (Starobinsky 1993; Stevens et al. 1993), even though the apparent nature of the covering space does permit structures that are larger than the Universe (Fig. 1, Roukema 1996). Small FLRW models have long been discussed (e.g., de Sitter 1917; Friedmann 1923, 1924; Lemaître 1927; Robertson 1935)1 The lack of structure on the largest scales is most simply seen in the spatial or angular two-point autocorrelation function of the temperature fluctuations, as spherical harmonical analysis requires a “conspiracy” between different harmonics in order to match the observed weak correlation at the largest scales (Spergel et al. 2003; Copi et al. 2007, 2009; Sarkar et al. 2011; Copi et al. 2010).
The locally homogeneous 3-manifolds that have most frequently been studied recently as candidates of comoving space in order to fit the WMAP data with an FLRW model include the 3-torus T3 (Spergel et al. 2003; Aurich et al. 2007; Aurich 2008; Aurich et al. 2008, 2010; Aslanyan & Manohar 2011) and the Poincaré dodecahedral space S3/I∗ (Luminet et al. 2003; Aurich et al. 2005a,b; Gundermann 2005; Caillerie et al. 2007; Roukema et al. 2008a,b). A full pre-WMAP classification of the positively curved spaces (including S3/I∗) and mathematical tools for studying them in the cosmological context were presented by Gausmann et al. (2001). Some analyses suggest that the Poincaré space may not provide a better fit than the infinite flat model or a hypersphere model2 (Key et al. 2007; Niarchou & Jaffe 2007). A heuristic argument in favour of the Poincaré space is that the residual gravity effect implied by imperfect cancellation of the gravitational signal from distant images of a nearby massive object singles out the Poincaré space as being better balanced than other spaces (Roukema et al. 2007; Roukema & Różański 2009).
If the Poincaré space hypothesis is correct, then the set of density perturbations in the Universe would not constitute a statistical ensemble of realisations of a model of density perturbation statistics, it would consist of a single physical realisation within a fundamental domain with a definite orientation and comoving size. Thus, it should be possible to find the optimal orientation and size of the fundamental domain in an astronomical coordinate system, rather than only estimate probabilities based on ensemble averages of simulated temperature fluctuations. The parameters of the optimal solution should then be usable to design observing strategies that should strengthen evidence either for or against the hypothesis.
Estimates of the optimal Poincaré space coordinates have been made (Roukema et al. 2008a,b). However, these estimates favoured the use of the moderately large-scale signal, up to ~4 h-1 Gpc. For geometrical reasons, this had the consequence that one of the fundamental domain parameters, the matched-circle observer-centred angular radius α, or equivalently, the (comoving) size of the Universe (2rinj, i.e. twice the injectivity radius, i.e. the length of the shortest closed spatial geodesic), was, in principle, only weakly constrained (Sect. 4.2, Fig. 9, Eq. (32), Roukema et al. 2008b). The random error in the estimate α ~ 21 ± 1° (Table 2, Roukema et al. 2008b) was suspected to be dominated by a systematic error of ~10°.
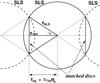 |
Fig. 1 Relation of matched discs to matched circles for the Poincaré dodecahedral space, with injectivity radius rinj = (π/10)RC, shown in the universal covering space S3 of radius RC. Multiple copies of the surface of last scattering (SLS) of radius rSLS intersect in circles lying in (flat) 2-planes that are orthogonal to the plane of the page. The interiors of the circles within these 2-planes constitute matched discs. The matched-circle (observer-centred) angular radius is α. Redshifts on either matched disc increase from zmin at the centre to zSLS on the boundary (the matched circle). The SLS can be replaced by the 2-sphere defined by z = 200 to obtain matched discs with 200 > z > zmin instead of zSLS > z > zmin. |
This uncertainty has critical consequences for the falsifiability of the model. If 32° ≲ α ≲ 48°, then multiply imaged objects should be observable at 40 ≳ z ≳ 10, respectively, near the centres of matched discs (Fig. 1). Matched discs and this redshift calculation are explained in Sect. 2.1 and the results are shown in Fig. 2. This redshift range is approximately that when 0.1% or so of baryons are expected to have formed H2-cooled protogalaxies within dark matter haloes of about 105 to 106 M⊙, in which very high mass Population III stars form and some explode as supernovae, while others may collapse directly into black holes (e.g., Glover 2005; Ciardi & Ferrara 2005; Greif et al. 2008, and references therein). Although the highest-redshift, spectroscopically confirmed, collapsed astrophysical object is a galaxy at z = 8.6 (Lehnert et al. 2010), it is generally expected that Population III stars may be detected as GRBs at z > 10 during the coming decades.
 |
Fig. 2 Upper panel: redshift zmin at the centre of a matched disc in a Poincaré space as a function of matched circle radius α, for Ωm = 0.26,0.28,0.30,0.32 as curved solid, dotted, dot-dashed and dashed lines, respectively (almost indistinguishable). Redshifts zmin = 10,40, and 200 are indicated as illustrations of epochs of successively rarer expected formation of galaxies with Population III stars. Lower panel: corresponding injectivity radius of the Universe rinj. |
However, if the Universe is larger, i.e. if 18° ≲ α ≲ 32°, then the corresponding redshifts are higher, in the range 200 ≳ z ≳ 40, respectively, so protogalaxies can have collapsed only in higher overdensity peaks, i.e. much more rarely. Their rareness at higher redshifts decreases the chance that observable objects will lie near the centres of the matched discs compared to the case for larger values of α.
The advantage of seeing two topologically lensed images of an object at nearly the same epoch is that evolutionary effects would be minimal, although there would still be a projection effect induced by seeing the same object “from front and back”. Significant evidence of the absence of a predicted topologically lensed image would be able to refute the Poincaré dodecahedral space model. Alternatively, well-matched topologically lensed pairs would increase the over-determined nature of the model, leading to successively more and more topological lensing predictions. Thus, it is important to see if the estimate of α can be made more accurate.
A more accurate estimate of α is made by using the cross-correlation method (Roukema et al. 2008a,b) at higher comoving spatial resolution ( ≲ 1 h-1 Gpc) than in the earlier work and updating to the WMAP 7-year data release. The method is presented in Sects. 2.2 and 2.3. Results are presented in Sect. 3 and conclusions are given in Sect. 4. All distances are FLRW comoving distances. The Hubble constant is written H0 = 100 h km s-1 Mpc-1.
2. Method
2.1. Matched discs
Here we introduce an observational corollary of the identified circles principle (Cornish et al. 1998; see also Fig. 2, Roukema 2000). Two circles on the surface of last scattering (SLS) are identified because in the comoving covering 3-space, they consist of the intersection of two copies of a single physical (flat) 2-plane with a 2-sphere (the SLS). Filled polygonal subsets of the two copies of the 2-plane constitute two faces of a copy of the fundamental domain that can be thought of as being pasted together. The flat interiors of the two matching circles – within the two copies of the flat 2-plane – constitute matched discs with sub-SLS redshifts, i.e. zmin ≤ z ≤ zSLS, where zmin occurs at the disc centre. This is illustrated in Fig. 1.
A large enough α (small enough 2rinj) would imply a low enough zmin for collapsed astrophysical objects (e.g. quasars, Lyman-break objects or gamma-ray bursts (GRBs) from early forming galaxies) located near the centres of these matched discs to be seen as nearly antipodal pairs at nearly identical redshifts. Objects successively further from the centres of the matched discs would be multiply imaged at successively higher redshifts z > zmin, i.e. at successively earlier, but still approximately equal, epochs. A survey whose selection criteria select a redshift band beyond zmin should detect an annulus of multiply imaged objects. For example, if zmin = 20 and the survey selects objects in the range 30 < z < 40, then there should be an annulus of multiply imaged objects.
The redshift to the centres of a pair of matched discs for a given matched circle radius α can be calculated by finding the value of the dark energy parameter ΩΛ that equates the curvature radius calculated locally with its value calculated globally using the injectivity radius. The former is RC = (c/H0)(Ωm + ΩΛ − 1)-0.5, where c is the spacetime unit conversion constant, Ωm is a fixed value of the matter density parameter, and H0 is the Hubble constant. The calculation using the injectivity radius is made using Eq. (15) of Roukema et al. (2008b), α and the comoving distance to the surface of last scattering rSLS(Ωm,ΩΛ,H0,zSLS), assuming zSLS = 1100. Thus, ![\begin{equation} \rC = \frac{c}{H_0} \frac{1}{\sqrt{\Omega_\Lambda + \Omm - 1}} = \frac{\rSLS(\Omm,\Omega_\Lambda,H_0)}{ \arctan \left[ \frac{\tan (\pi/10)}{\cos \alpha} \right]}\cdot \label{e-rC-equality} \end{equation}](/articles/aa/full_html/2011/09/aa17403-11/aa17403-11-eq58.png) (1)Given Ωm and H0, the latter equality can be solved numerically for ΩΛ, yielding RC from the former equality. The injectivity radius is
(1)Given Ωm and H0, the latter equality can be solved numerically for ΩΛ, yielding RC from the former equality. The injectivity radius is 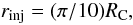 (2)so the redshift zmin to the centre of the matched discs is obtained by inverting
(2)so the redshift zmin to the centre of the matched discs is obtained by inverting 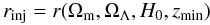 (3)where r is the standard FLRW radial comoving distance3.
(3)where r is the standard FLRW radial comoving distance3.
Figure 2 (upper panel) shows that if 32° ≲ α ≲ 48°, then the redshifts of objects lying in the matched discs would be in the range 40 ≳ z ≳ 10, respectively. For smaller matched circle radii 18° ≲ α ≲ 32°, the corresponding redshifts are higher, in the range 200 ≳ z ≳ 40, respectively.
Larger matched circle radii correspond to lower redshifts, but also higher total density and smaller curvature radii RC. For example, Fig. 15 of Gausmann et al. (2001) shows a multiple imaging spike with a minimum redshift lying in the range 1 < z < 3 when Ωm = 0.35, ΩΛ = 0.75. This can be calculated by using the left-hand equality of Eq. (1) to obtain RC = 9.48 h-1 Gpc, Eq. (2) to obtain rinj = 2.98 h-1 Gpc, and inverting Eq. (3), yielding z = 1.45. Use of the right-hand expression in Eq. (1) shows that the corresponding matched circle radius is α = 77°.
The lower panel of Fig. 2 shows the corresponding injectivity radius rinj of the Universe. While the redshift at the centre of a matched disc is insensitive to Ωm, the size of the Universe is sensitive to Ωm. When α = 0°, the injectivity radius is identical to the comoving distance to the surface of last scattering, i.e. rinj = rSLS (cf. Eqs. (1) and (2)).
2.2. Cross-correlation maximisation method
To improve the estimate of α, the cross-correlation method (Roukema et al. 2008a,b) is used over the single parameter α, using the previously found solution for the positions of the axes of the fundamental domain. The cross-correlation method can be thought of as reconstructing the spatial two-point correlation function of density fluctuations (using temperature fluctuations as a proxy) at sub-injectivity radius length scales, where an observed pair of points is only used if the observed spatial separation in the comoving covering space is larger than the injectivity radius. Holonomies gi are applied to one member y of a pair of observed spatial points (x,y) so that if the implied pair 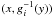 is a close pair, then the observed temperature fluctuation product ΔT(x) ΔT(y) is cumulated to the cross-correlation estimate at the separation
is a close pair, then the observed temperature fluctuation product ΔT(x) ΔT(y) is cumulated to the cross-correlation estimate at the separation ![\hbox{$d[x,g_i^{-1}(y)]$}](/articles/aa/full_html/2011/09/aa17403-11/aa17403-11-eq76.png) . The method can also be thought of as an extension of the identified circles principle (Cornish et al. 1998), but with a uniform sky weighting over observed points instead of a weighting that favours matched circle intersections. If a hypothesised set of sky orientation, injectivity radius and twist parameters are physically correct, then the locally isotropic components of the auto-correlation function should be reproduced by the cross-correlation function.
. The method can also be thought of as an extension of the identified circles principle (Cornish et al. 1998), but with a uniform sky weighting over observed points instead of a weighting that favours matched circle intersections. If a hypothesised set of sky orientation, injectivity radius and twist parameters are physically correct, then the locally isotropic components of the auto-correlation function should be reproduced by the cross-correlation function.
2.3. Correlation functions and optimisation criterion
The Markov chain Monte Carlo (MCMC) method used in (Roukema et al. 2008a,b) adopted Np = 2000 points per position in MCMC parameter space (Sect. 3.5, Roukema et al. 2008b). The optimisation criterion (a pseudo-probability) was aimed at maximising ξC − ξA at ≲ 4 h-1 Gpc scales. The definition of the criterion (Eqs. (25), (26), Roukema et al. 2008b) took into account the uncertainty in estimating the cross-correlation ξC(r) induced by using a small value of Np. This provided a practical method of exploring a large volume of parameter space, focussing on cross- and auto-correlations mostly at the upper end of the separation range r ≲ 4 h-1 Gpc.
Here, in order to optimise the estimate of α, a much higher number of points is used per correlation calculation, i.e. Np = 2 × 105, and only α is varied. This enables the use of the correlation signal at separations r ≲ 1 h-1 Gpc. From Fig. 11 of Roukema et al. (2008b), it is clear that ξA ≫ ξC at r ≲ 1 h-1 Gpc. Because of the complicated mix of different effects – the naïve Sachs-Wolfe effect, the integrated Sachs-Wolfe effect, the Doppler effect, and intrinsic temperature fluctuations – that contribute to ξC and the auto-correlation ξA, it is not obvious whether ξC should be as high as ξA at sub-Gpc scales. In other words, on these smaller scales, the increasing contribution of the Doppler effect – which is locally anisotropic – to the temperature fluctuations makes it less realistic to test the hypothesis that ξC and ξA are identical functions apart from calculational uncertainty. Moreover, the higher value of Np reduces the numerical usefulness of estimating the calculational uncertainty.
Hence, with the aim of maximising the cross-correlation of locally isotropic emission, the optimisation criterion is defined as the mean cross-correlation below a given length scale, without a direct comparison with the auto-correlation. However, since the comoving (spatial geodesic) separation d(θA,rSLS) between two fixed points on the SLS separated by an observer-centred angle θA varies with Ωm and ΩΛ, d needs to be replaced by a scaled separation β that to a good approximation depends only on θA, in order that ξA(β) has only a weak dependence on Ωm and ΩΛ. This can be done for small separations d, which are the ones of most interest. As in Eq. (16) of Roukema et al. (2008b), the spherical sine law gives ![\begin{equation} \frac{ \sin[ d(\theta_{\rm A},\rSLS) /(2\rC)]}{\rSLS} = \frac{1}{\rSLS} \sin \frac{\theta_{\rm A}}{2} \sin\frac{\rSLS}{\rC}, \label{e-autocorr-separation-A} \end{equation}](/articles/aa/full_html/2011/09/aa17403-11/aa17403-11-eq96.png) (4)i.e.
(4)i.e. 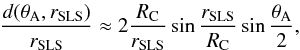 (5)where the second and higher order terms in the Taylor expansion of sin [d/(2RC)] are dropped, since for d ≲ 1 h-1 Gpc and RC ≳ 25 h-1 Gpc, d/(2RC) ≲ 0.02. Using Eq. (15) of Roukema et al. (2008b), the ratio
(5)where the second and higher order terms in the Taylor expansion of sin [d/(2RC)] are dropped, since for d ≲ 1 h-1 Gpc and RC ≳ 25 h-1 Gpc, d/(2RC) ≲ 0.02. Using Eq. (15) of Roukema et al. (2008b), the ratio 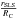 depends only on α, without any direct dependence on Ωm and ΩΛ. For 0° ≤ α ≤ 45°, we have
depends only on α, without any direct dependence on Ωm and ΩΛ. For 0° ≤ α ≤ 45°, we have 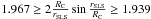 , respectively, i.e. the latter expression varies by less than 1.5% over this range. In contrast, for 0.25 ≤ Ωm ≤ 0.35, rSLS varies by about 14%. Thus, β: = d/rSLS depends mostly on θA and only weakly on Ωm and ΩΛ.
, respectively, i.e. the latter expression varies by less than 1.5% over this range. In contrast, for 0.25 ≤ Ωm ≤ 0.35, rSLS varies by about 14%. Thus, β: = d/rSLS depends mostly on θA and only weakly on Ωm and ΩΛ.
This is used for the mean cross-correlation, i.e. the latter is calculated below a fixed fraction β of the comoving distance to the surface of last scattering radius, 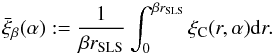 (6)The primary scales of interest are β = 0.033 and 0.1, corresponding to βrSLS ≈ 0.33 and 1 h-1 Gpc, respectively.
(6)The primary scales of interest are β = 0.033 and 0.1, corresponding to βrSLS ≈ 0.33 and 1 h-1 Gpc, respectively.
The primary estimate is the matched circle radius α that maximises 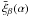 for β = 0.033 and 0.1 for the 7-year WMAP ILC map4, masking with the KQ85 mask to minimise galactic contamination. Estimates of the systematic error, assumed to dominate the random error, are made by considering the foreground-reduced V band5 and W band maps6, and by applying the KQ75 mask.
for β = 0.033 and 0.1 for the 7-year WMAP ILC map4, masking with the KQ85 mask to minimise galactic contamination. Estimates of the systematic error, assumed to dominate the random error, are made by considering the foreground-reduced V band5 and W band maps6, and by applying the KQ75 mask.
Since the aim here is to see whether the uncertainty in α can be reduced so that it no longer dominates the uncertainty in the optimal solution, the sky orientation parameters of the fundamental domain are fixed at (l,b,θ) = (184.0°,62.0°,34.0°), using the exact dodecahedral solution found in Roukema et al. (2008b, Fig. 11 caption) rather than the individual axis estimates.
3. Results
3.1. Matched circle radius α
Figure 3 shows a well-defined local peak in the mean correlation 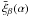 near α = 23°. Even for β = 0.4, i.e. using the ≲ 4 h-1 Gpc cross-correlations, a small local peak near the same value is present. The smaller scale cross-correlations clearly overcome the concern of a systematic error of about 10° in the estimate of α.
near α = 23°. Even for β = 0.4, i.e. using the ≲ 4 h-1 Gpc cross-correlations, a small local peak near the same value is present. The smaller scale cross-correlations clearly overcome the concern of a systematic error of about 10° in the estimate of α.
Several features of this figure can be interpreted simply if the overall Poincaré dodecahedral space solution is physically correct. Firstly, as would be expected for a true solution, the rough solution found using the larger scale signal becomes better defined using the smaller scale signal. Secondly, as α decreases down to 10°, 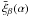 drops strongly. The smaller β is, the sharper the drop. This is consistent with the solution being correct, since matched circles for wrong values of α that are smaller than the would-be true value force small-scale cross-correlations to be estimated at large true separations, where the auto-correlation is weak.
drops strongly. The smaller β is, the sharper the drop. This is consistent with the solution being correct, since matched circles for wrong values of α that are smaller than the would-be true value force small-scale cross-correlations to be estimated at large true separations, where the auto-correlation is weak.
 |
Fig. 3 Gigaparsec-scale cross-correlation |
 |
Fig. 6 Gigaparsec-scale cross-correlation |
 |
Fig. 7 Spatial auto- and cross-correlation functions, ξA and ξC, respectively, for the WMAP7 ILC map for matched-circle radius α = 23°, shown as thin and thick (colour online) curves, respectively. The cross-correlation function is uniformly sampled only for β ≤ 0.44 (for calculation speed); at higher separations, it is, in principle, biased. In order to better compare the small-scale behaviour of ξA and ξC, the auto-correlation reduced (arbitrarily) by a factor of 4 is also shown. The mostly upper (lower) member of each close pair of functions is for the KQ85 (KQ75) galactic mask. |
Matched-circle radius α at which the Gpc-scale cross-correlation 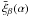 is maximised.
is maximised.
Figures 4 and 5 show that the peak in 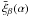 is present in both the V and W foreground-reduced maps. Figure 6 shows that the peak is a little weakened using a stronger galactic cut, but remains present. Because of the 36° rotation used in matching circles or discs, stronger galactic cuts severely reduce the numbers of matched pairs and nearly matched pairs.
is present in both the V and W foreground-reduced maps. Figure 6 shows that the peak is a little weakened using a stronger galactic cut, but remains present. Because of the 36° rotation used in matching circles or discs, stronger galactic cuts severely reduce the numbers of matched pairs and nearly matched pairs.
The matched circle radii that maximise 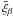 , after a Gaussian smoothing with σα = 0.2°, are listed in Table 1. In the ILC KQ85-masked map, the maximum cross-correlation is independent of the integration length scale β, giving α = 23.0° in all four cases. A sharp maximum cross-correlation is clearly present at about the same matched circle radius for the single-band V and W (foreground-reduced) maps, but with some dependence on β. The ≲ 1 h-1 Gpc scale V and W maps (β = 0.033,0.1) give 21.8° ≤ α ≤ 23°. The ILC KQ75-masked map again gives a maximum
, after a Gaussian smoothing with σα = 0.2°, are listed in Table 1. In the ILC KQ85-masked map, the maximum cross-correlation is independent of the integration length scale β, giving α = 23.0° in all four cases. A sharp maximum cross-correlation is clearly present at about the same matched circle radius for the single-band V and W (foreground-reduced) maps, but with some dependence on β. The ≲ 1 h-1 Gpc scale V and W maps (β = 0.033,0.1) give 21.8° ≤ α ≤ 23°. The ILC KQ75-masked map again gives a maximum 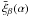 that is independent of β, i.e. α = 23.8°, a little higher than the other estimates. Conservatively taking the maximum differences to be independent and adding them in quadrature, the systematic error in the estimate of α induced by the choice of the map and the galactic mask is 1.4°, giving α = 23.0 ± 1.4° as the improved estimate of the matched circle radius.
that is independent of β, i.e. α = 23.8°, a little higher than the other estimates. Conservatively taking the maximum differences to be independent and adding them in quadrature, the systematic error in the estimate of α induced by the choice of the map and the galactic mask is 1.4°, giving α = 23.0 ± 1.4° as the improved estimate of the matched circle radius.
The cross-correlation functions for the ILC map for α = 23° are shown in Fig. 7. This should be compared with Fig. 11 of Roukema et al. (2008b). In Fig. 7, since the method of Roukema et al. (2008a) is used to speed up the calculations, only separations below β = 0.44, i.e. about 4.4 h-1 Gpc, are based on an underlying uniform sky distribution. Nevertheless, cross-correlations at higher scales are similar to those in Fig. 11 of Roukema et al. (2008b), i.e. they do not appear to be strongly affected by the potential bias.
The main new feature in Fig. 7 is that there is a sharp upturn at sub-Gpc scales, which was not visible in Fig. 11 of Roukema et al. (2008b), rather than a continuation of the approximately constant slope on 1 − 5 h-1 Gpc scales, visible in both figures. If the naïve Sachs-Wolfe effect, i.e. a locally isotropic effect, contributes about half of typical temperature fluctuation amplitudes on these scales, then the expected cross-correlation should be ξC ~ ξA/4. The latter function is plotted in Fig. 7, in addition to ξA. This shows that ξC ~ ξA/4 indeed gives a rough estimate of the cross-correlation on sub-Gpc scales with β > 0.011, i.e., βrSLS ≳ 0.11 h-1 Gpc. Thus, a possible order-of-magnitude interpretation would be that about half the temperature fluctuations on these scales are locally isotropic.
3.2. Inferred parameters: 2rinj,zmin,α200
As described above, for a choice of Ωm, H0, and α, Eqs. (1) and (2) can be used to find ΩΛ, RC, rinj and the redshift to the matched disc centres zmin. For Ωm = 0.28 ± 0.02 and α = 23 ± 1.4°, and assuming that these give Gaussian independent errors, twice the injectivity radius of the Universe is 2rinj = 18.2 ± 0.5 h-1 Gpc, and the redshift to the matched disc centres is zmin = 106 ± 18.
The angular radius of a matched disc from its centre at zmin = 106 ± 18 up to a redshift at which some of the very high density peaks should first collapse, z = 200, can be calculated analogously to Eq. (15) of Roukema et al. (2008b), i.e. ![\begin{equation} \alpha_{200} = \arccos \left[ \cos\alpha \, \frac{\tan (\rSLS/\rC)}{\tan (r_{200}/\rC)} \right], \label{e-alpha-200} \end{equation}](/articles/aa/full_html/2011/09/aa17403-11/aa17403-11-eq147.png) (7)where r200 is the comoving radial distance to z = 200 for the same values of Ωm,ΩΛ, and H0 as for the other parameters. This yields α200 = 14.8 ± 2.3°. These discs do not intersect with one another. Thus, for the full sky, the 12 matched discs for 200 > z > 106 would project to a fraction of 24π(1 − cosα200)/(4π) = 20 ± 6% of the sky. The fractional coverage of the unmasked sky should be similar.
(7)where r200 is the comoving radial distance to z = 200 for the same values of Ωm,ΩΛ, and H0 as for the other parameters. This yields α200 = 14.8 ± 2.3°. These discs do not intersect with one another. Thus, for the full sky, the 12 matched discs for 200 > z > 106 would project to a fraction of 24π(1 − cosα200)/(4π) = 20 ± 6% of the sky. The fractional coverage of the unmasked sky should be similar.
4. Conclusion
The sub-Gpc cross-correlation estimates shown in Figs. 3 − 6 show that the systematic uncertainty in the earlier estimate of the matched circle radius for the optimal fit of the Poincaré dodecahedral space model to WMAP sky maps is significantly reduced by using this high-resolution signal, giving α = 23 ± 1.4°. For Ωm = 0.28 ± 0.02, the inferred size of the Universe is 2rinj = 18.2 ± 0.5 h-1 Gpc.
This constraint on α pushes sub-SLS multiple-image testing of the Poincaré space model (at least) several decades into the future, given present plans for new telescope projects. Nevertheless, higher density peaks should collapse and form population III stars earlier than lower density peaks, so future surveys of very high density peaks that collapse early, during 200 > z > 106, should, in principle, be feasible. The objects would be (multiply) visible in 12 matched flat discs that project to about 20% of the full sky. The redshifts of the objects increase radially from z = 106 ± 18 at the centre of a disc out to the edge of the disc defined by z = 200. An annulus extending the disc further to zSLS ≈ 1100 on the SLS would define a multiply imaged region where collapsed objects would be extremely rare. The two topologically lensed images of a physical object are located at identical redshifts at widely separated directions in the sky in discs that are antipodal and matched with a twist of + 36° (right-handed). The redshift equality of the two images of an object implies that evolutionary effects would not be a problem for objects located exactly in the discs. Objects that are in the close foreground/background (foreground in one disc, background in
the other disc) would have small evolutionary differences between the two images of an object.
Lemaître (1927) is the paper in which Lemaître used redshift and distance estimates of 42 galaxies to estimate the value of what is now known as H0, finding 575 km s-1 Mpc-1 (unweighted) or 625 km s-1 Mpc-1 (weighted). An incomplete English translation that excludes almost all of the observational analysis was published four years later (Lemaître 1931). See van den Bergh (2011) and Block (2011) and references therein for discussion of this issue.
Acknowledgments
A part of this project has made use of Program Obliczeń Wielkich Wyzwań nauki i techniki (POWIEW) computational resources (grant 87) at the Poznań Supercomputing and Networking Center (PCSS). Use was made of the Centre de Données astronomiques de Strasbourg (http://cdsads.u-strasbg.fr), the GNU plotutils graphics package, and the GNU Octave command-line, high-level numerical computation software (http://www.gnu.org/software/octave).
References
- Aslanyan, G., & Manohar, A. V. 2011 [arXiv:1104.0015] [Google Scholar]
- Aurich, R. 2008, Class. Quant. Gra., 25, 225017 [Google Scholar]
- Aurich, R., Lustig, S., & Steiner, F. 2005a, Class. Quant. Gra., 22, 3443 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Aurich, R., Lustig, S., & Steiner, F. 2005b, Class. Quant. Gra., 22, 2061 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Aurich, R., Lustig, S., Steiner, F., & Then, H. 2007, Class. Quant. Gra., 24, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Aurich, R., Janzer, H. S., Lustig, S., & Steiner, F. 2008, Class. Quant. Gra., 25, 125006 [Google Scholar]
- Aurich, R., Lustig, S., & Steiner, F. 2010, Class. Quant. Gra., 27, 095009 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Block, D. L. 2011 [arXiv:1106.3928] [Google Scholar]
- Caillerie, S., Lachièze-Rey, M., Luminet, J.-P., et al. 2007, A&A, 476, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciardi, B., & Ferrara, A. 2005, Space Sci. Rev., 116, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Copi, C. J., Huterer, D., Schwarz, D. J., & Starkman, G. D. 2007, Phys. Rev. D, 75, 023507 [Google Scholar]
- Copi, C. J., Huterer, D., Schwarz, D. J., & Starkman, G. D. 2009, MNRAS, 399, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Copi, C. J., Huterer, D., Schwarz, D. J., & Starkman, G. D. 2010, Adv. Astron., 2010, 847541 [Google Scholar]
- Cornish, N. J., Spergel, D. N., & Starkman, G. D. 1998, Class. Quant. Gra., 15, 2657 [NASA ADS] [CrossRef] [Google Scholar]
- de Sitter, W. 1917, MNRAS, 78, 3 [NASA ADS] [Google Scholar]
- Friedmann, A. 1923, Mir kak prostranstvo i vremya, The Universe as Space and Time (Leningrad: Academia) [Google Scholar]
- Friedmann, A. 1924, Zeitschr. für Phys., 21, 326 [Google Scholar]
- Gausmann, E., Lehoucq, R., Luminet, J.-P., Uzan, J.-P., & Weeks, J. 2001, Class. Quant. Gra., 18, 5155 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. 2005, Space Sci. Rev., 117, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Greif, T. H., Johnson, J. L., Klessen, R. S., & Bromm, V. 2008, MNRAS, 387, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Gundermann, J. 2005, unpublished [arXiv:astro-ph/0503014] [Google Scholar]
- Key, J. S., Cornish, N. J., Spergel, D. N., & Starkman, G. D. 2007, Phys. Rev. D, 75, 084034 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Nesvadba, N. P. H., Cuby, J.-G., et al. 2010, Nature, 467, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaître, G. 1927, Annales de la Société Scientifique de Bruxelles, 47, 49 [NASA ADS] [Google Scholar]
- Lemaître, G. 1931, MNRAS, 91, 483 [NASA ADS] [Google Scholar]
- Luminet, J., Weeks, J. R., Riazuelo, A., Lehoucq, R., & Uzan, J. 2003, Nature, 425, 593 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Niarchou, A., & Jaffe, A. 2007, PRL, 99, 081302 [Google Scholar]
- Robertson, H. P. 1935, ApJ, 82, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Roukema, B. F. 1996, MNRAS, 283, 1147 [NASA ADS] [Google Scholar]
- Roukema, B. F. 2000, Bull. Astr. Soc. India, 28, 483 [NASA ADS] [Google Scholar]
- Roukema, B. F., & Różański, P. T. 2009, A&A, 502, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roukema, B. F., Bajtlik, S., Biesiada, M., Szaniewska, A., & Jurkiewicz, H. 2007, A&A, 463, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roukema, B. F., Buliński, Z., & Gaudin, N. E. 2008a, A&A, 492, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roukema, B. F., Buliński, Z., Szaniewska, A., & Gaudin, N. E. 2008b, A&A, 486, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarkar, D., Huterer, D., Copi, C. J., Starkman, G. D., & Schwarz, D. J. 2011, Astropart. Phys., 34, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Starobinsky, A. A. 1993, JETP Lett., 57, 622 [NASA ADS] [Google Scholar]
- Stevens, D., Scott, D., & Silk, J. 1993, PRL, 71, 20 [Google Scholar]
- van den Bergh, S. 2011, J. Roy. Ast. Soc. Canada, in press [arXiv:1106.1195] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Relation of matched discs to matched circles for the Poincaré dodecahedral space, with injectivity radius rinj = (π/10)RC, shown in the universal covering space S3 of radius RC. Multiple copies of the surface of last scattering (SLS) of radius rSLS intersect in circles lying in (flat) 2-planes that are orthogonal to the plane of the page. The interiors of the circles within these 2-planes constitute matched discs. The matched-circle (observer-centred) angular radius is α. Redshifts on either matched disc increase from zmin at the centre to zSLS on the boundary (the matched circle). The SLS can be replaced by the 2-sphere defined by z = 200 to obtain matched discs with 200 > z > zmin instead of zSLS > z > zmin. |
| In the text | |
 |
Fig. 2 Upper panel: redshift zmin at the centre of a matched disc in a Poincaré space as a function of matched circle radius α, for Ωm = 0.26,0.28,0.30,0.32 as curved solid, dotted, dot-dashed and dashed lines, respectively (almost indistinguishable). Redshifts zmin = 10,40, and 200 are indicated as illustrations of epochs of successively rarer expected formation of galaxies with Population III stars. Lower panel: corresponding injectivity radius of the Universe rinj. |
| In the text | |
 |
Fig. 3 Gigaparsec-scale cross-correlation |
| In the text | |
 |
Fig. 4 Gigaparsec-scale cross-correlation |
| In the text | |
 |
Fig. 5 Gigaparsec-scale cross-correlation |
| In the text | |
 |
Fig. 6 Gigaparsec-scale cross-correlation |
| In the text | |
 |
Fig. 7 Spatial auto- and cross-correlation functions, ξA and ξC, respectively, for the WMAP7 ILC map for matched-circle radius α = 23°, shown as thin and thick (colour online) curves, respectively. The cross-correlation function is uniformly sampled only for β ≤ 0.44 (for calculation speed); at higher separations, it is, in principle, biased. In order to better compare the small-scale behaviour of ξA and ξC, the auto-correlation reduced (arbitrarily) by a factor of 4 is also shown. The mostly upper (lower) member of each close pair of functions is for the KQ85 (KQ75) galactic mask. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


