| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201117322 | |
| Published online | 29 August 2011 | |
Alfvén instability of steady state flux tubes. Isothermal flow
Institute of Mathematics and Physics, Aberystwyth University,
Penglais,
Aberystwyth
SY23 3BZ,
UK
e-mail: yot@aber.ac.uk
Received:
23
May
2011
Accepted:
26
July
2011
Context. MHD instabilities are expected to play an important role in the dynamics and energetics of the solar atmosphere.
Aims. One application of a recently discovered MHD instability to an open magnetic flux tube is investigated. The flux tube is gravitationally stratified and permeated by a smooth isothermal flow.
Methods. The equilibrium structure is derived, and the stability of the tube with respect to small amplitude torsional perturbations generated at the footpoint by random convective motions analysed.
Results. It is shown that torsional perturbations are exponentially amplified in time if a narrow region exists where the flux tube rapidly expands while the plasma is flowing away from the footpoint. No high flow speeds are required for the instability to set in.
Conclusions. These obtained results may account for the nonthermal broadenings associated with upflows in magnetic regions of the lower solar atmosphere. However, additional studies that incorporate temperature variations are needed for more robust conclusions.
Key words: instabilities / magnetohydrodynamics (MHD) / Sun: atmosphere
© ESO, 2011
1. Introduction
In hydrodynamics, the interaction and energy exchange between small perturbations and flows has been extensively studied under different conditions. Reviews and applications to a wide range of astrophysical and laboratory systems can be found in Chandrasekhar (1961), Drazin & Reid (1981), and Drazin (2002). The inclusion of an ambient magnetic field introduces new types of waves and perturbations, and the interaction with the flow becomes more complex. Fundamental among those is the Alfvén wave arising from the competing effects between magnetic tension and plasma inertia. Since their discovery by Alfvén (1942) these waves have been extensively studied in various contexts including the heating of laboratory plasmas and the upper solar atmosphere, formation of spicules and the acceleration of the solar wind (Alfvén 1947; Obiki et al. 1977; Ionson 1978; Heinemann & Olbert 1980; Heyvaerts & Priest 1983; Hollweg 1992; Ofman & Davila 1995; Verth et al. 2010; Antolin & Shibata 2010; Murawski & Musielak 2010; McLaughlin et al. 2011; Vasheghani Farahani et al. 2011; Airapetian et al. 2011).
Flows in magnetic confinement devices, the solar wind, siphon flows in coronal loops, Evershed flows, jets, and spicules are all examples of flows in laboratory and astrophysical systems. The Doppler shift pattern of EUV emission lines was found to be linked with the field topology of solar atmospheric structures (Marsch et al. 2004, 2008). The blueshifts of Ne viii at the network junctions were observed to be long-lasting, and thus are expected to play a permanent role in the process of coronal mass circulation.
The magnetic field can either facilitate or inhibit the development of instabilities in magnetised plasma flows. The magnetorotational instability is an instance of the first case, whereas the shear flow instability of a planar tangential discontinuity corresponds to the second case.
The amplification of MHD waves due to their interaction with unstratified shear flows has been studied in relation to various problems in solar-terrestrial physics (Yang & Hollweg 1991; Miura 1992; Tirry et al. 1998; Ruderman & Goossens 1995; Joarder et al. 1997; Andries & Goossens 2001; Taroyan & Erdélyi 2003; Terradas et al. 2010; Zaqarashvili et al. 2010; Foullon et al. 2011).
Nonlinear circularly polarized Alfvén waves can become unstable when small amplitude compressible fluctuations are allowed. There are several different mechanisms by which this instability can take place, but they all belong to a class known as parametric instabilities. A parametric instability arises in situations where a system’s parameters are varied, or pumped, periodically. The perturbations may grow at the expense of the pump. Simpson & Ruderman (2005), and Simpson et al. (2006) have studied the absolute and convective instabilities of circularly polarized Alfvén waves propagating along an ambient magnetic field.
The interaction of MHD waves and flows in stratified media has also been studied. Erdelyi & Hargreaves (2008) investigated the propagation of longitudinal magnetic tube waves in a stratified isothermal flux tube with an internal equilibrium background flow. The effect of the background flow is to introduce an increase in the wave amplitude and change the phase shift when compared with the corresponding static case.The propagation of torsional Alfvén waves in a stratified and unbounded flowing atmosphere in the context of the solar wind was examined by, e.g., Belcher (1971), Heinemann & Olbert (1980), and Hollweg & Isenberg (2007).
Parker (1991) argued that photospheric convection is unlikely to produce Alfvén waves with large enough amplitudes to heat the corona or to power the solar wind. Recently, Taroyan (2008) has established the possibility of a new MHD instability associated with incompressible Alfvénic disturbances in compressible plasma flows.
It is well known that compressibility has a stabilising effect on the Kelvin-Helmholtz instability (e.g., Pu & Kivelson 1983). In this and other studies, the stability, in contrast to the strictly incompressible case, is due to the presence of small compressible perturbations. However, the flow remains incompressible: ∇·V = 0, where V is the bulk velocity. The instability studied in the present paper only arises when the flow is compressible. Also no shear is required, in contrast to the Kelvin-Helmholtz instability, so the physical mechanism is different. The linear Alfvénic disturbances are over-reflected and exponentially amplified due to the compressibility of the flow which is sub-Alfvénic and provides the required energy. The details of this process are discussed by Taroyan (2008).
An applications of the new instability to coronal loops with siphon flows was presented by Taroyan (2009). It was shown that in asymmetric loops with siphon flows linear torsional perturbations driven at the footpoints may become exponentially amplified.
The present paper extends these studies to gravitationally stratified isothermal flux tubes in which the plasma flow variations are smooth. The compressibility of the flow is due to variations in the cross-sectional surface area of the flux tube.
2. Governing equations
The focus of our study is an axisymmetric magnetic flux tube. The following model was introduced by Hollweg et al. (1982) to study the propagation of Alfvén waves in the lower solar atmosphere and the formation of spicules: we consider a single field line along which distance is denoted by s. The photospheric boundary is placed at s = 0. Distance from the axis of symmetry is denoted by r = r(s). The azimuthal angle about the axis of symmetry is denoted by θ. In the azimuthal direction, only axisymmetric motions are considered, so ∂/∂θ = 0. The main drawback of the model is that any radial expansion or contraction of the flux tube are assumed to be negligible. The model has been applied to both linear and nonlinear problems in various solar and stellar contexts (Sterling & Hollweg 1984; Mariska & Hollweg 1985; Kudoh & Shibata 1997; Moriyasu et al. 2004; Fujita et al. 2007; Musielak et al. 2007; Antolin & Shibata 2010).
The starting point for our analysis is the set of nonlinear equations of conservation of
mass, momentum, energy and induction for the mass density ρ,
pressure p, the s and θ components of
the magnetic field,
(Bs,Bθ),
and velocity,
(us,uθ):
![\begin{eqnarray} \label{eq1}&& \frac{\partial}{\partial t}\left(\frac{\rho}{B_s}\right) + \frac{\partial}{\partial s} \left(\frac{\rho u_s}{B_s}\right)=0, \\[1.5mm] \label{eq2} &&\frac{\partial}{\partial t}\left(\frac{\rho r u_\theta}{B_s}\right) + \frac{\partial}{\partial s} \left(\frac{\rho r u_\theta}{B_s} u_s\right) = \frac1{\mu_0}\frac{\partial}{\partial s} \left(r B_\theta\right), \\[1.5mm] &&\frac{\partial}{\partial t}\left(\frac{\rho u_s}{B_s}\right) + \frac{\partial}{\partial s} \left(\frac{\rho u_s}{B_s} u_s\right) = -\frac1{B_s}\frac{\partial p}{\partial s}+\frac{\rho g_s}{B_s}+\frac1{B_s}\nonumber \\[1.5mm] \label{eq3} &&\qquad\qquad\qquad\qquad\qquad\ \ \times\left[ \left(\rho u_{\theta}^2 \!-\! \frac{B_{\theta}^2}{\mu_0}\right) \frac{\partial \ln r}{\partial s}-\frac{\partial}{\partial s}\left(\frac{B_\theta^2}{2\mu_0}\right) \right], \\[1.5mm] \label{eq4} &&\frac{\partial}{\partial t}\left(\frac{p}{B_s}\right)+ \frac{\partial}{\partial s}\left(\frac{p}{B_s} u_s\right) = -(\gamma-1)p\frac{\partial}{\partial s}\left(\frac{u_s}{B_s}\right), \\[1.5mm] \label{eq5}&&\frac{\partial}{\partial t}\left(\frac{B_\theta}{r B_s}\right)+ \frac{\partial}{\partial s}\left(\frac{B_\theta}{r B_s} u_s\right)=\frac{\partial}{\partial s}\left(\frac{u_\theta}{r}\right), \end{eqnarray}](/articles/aa/full_html/2011/09/aa17322-11/aa17322-11-eq12.png) where
gs is the s component of the
gravitational acceleration, and γ is the adiabatic index. In the above
equations, Bs is a function
of s, but not of t. The condition for the conservation
of magnetic flux can be reduced to
where
gs is the s component of the
gravitational acceleration, and γ is the adiabatic index. In the above
equations, Bs is a function
of s, but not of t. The condition for the conservation
of magnetic flux can be reduced to 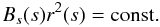 (6)provided the
chosen field line is near the axis of the flux tube.
(6)provided the
chosen field line is near the axis of the flux tube.
2.1. The steady equilibrium state
The equilibrium structure of the flux tube is shown in Fig. 1. The equilibrium quantities are denoted by a subscript 0. The magnetic
field B0 is untwisted, i.e., only
the s component is present. The flux tube is permeated by a
field-aligned mass flow u0. The steady
equilibrium is determined by the conservation equations of mass (1), momentum (3) and energy (4):
![\begin{eqnarray} \label{eq7}&&\frac{{\rm d}}{{\rm d} s}\left(\frac{\rho_0 u_0}{B_0}\right) = 0, \\[2.5mm] \label{eq8}&&\frac{{\rm d}}{{\rm d} s}\left(\frac{\rho_0 u_0}{B_0}u_0\right) = \frac1{B_0}\left(-\frac{{\rm d} p_0}{{\rm d} s} + \rho_0 g_s\right), \\[2.5mm] \label{eq9}&&\frac{{\rm d}}{{\rm d} s}\left(\frac{p_0 u_0}{B_0}\right) = -(\gamma-1)p_0\frac{\partial}{\partial s}\left(\frac{u_0}{B_0}\right), \end{eqnarray}](/articles/aa/full_html/2011/09/aa17322-11/aa17322-11-eq20.png) where
ρ0, p0,
B0 and u0 are the
time-independent density, pressure, field strength and flow speed along the chosen field
line. The quantity gs is
the s component of gravitational acceleration.
where
ρ0, p0,
B0 and u0 are the
time-independent density, pressure, field strength and flow speed along the chosen field
line. The quantity gs is
the s component of gravitational acceleration.
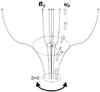 |
Fig. 1 A cartoon of an expanding flux tube in which plasma flows along the field lines. The s = 0 level represents the footpoint which is twisted by convective motions. |
Combining Eqs. (7) and (9) it can be shown that an adiabatic flow with
γ = 5/3 implies a decreasing temperature for decreasing density. In
order to replicate the temperature increase from photospheric to chromospheric/coronal
values, one has to include an extra heating term in the energy Eq. (9) that would balance losses due to advection.
In addition, the role of radiation and thermal conduction should be taken into account. In
the present paper, we make the simplifying assumption of an isothermal flow with
γ = 1. Thus the energy Eq. (9) is reduced to T0 = const. or
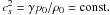 ,
where cs is the sound speed.
,
where cs is the sound speed.
Equations (7–9) can be solved to express the magnetic field, density and Alfvén
speed
(cA = B0/(μ0ρ0)1/2)
in terms of the flow speed: 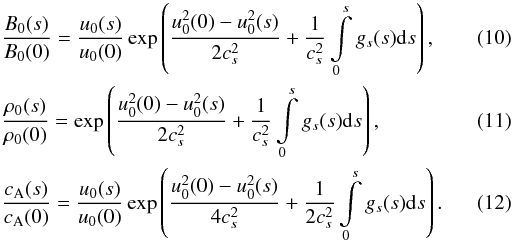
2.2. Linear torsional perturbations
Equations (1–5) can be linearised when small amplitude perturbations are considered.
The θ components of the magnetic field and velocity perturbations,
bθ
and vθ, become decoupled from the
corresponding s components and from the pressure and density
perturbations. These incompressible torsional perturbations are governed by the linearised
Eqs. (2) and (5): ![\begin{eqnarray} \label{eq13}&&\frac{\rho_0 r}{B_0} \frac{\partial v_\theta}{\partial t} + \frac{\partial}{\partial s} \left(\frac{\rho_0 r u_0}{B_0} v_\theta\right) = \frac1{\mu_0}\frac{\partial}{\partial s} \left(r b_\theta\right), \\[1.5mm] \label{eq14}&&\frac{1}{r B_0}\frac{\partial b_\theta}{\partial t} + \frac{\partial}{\partial s}\left(\frac{u_0}{r B_0} b_\theta\right) = \frac{\partial}{\partial s}\left(\frac{v_\theta}{r}\right)\cdot \end{eqnarray}](/articles/aa/full_html/2011/09/aa17322-11/aa17322-11-eq34.png) Equations (13) and (14) can be Fourier transformed with respect to t:
Equations (13) and (14) can be Fourier transformed with respect to t:
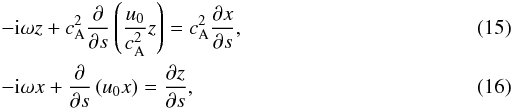 where
ω is the frequency. The newly introduced s-dependent
variables x, z are defined through the Fourier
transforms of the magnetic field and velocity perturbations:
where
ω is the frequency. The newly introduced s-dependent
variables x, z are defined through the Fourier
transforms of the magnetic field and velocity perturbations: 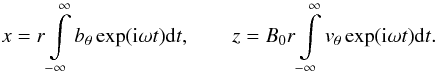 (17)Equations (15) and (16) can be rearranged and presented in the following canonical form:
(17)Equations (15) and (16) can be rearranged and presented in the following canonical form:
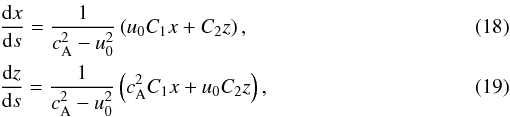 where
where
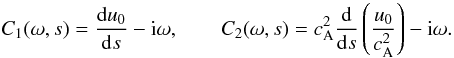 (20)The footpoint of
the flux tube is continually shaken by photospheric motions. The propagation of small
amplitude perturbations along the flux tube caused by footpoint twists is
determined by the system (13, 14). In order to establish the stability of the
steady equilibrium state with respect to arbitrary torsional motions, we consider a single
Dirac delta function pulse for vθ with no
variations for the magnetic field at s = 0:
(20)The footpoint of
the flux tube is continually shaken by photospheric motions. The propagation of small
amplitude perturbations along the flux tube caused by footpoint twists is
determined by the system (13, 14). In order to establish the stability of the
steady equilibrium state with respect to arbitrary torsional motions, we consider a single
Dirac delta function pulse for vθ with no
variations for the magnetic field at s = 0: 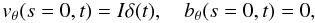 (21)where
I = const. The corresponding boundary conditions for the transformed
variables read
(21)where
I = const. The corresponding boundary conditions for the transformed
variables read  (22)where
Î = const. The system is at rest when t < 0.
The delta function velocity pulse corresponds to a unit twist. It must be pointed out that
due to linearity the results of the following stability analysis are applicable to systems
with different footpoint drivers, e.g., sinusoidal, random or damped twists.
(22)where
Î = const. The system is at rest when t < 0.
The delta function velocity pulse corresponds to a unit twist. It must be pointed out that
due to linearity the results of the following stability analysis are applicable to systems
with different footpoint drivers, e.g., sinusoidal, random or damped twists.
3. Horizontal flux tubes
It is instructive to begin our analysis by considering horizontal flux tubes. The
gravitational acceleration along the axis of a horizontal tube is zero. For field lines near
the tube axis gs = 0 and Eqs. (10–12) are reduced to 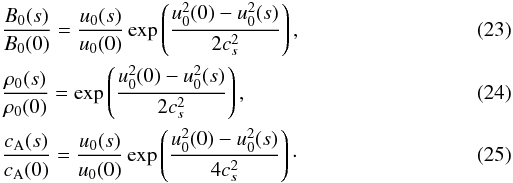 The
derivative of the equilibrium magnetic field can be expressed by the formula
The
derivative of the equilibrium magnetic field can be expressed by the formula 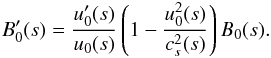 (26)The above equations also
describe the equilibrium of a flux tube in the absence of gravity. According to Eq. (6), a weakening magnetic field corresponds to an
expansion of the flux tube. We will consider an expanding flux tube from
s = 0, where the perturbations are driven, to
s = L. The cross-sectional area remains constant from
s = L to s = ∞. According to
Eqs. (23–25) this implies constant flow and Alfvén speeds. The flow profile is
smooth, subsonic and sub-Alfvénic throughout.
(26)The above equations also
describe the equilibrium of a flux tube in the absence of gravity. According to Eq. (6), a weakening magnetic field corresponds to an
expansion of the flux tube. We will consider an expanding flux tube from
s = 0, where the perturbations are driven, to
s = L. The cross-sectional area remains constant from
s = L to s = ∞. According to
Eqs. (23–25) this implies constant flow and Alfvén speeds. The flow profile is
smooth, subsonic and sub-Alfvénic throughout.
 |
Fig. 2 Profiles of the equilibrium quantities with cA(0) = 0.5, u0(0) = 0.45 and u0(L) = 0.2 for a horizontal flux tube are shown with different linestyles in the upper panel. All quantities are constant when s > L. Speed and distance are normalised with respect to the constant sound speed cs and the length of the nonuniform layer L, respectively (see text for an extended discussion). The middle and lower panels show the corresponding real and imaginary parts of the eigenmode frequencies plotted against u0(L). The solid, dotted, dashed and dot-dashed lines represent the first, second, third and fourth modes. |
Equation (26) shows that the sound speed
separates two distinct flow regimes: subsonic flows in expanding flux tubes decelerate
whereas supersonic flows accelerate. The following smooth profile for the flow speed is
chosen: ![\begin{equation} u_0(s) = \frac{u_0(0) \!+\! u_0(L)}{2} \!+\! \frac{u_0(L) \!-\! u_0(0)}{4} \left(\frac{2s \!-\! L}{L}\right)\left[3 \!-\! \left(\frac{2s \!-\! L}{L}\right)^2\right], \label{eq27} \end{equation}](/articles/aa/full_html/2011/09/aa17322-11/aa17322-11-eq61.png) (27)for
0 < s ≤ L and
u0(s) = u0(L)
for s > L.
(27)for
0 < s ≤ L and
u0(s) = u0(L)
for s > L.
Equations (18, 19) can be solved analytically in the region
s > L, where the flow speed is constant:
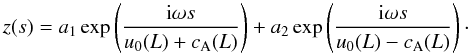 (28)Here
a1, a2 are arbitrary constants.
The first and second terms correspond to propagation in the positive and negative direction,
respectively, when
|u0| < cA. There are
no sources of perturbations in the region s > L and
so we set a2 = 0. The corresponding
counterpart x is easily determined through Eqs. (19) and (28).
(28)Here
a1, a2 are arbitrary constants.
The first and second terms correspond to propagation in the positive and negative direction,
respectively, when
|u0| < cA. There are
no sources of perturbations in the region s > L and
so we set a2 = 0. The corresponding
counterpart x is easily determined through Eqs. (19) and (28).
The shooting method is used to determine the complex frequencies of the eigenmodes. Equations (18, 19) are integrated numerically from s = 0 to s = L starting with the boundary conditions (22). The numerical integraion is carried out using a fourth order Runge-Kutta method. Matching the numerical solutions for 0 < s < L with the analytical solutions for s > L gives a numerical algebraic equation which is solved for ω.
In the following numerical results, distance and speed are normalised with respect to the length of the nonuniform layer L and the constant sound speed cs. For photospheric and lower chromospheric heights typical values could be cs = 8 km s-1 and L = 250 km. The flow speed is both subsonic and sub-Alfvénic.
The upper panel in Fig. 2 displays the variation of the equilibrium quantities with distance s when cA(0) < cs. The magnetic field and density are divided by B0(0) and ρ0(0), respectively. The expansion of the flux tube corresponds to a weakening magnetic field and a decelerating flow. The dependence of the eigenmode frequencies on u0(L) for cA(0) = 0.5 and u0(0) = 0.45 is shown in the lower two panels of Fig. 2. The fundamental mode (solid linestyle) and the first three harmonics are plotted. The real and imaginary parts of a given eigenmode frequency are indicated by the same linestyle. Negative values of imaginary part ωi correspond to damping and positive values correspond to instability. The first three modes are consecutively unstable for a wide range of flow speeds u0(L) including the one shown in the upper panel of Fig. 2.
The first panel of Fig. 3 displays the variation of the equilibrium quantities with distance s when cA(0) > cs. The flux tube expands and the flow decelerates. The dependence of the eigenmode frequencies on u0(L) for cA(0) = 1.1 and u0(0) = 0.8 is also shown. The fundamental mode can be unstable. The higher harmonics are damped. The equilibrium structure displayed in Fig. 3 is unstable.
Note that in both Figs. 2 and 3 the instability only occurs when u0(L) < u0(0), i.e., when the flow decelerates which is consistent with the findings of Taroyan (2008) who derived an instability criterion for a model with a discontinuous flow profile.
Figure 4 shows the frequencies of the first few modes as functions of the Alfvén speed cA(0) with a fixed flow profile shown in the upper panel. The growth rate of the instability decreases as the Alfvén speed increases supersonically until the instability eventually becomes suppressed.
4. Vertical flux tubes
In this section the focus is on the propagation of linear torsional pulses in a vertically
stratified isothermal flux tube with a steady background flow. For filed lines near the tube
axis gs = −g (see Hollweg
et al. 1982) and Eqs. (10–12) are reduced to
 where
where
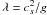 represents the pressure scale
height when the plasma flows with a constant speed.
represents the pressure scale
height when the plasma flows with a constant speed.
Similar to the horizontal tube case, the tube is divided into two parts: the flow speed is
variable in the lower region 0 < s < L and
constant for L < s < ∞. The flow varies
smoothly in the entire tube. Equations (18,
19) are treated numerically in the lower
region and analytically in the upper region s > L
where they can be reduced to the following second order equation for the
variable x: 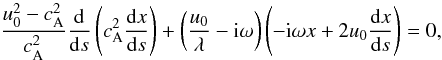 (32)where
u0 = const. and the Alfvén speed is expressed
through the formula (31). In order to
facilitate the analytical treatment we introduce a new variable τ:
(32)where
u0 = const. and the Alfvén speed is expressed
through the formula (31). In order to
facilitate the analytical treatment we introduce a new variable τ:
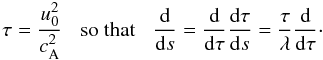 (33)In terms of the new
variable τ Eq. (32) is
recast in the following form:
(33)In terms of the new
variable τ Eq. (32) is
recast in the following form: 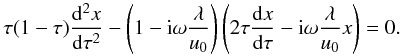 (34)This is the
hypergeometric differential equation (Abramowitz & Stegun 1972) with parameters
a = −iωλ/u0,
b = a + 1, c = 0. Note that in a
gravitationally stratified tube the Alfvén speed is no longer constant in the upper region,
s > L, but decays exponentially with height when
the flow speed is constant. The same is true for the magnetic field and density. Provided
the flow remains sub-Alfvénic in the lower region,
0 < s < L, there will be a point in the
upper region where
cA(τ = 1) = u0.
This is known as the Alfvén point (Heinemann & Olbert 1980). At the Alfvén point, τ = 1, Eq. (34) has a regular singularity. Since
c − a − b is not an integer the
solution around τ = 1 can be expressed as
(34)This is the
hypergeometric differential equation (Abramowitz & Stegun 1972) with parameters
a = −iωλ/u0,
b = a + 1, c = 0. Note that in a
gravitationally stratified tube the Alfvén speed is no longer constant in the upper region,
s > L, but decays exponentially with height when
the flow speed is constant. The same is true for the magnetic field and density. Provided
the flow remains sub-Alfvénic in the lower region,
0 < s < L, there will be a point in the
upper region where
cA(τ = 1) = u0.
This is known as the Alfvén point (Heinemann & Olbert 1980). At the Alfvén point, τ = 1, Eq. (34) has a regular singularity. Since
c − a − b is not an integer the
solution around τ = 1 can be expressed as ![\begin{eqnarray} x &=& a_1\times{_2F_1} \left(-{\rm i}\omega\frac{\lambda}{u_0}, 1 - {\rm i}\omega \frac{\lambda}{u_0}; 2 - 2{\rm i}\omega\frac{\lambda}{u_0};1-\tau\right)\nonumber\\[1.5mm] \label{eq35}&& + a_2(1-\tau)^{{\rm i}\omega\frac{\lambda}{u_0}-1}{_2F_1} \left({\rm i}\omega\frac{\lambda}{u_0}, {\rm i}\omega\frac{\lambda}{u_0}-1; 2{\rm i}\omega\frac{\lambda}{u_0};1-\tau\right), \end{eqnarray}](/articles/aa/full_html/2011/09/aa17322-11/aa17322-11-eq96.png) (35)where
2F1 is the hypergeometric function and a1,
a2 are arbitrary constants (Abramowitz & Stegun 1972). Only the first term on the right hand side of
Eq. (35) is physically acceptable as it
remains finite whereas the second term is infinite at the Alfvén point. Therefore
a2 = 0 has to be set in Eq. (35). In terms of the old variable s the solution in the
region s > L becomes
(35)where
2F1 is the hypergeometric function and a1,
a2 are arbitrary constants (Abramowitz & Stegun 1972). Only the first term on the right hand side of
Eq. (35) is physically acceptable as it
remains finite whereas the second term is infinite at the Alfvén point. Therefore
a2 = 0 has to be set in Eq. (35). In terms of the old variable s the solution in the
region s > L becomes 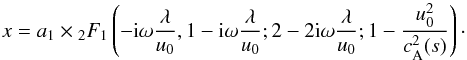 (36)The counterpart
z in the region s > L is
determined from Eqs. (18) and (36):
(36)The counterpart
z in the region s > L is
determined from Eqs. (18) and (36): ![\begin{eqnarray} z = \frac{a_1}{2}\cdot\frac{\lambda {\rm i} \omega}{1-{\rm i}\omega\lambda/u_0} \nonumber\\ &&\times\left[\left(1-\frac{u_0^2}{c_{\rm A}^2}\right) \times{_2F_1} \left(1-{\rm i}\omega\frac{\lambda}{u_0},2-{\rm i}\omega\frac{\lambda}{u_0}; 3-2{\rm i}\omega\frac{\lambda}{u_0};1-\frac{u_0^2}{c_{\rm A}^2}\right)\right. \nonumber\\ \label{eq37}&&\left.+2\times\,{_2F_1}\left(-{\rm i}\omega\frac{\lambda}{u_0}, 1-{\rm i}\omega\frac{\lambda}{u_0};2-2{\rm i}\omega\frac{\lambda}{u_0};1-\frac{u_0^2}{c_{\rm A}^2}\right)\right] \end{eqnarray}](/articles/aa/full_html/2011/09/aa17322-11/aa17322-11-eq99.png) (37)where
the differentiation formula for hypergeometric functions (Abramowitz & Stegun 1972) has been applied. Similar to the horizontal tube
case the eigenfrequencies are found by matching the numerically integrated solutions in the
region 0 < s < L with the analytical
solutions (36, 37) in
s > L and by solving the resulting numerical
algebraic equation for ω.
(37)where
the differentiation formula for hypergeometric functions (Abramowitz & Stegun 1972) has been applied. Similar to the horizontal tube
case the eigenfrequencies are found by matching the numerically integrated solutions in the
region 0 < s < L with the analytical
solutions (36, 37) in
s > L and by solving the resulting numerical
algebraic equation for ω.
 |
Fig. 5 Profiles of the equilibrium quantities with cA(0) = 0.8, u0(0) = 0.7 and u0(L) = 0.2 for a vertical flux tube are shown with different linestyles in the upper panel. The flow speed is constant when s > L. Speed and distance are normalised with respect to cs and L, respectively. The plotted equilibrium profiles are for a fixed scale height of λ = 2.5. The middle and lower panels show the variation of the corresponding real and imaginary parts of the eigenmode frequencies with respect to the scale height λ. The three dot dashed, solid, dotted, dashed and dot-dashed lines represent the first, second, third, fourth and fifth modes. |
The dependence of the real and imaginary frequencies on λ is plotted in Fig. 5. The upper panel shows the variation of the equilibrium quantities with s for the particular value of λ = 2.5. The flow and the Alfvén speeds are subsonic. Values of λ below about 2.3 would correspond to super-Alfvénic flows in the lower region where the equations are integrated numerically. As λ increases the mode represented by the solid line becomes unstable. An increase in λ corresponds to a more rapid deceleration of the flow as λ is normalised with respect to L. Note the appearance of a new damped mode with zero frequency which did not exist in the absence of gravitational acceleration.
 |
Fig. 6 Similar to Fig. 5 but for cA(0) = 1.2, u0(0) = 0.8, u0(L) = 0.2 and λ = 2. In the middle and lower panels, the real and imaginary parts of the eigenmode frequencies are plotted against the length of the intermediate layer Lm where the flow is constant. The upper panel corresponds to Lm = 0.3. |
We introduce an intermediate layer 0 < s < Lm with a constant flow. The upper panel of Fig. 6 shows the variation of the equilibrium quantities with s when Lm = 0.3. The Alfvén speed is supersonic and the flow is subsonic. Figure 6 shows how the variation in Lm influences the mode frequencies and their growth/damping. The value of the scale height is fixed at λ = 2. As Lm increases from 0 towards L more and more modes become unstable.
We also consider an accelerating flow in the intermediate region which then decelerates in
the upper parts of the atmosphere. The flow profile is always smooth and given by an
expression similar to Eq. (27). From
Eq. (29) we find the following expression
for the derivative of the magnetic field: ![\begin{equation} B_0^{\prime}(s) = \left[\frac{u_0^{\prime}(s)}{u_0(s)}\left(1-\frac{u_0^2(s)}{c_s^2(s)} \right)-\frac1{\lambda}\right] B_0(s). \label{eq38} \end{equation}](/articles/aa/full_html/2011/09/aa17322-11/aa17322-11-eq109.png) (38)The above equation shows
that the flux tube may expand even when the subsonic flow accelerates as long as the
pressure scale height remains finite.
(38)The above equation shows
that the flux tube may expand even when the subsonic flow accelerates as long as the
pressure scale height remains finite.
 |
Fig. 7 Similar to Fig. 5 but for cA(0) = 1.2, u0(0) = 0.5, λ = 1, Lm = 0.6 and 0.1 < u0(L) < 0.5. In the intermediate layer 0 < s < Lm, the flow accelerates and reaches a maximum of u0(Lm) = 0.9. |
The case with an accelerating and decelerating subsonic flow is studied in Fig. 7. The length of the intermediate region where the flow accelerates is Lm = 0.6 and the scale height is fixed at λ = 1. The variation of the equilibrium quantities is plotted in the upper panel for u0(L) = 0.4. The lower two panels show the complex frequencies as functions of u0(L). The mode plotted with a solid line is unstable for lower values of u0(L). It is also worth noting that the flow speed is rather moderate at s = 0 compared to the sound and Alfvén speeds. The magnetic field is a decreasing function throughout, whereas the density and the Alfvén speed decay exponentially in the upper region s > L.
The flow may also become supersonic as it accelerates in the intermediate region 0 < s < Lm. Such a case is studied and presented in Fig. 8. The flow returns to subsonic values as it slows down. The length of the intermediate layer is Lm = 0.6 and the scale height has a low value of λ = 0.5. The magnetic field profile in the upper panel indicates that the flux tube expands in the atmosphere. The Alfvén speed initially increases due to the flow acceleration. The lower two panels show that the instability may arise even for relatively high values of the Alfvén speed when the flow is slow at lower heights and becomes supersonic at intermediate heights. Similar to the previous case the growth rate of the instability depends on the rate of flow deceleration in the region Lm < s < L.
 |
Fig. 8 Similar to Fig. 5 but for cA(0) = 1.7, u0(0) = 0.5, λ = 0.5, Lm = 0.6 and 0.1 < u0(L) < 0.5. In the intermediate layer 0 < s < Lm, the flow accelerates and reaches a maximum of u0(Lm) = 1.4. |
5. Discussion and conclusions
The present work is an application of the instability found by Taroyan (2008) whereby incompressible perturbations become amplified in compressible plasma flows. The Alfvénic perturbations travelling from the footpoint are over-reflected back and transmitted forward as the decelerating plasma flow reduces their propagation speed in the direction of the flow.
We have shown that expanding isothermal flux tubes with smooth flow profiles can be unstable with respect to linear torsional perturbations which confirms that this is an ideal MHD instability that does not require the presence of shocks. We have first considered the case with no gravity or, alternatively, horizontal tubes. The instability arises when the flow decelerates in the positive direction. For subsonic flows this corresponds to expanding tubes. The Alfvén speed can be subsonic or supersonic. In both cases, the instability sets in when the flow deceleration is strong enough. Also the equilibrium becomes stable at large enough Alfvén speeds. These results are consistent with the instability criterion derived in Taroyan (2008): the flow speed on one side of the discontinuity, near the driver, must exceed the sum of the flow and Alfvén speeds on the other side. As the Alfvén speed increases the instability criterion is no longer satisfied and the system becomes stable.
The subsequent analysis is focused on stratified flux tubes where the plasma flows against the force of gravity. The flow is kept constant in the upper layer and the torsional perturbations are expressed in terms of generalised hypergeometric functions. In the presence of gravity, the decrease in density, Alfvén speed and the tube expansion continue in the upper layer with constant flow, although less rapidly. Due to the decreasing Alfvén speed the flow becomes super-Alfvénic above a certain height.
Figure 6 shows that the instability only appears when the flow deceleration is rapid enough. According to Eq. (38), a rapid deceleration of the plasma flow is equivalent to rapid expansion of the flux tube. Therefore reducing the size of the region, where the tube suffers largest expansion, has a destabilising effect on the modes (Fig. 6).
Another interesting result is the combined effect of flow acceleration and deceleration. In the case of a purely decelerating flow, relatively high flow speeds and low Alfvén speeds are required for the instability to set in. Figures 7 and 8 demonstrate that the flow acceleration in a fraction of the tube may account for both lower flow speeds at the footpoint and higher Alfvén speeds for which the tube still remains unstable. The flow may even become supersonic in the intermediate layers.
The fact that the plotted growth rates are small does not mean that the associated instability is not efficient in extracting the kinetic energy of the flow. One has to consider the growth rates ωi in conjunction with the corresponding frequencies ωr or periods.
We illustrate the obtained results using Fig. 7. In the linear regime, the amplitude growth over a single period T is proportional to exp(ωiT) = exp(2πωi/ωr), where T is the normalised period. According to Fig. 7, for u0(0) = 0.5 and u0(L) = 0.2 we have ωr = 1.5 and ωi = 0.2 for the unstable mode. Substituting in these values we find that the amplitude more than doubles in a single period and increases by a factor of 150 in 6 periods.
To express these estimates in dimensional periods,
Td = TL/cs = 2πL/(csωr),
we use a footpoint Alfvén speed of
cA(0) = 10 km s-1. According to Fig. 7, this leads to a sound speed of
cs = 8.3 km s-1 and a
footpoint flow speed of u0(0) = 4.15 km s-1. The
corresponding scale height is 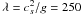 km
which also represents the distance over which the flow speed is variable since
λ = L. Therefore, the dimensional period,
Td = 2πcs/(gωr) = 127 s.
Hence the amplitudes will double in 127 s and will be amplified by a factor of 150 in about
760 s. The corresponding dimensional growth rate,
ωics/L = 0.006 s-1.
km
which also represents the distance over which the flow speed is variable since
λ = L. Therefore, the dimensional period,
Td = 2πcs/(gωr) = 127 s.
Hence the amplitudes will double in 127 s and will be amplified by a factor of 150 in about
760 s. The corresponding dimensional growth rate,
ωics/L = 0.006 s-1.
A number of observational studies of chromospheric and transition region lines have found periodic or non-periodic enhancements in the line width. Furthermore, these non-thermal broadenings interpreted as Alfvén waves are usually associated with upflows in magnetic structures of the solar atmosphere (Peter 2000, 2001; Xia et al. 2003, 2004; Hara et al. 2008; Tian et al. 2009; De Pontieu et al. 2009a,b, 2011; McIntosh et al. 2011). Estimates of the energy flux carried by these waves indicate that they could accelerate the solar wind, and possibly heat the corona. Observations in Hα by Jess et al. (2009) provided evidence for periodic torsional Alfvén waves associated with upflows. Oscillations with an amplitude of 2.6 km s-1 were accompanied by an average blueshift of 23 km s-1.
The majority of these studies were carried out using high temperature lines such as Ne viii, whereas the present study is mainly applicable to the lower parts of the solar atmosphere where the temperature is roughly constant. However, the presented instability mechanism may still offer an explanation for the association of upflows in magnetic flux tubes with non-thermal broadenings: provided the flux tube expansion is rapid enough, torsional perturbations, either periodic or not, may become amplified through interaction with the flow and thus account for the non-thermal broadenings that are large enough to be detected with current spectrometers.
The Alfvén and sound speeds are comparable at s = 0 which is a reasonable approximation for the lower parts of the solar atmosphere. However, temperature increase cannot be ignored at coronal heights. Also the Alfven speed decreases with height when the isothermal flow is constant. Therefore, caution is required in the interpretation of the obtained results. The consequences of a non-isothermal flow (adiabatic or non-adiabatic) will be addressed in a future study. However, even with the present model we are able to gain some useful information and insight into possible implications.
The results of our analysis do not give information about the nonlinear evolution of the amplified perturbations. The nonlinear coupling of Alfvén waves to longitudinal waves in magnetic structures with a static background has been the subject of several numerical studies (Hollweg et al. 1982; Sterling & Hollweg 1984; Mariska & Hollweg 1985; Kudoh & Shibata 1997; Moriyasu et al. 2004; Fujita et al. 2007; Vasheghani Farahani et al. 2011). The inclusion of an equilibrium flow makes the situation more complex since there is feedback on the flow: it is not clear what the effect of nonlinearity would be on the equilibrium flow.
As mentioned earlier, the present model also suffers the drawback of having a fixed tube radius. Once this restriction is removed, coupling between torsional and kink type perturbations is possible even in the linear regime. For example, Soler et al. (2011) have recently studied the resonant coupling between Alfvén and kink waves in the presence of a flow and transverse inhomogeneities. Such a coupling could also account for the transverse waves observed by Tomczyk et al. (2007) and De Pontieu et al. (2007). However, at this stage, we can only speculate about these effects until further studies are carried out.
The possibility of non-axisymmetric perturbations being subject to a similar amplification process cannot be excluded. Provided the instability exists, neither the required conditions nor the consequences are clear. One possibility is the generation of the above mentioned large amplitude transverse kink waves. However, the stability analysis of the flux tube with respect to non-axisymmetric perturbations requires a different model and a different set of governing equations.
Acknowledgments
The author is thankful to the anonymous referee for useful comments and suggestions.
References
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions, ed. Abramowitz, & Stegun [Google Scholar]
- Airapetian, V., Carpenter, K. G., & Ofman, L. 2011, ApJ, 723, 1210 [Google Scholar]
- Alfvén, H. 1942, Nature, 150, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Alfvén, H. 1947, MNRAS, 107, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Andries, J., & Goossens, M. 2001, A&A, 368, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antolin, P., & Shibata, K. 2010, ApJ, 712, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Belcher, J. 1971, ApJ, 168, 509 [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability (Oxford Clarendon Press) [Google Scholar]
- De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2007, Science, 318, 1574 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2009a, Science, 331, 55 [Google Scholar]
- De Pontieu, B., McIntosh, S. W., Hansteen, V. H., & Schrijver, C. J. 2009b, 701, L1 [Google Scholar]
- De Pontieu, B., McIntosh, S. W., Carlsson, M., Hansteen, V. H., et al. 2011, Science, 331, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Drazin, P. G. 2002, Introduction to hydrodynamic stability (Cambridge University Press) [Google Scholar]
- Drazin, P. G., & Reid, W. H. 1981, Hydrodynamic stability (Cambridge University Press) [Google Scholar]
- Erdélyi, R., & Hargreaves, J. 2008, A&A, 483, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foullon, C., Verwichte, E., Nakariakov, V. M., Nykyri, K., & Farrugia, C. J. 2011, ApJ, 729, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Suzuki, T., Kudoh, T., & Yokoyama, T. 2007, ApJ, 659, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Hara, H., Watanabe, T., Harra, L. K., et al. 2008, ApJ, 678, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Heinemann, M., & Olbert, S. 1980, J. Geophys. Res., 85, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvartes, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Hollweg, J. V. 1992, ApJ, 389, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Hollweg, J. V., & Isenberg, P. A. 2007, J. Geophys. Res., 112, A08102 [NASA ADS] [CrossRef] [Google Scholar]
- Hollweg, J. V., Jackson, S., & Galloway, D. 1982, Sol. Phys., 75, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Ionson, J. A. 1978, ApJ, 226, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Jess, D. B., Mathioudakis, M., Erdélyi, R., et al. 2009, Science, 323, 1582 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Joarder, P. S., Nakariakov, V. M., & Roberts, B. 1997, Sol. Phys., 176, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Kudoh, T., & Shibata, K. 1997, ApJ, 476, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Mariska, J. T., & Hollweg, J. V. 1985, ApJ, 296, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Wiegelmann, T., & Xia, L.-D. 2004, A&A, 428, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsch, E., Tian, H., Sun, J., Curdt, W., & Wiegelmann, T. 2008, ApJ, 684, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., de Moortel, I., & Hood, A. W. 2011, A&A, 527, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McIntosh, S. W., Leamon, R. J., & De Pontieu, B. 2011, ApJ, 727, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Miura, A. 1992, J. Geophys. Res., 97, 10, 655 [Google Scholar]
- Moriyasu, S., Kudoh, T., Yokoyama, T., & Shibata, K. 2004, ApJ, 601, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Murawski, K., & Musielak, Z. E. 2010, A&A, 518, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Musielak, Z. E., Routh, S., & Hammer, R. 2007, ApJ, 659, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Obiki, T., Mutoh, T., Adachi, S., et al. 1977, Phys. Rev. Lett., 39, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Davila, J. M. 1995, J. Geophys. Res., 100, 23413 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1991, ApJ, 372, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H. 2000, A&A, 360, 761 [NASA ADS] [Google Scholar]
- Peter, H. 2001, A&A, 374, 1108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pu, Z.-Y., & Kivelson, M. G. 1983, J. Geophys. Res., 88, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Goossens, M. 1995, J. Plasma Phys., 54, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, D., & Ruderman, M. S. 2005, Phys. Plasmas, 12, 2103 [Google Scholar]
- Simpson, D., Ruderman, M. S., & Erdélyi, R. 2006, A&A, 452, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, R., Terradas, J., & Goossens, M. 2011, ApJ, 734, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Sterling, A. C., & Hollweg, J. V. 1984, ApJ, 285, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Taroyan, Y. 2008, Phys. Rev. Lett., 101, 245001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Taroyan, Y. 2009, ApJ, 694, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Taroyan, Y., & Erdélyi, R. 2003, J. Geophys. Res., 10, 266 [Google Scholar]
- Terradas, J., Goossens, M., & Ballai, I. 2010, A&A, 515, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tian, H., Marsch, E., Curdt, W., & He, J. 2009, A&A, 704, 883 [Google Scholar]
- Tirry, W. J., Cadez, V. M., Erdélyi, R., & Goossens, M. 1998, A&A, 332, 786 [NASA ADS] [Google Scholar]
- Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verth, G., Erdélyi, R., & Goossens, M. 2010, ApJ, 714, 1637 [NASA ADS] [CrossRef] [Google Scholar]
- Vasheghani Farahani, S., Nakariakov, V. M., van Doorsselaere, T., & Verwichte, E. 2011, A&A, 526, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xia, L.-D., Marsch, E., & Curdt, W. 2003, A&A, 399, L5 [Google Scholar]
- Xia, L.-D., Marsch, E., & Wilhelm, K. 2004, A&A, 424, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, G., & Hollweg, J. V. 1991, J. Geophys. Res., 96, 13, 807 [Google Scholar]
- Zaqarashvili, T. V., Diaz, A. J., Oliver, R., & Ballester, J. L. 2010, A&A, 516, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 A cartoon of an expanding flux tube in which plasma flows along the field lines. The s = 0 level represents the footpoint which is twisted by convective motions. |
| In the text | |
 |
Fig. 2 Profiles of the equilibrium quantities with cA(0) = 0.5, u0(0) = 0.45 and u0(L) = 0.2 for a horizontal flux tube are shown with different linestyles in the upper panel. All quantities are constant when s > L. Speed and distance are normalised with respect to the constant sound speed cs and the length of the nonuniform layer L, respectively (see text for an extended discussion). The middle and lower panels show the corresponding real and imaginary parts of the eigenmode frequencies plotted against u0(L). The solid, dotted, dashed and dot-dashed lines represent the first, second, third and fourth modes. |
| In the text | |
 |
Fig. 3 Similar to Fig. 2 but for cA(0) = 1.1, u0(0) = 0.8 and 0.02 < u0(L) < 0.8. |
| In the text | |
 |
Fig. 4 Similar to Fig. 2 but for u0(0) = 0.9, u0(L) = 0.2 and 1 < cA(0) < 1.5. |
| In the text | |
 |
Fig. 5 Profiles of the equilibrium quantities with cA(0) = 0.8, u0(0) = 0.7 and u0(L) = 0.2 for a vertical flux tube are shown with different linestyles in the upper panel. The flow speed is constant when s > L. Speed and distance are normalised with respect to cs and L, respectively. The plotted equilibrium profiles are for a fixed scale height of λ = 2.5. The middle and lower panels show the variation of the corresponding real and imaginary parts of the eigenmode frequencies with respect to the scale height λ. The three dot dashed, solid, dotted, dashed and dot-dashed lines represent the first, second, third, fourth and fifth modes. |
| In the text | |
 |
Fig. 6 Similar to Fig. 5 but for cA(0) = 1.2, u0(0) = 0.8, u0(L) = 0.2 and λ = 2. In the middle and lower panels, the real and imaginary parts of the eigenmode frequencies are plotted against the length of the intermediate layer Lm where the flow is constant. The upper panel corresponds to Lm = 0.3. |
| In the text | |
 |
Fig. 7 Similar to Fig. 5 but for cA(0) = 1.2, u0(0) = 0.5, λ = 1, Lm = 0.6 and 0.1 < u0(L) < 0.5. In the intermediate layer 0 < s < Lm, the flow accelerates and reaches a maximum of u0(Lm) = 0.9. |
| In the text | |
 |
Fig. 8 Similar to Fig. 5 but for cA(0) = 1.7, u0(0) = 0.5, λ = 0.5, Lm = 0.6 and 0.1 < u0(L) < 0.5. In the intermediate layer 0 < s < Lm, the flow accelerates and reaches a maximum of u0(Lm) = 1.4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


