| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 4 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117267 | |
| Published online | 12 August 2011 | |
Nuclear de-excitation line spectrum of Cassiopeia A
Institut für Theoretische Physik und Astrophysik, Universität Würzburg, Campus Hubland Nord, Emil-Fischer-Str. 31, 97074 Würzburg, Germany
e-mail: asumma@astro.uni-wuerzburg.de
Received: 16 May 2011
Accepted: 9 July 2011
Context. The supernova remnant Cassiopeia A is a prime candidate for accelerating cosmic ray protons and ions. Gamma rays have been observed at GeV and TeV energies, which indicates hadronic interactions, but they could also be caused by inverse-Compton scattering of low-energy photons by accelerated electrons.
Aims. We seek to predict the flux of nuclear de-excitation lines from Cas A through lower-energy cosmic rays and to compare it with COMPTEL measurements.
Methods. Assuming a hadronic origin of the high-energy emission, we extrapolate the cosmic ray spectrum down to energies of 10 MeV, taking into account an equilibrium power-law momentum spectrum with a constant slope. We then calculate the nuclear line spectrum of Cassiopeia A, considering the most prominent chemical elements in the MeV band and their abundances as determined by X-ray spectroscopy.
Results. We show that the predicted line spectrum is close to the level of the COMPTEL sensitivity and agrees with conservative upper limits.
Key words: astroparticle physics / cosmic rays / ISM: supernova remnants
© ESO, 2011
1. Introduction
Cassiopeia A (Cas A) is one of the youngest known Galactic supernova remnants (SNR). Extensive observations in the radio, infrared, optical, and X-ray bands lead to an estimated explosion date of around 1680 AD (Thorstensen et al. 2001; Fesen et al. 2006). Being the brightest radio source in our Galaxy, it was first discovered in 1948 (Ryle & Smith 1948). Its distance can be estimated to 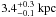 based on the combination of Doppler shifts and proper motions, whereas the angular size of 2.5′ corresponds to a physical size of 2.34 pc (Reed et al. 1995). The optical spectrum obtained from distant light echoes of the original blast indicates that Cas A was a type IIb supernova of a ~15 M⊙ main-sequence star and originated from the collapse of the helium core of a red supergiant that had lost most of its hydrogen envelope before exploding (Krause et al. 2008).
based on the combination of Doppler shifts and proper motions, whereas the angular size of 2.5′ corresponds to a physical size of 2.34 pc (Reed et al. 1995). The optical spectrum obtained from distant light echoes of the original blast indicates that Cas A was a type IIb supernova of a ~15 M⊙ main-sequence star and originated from the collapse of the helium core of a red supergiant that had lost most of its hydrogen envelope before exploding (Krause et al. 2008).
The blast wave drives an initially outgoing forward shock that can be seen as a thin X-ray edge expanding at roughly 5000 km s-1. The interaction with circumstellar material and the interstellar medium results in a reverse shock that is driven back into the outgoing ejecta and expanding at roughly half the rate of the forward shock (Gotthelf et al. 2001; DeLaney & Rudnick 2003). Emission at most wavelengths is dominated by a 30′′ thick “bright ring” where the ejecta are heated and ionized when they encounter Cas A’s reverse shock. Viewed in X-rays, this shell consists of undiluted ejecta rich in O, Si, S, and Fe (Willingale et al. 2002; Laming & Hwang 2003; Lazendic et al. 2006). Faint X-ray filaments outside of the shell mark the location of the forward shock where nonthermal X-ray synchroton radiation is produced by shock-accelerated electrons (Gotthelf et al. 2001; Vink & Laming 2003). Detected by HEGRA (Aharonian et al. 2001), MAGIC (Albert et al. 2007) and VERITAS (Humensky 2008), Cas A was the first SNR verified in TeV gamma rays. Recent observations with Fermi-LAT in the GeV range do not rule out either a leptonic or a hadronic emission scenario: a combination of nonthermal bremsstrahlung and inverse-Compton emission on the one hand as well as neutral pion decays on the other hand could be responsible for the measured spectrum (Abdo et al. 2010).
It has long been suggested that the shock waves associated with supernovae could be sites of acceleration of cosmic-ray particles (Baade & Zwicky 1934). The combination of diffusive shock acceleration (DSA) processes in SNR shocks with transport effects in our galaxy can in theory produce the observed power-law spectrum of cosmic rays up to the “knee” of about 1015 eV (Krymskii 1977; Axford et al. 1977; Bell 1978a,b; Blandford & Ostriker 1978; Drury 1983; Jones & Ellison 1991). To be consistent with the energy density of Galactic cosmic rays, the transfer of kinetic energy released in supernova explosions to cosmic rays must take place with an efficiency of ~10% (Ginzburg & Syrovatskii 1969). According to the DSA model, the charged particles scatter off irregularities in the magnetic field and increase their momentum by a fraction of the shock velocity v/c each round trip from the downstream to the upstream region and back again. Because of the feedback of the accelerated particles on the spatial profile of the flow velocity and therefore on the particle distribution itself, the DSA process can be significantly nonlinear. High-energy particles with considerable diffusion lengths sample a broader portion of the flow velocity profile and therefore experience a greater change in compression ratio than low-energy particles. That is why the particle spectrum and the resulting photon spectrum tend to flatten with increasing energy (Baring et al. 1999; Ellison et al. 2000; Bell & Lucek 2001; Ellison et al. 2005). The correspondence of electron and proton spectra at high energies (Ellison et al. 2000) renders it extremely difficult to prove the acceleration of cosmic ray protons at SNR shocks directly. Though the presence of cosmic ray protons could be inferred by gamma rays resulting from collisions with ambient gas and subsequent pion decays, TeV gamma rays can also be produced by inverse-Compton scattering of cosmic microwave background photons with the accelerated cosmic-ray electrons in SNRs.
The detection of nuclear de-excitation gamma-ray lines could point a way out of this dilemma: the line spectra produced in energetic collisions of cosmic rays with the ambient medium provide an unambiguous proof for the hadronic scenario of cosmic ray acceleration in SNRs. In contrast to other proposed scenarios (cf. Bozhokin & Bykov 1997), we expect the excitation processes to happen near the proton acceleration site, so effects through Coulomb losses regarding the proton spectrum can be neglected here. The following sections are devoted to a short summary concerning the theoretical concepts of nuclear de-excitation processes as well as the derivation of the resulting gamma-ray fluxes in the MeV range with respect to current and future detection limits. Finally, we discuss the results and their implications in the last section.
2. Theoretical framework
Inelastic scattering of energetic particles on heavier nuclei as well as spallation reactions leaving the product nucleus in an excited state are followed by the emission of gamma rays in the range from 1 to 20 MeV through de-excitation processes. The spectral structure of these gamma rays is determined both by the composition and the energy spectrum of the energetic particles and by the respective properties of the ambient medium. Especially cosmic rays with energies less than 100 MeV are suited well to be studied in gamma rays, because for cosmic rays with greater energies the gamma fluxes owing to p−p and p − α collisions followed by π0 desintegration are expected to be higher than the gamma fluxes resulting from nuclear de-excitations (Meneguzzi & Reeves 1975). That is why the observation of gamma-ray lines below 100 MeV offers the opportunity of studying astrophysical processes in great detail and of revealing the origin of hadronic cosmic rays in SNRs.
The basic ingredients in determining the profile of a gamma-ray line from energetic particle interactions can be summarized as follows: according to Ramaty et al. (1979), the probability of photon emission per second into solid angle d(cosθ0)dφ0 can be written as (the z-axis is chosen in the direction of the incident particle) 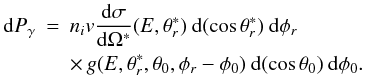 (1)In the center-of-mass frame, the interaction produces an excited nucleus with recoil velocity in
(1)In the center-of-mass frame, the interaction produces an excited nucleus with recoil velocity in  . E represents the energy of the incident particle before the interaction, ni the number density of the target particles. v is the incident particle’s velocity, dσ/dΩ∗ is the center-of-mass differential cross section, and g is the angular distribution of the resulting gamma rays. φr and φ0 are azimuth angles measured in the (x,y)-plane,
. E represents the energy of the incident particle before the interaction, ni the number density of the target particles. v is the incident particle’s velocity, dσ/dΩ∗ is the center-of-mass differential cross section, and g is the angular distribution of the resulting gamma rays. φr and φ0 are azimuth angles measured in the (x,y)-plane,  and θ0 are polar angles given with respect to the z-axis. To finally determine the gamma-ray spectrum, Eq. (1) can be integrated over
and θ0 are polar angles given with respect to the z-axis. To finally determine the gamma-ray spectrum, Eq. (1) can be integrated over 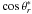 , φr, cosθ0 and E by using the Monte Carlo simulation technique. Choosing random numbers (uniformly distributed from 0 to 1), the integrations can be carried out by solving for
, φr, cosθ0 and E by using the Monte Carlo simulation technique. Choosing random numbers (uniformly distributed from 0 to 1), the integrations can be carried out by solving for 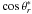 , φr, cosθ0 and E from the equations
, φr, cosθ0 and E from the equations 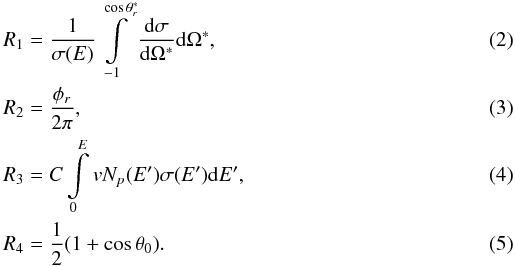 \arraycolsep1.75ptHere Np(E) is the number of incident particles per unit energy, C is a normalization constant. The probability of observing gamma rays of energies between Eγ and Eγ + ΔEγ is then proportional to the sum of all angular distributions g for which Eγ is in range. For a detailed description of the outlined methods above and a deeper insight into the different reaction types as well as the derivation of line production cross sections, we refer the reader to Ramaty et al. (1979) and Kozlovsky et al. (2002) and references therein.
\arraycolsep1.75ptHere Np(E) is the number of incident particles per unit energy, C is a normalization constant. The probability of observing gamma rays of energies between Eγ and Eγ + ΔEγ is then proportional to the sum of all angular distributions g for which Eγ is in range. For a detailed description of the outlined methods above and a deeper insight into the different reaction types as well as the derivation of line production cross sections, we refer the reader to Ramaty et al. (1979) and Kozlovsky et al. (2002) and references therein.
 |
Fig. 1 Calculated gamma-ray spectrum for the specific case of Cas A using the assumptions described in the text. 106 photons are binned into energy intervals of widths ranging from 2 to 5 keV as described in Ramaty et al. (1979). For example, the 12C line at 4.4 MeV has a flux that is comparable to the sensitivity of COMPTEL. Note that the continuum component caused by nonthermal electron bremsstrahlung is not taken into consideration here. |
3. Results
To validate the chances for success of the introduced approach concerning Cas A, we first study the exemplary case of the carbon line at 4.4 MeV. Considering a scenario in which the gamma-ray emission of Cas A is modeled by a hadronic fit based on the π0-decay of accelerated hadrons, the best-fit proton acceleration spectrum is given by Qp(p) ∝ p-2.3. The resulting proton energy content of Wp = ∫10 MeV/cQpp dp = 4 × 1049 erg corresponds to ~2% of the estimated SNR kinetic energy (Abdo et al. 2010). By extrapolating the high-energy proton spectrum down to the MeV-range, the gamma-ray flux emitted in the 4.4 MeV nuclear de-excitation line can be approximately calculated from 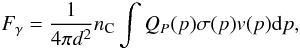 (6)where nC ~ 10 cm-3 is the adopted mean density of carbon atoms in the interaction region (cf. Laming & Hwang 2003), v the velocity of the accelerated protons and σ the cross section for the inelastic scattering processes. At first glance, line-broadening effects or additional contributions from unresolved gamma-ray lines in heavy nuclei and lines from long-term radioactive nuclei are neglected here. Using d = 3.4 kpc (see above) and the cross section for the reaction 12C(p,p′)12C ∗ given by Ramaty et al. (1979) yields a flux of ~10-6 cm-2 s-1 at 4.4 MeV. This flux value is close to the sensitivity limit of the COMPTEL experiment: following the analysis of Strong et al. (2000) concerning the MeV continuum emission from Cas A, only an upper limit of 1.4 × 10-5 cm-2 s-1 was obtained in the 3−10 MeV energy range. According to Iyudin et al. (1995), the COMPTEL line sensitivity is indicated with ~10-5 cm-2 s-1. So only a future gamma-ray mission with enhanced sensitivity in the MeV range will be able to obtain final results concerning the detection of de-excitation lines in Cas A.
(6)where nC ~ 10 cm-3 is the adopted mean density of carbon atoms in the interaction region (cf. Laming & Hwang 2003), v the velocity of the accelerated protons and σ the cross section for the inelastic scattering processes. At first glance, line-broadening effects or additional contributions from unresolved gamma-ray lines in heavy nuclei and lines from long-term radioactive nuclei are neglected here. Using d = 3.4 kpc (see above) and the cross section for the reaction 12C(p,p′)12C ∗ given by Ramaty et al. (1979) yields a flux of ~10-6 cm-2 s-1 at 4.4 MeV. This flux value is close to the sensitivity limit of the COMPTEL experiment: following the analysis of Strong et al. (2000) concerning the MeV continuum emission from Cas A, only an upper limit of 1.4 × 10-5 cm-2 s-1 was obtained in the 3−10 MeV energy range. According to Iyudin et al. (1995), the COMPTEL line sensitivity is indicated with ~10-5 cm-2 s-1. So only a future gamma-ray mission with enhanced sensitivity in the MeV range will be able to obtain final results concerning the detection of de-excitation lines in Cas A.
To compute the whole nuclear de-excitation spectrum for the specific case of Cas A, we used the Monte-Carlo code developed by Ramaty et al. (1979)1 (see also Sect. 2). Besides the ingredients already mentioned in the previous paragraph, the calculations take into account the following assumptions: the acceleration scenario for cosmic rays is assigned to the reverse-shock side and the chemical composition of the accelerated cosmic rays is inferred from Engelmann et al. (1990). The composition of the ambient gas, in fact a mixture of both massive Wolf-Rayet winds and subsequent supernova ejecta (cf. Lingenfelter & Higdon 2007), is described by the use of results from X-ray spectroscopy (cf. Table 1). The abundances of H and He are deduced from optical measurements by Chevalier & Kirshner (1979). The resulting total mass is in line with the Wolf-Rayet-supernova scenario, i.e. there is no room for additional amounts of hydrogen that would enhance the pion vs. the nuclear de-excitation yields. Unresolved gamma-rays from heavy nuclei and lines from long-term radioactive nuclei are also included. Together with the consideration of recoiling target particles, this leads to a significant broadening of the lines. Although some nonthermal emission is associated with the forward shock, recent studies showed that electron acceleration to multi-TeV energies is likely to take place mainly at the reverse shock within the supernova ejecta (Helder & Vink 2008), making Cas A to a unique object for studying particle acceleration at the reverse-shock side. The resulting spectrum is depicted in Fig. 1 and agrees well with the approximate calculation above.
Mean measured abundance mass ratios and rms scatter resp. upper limits according to the results of Willingale et al. (2002), Docenko & Sunyaev (2010) and Chevalier & Kirshner (1979).
4. Discussion
As can be seen in Fig. 1, the adopted acceleration scenario for cosmic rays in Cas A leads to a flux of nuclear de-excitation lines that would be clearly detectable by a gamma-ray telescope with enhanced sensitivity as sucessor to the COMPTEL mission (e.g. the proposed GRIPS mission by Greiner et al. 2009). The line emissivity is additionally boosted because the thermal target gas reflects the heavily enriched abundances of the Wolf-Rayet progenitor star. Though the detailed line characteristics always depend on the precise knowledge of the supernova ejecta’s composition, the natural process of element synthesis in the progenitor star and the supernova explosion mechanisms lead to peculiar properties in the gamma-ray spectrum. A unique feature arises because the C and O lines in the 4−6 MeV band dominate the line flux from the Ne-Fe group in the 1 − 3 MeV band. Of course, the reasonability of extrapolating the proton spectrum obtained from high-energy measurements down to the MeV range has to be discussed: it is commonly believed that strong Coulomb losses would quench the particle spectra of nonthermal particles below GeV energies, but the steep spectra of nonthermal particles in solar flares may tell a different story. Furthermore, the results of modeling the acceleration process of cosmic rays and the evolution of SNRs should be taken into account: according to the kinetic models of Berezhko & Völk (1997) and Berezhko & Völk (2000), the overall proton momentum spectrum at the shock front is close to a pure power law in the entire momentum range down to MeV at low injection rates, for high injection rates the low-energy part (p ≪ mc) of the overall cosmic ray spectrum is slightly steeper than the high-energy part. The application of the kinetic model approach with respect to the specific case of Cas A confirms these results (Berezhko et al. 2003). So the assumption of an in-situ cosmic ray spectrum that is as steep as at higher energies and a localization of the inelastic scattering processes near the reverse shock site seem to be quite reasonable and theoretically motivated.
5. Conclusion
We have shown that if cosmic rays are accelerated at the reverse shock in the Wolf-Rayet supernova remnant Cas A, as indicated by its strong GeV and TeV emission, the resulting flux of carbon and oxygen de-excitation lines is marginally detectable with COMPTEL. Precision spectroscopy with future MeV-missions such as GRIPS (Greiner et al. 2009) will put the theory of cosmic ray acceleration to a crucial test and will permit us to determine the overall efficiency of cosmic ray acceleration. As a corollary, these measurements would also determine the yields of spallation products from nuclear collisions that affect the abundances of the cosmologically relevant light elements such as Li, Be, and B. It must be noted that the prediction of the line flux rests on an extrapolation of the cosmic ray spectrum determined at high energies, which is in line with diffusive shock acceleration theory, but which is still subject to major systematic uncertainties associated to nonlinear effects such as shock broadening caused by back reactions.
Acknowledgments
The authors thank Werner Collmar for helpful discussions and the referee for the constructive comments on the manuscript. This work was funded by DFG through GRK 1147.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 710, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A., Barrio, J., et al. 2001, A&A, 370, 112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, A&A, 474, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Axford, W. I., Leer, E., & Skadron, G. 1977, in International Cosmic Ray Conference, 11, 132 [Google Scholar]
- Baade, W., & Zwicky, F. 1934, Proceedings of the National Academy of Science, 20, 259 [Google Scholar]
- Baring, M. G., Ellison, D. C., Reynolds, S. P., Grenier, I. A., & Goret, P. 1999, ApJ, 513, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R., & Lucek, S. G. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E. G., & Völk, H. J. 1997, Astropart. Phys., 7, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E. G., & Völk, H. J. 2000, A&A, 357, 283 [NASA ADS] [Google Scholar]
- Berezhko, E. G., Pühlhofer, G., & Völk, H. J. 2003, A&A, 400, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Bozhokin, S. V., & Bykov, A. M. 1997, Astron. Lett., 23, 212 [NASA ADS] [Google Scholar]
- Chevalier, R. A., & Kirshner, R. P. 1979, ApJ, 233, 154 [NASA ADS] [CrossRef] [Google Scholar]
- DeLaney, T., & Rudnick, L. 2003, ApJ, 589, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Docenko, D., & Sunyaev, R. A. 2010, A&A, 509, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drury, L. 1983, Space Sci. Rev., 36, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Berezhko, E. G., & Baring, M. G. 2000, ApJ, 540, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Decourchelle, A., & Ballet, J. 2005, A&A, 429, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engelmann, J. J., Ferrando, P., Soutoul, A., Goret, P., & Juliusson, E. 1990, A&A, 233, 96 [NASA ADS] [Google Scholar]
- Fesen, R. A., Hammell, M. C., Morse, J., et al. 2006, ApJ, 645, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1969, The origin of cosmic rays, ed. V. L. Ginzburg, & S. I. Syrovatskii [Google Scholar]
- Gotthelf, E. V., Koralesky, B., Rudnick, L., et al. 2001, ApJ, 552, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Iyudin, A., Kanbach, G., et al. 2009, Exp. Astron., 23, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Helder, E. A., & Vink, J. 2008, ApJ, 686, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Humensky, T. B. 2008, in AIP Conf. Ser. 1085, ed. F. A. Aharonian, W. Hofmann, & F. Rieger, 357 [Google Scholar]
- Iyudin, A. F., Bennett, K., Bloemen, H., et al. 1995, A&A, 300, 422 [NASA ADS] [Google Scholar]
- Jones, F. C., & Ellison, D. C. 1991, Space Sci. Rev., 58, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Kozlovsky, B., Murphy, R. J., & Ramaty, R. 2002, ApJS, 141, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, O., Birkmann, S. M., Usuda, T., et al. 2008, Science, 320, 1195 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Laming, J. M., & Hwang, U. 2003, ApJ, 597, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Lazendic, J. S., Dewey, D., Schulz, N. S., & Canizares, C. R. 2006, ApJ, 651, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Lingenfelter, R. E., & Higdon, J. C. 2007, ApJ, 660, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Meneguzzi, M., & Reeves, H. 1975, A&A, 40, 91 [NASA ADS] [Google Scholar]
- Ramaty, R., Kozlovsky, B., & Lingenfelter, R. E. 1979, ApJS, 40, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, J. E., Hester, J. J., Fabian, A. C., & Winkler, P. F. 1995, ApJ, 440, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Ryle, M., & Smith, F. G. 1948, Nature, 162, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Bloemen, H., Collmar, W., et al. 2000, in AIP Conf. Ser. 510, ed. M. L. McConnell, & J. M. Ryan, 60 [Google Scholar]
- Thorstensen, J. R., Fesen, R. A., & van den Bergh, S. 2001, AJ, 122, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., & Laming, J. M. 2003, ApJ, 584, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Bleeker, J. A. M., van der Heyden, K. J., Kaastra, J. S., & Vink, J. 2002, A&A, 381, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Mean measured abundance mass ratios and rms scatter resp. upper limits according to the results of Willingale et al. (2002), Docenko & Sunyaev (2010) and Chevalier & Kirshner (1979).
All Figures
 |
Fig. 1 Calculated gamma-ray spectrum for the specific case of Cas A using the assumptions described in the text. 106 photons are binned into energy intervals of widths ranging from 2 to 5 keV as described in Ramaty et al. (1979). For example, the 12C line at 4.4 MeV has a flux that is comparable to the sensitivity of COMPTEL. Note that the continuum component caused by nonthermal electron bremsstrahlung is not taken into consideration here. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


