| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116942 | |
| Published online | 18 August 2011 | |
Entropy mode at a magnetic null point as a possible tool for indirect observation of nanoflares in the solar corona
1
Group of Astrophysics, Institute of Physics,
UMCS, ul. Radziszewskiego 10,
20-031
Lublin,
Poland
e-mail: kmur@kft.umcs.lublin.pl
2
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz,
Austria
e-mail: teimuraz.zaqarashvili@oeaw.ac.at
3
Centre for Fusion, Space and Astrophysics, Department of Physics,
University of Warwick, Coventry, CV4
7AL, UK
e-mail: V.Nakariakov@warwick.ac.uk
4 Abastumani Astrophysical Observatory, Ilia State University,
University St. 2, Tbilisi, Georgia
5
Central Astronomical Observatory, Russian Academy of Sciences,
Pulkovo,
196140
St Petersburg,
Russia
Received:
23
March
2011
Accepted:
12
July
2011
Aims. We aim to explore the dynamics of the entropy mode perturbation excited by an energy release in the vicinity of a magnetic null point that is embedded in a gravitationally stratified solar corona.
Methods. We solve two-dimensional, time-dependent magnetohydrodynamic equations numerically to find spatial and temporal signatures of the entropy mode that is triggered impulsively by a spatially localized pulse of the gas pressure.
Results. We find that the properties of the entropy mode are determined by the sign of the initial pressure pulse. The initial increase in the gas pressure creates, together with the magnetoacoustic-gravity waves, a stationary void of the rarefied plasma at the launching place, associated with the entropy mode. In contrast, an initial decrease in the gas pressure, which corresponds to a rapid (or catastrophic) cooling, forms a blob of the dense plasma at the launching place.
Conclusions. The cool, dense blobs at magnetic null points may be observed in transition region and chromospheric spectral lines at coronal heights off the solar limb and may be associated with the places of nanoflare occurrence. Therefore, extensions of entropy mode studies may produce a diagnostic tool for indirect observations of nanoflares. The dense cool blobs may be affected by the gravity or carried by downflows, hence may initiate a coronal rain.
Key words: magnetohydrodynamics (MHD) / Sun: corona / Sun: oscillations
© ESO, 2011
1. Introduction
Sudden energy releases in the solar corona are subject to intensive investigation in the context of solar flares. Special attention is directed to the low-energy releases, so-called nanoflares, with energy of about 1024 erg, which arguably can significantly contribute to coronal heating (Parker 1988). In particular, Cargill (1994) constructed a model of the active corona that consists of many small-scale loops and is heated by nanoflares (but see Aschwanden 2008, for an alternative view). There is some observational evidence of nanoflares in the coronal X-ray emission (Katsukawa & Tsuneta 2001; Schmelz et al. 2009). The bright points in coronal EUV lines (Madjarska et al. 2003; Tian et al. 2008) and the phenomenon of coronal rain (De Groof et al. 2004; Antolin et al. 2010) may also be associated with nanoflares. But the firm observational evidence of nanoflare heating of the solar corona is still absent. Understanding the observables that can shed light on the presence of nanoflares is therefore an important task.
From the point of view of generating bulk plasma motions, the energy releases in nanoflares can be approximately described as a sudden enhancement of the plasma temperature in the vicinity of the reconnection site, e.g. a magnetic null point. The increased temperature can create a region of increased gas pressure. Also, the hot plasma then can be quickly cooled down to the transition region or chromospheric temperatures owing to “catastrophic cooling” (Antiochos & Klimchuk 1991; Schrijver 2001; Müller et al. 2003; 2004; Karpen et al. 2006; Klimchuk et al. 2010). The resulting dense and cool plasma blobs may then be attracted by gravity, slide down along the magnetic field lines, and result in “coronal rain” (De Groof et al. 2004; Antolin et al. 2010). In addition, such a compressible perturbation would generate an outgoing magnetoacoustic wave (Longcope & Priest 2007), which can be subject to steepening.
Interaction of magnetohydrodynamic (MHD) waves with magnetic null points leads to interesting physical processes. McLaughlin & Hood (2004; 2005) have studied the interaction of magnetoacoustic waves with two-dimensional (2D) single and double null points. They find that fast magnetoacoustic waves are refracted towards the null points and can dissipate leading to plasma heating in the near vicinity of the null point (see also recent review of McLaughlin et al. 2011). Moreover, these waves can trigger magnetic reconnection by the generation of steep spikes in the electric current density, which can produce anomalous resistivity (Foullon et al. 2005; Nakariakov et al. 2006).
All these works have only considered MHD propagating waves and paid no attention to the other MHD mode, a non-propagating entropy wave. The entropy wave is also a solution to ideal MHD equations with zero frequency, and it is associated with a perturbation of the entropy (see, e.g. Goedbloed & Poedts 2004). Frequency of the entropy mode becomes purely imaginary when the thermal conduction is taken into account. In this case, it is called a thermal mode, and its coupling to acoustic waves leads to their damping due to the thermal conduction (De Moortel & Hood 2003). Thus, impulsive energy releases in the vicinity of a magnetic null point can excite both propagating MHD waves and the entropy mode. The generated MHD waves leave the region of the initial excitation, while the entropy mode stays at the null point whenever it is embedded in plasma, producing a stationary compressible perturbation. This perturbation is subject to thermal and gravitational effects.
Here we suggest that the entropy mode, and the compressible disturbances associated with it, can be used as an observational signature of sudden, spatially localized energy releases in the corona (in particular, nanoflares). Working in terms of a simple 2D magnetic null point model, we numerically study the excitation of the entropy mode by positive or negative pressure pulses and its subsequent evolution in the presence of gravity. This paper is organized as follows. The numerical model is described in Sect. 2, where we also briefly review properties of linear entropy mode. The numerical results are presented in Sect. 3. Summary of the obtained results is given in Sect. 4.
2. The numerical model
We perform the numerical simulations in a magnetically structured atmosphere. The plasma is
described by the following magnetohydrodynamic equations: 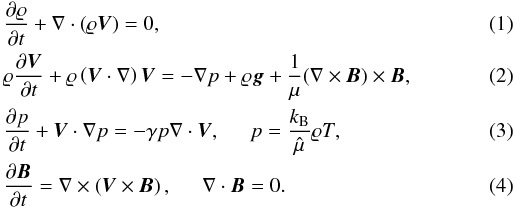 Here
γ = 5/3 is the adiabatic index, μ the magnetic
permeability, ϱ the mass density, p the gas pressure,
V = [Vx,Vy,Vz]
is the flow velocity, T plasma temperature,
B = [Bx,By,Bz]
the magnetic field, g = [0,−g,0] a
constant gravity with g = 274 ms-2,
kB is Boltzmann’s constant
and
Here
γ = 5/3 is the adiabatic index, μ the magnetic
permeability, ϱ the mass density, p the gas pressure,
V = [Vx,Vy,Vz]
is the flow velocity, T plasma temperature,
B = [Bx,By,Bz]
the magnetic field, g = [0,−g,0] a
constant gravity with g = 274 ms-2,
kB is Boltzmann’s constant
and 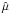 denotes mean mass. Henceforth, we assume that the z-direction is invariant
(∂/∂z = 0), and z components of
velocity and magnetic field are identical to
zero: Vz = Bz = 0. This assumption
removes Alfvén waves from the system.
denotes mean mass. Henceforth, we assume that the z-direction is invariant
(∂/∂z = 0), and z components of
velocity and magnetic field are identical to
zero: Vz = Bz = 0. This assumption
removes Alfvén waves from the system.
The MHD equations describe propagating waves. However, this system also possesses another solution called the entropy mode (Goedbloed & Poedts 2004). This mode does not lead to changes in plasma variables such as velocity, gas pressure, and magnetic field, but this mode effects entropy and mass density. The mode has zero frequency, ω = 0, and it does not propagate in the static medium. The mode can be represented as a local increase (decrease) in the temperature and a decrease (increase) in the mass density with no net pressure changes. However, if thermal conduction is present in the system, then the entropy mode gains a purely imaginary frequency, and the dispersion relation in magnetic field-free medium becomes quartic in wavenumber k and cubic in cyclic frequency ω (Field 1965; De Moortel & Hood 2003; Macnamara & Roberts 2010). See also the quasi-isentropic dispersion relations in Nakariakov et al. (2000). There are three solutions to this dispersion relation. Two of them correspond to the damped counter-propagating acoustic waves. The other, with a purely imaginary ω, is associated with the entropy mode and is called a thermal mode. This mode does not propagate, but its amplitude gradually decays in time because of the thermal conduction. Therefore, the thermal mode in the system with thermal conduction corresponds to the entropy mode (ω = 0) in ideal MHD.
The thermal conduction simply leads to the decay in entropy mode amplitude in time. However, the strong coronal magnetic field prohibits thermal conduction in the perpendicular direction. On the other hand, the thermal conduction is still important in the parallel direction, which may smooth out the entropy mode over a long time. However, for our purposes, the thermal conduction does not play an important role, so we ignore it in Eqs. (1)−(4) and consider pure entropy mode in the frame of ideal MHD.
2.1. Initial numerical setup
In this section, we detail the initial setup used in this study. The solar corona is modeled as a low mass density, highly magnetized plasma overlaying a dense photosphere/chromosphere.
2.1.1. Initial equilibrium
We assume that the corona is settled in a magnetic force-free
((∇ × Be) ×
Be/μ = 0) and static
(Ve = 0) equilibrium in which the pressure
gradient force is balanced by the gravity, that is, 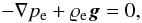 (5)where the
subscript e corresponds to a background quantity.
(5)where the
subscript e corresponds to a background quantity.
 |
Fig. 1 The initial equilibrium magnetic field lines with the x-point located at (x = 0, y = 15) Mm and the separatrices along which the magnetic field lines remain straight. |
We adopt a constant equilibrium temperature
T = const. for the solar corona. Using the ideal gas
law and the y-component of hydrostatic pressure balance given by
Eq. (5), we express the background gas
pressure and mass density as 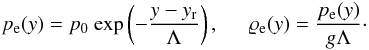 (6)Here
(6)Here
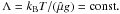 is the pressure atomic mass, and p0 denotes the gas pressure
at the reference level that is chosen at yr = 10 Mm. From
Eq. (6) we infer
that ϱe(y) falls off exponentially with
height.
is the pressure atomic mass, and p0 denotes the gas pressure
at the reference level that is chosen at yr = 10 Mm. From
Eq. (6) we infer
that ϱe(y) falls off exponentially with
height.
We assume a current-free magnetic field,
∇ × Be = 0 such that
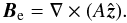 (7)Here
(7)Here
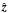 is a unit vector along the z-direction and A is the
magnetic flux function (chosen as in McLaughlin et al. 2006):
is a unit vector along the z-direction and A is the
magnetic flux function (chosen as in McLaughlin et al. 2006): ![\begin{equation} A(x,y) = B_{\rm 0} \left[ \frac{ y-y_{\rm d} } { (x+x_{\rm d})^2+(y-y_{\rm d})^2 } + \frac{ y-y_{\rm d} } { (x-x_{\rm d})^2+(y-y_{\rm d})^2 } \right], \label{eq:A_func} \end{equation}](/articles/aa/full_html/2011/09/aa16942-11/aa16942-11-eq42.png) (8)with
B0 denoting the magnetic field at
y = yr, and
(± xd,yd) correspond to the
coordinates of two dipoles. We have chosen and held fixed
xd = 10 Mm and yd = 5 Mm.
Magnetic field vectors are illustrated in Fig. 1.
The x-point is located at x = 0 Mm and
y = 15 Mm.
(8)with
B0 denoting the magnetic field at
y = yr, and
(± xd,yd) correspond to the
coordinates of two dipoles. We have chosen and held fixed
xd = 10 Mm and yd = 5 Mm.
Magnetic field vectors are illustrated in Fig. 1.
The x-point is located at x = 0 Mm and
y = 15 Mm.
2.1.2. Initial pressure pulse
Consider an impulsively excited entropy mode within the magnetic null-point
configuration. This mode is triggered by the initial pulse in gas pressure, which is
![\begin{equation} {p(x,y,t=0)}= p_{\rm e} \left[ 1 + A_{\rm p} \exp{ \left( -\frac{x^2+(y-y_{\rm 0})^2}{w^2} \right) } \right], \label{eq:perturb_p} \end{equation}](/articles/aa/full_html/2011/09/aa16942-11/aa16942-11-eq50.png) (9)where
Ap denotes the amplitude of the initial pulse,
w is its width, and y0 its vertical
location. Positive (negative) Ap indicates sudden heating
(cooling) of plasma near the null point. We choose and hold fixed
y0 = 15 Mm and so we launch the initial pulse at the
x-point.
(9)where
Ap denotes the amplitude of the initial pulse,
w is its width, and y0 its vertical
location. Positive (negative) Ap indicates sudden heating
(cooling) of plasma near the null point. We choose and hold fixed
y0 = 15 Mm and so we launch the initial pulse at the
x-point.
It is noteworthy that the entropy mode has already been observed in a number of numerical simulations of coronal dynamics. For instance, Mȩdrek et al. (2000) simulated sunquakes by pressure pulses. They observed that the entropy mode leads to remnants of the initial pulse, seen in the mass density profiles at the launching place.
3. Numerical results
Equations (1)−(4) are solved numerically using the code FLASH (Fryxell et al. 2000; Lee & Deane 2009). This code implements a second-order unsplit Godunov solver with various slope limiters and Riemann solvers as well as Adaptive Mesh Refinement (AMR) which is adopted in Paramesh package (MacNeice et al. 1999). We use the minmod slope limiter and the Roe Riemann solver (e.g., Toro 2009).
We set the simulation box as (−3 Mm,3 Mm) × (12 Mm,18 Mm) and impose fixed in time boundary conditions for all plasma quantities in the x- and y-directions, while all plasma quantities remain invariant along the z-direction. In our studies we always use AMR grid with a minimum (maximum) level of refinement set to 4 (7). The refinement strategy is based on controlling numerical errors in temperature. This results in an excellent resolution of steep spatial profiles and greatly reduces numerical diffusion at these locations. The convergence tests we carried out have confirmed that such resolution is sufficient to adequately represent the system.
3.1. Rapid heating
First we consider the case of positive Ap = 5 i.e. the sudden, spatially localized increase in the gas pressure around the null point. This corresponds to the deposition of heat and could be associated with a flare or a nanoflare (e.g., Aschwanden & Alexander 2001). Flare models usually assume that energy is stored in the solar corona for hours or days. The onset of the flare takes place after this energy storage phase and is associated with a sudden (usually shorter than 30 min) energy release. Such a strong pulse in the gas pressure pushes the plasma out, creating a region of the density decrease around the x-point.
 |
Fig. 2 Mass density profiles (color maps) and velocity vectors at t = 250 s (top panel) and t = 2 × 103 s (bottom panel) for the positive value of Ap = 5 (i.e. rapid heating). Mass density and velocity are measured in units of 10-15 kg m-3 and 1 km s-1, respectively. |
The pulse (Eq. (9)) triggers outgoing fast and slow magnetoacoustic-gravity waves, as well as the entropy mode. Fast waves propagate quasi-isotropically in the radial direction near the null point (however, the propagation may become anisotropic near the loci of the two dipoles, which is not shown here, McLaughlin & Hood 2006), while slow waves are guided along the separatrices.
Figure 2 shows the snapshot at the instant of time when the fast and slow waves have already left the region around the x-point. The entropy mode is manifested as the stationary void blob around the x-point. This blob starts to evolve according to buoyancy force, which pushes the plasma upwards along the separatrices. Such upward flow is seen at t = 2 × 103 s (Fig. 2, bottom panel).
 |
Fig. 3 Time signature of relative mass density, collected at the x-point for the case of Ap = 5. |
Figure 3 displays the time signature that is drawn
by collecting wave signals in 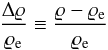 (10)at
the x-point. This time signature reveals the initial phase at which the
mass density abruptly falls off in time due to the action of the initial pressure pulse.
This phase lasts until t ≃ 10 s. Later on, mass density oscillates as a
result of propagating fast and slow waves. This oscillatory phase lasts to about
t = 100 s, and it is followed by a gradual rarefaction of plasma.
(10)at
the x-point. This time signature reveals the initial phase at which the
mass density abruptly falls off in time due to the action of the initial pressure pulse.
This phase lasts until t ≃ 10 s. Later on, mass density oscillates as a
result of propagating fast and slow waves. This oscillatory phase lasts to about
t = 100 s, and it is followed by a gradual rarefaction of plasma.
3.2. Rapid cooling
 |
Fig. 4 Mass density profiles (color maps) and velocity vectors at t = 250 s (top panel) and t = 2 × 103 s (bottom panel) for the negative value of Ap = −0.75 (i.e. rapid cooling). Mass density and velocity are measured in units of 10-15 kg m-3 and 0.2 km s-1, respectively. |
Since the radiation term is absent in the MHD equations, the cooling of hot plasma due to radiative losses is not considered here. On the other hand, the radiation losses can be important just after the onset of flare/nanoflare, which may lead to “catastrophic cooling” of the hot plasma to transition region/chromospheric temperatures once the temperature and mass density reach some critical values (Schrijver 2001). The one-dimensional loop models show that the catastrophic cooling is a loss of equilibrium; i.e., the radiative losses become stronger than heating and heat conduction (Antiochos & Klimchuk 1991; Müller et al. 2003; 2004; Karpen et al. 2006; Klimchuk et al. 2010). Including a magnetic field, i.e. considering two-dimensional loops, may modify the non-equilibrium state. However, the solution of full MHD equations with heating, heat conduction, and radiative losses is a formidable task. Therefore, all non-adiabatic processes are ignored in our study, and the sudden cooling is modeled by a negative value of Ap, i.e., sudden decrease in the plasma pressure at the null point.
The pulse of Eq. (9) with Ap = −0.75 again triggers fast and slow magnetoacoustic-gravity waves, as well as the entropy mode (Fig. 4). But now the entropy mode is represented by mass density enhancement at the x-point. We observe that the density enhancement, corresponding to the cooler region, persists for a long time at the null point, while being weakly affected by the gravity. Therefore, when a nanoflare occurs at a null point, its location can be traced through the density enhancement of a lower temperature.
 |
Fig. 5 Time signature of relative mass density, collected at the x-point for the case of Ap = −0.75. |
Figure 5 displays the time signature that is drawn by collecting wave signals in Δϱ/ϱe at the x-point. Similar to Fig. 3 this time signature reveals the initial phase at which the mass density varies in time because of the action of the initial pressure pulse and resulting propagation of fast and slow waves. This phase lasts until t ≃ 100 s. Later on, mass density remains essentially constant.
4. Discussion and summary
We developed a two-dimensional model of the evolution of an initial gas pressure pulse at a coronal magnetic x-point. This pulse leads to the excitation of magnetoacoustic-gravity waves that propagate away from the null point. In addition, an entropy mode is triggered in the vicinity of the energy release location, in the form of either a plasma void or a dense blob. The rapid initial enhancement of the plasma pressure, which is associated with the rapid energy release, is accompanied by the entropy mode with higher temperature and lower density plasma void. On the other hand, the initial rapid decrease in the plasma pressure, which is associated with the rapid cooling, is accompanied by the entropy mode with lower temperature and higher density, that is to say a blob. The dense, cool blob remains weakly altered at the null point for a long time (Fig. 4). In principle, the rarefaction (compression) of mass density is subject to buoyancy (gravity) force, and its influence is expressed by changing the void (or blob) shape. However, strong perpendicular magnetic field inhibits any movement of the whole blob (or void) in the vertical direction. Therefore, both the blob and void remain near the place of initial energy deposition, i.e. near the x-point, for a long time.
Dense plasma blobs may be observed in the transition region or chromospheric spectral lines off the solar limb. Locations of the observed blobs then may correspond to nanoflares, which may provide the opportunity for indirect observations of
these events. In some cases, these blobs may be carried away by downflows while the entropy mode is embedded in plasma. In this case, the entropy modes may be observed as coronal rains.
Acknowledgments
The authors express their thanks to the referee for his/her comments. The software used in this work was in part developed by the DOE-supported ASC/Alliance Center for Astrophysical Thermonuclear Flashes at the University of Chicago. The work of T.Z. was supported by the Austrian Fond zur Förderung der wissenschaftlichen Forschung (project P21197-N16) and the Georgian National Science Foundation (under grant GNSF/ST09/4-310).
References
- Antiochos, S. K., & Klimchuk, J. A. 1991, ApJ, 378, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Antolin, P., Shibata, K., & Vissers, G. 2010, ApJ, 716, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J. 2008, ApJ, 672, 135 [Google Scholar]
- Aschwanden, M. J., & Alexander, D. 2001, Sol. Phys., 204, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J. 1994, ApJ, 422, 381 [Google Scholar]
- De Groof, A., Berghmans, D., van Driel-Gesztelyi, L., & Poedts, S. 2004, A&A, 415, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2003, A&A, 408, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Foullon, C., Verwichte, E., Nakariakov, V. M., & Fletcher, L. 2005, A&A, 440, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Goedbloed, H., & Poedts, S. 2004, Principles of Magnetohydrodynamics (Cambridge University Press) [Google Scholar]
- Karpen, J. T., Antiochos, S. K., & Klimchuk, J. A. 2006, ApJ, 637, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Katsukawa, Y., & Tsuneta, S. 2001, ApJ, 557, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A., Karpen, J. T., & Antiochos, S. K. 2010, ApJ, 714, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, D., & Deane, A. E. 2009, J. Comput. Phys., 228, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Priest, E. R. 2007, Phys. Plasmas, 14, 122905 [NASA ADS] [CrossRef] [Google Scholar]
- Macnamara, C. K., & Roberts, B. 2010, A&A, 515, 41 [Google Scholar]
- MacNeice, P., Olson, K. M., Mobarry, C., de Fainchtein, R., & Packer, C. 1999, CPC, 126, 3 [Google Scholar]
- Madjarska, M. S., Doyle, J. G., Teriaca, L., & Banerjee, D. 2003, A&A, 398, 775 [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2004, A&A, 420, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2005, A&A, 435, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2006, A&A, 452, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., Hood, A. W., & De Moortel, I. 2011, Space Sci. Rev., DOI: 10.1007/s11214-010-9654-y [Google Scholar]
- Mȩdrek, M., Murawski, K., & Nakariakov, V. M. 2000, Acta Astron., 50, 405 [NASA ADS] [Google Scholar]
- Müller, D. A. N., Hansteen, V. H., & Peter, H. 2003, A&A, 411, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, D. A. N., Peter, H., & Hansteen, V. H. 2004, A&A, 424, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Mendoza-Briceño, C. A., Ibáñez, S., & Miguel, H. 2000, ApJ, 528, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Foullon, C., Verwichte, E., & Young, N. P. 2006, A&A, 452, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Schmelz, J. T., Saar, S. H., DeLuca, E. E., et al. 2009, ApJ, 693, 131 [Google Scholar]
- Schrijver, C. J. 2001, Sol. Phys., 198, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, H., Curdt, W., Marsch, E., & He, J. 2008, ApJ, 681, 121 [Google Scholar]
- Toro, E. 2009, Riemann solvers and numerical methods for fluid dynamics (Berlin: Springer) [Google Scholar]
All Figures
 |
Fig. 1 The initial equilibrium magnetic field lines with the x-point located at (x = 0, y = 15) Mm and the separatrices along which the magnetic field lines remain straight. |
| In the text | |
 |
Fig. 2 Mass density profiles (color maps) and velocity vectors at t = 250 s (top panel) and t = 2 × 103 s (bottom panel) for the positive value of Ap = 5 (i.e. rapid heating). Mass density and velocity are measured in units of 10-15 kg m-3 and 1 km s-1, respectively. |
| In the text | |
 |
Fig. 3 Time signature of relative mass density, collected at the x-point for the case of Ap = 5. |
| In the text | |
 |
Fig. 4 Mass density profiles (color maps) and velocity vectors at t = 250 s (top panel) and t = 2 × 103 s (bottom panel) for the negative value of Ap = −0.75 (i.e. rapid cooling). Mass density and velocity are measured in units of 10-15 kg m-3 and 0.2 km s-1, respectively. |
| In the text | |
 |
Fig. 5 Time signature of relative mass density, collected at the x-point for the case of Ap = −0.75. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


