| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116933 | |
| Published online | 12 September 2011 | |
Leakage of long-period oscillations from the chromosphere to the corona
1
Centre for Fusion, Space and Astrophysics, Department of PhysicsUniversity
of Warwick,
Coventry
CV4 7AL,
UK
e-mail: Ding.Yuan@warwick.ac.uk
2
Central Astronomical Observatory at Pulkovo of the Russian Academy
of Sciences, 196140
St Petersburg,
Russia
Received:
21
March
2011
Accepted:
7
August
2011
Long-period oscillations in a coronal diffuse structure are detected with the Transition Region And Coronal Explorer (TRACE). The EUV images of the NOAA active region 8253 are available in 171 Å and 195 Å bandpasses from 30 June to 4 July 1998. The average intensity variation is found to be connected with the CCD temperature, which varies with the orbital motion of the spacecraft. Hence, oscillations with the orbital period and its higher harmonics appear as artifacts in the light curves. After the exclusion of the orbital effects, we identified several long-period oscillations in the diffuse fan-like structure of the active region. Similar periodicities were detected in the radio emission from the chromospheric part of that active region, observed with the ground-based Nobeyama Radioheliograph (NoRH) in the 17 GHz channel. It was found that 0.221, 0.312 and 0.573 mHz oscillations were present in both EUV emission lines in the corona and the radio signal from the sunspot in the chromosphere, just beneath the active region. From the frequency values, the 1st and 3rd detected oscillations could be associated with the l = 2, n = −3 or l = 3, n = −5 and l = 1 gravity-driven solar interior modes, respectively. The appearance of these oscillations in the coronal part of the active region can be connected with the wave leakage or the evanescence of chromospheric oscillations.
Key words: Sun: oscillations / Sun: corona / Sun: UV radiation / Sun: atmosphere / sunspots / instrumentation: miscellaneous
© ESO, 2011
1. Introduction
Propagating intensity disturbances in Extreme UltraViolet (EUV) bandpasses were first observed in the polar plumes (Deforest & Gurman 1998) and over the strands of large coronal loops (Berghmans & Clette 1999) with SOHO/EIT. This stimulated a number of follow-up studies, mainly in the 171 Å and 195 Å bandpasses of TRACE (e.g. De Moortel et al. 2000, 2002a,b; King et al. 2003). The intensity disturbances are observed to propagate at the speeds lower than the local sound speed due to projection effects. The typical periods of these disturbances were found to cluster near 3 and 5 min in the power spectrum (De Moortel et al. 2002a). Hence, they are likely to be associated with the chromospheric 3-min oscillations and the photospheric 5-min oscillations, respectively. The 3-min oscillations were found to leak from sunspot umbra to the corona (Shibasaki 2001; Sych et al. 2009). The 5-min oscillations, above the acoustic cut-off period, can be channelled to the corona by the inclined magnetic field lines (e.g above the plage region, see De Pontieu et al. 2005). The coronal propagating disturbances are usually interpreted as propagating slow magnetoacoustic waves (Nakariakov et al. 2000; Verwichte et al. 2010).
Longer period oscillations are detected in sunspot chromosphere and transition region (Nagovitsyna & Nagovitsyn 2001, 2002). The oscillations of tens up to hundreds of minutes were observed as modulations of the radio emission (Gelfreikh et al. 2006). The line-of-sight velocity oscillations with periods ranging from 60 to 80 min were found in the analysis of the Doppler shift of spectral lines in sunspots (Efremov et al. 2009). Long-period oscillations (16–88 min) of the radio emission intensity over sunspots were recently studied with the Nobeyama Radioheliograph (NoRH) (Chorley et al. 2010, 2011).
Theoretical studies argue that these long-period (low frequency) oscillations are well below the cut-off frequency (e.g. Bel & Leroy 1977), thus cannot appear in the corona. However, in the corona, long-period oscillations have been detected in the EUV emission with multiple instruments and in different bandpasses. For example, propagating waves with long periods (10–15 min) were observed in coronal loops with EIT (Berghmans & Clette 1999), TRACE (McIntosh et al. 2008) and STEREO/EUVI (Marsh et al. 2009). Wang et al. (2009) reported two significant periodicities of 12 and 25 min in the intensity and Doppler shift variations over a coronal diffuse structure with Hinode/EIS. Prominence oscillations with periods ranging from 20 min up to several hours were reported as well (Foullon et al. 2004, 2009; Tripathi et al. 2009; Hershaw et al. 2011).
 |
Fig. 1 a) The field of view over AR8253 taken at 1998-07-01 01:01 UT in TRACE 171 Å bandpass, the region of interest (ROI) in the white box includes the fan-like structure and is re-sized to the left, an off-ROI region including the weakest intensity area is marked to the top. b) The region of interest (128 × 128 pixels) showing the fan-like structure; a slit of the macro-pixels (3 × 3) is selected along the fan. c) The intensity map of 17 GHz radio emission over AR8253 at 1998-07-01 01:01 UT. The contour in dashed line marked the sunspot area. |
Likewise, long-period oscillations have been observed in the upper corona and the solar wind. In particular, Ofman et al. (2000) detected an oscillation of the polarised white-light brightness with a 30 min period at 1.9 R⊙ in a polar coronal hole. Similar periodicities in the low-energy charged particle flux were found to be modulated by the variation of the interplanetary magnetic field, which may be of solar origin (Thomson et al. 1995). Moreover, Kepko & Spence (2003) established a high correlation of solar wind density variations and the ultra low frequency (ULF) oscillations of the Earth’s magnetosphere, with the power spectrum peaks being located at 0.1, 0.2 and 0.6 mHz.
Thus, there appear questions as to whether the long-period oscillatory phenomena, observed in different parts of the solar atmosphere, are connected with one another, and how this connectivity is carried out. For example, for 3-min chromospheric oscillations in sunspots, the possibility of the acoustic wave leakage into the corona has recently been demonstrated numerically (Botha et al. 2011), but for longer periods a similar mechanism has not been developed. Also, a related question is whether the atmospheric long-period oscillations are anyhow connected with the long-period gravity-driven oscillations of the solar interior. Indeed, the solar g-mode periods are estimated in the range of 16 min to 28 h (e.g. Appourchaux et al. 2010), these are similar to the periods of the atmospheric oscillations. The aim of this paper is to contribute to our understanding of this connectivity.
Here, we analyse long-duration observations of active region AR8253 in the 171 Å and 195 Å bandpasses of TRACE, for five days. We aim to fully take advantage of the long dataset and search for the long-period oscillations and its originality in combination with NoRH 17 GHz radio data. The dataset and its pre-processing are described in Sect. 2; the orbital effects are discussed in Sect. 3; the power spectrum analysis and the elimination of the orbital artifacts are presented in Sect. 4, and final conclusions are given in Sect. 5.
2. Dataset
2.1. Observations
TRACE targeted AR8253 almost continuously for about 5 days, from 30 Jun. to 4 Jul. 1998. The images were taken with the half field-of-view (FOV), 512 × 512 pixels, at the full resolution of 0.5 arcsec/pixel in 171 Å and 195 Å bandpasses. The typical cadence time was either ~41 or ~30 s. The imaging interval between 171 Å and 195 Å was normally 11 s. The data contained several gaps, lasting from ~20 min to ~4 h, but the total observation time covered about ~70% of the time span in both EUV bandpasses. Radio observations at 17 GHz were provided by NoRH. It operates daily from 22:45 to 6:30 UT of the next day, providing data at 10 s cadence with spatial resolution of 10 arcsec/pixel.
2.2. Pre-processing
The TRACE datacubes were prepared with the standard routine TRACE_PREP in Solar Software with standard pre-processing keywords. The EUV images were calibrated with white-light pointing; the spikes and streaks from radiation belts and cosmic rays, plus the readout noise, were removed; the flux intensities were normalised to the exposure time. The image coordinates were co-aligned at the origin of the solar disk in Heliocentric-Cartesian Coordinates to correct the spacecraft re-targeting. The fan-like structure (Fig. 1a) was tracked with the co-moving frame following the solar surface differential rotation. The spacecraft pointing drifts (Handy et al. 1999), plus the uncertainties of solar rotational model, were minimised by cross-correlation offsets. Two co-aligned sub-datasets (128 × 128 pixels) were taken for further analysis (Fig. 1b).
The NoRH 17 GHz radio data was synthesised with the Koshix algorithm. The sunspot was located in the full-disk image and followed with a solar co-rotating box of size (36 × 36 pixels) (see details in Chorley et al. 2010). The FOV was chosen to coincide with the EUV observations. The position of the region of the microwave emission intensity is contoured in dashed line in the EUV image in Fig. 1c. The strong gyro-resonant emission is situated in the sunspot chromosphere. Above it, the fan-like diffuse structure in the corona is an magnetic field extension from the sunspot (Fig. 1a).
2.3. Co-alignment and dejittering
As the TRACE observation spans over 100 h, the images had to be co-aligned and de-jittered. Four images were selected for each day as the reference for cross-correlation and were co-aligned by overlapping the footpoint within an accuracy of less than 1.5 pixels. The rest of the images were smoothed with boxcar of 10 × 10 pixels, then aligned by the offset calculated by cross-correlating to the corresponding reference image. The offsets were treated as time series and smoothed by running averaging to suppress the noise. This approach is more efficient than any smoothing in the images. However it becomes very unstable to the outliers introduced by disruption(s) to the image topology.
 |
Fig. 2 Observational coverage over AR8253 by TRACE 171 Å (red) and 195 Å (blue), and NoRH 17 GHz (green) in the analysed time interval. Small gaps in EUV observations of order 100 s are due to channel switching, and large ones are due to routine observations on the solar limb (including polar regions), re-pointing or to avoid radiation belts. |
There are three types of outliers (Gounder et al. 2007) in the offsets: 1) additive outliers (AO) are single exotic values, normally due to CCD saturation bleeds that ruin part(s) of an image. AOs are easily detected by thresholding and replaced with neighbouring values; 2) innovational outliers (IO) appear as an abrupt step of the average, during which part of the region of interest is out of the FOV; IOs are corrected by restoring the mean; 3) transitory change outliers (TCO) are spikes in the time series that disappear gradually. A flare or a bright point normally induces TCO. TCOs are replaced by linearly interpolated values between the points before and after the event (about 0.5–1 h).
The global accuracy of the co-alignment over 5 days is less than 1.5 pixels, the local relative accuracies (over several hours) are normally as good as 0.5 pixel. The appearances of TCOs deteriorate the co-alignment accuracy to ~2 or 3 pixels for about 0.5–1 h, these parts are deliberately avoided in later analysis.
2.4. Spectral analysis
In the selected time interval, the active region AR8253 was observed for the time sufficiently long for the detection of long-period oscillations, with least disruptions. In the selection of a suitable time interval, we opted to minimise the presence of large data gaps, as a time series containing them lacks a significant portion of information, the power spectrum may be totally erroneous irrespective of the spectral analysis technique. The analysed series of the EUV images were not uniformly sampled, and the data has to be re-sampled into uniform time grid by interpolation. Even though, as the data contained some gaps, its power spectrum was obtained with the Lomb-Scargle periodogram technique (Scargle 1982; Horne & Baliunas 1986). This technique is specifically applicable to the analysis of unevenly sampled data. It overcomes the difficulty posed by unevenness, reduces side-lobe effect and can focus on a certain range of frequencies.
De-trending is applied to the time series by removing the running average before spectral analysis. This process removes ultra-long period trend, it is normally comparable to the range of the time series and contains the large portion of the total power. De-trending relatively suppress the low-frequency bandpass and levitate the high-frequency part. We remove 30 min running average in the time series in studying the orbital effect (Fig. 3), a different averaging time only results in changes in relative power of the peaks. In obtaining Fig. 4, we subtracted 60-min running average from the time series.
In order to distinguish the peaks out of orbital artifacts (see Sect. 3), we applied temporal filtering to the time series. The
orbital harmonics are removed by subtracting sinusoidal functions from the time series
iteratively with date-compensated discrete Fourier transform (DCDFT), ![\begin{equation} \label{eq:filter} \hat{y}(t)=y(t)-[d_0+d_1\sin (2\pi ft)+d_2\cos(2\pi ft)] \end{equation}](/articles/aa/full_html/2011/09/aa16933-11/aa16933-11-eq20.png) (1)where f
is a orbital harmonic frequency, the coefficients d0,
d1, d2 are estimated according
to Ferraz-Mello (1981). Spectral filtering was also
attempted, an abrupt window would bring in edge effects to the spectrum, while a smooth
one may not completely remove the peak (see Inglis
& Nakariakov 2009). DCDFT can be done without tackling the spectral
domain, it calculates the accurate magnitude of the frequencies, but sometimes residual
peaks may appear around the removed component (see Fig. 4e, f and discussions in Sect. 5).
(1)where f
is a orbital harmonic frequency, the coefficients d0,
d1, d2 are estimated according
to Ferraz-Mello (1981). Spectral filtering was also
attempted, an abrupt window would bring in edge effects to the spectrum, while a smooth
one may not completely remove the peak (see Inglis
& Nakariakov 2009). DCDFT can be done without tackling the spectral
domain, it calculates the accurate magnitude of the frequencies, but sometimes residual
peaks may appear around the removed component (see Fig. 4e, f and discussions in Sect. 5).
 |
Fig. 3 Left column: time series (1998-07-03 00:47–12:00 UT).Right column: the corresponding normalised power spectra, a 30-min running average is removed from the intensity time series beforehand, the harmonics of the orbital periods are marked with the vertical dash-dot-dot lines, corresponding to the periods 96, 48, 32, 24 min. From top to bottom row: TRACE CCD temperature variation (°C), the average intensity (DN) of the ROI, and off ROI. |
Referring to the significance level of the detected peaks, no scheme is well accepted by the community, as the distribution of random noise is unknown, a certain assumption of noise distribution has to be made. Moreover, the processing of the data, e.g. de-trending, filtering, destroys the independence of the measurements and coherence of the time series (Hernandez 1999), while these steps are normally unavoidable.
 |
Fig. 4 a), b) Power spectra of the time series (1998-07-03 00:47–09:00 UT) of a macro-pixel (3 × 3 pixels) situated along the mid-way of the slit (Fig. 1b in EUV 171 Å (left) and 195 Å (right). c), d) The corresponding spectra of an enlarged macro-pixel (20 × 20 pixels). e), f) The power spectra after filtering out the orbital frequencies. g) The power spectrum of NoRH 17 GHz radio emission, (1998-07-03 02:55–06:30 UT). The vertical dot-dot-dashed lines are the orbital frequency and its higher harmonics. A horizontal dashed line indicates the 99% confidence level in all the panels (see Sect. 2.4). The detected peaks in all the bandpasses are summarised in Table 1. |
 |
Fig. 5 Lomb-Scargle periodograms of 171 Å data shown after iteratively subtracting the highest peak in the spectrum with power above 1% of FAP (dashed line). The iteration is displayed in order from left to right, top to bottom. |
We estimated the false alarm probability (FAP) at 0.01 to the spectrum, assuming Gaussian noise distribution based on Horne & Baliunas (1986). FAP is the probability to reject a detected peak, it only applies to the highest peak in the spectrum, thus, we subtract the highest peak from the time series using Eq. (1)and repeat this process to the rest of the peaks until all whole spectrum is below the significant level. All peaks quoted in the following text are lower than 0.01 significance level by default, unless specified such as the bracketed numbers in Table 1, they are illustrated in iteration order in Fig. 5 (171 Å), Fig. 6 (195 Å) and Fig. 7 (17 GHz radio).
 |
Fig. 6 The same analysis to 195 Å data as in Fig. 5. The iteration stops earlier than those for 171 Å data, but we note peaks with power below 99% confidence level, near 0.202 and 0.320 mHz, that may be of relevance. |
We also perform Fisher’s randomisation test (Linnell Nemec & Nemec 1985; O’Shea et al. 2001) to all the detected peaks in the power spectrum. This is an unbiased distribution-free test, that estimates the significance level (p-value) of the peaks. Consider a time series, yi = y(ti) and its periodogram, F0(ω). By randomly permuting pairs of data points, yδk ↔ yδj, the time series is rearranged, while the noise remains intact. If there is a significant periodic component in the data, say Tn = 2π/ωn, and |tδi − tδj| = Tn, there is a certain probability that we detect a higher peak at ωn. Repeat this process M times, if a higher peak is recorded K times at ωn, the Fisher’s randomisation estimates the false alarm probability as p = K/M (p-value is alternative to FAP in Horne & Baliunas 1986, test), the standard error is (p(1 − p)/M)0.5. We run 1000 permutations in our studies, the maximum uncertainty is σ(p) = 0.5 M-0.5 = 0.016. If p = 0.0 is obtained, we quote as p < 0.01 by considering the error bar. It is done by iteratively removing the highest peak in the spectrum as described by Eq. (1). We use the time series analysis package PERIOD developed by the Starlink Project (Dhillon et al. 2001). All results are included in Table 1.
3. Orbital effect
TRACE orbits in a polar sun-synchronous orbit, roughly following the solar terminator (twilight zone). The orbital period is ~96 min (0.17 mHz). Because of the orbital motion, the EUV flux incident on the detector changes periodically, thus the CCD temperature is modulated and varies with the orbital period (see Fig. 3, top row). The changes in temperature introduce variability to the pedestal value of the observed intensity and the readout noise (Aschwanden et al. 2000). It should be accounted for when studying long-period intensity oscillations.
The analysis of the time variation of pixel count averaged over the ROI in 171 Å data (see Fig. 1a) in 1998-07-03 00:47–12:00 UT (Fig. 3, middle row) revealed pronounced peaks at the frequency corresponding to the orbital period 0.17 mHz (96 min) and its higher harmonics 0.35 mHz (48 min), 0.52 mHz (32 min), 0.69 mHz (24 min). The same periodicities were detected in a rather quiet region (Fig. 3, bottom row), chosen off the ROI region (Fig. 1a). The same result are found in both 171 Å and 195 Å data. The presence of the higher harmonics of the orbital period is connected with nonlinear dependence of the image intensity to the CCD temperature (Fig. 3, top row).
By assuming the CCD temperature 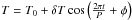 , we
expand the average intensity F(T) of the images in to
Taylor series and re-arrange it by trigonometric operations:
, we
expand the average intensity F(T) of the images in to
Taylor series and re-arrange it by trigonometric operations:
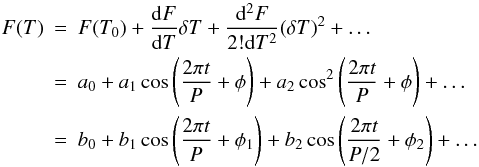 Here
the harmonics periods affect the image intensities, as the telescope orbits around the
Earth, it is due to the non-linearity of the orbital environment, the detection efficiency,
the telescope system. The orbital effect applies to other space missions as well, e.g.
Yohkoh, Hinode and CORONAS-Photon. It varies between instruments and has to be studied
systematically to avoid misleading results.
Here
the harmonics periods affect the image intensities, as the telescope orbits around the
Earth, it is due to the non-linearity of the orbital environment, the detection efficiency,
the telescope system. The orbital effect applies to other space missions as well, e.g.
Yohkoh, Hinode and CORONAS-Photon. It varies between instruments and has to be studied
systematically to avoid misleading results.
4. Results
We selected a time series (1998-07-03 00:47-09:00 UT) of a de-rotated macro-pixel (3 × 3 pixels) situated along the mid-way of the slit (Fig. 1b) in the image in 171 Å. A time interval affected by a C1.3 GOES-class flare (11:19–11:33 UT) was cropped. There are several images corrupted by CCD saturation bleeding between 09:00–10:00 UT, and we simply crop this part. We attempted removing the bad images manually, and included one more hour to the time series, but it resulted in tiny difference compared to Fig. 4. The power spectrum of the signal is shown in Fig. 4a. It contains a mixture of peaks, including the orbital artifacts.
We did the same spectral analysis to macro-pixels out of the fan structure, only the orbital artifacts and/or other random peaks due to noise or unknown sources were found. It suggests that the peaks possibly of solar origin are only localised to the diffuse structure. We enlarged the macro-pixel size from 3 × 3 pixels to 20 × 20 pixels, the corresponding power spectrum is shown in Fig. 4c. Since the orbital artifact exist in all pixels, it is seen that the rest of the peaks are smoothed out and buried relatively in the enhanced orbital harmonics. In order to identify the disappearing peaks and distinguish signals of solar origin from the noise within the data and artifacts due to spectral leakage of the orbital harmonics, we also performed filtering to the signal, as specified in Sect. 2.4. The spectrum (see Fig. 4e) after filtering out the orbital harmonics, shows significant peaks. The result is confirmed by the 195 Å data, displayed in Fig. 4b,d and f. The results are summarised in Table 1.
Outside the orbital periodicity and its higher harmonics, we detected significant spectral peaks at 0.123, 0.222, 0.262, 0.302, 0.382, 0.421 and 0.579 mHz in the TRACE EUV 171 Å emission from a fan-like coronal structure in the active region. These peaks are detected with FAP (p < 0.01) in both Horne & Baliunas (1986) and Fisher randomisation test (see Fig. 5 and Table 1). In the EUV 195 Å data, we only detected 0.262 and 0.559 mHz with FAP < 0.01 in both two significance tests. In the Horne & Baliunas (1986) test, the peaks at 0.202 and 0.320 mHz were found to have FAP > 0.01, while in the Fisher randomisation test, the former peak was found significant (p < 0.01) and the latter was detected with poor confidence (p = 0.20). The FAPs of 0.440 and 0.500 mHz are both <0.01 in Horne & Baliunas (1986) test and estimated at p = 0.018 and p = 0.025 in randomisation test respectively (see Fig. 6 and Table 1).
Similar analysis was performed to the 17 GHz radio intensity data obtained with NoRH, which is ground-based and free of the orbital effects. The available time series was 1998-07-03 02:55–06:30 UT. The power spectrum indicates the existence of long-period oscillations (Fig. 4g). We found spectral peaks in 0.220, 0.314, 0.467 and 0.582 mHz with very good confidence (p < 0.01) in both Horne & Baliunas (1986) and Fisher randomisation tests (see Fig. 7 and Table 1).
5. Conclusions
In this study, we selected time sequences from a five day sample of TRACE observation data over AR8253 to study the long period coronal oscillations. The spacecraft orbital period creates a strong artificial periodicity in the light curves. We found that the TRACE orbital frequency (0.17 mHz) and its higher harmonics (0.35, 0.52 and 0.69 mHz) are pronounced in the EUV intensity images, because of its nonlinear dependence on the CCD temperature variation. A similar artifact can be present in the data obtained with other sun-synchronous space missions, e.g. Yohkoh, Hinode and CORONAS-Photon.
Summary of the detected peaks and significance tests.
We note that 0.221, 0.312, 0.573 mHz (average values, see Table 1) oscillations are present in both EUV emissions in the corona and radio signal in the chromosphere, they are found with with good confidence in both Horne & Baliunas (1986) and Fisher randomisation test at both levels of the solar atmosphere. We conclude that the 0.221, 0.312, 0.573 mHz spectral peaks are of solar origin, and are present in the chromosphere and in the corona. Since the diffuse structure in the corona is the magnetic field extension of the sunspot, propagating EUV disturbance (slow magnetoacoustic wave, see introduction in Sect. 1) was seen persistent for days in the datasets, they were found to leak from the sunspot (Shibasaki 2001; Sych et al. 2009), it strongly implies as well the connectivity of the long period oscillations in the chromosphere and corona.
The nature of the long-period oscillations has not been understood yet. It can have several interpretations. For example, the 0.312 mHz oscillation was also well detected in 17 GHz radio emission in sunspot oscillations (Chorley et al. 2010, 2011). The 0.221 mHz oscillations are very close to the l = 2,n = −3 or l = 3,n = −5 g-mode (note: the same 2l + s combinations pronounce the same frequency, see Turck-Chièze et al. 2004), while the 0.583 mHz could be associated with the l = 1 g-mode (see García et al. 2007). The slight discrepancy can be attributed to observational uncertainties, unresolved multiplet splitting at azimuthal order m due to solar interior rotation or other dynamical processes. In this case, one can speculate that the energy of g-modes, which cannot reach the solar surface, can be channelled by the magnetic field from the deeper layers of the solar interior, especially the less efficiently trapped low-l modes, and hence be seen in the regions of the magnetic concentrations such as the sunspots. The variations of the parameters of the plasma surrounding a magnetic flux tube in the convection zone by a g-mode could excite trapped MHD waves propagating along the tube to the solar surface. Thus, the magnetic flux tubes forming the sunspot could act as a waveguide with little attenuation of the g-mode signal. However, rigorous analysis of this mechanism remains to be performed. Another possibility is the global oscillations of the sunspot, proposed in terms of the shallow sunspot model (Solov’ev & Kirichek 2008).
Another puzzle is the presence of the long-period oscillations in the corona, found in this study. Waves with the periods much longer than the acoustic cut-off period (normally 200–300 s in the chromospheric plasma) (Bel & Leroy 1977) are believed to be constrained to the chromosphere. One possibility is that the wave is indeed evanescent above the chromosphere, but its penetration depth is sufficiently large to be detected in the corona. Another option could be some kind of wave-guiding by the magnetic field, while its nature needs to be revealed. However, it could not be ruled out that the detected long-period oscillations in the chromosphere and in the corona have the same period by pure coincidence.
In any case, the detection of long-period oscillations in the lower corona is a promising signal to help the understanding of the magnetic connectivity of the different layers of the Sun and beyond.
Acknowledgments
D.Y. acknowledges the MPAGS funding for studentship. N.C. is supported by EPSRC studentship. C.F. acknowledges financial support from the UK Science and Technology Facilities Council (STFC) on the CFSA Rolling Grant. We thank the anonymous referee for helpful comments. We acknowledge the TRACE team for providing data. NoRH is operated by the Nobeyama Solar Radio Observatory.
References
- Appourchaux, T., Belkacem, K., Broomhall, A. M., et al. 2010, A&ARv, 18, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Nightingale, R. W., Tarbell, T. D., & Wolfson, C. J. 2000, ApJ, 535, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Bel, N., & Leroy, B. 1977, A&A, 55, 239 [NASA ADS] [Google Scholar]
- Berghmans, D., & Clette, F. 1999, Sol. Phys., 186, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Botha, G. J. J., Arber, T. D., Nakariakov, V. M., & Zhugzhda, Y. D. 2011, ApJ, 728, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Chorley, N., Hnat, B., Nakariakov, V. M., Inglis, A. R., & Bakunina, I. A. 2010, A&A, 513, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chorley, N., Foullon, C., Hnat, B., Nakariakov, V. M., & Shibasaki, K. 2011, A&A, 529, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., Ireland, J., & Walsh, R. W. 2000, A&A, 355, L23 [NASA ADS] [Google Scholar]
- De Moortel, I., Hood, A. W., Ireland, J., & Walsh, R. W. 2002a, Sol. Phys., 209, 89 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., Ireland, J., Walsh, R. W., & Hood, A. W. 2002b, Sol. Phys., 209, 61 [NASA ADS] [CrossRef] [Google Scholar]
- De Pontieu, B., Erdélyi, R., & De Moortel, I. 2005, ApJ, 624, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Deforest, C. E., & Gurman, J. B. 1998, ApJ, 501, L217 [NASA ADS] [CrossRef] [Google Scholar]
- Dhillon, V. S., Privett, G. J., & Duffey, K. P. 2001, PERIOD, A Time-Series Analysis Package Version 5.0 User’s Manual [Google Scholar]
- Efremov, V. I., Parfinenko, L. D., & Soloviev, A. A. 2009, Cosmic Research, 47, 279 [Google Scholar]
- Ferraz-Mello, S. 1981, AJ, 86, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Foullon, C., Verwichte, E., & Nakariakov, V. M. 2004, A&A, 427, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foullon, C., Verwichte, E., & Nakariakov, V. M. 2009, ApJ, 700, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., et al. 2007, Science, 316, 1591 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gelfreikh, G. B., Nagovitsyn, Y. A., & Nagovitsyna, E. Y. 2006, PASJ, 58, 29 [NASA ADS] [Google Scholar]
- Gounder, M. K., Shitan, M., & Imon, R. A. 2007, in Festschrift in honor of Distinguished Professor Mir Masoom Ali On the occasion of his retirement, 213 [Google Scholar]
- Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, G. 1999, J. Geophys. Res., 104, 10355 [NASA ADS] [CrossRef] [Google Scholar]
- Hershaw, J., Foullon, C., Nakariakov, V. M., & Verwichte, E. 2011, A&A, 531, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Inglis, A. R., & Nakariakov, V. M. 2009, A&A, 493, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kepko, L., & Spence, H. E. 2003, J. Geophys. Res. (Space Physics), 108, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- King, D. B., Nakariakov, V. M., Deluca, E. E., Golub, L., & McClements, K. G. 2003, A&A, 404, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linnell Nemec, A. F., & Nemec, J. M. 1985, AJ, 90, 2317 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, M. S., Walsh, R. W., & Plunkett, S. 2009, ApJ, 697, 1674 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., de Pontieu, B., & Tomczyk, S. 2008, Sol. Phys., 252, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Nagovitsyna, E. Y., & Nagovitsyn, Y. A. 2001, Astron. Lett., 27, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Nagovitsyna, E. Y., & Nagovitsyn, Y. A. 2002, Astron. Lett., 28, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Verwichte, E., Berghmans, D., & Robbrecht, E. 2000, A&A, 362, 1151 [NASA ADS] [Google Scholar]
- Ofman, L., Romoli, M., Poletto, G., Noci, G., & Kohl, J. L. 2000, ApJ, 529, 592 [NASA ADS] [CrossRef] [Google Scholar]
- O’Shea, E., Banerjee, D., Doyle, J. G., Fleck, B., & Murtagh, F. 2001, A&A, 368, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Shibasaki, K. 2001, ApJ, 550, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Solov’ev, A. A., & Kirichek, E. A. 2008, Astrophys. Bull., 63, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Sych, R., Nakariakov, V. M., Karlicky, M., & Anfinogentov, S. 2009, A&A, 505, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomson, D. J., Maclennan, C. G., & Lanzerotti, L. J. 1995, Nature, 376, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, D., Isobe, H., & Jain, R. 2009, Space Sci. Rev., 149, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Turck-Chièze, S., García, R. A., Couvidat, S., et al. 2004, ApJ, 604, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Marsh, M., Foullon, C., et al. 2010, ApJ, 724, L194 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Ofman, L., Davila, J. M., & Mariska, J. T. 2009, A&A, 503, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 a) The field of view over AR8253 taken at 1998-07-01 01:01 UT in TRACE 171 Å bandpass, the region of interest (ROI) in the white box includes the fan-like structure and is re-sized to the left, an off-ROI region including the weakest intensity area is marked to the top. b) The region of interest (128 × 128 pixels) showing the fan-like structure; a slit of the macro-pixels (3 × 3) is selected along the fan. c) The intensity map of 17 GHz radio emission over AR8253 at 1998-07-01 01:01 UT. The contour in dashed line marked the sunspot area. |
| In the text | |
 |
Fig. 2 Observational coverage over AR8253 by TRACE 171 Å (red) and 195 Å (blue), and NoRH 17 GHz (green) in the analysed time interval. Small gaps in EUV observations of order 100 s are due to channel switching, and large ones are due to routine observations on the solar limb (including polar regions), re-pointing or to avoid radiation belts. |
| In the text | |
 |
Fig. 3 Left column: time series (1998-07-03 00:47–12:00 UT).Right column: the corresponding normalised power spectra, a 30-min running average is removed from the intensity time series beforehand, the harmonics of the orbital periods are marked with the vertical dash-dot-dot lines, corresponding to the periods 96, 48, 32, 24 min. From top to bottom row: TRACE CCD temperature variation (°C), the average intensity (DN) of the ROI, and off ROI. |
| In the text | |
 |
Fig. 4 a), b) Power spectra of the time series (1998-07-03 00:47–09:00 UT) of a macro-pixel (3 × 3 pixels) situated along the mid-way of the slit (Fig. 1b in EUV 171 Å (left) and 195 Å (right). c), d) The corresponding spectra of an enlarged macro-pixel (20 × 20 pixels). e), f) The power spectra after filtering out the orbital frequencies. g) The power spectrum of NoRH 17 GHz radio emission, (1998-07-03 02:55–06:30 UT). The vertical dot-dot-dashed lines are the orbital frequency and its higher harmonics. A horizontal dashed line indicates the 99% confidence level in all the panels (see Sect. 2.4). The detected peaks in all the bandpasses are summarised in Table 1. |
| In the text | |
 |
Fig. 5 Lomb-Scargle periodograms of 171 Å data shown after iteratively subtracting the highest peak in the spectrum with power above 1% of FAP (dashed line). The iteration is displayed in order from left to right, top to bottom. |
| In the text | |
 |
Fig. 6 The same analysis to 195 Å data as in Fig. 5. The iteration stops earlier than those for 171 Å data, but we note peaks with power below 99% confidence level, near 0.202 and 0.320 mHz, that may be of relevance. |
| In the text | |
 |
Fig. 7 The same analysis to NoRH 17 GHz data as in Fig. 5 . |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


