| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201116808 | |
| Published online | 30 August 2011 | |
Implications for the structure of the relativistic jet from multiwavelength observations of NGC 6251
1
SISSA/International School for Advance Studies, via Bonomea 265, 34136 Trieste, Italy
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden St, Cambridge, MA 02138, USA
e-mail: migliori@head.cfa.harvard.edu
3
Istituto di Astrofisica e Fisica Cosmica - Bologna, INAF, via Gobetti 101, 40129 Bologna, Italy
4
Dipartimento di Astronomia, Università di Bologna, via Ranzani 1, 40127 Bologna, Italy
5
Space Science Division, Naval Research Laboratory, Washington, DC 20375, USA
6
Department of Physics and Astronomy, Barnard College, Columbia University, New York NY 10027, USA
7
Istituto Nazionale di Fisica Nucleare, Sezione di Bari, 70126 Bari, Italy
8
Dipartimento di Fisica “M. Merlin” dell’Università e del Politecnico di Bari, 70126 Bari, Italy
9
INAF Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
Received: 1 March 2011
Accepted: 15 June 2011
NGC 6251 is a luminous radio galaxy ≈104 Mpc away that was detected significantly with the Fermi Gamma-ray Space Telescope, and before that with EGRET (onboard the Compton Gamma-ray Observatory). Different observational constraints favor a nuclear origin for the γ-ray emission. Here we present a study of the spectral energy distribution of the core of NGC 6251, and give results of modeling in the one-zone synchrotron/SSC framework. The SSC model provides a good description of the radio to γ-ray emission but, as for other misaligned sources, predicts a lower Lorentz factor (Γ ~ 2.4) than typically found when modeling blazars. If the blazar unification scenario is correct, this seems to point to the presence of at least two emitting regions in these objects, one with a higher and one with a lower Lorentz factor. The solution of a structured jet, with a fast moving spine surrounded by a slow layer, is explored and the consequences of the two models for the jet energetics and evolution are discussed.
Key words: galaxies: jets / galaxies: active / gamma rays: galaxies / galaxies: individual: NGC 6251
© ESO, 2011
1. Introduction
The Fermi Gamma-ray Space Telescope has confirmed misaligned AGNs (MAGNs), including radio galaxies (RGs) and steep-spectrum radio quasars (SSRQs), as a new and important class of γ-ray emitters (Abdo et al. 2010c,e). In the first year of activity, the Large Area Telescope (LAT, Atwood et al. 2009) onboard Fermi detected 11 MAGNs belonging to the 3CRR, 3CR, and MS4 catalogs at 178 and 408 MHz. At these low frequencies, the Cambridge and Molonglo surveys favor the detection of radio galaxies over blazars. Seven of the 11 Fermi MAGNs are nearby (z ≲ 0.06) Fanaroff-Riley type I (FRI; Fanaroff & Riley 1974) radio galaxies, while the rest are FRII radio galaxies.
The FRI radio galaxies detected with Fermi are significantly less γ-ray luminous than BL Lac objects. The BL Lac objects have isotropic 100 MeV–10 GeV luminosities Lγ ≈ 1044−1046 erg s-1, significantly higher than the FRI radio galaxies, which have Lγ ≈ 1041−1044 erg s-1. They also have spectral slopes that are consistent with low- or intermediate-synchrotron-peaked blazars (Abdo et al. 2010c,a). This is consistent with AGN unified schemes, according to which an increase in the inclination angle of the jet axis with respect to the observer’s line-of-sight implies a de-amplification of the observed flux and a general shift in the emission to lower energies (Urry & Shafer 1984; Urry & Padovani 1995, and references therein). The classification itself of misaligned sources is relative to our expectations of detecting in radio galaxies strongly beamed jet radiation from highly relativistic (Γ ≳ 10) bulk flows, as in the case of blazars. Thus, for the sake of clarity, by misaligned here we do not mean that the observer line-of-sight is outside the radiation cone of the source but rather that it falls outside the (narrow) beaming cone we would expect in the case of a highly relativistic core.
A full comparison with the expectations of the unification scenarios for AGNs has not yet been considered, but the addition of a substantial number of misaligned AGNs at 100 MeV–10 GeV energies now enables this to be made.
Here we present our study of the spectral energy distribution (SED) of the core of NGC 6251, identified with 1FGLJ1635.4+8228 in the First Fermi-LAT Catalog (Abdo et al. 2010b,c, First Fermi-LAT Source Catalog, 1FGL, and First Fermi-LAT AGN Catalog, 1LAC, respectively). NGC 6251 is the fifth γ-ray brightest radio galaxy in the MAGN sample with an integrated flux F-9 = (36 ± 8) in units of 10-9 ph (>100 MeV) cm-2 s-1. It is associated with the EGRET source 3EG J1621+8203 (Mukherjee et al. 2002), being after Centaurus A one of the most likely associations of an EGRET source with a radio galaxy (also of interest are NGC 1275, 3C 111, and M 87). Being bright and relatively close (z = 0.02471 Wegner et al. 2003), NGC 6251 provides a nearby cosmic laboratory to explore the jet structure of radio sources hosting a supermassive black hole.
After describing the source in more detail (Sect. 2), we describe the multiwavelength datasets used to assemble the spectrum of NGC 6251 (Sect. 3). In Sect. 4, we illustrate some uncertainties regarding jet orientation and location, before presenting the results of one-zone synchrotron self-Compton (SSC) modeling in Sect. 5. There we derive magnetic fields, outflow Lorentz factors, and absolute power estimates for comparison with blazars. Parameter comparisons between SSC models of BL Lacs and FRI galaxies reveal the incongruity between these two classes of sources, which we discuss in light of the unification scenario and explore the feasibility of an alternative scenario. In Sect. 6, we consider the connection between the jet power, the disk luminosity, and the accretion. The results are summarized in Sect. 7.
2. NGC 6251
X-ray data analysis results.
NGC 6251 is classified as a FRI radio galaxy (Laing et al. 1983) based on its morphology and monochromatic radio luminosity1 of ≈ 0.94 × 1031 erg s-1 sr-1 at 178 MHz (Waggett et al. 1977)2. Nevertheless, it exhibits an unusual radio morphology, with an ≈ 1° extension of bright radio emission to the northwest (Waggett et al. 1977), and characteristics typical of both FRI and FRII radio galaxies (see the radio maps at 327 and 608 MHz in Mack et al. 1997). At a distance of ≈ 104 Mpc, this corresponds to a linear extension of ≈1.8 Mpc (1″ ≅ 0.5 kpc).
High resolution 1.48 and 4.9 GHz VLA studies reveal a radio core and a complex jet, that is bright and structured within 4.4′ of the core (~113 kpc), and then faint and curved at larger size scales (Perley et al. 1984). On the basis of radio images, Sudou & Taniguchi (2000) showed that the angle between the jet axis and the line of sight increases by ≳ 10°, going from 33° at 50″ from the core to 45° at 200″. The VLBI maps show an asymmetric core-jet radio structure aligned with the VLA jet (Jones et al. 1986).
Both non-thermal and thermal SED components contribute to the core emission of NGC 6251. At wavelengths between ≈ 15 and 30 μm, thermal dust emission appears to dominate over an estimated ~30% nonthermal contribution to the total mid-IR Spitzer flux (Leipski et al. 2009). Synchrotron radiation probably also accounts for the bulk of the optical to UV emission within ≈ 0.2″ of NGC 6251’s core (Chiaberge et al. 2003). The nuclear region in the optical band is complex. A warped dusty disk ≈ 1.43″ in extension unevenly reflects UV radiation from the nucleus, as seen in Hubble Space Telescope images (Ferrarese & Ford 1999). Ionized gas in the 0.3″ region ( ≈ 150 pc) surrounding the nucleus implies that the nucleus of NGC 6251 harbors a black hole with mass ≈ (4–8) × 108 M⊙ (Ferrarese & Ford 1999).
NGC 6251 has been observed with space-based observatories at X-ray energies. The unresolved core is the main X-ray emitter, although high-resolution imaging with Chandra resolves distinct X-ray emission in three different jet regions (Evans et al. 2005). The detection of the Fe Kα line is still debated (Turner et al. 1997; Guainazzi et al. 2003; Gliozzi et al. 2004; Evans et al. 2005). An extended, ~100 kpc X-ray (kBT ≈ 1.7 keV) thermal halo was detected with ROSAT (Birkinshaw & Worrall 1993; Mack et al. 1997), Chandra (Evans et al. 2005), and XMM-Newton (Sambruna et al. 2004). A drop in the surface brightness of the X-ray halo, in positional agreement with the northern radio lobe, suggests that the lobe has evacuated a cavity in the surrounding X-ray gas (Kerp & Mack 2003; Evans et al. 2005).
NGC 6251 has also been detected at hard (>10 keV) X-ray energies by Beppo-Sax (Guainazzi et al. 2003; Grandi et al. 2006) and INTEGRAL (Foschini et al. 2005) and, as previously noted, was proposed as a counterpart to the EGRET source 3EG J1621+8203 (Mukherjee et al. 2002). Observations from Fermi confirmed that NGC 6251 is a GeV source (Abdo et al. 2010b,c). The origin of the nuclear SED of NGC 6251 has been discussed in several papers (Chiaberge et al. 2003; Guainazzi et al. 2003; Ghisellini et al. 2005; Foschini et al. 2005), which have concluded overall that the observed nuclear emission is likely to be dominated by emission from a relativistic jet. The observed SED indeed shows the typical double-hump shape characteristic of blazar sources.
3. SED Data
3.1. Radio to optical/UV data
The radio to UV data collected from literature and shown in Table 4 are used to assemble the nuclear broadband SED of NGC 6251. We note that radio fluxes are taken at different angular resolution and sample nuclear regions of different dimensions. Moreover, the data are not simultaneous and variability could be an issue. Evans et al. (2005), however, inspected VLBI core radio fluxes over 17 years and limited the maximum radio flux variability to a factor of ≤ 2 (see Table 9 in Evans et al. 2005). Data in the microwave region are provided by the five-year Wilkinson Microwave Anisotropy Probe (WMAP) catalog (Wright et al. 2009) and by the published Planck Early Release Compact Source list (Planck Collaboration et al. 2011). The IR flux (15–30 μm) is decomposed into ~30% synchrotron jet emission extrapolated from the radio data and the remainder thermal radiation (Leipski et al. 2009).
The non-thermal origin of the bulk of the nuclear optical emission is supported by the high degree of polarization of the UV emission (close to 50%) and the position of NGC 6251 in diagnostic diagrams for radio galaxies, in common with the other FRI sources (Chiaberge et al. 2003, and references therein). The drop in the optical-UV band might be either real or caused by the dust extinction of the intrinsic optical and UV flux. It is important to establish wether the IR to X-ray flux can be ascribed to a single non-thermal process. The interpretation of the available data is partly controversial. Chiaberge et al. (2003) argued against significant dust reddening because the progressive steepening of the optical-UV slope, related to the increase in the dust extinction with frequency, is not observed. By visual inspection, the optical nucleus appears to be very bright and unobscured by the dust lane. Ferrarese & Ford (1999) estimated a mean intrinsic visual extinction (AV) of 0.61 ± 0.12 mag. The total extinction, which also accounts for the foreground reddening in the direction of NGC 6251, is AV = 0.88 ± 0.13 mag. This value indeed relies on some assumptions, such as that the reddening law follows Cardelli et al. (1989) and RV ≡ AV/E(B − V) is equal to 3.1. An upper limit of 1.0–1.5 to the value of AV was derived in Chiaberge et al. (2003).
In the SED (Fig. 4), we show both the optical fluxes for no absorption (black solid triangles) and after de-reddening (empty circles) for AV = 0.88 mag (using the extinction curves of Cardelli et al. 1989). The SED has a clear double-peaked shape. However, even in the case of absorption (AV < 1.01), a unique emission process for the IR to X-ray data seems unlikely as the IR and optical fluxes do not lie on the extrapolation of the X-ray slope to the lower frequencies (see also Fig. 13 in Evans et al. 2005).
3.2. High energy data
All data from XMM-Newton, Swift, and Chandra observations available in the public archives were re-analyzed and included in the SED. For EGRET and Fermi-LAT data, we use the spectra provided by Mukherjee et al. (2002) and Abdo et al. (2010e).
3.2.1. X-ray spectral analysis
The XMM-Newton observation of NGC 6251, performed in March 2002, was analyzed using the SAS v.9.0 software and available calibration files. We excluded time intervals affected by high background. After this data cleaning, we obtained a net exposure and count rate of 8.7 ks and 1.867 ± 0.015 count s-1 for the pn, 13.9 ks and 0.553 ± 0.006 count s-1 for MOS1, and 13.5 ks and 0.556 ± 0.006 count s-1 for MOS2, respectively. The source and background spectra were extracted from circular regions of 27′′ radius. The response matrices were created using the SAS commands RMFGEN and ARFGEN. The nuclear data are not piled up. Data were grouped into 25 counts per bins in order to be able to apply the χ2 statistic. The best-fit model for the pn (0.3–10 keV) data consists of an absorbed power-law plus an APEC component which models a collisional gas emission (χ2 = 410 for 372 degrees of freedom). The parameter values, reported in Table 1, agree with the results of Evans et al. (2005). The same results (not shown in Table 1) were obtained using MOS data. There is no significant evidence of the Fe Kα emission line in the XMM data.
The Swift X-Ray Telescope observed NGC 6251 three times between April 2007 and May 2009. The X-ray data were reduced using the on-line XRT data analysis provided by the ASDC3. Source spectra for each observation were extracted from a circular region of 20″ radius, while the background was taken from an annulus with an inner radius of 40″ and outer radius of 80″. The data were re-binned to 20 counts per bin in order to calculate χ2. All spectral fits were performed in the 0.5–10 keV band. Data can be well described by an absorbed power-law with column density slightly in excess of the Galactic value (NHGal = 5.4 × 1020 cm-2). Unlike XMM Newton, the XRT spectra, characterized by a lower signal-to-noise ratio, do not require the addition of a soft thermal emission component (see Table 1). We note that, during the 2002 observation, the source appeared in a higher state (see Sect. 3.2.2).
We analyzed only the most recent and longest Chandra observation of the source that was performed in November 2003 in ACIS–S (S3 and S4 chips) configuration. The Chandra pointing of September 2000 was not taken into account because in this observation the core fell in a chip gap. Data were reprocessed using the Chandra Interactive Analysis of Observation (CIAO v.4.1) and the Chandra Calibration Database CALDB 4.1. After correction for high particle background, the total exposure time is reduced to 45 ks. The nuclear spectrum was extracted from a circular region of 5″ radius centered on the source. The background was chosen in an adjacent circular region with 12″ radius. Because of the brightness of NGC 6251 at X-ray energies, the data are affected by pile-up, which was estimated to be ≈ 13% using the PIMMS software4. For this reason, we decided not to consider the Chandra nuclear fluxes in the SED. As an extended extranuclear emission associated with the kpc jet is clearly visible in the Chandra image, a spectrum was also extracted for this component. The accumulation region is a box of 20″ and 5.3″ each side, far ( ≈ 6″) from the nucleus. A box of similar size was chosen to estimate of the background. A good fit is obtained by an absorbed power law with 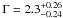 and NHGal = 5.7 × 1020 cm-2. The photon index value is in good agreement with the one (
and NHGal = 5.7 × 1020 cm-2. The photon index value is in good agreement with the one (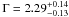 ) reported in Evans et al. (2005) for the region containing the inner jet (extending from about 1.5″ to 27″ from the nucleus). The 0.5–2 keV unabsorbed flux is 3.1 × 10-14 erg cm-2 s-1, while the 2–10 keV flux is 2.3 × 10-14 erg cm-2 s-1.
) reported in Evans et al. (2005) for the region containing the inner jet (extending from about 1.5″ to 27″ from the nucleus). The 0.5–2 keV unabsorbed flux is 3.1 × 10-14 erg cm-2 s-1, while the 2–10 keV flux is 2.3 × 10-14 erg cm-2 s-1.
 |
Fig. 1 Unfolded spectral model of the combined XMM-Newton and Swift datasets. Black points: Swift observation of April 2007; red: Swift observation of May 2009; green: Swift observation of June 2009; blue: XMM-Newton observation of March 2002. |
3.2.2. High energy variability
We first explored fast (hour-scale) temporal variability of the nuclear X-ray flux during the XMM and Swift observations producing a lightcurve in the 0.5–10 keV band for each observation. None of the four lightcurves reveal a statistically significant change of flux. To investigate the presence of X-ray flux variability on timescales of months/years, we successively performed a simultaneous fit of the XMM and Swift spectra. The four datasets were simultaneously fit with a composite model, an absorbed power law, and a thermal (APEC) component, which correspond collectively to the best-fit model for the spectrum with the highest signal-to-noise ratio (i.e. the XMM-Netwon dataset). An energy-independent multiplicative factor (n) allows us to compare the fits of the four datasets. The results of the simultaneous fit are reported in the last column of Table 1. The values of the model parameters are driven by the XMM dataset. As also shown in Fig. 1, there is an evident flux variation over the entire 0.5–10 keV band between the XMM and Swift observations, expressed by the different n values. The X-ray flux decreases by about 40% between the XMM and the first Swift observations and then an additional ~15% by the two last Swift observations (the values of n parameter for the three observations being nXMM = 1, nSwift1 = 0.60 ± 0.04 and nSwift2 = 0.45 ± 0.05 respectively). The close to two years between the first and the second Swift observations, performed on April 6, 2007 and May 5, 2009, respectively, provide us with the shortest interval during which X-ray flux variability has been detected. Thus, we consider this as an upper limit to the X-ray flux variability timescale.
No time variability in the γ-ray band was detected in the first 15 months of LAT observations of the Fermi source 1FGLJ1635.4+8228, which is associated with NGC 6251 (Abdo et al. 2010e). In Fig. 2, we show the 100 MeV–100 GeV lightcurve of the 15-month LAT dataset generated by dividing the total observation period in 5 time intervals of 3-month duration.
 |
Fig. 2 Fermi-LAT lightcurve of the source 1FGL1635.4+8228, associated with the radio galaxy NGC 6251, between 100 MeV and 100 GeV. The time is measured from 2008 August 4 and covers 15 months of Fermi operation. Each bin corresponds to 3 months of observations. The horizontal line is the constant flux. |
We considered longer timescales when comparing the LAT and EGRET results. The LAT flux F-9 = 36 ± 8 is lower in comparison with the γ-ray flux measured by EGRET, F-9 = 74 ± 23. However, the large uncertainties in the fluxes make it difficult to firmly establish whether this is related to an actual variation in the γ-ray flux of the source on timescales of years rather than to contamination of the EGRET flux from other sources. At a distance in the range of ≈2°–5° from 1FGLJ1635.4+8228, there are at least three other γ-ray sources in the 1FGL with a flux similar to or brighter than 1FGLJ1635.4+8228, none of which has an EGRET counterpart.
4. Observational constraints
We must now consider our observational constraints when developing a multiwavelength database for modeling, including the relative imaging capabilities of different detectors, epochs of different observations, separate spectral components, and questions about whether there is either intrinsic or Galactic extinction.
4.1. Location of the γ-ray emission region
The construction and interpretation of NGC 6251’s SED depends on the site of production of the γ-ray photons. Because of the limited imaging capability of the Fermi-LAT, with a PSF of ≈ 0.6° at 1 GeV (Atwood et al. 2009), Fermi can distinguish the central regions from sites coincident with the extended radio structures in NGC 6251, but is unable to resolve details on length-scales ≲ 3′ (1′ corresponds to ≈ 30 kpc). Radio galaxies are expected to be sources of γ-ray emission produced in both the compact core and inner jet (Marscher et al. 2008; Fermi-Lat Collaboration et al. 2010), as well as emitting extended γ-ray emission from, at least, photons of the cosmic microwave and extragalactic background light (CMB and EBL respectively) that are Compton-scattered by the radio-emitting electrons in the lobes (Cheung 2007; Georganopoulos et al. 2008; Hardcastle et al. 2009).
If the source varies, simultaneous multi-frequency VLBI, X-ray/Swift, and Fermi campaigns (Sokolovsky et al. 2010; Giovannini et al. 2010) can help to constrain the origin of the γ-ray emission as well as the physical parameters of the region. For blazars, results based on high frequency radio observations, rapid γ-ray variability, and correlated variability in different wavebands make locations in the vicinity of the bright radio core the favored candidate for the site of intense γ-ray production.
The same approach might be more difficult for MAGNs. Seven of the 11 MAGNs have a flux of F-9 < 40, and two of them (3C 78/NGC 1218 and PKS 0625-354) have F-9 ≲ 5. With the exception of NGC 1275, no significant γ-ray variability has been detected so far with the Fermi-LAT in MAGNs (Abdo et al. 2009a; Kataoka et al. 2010; Abdo et al. 2010c), but, at these low γ-ray fluxes, we are unable to detect variability even when present.
Significant contributions from other components can further dilute and hide the flux variability. For the first time, Fermi-LAT has detected γ-ray emission from the lobes of the radio galaxy Cen A (Fermi-LAT Collaboration et al. 2010): the >100 MeV emission from the lobes is a large fraction ( ≳ 1/2) of the total flux, with the fluxes of the northern lobe, the southern lobe and the core, being ≈ 0.77 ± 0.3 × 10-7, 1.09 ± 0.3 × 10-7, and 1.50 ± 0.3 × 10-7 ph cm-2 s-1 respectively.
As discussed in Sect. 3.2.2, γ-ray variability on month timescales has not been observed by Fermi, although flux variability over several years is not completely ruled out. Since no variability has yet been clearly detected, a significant fraction of the γ-ray flux could originate from the lobes. The γ-ray spectral index is soft (Γγ = 2.52 ± 0.12), implying that most of the power detected in the Fermi band is dominated by photons in the 100 MeV–10 GeV range. At these energies, the LAT PSF is unable to resolve the core from the lobes. As a rough estimate, we can rescale the γ-ray flux of Cen A lobes at the proper luminosity distance (~104 Mpc) and lobe dimensions of NGC 6251. We use the γ-ray brightest lobe of Cen A (i.e. the southern lobe) and assume a simple spherical geometry for the NGC 6251 lobe with a diameter D = 1.9 Mpc/2 = 850 kpc, equal to half of the NGC 6251 linear dimension, and thus an overestimate of the actual lobe dimensions. In this way, the γ-ray flux rescaled to the NGC 6251 lobe is F-9 ≈ 8, comparable to the statistical error in the LAT flux of the source associated with NGC 6251 (F-9 = 36 ± 8). There are indeed uncertainties in this estimate: we assume a similar SED for the lobes of the two radio galaxies while this cannot be assessed not even in the radio-IR band as the lobes of NGC 6251 are not well sampled. For this reason, we discuss the effects on the nuclear SED modeling of a possible extended contribution in Sect. 5.
Even though γ-ray emission on the hundred parsec scale might also contribute, the non-thermal nuclear emission of the core likely dominates the source SED at radio, X-ray, and γ-ray wavelengths. In Fig. 12 of Jones et al. (1986), the core and jet-knot radio fluxes are compared at different frequencies: the core is optically thick below ~13.5 GHz, and becomes dominant at higher radio frequencies. The X-ray spectral analysis, using high resolution Chandra data, has shown that the bulk of the X-ray emission comes from the nuclear region (r ≤ 4″), while the knot accounts for ≲ 10% of the total observed X-ray flux (Evans et al. 2005).
4.2. Jet orientation
Another key question for MAGNs is the jet orientation, which is expected to be a large angle in objects with no extreme blazar characteristics. The jet inclination angle, a difficult quantity to observationally establish, must be measured before constraining the physical properties of relativistic sources. Here we consider a range of jet inclinations for NGC 6251 based on different observational quantities: the jet sidedness (J), the VLBI apparent velocity βa = vac of the jet knots, and the core dominance. If an intrinsic symmetry is assumed, the jet and counter-jet brightness ratio J can be expressed in terms of the jet velocity (β = vc) and orientation (θ): J = [(1 + βcosθ)/(1 − βcosθ)](2 + α), where α is the radio spectral index, defined such that S(ν) ∝ ν − α, and assumed here to be α = 0.5. In a similar way the apparent transverse velocity of a relativistic moving blob βa is related to β and θ via βa = βsinθ/(1 − βcosθ) (Urry & Padovani 1995). Giovannini et al. (2001) found a general correlation, albeit with significant spread, between the core and total radio power in radio galaxies log Pc = 0.62log Ptot + 7.6, where Pc is the arcsecond core radio power at 5 GHz and Ptot is the total radio power at 408 MHz in units of W Hz-1. This relation can be used to derive upper and lower limits to β and θ (for details, see Giovannini et al. 1994), allowing the core density to vary within a factor of 2. Thus, if Pc and Ptot are known, and values or upper limits to J and βa are available, a narrow region of permitted values can be defined in the β versus θ plot. This implicitly assumes that the pattern speed inferred from the apparent motion and the bulk motion of the emitting plasma do not differ (Urry & Padovani 1995, and references therein).
In NGC 6251, the counter jet observed in VLA maps (Perley et al. 1984) disappears on mas scales. Jones & Wehrle (2002) investigated the possibility that free-free absorption by an ionized accretion disk could hide the receding jet, but concluded on the basis of the high electron density required that relativistic boosting effects better explain the observations. In line with their considerations, we assume that the brightness ratio of ≈100:1 measured within 6 mas of the core is a plausible lower limit to J (Jones & Wehrle 1994). The superluminal velocity of the jet has not been measured in NGC 6251, only a lower limit of βa > 1.2 having been reported (Jones & Wehrle 1994). The values of Pc and Ptot that we considered here to estimate the jet inclinations and velocities allowed by the core dominance correlation, were calculated from the 5 GHz core flux Fc(5 GHz) = 0.4 Jy (Perley et al. 1984) and the total 408 MHz flux Ftot(408 MHz) = 5.3 Jy (Waggett et al. 1977).
The final β-θ plot is shown in Fig. 3. The permitted values, shown by the gray region, are within the area delimited by J > 100, βa > 1.2, and the core dominance relation. Only bulk motions larger than ~ 0.78 and inclination angles in the range of about ≈ 10°–40° are compatible with the observed properties of the NGC 6251 jet.
 |
Fig. 3 Constraints on the angle θ between the jet and the line of sight and the jet velocity β in units of the speed of light. Blue and black curves correspond to J = 100 and βa = 1.2, respectively. The red curve is from the Pc versus Ptot relation. The dot-dashed red lines are obtained allowing the core density to vary by a factor two. The gray area corresponds to the permitted values of β and θ. |
5. SED modeling
5.1. One-zone SSC model
In the context of the emission from a relativistic jet, the double-hump shape of the nuclear SED is accounted for the nonthermal synchrotron and inverse Compton (IC) radiation. The radio to optical/UV radiation originates from the synchrotron mechanism by relativistic electrons, while the same electrons are supposed to Compton-upscatter seed-photons to X-ray and γ-ray energies.
We first model the SED of NGC 6251 with a one-zone synchrotron self-Compton (SSC) model, where the seed photons for Compton scattering are the local synchrotron photons themselves. We assume a homogeneous spherical blob. VLBI observations (Jones et al. 1986) place an upper limit of ≲ 0.20 mas ( ≈ 3 × 1017 cm) on the size of the nuclear region. There is no clear evidence of flux variability on short timescales that could provide more stringent limits. VLBI radio fluxes vary by a factor of close to two on timescales of years (Evans et al. 2005), corresponding to a region radius R ~ 1018 cm ~ 1 pc. Gliozzi et al. (2004) reported the detection of short-time (~104 s), low-amplitude X-ray flux variations. Evans et al. (2005), analyzing XMM-Newton and Chandra data, concluded that variations in 2–10 keV fluxes are plausible but uncertain.
We derive upper limits similar to the radio ones on the basis of our X-ray temporal analysis of XMM and Swift observations (Sect. 3.2.2). The assumption is that the nuclear X-ray emission is produced in the same region as the radio and γ-ray radiation.
As discussed in Sect. 4.2, the jet/counter-jet flux ratio, apparent velocity, and the core-dominance relation define a range of allowed values for the core jet speed β and relative inclination θ. We consider as reference values for the modeling θ = 25° and β = 0.91, values that fall roughly at the center of the area of permitted values (see Fig. 3). The resulting Doppler factor is δ = 2.4. This value agrees with the constraints inferred by assuming that the region is transparent to γ-ray absorption via the γγ to e+e− process, δ ≥ 0.44 (calculated using Eq. (A4) in Abdo et al. 2010d, Appendix).
Looking at the broad-band SED (Fig. 4), the synchrotron and Compton peaks can be approximately located in the frequency intervals 1013–1014 Hz and 1021–1022 Hz, respectively. Quillen et al. (2003) report a spectral index αO − S = 1.1 between the sub-millimeter (870 μm) and the optical band, while the IR-to-UV slope between 16 000 and 2200 Å is αIR − UV = 1.75 ± 0.16 (Chiaberge et al. 2003). The spectral index values in the high energy band, αX = 0.88 ± 0.04 in the range 2–10 keV and αΓ = 1.52 ± 0.12 in the Fermi-LAT frequency interval, are slightly flatter than, but still consistent with, the sub-mm/UV α values. Quillen et al. (2003) noted that dust extinction can partially reduce the flux of the optical continuum in the core, and determine the spectral steepening.
The four spectral indices give the slope below (αO − S, αX) and above (αIR − UV, αΓ) the synchrotron and Compton peaks, respectively. Therefore, as a reasonable approximation, we assume the same spectral indices for the synchrotron and IC curves below (α1 = 0.88) and above (α2 = 1.52) the peaks, and adopt a broken power-law to describe the electron energy distribution (EED) 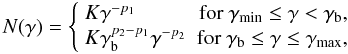 (1)where γ is the electron Lorentz factor in the range γmin ≤ γ ≤ γmax, K is the EED normalization, p1 = 2α1 + 1 and p2 = 2α2 + 1 are the low and high energy EED spectral indices, and γb is the energy break of the distribution. From the ratio of the synchrotron (νs) and IC (νc) peak frequencies
(1)where γ is the electron Lorentz factor in the range γmin ≤ γ ≤ γmax, K is the EED normalization, p1 = 2α1 + 1 and p2 = 2α2 + 1 are the low and high energy EED spectral indices, and γb is the energy break of the distribution. From the ratio of the synchrotron (νs) and IC (νc) peak frequencies 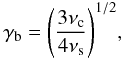 (2)which yields values for γb spanning the range between ≈ 3 × 103 and ≈ 3 × 104.
(2)which yields values for γb spanning the range between ≈ 3 × 103 and ≈ 3 × 104.
The best SSC model “fit” for the nuclear SED of NGC 6251 is shown in Fig. 4 (left panel), and the corresponding model parameters (in the comoving frame) are reported in Table 2.
 |
Fig. 4 Nuclear broadband SED of NGC 6251 compiled using multi-epoch data. Radio to optical-UV data are reported in Table 4. Solid black triangles are the total IR flux. The solid IR points are the extrapolated non-thermal synchrotron fluxes given in Leipski et al. (2009). Empty optical-UV data are dereddened (see text). X-ray emission is presented in Sect. 3.2: black dots are for XMM-Netwon data and red from Swift satellite. Black γ-ray points correspond to EGRET flux (Mukherjee et al. 2002). Red γ-ray points are Fermi data (Abdo et al. 2010c). Left panel: the SED is modeled with a one-zone SSC model (solid black line: synchrotron curve, solid red line: IC emission). Right panel: the SED is modeled with the spine-layer model illustrated in Ghisellini et al. (2005). Solid black and red lines reproduce the SSC emission of the layer. Dashed black and red curves are the SSC model for the spine. The long-dashed blue line is the IC emission of the spine synchrotron photons scattered by the layer relativistic electrons. |
Interestingly the nuclear SED can be broadly reproduced by assuming a mildly relativistic motion (Γ = 2.4), i.e. significantly lower than that required to account for several observational properties of blazars (i.e. the apparent superluminal motion observed on milliarcsecond scales, see Kellermann et al. 2004; Lister et al. 2009; and SED modeling, Tavecchio et al. 2010), but with values of the source size (R = 1.2 × 1017 cm) and magnetic field (B = 0.037 G) consistent with those inferred for BL Lac objects. Similar results have also been found when a single-zone synchrotron/SSC model is applied to the nuclear SED of other members of the MAGN sample detected by Fermi-LAT (see the studies on Cen A, NGC 1275, and M 87, Abdo et al. 2010d, 2009a,b, respectively). For comparison, typical bulk Doppler factors and magnetic fields of BL Lac objects are δ = 12 and B = 1.5 × 10-2 G for Mrk 501 (Abdo et al. 2011), while for the extreme case of PKS 2155-304 during flaring states, detailed SSC modeling gives δ ≅ 100 and B ≅ 0.1 G (Finke et al. 2008).
We note that the adopted bulk motion value implies a jet radiation cone θrad = 1/Γ ~ 24°. Thus, the observer line of sight falls roughly inside the radiation cone of the emitting region and NGC 6251 is aligned in the sense that it is within 1/Γ. Once again, we underline that the definition of MAGN is strictly related to the expectation of detecting radiation from a blazar-like (i.e. highly relativistic) region even in those radio sources whose jet physical axis is oriented at larger inclination angles (θ ≳ 10°) with respect to the line of sight.
The values of the main parameters are similar to the results of the SSC model fitting of NGC 6251 in Chiaberge et al. (2003), where θ = 18° and Γ = 3.2 were assumed. The particle-to-magnetic field energy density ratio is 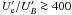 , where
, where 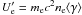 (me is the electron mass, ⟨ γ ⟩ is the average electron Lorentz factor) and
(me is the electron mass, ⟨ γ ⟩ is the average electron Lorentz factor) and 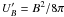 . The violation of the minimum energy assumption is then rather severe already without considering any contribution from the protons.
. The violation of the minimum energy assumption is then rather severe already without considering any contribution from the protons.
In summary, the SSC model provides a good overall fit to the data, but requires a large departure from the equipartition between relativistic electrons and magnetic field and a relatively slow speed of the jet. We note incidentally that Sudou et al. (2000) discussed a possible sub-parsec scale acceleration of the jet from β ~ 0.13 ≈ 0.5 pc to β ~ 0.42 at ≈ 1 pc. According to this, we should be observing the jet before it becomes relativistic.
How robust are these results? The source orientation (with the related quantities, Γ and δ) is indeed a crucial assumption. A smaller θ, say ~10°, while requiring a higher bulk Lorentz factor, Γ ≈ 15, is disfavored by radio observations: this θ would imply either a large linear size of the source, ≳ 5.5 Mpc, or a significantly bent jet (Chiaberge et al. 2003).
We note that θ and Γ, as also R, affect in the same way the synchrotron and IC curves and will not change our results for the particle to magnetic field relative energy densities. Beyond the uncertainties related to the assumed parameters (e.g. θ), we also considered those caused by observational uncertainties and examined three possibilities: (i) the γ-ray flux was overestimated because of contamination from an external contribution (for example the kpc jet or the lobes, as in the case of Cen A, see Fermi-LAT Collaboration et al. 2010; Abdo et al. 2010d; Böttcher et al. 2008); (ii) both the γ-ray and X-ray fluxes are overestimated, because of the limits of the X-ray and γ-ray observatories in resolving the dimensions of the emitting region (R ≈ 1017 cm); and (iii) the flux contamination introduces uncertainties in the values of spectral indices. As a test, we considered the case where the fluxes were overestimated by at most a factor of 5. We assumed an intrinsically harder source, assigning to α1 and α2 the values 0.84 and 1.4 respectively, based on the uncertainties on the X-ray and γ-ray spectral indices. Summarizing the results for the three cases, we have that B, K, and γb vary in the ranges (3.7 − 6) × 10-2 G, (1.5 − 0.25) × 106 cm-3, and (0.8 − 2) × 104 respectively. It follows that 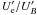 may be reduced by at most an order of magnitude but still the jet remains particle-dominated.
may be reduced by at most an order of magnitude but still the jet remains particle-dominated.
NGC 6251 nuclear SED-models.
5.2. Structured jet models
Chiaberge et al. (2000) pointed out that the luminosities of FRI radio sources exceed those predicted by a simple unification scenario, which assumes that FRI radio galaxies represent the de-beamed counterparts of BL Lac objects whose emission is produced, via SSC, by a single region. Moreover, model fitting of NGC 6251, as also of other radio galaxies, do require (modest) beaming factors (Chiaberge et al. 2001; Abdo et al. 2009a,b, 2010d). If the condition of a homogeneous one-zone emitting blob is relaxed, other possible interpretations are viable. For example, Ghisellini et al. (2005) proposed a stratified jet structure, with a fast narrow spine responsible for the BL Lac-like emission, and a slower layer, whose emission would dominate that of the fast spine at larger angles, i.e. as in FRI radio sources. If true, there would be a strong feedback between the two components. The spine provides additional seed photons via synchrotron emission that can be IC scattered by the relativistic electrons of the layer (and vice versa). Similar solutions, assuming a complex velocity axial/radial structure in jets, were also proposed by other authors (Stawarz & Ostrowski 2002; Georganopoulos & Kazanas 2003). The presence of these structures are also supported by the transversely resolved brightness profile observed in parsec scale jets (Giroletti et al. 2004, 2006).
In view of the new Fermi detection and additional (Spitzer and Planck) data in the mm-IR band, we reconsider the spine-layer scenario previously proposed for NGC 6251 in Ghisellini et al. (2005). The “fit” to NGC 6251 nuclear SED thus obtained is shown in Fig. 4 (right panel). The geometry of the two regions is cylindrical (L is the cylinder length), with the spine nested inside the hollow layer cylinder. The spine parameters in Table 2 are chosen to reproduce a standard BL Lac object, with Γspine = 15 for a region of radius Rspine = 1016 cm in a magnetic field Bspine = 1.8 G. The spine EED is a broken power-law with p1 = 2.1 and p2 = 3.0 and an energy break γb,spine = 3.0 × 103. We keep the same spectral shape as before for the EED of the layer (p1 = 2.76 and p2 = 4.04), and the same δ and θ. The red and black solid (dashed) curves in Fig. 4 (right panel) represent the layer (spine) synchrotron and SSC contributions, respectively. The blue long-dashed curve is the layer IC emission of the spine synchrotron photons. The interaction between the spine and the layer helps reproduce the observed X-ray to γ-ray emission and requires a reduced number of relativistic electrons and a larger magnetic field (Blayer = 0.7 G) than the SSC model values. On the other hand, the debeaming (δspine ~ 0.7) of the spine emission at θ = 25° hides the presence of the emission from the fast flow. When the jet axis inclination with respect to the line of sight is reduced, to say θ ≲ 5°, the blazar-like emission from the spine dominates the SED (as also shown in Fig. 5 in Ghisellini et al. 2005, for similar parameter values).
A critical point is that the spine-layer model assumes a flux variability in the spine radiation similar to that observed in blazar sources. Rapid changes in the spine synchrotron flux should be reflected by those of Comptonized emission coming from the layer, on timescales of about tvar ~ (Rspine/c)δlayer ≈ 0.02 yrs. In NGC 6251, no clear indication of variability in γ-rays has been found, while the X-ray emission has varied on a shorter than two-year timescale. The lack of significant variability in the γ-ray band, however, cannot by itself rule out the model. Even without considering the source detectability, clearly the volume of the layers could partly dilute the variability and of course the real jet structure is likely to be more complex than assumed in this simplified description.
Though beyond the aim of this work, we recall that more recently two classes of models have been proposed to explain the high energy emission in blazars and radio galaxies. In the first case, beams of particles or “jets in a jet” emitting also off the jet axis are invoked to explain the observed TeV flares in both blazars (e.g. Ghisellini et al. 2009; Giannios et al. 2009) and the misaligned AGN M 87 (Giannios et al. 2010). In the second scenario, the high-energy emission is produced by colliding shells with different bulk motions. In a schematic and simplified view, (internal) shocks are caused by the broad range of velocities characterizing the different “shells”: the slower ones would naturally lead to emission at larger viewing angles (Dermer 2011).
5.3. Jet power
While from the modeling of the SED and its variability properties it is not possible to discriminate between the SSC and spine-layer scenarios, these have different implications as far as the jet energetics is concerned as inferred here. Jet powers for electrons (Le), protons (Lp), and Poynting flux (LB) are estimated as, 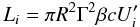 (3)where
(3)where 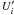 is the energy density, in the comoving frame, of electrons,
is the energy density, in the comoving frame, of electrons, 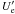 , cold protons,
, cold protons, 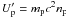 (mp proton mass), and magnetic field,
(mp proton mass), and magnetic field, 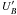 . Here, we assume that there is one cold proton per emitting electron (np = ne). The radiation luminosity is
. Here, we assume that there is one cold proton per emitting electron (np = ne). The radiation luminosity is 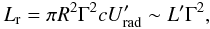 (4)where L′ is the intrinsic total (synchrotron and IC) luminosity. The kinetic, magnetic, and radiative powers for the two applied models, SSC and spine-layer, are shown in Table 3.
(4)where L′ is the intrinsic total (synchrotron and IC) luminosity. The kinetic, magnetic, and radiative powers for the two applied models, SSC and spine-layer, are shown in Table 3.
NGC 6251 Jet Powers for the SSC and spine-layer models.
NGC 6251 nuclear SED-data.
As noted before, the SSC model implies a strong particle dominance (Le ≈ 1.6 × 1044 erg s-1 and Lp ≈ 5 × 1044 erg s-1) over the magnetic field (LB ≈ 3.6 × 1041 erg s-1). The radiative power is Lr ≈ 2 × 1043 erg s-1, about an order of magnitude lower than the kinetic one. In this case, the bulk of the jet power is conserved and goes into the formation of the large radio structures. The values are in the range of powers found by modeling the SEDs of typical BL Lacs (Celotti & Ghisellini 2008; Ghisellini et al. 2010; Tavecchio et al. 2010), even though we note that NGC 6251 is in the low tail of LB values for BL Lacs (Celotti & Ghisellini 2008).
The SSC model – if correct – would have two interesting implications: (i) Le and Lp are comparable to those of BL Lacs with similar Lr, despite of the different Lorentz factor, and thus the jet is relatively heavier; and (ii) the low Poynting flux seems to exclude a magnetically confined jet. On kpc scales, the jet expands at variable lateral velocity, and exhibits the presence of re-confinement sites (Perley et al. 1984). Several authors (Perley et al. 1984; Mack et al. 1997; Evans et al. 2005) have shown that the pressure exerted by the extended (out to 100 kpc) halo of X-ray emitting gas around the radio source can account for the jet confinement on kpc scales. On the other hand, in the inner few arcseconds the jet is rapidly expanding and thermal confinement would require an X-ray luminosity incompatible with the observed one. An initial regime of free expansion seems then more likely (Perley et al. 1984), requiring a re-collimation mechanism.
In contrast, in the spine-layer model the jet is faster and less heavy. Thus, magnetic fields could play a fundamental role in its confinement. The total jet kinetic power derived from the spine-layer model parameters is just slightly smaller (Lkin = Le + Lp ≈ 3 × 1044 erg s-1) than Lkin of the SSC model. However, in this scenario, because of the higher energy density in seed photons than in the SSC model, the required emitting particle density is lower. This leads also to quasi-equipartition between 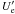 and
and 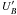 (Ghisellini et al. 2005). The bulk of the jet kinetic power is carried by the fast spine. The radiative dissipation (Lr = 9 × 1043 erg s-1) is rather high in the spine. The jet converts about 30% of its total power into radiation, and should then undergo a progressive deceleration, as also predicted by the Compton rocket effect (Ghisellini et al. 2005), while we recall that NGC 6251 has an extraordinary linear extension of ~ 1.9 Mpc.
(Ghisellini et al. 2005). The bulk of the jet kinetic power is carried by the fast spine. The radiative dissipation (Lr = 9 × 1043 erg s-1) is rather high in the spine. The jet converts about 30% of its total power into radiation, and should then undergo a progressive deceleration, as also predicted by the Compton rocket effect (Ghisellini et al. 2005), while we recall that NGC 6251 has an extraordinary linear extension of ~ 1.9 Mpc.
5.4. Checking the jet kinetic power
The inferences about Lkin rely on some key assumptions, the ratio of the number density of cold protons to that of electrons above all. A check on these estimates can be done using an alternative approach, based on the measure of the pdV work done by the source in forming the lobes in the hot surrounding gas (Willott et al. 1999; Fabian et al. 2002; Allen et al. 2006). Here, we adopted the correlation reported by Willott et al. (1999)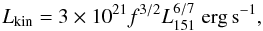 (5)where L151 [erg s-1 Hz-1 sr-1] is the monochromatic radio power at 151 MHz. In the revised formula considered here, a factor f takes into account possible systematic underestimates intrinsic to the technique. Hardcastle et al. (2007) estimated f to be in the range between 10 and 20 for a sample of FRI and FRII sources. Given the 151 MHz luminosity of NGC 6251, L151 = 2.46 × 1031 erg s-1 Hz-1 sr-1, the kinetic power, setting f respectively equal to 10 and 20, is in the range 7.5 × 1043–2.2 × 1044 erg s-1, just slightly below the value of Lkin found for the two models, thus in agreement with the above estimates.
(5)where L151 [erg s-1 Hz-1 sr-1] is the monochromatic radio power at 151 MHz. In the revised formula considered here, a factor f takes into account possible systematic underestimates intrinsic to the technique. Hardcastle et al. (2007) estimated f to be in the range between 10 and 20 for a sample of FRI and FRII sources. Given the 151 MHz luminosity of NGC 6251, L151 = 2.46 × 1031 erg s-1 Hz-1 sr-1, the kinetic power, setting f respectively equal to 10 and 20, is in the range 7.5 × 1043–2.2 × 1044 erg s-1, just slightly below the value of Lkin found for the two models, thus in agreement with the above estimates.
6. Jet power versus accretion
The SED of NGC 6251 in the optical-UV band is dominated by the non-thermal emission of the jet. No sign of a big blue bump is identified and there is no strong evidence in the X-ray spectrum of a broad Fe Kα emission line, which are both considered to be signatures of emission by an accretion disk. The nonthermal flux can be used to derive an upper limit to the disk luminosity, Ldisk ≲ 1043 erg s-1 (Ferrarese & Ford 1999; Ho 2009), which in units of Eddington luminosity, LEdd, is Ldisk/LEdd ≲ 10-4 for an estimated black hole mass MBH = 6 × 108 M⊙ (Ferrarese & Ford 1999). The sub-Eddington regime could indicate the presence of a radiatively inefficient disk (here we generically refer to the class of models as radiatively inefficient accretion flows, RIAFs, see Narayan 2002, for a review). Ghisellini & Celotti (2001) demonstrated that the FRI–FRII dividing line in the radio luminosity vs optical galaxy luminosity plane (proposed by Ledlow & Owen 1996) can be expressed in terms of a critical accretion rate of 10-2 − 10-3, in units of Eddington accretion, and suggested that this might reflect a change in the accretion mode from a standard optically thick geometrically thin efficient Shakura-Sunyaev disk (Shakura & Sunyaev 1973) to a RIAF.
Ferrarese & Ford (1999) estimated for NGC 6251 a Bondi accretion rate of ṀBondi ~ 5 × 10-4 M⊙ yr-1 and a corresponding accretion power of 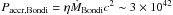 erg s-1, assuming an efficiency for the conversion of the accreted rest mass into energy of η = 0.1. Given the observed (non-thermal) luminosity, they argued that a RIAF would require an accretion rate 102 − 103 higher. However, as they pointed out, this accretion rate value is likely to be a lower limit based on lower limits to the pressure and density of the interstellar matter (ISM). If we assume that the jet is completely powered by the accretion process, the jet kinetic power provides us with an even higher lower-limit5 to the accretion power Paccr ≳ Lkin ≈ 1044 − 1045 erg s-1. When we adopt typical gas densities found for the central regions of elliptical galaxies, nd ≈ 0.1 − 0.5 cm-3 (Di Matteo et al. 2001; Pellegrini 2005), we obtain a Bondi accretion rate ṀBondi ~ 5 × 10-2 M⊙ yr-1, which gives Paccr,Bondi ≈ 1045 erg s-1. If this is the case, a radiatively inefficient disk can in principle provide the required jet power, though the mechanism that converts the accretion into the jet power is very efficient. A study of nearby X-ray luminous elliptical galaxies have found that Paccr,Bondi and the jet power, inferred from the work done to expand the cavities observed in the surrounding X-ray gas, have similar values. This suggests that a significant fraction of the mass entering the Bondi accretion radius eventually goes into the relativistic jet (Allen et al. 2006). Interestingly, it has been proposed for blazars (Celotti & Ghisellini 2008; Ghisellini et al. 2010, and references therein) that the jet power maintains a linear dependence on Ṁ/ṀEdd with a transition to a quadratic dependence at low accretion rates, as also expected in RIAF solutions (Narayan & Yi 1995; Mahadevan 1997).
erg s-1, assuming an efficiency for the conversion of the accreted rest mass into energy of η = 0.1. Given the observed (non-thermal) luminosity, they argued that a RIAF would require an accretion rate 102 − 103 higher. However, as they pointed out, this accretion rate value is likely to be a lower limit based on lower limits to the pressure and density of the interstellar matter (ISM). If we assume that the jet is completely powered by the accretion process, the jet kinetic power provides us with an even higher lower-limit5 to the accretion power Paccr ≳ Lkin ≈ 1044 − 1045 erg s-1. When we adopt typical gas densities found for the central regions of elliptical galaxies, nd ≈ 0.1 − 0.5 cm-3 (Di Matteo et al. 2001; Pellegrini 2005), we obtain a Bondi accretion rate ṀBondi ~ 5 × 10-2 M⊙ yr-1, which gives Paccr,Bondi ≈ 1045 erg s-1. If this is the case, a radiatively inefficient disk can in principle provide the required jet power, though the mechanism that converts the accretion into the jet power is very efficient. A study of nearby X-ray luminous elliptical galaxies have found that Paccr,Bondi and the jet power, inferred from the work done to expand the cavities observed in the surrounding X-ray gas, have similar values. This suggests that a significant fraction of the mass entering the Bondi accretion radius eventually goes into the relativistic jet (Allen et al. 2006). Interestingly, it has been proposed for blazars (Celotti & Ghisellini 2008; Ghisellini et al. 2010, and references therein) that the jet power maintains a linear dependence on Ṁ/ṀEdd with a transition to a quadratic dependence at low accretion rates, as also expected in RIAF solutions (Narayan & Yi 1995; Mahadevan 1997).
7. Summary
We have presented a study of the broad-band nuclear SED of the radio galaxy NGC 6251, one of the MAGNs detected by Fermi-LAT. In agreement with previous studies, the nuclear SED is dominated by non-thermal emission related to the sub-pc jet. A nuclear origin appears to be the most likely hypothesis for the γ-ray emission. This is also supported by the results of our X-ray analysis of archival XMM-Newton, Chandra, and Swift observations. Both models, SSC and spine-layer, adopted to reproduce the observed SED, provide a good overall fit. In the following, we summarize the main results of the SED modeling.
A single-zone SSC model assumes a slow and heavy jet. The particle power dominates over the magnetic field power by about three orders of magnitude. This seems to rule out a magnetically accelerated and confined jet. The X-ray halo surrounding the jet can account for its confinement on kpc scales but the core region remains poorly constrained. A low bulk Lorentz factor, when a one-zone SSC model is adopted, is also shared with other MAGNs detected by Fermi-LAT (Abdo et al. 2009a,b; Kataoka et al. 2010; Abdo et al. 2010d). This suggests the presence of at least a second site of γ-ray emission in addition to the one we observe when the jet is pointing directly toward us (Chiaberge et al. 2000). A significant reduction of the jet inclination angle, which would allow higher bulk Lorentz factors, is unsupported by the radio observations. These results should not be significantly affected by an overestimate of the γ-ray flux of a factor of a few ( ≈ 5).
A structured jet with a fast inner component and a slower layer is a possible explanation. In the spine-layer model proposed in Ghisellini et al. (2005), the jet is relatively light and could be magnetically confined. The fast inner component carries the bulk of the jet power. On the other hand, the strong radiative dissipation (Lr ~ 0.3 Lkin) is at odds with the Mpc-length of the jet and the flux variability predicted by the model in the high energy band has not yet been observed.
The derived jet powers, ≈ 1044–1045 erg s-1, are model-dependent and rely on some important assumptions. However, similar values were derived using the 151 MHz luminosity (Willott et al. 1999).
The disk component appears to be completely hidden by the jet emission. The sub-Eddington luminosity regime (Ldisk/LEdd ≲ 10-4) could be related to the presence of a RIAF. Support to this hypothesis is provided by the estimates of the Bondi accretion rate, albeit with significant uncertainties in the ISM physical parameters. As has been found for blazar sources, the mechanism channeling the accretion power into the jet seems to work in a more efficient way (Lkin/Ldisk ≳ 10 and Lkin ~ 0.1 − 1Paccr).
According to the classification proposed by Fanaroff & Riley (1974), the flux density at the FRI/FRII boundary, corrected for the adopted cosmological values, is 1 × 1032 erg s-1 sr-1.
Acknowledgments
We thank the anonymous referee for her/his contribution to improve the paper. G. Migliori thanks A. Capetti and D. Thompson for useful comments, professor A.J. Buras for hospitality at TUM-IAS and F. Civano for helpful suggestions.
This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. The authors would like to thanks the ASI Science Data Center (ASDC) for providing on-line facilities for the Swift/XRT data analysis. G.M. research is supported by Chandra grant GO0-11133X.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 699, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 707, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010a, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 715, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, ApJ, 719, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010e, ApJ, 720, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 727, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Dunn, R. J. H., Fabian, A. C., Taylor, G. B., & Reynolds, C. S. 2006, MNRAS, 372, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Birkinshaw, M., & Worrall, D. M. 1993, ApJ, 412, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., Dermer, C. D., & Finke, J. D. 2008, ApJ, 679, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., & Ghisellini, G. 2008, MNRAS, 385, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, C. C. 2007, in The First GLAST Symposium, ed. S. Ritz, P. Michelson, & C. A. Meegan, 921, AIP Conf. Ser., 325 [Google Scholar]
- Chiaberge, M., Celotti, A., Capetti, A., & Ghisellini, G. 2000, A&A, 358, 104 [NASA ADS] [Google Scholar]
- Chiaberge, M., Capetti, A., & Celotti, A. 2001, MNRAS, 324, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Gilli, R., Capetti, A., & Macchetto, F. D. 2003, ApJ, 597, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M. H., & Readhead, A. C. S. 1979, ApJ, 233, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D. 2011, Jets at all Scales, Proc. IAU, IAU Symp. 275, 111 [Google Scholar]
- Di Matteo, T., Carilli, C. L., & Fabian, A. C. 2001, ApJ, 547, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, D. A., Hardcastle, M. J., Croston, J. H., Worrall, D. M., & Birkinshaw, M. 2005, MNRAS, 359, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Celotti, A., Blundell, K. M., Kassim, N. E., & Perley, R. A. 2002, MNRAS, 331, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Fermi-LAT Collaboration, Members Of The 3C 279 Multi-Band Campaign, Abdo, A. A., Ackermann, M., Ajello, M., Axelsson, M., Baldini, L., Ballet, J., Barbiellini, G., Bastieri, D., et al. 2010a, Nature, 463, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fermi-LAT Collaboration, Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Science, 328, 725 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ferrarese, L., & Ford, H. C. 1999, ApJ, 515, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Finke, J. D., Dermer, C. D., & Böttcher, M. 2008, ApJ, 686, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Chiaberge, M., Grandi, P., et al. 2005, A&A, 433, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georganopoulos, M., & Kazanas, D. 2003, ApJ, 594, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Georganopoulos, M., Sambruna, R. M., Kazanas, D., et al. 2008, ApJ, 686, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Celotti, A. 2001, A&A, 379, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Bodo, G., & Celotti, A. 2009, MNRAS, 393, L16 [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2010, MNRAS, 402, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D., Uzdensky, D. A., & Begelman, M. C. 2009, MNRAS, 395, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D., Uzdensky, D. A., & Begelman, M. C. 2010, MNRAS, 402, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Feretti, L., Venturi, T., et al. 1994, ApJ, 435, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Cotton, W. D., Feretti, L., Lara, L., & Venturi, T. 2001, ApJ, 552, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Casadio, C., Giroletti, M., et al. 2010 [arXiv:astro-ph/1010.4170] [Google Scholar]
- Giroletti, M., Giovannini, G., Feretti, L., et al. 2004, ApJ, 600, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Giroletti, M., Giovannini, G., Taylor, G. B., & Falomo, R. 2006, ApJ, 646, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Gliozzi, M., Sambruna, R. M., Brandt, W. N., Mushotzky, R., & Eracleous, M. 2004, A&A, 413, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grandi, P., Malaguti, G., & Fiocchi, M. 2006, ApJ, 642, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Guainazzi, M., Grandi, P., Comastri, A., & Matt, G. 2003, A&A, 410, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Cheung, C. C., Feain, I. J., & Stawarz, Ł. 2009, MNRAS, 393, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C. 2009, ApJ, 699, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. L., & Wehrle, A. E. 1994, ApJ, 427, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. L., & Wehrle, A. E. 2002, ApJ, 580, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. L., Unwin, S. C., Readhead, A. C. S., et al. 1986, ApJ, 305, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, J., Stawarz, Ł., Cheung, C. C., et al. 2010, ApJ, 715, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Kerp, J., & Mack, K. 2003, New Astron. Rev., 47, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Knapp, G. R., Bies, W. E., & van Gorkom, J. H. 1990, AJ, 99, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., Riley, J. M., & Longair, M. S. 1983, MNRAS, 204, 151 [Google Scholar]
- Ledlow, M. J., & Owen, F. N. 1996, AJ, 112, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Leipski, C., Antonucci, R., Ogle, P., & Whysong, D. 2009, ApJ, 701, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Mack, K., Kerp, J., & Klein, U. 1997, A&A, 324, 870 [NASA ADS] [Google Scholar]
- Mahadevan, R. 1997, ApJ, 477, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mukherjee, R., Halpern, J., Mirabal, N., & Gotthelf, E. V. 2002, ApJ, 574, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R. 2002, in Lighthouses of the Universe: The Most Luminous Celestial Objects and Their Use for Cosmology, ed. M. Gilfanov, R. Sunyeav, & E. Churazov, 405 [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, S. 2005, MNRAS, 364, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., Bridle, A. H., & Willis, A. G. 1984, ApJS, 54, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration, Ade, P. A. R., Aghanim, N., Arnaud, M., et al. 2011, A&A, in press, DOI: 10.1051/0004-6361/201116474 [arXiv:astro-ph/1101.2041] [Google Scholar]
- Quillen, A. C., Almog, J., & Yukita, M. 2003, AJ, 126, 2677 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Gliozzi, M., Donato, D., et al. 2004, A&A, 414, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sokolovsky, K. V., Kovalev, Y. Y., Lobanov, A. P., et al. 2010 [arXiv:1006.3084] [Google Scholar]
- Stawarz, Ł., & Ostrowski, M. 2002, ApJ, 578, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Sudou, H., & Taniguchi, Y. 2000, AJ, 120, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Sudou, H., Taniguchi, Y., Ohyama, Y., et al. 2000, PASJ, 52, 989 [Google Scholar]
- Tavecchio, F., Ghisellini, G., Ghirlanda, G., Foschini, L., & Maraschi, L. 2010, MNRAS, 401, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., George, I. M., Nandra, K., & Mushotzky, R. F. 1997, ApJS, 113, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Shafer, R. A. 1984, ApJ, 280, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Waggett, P. C., Warner, P. J., & Baldwin, J. E. 1977, MNRAS, 181, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Wegner, G., Bernardi, M., Willmer, C. N. A., et al. 2003, AJ, 126, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Chen, X., Odegard, N., et al. 2009, ApJS, 180, 283 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Unfolded spectral model of the combined XMM-Newton and Swift datasets. Black points: Swift observation of April 2007; red: Swift observation of May 2009; green: Swift observation of June 2009; blue: XMM-Newton observation of March 2002. |
| In the text | |
 |
Fig. 2 Fermi-LAT lightcurve of the source 1FGL1635.4+8228, associated with the radio galaxy NGC 6251, between 100 MeV and 100 GeV. The time is measured from 2008 August 4 and covers 15 months of Fermi operation. Each bin corresponds to 3 months of observations. The horizontal line is the constant flux. |
| In the text | |
 |
Fig. 3 Constraints on the angle θ between the jet and the line of sight and the jet velocity β in units of the speed of light. Blue and black curves correspond to J = 100 and βa = 1.2, respectively. The red curve is from the Pc versus Ptot relation. The dot-dashed red lines are obtained allowing the core density to vary by a factor two. The gray area corresponds to the permitted values of β and θ. |
| In the text | |
 |
Fig. 4 Nuclear broadband SED of NGC 6251 compiled using multi-epoch data. Radio to optical-UV data are reported in Table 4. Solid black triangles are the total IR flux. The solid IR points are the extrapolated non-thermal synchrotron fluxes given in Leipski et al. (2009). Empty optical-UV data are dereddened (see text). X-ray emission is presented in Sect. 3.2: black dots are for XMM-Netwon data and red from Swift satellite. Black γ-ray points correspond to EGRET flux (Mukherjee et al. 2002). Red γ-ray points are Fermi data (Abdo et al. 2010c). Left panel: the SED is modeled with a one-zone SSC model (solid black line: synchrotron curve, solid red line: IC emission). Right panel: the SED is modeled with the spine-layer model illustrated in Ghisellini et al. (2005). Solid black and red lines reproduce the SSC emission of the layer. Dashed black and red curves are the SSC model for the spine. The long-dashed blue line is the IC emission of the spine synchrotron photons scattered by the layer relativistic electrons. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


