| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201117016 | |
| Published online | 03 August 2011 | |
Investigating the variation of latitudinal stellar spot rotation and its relation to the real stellar surface rotation⋆
1
Finnish Centre for Astronomy with ESO (FINCA), University of
Turku,
Väisäläntie 20,
21500
Piikkiö,
Finland
e-mail: heidi.h.korhonen@utu.fi
2
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6,
79104
Freiburg,
Germany
3
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte
16, 14482
Potsdam,
Germany
e-mail: delstner@aip.de
Received: 4 April 2011
Accepted: 6 June 2011
Aims. In this work the latitude-dependent stellar spot rotation is investigated based on dynamo models, and with similar analysis techniques as for real observations. The resulting surface differential rotation patterns are compared to the known input rotation law used in the calculation of the dynamo model.
Methods. Snapshots of the dynamo simulations are used to measure the surface differential rotation. The maps of the magnetic pressure at the surface are treated similarly to the temperature maps obtained using Doppler imaging techniques, and a series of snapshots from the dynamo models are cross-correlated to obtain the shift of the magnetic patterns at each latitude and time point. These shifts are used to study the surface rotation pattern over a wide latitude range at different epochs during the activity cycle, and are compared to the known input rotation law.
Results. Two different rotation laws are investigated, one solar-type law and one with axis-distance-dependent rotation. Three different dynamo calculations are carried out based on the axis-distance-dependent law: one with a large-scale dynamo field only, one with an additional strong small-scale field and one with a weaker small-scale field. The surface differential rotation patterns obtained from the snapshots of all four dynamo calculations show variability over the activity cycle. Clear evolution and variation in the measured surface rotation patterns is seen, but in the models using only the large-scale dynamo field the measured rotation patterns are only at times similar to the input rotation law. This is because the spot motion is mainly determined by the geometric properties of the large-scale dynamo field. In the models with an additional small-scale magnetic field the surface differential rotation measured from the model follows the input rotation law well.
Conclusions. Here, the surface differential rotation patterns are investigated in detail based on dynamo calculations for the first time. The results imply that the stellar spots caused by the large-scale dynamo field are not necessarily tracing the stellar differential rotation, whereas the spots formed from small-scale fields trace the surface flow patterns well. One may wonder whether the large spots observed in active stars could be caused by small-scale fields. Therefore, it is still unclear if the true stellar surface rotation can be recovered using measurements of large starspots, which are currently the only observable feature.
Key words: magnetic fields / magnetohydrodynamics (MHD) / stars: activity / stars: rotation / starspots
Figures 3, 4, 7, and 8 are available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
Differential rotation (DR) is one of the key ingredients in stellar dynamo models. Together with the helical turbulence and meridional flow it is responsible for the main features of the solar and stellar magnetic activity (see, e.g., Rüdiger et al. 1986; Choudhuri et al. 1995; Brun & Toomre 2002). The surface DR of the Sun has been known for a long time from observing the rotation of sunspots and other magnetic elements at different latitudes (e.g., Balthasar et al. 1986). The rotation period at the solar equator is approximately 30% shorter than the period at the poles. Helioseismology has revealed that this pattern persists throughout the entire convection zone (e.g., Thompson et al. 1996; Schou et al. 1998), while the radiative core rotates rigidly. Between the core and the convection zone there is a transition layer, tachocline, with a strong radial shear (Spiegel & Zahn 1992).
Theoretical calculations predict that across the Hertzsprung-Russel diagram the DR becomes stronger with increasing rotation period and evolutionary status (Kitchatinov & Rüdiger 1999). In general, models for global circulation in outer stellar convection zones predict solar-type DR, where the equator is rotating faster than the poles. However, Kitchatinov & Rüdiger (2004) have shown that anti-solar DR, which was suggested by observations of several active stars (e.g., Weber 2007), could arise as a result of intensive meridional circulation.
Stellar differential rotation is usually characterised by the surface shear δΩ = Ωeq−Ωpole, where Ωeq and Ωpole are the rotation rates at the equator and the poles, respectively. The surface shear is related to the lapping time, tlap = 2π/δΩ. For stars, a surface rotation law of the form Ω = Ωeq(1 − ksin2θ) is usually assumed, where θ is the latitude. The measurements of surface DR on rapidly rotating cool stars is summarised by Barnes et al. (2005). These measurements seem to show an increase in the magnitude of differential rotation towards earlier spectral types, which is consistent with the theoretical calculations of Rüdiger & Küker (2002). Recently, a comparison of the models and observations was carried out by Küker & Rüdiger (2008).
Intriguingly, temporal evolution of the surface DR has been reported for two young single K-dwarfs, AB Dor and LQ Hya (see, e.g., Donati et al. 2003; Jeffers et al. 2007). Donati et al. (2003) hypothesise that these temporal variations could be caused by the stellar magnetic cycle periodically converting kinetic energy within the convective zone into large-scale magnetic fields and vice versa, as originally proposed by Applegate (1992).
Measuring stellar differential rotation is not straightforward. Stars are faint and far away, thus only the closest super giants can be directly spatially resolved with the current instruments and methods (e.g., Gilliland & Dupree 1996; Monnier et al. 2007). Currently the best way to study stellar surface DR in detail, both the strength and the sign, is by using surface maps obtained with the Doppler imaging technique (see, e.g., Vogt et al. 1987; Piskunov et al. 1990). One way, similar to using sunspots and other magnetic features to study the solar DR, is to use several of the surface maps and cross-correlate them to investigate the changes in the locations of the spots (see, e.g., Barnes et al. 2000; Weber et al. 2005; Kővári et al. 2007). The other frequently used way is the so-called χ2-landscape technique, in which a DR law is implemented into the Doppler imaging code, and many maps are obtained for studying which parameters give the best solution (e.g., Petit et al. 2002; Marsden et al. 2006; Dunstone et al. 2008). Stellar surface DR has also been studied by combining spot latitude information from Doppler images and the spot rotation period from contemporaneous photometry (Korhonen et al. 2007) as well as by using Fourier transforms to study shapes of the spectral line profiles (see, e.g., Reiners & Schmitt 2003).
All methods for measuring stellar surface DR using Doppler imaging results suffer from the often restricted latitude range that the starspots occur on, and from possible artefacts in the maps caused by systematic errors. These systematics can for example arise from incorrect modelling of the spectral line profiles. Additionally, in the χ2-landscape technique a predefined rotation law is assumed. On the other hand, the time difference between the maps is crucial in cross-correlation, if the difference is too small no change has time to occur, and if the difference is too long spot evolution owing to flux emergence and disappearance may have occurred. Therefore, it is very demanding to obtain reliable measurements of stellar surface differential rotation, and currently it is basically impossible to obtain information on the internal rotation of stars other than the Sun.
In this study we investigate the surface differential rotation obtained from snapshots of dynamo models using cross-correlation methods. These snapshots provide a very good temporal base for studying the measured surface differential rotation at different times over the stellar activity cycle. The obtained surface DR values are compared to the known internal rotation law used in the dynamo modelling.
2. Dynamo model and analysis methods
2.1. Model
The model used here was first developed to theoretically study the flip-flop dynamo behaviour. In the flip-flop phenomenon the spots concentrate on two permanent active longitudes that are separated by 180°, and the main spot-activity switches between the longitudes every few years (e.g., Jetsu et al. 1993; Berdyugina & Tuominen 1998; Järvinen et al. 2005).
The dynamo is modelled with a turbulent fluid in a spherical shell. Two different rotation laws are chosen for investigation: one similar to the solar one but with a smaller difference between core and surface rotation (L1), and another one with axis-distance-dependent rotation (L2), similar to the models presented by Moss (2004). The mean electromotive force contains an anisotropic alpha-effect and a turbulent diffusivity. The nonlinear feedback of the magnetic field acts on the turbulence only. The boundary conditions describe a perfect conducting fluid at the bottom of the convection zone and the magnetic field matches the vacuum field at the stellar surface. The model is discussed in detail in Elstner & Korhonen (2005) and Korhonen & Elstner (2005).
The rotation laws used in this study are illustrated in Fig. 1. In L1 the internal rotation is solar-type, i.e., the equator is rotating faster than the polar regions. The inner boundary of the convective zone is at the radius 0.4 R⋆. L2 is an axis-distance-dependent rotation law, where the parts farthest away from the rotation axis are rotating the fastest. The areas close to the axis, i.e., on the surface the polar regions, do not rotate at all. In this model the inner boundary of the convective zone is at the radius 0.27 R⋆. The dynamo numbers Cα = α ∗ R⋆/ηT and 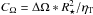 , and the distribution of magnetic energy (e0 in the axisymmetric mode, e1 in the mode with azimuthal wavenumber m = 1, and en in the higher modes) are given in Table 1.
, and the distribution of magnetic energy (e0 in the axisymmetric mode, e1 in the mode with azimuthal wavenumber m = 1, and en in the higher modes) are given in Table 1.
 |
Fig. 1 Illustration of the internal rotation laws used in this study. a) The solar-type rotation law with the equator rotating faster than the poles (L1). b) Axis-distance-dependent law, where the parts farthest away from the axis are rotating the fastest (L2). |
 |
Fig. 2 Illustration of the clockwise spot motion (circles) during the flip-flop event. Shown is the surface magnetic pressure of the non-axisymmetric mode. The circles along the latitude mark the maximum of the poleward migrating axisymmetric field at different times. Spots appear only at one spiral, where the signs of the two modes are equal. Note that the stellar rotation and the magnetic pattern are anti-clockwise. |
Dynamo models.
Both models lead to a mixed field of a non-axisymmetric and an oscillating axisymmetric mode. The non-axisymmetric modes rotate rigidly with Ωm = −0.32 degrees/day for L1 and Ωm = −2.9 degrees/day for L2. This corresponds to the surface rotation at about 55° latitude for L1 and 65° for L2. The oscillation period for the full cycle of the axisymmetric mode is 6.8 years for L1 and 2.7 years for L2. In Fig. 2 the surface magnetic pressure of the non-axisymmetric mode for L2 is shown. The schematic rings demonstrate the upward motion of the axisymmetric field belt of one polarity during half a cycle. The small circles indicate the spot motion owing to the field geometry (in the corotating frame of the field pattern). The spots move during one third of a half cycle (latitudes 40° to 70°) about 100° opposite to the stellar rotation. Therefore we expect the spot rotation to almost stop during the flip-flop cycle. The individual behaviour depends on the spiral pattern of the field and the migration speed of the axisymmetric field. A similar explanation for the differential rotation of active longitudes on the sun was already discussed in Berdyugina et al. (2006).
In order to study the effect of small-scale spots, additional simulations were run for the model L2, where small poloidal field loops were randomly added to the convection zone once per day (laws L2a and L2b). The magnetic energy caused by the additional field injection in model L2a is about half of the energy of the axisymmetric field component in the quasi-stationary regime. The fields appear as localised spots on the surface that move with the surface rotation. With that strong field injection (L2a) the field structure of the global dynamo mode is nearly hidden by the small-scale spots. Therefore, we added 10 times weaker field loops (model L2b) in a second run, which led to a final energy of the small-scale component of only 1/100th of the axisymmetric field. Here the global field again dominates the surface spot structure. One could also correlate the small-scale field injection with the large-scale magnetic field, but for simplicity a totally uncorrelated field injection was chosen.
2.2. Measuring the surface differential rotation
When using the dynamo models to study the surface differential rotation, the temporal resolution can be made sufficiently high for standard cross-correlation methods to work. Snapshot maps of the surface magnetic pressure are taken from the dynamo calculations and treated as representations of the magnetic structures at that time point. These maps can be treated the same way as the temperature maps obtained from Doppler imaging, therefore the same techniques as for the real observations can be used to analyse the model snapshots. Magnetic pressure maps have been taken from 36 time points over the activity cycle. These time points are relatively close to each other: separated by about 50 days in L1, and by about 18 days with L2. Examples of snapshots for L1 and L2 are shown in Figs. 3 and 4, respectively.
In the analysis each time point is cross-correlated with the following one and the behaviour is studied from equator to the visible pole. The dynamo model has a grid of 43 × 43 surface points. This yields longitudinal resolution of 8.4° and latitudinal of 4.2°. The equator lies in the middle of the 22nd latitude strip. The cross-correlations are obtained for each latitude between the latitudes centred at 4.2° and 83.7°. The last latitude strip closest to the pole is not used owing to the lack of signal. The measured shift in degrees/day at each latitude is compared to the expected shift obtained from the rotation law used in the dynamo model. The spots are migrating in the dynamo simulation; to remove this field migration all measured shifts are normalised to the shift at the lowest latitude used in the investigation.
3. Results
Examples of results from cross-correlating the 36 maps for L1 are shown in Fig. 5. The plots give the shift in degrees/day for each latitude on the visible hemisphere (crosses). The last plot shows the average of the measurements from all cross-correlations with the standard deviation of the measurements as error. In the plots the dashed line is the input rotation at the stellar surface.
 |
Fig. 5 Examples of the cross-correlation results using the 36 individual snapshots from the dynamo model L1. The crosses give the shift in degrees/day for each latitude between 4.2° and 83.7°. The solid line in the plots shows the input rotation law for the dynamo model at the surface. The last plot is the average behaviour obtained from all snapshots with using the standard deviation of the measurements as the error. |
 |
Fig. 6 Same as Fig. 5, but using L2. Note that occasionally very high negative shifts are measured and one point can fall outside the plotting range. |
The behaviour of the measured spot rotation clearly changes from cross-correlation to cross-correlation, indicating that the appearing surface rotation pattern changes during the activity cycle. Furthermore, the measured surface rotation can take numerous different forms: typical solar-type rotation law (e.g., cross-correlation 11), almost no difference between the latitudes (e.g., cross-correlation 01) and even completely anti-solar rotation law with the pole rotating faster (e.g., cross-correlation 25). In general, evidently the measured surface differential rotation at low latitudes for L1 often is what one would expect from the models, but at higher latitudes the correlation is very poor.
The examples of cross-correlation results from L2, shown in Fig. 6, also exhibit large variations in the surface rotation patterns over the activity cycle. In some cases the measured surface rotation at the lower latitudes is similar to the input rotation (e.g., cross-correlation 14), at times the surface rotation at the equator and at the polar region is similar to the input rotation, but the exact shape of the rotation curve is different from the expected (e.g., cross-correlation 16), but in most cases the rotation shows much less latitudinal variation than expected based on the input rotation.
4. Discussion
4.1. Surface differential rotation patterns over the activity cycle
4.1.1. Model L1
The surface DR measurements for model L1, shown in Fig. 5, cover slightly more than one activity cycle, which also includes a flip-flop event. A similar phase in the cycle as in map 1 is reached in map 28. Clear evolutions in the surface rotation patterns are seen throughout the cycle.
In general, the shape of the surface rotation pattern over the latitude can be divided into four parts. Closest to the equator the surface rotation follows the internal rotation law, and in most maps three abrupt changes in the surface rotation occur at higher latitudes. Clear evolution in the latitude at which the breaks occur is seen over the activity cycle. When the cycle advances, the breaks drift towards the higher latitudes. Even at the point where the spots move to lower latitude, the breaks continue drifting towards the polar regions. The highest latitudes for the breaks are obtained just before the time when the second spot starts to appear in the flip-flop event. When the breaks abruptly move towards the equator again, the rotation measurements for the lower latitudes become less ordered and appear chaotic.
In this model the axisymmetric dynamo wave is not only a poleward migration as indicated in Fig. 2. It starts at the bottom of the convection zone at 30° latitude and expands outwards in radius and latitude. For lower latitudes the expansion along the non-axisymmetric spiral now gives a counter-clockwise acceleration. This leads to the qualitative agreement with the stellar rotation law near the equator. The effect depends on the expansion speed and the pitch angle of the underlying non-axisymmetric field. For the rotation-law-dependent small pitch angle near the equator this is a huge effect. At higher latitudes the spot motion is determined by the field geometry and the migration speed of the poleward-moving dynamo wave, and therefore the rotation is reduced by the clockwise motion of the spot along the spiral. At the very polar region the wave moves slower and the rotation again appears faster. This behaviour depends on the phase of the cycle. If the field reversal between two cycles lies at mid-latitudes (50°), we see the rotation of the non-axisymmetric field, which coincides here with the stellar rotation (cf. cross-correlation 1 to 5 and 26 to 30).
4.1.2. Model L2
The measurements of the surface DR using model L2 shown in Fig. 6 cover almost two activity cycles. The same epoch as in the first cross-correlation is again obtained around the time of cross-correlation 18. Evolution in the surface rotation patterns are seen, but they are not as clear as for L1.
For most epochs the surface rotation is similar at all the latitudes, showing relatively small differential rotation. Often two areas with distinctly different rotation behaviour are seen, though, one where the magnetic surface patterns lag behind, and one where they rotate faster than the general surface rotation. The mainly constant spot velocity in this model goes back to the much more clear poleward migration of the oscillating mode because of the different shape of the inner rotation law. Here we are missing the equatorward motion of the axisymmetric mode and do not see any correspondence to the input rotation law. The low positive values sometimes seen near the equator may be some similar effect as in model L1, but much weaker. The negative jumps migrating poleward are connected to the rigid rotation of the non-axisymmetric dynamo mode, which appear where the poleward migrating axisymmetric mode is about zero.
The DR measurements for L2 usually show very rigid rotation. During the activity cycle the most rigid rotation occurs around the time of the flip-flop event, and the best fit to the rotation law around the equator and the polar region is obtained just before the flip-flop event starts. Still, even at these time points the shape of the measured rotation law is very different from the shape of the input rotation law. Two deviations from the generally rigid rotation are often seen. In many cases a small latitude range shows higher than normal positive shifts. This area is restricted to latitudes >20°. Also, an area of negative shifts is seen. This area migrates polewards with the general migration of the magnetic elements. At the time leading to a flip-flop event, this area occurs in between the two latitudinal spot belts.
4.2. Small-scale spots versus large-scale dynamo spots
Interestingly, the DR measured from the models that only include large-scale dynamo field follows the input DR best at the latitudes close to the equator, and breaks down completely closer to the poles where the magnetic pressure is the highest. This could imply that the strongly magnetic regions do not follow the differential rotation as well as the less magnetic areas.
At first glance, a correspondence of the large-scale dynamo field with the local differential rotation cannot be expected. Only the non-axisymmetric features lead to an observable rotation. The main component here is a large-scale field with azimuthal wavenumber m = 1. This field rotates rigidly with a value between the minimum and maximum rotation speed. Because of the faster rotation at the equator, this field is shaped like a leading spiral. Together with the oscillating poleward-migrating axisymmetric field mode, a counter-clockwise spot motion is introduced, which may be latitude-dependent (cf. Fig. 2). All these effects have no direct connection to the differential rotation of the stellar surface. Therefore, the rotation law cannot be recovered by measuring the spot motion of the large-scale field. On the other hand, at least for L1, a good agreement of the cross correlation result with the actual rotation law is found at low latitudes. This is a consequence of the equatorward extension of the field. Here, a connection to the stellar rotation law is obtained through the pitch angle.
We tested whether the DR patterns can be recovered from models that also include small-scale fields by adding these fields to the model L2. Two different strengths for the small-scale fields were used: a strong field (L2a) and a 10 times weaker field (L2b). For more details on the models see Sect. 2.1 and Table 1.
The examples of snapshots for L2a and L2b are shown in Figs. 7 and 8, respectively. In the analysis 99 maps are used. In these models, especially in L2a, which has strong small-scale field, the changes are so rapid that the time step between the snapshots is now reduced to approximately six days. This means that with the 99 snapshots we cover more or less the same time period as with the 36 snapshots earlier.
 |
Fig. 9 Examples of the cross-correlation results using all 99 individual snapshots from the dynamo model L2a. The symbols are the same as in Fig. 5. The last plot is the average behaviour obtained from all 99 snapshots with the standard deviation of the measurements as error. Latitude 12.6° is used as the reference latitude. |
Examples of the cross-correlation results from L2a are shown in Fig. 9. The cross-correlation was made for 99 snapshots of magnetic pressure, but only every other cross-correlation curve for the time period covering a bit more than one flip-flop cycle is shown in the plot. Here, the latitude 12.6° is used as the reference latitude because of the anomalous shifts occasionally measured at the lower latitudes. As can be seen, now the recovered surface DR follows the input rotation well. Still, some time points of anomalous rotation are seen, but, as shown by the average rotation, in general the rotation is well reproduced.
The results for L2b are shown in Fig. 10. Now the latitude 4.2° is used again as the reference latitude. With a weaker small-scale field of the model L2b, the results are between the results from the original L2 and from L2a, in which a stronger small-scale field was used. Again, the general rotation law is recovered, but the high latitudes start to again show almost rigid rotation.
The addition of the small-scale fields to the dynamo model enables us to recover the input rotation law. But it remains an open question if the observable large spots can be attributed to small-scale magnetic features. Recently, Lehtinen et al. (2011) found active longitudes rotating significantly slower than the star, which according to the current investigation favours spots as signs for the large-scale field.
4.3. Comparison to observations
The results presented here clearly show that the rotation law obtained from dynamo models with large-scale fields breaks at the latitudes where most of the spots occur.
A literature search was carried out to investigate whether or not this phenomenon is also seen when cross-correlating Doppler images. One significant difference between the model calculations used here and the real Doppler images is that when cross-correlating the models there is always signal, even if the signal is weak, i.e., not resulting in a starspot, whereas in Doppler images the latitudes devoid of spots only result in noise in the cross-correlation.
The literature search reveals that at times the cross-correlation result reproduces the sin2-type surface rotation law very well within observational errors, which at times can be very large. A relatively good fit is seen for example in RS CVn-type binaries IM Peg (Weber et al. 2005) and IL Hya (Weber & Strassmeier 1998), young single K-dwarfs AB Dor (Donati & Collier Cameron 1997) and LQ Hya (Kővári et al. 2004), and for a post-T Tauri star RX J1508.6 ± 4423 (Donati et al. 2000). Occasionally, the sin2-law has the same general shape as that is obtained from cross-correlating latitude strips in the Doppler images. For example, the shifts measured for a late-type single star PZ Tel follow the general shape of the sin2-law well, but there are latitudes, especially around the equator, where the measurements deviate significantly from the sin2-law (Barnes et al. 2000). The general shape of the rotation law is also reproduced for V1192 Ori, but deviations are seen at the higher latitudes (Strassmeier et al. 2003). On KU Peg the latitudinal rotation rates form a complex double-peaked pattern, where the equator and the latitudes around 45° rotate faster than the general rotation (Weber & Strassmeier 2001; Weber et al. 2005). There are also examples of targets where Doppler images obtained from different spectral lines give slightly different latitudinal rotation behaviour, e.g., σ Gem (Kővári et al. 2007) and UZ Lib (Vida et al. 2007).
Moreover, the results on cross-correlating Doppler images do not commonly extend to higher latitudes than 60°. Often this is because of the polar spot, which is seen in many of the maps. This constant feature would not result in shifts in spot configuration between two consecutive Doppler images, and thus it would not give any signal in the cross-correlation. Still, this feature is often large and the strongest spot on the surface, i.e., analogous to the maximum magnetic pressure in the dynamo models, and exactly the location where the rotation behaviour is seen to deviate from the input rotation. Thus, it is very difficult to conclude based on the Doppler images whether or not the observations also show the behaviour where the surface rotation in strongly magnetic features deviates from the general rotation.
5. Conclusions
Starspots are generally used as tracers of the stellar surface differential rotation. If starspots are direct signs of the global stellar magnetic field, this assumption does not seem to be valid, because in this case the spot motion would mainly be determined by the geometric properties of the large-scale dynamo field. Based on the dynamo calculations presented here, the surface differential rotation can only be recovered by following the spot motion of small-scale spots frozen into the flow.
In the dynamo models presented here the usual assumption of a positive alpha in the northern hemisphere is made, implying a poleward migration of the axisymmetric dynamo wave. This together with the leading spiral of the non-axisymmetric field geometry gives a strongly reduced or even counter-rotating spot motion. This could possibly explain the reported detections of anti-solar differential rotation in some stars (e.g., Vogt et al. 1999; Weber et al. 2005). Nevertheless, for equatorward-drifting dynamo waves, as in the Sun, the spot motion will more or less coincide with the surface differential rotation. In our model L1 it coincides even quantitatively in the equatorial region. This may be due to a connection of the strength of the differential rotation to the pitch angle of the non-axisymmetric mode. The fact that mainly solar type rotation laws have been observed (see, e.g., Barnes et al. 2005) would imply that the dynamos in general show an equatorward drift. Additional models with more solar type dynamos are needed. If the observed spots are more local phenomena, we have a direct correspondence of the spot motion to the stellar rotation law. This was nicely reproduced using the cross-correlation method.
Here, stellar surface differential rotation was for the first time investigated in detail based on dynamo calculations. We draw the following conclusions from this study:
-
1.
Cross-correlation is a powerful method to follow differentialrotation using starspots as tracers, if the time difference betweenthe maps that are cross-correlated is appropriate for detecting thedifferential-rotation-induced changes.
-
2.
Spots caused by the large-scale dynamo field are not necessarily tracing the real surface differential rotation.
-
3.
Equatorward drift of the dynamo field gives at least a qualitative agreement with the differential rotation, as was seen for the model with a solar-type rotation law (L1).
-
4.
The differential rotation obtained from the spot motion varies during the dynamo cycle.
-
5.
Spots caused by small-scale magnetic fields are good tracers of the stellar differential rotation.
-
6.
Comparing direct tracers of differential rotation (e.g., analysing shapes of spectral lines) and obtaining the spot motion from cross-correlation can probably clarify the nature of the spots, i.e, whether they are caused by small-scale field or are signs of the large-scale dynamo field.
Online material
 |
Fig. 3 Examples of snapshots from the dynamo model L1. In total 36 individual magnetic pressure maps covering slightly more than one flip-flop event are used in the analysis. |
 |
Fig. 7 Examples of the snapshots from the dynamo model L2a. In total 99 magnetic pressure maps are used in the analysis. |
Acknowledgments
With this article we would like to remember Prof. Ilkka Tuominen, who died in March 2011. He will be missed by his colleagues, but also remembered by his work on stellar activity and dynamos. Part of this work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number KO 2320.
References
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Balthasar, H., Vazquez, M., & Woehl, H. 1986, A&A, 155, 87 [NASA ADS] [Google Scholar]
- Barnes, J. R., Collier Cameron, A., James, D. J., & Donati, J.-F. 2000, MNRAS, 314, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Collier Cameron, A., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
- Berdyugina, S. V., Moss, D., Sokoloff, D., & Usoskin, I. G. 2006, A&A, 445, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brun, A. S., & Toomre, J. 2002, ApJ, 570, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choudhuri, A. R., Schüssler, M., & Dikpati, M. 1995, A&A, 303, L29 [NASA ADS] [Google Scholar]
- Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Mengel, M., Carter, B. D., et al. 2000, MNRAS, 316, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Collier Cameron, A., Semel, M., et al. 2003, MNRAS, 345, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Dunstone, N. J., Hussain, G. A. J., Collier Cameron, A., et al. 2008, MNRAS, 387, 1525 [NASA ADS] [CrossRef] [Google Scholar]
- Elstner, D., & Korhonen, H. 2005, Astron. Nachr., 326, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., & Dupree, A. K. 1996, ApJ, 463, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Järvinen, S. P., Berdyugina, S. V., Tuominen, I., Cutispoto, G., & Bos, M. 2005, A&A, 432, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffers, S. V., Donati, J.-F., & Collier Cameron, A. 2007, MNRAS, 375, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Jetsu, L., Pelt, J., & Tuominen, I. 1993, A&A, 278, 449 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1999, A&A, 344, 911 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 2004, Astron. Nachr., 325, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Korhonen, H., & Elstner, D. 2005, A&A, 440, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Hackman, T., et al. 2007, A&A, 476, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Strassmeier, K. G, Granzer, T., et al. 2004, A&A, 417, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Bartus, J., Strassmeier, K. G., et al. 2007, A&A, 474, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Küker, M., & Rüdiger, G. 2008, J. Phys. Conf. Ser., 118, 2029 [NASA ADS] [Google Scholar]
- Lehtinen, J., Jetsu, L., & Mantere, M. J. 2011 [arXiv:1103.0663v1] [Google Scholar]
- Marsden, S. C., Donati, J.-F., Semel, M., Petit, P., & Carter, B. D. 2006, MNRAS, 370, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Moss, D. 2004, MNRAS, 352, 17 [Google Scholar]
- Petit, P., Donati, J.-F., & Collier Cameron, A. 2002, MNRAS, 334, 374 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Piskunov, N. E., Tuominen, I., & Vilhu, O. 1990, A&A, 230, 363 [NASA ADS] [Google Scholar]
- Reiners, A., & Schmitt, J. H. M. M. 2003, A&A, 398, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüdiger, G., & Küker, M. 2002, A&A, 385, 308 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüdiger, G., Krause, F., Tuominen, I., & Virtanen, H. 1986, A&A, 166, 306 [NASA ADS] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, E. A., & Zahn, J.-P. 1992 A&A, 265, 106 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Kratzwald, L., & Weber, M. 2003 A&A, 408, 1103 [Google Scholar]
- Thompson, M. J., Toomre, J., Anderson, E. R., et al. 1996, Science, 272, 1300 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vida, K., Kővári, Zs., Švanda, M., et al. 2007, Astron. Nachr., 328, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Penrod, G. D., & Hatzes, A. P. 1987, ApJ, 321, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Hatzes, A. P., Misch, A., & Kürster, M. 1999, ApJS, 121, 546 [Google Scholar]
- Weber, M. 2007, Astron. Nachr., 328, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., & Strassmeier, K. G. 1998, A&A, 330, 1029 [NASA ADS] [Google Scholar]
- Weber, M., & Strassmeier, K. G. 2001, A&A, 373, 974 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weber, M., Strassmeier, K. G., & Washuettl, A. 2005, Astron. Nachr., 326, 287 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Illustration of the internal rotation laws used in this study. a) The solar-type rotation law with the equator rotating faster than the poles (L1). b) Axis-distance-dependent law, where the parts farthest away from the axis are rotating the fastest (L2). |
| In the text | |
 |
Fig. 2 Illustration of the clockwise spot motion (circles) during the flip-flop event. Shown is the surface magnetic pressure of the non-axisymmetric mode. The circles along the latitude mark the maximum of the poleward migrating axisymmetric field at different times. Spots appear only at one spiral, where the signs of the two modes are equal. Note that the stellar rotation and the magnetic pattern are anti-clockwise. |
| In the text | |
 |
Fig. 5 Examples of the cross-correlation results using the 36 individual snapshots from the dynamo model L1. The crosses give the shift in degrees/day for each latitude between 4.2° and 83.7°. The solid line in the plots shows the input rotation law for the dynamo model at the surface. The last plot is the average behaviour obtained from all snapshots with using the standard deviation of the measurements as the error. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but using L2. Note that occasionally very high negative shifts are measured and one point can fall outside the plotting range. |
| In the text | |
 |
Fig. 9 Examples of the cross-correlation results using all 99 individual snapshots from the dynamo model L2a. The symbols are the same as in Fig. 5. The last plot is the average behaviour obtained from all 99 snapshots with the standard deviation of the measurements as error. Latitude 12.6° is used as the reference latitude. |
| In the text | |
 |
Fig. 10 As for Fig. 9, but now for L2b and using latitude 4.2° as the reference latitude. |
| In the text | |
 |
Fig. 3 Examples of snapshots from the dynamo model L1. In total 36 individual magnetic pressure maps covering slightly more than one flip-flop event are used in the analysis. |
| In the text | |
 |
Fig. 4 The same as for Fig. 3, now for model L2. |
| In the text | |
 |
Fig. 7 Examples of the snapshots from the dynamo model L2a. In total 99 magnetic pressure maps are used in the analysis. |
| In the text | |
 |
Fig. 8 The same as for Fig. 7, now for model L2b. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


