| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 5 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201016339 | |
| Published online | 19 July 2011 | |
Research Note
Mutual occultations between Galilean satellites observed at Yunnan Observatory in 2009⋆
1
National Astronomical Observatories/Yunnan Observatory, Joint Laboratory for Optical Astronomy, Chinese Academy of Sciences, Kunming, PR China
e-mail: zhangxiliang@ynao.ac.cn
2
Graduate School of Chinese Academy of Sciences, Beijing 100039, PR China
3
Institut de mecanique celeste et de calcul des ephemerides, Observatoire de Paris, UMR 8028 du CNRS, 77 avenue Denfert-Rochereau, 75014 Paris, France
Received: 16 December 2010
Accepted: 13 June 2011
Context. Photometry of mutual events between natural satellites has been shown to be a most effective and accurate ground-based method for obtaining accurate astrometric data by fitting the light curves observed during these events, and is invaluable for developing the orbital models of the natural satellites.
Aims. Mutual occultations of J2 Europa by J1 Io (Aug. 28, 2009), J1 Io by J2 Europa (Nov. 9 and Dec. 11, 2009), and J1 Io by J3 Ganymede (Nov. 28, 2009) were observed at Yunnan Observatory during the PHEMU09 international campaign. We calculate the astrometric data of satellites by analyzing and fitting the light curves that we derived.
Methods. The model proposed by Emelianov (2003, Sol. Syst. Res., 37, 314) was used to fit the light curves, while taking the Lommel-Seeliger scattering law into account.
Results. For each event, we derive dynamical quantities such as the deviation of the observed relative satellite motion from the theoretical motion provided by the relevant ephemeris denoted as Dx and Dy, and the impact parameter and its corresponding mid-time. These results have an accuracy of between about several mas and 90 mas for Dx and Dy, and 0.31–2.97 s for the mid-time. The residuals of the longitude shifts (δl1 for J1 Io and δl2 for J2 Europa) that represent the shifts of the mid-times of the events, are also calculated to be around 10 km with the most accurate available ephemerides.
Key words: techniques: photometric / occultations / planets and satellites: dynamical evolution and stability / celestial mechanics
Photometry is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/532/A36
© ESO, 2011
1. Introduction
The dynamics of the Galilean satellites of Jupiter is one of the most interesting but also most difficult problems of the solar system because of the wide range of gravitational influences that they suffer. Therefore, accurate astrometric data of Galilean satellites is very invaluable. The photometry of mutual events between natural satellites has been found to be a most effective and accurate ground-based means of obtaining astrometric data of the natural satellites.
Mutual events are caused by the relative positions of the Sun, satellites, and Earth (observer), and occur twice during one orbital period of Jupiter, that is to say every six years for the Galilean satellites. Since 1979, the first worldwide campaign had been operated by IMCCE (Paris Observatory, France), and six observational campaigns of the mutual events between Galilean satellites have been performed.
In 2009, four mutual occultations between Galilean satellites that had been predicted by Arlot (2008), were observed at Yunnan Observatory. The main objectives of our current paper is to model the deviation of the observed relative satellite-motion from the theoretical motion provided by the relevant ephemeris, and to calculate several physical and dynamical quantities of these events. In the following sections, we provide detailed descriptions of the observations, reductions, analysis and fitting of light curves, and the astrometric results of these mutual occultations.
2. CCD photometric observations
2.1. Observation
Our observations were carried out with DW436 2048 × 2048 CCD, attached to the 1-m telescope and 60-cm telescope at Yunnan Observatory (102°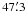 E,
E, 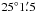 N, altitude = 2000 m, IAU code 286) from Aug. 28 to Dec. 11, 2009. The effective field of view of the 1-m telescope at the Cassegrain focus is about 7 × 7 square arcmin, and that of the 60-cm telescope is 12 × 12 square arcmin. During the observations, we used a Johnson R filter. There are three choices of CCD readout rates (50, 100 and 150 kHz), and to obtain as many data points as possible, we chose the fastest readout mode (150 kHz). Table 1 outlines the properties of both the 1-m telescope and 60-cm telescope at Yunnan Observatory, and their attached CCDs.
N, altitude = 2000 m, IAU code 286) from Aug. 28 to Dec. 11, 2009. The effective field of view of the 1-m telescope at the Cassegrain focus is about 7 × 7 square arcmin, and that of the 60-cm telescope is 12 × 12 square arcmin. During the observations, we used a Johnson R filter. There are three choices of CCD readout rates (50, 100 and 150 kHz), and to obtain as many data points as possible, we chose the fastest readout mode (150 kHz). Table 1 outlines the properties of both the 1-m telescope and 60-cm telescope at Yunnan Observatory, and their attached CCDs.
Properties of the 1-m and 60-cm telescopes at Yunnan Observatory, with attached CCDs.
2.2. Reduction
Each image observed during the mutual events corresponds to one flux data point of the satellites involved (occulting and occulted satellites in this paper). The main idea behind the photometry of mutual events is to calculate the physical and dynamical quantities of the satellites involved by means of analyzing and fitting their flux variations during the events.
Before the flux of the satellites involved was calculated, each image was bias-corrected and flat-fielded, and curves of flux variations relative to UT time were then obtained for each event. Table 2 shows the details of our observations and reductions, where J1, J2, and J3 are the Galilean satellites Io, Europa, and Ganymede, respectively, and “J1OJ2” means the event of Io that occults Europa. “Ref.” indicates the satellite used as a reference for the photometry, which in this paper is Europa for the event of Ganymede occulting Io and Ganymede for the events between Io and Europa. “Telescope” indicates the apertures of the two different telescopes used whose complete descriptions are provided in Table 1. We switched from the 60 cm telescope to the 1m telescope to obtain higher quality images during the observations, and all observations used a Johnson R filter during the 0.2 s exposures.
Observational details of mutual occultations at Yunnan Observatory in 2009.
3. Analysis and adjustment
As mentioned above, mutual events depend on the relative positions of the Sun, satellites, and Earth (observer). Mutual occultations between Galilean satellites occur twice every Jovian orbital period, when the Earth goes through their common orbital plane. Figure 1 shows the geometrical projection of the two satellites involved during the mutual occultation of “J1OJ2” as seen from the center of Earth, where disks S1 and S2 are assumed to be uniform.
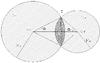 |
Fig. 1 Geometry of a partial occultation where the disks S1 and S2 of radius R2 < R1 partially intercept each other with an area A, S1 and S2 representing the two satellites involved. |
3.1. Dynamical model and formula
The model of Emelianov (2003) was used to fit the observed light curves, with two assumptions being made. One assumption is that the occulted satellite is assumed to be unmovable, while the occulting satellite has a linear uniform motion relative to the occulted one (as shown in Fig. 2). The other assumption is that the deviation of the observed relative satellite motion from the theoretical motion are constants in Δαcosδ and Δδ during the mutual occultations.
In spite of the surfaces of satellites being nonuniform, the values of albedo ratios of the occulting to the occulted satellites are usually assumed to be constants during the fitting of mutual events because of their short durations. After the dynamical model had been established, the corresponding formula used to perform the fitting of the light curves, was given below.
As shown in Fig. 1, during mutual occultation, the flux variation of the satellites involved is mainly determined by the occulted area A of S2 by S1 and their different albedos. Equation (1) (Assafin et al. 2009) shows the expression of flux variation of the satellites involved, which has been normalized to 1 before and after mutual occultation, where F1o2 represents the flux of the satellites involved during the mutual occultation, F1 + 2, that of before and after the occultation, and R1, k1 and R2, k2, the radius and albedos of S1 and S2, respectively, such that 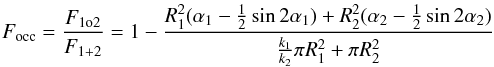 (1)where,
(1)where, 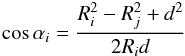 (2)
(2)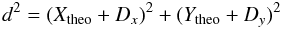 (3)
(3)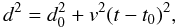 (4)and i = 1 or 2 and j = 2 or 1.
(4)and i = 1 or 2 and j = 2 or 1.
When modeling a mutual occultation, the deviations of the observed relative satellite motion from the theoretical motion provided by the relevant ephemeris have been assumed to be constants, denoted as Dx and Dy in Eq. (3), where d is the real distance between the centers of occulting satellite S2 and the occulted one S1, and Xtheo and Ytheo represent the theoretical calculated values of Δαcosδ and Δδ.
Equation (4), which is based on the first of the previous assumptions, is used to calculate the mid-times t0 and impact parameters d0, where d and v are the relative distance and velocity of occulting satellite from to the occulted one respectively, and t is the time of observation.
3.2. Analysis and results
Since the dynamical model and corresponding formula had been determined, we used the algorithm of Gauss-Newton iteration (Teunissen 1990) to carry out the least-squares fit to the light curves. The initial values of the dynamical parameters were derived from the MULTISAT ephemerides available at WWW.IMCCE.FR/SAT using the available ephemerides (Emelianov and Arlot 2008).
To get higher accuracy astrometric data of Galilean satellites, we considered the effects of both the phase angle and light scattering over the surfaces of satellites during the fitting of the light curves. In addition, we chose to adopt the Lommel-Seeliger scattering law (Surdej & Surdej 1978).
We derived two different solutions, first by treating the albedo ratios as unknown parameters, and second using the geometry albedo of 0.63, 0.67, and 0.43 for the Galilean satellites Io (Simonelli 1984), Europa (Buratti 1983), and Ganymede (Morrison 1977), respectively, to calculate the quantities of the deviations of observed Δαcosδ and Δδ from that of the relevant ephemeris, impact parameters, and mid-times.
Table 3 shows the parameters derived for each event, in which the first to third columns denote the observed dates, types, and observed mid-times of each event, the fourth column is the albedo ratios of the occulting to occulted satellites that are either unknown in the solution or were given in previous publications, the fifth and sixth columns are the residuals Δαcosδ and Δδ for the relevant ephemeris which are usually expressed as O–C(x) and O–C(y), and the following two columns give the observed values of Δαcosδ and Δδ. The impact parameters and declines in flux are presented in the next two columns. In the last column of “Albedo”, “Variable” means that the albedos of the satellites are unknown, whereas “Fixed” means that it is fixed to values from the literature.
The observed and fitted light curves, indicated by dots and bold lines respectively, are plotted in Fig. 3, with the flux of the satellites involved being normalized to 1 before and after the occultations.
 |
Fig. 3 Observed and fitted light curves of involved satellites. The dots and bold lines represent the observed and fitted flux variations of involved satellites normalized to 1 before and after the event, respectively. The x-axis corresponds to the date (in hours) and the y-axis to the relative flux. |
Astrometric results.
4. Discussion and interpretation
Table 3 provides the results that we obtained for the four mutual events observed. For three of the observed events, the (O–C)s and the errors appear to be small but for the event of November 28 the signal-to-noise ratio is too small. It is easy to see in Fig. 3 that this event is not clearly visible in the light curve. The predicted flux drop was about 3.5% and the observed one is determined to be around 2% even it is not visible in the light curve.
As we know, the photometric noise of satellites influence the error bars of Dx and Dy. However, the error bar of midtime not only depends on the variances of Dx and Dy but also on the theoretical model of the satellites that we chose. In Table 3, the error bars of the midtimes are therefore not completely consistent with the photometric noise.
The error in the midtimes for all the mutual events in Table 3 were calculated to be: 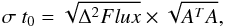 (5)where the parameter “Flux” represents the flux of satellites during the events, A is the differential coefficient matrix of distance d for parameters of d0, and v and t0 were derived using Eq. (4).
(5)where the parameter “Flux” represents the flux of satellites during the events, A is the differential coefficient matrix of distance d for parameters of d0, and v and t0 were derived using Eq. (4).
All the error bars are coherent, the worse being for the events Aug. 28 and Nov. 28 where the photometric noise is large. The O–C are larger for the event of Nov. 28 because the magnitude drop is very small and the mid time difficult to detect.
We propose two solutions either using albedos provided by previous authors or considering the ratio of the albedos k1 to k2 as unknowns. We do not immediately adopt published values of albedos because authors do not agree on these values, and the images of the space probes, made in specific filters at large phase angles, do not help us to determine the albedos as seen from the Earth in the standard filter systems. Hence we appear to be justified in our attempt to determine these albedos from our photometric observations as proposed by Emelianov (2003).
The change in the ratio k1 to k2 causes a change in the observed decline in the brightness of the events, which we see mainly for the first event whose signal is noisier than both the second and fourth events. These two events (November 9 and December 11) are those for which we have gathered the most reliable data with errors of about 10 mas in the determination of the relative positions of the two satellites. The two other events (August 28 and November 28) have larger errors. However, its value of around 75 mas is still smaller than the errors in the positions observed directly by imaging, which used to reach 100 mas or more. We note that 10 mas corresponds to 30 km in situ when the space probes provide astrometric observations with an accuracy of 10 km.
We now discuss the conclusions that can be drawn from the events that we observed.
From our observed events, we have been able to calculate the drift in the longitude of satellites J1 and J2 from the three events involving J1 and J2 based on different theoretical models: L2 (2009) and L1 (2006) by Lainey, G5 by Arlot (1982) and E5 by Lieske (1998). During one event, the difference between the observed longitude and the calculated one depended on the difference between the observed mid-time and the calculated one through Eq. (5) (Arlot et al. 2008). We have 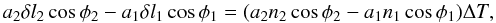 (6)where
(6)where
-
a1 and a2 are the semi major axes of J1 Io and J2 Europa;
-
n1 and n2 are the mean motions of the same;
-
φ1 and φ2 are the geocentric synodic longitudes of the satellites;
-
δl1 and δl2 are the shifts in longitude explaining the shift of the mid-time of the event;
-
ΔT is the C–O of the date of the minimum of flux.
We obtain a relationship between the two shifts in longitude of the satellites for each event, so we are able to calculate each individual shift in longitude using data for two events. Since we have three events, we may calculate two different values for each shift. However, the events on November 9 and December 11 are too close to be independent (the configurations are similar so that the relationships between δl1 and δl2 are not independent).
(O–C)s in longitude for Io and Europa depending on the ephemeris.
Table 4 provides the results and shows the accuracy in the determination of the longitudes of the satellites. For the highest quality ephemerides, the differences in the determination of the longitudes shifts is around 10 km. Our observations will be useful for determining small effects such as tidal ones in the dynamics of the satellites, these effects being of small amplitude but larger than the accuracy of our data.
By comparison to Table 4, the drifts in longitude of Io and Europa, presented in Table 5 from the three observed events involving these satellites, appear to be significantly smaller than those obtained during previous PHEMU campaigns by Vasundhara et al. (2003) and Dourneau et al. (2005) for the same satellites. The O–Cs presented in Vasundhara (2003) are not reliable because the data analysis of that study was performed using too few parameters as pointed out by Emelianov (2003).
Previous published results of (O–C)s in longitude for observations made in 1997.
5. Conclusion
The results of our observations that we have presented demonstrate the high angular resolution of the mutual events of the Jovian satellites. We have shown that the dynamical models of the Galilean satellites are very accurate. The observations
provided in this paper should be added to the others made during the 2009 occurrence to improve the dynamics of the Galilean satellites. The data analysis presented here could be applied to a wide range of observations to determine the observed astrometric positions that are useful for dynamical purposes. We look forward to the next occurrence in 2014-15 to get more data at a time when the space probes will be unable to provide data, and preparing the EJSM mission to the Jovian system.
Note that our data (photometric light curves) will be available at http://www.imcce.fr/nsdc.
Acknowledgments
We would like to thank Dr. Nicolai Emelianov for his valuable help. We also would like to thank Dr. Zhu Liying along with the staff of 1-m and 60-cm telescopes team of Yunnan Observatory for their help and support for our work. This work was supported by Project of MOST(2011CB811400), China and the Joint Doctoral Promotion Programme of Chinese Academy of Science.
References
- Arlot, J.-E. 1982, A&A, 107, 305 [NASA ADS] [Google Scholar]
- Arlot, J.-E. 2008, A&A, 478, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlot, J.-E., Dumas, C., & Sicardy, B. 2008, A&A, 492, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Assafin, M., Viera-Martins, R., Braga-Ribas, F., et al. 2009, AJ, 137, 4046 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buratti, B., & Veverka, J. 1983, Icarus 55, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Dourneau, G., LeCampion, J. F., & Baratchart, S. 2005, A&A, 437, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emelianov, N. V. 2003, Sol. Syst. Res., 37, 314 [Google Scholar]
- Emelianov, N. V., & Arlot, J.-E. 2008, A&A, 487, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lainey, V., Duriez, L., & Vienne, A. 2006, A&A, 456, 786 [Google Scholar]
- Lainey, V., Arlot, J. E., Karatekin, O., et al. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lieske, J. H. 1998, A&A, 129, 205 [Google Scholar]
- Morrison, D., & Morrison, N. D. 1977, Planetary satellites, 363 [Google Scholar]
- Simonelli, D. P., & Veverka, J. 1984, Icarus, 59, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Surdej, A., & Surdej, J. 1978, A&A, 66, 31 [NASA ADS] [Google Scholar]
- Teunissen, P. J. G. 1990, Manuscripta Geodaetica 15, 137 [Google Scholar]
- Vasundhara, R., Arlot, J.-E., Lainey, V., et al. 2003, A&A, 410, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Properties of the 1-m and 60-cm telescopes at Yunnan Observatory, with attached CCDs.
All Figures
 |
Fig. 1 Geometry of a partial occultation where the disks S1 and S2 of radius R2 < R1 partially intercept each other with an area A, S1 and S2 representing the two satellites involved. |
| In the text | |
 |
Fig. 2 Dynamical model of the mutual occultation corresponding to Fig. 1. |
| In the text | |
 |
Fig. 3 Observed and fitted light curves of involved satellites. The dots and bold lines represent the observed and fitted flux variations of involved satellites normalized to 1 before and after the event, respectively. The x-axis corresponds to the date (in hours) and the y-axis to the relative flux. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


